0 引言

海底四分量（4C）地震勘探因宽方位照明、高信噪比、可重复观测、受海况风浪因素影响小等优势而备受地球物理勘探界的关注^[1-2]。海底4C采集比陆地三分量采集多了一个压力分量，为复杂海底结构成像提供了更大的挑战和机遇。对于海底4C数据的处理，传统上是将速度记录(或位移记录)的水平分量作为转换横波，将压力记录作为纵波进行处理、解释，而工业界则通常是直接叠加压力分量和速度记录的垂直分量抑制鬼波干扰^[3]。这些处理方法效果有限，未能充分使用4C地震数据的信息，因此迫切需要研究新的数据处理技术充分挖掘4C地震记录中的弹性矢量波场信息。目前，多波多分量高斯束偏移方法已经可以实现复杂地质构造的高效、准确成像，但是还不能完美处理海底4C数据，充分利用4C地震数据进行弹性波叠前深度偏移成像仍然是一个难题。

基于弹性波动理论的多分量偏移方法出现于20世纪80年代，主要分为弹性Kirchhoff偏移^[4-5]和弹性逆时偏移^[6-7]。Kirchhoff偏移是射线类方法的代表，具有计算高效、适应性强的优势，但无法对复杂地质体和高陡构造成像。而作为波动方程类方法代表的逆时偏移成像精度高但计算量过大。因此，Hill^[8]提出了兼具两种偏移算法优势的高斯束偏移方法，可以多路径成像，不仅信噪比高、成像精度高，而且计算效率高^[9-10]，能适应崎岖的地表和复杂海底。

海底地震数据的特殊性使上述方法存在一定的适用性问题。使用传统的三分量地震观测数据只能够获取边界点的位移或速度矢量，这作为弹性波动方程的边界条件是不完整的^[11]。准确求解弹性波波动方程还需要知道应力边界条件，不完整的海底边界条件会使P波和S波分离不彻底。Ravasi等^[12]提出4C数据的水压信息恰好可以作为应力信息组成完整的边界条件。另外，上、下行波会在海底的记录方式下发生混叠，使偏移成像受到自由表面多次波的干扰，造成最终成像结果中的假象。栗学磊等^[13]在假设观测数据只有上行波信号的基础上建立了精确的海底界面应力与位移关系式，实现了准确的海底波场延拓，但是实际海底地震记录中既有上行波也有下行波。Shi等^[14]在此基础上作出改进，提出海底4C地震数据高斯束偏移方法。该方法能够获得完整的弹性波场信息，实现海底的多波型自动分离和准确成像，解决矢量波场偏移成像中存在的多波型耦合和非物理成像噪声问题。Qu等^[15]提出了一种基于OBD(海底双检)数据的声弹最小二乘逆时偏移方法, 同时利用数据中的压力和位移观测记录进行声弹联合反演，提高了成像精度。

在海底存在周期性沉积薄层的情况下，各向异性的影响不容忽略。对复杂各向异性地层使用常规各向同性成像算法，会导致反射波归位不准确、绕射波收敛不彻底等问题，造成地下结构的错位成像和低分辨率，影响储层预测的可靠性^[16]。近年来，随着探测区域的复杂深入和计算能力的提升，勘探目标也由各向同性介质转向复杂各向异性区域。而TI(横向各向同性)介质模型是应用最广泛的各向异性介质模型。其中，VTI(具有垂直对称轴的横向各向同性)模型最为典型，符合一般的沉积规律，方法理论相对简单，需要的模型表达参数最少。自Alkhalifah^[17]提出适用于各向异性介质的高斯束偏移方法，人们不断在此基础上加以改进和完善并发展至多分量，研究了转换波高斯束偏移^[18]和高斯束逆时偏移^[19]。这些方法大多是针对复杂地表条件的三分量数据，Li等^[20]对这些技术的发展历程和成像原理作出了详细的介绍和总结。

目前，有关海底4C矢量波场弹性高斯束偏移方法的研究还不多，考虑到各向异性介质的更少。Yu等^[21]兼顾海底4C、基于声弹耦合方程，将适用于海底4C地震数据的弹性波逆时偏移方法从各向同性介质扩展到各向异性介质，实现了qP波准确、快速的分离，通过抑制伪影噪声提高了成像质量。Shi等^[14]将高斯束偏移从3C陆地数据扩展至海底4C数据，考虑了精确的边界条件，但是此方法没有考虑实际地下介质的各向异性，无法消除界面位置与断层成像误差，对各向异性地层的成像效果不佳。

为解决复杂海底成像分辨率低的问题，本文使用4C数据进行偏移，有效抑制了不完整边界条件造成的成像假象，并在偏移过程中考虑地层介质各向异性的影响，将弹性波高斯束偏移从各向同性介质成像推广至各向异性介质成像。以弹性波高斯束和Kirchhoff-Helmholtz积分为基础，推导出海底模型的积分延拓和成像公式，得到4C数据的波型分离矩阵，再结合各向异性射线追踪和动力学参数近似，实现了VTI介质的弹性波高斯束偏移。2D层状模型和北海Gullfaks区域模型的数值模拟成像结果验证了本文提出的4C各向异性介质高斯束偏移方法的可行性和有效性。

1 方法原理 1.1 弹性波高斯束

高斯束是波动方程在中心射线坐标系下的高频近似解，表示局部范围内的地震波场。栗学磊等^[13]给出了三维弹性非均匀各向同性介质的高斯束归一化多波表示形式

$ \begin{array}{l}{\boldsymbol{u}}_{\mathrm{G}\mathrm{B}}^{\psi }(\boldsymbol{x};\boldsymbol{r},{\boldsymbol{p}}^{\psi };\omega )=\sqrt{\frac{v\left({s}_{0}\right)\rho \left({s}_{0}\right)\mathrm{d}\mathrm{e}\mathrm{t}\boldsymbol{Q}\left({s}_{0}\right)}{v\left(s\right)\rho \left(s\right)\mathrm{d}\mathrm{e}\mathrm{t}\boldsymbol{Q}\left(s\right)}}{\boldsymbol{g}}^{\psi }\left(x\right)\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\omega \tau \left(s\right)+\frac{\mathrm{i}\omega }{2}{\boldsymbol{q}}^{T}\boldsymbol{M}\left(s\right)\boldsymbol{q}\right]\end{array} $

(1)

式中：$ {\boldsymbol{u}}_{\mathrm{G}\mathrm{B}}^{\psi } $表示点$ \boldsymbol{x} $处的$ \psi $波高斯束位移矢量，上标$ \psi $代表不同地震波型(P，S1，S2)；$ \boldsymbol{r} $和$ {\boldsymbol{p}}^{\psi } $分别为高斯束的入射点和入射慢度矢量；$ \omega $和$ v $分别为角频率和波速；$ {s}_{0} $为二维中心射线坐标系的点位；$ \rho $为密度；$ \tau $为走时；$ \boldsymbol{q}=({q}^{1},{q}^{2}{)}^{\mathrm{T}} $为垂直射线的平面坐标系；$ \boldsymbol{Q} $是一个2×2矩阵，为反映波场能量几何扩散情况的动力学参数；$ {\boldsymbol{g}}^{\psi } $为$ \psi $波偏振方向矢量，有如下关系式

$ \left\{\begin{array}{l}{\boldsymbol{g}}^{\mathrm{P}}=\boldsymbol{E}+\alpha \left(s\right){M}_{IJ}{q}_{J}{\boldsymbol{e}}_{1}\\ {\boldsymbol{g}}^{\mathrm{S}1}={\boldsymbol{e}}_{1}-\beta \left(s\right){M}_{1J}{q}_{J}\boldsymbol{E}\;\;\;\;\;\;\;\;I,J=\mathrm{1,2}\\ {\boldsymbol{g}}^{\mathrm{S}2}={\boldsymbol{e}}_{2}-\beta \left(s\right){M}_{2J}{q}_{J}\boldsymbol{E}\end{array}\right. $

(2)

式中：$ {M}_{IJ} $是$ 2\times 2 $矩阵$ \boldsymbol{M} $中的元素，为波前走时在$ ({q}^{1},{q}^{2}) $坐标系的二阶偏导，满足$ \boldsymbol{M}=\boldsymbol{T}{\boldsymbol{Q}}^{-1} $，T为动力学参数；$ \alpha $和$ \beta $分别为横波速度和纵波速度；$ {\boldsymbol{e}}_{1},{\boldsymbol{e}}_{2} $，$ {\boldsymbol{e}}_{3}\equiv \boldsymbol{E} $是三维中心射线坐标系$ ({q}_{1},{q}_{2},s) $对应的坐标基；与$ {q}_{J} $相关的附加项是偏振方向矢量的校正项，当$ \boldsymbol{x} $离射线中心很近时很小，可以忽略不计。

1.2 波场延拓

弹性Kirchhoff-Helmholtz积分相当于弹性波波动方程的积分表示形式。积分方程反向延拓可以表示为

$ \begin{array}{l}{u}_{n}(\boldsymbol{x},\omega )=\left[{\tau }_{ij}(\boldsymbol{r},\omega ){G}_{ni}^{*}(\boldsymbol{x},\boldsymbol{r},\omega )-\right.\\ \left.{u}_{i}(\boldsymbol{r},\omega ){H}_{nji}^{\mathrm{*}}(\boldsymbol{x},\boldsymbol{r},\omega )\right]{n}_{j}\mathrm{d}{S}^{\boldsymbol{r}}\end{array} $

(3)

式中：$ {u}_{n}(\boldsymbol{x},\omega ) $表示位移的第$ n $个分量；$ {u}_{i}(\boldsymbol{r},\omega ) $为点$ \boldsymbol{r} $处的第$ i $个位移分量；$ {\tau }_{ij} $为应力分量；符号“*”代表复共轭；$ \mathrm{d}{S}^{\boldsymbol{r}} $为边界点$ \boldsymbol{r} $在$ \sum $的微元面；$ {n}_{j} $为边界$ \sum $的外法线方向向量；$ {G}_{ni}(\boldsymbol{x},\boldsymbol{r},\omega ) $为格林函数分量；$ {H}_{nji}^{}(\boldsymbol{x},\boldsymbol{r},\omega ) $为格林应力分量，其中nji为定义三阶张量。设定$ \sum $的外法线方向为$ (-\mathrm{1,0},0) $。从式(3)可以看出，求解该弹性波波动方程需要同时知道应变信息和应力信息。在只有位移分量$ {u}_{i}(\boldsymbol{r},\omega ) $的情况下，不能得到波场的唯一解。当前的多波多分量偏移方法研究大都是基于自由地表模型进行的，这种条件下可以直接认为应力分量$ {\tau }_{ij}(\boldsymbol{r},\omega )=0 $。但是对于海底模型，显然$ {\tau }_{ij}(\boldsymbol{r},\omega )\ne 0 $。栗学磊等^[13]提出假设，如果观测数据只包含上行波信号，海底界面上的应力与位移有精确的关系式，那么可以通过地震记录提供的应变信息求取应力，而实际海底地震记录通常既有上行波，也有下行波。对此，可直接利用水压分量作为应力。

据广义胡克定律，可以用格林函数张量表示格林应力张量

$ {H}_{nji}^{}(\boldsymbol{x},\boldsymbol{r},\omega )={c}_{ijkl}\left(\boldsymbol{r}\right)\frac{\partial {G}_{nk}^{}(\boldsymbol{x},\boldsymbol{r},\omega )}{\partial {x}_{l}^{r}} $

(4)

式中：$ {G}_{nk}^{}(\boldsymbol{x},\boldsymbol{r},\omega ) $为r点处的力震源沿第n维方向激起波场、传导到x点处的位移矢量；$ {c}_{ijkl} $为四阶弹性参数张量。

考虑到理想、严格的弹性各向异性波型分离是极其复杂的，涉及过多参数，在弹性波高斯束偏移框架下的多波型分离只与接收界面的弹性参数和多波几何参数有关，与地下介质参数无关。因此如果假设海底接收界面为各向同性或弱各向异性，则VTI介质的波型分离可以利用弹性各向同性介质波型分离方法实现，从而大大降低方法实现的难度。$ {c}_{ijkl} $在海底接收界面为各向同性的假设条件下可由拉梅系数$ \lambda $和$ \mu $表示为

$ {c}_{ijkl}=\lambda {\mathrm{\delta }}_{ij}{\mathrm{\delta }}_{kl}+\mu ({\mathrm{\delta }}_{ik}{\mathrm{\delta }}_{jl}+{\mathrm{\delta }}_{il}{\mathrm{\delta }}_{jk}) $

(5)

拉梅系数与速度和密度有关系式$ \lambda =\rho ({\alpha }^{2}-2{\beta }^{2}) $，$ \mu =\rho {\beta }^{2} $。可以利用射线理论高频近似关系求解式(4)

$ \frac{\partial {G}_{nk}^{}}{\partial {x}_{l}^{r}}\approx \sum\limits_{\psi }-\text{i}\omega {p}_{l}^{\psi }\left(\boldsymbol{r}\right){G}_{nk}^{\psi } $

(6)

Hill^[8]用弹性波高斯束的叠加形式表示弹性介质中的格林函数张量

$ {G}_{ni}(\boldsymbol{x},\boldsymbol{r},\omega )=\sum\limits_{\psi }\frac{\mathrm{i}\omega }{8{\mathrm{\pi }}^{2}\rho {v}_{}^{2}}\iint \frac{\mathrm{d}{p}_{x}\mathrm{d}{p}_{y}}{{p}_{z}^{\gamma }}{\boldsymbol{u}}_{GB}^{\psi }(\boldsymbol{x};\boldsymbol{r},{\boldsymbol{p}}^{\psi };\omega ) $

(7)

式中：下标$ x $、$ y $、$ z $为三维笛卡尔坐标系的方向；$ {p}_{x}\mathrm{和}{p}_{y} $分别是x和y方向上的慢度。

$ {\boldsymbol{u}}_{\mathrm{G}\mathrm{B}}^{\psi } $可简化为

$ {\boldsymbol{u}}_{\mathrm{G}\mathrm{B}}^{\psi }(\boldsymbol{x};\boldsymbol{r},{\boldsymbol{p}}^{\psi };\omega )={u}_{\mathrm{G}\mathrm{B}}^{\psi }(\boldsymbol{x};\boldsymbol{r},{\boldsymbol{p}}^{\psi };\omega ){\boldsymbol{g}}^{\psi }\left(\boldsymbol{x}\right) $

(8)

Ravasi等^[12]提出了海底边界条件应该满足

$ \left\{\begin{array}{l}{\tau }_{12}(r,t)=0\\ {\tau }_{13}(r,t)=0\\ {\tau }_{11}(r,t)=-{u}_{\mathrm{p}}(r,t)\end{array}\right. $

(9)

式中：$ t $为时间；$ {u}_{\mathrm{p}}(r,t) $代表压力记录。对多分量地震记录进行局部倾斜叠加实现局部平面波分解，分离后的波场延拓方程最终表示为

$ \begin{array}{l}{u}_{n}^{\psi }(\boldsymbol{x},\omega )=\frac{\sqrt{3}}{4\mathrm{\pi }}{\left(\frac{{\omega }_{l}a}{{w}_{l}}\right)}^{2}\sum\limits_{L}\frac{1}{8{\mathrm{\pi }}^{2}\rho {v}^{2}}\iint \frac{\mathrm{d}{p}_{x}\mathrm{d}{p}_{y}}{{p}_{z}^{\psi }}\times \\ {u}_{\mathrm{G}\mathrm{B},n}^{\psi \mathrm{*}}(\boldsymbol{x};L,{\boldsymbol{p}}^{\psi };\omega ){\widehat{D}}^{\psi }(L,\boldsymbol{p},\omega )\end{array} $

(10)

式中：$ {u}_{\mathrm{G}\mathrm{B},n}^{\psi } $为点$ \boldsymbol{x} $处的$ \psi $波高斯束位移矢量$ {\boldsymbol{u}}_{\mathrm{G}\mathrm{B}}^{\psi } $的第n个分量；$ a $为束中心间隔；$ {w}_{l} $和$ {\omega }_{l} $分别为参考有效半宽度和高斯束参考角频率；$ L $代表高斯束中心坐标；$ \boldsymbol{p} $为慢度矢量；$ {\widehat{\boldsymbol{D}}}^{\psi } $是多波型分解后的标量局部平面$ \psi $波，有

$ {\widehat{\boldsymbol{D}}}^{\psi }(L,\boldsymbol{p},\omega )={\boldsymbol{W}}_{n}^{\psi }\left[\begin{array}{l}{D}_{n}(L,\boldsymbol{p},\omega )\\ {\left(\mathrm{i}\omega \right)}^{-1}{u}_{\mathrm{p}}(L,\boldsymbol{p},\omega )\end{array}\right] $

(11)

式中：$ {D}_{n}(L,\boldsymbol{p},\omega ) $表示第$ n $个位移分量经局部倾斜叠加后形成的局部平面波；$ {u}_{\mathrm{p}}(L,\boldsymbol{p},\omega ) $为压力分量经局部倾斜叠加后形成的局部平面波。因此，可以认为$ {\boldsymbol{D}}^{\psi } $是多个位移分量与水压分量的加权求和（如果$ {D}_{n} $表示速度分量，则压力分量$ {u}_{\mathrm{p}} $前的$ {\left(\mathrm{i}\omega \right)}^{-1} $可以去掉并取负，其余不变）。可得权重矩阵

$ {\boldsymbol{W}}_{n}^{\psi }=\left(\begin{array}{cccc}\lambda {\alpha }^{-1}+2\mu {p}_{1}^{\mathrm{P}}{\boldsymbol{e}}_{1}^{\mathrm{P}}& 2\mu {p}_{2}^{\mathrm{P}}{\boldsymbol{e}}_{1}^{\mathrm{P}}& 2\mu {p}_{3}^{\mathrm{P}}{\boldsymbol{e}}_{1}^{\mathrm{P}}& {\boldsymbol{e}}_{1}^{\mathrm{P}}\\ 2\mu {p}_{1}^{\mathrm{S}1}{\boldsymbol{e}}_{1}^{\mathrm{S}1}& \mu \left({p}_{2}^{\mathrm{S}1}{\boldsymbol{e}}_{1}^{\mathrm{S}1}+{p}_{1}^{\mathrm{S}1}{\boldsymbol{e}}_{2}^{\mathrm{S}1}\right)& \mu \left({p}_{3}^{\mathrm{S}1}{\boldsymbol{e}}_{1}^{\mathrm{S}1}+{p}_{1}^{\mathrm{S}1}{\boldsymbol{e}}_{3}^{\mathrm{S}1}\right)& {\boldsymbol{e}}_{1}^{\mathrm{S}1}\\ 2\mu {p}_{1}^{\mathrm{S}2}{\boldsymbol{e}}_{1}^{\mathrm{S}2}& \mu \left({p}_{2}^{\mathrm{S}2}{\boldsymbol{e}}_{1}^{\mathrm{S}2}+{p}_{1}^{\mathrm{S}2}{\boldsymbol{e}}_{2}^{\mathrm{S}2}\right)& \mu \left({p}_{3}^{\mathrm{S}2}{\boldsymbol{e}}_{1}^{\mathrm{S}2}+{p}_{1}^{\mathrm{S}2}{\boldsymbol{e}}_{3}^{\mathrm{S}2}\right)& {\boldsymbol{e}}_{1}^{\mathrm{S}2}\end{array}\right) $

(12)

式中：$ {p}_{i} $(i=1, 2, 3)分别为z，x和y方向的慢度分量；$ {\boldsymbol{e}}_{i} $代表$ \psi $波偏振方向单位矢量坐标基。该权重矩阵中的弹性参数和多波几何参数只和接收界面有关，而接收界面简化为各向同性。

1.3 成像条件

四分量和三分量偏移成像算法的区别主要在于波型分离时所用的数据，在成像条件部分则是完全一致的。常规的互相关条件不适用于弹性矢量波场，Li等^[22]给出了三分量的弹性波高斯束偏移成像的详细推导，基于旋度和散度关系得出了PP波和PS波成像公式

$ \begin{array}{l}{I}_{\mathrm{P}\mathrm{P}}\left(\boldsymbol{x}\right)=\frac{\sqrt{3}}{4\mathrm{\pi }{\alpha }_{x}^{2}}{\left(\frac{{\omega }_{l}a}{{w}_{l}}\right)}^{2}\sum\limits_{L}\int \mathrm{d}\omega \frac{\mathrm{i}{\omega }^{3}}{64{\mathrm{\pi }}^{4}{\rho }_{m}{\alpha }_{m}^{2}{\rho }_{r}{\alpha }_{r}^{2}}\times \\ \iint \frac{\mathrm{d}{p}_{mx}\mathrm{d}{p}_{my}}{{p}_{mz}^{\mathrm{P}}}\iint \frac{\mathrm{d}{p}_{rx}\mathrm{d}{p}_{ry}}{{p}_{rz}^{\mathrm{P}}}\times \\ {u}_{\mathrm{G}\mathrm{B}}^{\mathrm{P}\mathrm{*}}(\boldsymbol{x};s,{\boldsymbol{p}}_{m}^{\mathrm{P}};\omega )\cdot {u}_{\mathrm{G}\mathrm{B}}^{\mathrm{P}\mathrm{*}}(\boldsymbol{x};L,{\boldsymbol{p}}_{r}^{\mathrm{P}};\omega )\cdot {\widehat{D}}^{\mathrm{P}}(L,\boldsymbol{p},\omega )\end{array} $

(13)

$ \begin{array}{l}{I}_{\mathrm{P}\mathrm{S}}\left(\boldsymbol{x}\right)=\frac{\sqrt{3}}{4\mathrm{\pi }{\alpha }_{x}{\beta }_{x}}{\left(\frac{{\omega }_{l}a}{{w}_{l}}\right)}^{2}\sum\limits_{L}\int \mathrm{d}\omega \frac{\mathrm{i}{\omega }^{3}}{64{\mathrm{\pi }}^{4}{\rho }_{m}{\alpha }_{m}^{2}{\rho }_{r}{\beta }_{r}^{2}}\times \\ \iint \frac{\mathrm{d}{p}_{mx}\mathrm{d}{p}_{my}}{{p}_{mz}^{\mathrm{P}}}\iint \frac{\mathrm{d}{p}_{rx}\mathrm{d}{p}_{ry}}{{p}_{rz}^{\mathrm{S}}}\times \\ {u}_{\mathrm{G}\mathrm{B}}^{\mathrm{P}\mathrm{*}}(\boldsymbol{x};s,{\boldsymbol{p}}_{m}^{\mathrm{P}};\omega )\cdot {u}_{\mathrm{G}\mathrm{B}}^{\mathrm{S}\mathrm{*}}(\boldsymbol{x};L,{\boldsymbol{p}}_{m}^{\mathrm{S}};\omega )\cdot \mathrm{S}\mathrm{g}\mathrm{n}\left(\boldsymbol{x}\right)\cdot {\widehat{D}}^{\mathrm{S}}\end{array} $

(14)

式中：r为接收点；$ m $为震源点；$ {\widehat{D}}^{\mathrm{P}} $、$ {\widehat{D}}^{\mathrm{S}} $为倾斜叠加后的局部平面波；a_x为x方向上的横波速度；a_r为r点的横波速度。

$ {\widehat{D}}^{\mathrm{S}}={\widehat{D}}^{\mathrm{S}1}(L,{\boldsymbol{p}}_{r},\omega ){\boldsymbol{e}}_{2}\left(x\right)-{\widehat{D}}^{\mathrm{S}2}(L,{\boldsymbol{p}}_{r},\omega ){\boldsymbol{e}}_{1}\left(x\right) $

(15)

为解决PS波成像的偏振反转问题，有单位矢量函数

$ \mathrm{S}\mathrm{g}\mathrm{n}\left(x\right)=\frac{{\boldsymbol{p}}_{r}\left(x\right)\times {p}_{m}\left(x\right)}{\left|{\boldsymbol{p}}_{r}\left(x\right)\times {\boldsymbol{p}}_{m}\left(x\right)\right|} $

(16)

1.4 各向异性射线追踪

运动学和动力学射线追踪是实现各向异性介质弹性波高斯束偏移的关键。运动学射线追踪可以确定中心射线轨迹，动力学射线追踪可以计算射线的能量分布。Zhu等^[23]利用群速度和相速度给出了各向异性运动学射线追踪的表达式，秦宁^[24]将其推广到各向异性弹性波

$ \left\{\begin{array}{l}\frac{\mathrm{d}{x}_{h1}}{\mathrm{d}\tau }={V}_{{\mathrm{P}}_{h1}}\\ \frac{\mathrm{d}{p}_{{\mathrm{P}}_{h1}}}{\mathrm{d}\tau }=-\frac{1}{{V}_{0\mathrm{P}}}\frac{\partial {{V}_{0\mathrm{P}}}_{{}_{}}}{\partial {x}_{h1}}\\ \frac{\mathrm{d}{x}_{h2}}{\mathrm{d}\tau }={V}_{{\mathrm{S}}_{h2}}\\ \frac{\mathrm{d}{p}_{{\mathrm{S}}_{h2}}}{\mathrm{d}\tau }=-\frac{1}{{V}_{0\mathrm{S}}}\frac{\partial {V}_{0\mathrm{S}}}{\partial {x}_{h2}}\end{array}\right. $

(17)

式中：V和V₀分别为群速度和相速度；下标P和S代表P波和S波；h1和h2分别代表水平方向和垂直方向。该射线追踪表达适用于一般的各向异性介质。在VTI介质中，有用Thomosen参数表示相速度

$ \left\{\begin{array}{l}{V}_{\mathrm{S}\mathrm{H}}\left(\theta \right)={V}_{\mathrm{S}0}\sqrt{1+2\gamma \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }\\ \frac{{V}^{2}\left(\theta \right)}{{{V}_{\mathrm{P}0}}^{2}}=1+ε \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta -\frac{f}{2}\pm \frac{1}{2}\sqrt{(f+2ε \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta )}^{2}-2f(ε -\delta )\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}2\theta }\\ f=1-\frac{{V}_{\mathrm{S}0}^{2}}{{V}_{\mathrm{P}0}^{2}}\end{array}\right. $

(18)

式中：$ {V}_{\mathrm{S}0} $、$ {V}_{\mathrm{P}0} $分别为S波、P波的垂直速度；取“+”为P波相速度，取“-”为SV波相速度；$ \delta $、$ ε $和$ \gamma $为Thomosen参数^[25]，可与弹性参数建立联系；$ \theta $为射线传播方向与VTI对称轴的夹角。

利用以上方程进行射线追踪，即可得到P波和SV波中心射线走时和路径。

相比之下，Červený^[26]给出的各向异性动力学射线追踪表达式更复杂

$ \left\{\begin{array}{l}\frac{\mathrm{d}\boldsymbol{Q}}{\mathrm{d}\tau }=A\boldsymbol{Q}+\boldsymbol{BT}\\ \frac{\mathrm{d}T}{\mathrm{d}\tau }=-C\boldsymbol{Q}-\boldsymbol{DT}\end{array}\right. $

(19)

式中：A、B、C、D为$ 2\times 2 $阶系数矩阵；矩阵$ T $和Q在局部正交坐标系$ ({y}_{1},{y}_{2},{y}_{3}) $中具有微分形式

$ {\boldsymbol{Q}}_{IJ}^{\left(y\right)}={\left.\frac{\partial {y}_{I}}{\partial {\gamma }_{J}}\right|}_{\tau =\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}},\boldsymbol{T}_{IJ}^{\left(y\right)}={\left.\frac{\partial {{p}_{I}}^{\left(y\right)}}{\partial {\gamma }_{J}}\right|}_{\tau =\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}} $

(20)

式中：I，J=1, 2, 3; $ ({y}_{1},{y}_{2},{y}_{3}) $为笛卡尔坐标系；$ \gamma $是射线坐标系；const表示常数。局部坐标系中$ {y}_{1} $和$ {y}_{2} $与波前平行，$ {y}_{3} $与波前垂直。在各向异性介质中为

$ \left\{\begin{array}{l}{A}_{IJ}=\frac{{V}_{GI}}{V}\frac{\partial V}{\partial {y}_{J}}+\frac{\partial {V}_{GI}}{\partial {y}_{J}}\\ {B}_{IJ}={V}_{GI}{V}_{GJ}+\frac{\partial {V}_{GI}}{\partial {p}_{J}}\\ {C}_{IJ}=\frac{1}{{V}^{2}}\frac{\partial V}{\partial {y}_{I}}\frac{\partial V}{\partial {y}_{J}}+\frac{1}{V}\frac{{\partial }^{2}V}{\partial {y}_{I}{y}_{J}}\\ {D}_{IJ}={A}_{JI}\end{array}\right. $

(21)

计算该系数矩阵在实际中较困难，因此一般会将动力学射线追踪进行特殊处理。Červený等^[27]指出，对于较高的各向异性对称性，例如横向各向同性(TI）或正交介质，可以得到相当大的简化。段鹏飞等^[28]假设介质为各向异性，可以将其几何扩散近似为各向同性介质，即

$ {A}_{IJ}={D}_{IJ}=0,{B}_{IJ}={V}^{2},{C}_{IJ}=\frac{1}{V}\frac{{\partial }^{2}V}{\partial {y}_{I}\partial {y}_{J}} $

(22)

动力学参数对偏移成像效果的影响很小，利用各向同性替代各向异性同样可以得到非常准确的成像效果。

2 数值试算

三维情况下对应的4C数据包括水压和位移矢量，3C数据只有位移矢量；二维情况下进行成像时则都减少一个位移分量。上述公式推导部分对应的是三维情况，如下数值试算只给出了二维结果。

2.1 水平层状模型

为了验证本文方法的效果，首先采用水平层状模型测试成像效果，使用二维有限差分波场正演模拟程序计算模型记录。

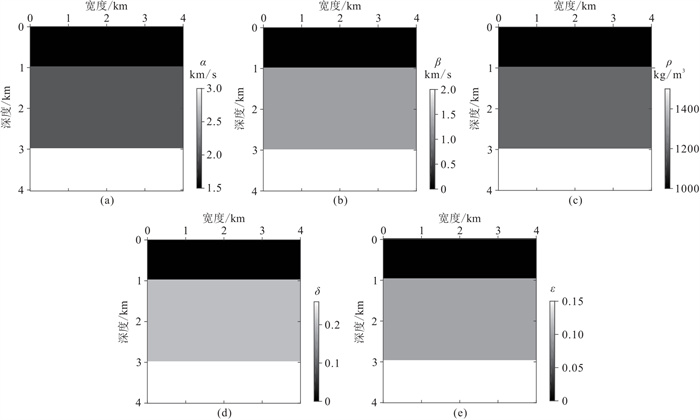
图 1为层状模型的速度场、密度和各向异性参数。模型网格数为801×801，x方向和z方向的网格间距dx=dz=5 m，最上面一层为水层(α=1500 m/s, β=0, ρ=1000 kg/m³)，反射界面在深度z=1000 m和z=3000 m处，炮点布设于海面（z=0）、x=0~4000 m处，间隔为200 m。四分量检波器于海底(z=1000 m)成水平排列，布设间隔为25 m，顶部边界条件为自由表面，便于产生多次波，从而能同时记录上行波和下行波，侧面和底部为PML吸收边界条件。震源是主频为10 Hz的雷克子波，生成的数据只包含了反射波和检波点端的鬼波效应，没有包含炮点端鬼波，地震记录时长为4 s，采样间隔为2 ms。

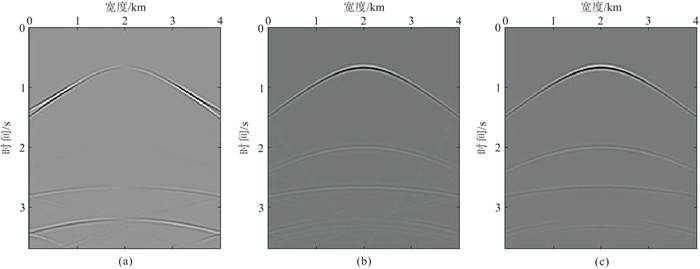
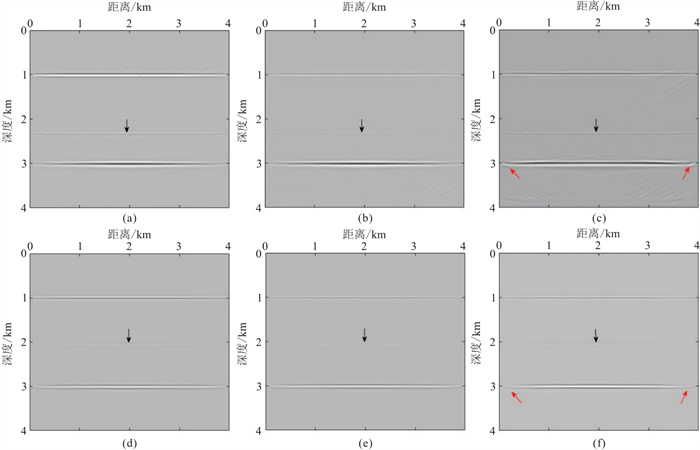
图 2展示了各向异性介质弹性波单炮地震记录，对比x分量(图 2a)和z分量(图 2b)可知，PS波在x分量上更明显，而PP波在z分量上更明显，它们在另一分量(图 2c)也清晰可见，因此不同的波型在成像时会导致串扰现象。图 3是PP波和PS波偏移成像结果。由图可见PP波(图 3a~图 3c)和PS波(图 3d~图 3f)均可以准确成像，并且PP波和PS波之间不存在明显的串扰噪声，PS波成像比PP波成像有更高的分辨率。因为忽略了各向异性的影响，各向同性介质弹性波高斯束偏移成像结果(图 3c)的构造位置不准确，红色箭头处出现上翘现象，不能把地震信号聚集在准确的位置，成像品质较低。而各向异性介质高斯束偏移结果的信噪比高，构造位置更准确，同相轴连续性更好。图 3b和图 3e偏移成像比图 3a和图 3d得到的结果更准确，分辨率更高，抑制了由下行的检波点端鬼波引起的虚影假象(黑色箭头处)。层状模型的试算结果证明了本文方法的有效性。

2.2 北海Gullfaks区域模型

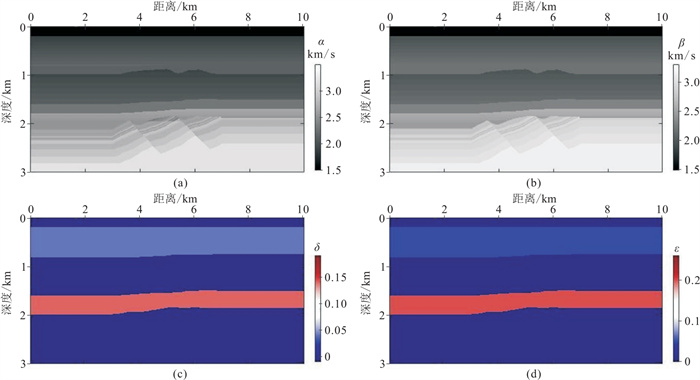
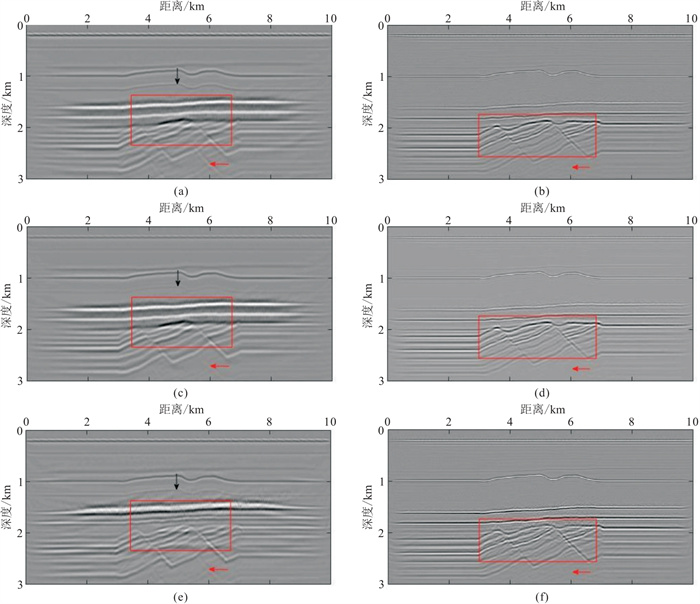
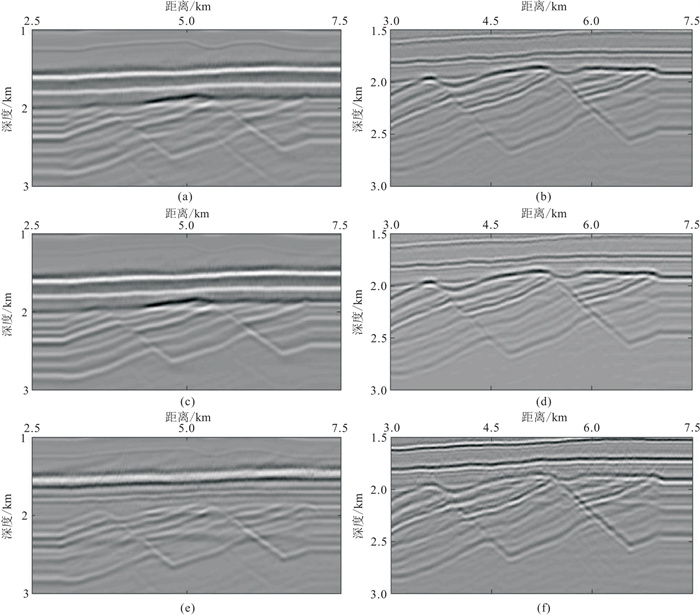
图 4为北海Gullfaks区域速度模型及各向异性参数，模型采取常密度ρ=1000 kg/m³。正演模拟采用的模型网格数为2001×601，网格间距dx=dz=5 m，震源采用主频为10 Hz的雷克子波，共401炮，均匀分布在深度5 m处，炮间距为25 m，检波器位于海底z=200 m，每炮排列为2001道，道间距为5 m。图 5是高斯束偏移成像结果，对三分量和四分量数据、各向同性和各向异性算法成像结果进行对比分析。红色方框与箭头所指为成像效果差异显著部分。图 6是图 5中的局部成像放大展示, 由图可知：①图 6c和图 6d使用4C数据联合成像, 消除了检波器鬼波的影响，比只使用三分量数据得到的结果(图 6a、图 6d)分辨率更高，抑制了假象的形成，地层界面与断层构造处更清晰；②图 6c和图 6d是VTI介质弹性波高斯束偏移成像结果，能量聚焦性更好，信噪比高，同向轴连续性好，构造位置更准确；③VTI介质的PP波成像结果的同向轴能量强于PS波，PS波成像的分辨率高于PP波，成像更细腻，PP波成像存在明显的重影和假象；④忽略各向异性因素影响的各向同性介质弹性波高斯束偏移成像结果，图 6e和图 6f的构造位置不准确，出现了成像假象，地下层位界面不清晰。北海Gullfaks区域模型的试算结果进一步证明本文方法的有效性。

总体来说，利用各向异性介质弹性波高斯束偏移方法对PP波和PS波分别成像，从不同角度刻画洋底构造，提高了成像质量，对复杂各向异性介质海底模型的成像效果优于各向同性算法，四分量数据效果优于三分量数据。

3 结论

本文通过假设海底接收界面为各向同性，利用动力学参数近似和Zhu等^[23]提出的运动学射线追踪，将各向异性理论与高斯束偏移成像方法相结合，并应用于VTI介质的弹性波高斯束偏移成像，提出了海底四分量各向异性介质高斯束偏移方法，通过考虑各向异性参数对地震波场的影响，实现海底各向异性介质中的多波型以及上下行波的自动分离与准确成像。该方法适用于一般各向异性介质(但本文只给出了VTI介质的数值算例)。

VTI层状介质模型和北海Gullfaks区域模型试算结果表明，与各向同性介质弹性波高斯束偏移算法相比，各向异性介质弹性波高斯束偏移成像结果的信噪比更高，同向轴连续性更好，构造位置更准确。另外，利用四分量数据中的横波、纵波以及压力场信息，能够获得完整的海底边界条件，消除海底成像中的串扰和假象，有效提高了海底成像分辨率。