2. 吉林大学地球探测科学与技术学院, 吉林长春 130026;
3. 北京工商大学数学与统计学院, 北京 100048
2. College of Geoexploration Science and Technology, Jilin University, Changchun, Jilin 130026, China;
3. School of Mathematics and Statistics, Beijing Technology and Business University, Beijing 100048, China
社会经济的高速发展,带动了各行业的快速进步,对于相关资源的需求也在不断增加。石油、天然气的开发和应用对于中国经济的发展有着重要影响。在油气勘探领域,地震勘探技术处于核心地位,发展新型的勘探方法和偏移技术,对了解地震波传播规律和提高地震成像分辨率具有重要意义。
逆时偏移(RTM)可为岩性储层估计提供保真的、分辨率高的成像剖面,是地震成像技术的研究热点[1-2]。地震波在传播过程中会出现频散和衰减效应。使用品质因子(Q)描述的黏滞声波方程将有助于补偿能量损失,进而获得高分辨率的成像结果[3]。
RTM的核心步骤是波动方程数值求解。常用的数值模拟方法包括有限差分法、伪谱法和有限元法等。有限元法能灵活地进行网格剖分、精度高、适用于复杂边界区域的成像,但计算量大,很难高效实现并行计算[4]。伪谱法在指定精度下,所需网格数量少于有限元法和有限差分法,但其局部性能差、不易并行、边界处理困难,并且可能出现吉布斯现象。有限差分法具有编程简单、计算速度快、存储需求少、易并行等优点,在地球物理领域的数值模拟中被广泛应用[5],能求解多种波动方程,包括声波、弹性波和黏弹性波方程[5]。然而,传统的有限差分法,例如Laxwendroff Correction(LWC)方法,在粗网格下或介质存在较大速度反差时会产生严重的数值频散[6]。高阶格式或加细网格可以压制数值频散,但会令计算量和存储量大幅增加,从而难以满足大规模波场数值模拟的需求。Yang等[7-9]提出应用Stereomodeling法(STEM)求解声波和弹性波方程。不同于传统的有限差分法,STEM应用位移及其空间梯度共同逼近空间高阶偏导数,能够有效压制数值频散并达到较高的数值精度。Li等[10-11]将STEM应用于逆时偏移,结果表明,相比于传统有限差分法,STEM的偏移结果分辨率更高。
以上有限差分法是在牛顿力学体系中构造的,在格式构造过程中较少考虑能量守恒、保持结构不变等物理性质,会因为数值离散和求解过程等引发系统能量损失。解决的方法之一就是使用保辛方法[12]。保辛方法是一种在哈密顿系统下构造的数值格式,可以保持哈密顿系统随时间演化中的一系列量不变,具有长时计算稳定性。Feng等[13]根据函数生成理论,针对常微分方程构建了保辛方法的理论框架,发展了许多不同类型的保辛方法。Qin等[14]提出了波动方程的哈密顿形式,并构造了多个时间上的多级保辛方法。Li等[15]提出了时间上的三阶保辛可分Runge-Kutta (SPRK)法。马啸等[16]基于声波方程和弹性波方程的哈密顿系统表述,结合STEM和SPRK法,提出了近似解析的SPRK(NSPRK)法。Birkhoffian系统比哈密尔顿系统能够描述的情况更广泛,王美霞[17]将STEM应用到达朗贝尔介质中的纵波和PSV波方程,构建了广义Birkhoffian系统,并提出了求解该系统的保辛方法SSM(Symplectic Stereo-modeling Method)。Yang等[18] 将SSM推广至求解双相介质中的弹性波方程。
本文将SSM推广至求解黏滞声波方程,并进行振幅补偿的逆时偏移成像。具体为:首先,将黏滞声波方程构造为一个广义Birkhoffian系统;然后,采用二阶保辛Runge-Kutta法进行时间推进,并采用低数值频散的STEM进行空间离散,从而获得求解黏滞声波方程的SSM;再通过数值频散、计算效率和长时计算稳定性对比等分析方法的优势;最后,应用多个模型,进行基于黏滞声波方程的正演数值模拟和衰减补偿的逆时偏移。结果表明,所提方法具有低数值频散、成像分辨率更高的优势。
1 求解黏滞声波方程的保辛格式 1.1 方法理论本文应用的黏滞声波方程为[19]
| $ \begin{array}{l}\frac{1}{v{\left(\boldsymbol{x}\right)}^{2}}\frac{{\partial }^{2}u(\boldsymbol{x}, t)}{\partial {t}^{2}}+\frac{\psi g}{v\left(\boldsymbol{x}\right)}\frac{\partial u(\boldsymbol{x}, t)}{\partial t}\\ ={\nabla }^{2}u(\boldsymbol{x}, t)+\mathrm{\delta }(\boldsymbol{x}-{\boldsymbol{x}}_{\mathrm{s}})s\left(t\right)\end{array} $ | (1) |
式中:x=(x, z)表示空间位置;s(t)为震源函数;v(x)为波速;u(x, t)为t时刻的波场值;
黏滞声波方程(式(1))可构造成Birkhoffian系统形式
| $ \left\{\begin{array}{l}\frac{\mathrm{d}u}{\mathrm{d}t}={\mathrm{e}}^{-rt}p\\ \frac{\mathrm{d}p}{\mathrm{d}t}={\mathrm{e}}^{rt}Lu\end{array}\right. $ | (2) |
式中:
| $ \left\{\begin{array}{l}{p}_{1}={p}^{n}+\frac{\mathrm{\Delta }t}{2}{\mathrm{e}}^{r{t}_{n}}{L}_{s}{u}^{n}\\ {u}^{n+1}={u}^{n}+\mathrm{\Delta }t{\mathrm{e}}^{-r{t}_{n+1/2}}{p}_{1}\\ {p}^{n+1}={p}_{1}+\frac{\mathrm{\Delta }t}{2}{\mathrm{e}}^{r{t}_{n+1}}{L}_{s}{u}^{n+1}\end{array}\right. $ | (3) |
式中:n为时间方向离散序号;
定义
| $ \left\{\begin{array}{l}\frac{\mathrm{d}\boldsymbol{u}}{\mathrm{d}t}={\mathrm{e}}^{-rt}\boldsymbol{p}\\ \frac{\mathrm{d}\boldsymbol{p}}{\mathrm{d}t}={\mathrm{e}}^{rt}{\boldsymbol{L}}_{1}\boldsymbol{u}\end{array}\right. $ | (4) |
其中
| $ {\boldsymbol{L}}_{1}=\left[\begin{array}{ccc}L& 0& 0\\ 0& L& 0\\ 0& 0& L\end{array}\right] $ | (5) |
针对式(4),同样应用Lobatto IIIAIIIB法进行时间离散,即可得到类似于式(3)的时间推进格式,同时空间上采用四阶STEM离散高阶空间偏导数,即可得到求解黏滞声波方程式(1)的SSM。CSM与SSM具有同样的理论精度,即空间和时间均为四阶精度。区别在于,CSM离散空间偏导数只用到函数值,而SSM同时用到函数和梯度值。
例如,对于二阶空间偏导数
| $ \begin{array}{l}{\left(\frac{{\partial }^{2}u}{\partial {x}^{2}}\right)}_{i, j}^{n}=\frac{2}{\mathrm{\Delta }{x}^{2}}\left({u}_{i-1, j}^{n}-2{u}_{i, j}^{n}+{u}_{i+1, j}^{n}\right)-\\ \frac{1}{2\mathrm{\Delta }x}\left[{\left(\frac{\partial u}{\partial x}\right)}_{i+1, j}^{n}-{\left(\frac{\partial u}{\partial x}\right)}_{i-1, j}^{n}\right]\end{array} $ | (6) |
式中∆x、∆z为空间网格步长。而CSM的四阶离散格式为
| $ \begin{array}{l}{\left(\frac{{\partial }^{2}u}{\partial {x}^{2}}\right)}_{i, j}^{n}=\frac{4}{3\mathrm{\Delta }{x}^{2}}\left({u}_{i+1, j}^{n}+{u}_{i-1, j}^{n}\right)-\\ \frac{1}{12\mathrm{\Delta }{x}^{2}}\left({u}_{i+2, j}^{n}+{u}_{i-2, j}^{n}\right)-\frac{5}{2\mathrm{\Delta }{x}^{2}}{u}_{i, j}^{n}\end{array} $ | (7) |
其他空间偏导数的具体离散格式见参考文献[5]。
1.2 数值频散分析和计算效率对比根据Moczo等[22]的分析,定义数值频散比率为
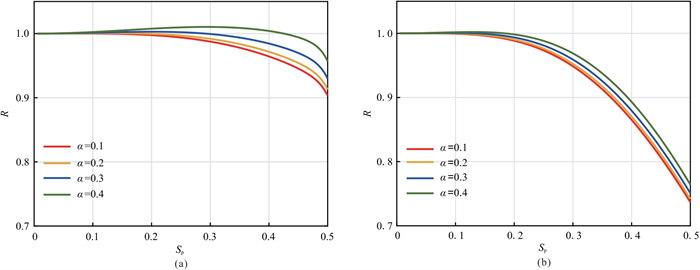
|
图 1 SSM(a)和CSM(b)的频散曲线对比 |
通过波形和波场快照对比进一步分析SSM与CSM的数值频散。实验选取二维均匀各向同性介质模型,其中v=4 km/s、Q=80、α=0.32,计算区域为0≤x、z≤10 km。中心频率f0=20 Hz的震源子波
| $ \begin{array}{l}{s}_{1}\left(t\right)=-5.76{f}_{0}^{2}\left[1-16{\left(0.6{f}_{0}t-1\right)}^{2}\right]\times \\ {\mathrm{e}}^{-8{\left(0.6{f}_{0}t-1\right)}^{2}}\end{array} $ | (8) |
放置在模型的中心。另外,本文实验中fd均取f0/2。
图 2a和图 2b分别为粗网格(h=50 m)情况下SSM和CSM在1.0 s时获得的波场快照,可以看出,CSM方法存在较严重的数值频散,而SSM方法几乎无可见的数值频散。图 3为检波器在(6.5 km,5 km)处接收到的波形记录与解析解[23]的对比。由图 3可以看出,SSM数值解与解析解非常吻合,误差很小,而CSM数值解存在严重数值频散,与解析解匹配较差。当网格细化到h=25 m时,CSM波场快照(图 2c)几乎与图 2a一致,但网格节点需要从201×201增加到401×401。表 1列出了此时两种方法的CPU时间和存储需求。从表 1可以看出,当波场快照基本一致时,SSM的存储需求大约是CSM的75.4%,而计算效率大约是CSM的2.03倍。

|
图 2 均匀模型两种方法波场快照对比 (a)SSM,h=50 m;(b)CSM,h=50 m;(c)CSM,h=25 m |
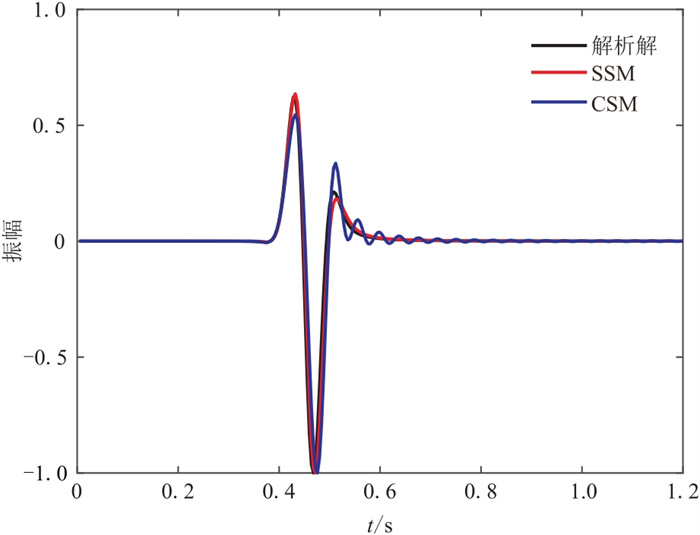
|
图 3 SSM和CSM数值解与解析解的波形对比 |
|
|
表 1 SSM和CSM的CPU时间和内存需求对比 |
选择没有物理耗散的声波方程和没有几何扩散的一维各向同性均匀介质模型进行长时间的正演波场数值模拟,观察能量随时间的变化,测试SSM的长时计算稳定性。实验参数为:v=4 km/s,∆t=2 ms,h=20 m,总传播时间=80 s;震源放置在计算区域的中心,f0=25 Hz。另外,格式的保辛性体现在时间域的离散上,因此为排除空间离散的干扰,实验的对比方法选择与SSM相同的空间离散格式,但时间上采用非保辛的四阶泰勒展开方法NADM(Nearly Analytic Discrete Method)[7]。定义相对能量为
| $ E\left(u\right)=\frac{1}{2}\int \left[{\left(\frac{\partial u}{\partial t}\right)}^{2}+uLu\right]\mathrm{d}x $ | (9) |
SSM和NADM两种方法一维波场数值模拟的相对能量随时间变化如图 4所示,可以看到,随着时间的演化,SSM的能量基本保持稳定,整体波动范围很小;然而,由于NADM的能量随着时间的增长,存在显著的波动和耗散。这说明在时间推进上采用保辛格式的SSM具有长时的计算稳定性。
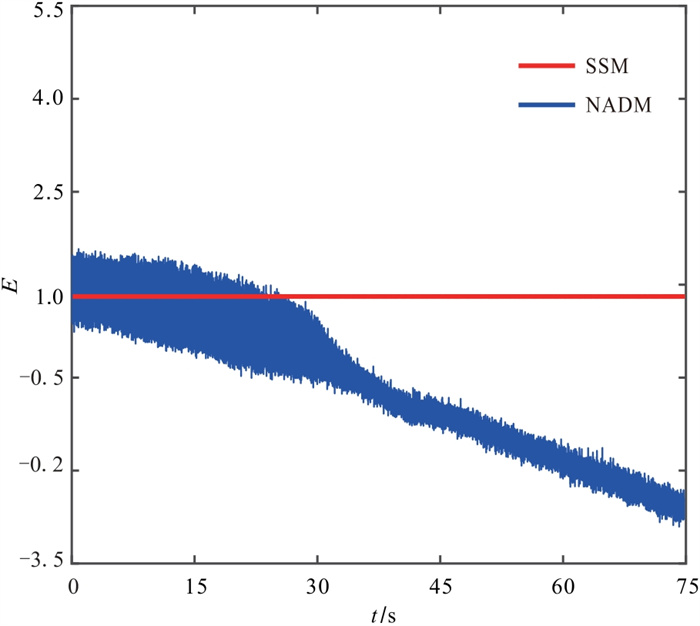
|
图 4 SSM与NADM一维模拟的相对能量对比 |
通过断层模型验证SSM求解黏滞声波方程正确性和优势。断层模型网格数为210×90,上层介质v=1.6 km/s、Q= 30;下层介质v=2.3 km/s、Q=60(图 5)。实验参数为:h=10 m,∆t=0.6 ms。震源位于(1.05 km,0.02 km)处,主频为30 Hz,总记录时长为1.56 s。
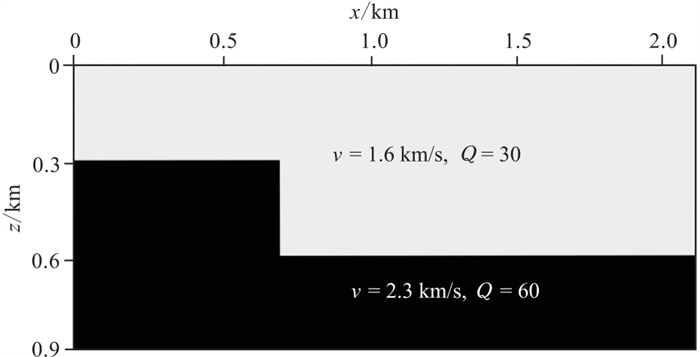
|
图 5 断层模型 |
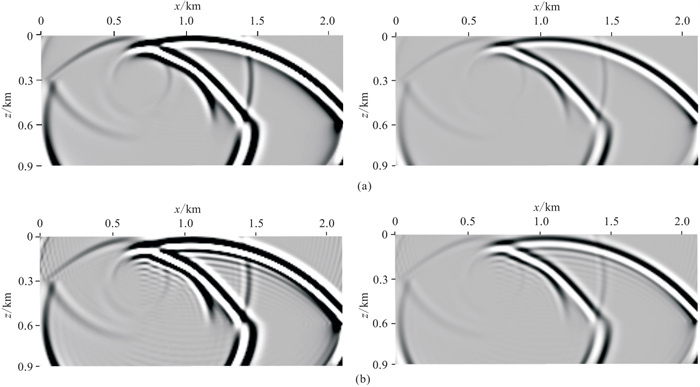
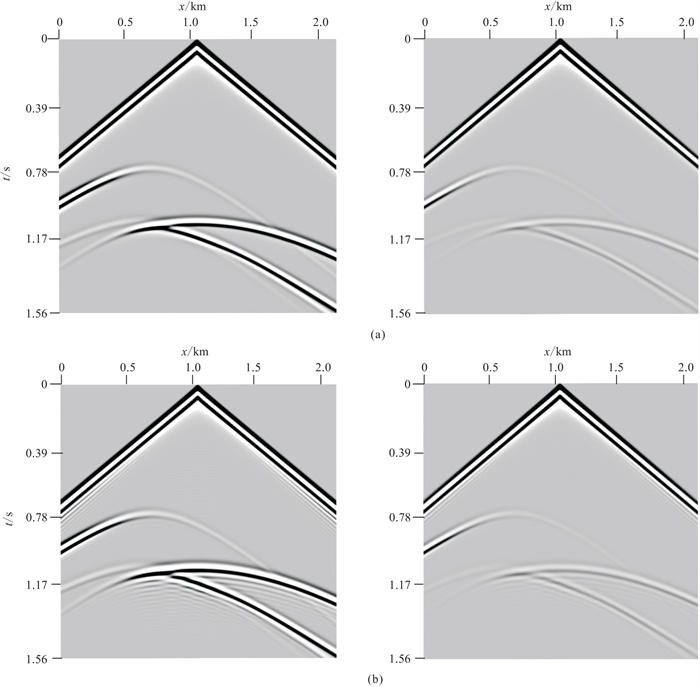
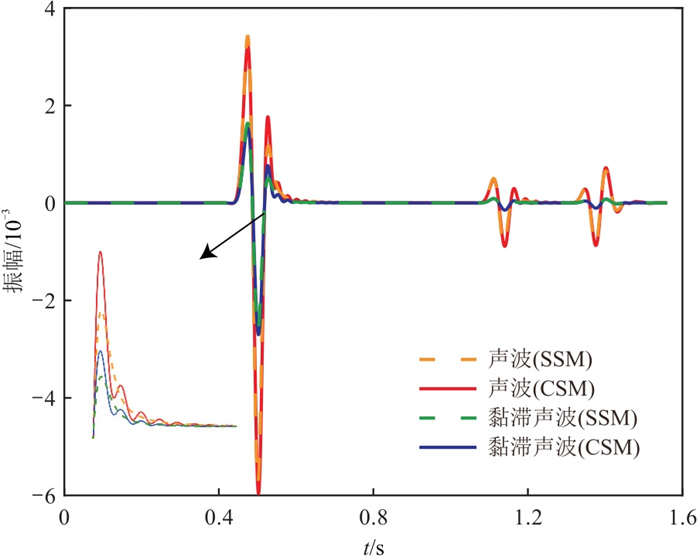
由SSM和CSM基于声波和黏滞声波方程计算的波场快照如图 6所示,可以看出,SSM方法的波场快照没有明显的数值频散(图 6a),而CSM方法的波场快照存在很严重的数值频散(图 6b)。同时,对比声波与黏滞声波波场快照可以发现,后者的振幅要比前者低,出现了衰减。由图 7的炮集记录中也可以看到这两个现象。进一步,从图 7中提取距离x = 1.75 km处的波形(图 8),进一步证明了SSM方法比CSM方法能更有效压制数值频散,且黏滞声波相比于声波出现了衰减。
|
图 6 断层模型两种方法模拟的声波(左)和黏滞声波(右)的波场快照对比 (a)SSM;(b)CSM |
|
图 7 断层模型两种方法模拟的声波(左)和黏滞声波(右)炮集对比 (a)SSM;(b)CSM |
|
图 8 断层模型SSM与CSM模拟的波形对比 |
本文应用断层模型、Marmousi模型和油气藏模型验证将SSM应于黏滞介质振幅补偿逆时偏移可行性。
3.1 逆时偏移成像原理逆时偏移成像的主要步骤为:首先,从0时刻开始到最大时刻T,基于式(1)(ψ=1)正演计算各个时刻的震源波场
| $ I\left(\boldsymbol{x}\right)=\frac{{\int }_{0}^{T}u(\boldsymbol{x}, t)q(\boldsymbol{x}, t)\mathrm{d}t}{{\int }_{0}^{T}u(\boldsymbol{x}, t)u(\boldsymbol{x}, t)\mathrm{d}t+ε } $ | (10) |
式中
首先通过断层模型测试基于SSM的声波方程和黏滞声波方程RTM。使用的震源函数为
| $ {s}_{2}\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(2\mathrm{\pi }{f}_{0}t\right)\times {\mathrm{e}}^{-\frac{{\mathrm{\pi }}^{2}{f}_{0}^{2}{t}^{2}}{4}} $ | (11) |
式中f0=15 Hz。其它参数与断层模型的正演数值模拟时相同。从x = 0.56 km开始设置炮点,共41炮,炮间距为50 m,地表均匀放置210个检波器。使用SSM求解黏滞声波方程得到正演模拟数据。
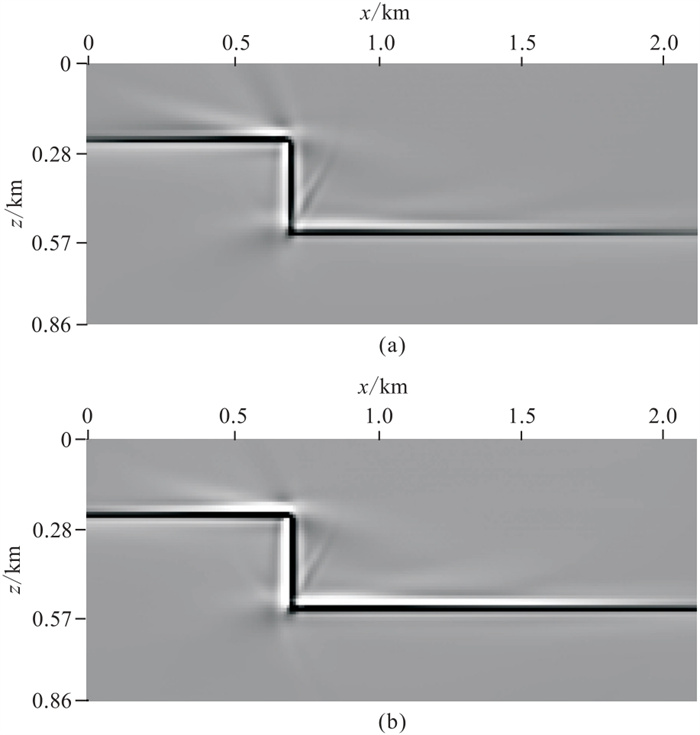
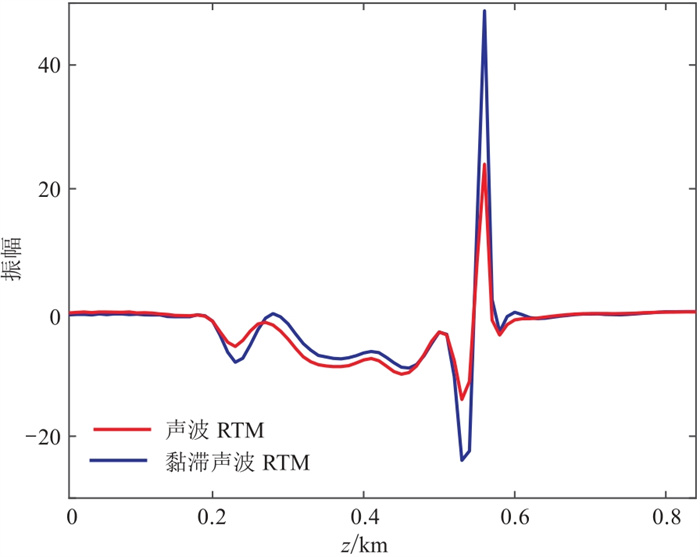
图 9为基于声波方程和黏滞声波方程的RTM成像结果,二者使用的都是黏滞声波衰减数据。由图 9可以看出,振幅补偿的黏滞声波RTM的成像振幅更大,结果更清晰。从图 9提取x=0.74 km处的RTM偏移波形(图 10)进行对比,可进一步验证该结论。
|
图 9 断层模型声波(a)和黏滞声波(b)RTM偏移结果对比 |
|
图 10 断层模型x=0.74 km处声波与黏滞声波RTM的波形对比 |
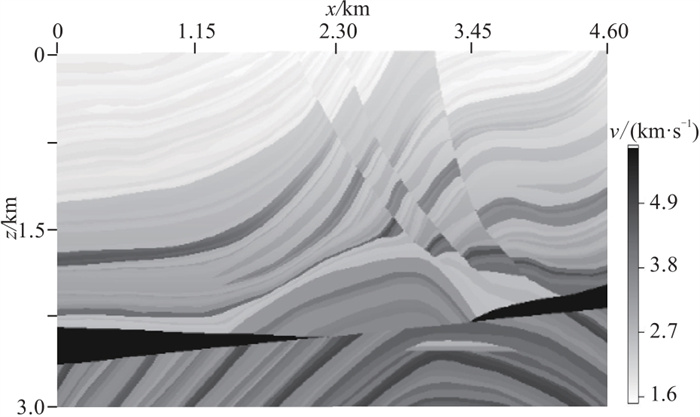
Marmousi模型的速度结构如图 11所示。该模型的网格点数为461×301,速度范围为1.5~5.5 km/s。Q取值范围为34.2~688.4,由与速度的经验公式
| $ Q=3.516\times {v}^{2.2}\times {10}^{-6} $ | (12) |
|
图 11 Marmousi模型 |
计算所得。实验中,h=10 m、∆t=0.6 ms、f0=15 Hz,炮点深度均为20 m,从x = 0.35 km开始每隔50 m设置一炮,共87炮。每炮均在地表布设461个检波器。同样使用SSM求解黏滞声波方程得到正演模拟数据。
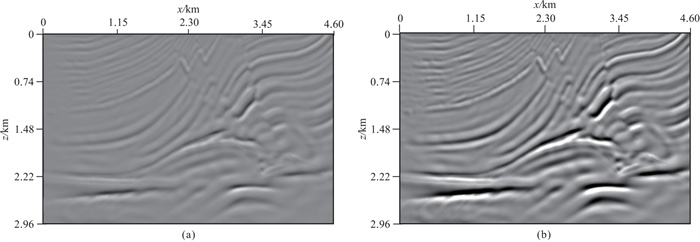
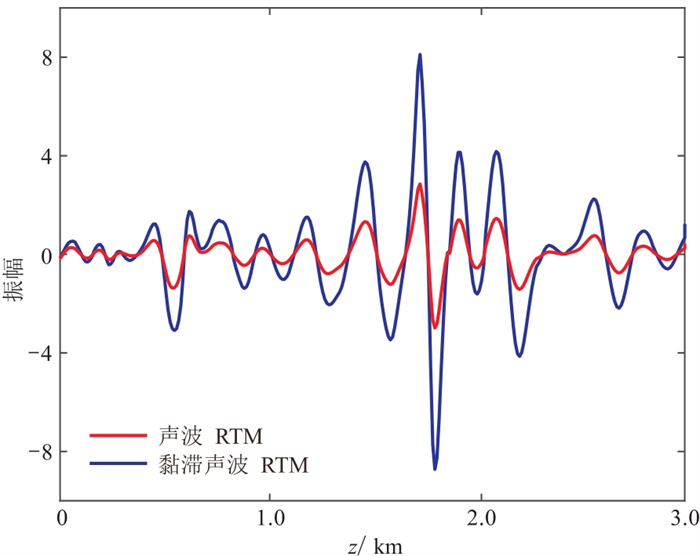
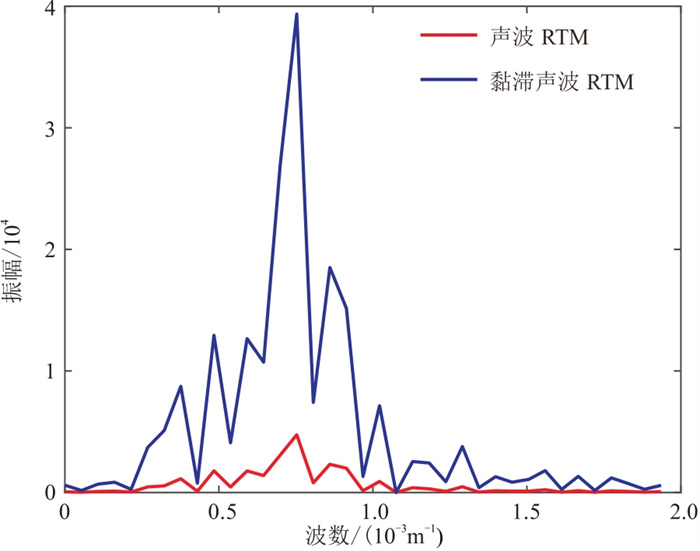
图 12为基于声波方程和黏滞声波方程的RTM成像结果,二者均采用黏滞声波数据。可以看到,黏滞声波RTM的振幅更大,细节刻画得更明显,衰减效应得到了补偿,特别是在浅层和中间大倾角目标层处。从图 12提取x=2.3 km处的RTM单道波形并计算其波数谱,分别如图 13和图 14所示,带振幅补偿的黏滞声波RTM成像振幅更大、分辨率更高。
|
图 12 Marmousi模型声波(a)与黏滞声波(b)RTM结果对比 |
|
图 13 Marmousi模型x=2.3 km处声波与黏滞声波RTM单道波形对比 |
|
图 14 Marmousi模型x=2.3 km处声波与黏滞声波RTM单道波数谱对比 |
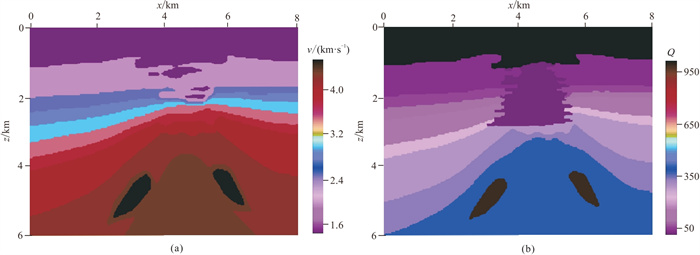
油气藏模型的速度结构和Q值分布如图 15所示。该模型网格数为401×301,速度范围为1.5 ~4.5 km/s,品质因子Q取值范围为20~1000,油气藏处(Q=20)为小Q值区域,水层(Q=1000)和盐丘(Q=980)为大Q值区域。实验参数为:h=20 m,∆t=1.5 ms;震源函数用s1,f0为15 Hz,从x=0.7 km开始每隔0.1 km设置一炮,共75炮,放置在地表下40 m处;在地表均匀布设401个检波器。
|
图 15 油气藏速度(a)和Q(b)模型 |
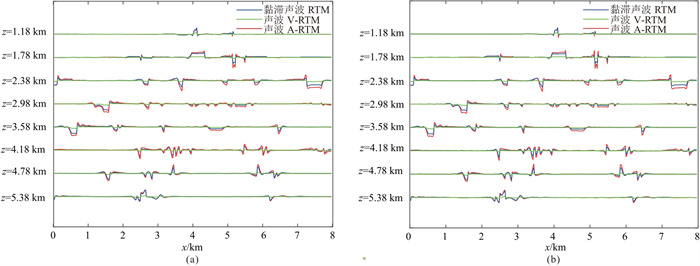
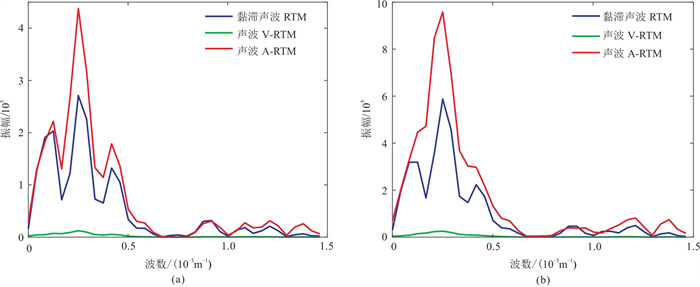
图 16为基于SSM和CSM得到的黏滞声波RTM(分别基于SSM和CSM的黏滞声波正演数据)、声波V-RTM(分别基于SSM和CSM的黏滞声波正演数据)和声波A-RTM(分别基于SSM和CSM的声波正演数据)成像结果。一方面,无论是SSM还是CSM,声波V-RTM成像振幅最小,声波A-RTM成像振幅最大,而黏滞声波RTM除了盐丘部分成像振幅相对较弱,其他区域几乎可以与声波A-RTM一样强。图 17为从不同深度提取的RTM波形,图 18为深度z=1.72 km处波数谱对比,进一步验证了上述结论。另一方面,对比图 16的CSM和SSM的成像结果,可以看出,CSM方法的偏移结果存在数值频散。由图 17可以看出,相比于CSM,基于SSM的黏滞声波RTM经过振幅补偿后更接近于声波A-RTM,表明基于SSM的RTM比CSM更有效。

|
图 16 油气藏模型不同数据基于SSM(左)与CSM(左)的RTM结果对比 (a)黏滞声波RTM;(b)声波V-RTM;(c)声波A-RTM |
|
图 17 油气藏模型不同深度基于SSM(a)与CSM(b)的RTM波形对比 |
|
图 18 油气藏模型z=1.72 km处基于SSM(a)与CSM(b)的RTM波数谱对比 |
本文针对黏滞介质逆时偏移,在Birkhoffian系统框架下求解黏滞声波方程,使用STEM方法进行空间离散,使用保辛的SSM进行时间推进。由模型数据试算可以得到如下结论。
(1) 在Birkhoffian系统下求解黏滞声波方程,与CSM相比,SSM可更好地压制数值频散,计算效率更高,数值解与解析解更接近。
(2) 长时计算稳定性测试表明,与使用四阶泰勒展开格式的NADM相比,使用保辛格式的SSM进行时间递推具有更强的长时计算稳定性。
(3) 多个模型的RTM结果表明:与CSM相比,SSM的成像结果分辨率更高、数值频散更小;与声波RTM相比,考虑了衰减补偿的黏滞声波RTM成像分辨率更高、振幅更强、成像更清晰。
| [1] |
王喜鹏, 张庆臣, 毛伟建. 基于上下行波分解的分数阶拉普拉斯算子黏滞声波逆时偏移成像方法[J]. 石油地球物理勘探, 2023, 58(4): 872-882. WANG Xipeng, ZHANG Qingchen, MAO Weijian. Viscoacoustic reverse-time migration imaging based on fractional Laplacian with up-going and down-going wave decomposition[J]. Oil Geophysical Prospecting, 2023, 58(4): 872-882. |
| [2] |
张艺山, 国九英, 张明玉, 等. 提高逆时偏移成像效果的若干关键处理技术[J]. 石油地球物理勘探, 2020, 55(4): 774-781. ZHANG Yishan, GUO Jiuying, ZHANG Mingyu, et al. Research on seismic processing technologies for im - proving RTM imaging[J]. Oil Geophysical Prospecting, 2020, 55(4): 774-781. |
| [3] |
SONG C, ALKHALIFAH Y L T. A sequential inversion with outer iterations for the velocity and the intrinsic attenuation using an efficient wavefield inversion[J]. Geophysics, 2020, 85(6): 1-62. |
| [4] |
薛东川, 王尚旭. 波动方程有限元叠前逆时偏移[J]. 石油地球物理勘探, 2008, 43(1): 17-21. XUE Dongchuan, WANG Shangxu. Wave-equation finite - element prestack reverse - time migration[J]. Oil Geophysical Prospecting, 2008, 43(1): 17-21. |
| [5] |
DABLAIN M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. |
| [6] |
FEI T, LARNER K. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport[J]. Geophysics, 1995, 60(6): 1830-1842. |
| [7] |
YANG D H, TENG J W, ZHANG Z J, et al. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media[J]. Bulletin of the Seismological Society of America, 2003, 93(2): 882-890. |
| [8] |
YANG D H, PENG J M, LU M, et al. Optimal nearly analytic discrete approximation to the scalar wave equation[J]. Bulletin of the Seismological Society of America, 2006, 96(3): 1114-1130. |
| [9] |
YANG D H, TONG P, DENG X Y. A central difference method with low numerical dispersion for solving the scalar wave equation[J]. Geophysical Prospecting, 2012, 60(5): 885-905. |
| [10] |
LI J S, YANG D H, LIU F Q. An efficient reverse-time migration method using the local nearly analytic discrete operator[J]. Geophysics, 2013, 78(1): S15-S23. |
| [11] |
LI J S, FEHLER M, YANG D H, et al. 3D weak-dispersion reverse time migration using a stereo-modeling operator[J]. Geophysics, 2015, 80(1): S19-S30. |
| [12] |
冯康, 秦孟兆. 哈密尔顿系统的辛几何算法[M]. 浙江杭州: 浙江科技出版社, 2003. FENG Kang, QIN Mengzhao. Symplectic Geometric Algorithms for Hamiltonian Systems[M]. Hangzhou, Zhejiang: Zhejiang Science and Technology Publishing House, 2003. |
| [13] |
FENG K, QIN M Z. Symplectic Geometric Algorithms for Hamiltonian Systems[M]. Heidelberg: Springer Berlin Press, 2010: 165-186.
|
| [14] |
QIN M Z, ZHANG M Q. Multi-stage symplectic schemes of two kinds of Hamiltonian systems for wave equations[J]. Computers & Mathematics with Applications, 1990, 19(10): 51-62. |
| [15] |
LI X F, LI Y Q, ZHANG M G, et al. Scalar seismic-wave equation modeling by a multisymplectic discrete singular convolution differentiator method[J]. Bulletin of the Seismological Society of America, 2011, 101(4): 1710-1718. |
| [16] |
马啸, 杨顶辉, 张锦华. 求解声波方程的辛可分Runge-Kutta方法[J]. 地球物理学报, 2010, 53(8): 1993-2003. MA Xiao, YANG Dinghui, ZHANG Jinhua. Symplectic partitioned Runge-Kutta method for solving the acoustic wave equation[J]. Chinese Journal of Geophysics, 2010, 53(8): 1993-2003. |
| [17] |
王美霞. 双相及黏弹性介质中波传播方程的保辛算法及其波场模拟[D]. 北京: 清华大学, 2012. WANG Meixia. Symplectic Stereomodelling Method for Wave Equations in Two - phase and Viscoelastic Media and Its Numerical Simulations[D]. Tsinghua University, Beijing, 2012. |
| [18] |
YANG D H, WANG M X, MA X. Symplectic stereomodelling method for solving elastic wave equations in porous media[J]. Geophysical Journal International, 2013, 196(1): 560-579. |
| [19] |
YAN H Y, LIU Y. Visco-acoustic prestack reversetime migration based on the time - space domain adaptive high-order finite difference method[J]. Geophysical Prospecting, 2013, 61(5): 941-954. |
| [20] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5729-5791. |
| [21] |
孙耿. 波动方程的一类显式辛格式[J]. 计算数学, 1997, 19(1): 1-10. SUN Geng. A class of explicitly symplectic schemes for wave equations[J]. Mathematica Numerica Sinica, 1997, 19(1): 1-10. |
| [22] |
MOCZO P, KRISTEK J, HALADA L. 3D fourthorder staggered-grid finite-difference schemes: Stability and grid dispersion[J]. Bulletin of the Seismological Society of America, 2000, 90(3): 587-603. |
| [23] |
CARCIONE J M, KOSLOFF D, KOSLOFF R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 90(3): 393-401. |
| [24] |
LI Y, MATAR O B. Convolutional perfectly matched layer for elastic second-order wave equation[J]. Journal of the Acoustical Society of America, 2010, 127(3): 1318-1327. |
| [25] |
焦峻峰, 赵爱国, 廉西猛, 等. 基于照明补偿的变"子波"模拟成像方法[J]. 石油地球物理勘探, 2023, 58(4): 883-892. JIAO Junfeng, ZHAO Aiguo, LIAN Ximeng, et al. Variable"wavelet"simulated imaging method based on illumination compensation[J]. Oil Geophysical Prospecting, 2023, 58(4): 883-892. |



 张向佳, 吉林省长春市朝阳区西民主大街938号吉林大学地球探测科学与技术学院,130026。Email:
张向佳, 吉林省长春市朝阳区西民主大街938号吉林大学地球探测科学与技术学院,130026。Email: