2. 崂山实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266237;
3. 南方科技大学地球与空间科学系, 广东深圳 518055
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266237, China;
3. Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China
面波在早期地震勘探中被视为一种强干扰波,一般具有低速、高能量的特点,陆地勘探中的常见面波类型有瑞利波和勒夫波。随着地震勘探技术的发展,研究人员发现面波在层状介质中具有很强的频散特性,因此提出了一种新的近地表勘探方法——面波勘探,其基本思想是利用面波的频散特征勘查地质结构[1-2]。面波勘探中的一个重要研究领域是面波的正演模拟,尤其是横向各向同性(TI)介质中的面波模拟[3-5]。
一直以来,有限差分法是研究体波正演模拟的重要手段,现也被应用到面波的模拟研究中[6]。相比体波波场的正演模拟,面波波场的正演模拟对自由表面有更严格的要求。自由表面的实现直接影响模拟波场的精度和准确性[7-8]。
目前,基于标准交错网格(Standard Staggered Grid, SSG)的有限差分法在面波正演模拟中应用最广泛。Mittet[9]实现了基于弹性波交错网格有限差分法的瑞利波波场模拟,并分析了其准确性和精度;Bohlen[10]通过对比实验,给出了SSG方法下水平界面瑞利波模拟压制数值频散的频散准则;秦臻等[11]实现了高精度的有限差分瑞利波模拟并分析了正演结果的频散特征;Zeng等[12]将多轴完美匹配层技术(M-PML)应用到瑞利波数值模拟,解决了传统PML技术在高泊松比介质中不稳定的问题;邵广周等[13]基于波场模拟方法分析了瑞利波的频散曲线及多模式能量分布;杜兴忠等[14]利用GPU并行编程架构实现了基于MC-PML的二维瑞利波正演模拟。
当介质性质变化剧烈或地表起伏较大时,SSG有限差分法的稳定性和精度均较差,且需要内插介质参数影响模拟效果。对此,Saenger等[15]提出一种稳定性更好且更适用于复杂介质情况的旋转交错网格(Rotated Staggered Grid, RSG)有限差分法。Saenger等[16]又将RSG有限差分法应用到各向异性介质,证明了其在各向异性介质中进行地震波波场模拟的优势。Bohlen[10]实现了基于RSG的瑞利波波场模拟,并与传统交错网格有限差分法的瑞利波波场模拟结果对比,认为二者在水平界面的模拟精度相当,在倾斜界面的RSG有限差分法的稳定性和精度更高。但是,Bohlen仅定性对比了波形,没有从多方面定量对比两种方法的模拟效果。
近年来,许多学者将RSG差分方法应用到各向异性介质尤其是TI介质的正演模拟研究,取得了相当不错的效果[17-18]。在基于SSG的面波模拟中,瑞利波和勒夫波模拟一般分别进行P-SV波和SH波方程模拟。随着面波勘探方法的发展,单一的瑞利波和勒夫波方法已经不能满足勘探需求,研究人员开始发展联合反演方法[19]和全波形反演方法[20-21]。此外各向异性介质中的面波波场研究也开始被研究人员所重视[22]。
本文基于TI介质一阶速度—应力二维三分量波动方程将P-SV波方程和SH波方程联合,利用RSG有限差分法进行二维三分量波动方程模拟,实现瑞利波和勒夫波的同步模拟。并从波前快照、波形曲线和频散曲线三个方面定性和定量地对比RSG和SSG有限差分法在二维各向同性介质均匀半空间中面波模拟的效果和精度。通过分析三种典型层状介质中RSG有限差分法模拟面波地震记录对应的频散曲线与理论频散曲线的吻合程度,以验证文中方法。进一步将基于RSG的面波模拟方法推广到TI介质,实现VTI、HTI和TTI介质的二维三分量面波模拟,并分析TI介质中的面波波形特征、频散曲线特征和地震记录特征,同时进行两层速度递增的TTI介质模型的二维三分量面波模拟。
1 二维三分量速度—应力波动方程TI介质的二维三分量速度—应力波动方程为[17]
| $ \left\{\begin{array}{l}\frac{\partial {v}_{x}}{\partial t}=\frac{1}{\rho }\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xz}}{\partial z}\right)\\ \frac{\partial {v}_{y}}{\partial t}=\frac{1}{\rho }\left(\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial z}\right)\\ \frac{\partial {v}_{z}}{\partial t}=\frac{1}{\rho }\left(\frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{zz}}{\partial z}\right)\\ \frac{\partial {\tau }_{xx}}{\partial t}={C}_{11}\frac{\partial {v}_{x}}{\partial x}+{C}_{16}\frac{\partial {v}_{y}}{\partial x}+{C}_{15}\left(\frac{\partial {v}_{z}}{\partial x}+\frac{\partial {v}_{x}}{\partial z}\right)+{C}_{14}\frac{\partial {v}_{y}}{\partial z}+{C}_{13}\frac{\partial {v}_{z}}{\partial z}\\ \frac{\partial {\tau }_{zz}}{\partial t}={C}_{13}\frac{\partial {v}_{x}}{\partial x}+{C}_{36}\frac{\partial {v}_{y}}{\partial x}+{C}_{35}\left(\frac{\partial {v}_{z}}{\partial x}+\frac{\partial {v}_{x}}{\partial z}\right)+{C}_{34}\frac{\partial {v}_{y}}{\partial z}+{C}_{33}\frac{\partial {v}_{z}}{\partial z}\\ \frac{\partial {\tau }_{yz}}{\partial t}={C}_{14}\frac{\partial {v}_{x}}{\partial x}+{C}_{46}\frac{\partial {v}_{y}}{\partial x}+{C}_{45}\left(\frac{\partial {v}_{z}}{\partial x}+\frac{\partial {v}_{x}}{\partial z}\right)+{C}_{44}\frac{\partial {v}_{y}}{\partial z}+{C}_{34}\frac{\partial {v}_{z}}{\partial z}\\ \frac{\partial {\tau }_{xz}}{\partial t}={C}_{15}\frac{\partial {v}_{x}}{\partial x}+{C}_{56}\frac{\partial {v}_{y}}{\partial x}+{C}_{55}\left(\frac{\partial {v}_{z}}{\partial x}+\frac{\partial {v}_{x}}{\partial z}\right)+{C}_{45}\frac{\partial {v}_{y}}{\partial z}+{C}_{35}\frac{\partial {v}_{z}}{\partial z}\\ \frac{\partial {\tau }_{yx}}{\partial t}={C}_{16}\frac{\partial {v}_{x}}{\partial x}+{C}_{66}\frac{\partial {v}_{y}}{\partial x}+{C}_{56}\left(\frac{\partial {v}_{z}}{\partial x}+\frac{\partial {v}_{x}}{\partial z}\right)+{C}_{46}\frac{\partial {v}_{y}}{\partial z}+{C}_{36}\frac{\partial {v}_{z}}{\partial z}\end{array}\right. $ | (1) |
式中:vk(k=x, y, z)为不同方向的振动速度分量;
当介质为各向同性时,式(1)中的弹性参数组成的弹性参数矩阵为
| $ \left[\begin{array}{cccccc}{C}_{11}& {C}_{12}& {C}_{13}& {C}_{14}& {C}_{15}& {C}_{16}\\ {C}_{21}& {C}_{22}& {C}_{23}& {C}_{24}& {C}_{25}& {C}_{26}\\ {C}_{31}& {C}_{32}& {C}_{33}& {C}_{34}& {C}_{35}& {C}_{36}\\ {C}_{41}& {C}_{42}& {C}_{43}& {C}_{44}& {C}_{45}& {C}_{46}\\ {C}_{51}& {C}_{52}& {C}_{53}& {C}_{54}& {C}_{55}& {C}_{56}\\ {C}_{61}& {C}_{62}& {C}_{63}& {C}_{64}& {C}_{65}& {C}_{66}\end{array}\right]=\left[\begin{array}{cccccc}\rho {V}_{\mathrm{P}}^{2}& \rho \left({V}_{\mathrm{P}}^{2}-2{V}_{\mathrm{S}}^{2}\right)& \rho \left({V}_{\mathrm{P}}^{2}-2{V}_{\mathrm{S}}^{2}\right)& 0& 0& 0\\ \rho \left({V}_{\mathrm{P}}^{2}-2{V}_{\mathrm{S}}^{2}\right)& \rho {V}_{\mathrm{P}}^{2}& \rho \left({V}_{\mathrm{P}}^{2}-2{V}_{\mathrm{S}}^{2}\right)& 0& 0& 0\\ \rho \left({V}_{\mathrm{P}}^{2}-2{V}_{\mathrm{S}}^{2}\right)& \rho \left({V}_{\mathrm{P}}^{2}-2{V}_{\mathrm{S}}^{2}\right)& \rho {V}_{\mathrm{P}}^{2}& 0& 0& 0\\ 0& 0& 0& \rho {V}_{\mathrm{S}}^{2}& 0& 0\\ 0& 0& 0& 0& \rho {V}_{\mathrm{S}}^{2}& 0\\ 0& 0& 0& 0& 0& \rho {V}_{\mathrm{S}}^{2}\end{array}\right] $ | (2) |
式中VP、VS分别为纵波速度和横波速度。
为证明基于式(1)实现P-SV波[11]和SH波[21]方程的联合是可行的,将式(2)代入式(1)可得各向同性介质P-SV波、SH波的一阶速度—应力方程
| $ \left\{\begin{array}{l}\frac{\partial {v}_{x}}{\partial t}=\frac{1}{\rho }\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xz}}{\partial z}\right)\\ \frac{\partial {v}_{z}}{\partial t}=\frac{1}{\rho }\left(\frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{zz}}{\partial z}\right)\\ \frac{\partial {\tau }_{xx}}{\partial t}=\rho \left[{V}_{\mathrm{p}}^{2}\frac{\partial {v}_{x}}{\partial x}+\left({V}_{\mathrm{p}}^{2}-2{V}_{\mathrm{S}}^{2}\right)\frac{\partial {v}_{z}}{\partial z}\right]\\ \frac{\partial {\tau }_{zz}}{\partial t}=\rho \left[\left({V}_{\mathrm{p}}^{2}-2{V}_{\mathrm{S}}^{2}\right)\frac{\partial {v}_{x}}{\partial x}+{V}_{\mathrm{p}}^{2}\frac{\partial {v}_{z}}{\partial z}\right]\\ \frac{\partial {\tau }_{xz}}{\partial t}=\rho {V}_{\mathrm{S}}^{2}\left(\frac{\partial {v}_{z}}{\partial x}+\frac{\partial {v}_{x}}{\partial z}\right)\end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l}\rho \frac{\partial {v}_{y}}{\partial t}=\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial z}\\ \frac{\partial {\tau }_{yx}}{\partial t}=\rho {V}_{\mathrm{S}}^{2}\frac{\partial {v}_{y}}{\partial x}\\ \frac{\partial {\tau }_{yz}}{\partial t}=\rho {V}_{\mathrm{S}}^{2}\frac{\partial {v}_{y}}{\partial z}\end{array}\right. $ | (4) |
式(1)包含P-SV波和SH波,式(3)、式(4)等价式(1),所以通过数值求解式(1)能够实现包含瑞利波和勒夫波的波场模拟。
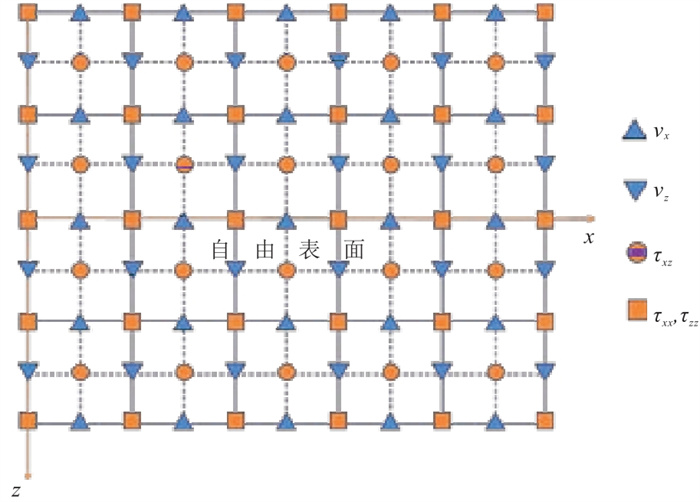
2 RSG有限差分法 2.1 RSG差分格式相比于SSG速度分量和应力分量都在整网格节点(图 1),RSG进行了网格旋转,将速度分量定义在整网格节点,应力分量定义在网格中心点(图 2),并将密度和弹性参数定义在计算所需的网格点,避免了计算过程中弹性参数和密度的插值,提高了计算精度[15]。
|
图 1 SSG示意图 |

|
图 2 RSG示意图 |
RSG方法设计了两套坐标系计算微分,其一是对角线方向的
| $ \left\{\begin{array}{l}\frac{\partial }{\partial x}=\frac{\sqrt{\mathrm{\Delta }{x}^{2}+\mathrm{\Delta }{z}^{2}}}{2\mathrm{\Delta }x}\left(\frac{\partial }{\tilde{z}}+\frac{\partial }{\tilde{x}}\right)\\ \frac{\partial }{\partial z}=\frac{\sqrt{\mathrm{\Delta }{x}^{2}+\mathrm{\Delta }{z}^{2}}}{2\mathrm{\Delta }z}\left(\frac{\partial }{\tilde{z}}-\frac{\partial }{\tilde{x}}\right)\end{array}\right. $ | (5) |
式中
Saenger等[15]基于冯诺伊曼方法推导了时间二阶、空间2M阶RSG差分法的稳定性条件,并通过下式指出其在二维和三维情况下稳定性一致
| $ \begin{array}{c}\frac{\mathrm{\Delta }t{V}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }h}\sum\limits_{m=1}^{M}\left|{C}_{m}^{M}\right|\le 1\end{array} $ | (6) |
式中:
对应时间二阶、空间2M阶精度的SSG差分法的稳定性条件为
| $ \begin{array}{c}\frac{\mathrm{\Delta }t{V}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }h}\sum\limits_{m=1}^{M}\left|{C}_{m}^{M}\right|\le \end{array}\frac{1}{\sqrt{D}} $ | (7) |
式中D为空间维度。
对比式(6)和式(7)可以发现,理论上RSG方法比SSG方法的稳定性更强。
2.3 吸收边界传统PML(Perfectly Matched Layer)方法在求解区域外镶嵌厚度有限的吸收衰减层时,将传播到镶嵌层中的波场按传播方向分为
| $ \left\{\begin{array}{l}{v}_{x}={v}_{x}^{\Vert }+{v}_{x}^{\perp }\\ \frac{\partial {v}_{x}^{\perp }}{\partial t}+{d}_{x}{v}_{x}^{\perp }=\frac{1}{\rho }\frac{\partial {\tau }_{xx}}{\partial x}\\ \frac{\partial {v}_{x}^{\Vert }}{\partial t}+{d}_{z}{v}_{x}^{\Vert }=\frac{1}{\rho }\frac{\partial {\tau }_{xz}}{\partial z}\end{array}\right. $ | (8) |
式中:
| $ \left\{\begin{array}{l}{d}_{x}\left({h}_{x}\right)=\mathrm{l}\mathrm{g}\frac{1}{R}\frac{2{V}_{\mathrm{P},\mathrm{m}\mathrm{a}\mathrm{x}}}{L}{\left(\frac{{h}_{x}}{L}\right)}^{4}\\ {d}_{z}\left({h}_{z}\right)=\mathrm{l}\mathrm{g}\frac{1}{R}\frac{2{V}_{\mathrm{P},\mathrm{m}\mathrm{a}\mathrm{x}}}{L}{\left(\frac{{h}_{z}}{L}\right)}^{4}\end{array}\right. $ | (9) |
式中:
当地震波场变复杂时,PML边界的吸收效果会变差甚至不稳定。为解决这一问题,Meza等[24]提出了一种多轴PML(M-PML)方法,分析了其在各向同性介质复杂波场和各向异性介质波场中的适用性和稳定性,并给出了数学意义上的稳定性分析结果,证明了M-PML边界的适用性;Zeng等[12]验证了不同泊松比介质情况下M-PML吸收边界的稳定性和效果;刘东洋等[25]将M-PML应用到TTI介质的正演模拟,取得了良好的效果。M-PML是PML方法的进一步发展,它在PML基础上对镶嵌层内分裂的波场进行
| $ \left\{\begin{array}{l}x:{d}_{x}={d}_{x}\left({h}_{x}\right),{d}_{z}={p}^{(z/x)}{d}_{x}\left({h}_{x}\right)\\ z:{d}_{x}={p}^{(x/z)}{d}_{z}\left({h}_{z}\right),{d}_{z}={d}_{z}\left({h}_{z}\right)\end{array}\right. $ | (10) |
式中:
面波正演模拟研究中,自由表面边界条件会直接影响模拟波场的精度和准确性。Aki等[8]给出了自由表面应力条件的理论表达式,二维自由表面边界条件的数学表达式为
| $ \left\{\begin{array}{l}{\tau }_{zz}=0\\ {\tau }_{xz}=0\\ {\tau }_{yz}=0\end{array}\right. $ | (11) |
基于上式发展了诸多自由表面处理方法,其中有直接对自由表面应力进行处理的显式表达法,如应力镜像法(Stress Image Method, SIM)等。还有通过调整自由表面物性参数间接实现自由表面的隐式表达法,文中所使用的方法就属于这一类。Mittet[9]在前人研究的基础上基于气—固界面物性变化给出了一种调整自由表面物性参数的方法,称为横向各向同性介质替换(MS)法,其二维表达式为
| $ \left\{\begin{array}{l}{\tau }_{zz}=0\\ \rho =0.5{\rho }_{{}_{{}_{0}}}\\ \lambda =0\\ \mu =0.5{\mu }_{{}_{0}}\end{array}\right. $ | (12) |
式中:
使用RSG差分法能更简单地实现MS法相应的自由表面条件。由于应力分量定义在同一网格点,自由表面位于速度分量采样点所在的整网格点,故只需要对自由表面的密度进行处理,而不需要调整其他物性参数,自由表面的密度满足[10]
| $ \rho =0.5{\rho }_{0} $ | (13) |
对于自由表面上方的波场分量,直接赋值为零。波场初始化后,从自由表面开始更新波场,隐式满足了自由表面的应力条件。后文通过数值测试证明了这一处理方式的正确性。
3 数值模拟分析设计各向同性的均匀半空间模型和层状介质模型验证文中面波模拟方法,然后将模拟方法推广到TI介质,并分析TI介质的面波特征。正演模拟使用的震源函数为雷克子波,主频为40 Hz,延时为30 ms。
3.1 各向同性介质均匀半空间模型建立各向同性介质均匀半空间模型(模型1),弹性参数见表 1。针对该模型使用文中所提方法和SSG方法进行面波模拟。使用SSG方法模拟面波时,针对自由表面分别采用SIM、声学—弹性边界近似(Acoustic-elastic Boudary Approach, AEA)法,从波场快照、波形曲线和频散曲线三个角度对比分析三种方法面波模拟的精度。
|
|
表 1 模型1参数 |
理论上可以通过同时在式(1)中的
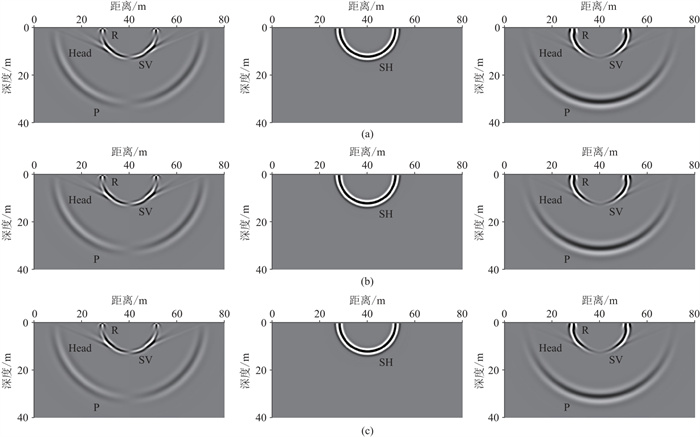
|
图 3 模型1不同方法模拟的波场快照(t=0.15 s) (a)SSG-SIM;(b)SSG-AEA;(c)RSG。从左至右依次为vx、vy、vz。 |
面波模拟精度与网格剖分的精细程度有重要关系,引入参数ppw(points per minimum wavelength,面波最小波长
| $ \begin{array}{c}\mathsf{ppw}=\frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\mathrm{\Delta }h}=\frac{{V}_{\mathrm{S},\mathrm{m}\mathrm{i}\mathrm{n}}^{}}{2{f}_{0}\mathrm{\Delta }h}\end{array} $ | (14) |
式中:
|
|
表 2 模型1网格剖分参数 |
以ppw=10,RSG为例,地震记录如图 4所示,可见低速强能量的瑞利波和体波,体波相比瑞利波能量很弱,在地震记录上波形不明显,由
| $ E=\frac{\sum\limits_{l={l}_{\mathrm{s}}}^{{l}_{\mathrm{e}}}\left[f\right(l\mathrm{\Delta }t)-q{\left(l\mathrm{\Delta }t\right)]}^{2}}{\sum\limits_{l={l}_{\mathrm{s}}}^{l\mathrm{e}}{q}^{2}\left(l\mathrm{\Delta }t\right)} $ | (15) |

|
图 4 模型1炮集记录
(a) |
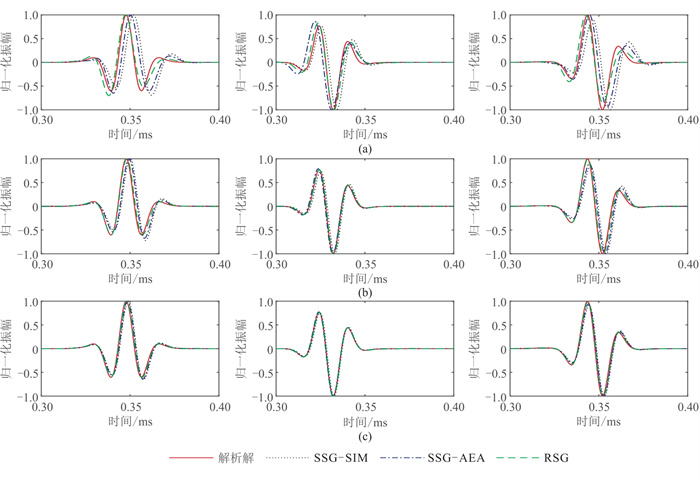
|
图 5 不同网格剖分参数下三种边界处理方法所得单道面波记录对比 (a)ppw=10;(b)ppw=25;(c)ppw=50。从左至右依次为vx、vy、vz。 |
式中:f为数值解;q为解析解;
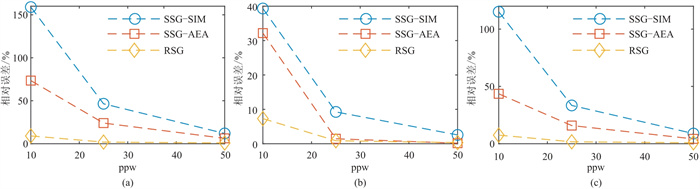
|
图 6 三种边界处理方法对应波形曲线L2范数误差随ppw的变化
(a) |
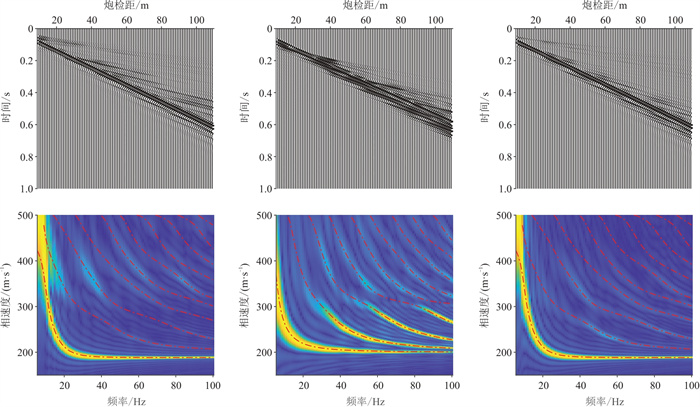
在面波相关研究中,除了波场和波形特征,频散特征也是研究人员关注的重点,且频散特征是对地震记录的综合反应。通过高分辨率线性拉东变换方法(LRT)提取图 5中对应模拟地震记录的频散能量,再提取地震记录对应的频散曲线,并与快速矢量传递算法正演所得的理论频散曲线对比,计算二者的L2范数误差(图 7)。由图可见,RSG方法模拟所得地震记录对应的频散能量分布(图 7a左、图 7b左、图 7c左)与理论频散曲线的拟合较好,可见三种方法在不同的网格剖分精度下频散曲线的误差都很小,且RSG方法的误差最小。
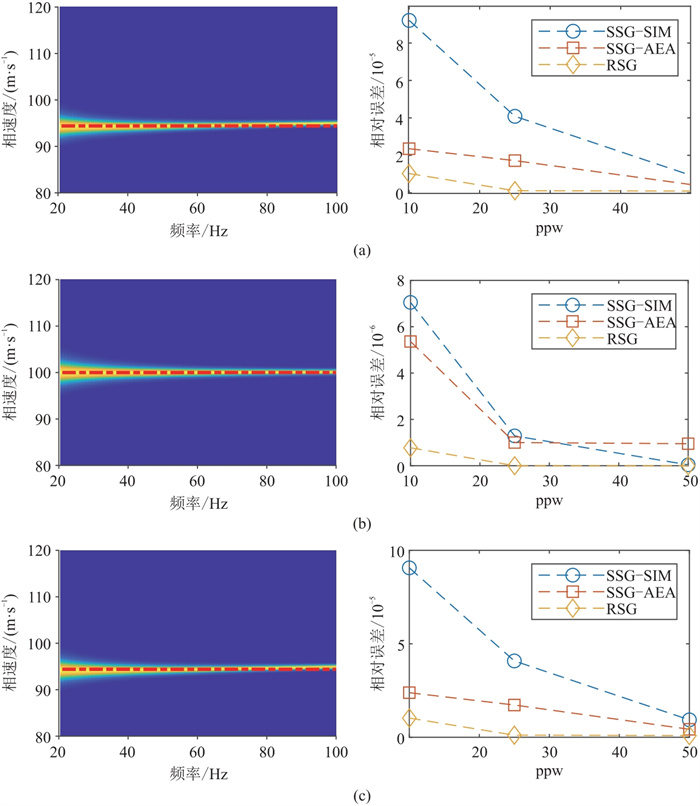
|
图 7 RSG方法频散图(左)和三种边界处理方法对应频散曲线L2范数误差随ppw的变化(右) (a) |
各向同性介质均匀半空间模型中波场快照、波形曲线和频散曲线的定性—定量对比,已经证明RSG方法的模拟精度和稳定性明显优于SSG-AEA和SSG-SIM方法。为了进一步验证RSG方法,设计了速度递增、含低速软夹层和含高速硬夹层三种典型层状模型,模型参数分别如表 3~表 5所示。震源加载于自由表面的
|
|
表 3 速度递增型层状模型(模型2)参数 |
|
|
表 4 含低速软夹层层状模型(模型3)参数 |
|
|
表 5 含高速硬夹层模型(模型4)参数 |
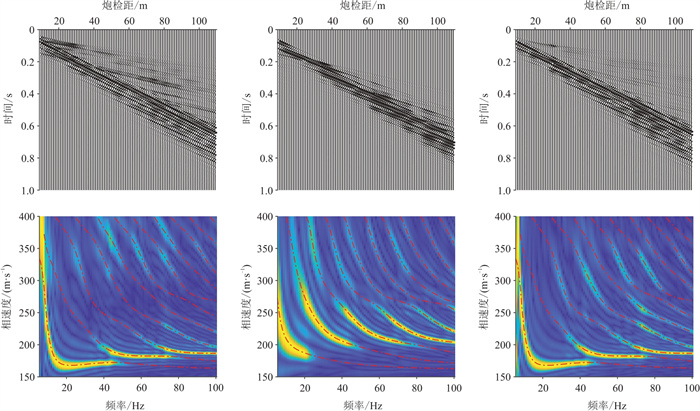
|
图 9 模型3模拟地震记录(上)及其频散能量图(下) |
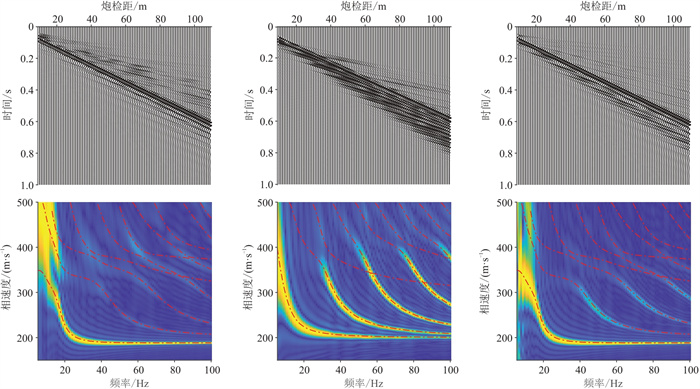
|
图 10 模型4模拟地震记录(上)及其频散能量图(下) |
各向同性介质模型的测试结果,证明了RSG方法在面波模拟中的适用性。本文将其推广到TI介质,设计了VTI、HTI和TTI介质均匀半空间模型,其模型参数如表 6所示,表中
|
|
表 6 均匀半空间TI介质模型参数 |
用RSG方法进行面波模拟,将震源分别加载在自由表面的
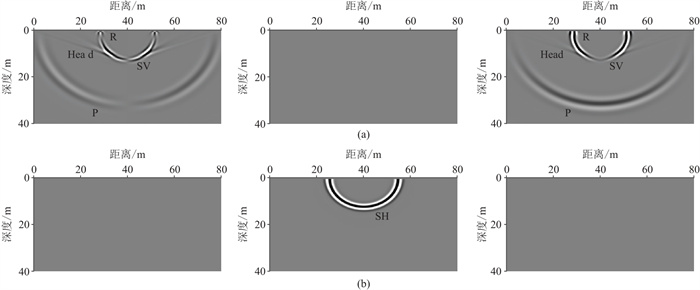
|
图 11 模型5波场快照(t=0.15 s) (a)震源加载于 |

|
图 12 模型6波场快照(t=0.15 s) (a)震源加载于 |
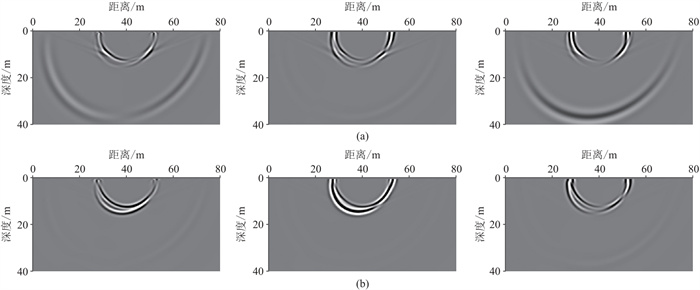
|
图 13 模型7波场快照(t=0.15 s) (a)震源加载于 |
在自由表面上设置接收点,最小炮检距为10 m,道间距为1 m,接收道数为70,记录长度为1 s,得到模型7的三分量炮集地震记录,并提取各自对应的频散能量(图 14), 可见由于介质各向异性,导致地震记录复杂、横波分裂现象明显、横波能量更强,三分量的频散曲线相近,
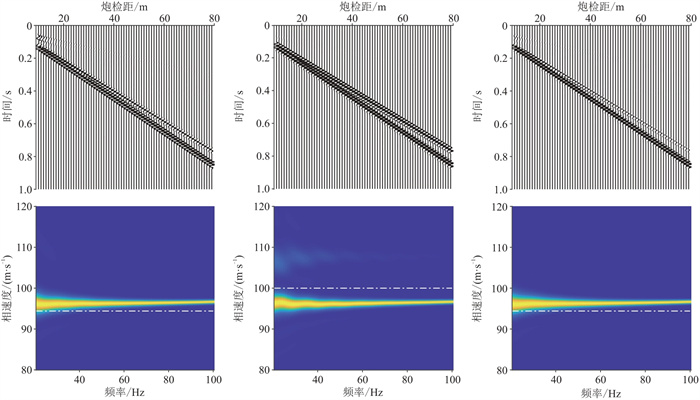
|
图 14 模型7模拟地震记录(上)及其频散能量图(下) 从左至右分别为 |
为进一步探究各向异性对频散特征的影响,设计了三个模型组,分别控制
|
|
表 7 模型组1: |
|
|
表 8 模型组2: |
|
|
表 9 模型组3: |
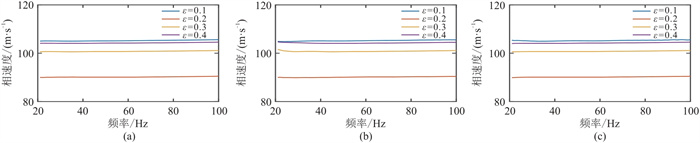
|
图 15 模型组1模拟记录对应的频散曲线对比
(a) |
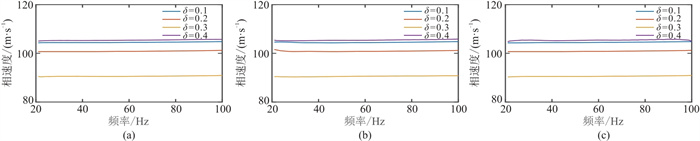
|
图 16 模型组2模拟记录对应的频散曲线对比
(a) |
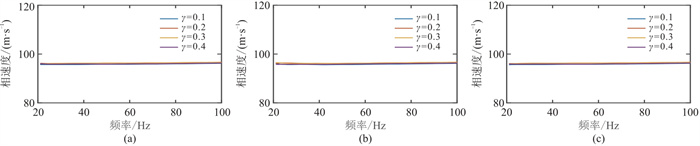
|
图 17 模型组3模拟记录对应的频散曲线对比
(a) |
为进一步研究TI介质中面波的特性,设计了一个两层的速度递增模型,其模型参数如表 10所示。将震源加载于自由表面的
|
|
表 10 模型8:两层速度递增模型参数 |
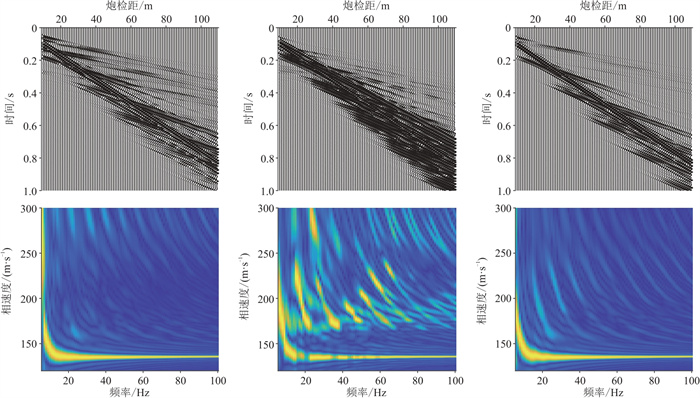
|
图 18 模型8模拟地震记录(上)及其频散能量图(下)
从左至右分别为 |
由频散能量图(图 18下)可见层状介质中存在多阶面波,基阶面波的能量在其中占据主导地位,
本文基于TI介质一阶速度—应力二维三分量波动方程,通过旋转交错网格有限差分法结合M-PML边界法,并联合P-SV波方程和SH波方程,实现了包含瑞利波模拟和勒夫波模拟的二维三分量面波模拟。在证明文中模拟方案有效的基础上,将方案应用到TI介质二维三分量面波模拟,通过波场快照、地震记录和频散能量图分析TI介质中的面波特征和各向异性参数对面波频散特征的影响。结果表明:①TI介质面波波场相比各向同性介质变得复杂,普遍存在各向异性导致的极化现象;②VTI介质中面波波场特征与各向同性介质中面波波场特征相似,其中P-SV波和SH波的传播过程互不干扰;③HTI、TTI介质中P-SV波和SH波的传播过程相互影响,面波波场更复杂且与各向同性介质存在较大差异;④描述TI介质各向异性强度的三个Thomsen参数中,与纵波各向异性有关的
本文提出的二维三分量面波模拟方案为各向同性介质中瑞利波和勒夫波的模拟提供了精度更高、稳定条件更宽松、效率更高的模拟方法,实现了用同一个方程模拟瑞利波和勒夫波,为二维全波场地震波模拟甚至是全波场反演提供了重要参考,对TI介质中面波三分量波场的研究更接近真实面波勘探情况,对进一步认识各向异性介质中面波的传播特征具有重要意义。
| [1] |
XIA J, MILLER R D, PARK C B. Estimation of near-surface shear-wave velocity by inversion of Raleigh waves[J]. Geophysics, 1999, 64(3): 659-992. |
| [2] |
XU Yixian, LUO Yinhe, CHEN Chao, et al. High-frequency rayleigh-Wave Method[J]. Journal of Earth Science, 2009, 20(3): 563-579. |
| [3] |
YANG L, YAN H Y, LIU H. Optimal rotated staggered-grid finite-difference schemes for elastic wave modeling in TTI media[J]. Journal of Applied Geophysics, 2015, 122: 40-52. |
| [4] |
THOMSEN L, ANDERSON L D. Weak elastic anisotropy in global seismology[J]. Geological Society of America Special Papers, 2015, 514: 39-50. |
| [5] |
张建中, 安全, 于建明, 等. 倾斜层状TI介质反射波旅行时快速计算[J]. 石油地球物理勘探, 2022, 57(1): 111-117. ZHANG Jianzhong, AN Quan, YU Jianming, et al. Rapid calculation of reflected wave travel time in layered TI media with dipping interfaces[J]. Oil Geophysical Prospecting, 2022, 57(1): 111-117. |
| [6] |
宋先海. 瑞雷波勘探理论及其应用[M]. 北京: 中国水利水电出版社, 2010.
|
| [7] |
袁士川, 宋先海, 蔡伟, 等. 瑞雷波有限差分数值模拟中不同自由表面边界条件的对比[J]. 石油地球物理勘探, 2017, 52(6): 1156-1169. YUAN Shichuan, SONG Xianhai, CAI Wei, et al. Comparison of different free-surface boundary conditions for Rayleigh waves finite-difference modeling[J]. Oil Geophysical Prospecting, 2017, 52(6): 1156-1169. |
| [8] |
AKI K, RICHARDS P G. Quantitative Seismology: Theory and Methods[M]. Sansalito, CA: University Science Books, 2009.
|
| [9] |
MITTET, R. Free-surface boundary conditions for elastic staggered-grid modeling schemes[J]. Geophysics, 2002, 67(5): 1616-1623. |
| [10] |
BOHLEN T. Accuracy of heterogeneous staggered-grid finite-difference modeling of Rayleigh waves[J]. Geophysics, 2006, 71(4): T109-T115. |
| [11] |
秦臻, 张才, 郑晓东, 等. 高精度有限差分瑞雷面波模拟及频散特征提取[J]. 石油地球物理勘探, 2010, 45(1): 40-46. QIN Zhen, ZHANG Cai, ZHENG Xiaodong, et al. High precision finite difference Rayleigh wave simulation and frequency dispersion characteristics extraction[J]. Oil Geophysical Prospecting, 2010, 45(1): 40-46. |
| [12] |
ZENG C, XIA J, MILLER R D, et al. Application of the multiaxial perfectly matched layer(M-PML) to near-surface seismic modeling with Rayleigh waves[J]. Geophysics, 2011, 76(3): T43-T52. |
| [13] |
邵广周, 李庆春, 吴华. 基于波场数值模拟的瑞利波频散曲线特征及各模式能量分布[J]. 石油地球物理勘探, 2015, 50(2): 306-315. SHAO Guangzhou, LI Qingchun, WU Hua. Dispersion curves and mode energy distribution of Rayleigh wave based on wavefield numerical simulation[J]. Oil Geophysical Prospecting, 2015, 50(2): 306-315. |
| [14] |
杜兴忠, 黄金强, 胡昌荣, 等. 基于MC-PML的二维Rayleigh波正演模拟及频散特征分析[J]. 地球物理学进展, 2024, 39(2): 542-560. DU Xingzhong, HUANG Jinqiang, HU Changrong, et al. 2D Rayleigh wave modeling based on MC-PML and its dispersion characteristics analysis[J]. Progress in Geophysics, 2024, 39(2): 542-560. |
| [15] |
SAENGER E H, GOLD N, SHAPIRO S A. Modeling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 2000, 31(1): 77-92. |
| [16] |
SAENGER E H, BOHLEN T. Finite-difference mo-deling of viscoelastic and anisotropic wave propagation using the rotated staggered grid[J]. Geophysics, 2004, 69(2): 318-628. |
| [17] |
杜启振, 孙瑞艳, 张强. 组合边界条件下二维三分量TTI介质波场数值模拟[J]. 石油地球物理勘探, 2011, 46(2): 187-195. DU Qizhen, SUN Ruiyan, ZHANG Qiang. Numerical simulation of three-component elastic wavefield in 2D TTI media in the condition of the combined boundary[J]. Oil Geophysical Prospecting, 2011, 46(2): 187-195. |
| [18] |
赵明哲, 杨军, 张陆军, 等. 基于CUDA的高阶旋转交错网格有限差分法的弹性波正演模拟[J]. 地球物理学进展, 2022, 37(4): 1697-1703. ZHAO Mingzhe, YANG Jun, ZHANG Lujun, et al. Forward modeling of elastic wave based on CUDA finite difference method with high order rotating staggered grid[J]. Progress in Geophysics, 2022, 37(4): 1697-1703. |
| [19] |
夏江海, 高玲利, 潘雨迪, 等. 高频面波方法的若干新进展[J]. 地球物理学报, 2015, 58(8): 2591-2605. XIA Jianghai, GAO Lingli, PAN Yudi, et al. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2591-2605. |
| [20] |
GROOS, LISA, SCHAEFER, et al. Application of a complete workflow for 2D elastic full-waveform inversion to recorded shallow-seismic Rayleigh waves[J]. Geophysics, 2017, 82(2): R109-R117. |
| [21] |
CHEN R Y, TRAN K T. 2D Gauss-Newton full waveform inversion of SH-and Love-waves in the time domain[J]. Journal of Applied Geophysics, 2021, 191: 104363. |
| [22] |
袁士川. 粘弹性VTI介质瑞雷波有限差分模拟及其特性分析[D]. 湖北武汉: 中国地质大学, 2018.
|
| [23] |
王辉, 何兵寿, 邵祥奇. 一阶速度—胀缩—旋转弹性波方程交错网格数值模拟[J]. 石油地球物理勘探, 2022, 57(6): 1352-1361. WANG Hui, HE Bingshou, SHAO Xiangqi. Numerical simulation of first-order velocity-dilatation-rotation elastic wave equation with staggered grid[J]. Oil Geophysical Prospecting, 2022, 57(6): 1352-1361. |
| [24] |
MEZA F K C, Papageorgiou A S. A nonconvolutional, split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media: stability analysis[J]. Bulletin of the Seismological Society of America, 2008, 98(4): 1811-1836. |
| [25] |
刘东洋, 彭苏萍, 师素珍, 等. 基于Lebedev网格的TTI介质二维三分量正演模拟[J]. 石油地球物理勘探, 2018, 53(2): 288-296. LIU Dongyang, PENG Suping, SHI Suzhen, et al. 2D three-component seismic forward modeling in TTI media based on the Lebedev grid[J]. Oil Geophysical Prospecting, 2018, 53(2): 288-296. |
| [26] |
BERG P, IF F, NIELSEN P, et al. Analytical reference solutions, advanced seismic modeling[M]//Modeling the Earth for Oil Exploration. Pergamon Press, New York, 1994, 421-427.
|



 童思友, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email:
童思友, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email: