为了处理油气勘探中日益复杂的地下介质情况以及产生的新问题,新的偏移理论不断被提出,更先进的成像技术也相应发展并应用到各个领域,不仅提高了计算效率,成像精度也在不断提高。但是获取叠前深度偏移剖面时流程繁琐的根本问题依旧未能得到解决。为简化这一复杂流程、快速获得高精度偏移剖面,研究人员也做了很多工作:Fletcher等[1]首先提出了深度域等效子波的概念,利用等效子波完成了快速成像;周东勇等[2]在总结了已有的研究基础上推导了深度域等效子波的表达式,并基于这一理论完成了深度域合成地震记录;向晨等[3]、郝洪鉴等[4]相继完成了基于点扩散函数的深度域快速成像技术以及深度域反演;段伟国等[5]、张庆臣[6]及姚振岸等[7]分别完成了基于点扩散函数的迭代加权最小二乘反演、高精度逆时偏移和预条件黏声最小二乘偏移;岳玉波等[8]利用射线理论计算点扩散函数;袁江洋等[9]对深度域合成地震记录的精度问题进行了分析。
快速成像技术虽然在不断发展和完善,但是成像结果仍需考虑很多方面,成像理论也有待完善。Gelius等[10-11]提出广义散射层析方法,率先引入成像算子;Hamran等[12-13]也实现了基于局部平面波的散射层析成像;徐海等[14]系统分析了现有地震数据高分辨率处理方法的适用性及不足,探索了一种基于高频噪声定量约束函数的高分辨率处理方法,有效且保真地提高地震资料信噪比与分辨率;Lecomte等[15-18]分析了叠前深度偏移成像分辨率算子,提出用散射波数算子表征地震成像分辨率函数,并以此实现局部小区域的叠前深度地震记录直接模拟成像;吴涵等[19-20]提出了一种基于深度域广义卷积技术的叠前深度偏移地震记录直接模拟方法;焦峻峰等[21]对模拟成像方法进行了改善,考虑了地震子波在深度域中的空变。
在已有基础上,本文发展了一种基于粗网格的多算子叠前深度直接模拟成像方法,此方法对已知的速度模型先进行粗网格离散,构建粗成像算子,测试并选取最优插值方法对算子进行插值,使用插值后成像算子进行直接模拟成像,以提高计算效率。后续又在粗网格的基础上计算了多算子并进行模拟成像,使用多个算子控制模拟成像,得到更符合理论的成像结果,对观测系统的建立与优化有一定的指导意义。
1 模拟成像方法原理模拟叠前局部成像方法是一种卷积技术,不需要首先生成合成数据,然后进行偏移以计算储层模型的偏移地震响应。根据测量、激发子波、波模式和局部储层结构,快速获得模拟叠前偏移剖面。此方法源于对地震分辨率[12, 14-15]和地震成像新方法[16-18]进行的研究,最初是为了更好地理解偏移剖面而开发的。
研究此方法,就必须首先定义模拟叠前局部成像方法的关键参数,即散射波数向量
| $ \boldsymbol{K}(\omega ,{r}_{0},{r}_{\mathsf{s}},{r}_{\mathsf{g}})={\boldsymbol{k}}_{\mathsf{g}}(\omega ,{r}_{0},{r}_{\mathsf{g}})-{\boldsymbol{k}}_{\mathsf{s}}(\omega ,{r}_{\mathsf{s}},{r}_{0}) $ | (1) |

|
图 1 散射向量示意图 |
式中:
如果分别用算子的形式描述模型的正演过程和成像过程,则有
| $ \boldsymbol{U}(\omega ,{r}_{\mathsf{g}},{r}_{\mathsf{s}})=\boldsymbol{D}(\omega ,{r}_{\mathsf{g}},{r}_{\mathsf{s}})\boldsymbol{V}\left(r\right) $ | (2) |
式中:
引入成像算子
| $ \begin{array}{l}\boldsymbol{I}\left({r}^{\text{'}}\right)=\boldsymbol{T}\left({r}^{\text{'}}\right|\omega ,{r}_{\mathsf{g}},{r}_{\mathsf{s}}\left)\boldsymbol{U}\right(\omega ,{r}_{\mathsf{g}},{r}_{\mathsf{s}})\\ =\boldsymbol{T}\left({r}^{\text{'}}\right|\omega ,{r}_{\mathsf{g}},{r}_{\mathsf{s}}\left)\boldsymbol{D}\right(\omega ,{r}_{\mathsf{g}},{r}_{\mathsf{s}}\left)V\right(r)\\ =\boldsymbol{F}(\omega ,{r}_{\mathsf{g}},{r}_{\mathsf{s}})\boldsymbol{V}\left(r\right)\end{array} $ | (3) |
式中
| $ {\nabla }^{2}\boldsymbol{P}(r,t)=\frac{1}{{v}^{2}\left(r\right)}\frac{{\partial }^{2}\boldsymbol{P}(r,t)}{\partial {t}^{2}} $ | (4) |
式中:
| $ \boldsymbol{P}_{\mathsf{s}\mathsf{c}}({r}_{\mathsf{g}},{r}_{\mathsf{s}})=-{\int }_{\boldsymbol{\varOmega }}\boldsymbol{P}_{in}(r,{r}_{s})\boldsymbol{k}_{0}^{2}O\left(r\right)\boldsymbol{G}({r}_{\mathsf{g}},r)\mathsf{d}r $ | (5) |
式中:
对于非均匀且无衰减的背景场,使用动态射线追踪得到其格林函数
| $ \begin{array}{l}\stackrel{}{\widehat{\boldsymbol{O}}}={\int }_{\boldsymbol{\varOmega }}O\left(r\right)\iiint \frac{\boldsymbol{a}\left({r}_{\mathsf{g}},{r}_{\mathsf{s}},r\right)}{\boldsymbol{a}\left({r}_{\mathsf{g}},{r}_{\mathsf{s}},{r}^{\mathsf{\text{'}}}\right)}\boldsymbol{m}\left[\boldsymbol{a}\left({r}_{\mathsf{g}},{r}_{\mathsf{s}},{r}^{\mathsf{\text{'}}}\right)\right]\times \\ \mathsf{e}\mathsf{x}\mathsf{p}\left\{\mathsf{i}\omega \left[\boldsymbol{\tau }\right({r}_{g},{r}_{s},r)-\boldsymbol{\tau }({r}_{g},{r}_{s},r\mathsf{\text{'}}\left)\right]\right\}\mathsf{d}{r}_{\mathsf{g}}\mathsf{d}{r}_{\mathsf{s}}\mathsf{d}r\\ ={\int }_{\boldsymbol{\varOmega }}\boldsymbol{O}\left(r\right)\boldsymbol{F}(r,r\mathsf{\text{'}})\mathsf{d}r\end{array} $ | (6) |
式中
| $ \boldsymbol{\alpha }({r}_{\mathsf{g}},{r}_{\mathsf{s}},r)=-\frac{\gamma {\boldsymbol{k}}_{0}}{2}\sqrt[]{\frac{\mathsf{i}{\boldsymbol{k}}_{0}}{2\mathsf{\pi }}}\frac{1}{\sqrt[]{|r-{r}_{\mathsf{s}}|}\sqrt[]{|{r}_{\mathsf{g}}-r|}} $ | (7) |
| $ \boldsymbol{\tau }({r}_{\mathsf{g}},{r}_{\mathsf{s}},r)=\frac{|r-{r}_{\mathsf{s}}|+|{r}_{\mathsf{g}}-r|}{{v}_{0}} $ | (8) |
式中
结合Beylkin等[23-24]提出的理论,在成像点的邻域内将振幅项和相位项Talor展开,结合程函方程并使点扩散算子趋近于
| $ \boldsymbol{M}(r,r\mathsf{\text{'}})=\iint \boldsymbol{S}\left(\omega \right)\mathsf{e}\mathsf{x}\mathsf{p}\left[\mathsf{i}\boldsymbol{K}\right(r-r\mathsf{\text{'}}\left)\right]{\mathsf{d}}^{2}\boldsymbol{K} $ | (9) |
式中:
此处的成像算子实质上就是由地下速度模型及观测系统共同构建的滤波器,模拟成像结果则是地下真实反射率经过此滤波器得到的理论成像结果。
多算子协同模拟成像则是在模拟成像的基础上,设置合适的偏移成像窗,在相同的速度模型和观测系统的前提下构造多个控制成像的点扩散算子
| $ \left[\begin{array}{c}{I}_{1}\\ {I}_{2}\\ ⋮\\ {I}_{n}\end{array}\right]=\left[\begin{array}{c}{F}_{1}\\ {F}_{2}\\ ⋮\\ {F}_{n}\end{array}\right]\left[\begin{array}{cccc}{R}_{1}& {R}_{2}& \cdots & {R}_{n}\end{array}\right] $ | (10) |
式中R为反射系数。
2 算子插值与模拟成像模型试算 2.1 不同插值方法求取散射点处的散射波数向量需要预先求取散射点处的射线路径,本文选用算法稳定的多模板快速行进法计算走时,再使用最短路径法求取射线路径信息[25-28]。
为提高计算效率,先对模型进行粗网格离散,建立粗点扩散算子并进行不同方法插值测试。此方法区别于常见的对地震射线追踪的走时线性插值[29-30],插值域也从空间域变为波数域。
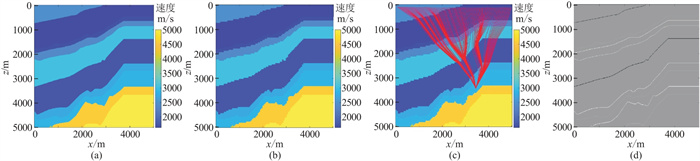
2.2 简单模型模拟成像先使用一个501×501大小的网格且夹带低速层的简单速度模型(图 2a),使用粗网格对模型进行剖分以提高计算效率。使用1∶5比例网格抽稀原速度模型(图 2b),求取射线路径(图 2c)、反射系数(图 2d)。观测系统参数:均匀激发20炮,每炮100道接收,地震子波为主频30 Hz的Ricker子波。点扩散算子布置在(3500 m,3500 m)处。
|
图 2 粗网格速度模型射线路径求取过程 (a)原速度模型;(b)粗网格速度模型;(c)粗网格速度模型射线路径;(d)反射系数 |
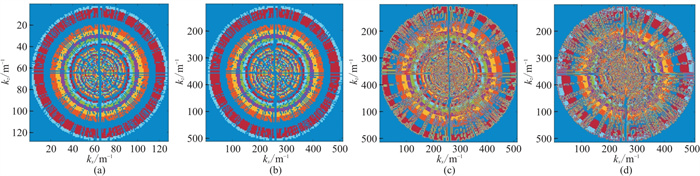
散射波数向量的不完备导致粗算子很多方向存在信息缺失,这将会对模拟成像结果造成影响。由图 3可见,不同的插值方法得到的算子在形态上与未插值算子保持一致,但也有明显区别。相比于粗点扩散算子(图 3a),最近邻插值法(图 3b)得到的算子仅相当于等比例放大,依旧缺失信息。双线性插值(图 3c)与双三次插值(图 3d)不仅将原有的小波数图放大,以便与反射系数波数图在波数域相乘的大小,而且通过线性计算补充了部分新的值。双三次插值算子产生的新数值数量明显多于双线性插值算子,新值虽然可以填补算子缺失信息,但也可能对成像结果造成影响。
|
图 3 不同插值方法点扩散算子 (a)粗算子;(b)最近邻插值算子;(c)双线性插值细算子;(d)双三次插值细算子。kx、kz分别表示横向、纵向波数 |
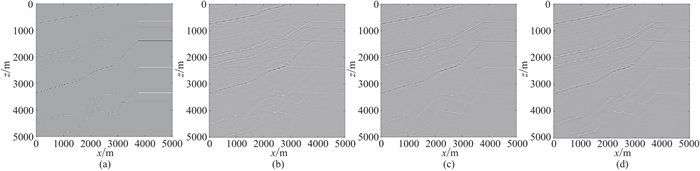
使用反射系数与地震子波在深度域做非稳态褶积,可以得到未经点扩散算子作用的理想情况的成像结果,以此作为标准对比不同插值方法的点扩散算子的成像效果。相比于双线性插值法(图 4c)与双三次插值法(图 4d),最近邻插值法模拟成像结果干扰明显较多,信噪比相对较低(图 4b)。使用双线性插值法和双三次插值法得到的结果都能较好地减少噪声,对反射系数的模糊程度较低。但是由于双三次插值法使点扩散算子插值回原来大小的同时,在原本没有散射向量的区域产生了更多的数值,这些数值不一定有益于模拟成像结果,故其与双线性插值法模拟结果还是有微弱的区别。
|
图 4 不同插值算子成像结果对比 (a)理想成像结果;(b)最近邻插值算子;(c)双线性插值算子;(d)双三次插值算子 |
用反射系数与单位脉冲作褶积,得到理想成像结果,选用三种插值法模拟成像结果与理想成像结果的第100、第300道地震记录进行对比(表 1)。由表可见,同一速度模型相同粗网格的情况下,三种插值方法提升的计算效率几乎相等,综合考虑了成像效果,采用双线性插值方法得到的模拟成像结果受粗网格因素的影响也最小,因此,此插值方法是较好的选择,后续对算子插值均采用双线性插值方法。
|
|
表 1 不同插值方法效果对比 |
使用1361×561网格的Marmousi模型进行复杂速度模型的粗网格模拟成像。地震子波为主频30 Hz的Richer子波,地面激发20炮,道间距20 m,每炮227道接收,计算(1800 m, 1800 m)处算子。分别使用横向1∶3、纵向1∶2和横向1∶6、纵向1∶4的两种粗网格速度模型求取射线路径构建粗点扩散算子。
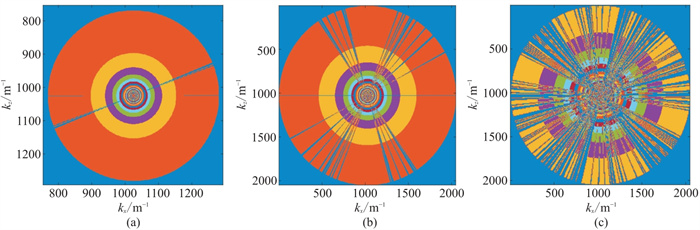
可以由射线路径图(图 5)看出,(1800 m, 1800 m)处射线路径在原速度模型基础上求取的射线覆盖面积要大于粗网格速度模型,表明了原模型射线路径携带的照明信息更多。即原速度模型射线在理论照明程度上要优于粗网格模型。反映到点扩散算子上,即使用粗网格速度模型建立的点扩散算子(图 6b、图 6c)即使通过插值得到与原点扩散算子大小相同的算子也会缺失不少信息,而且网格越粗,信息缺失越严重。

|
图 5 不同粗网格速度模型的射线路径 (a)原速度模型;(b)原速度模型射线路径;(c)横向1∶3粗网格模型射线路径;(d)横向1∶6粗网格模型射线路径 |
|
图 6 不同粗网格速度模型散射点处点扩散算子 (a)原模型构建算子;(b)横向1∶3粗网格模型插值后算子;(c)横向1∶6粗网格模型插值后算子kx、kz分别表示横向、纵向波数,图 9同。 |
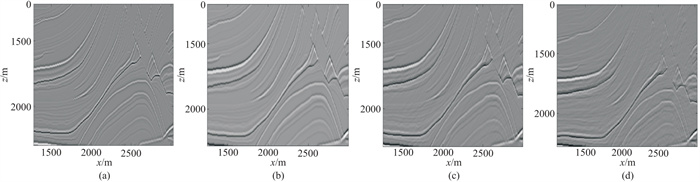
在相同观测系统下,使用粗网格速度模型进行射线追踪虽然可以节省计算时间,但是对于散射点附近的成像效果会造成影响。计算粗网格算子(图 7c、图 7d)与原模型算子(图 7b)成像结果的相关系数分别为0.7902和0.7713,总计算效率提高了约84%和89%。综合考虑计算效率、模拟成像结果和可能存在的不确定因素,对于复杂模型也可以使用粗网格构建点扩散算子进行模拟成像。
|
图 7 粗算子插值模拟成像结果对比 (a)理想成像结果;(b)原模型算子成像结果;(c)横向1∶3粗网格插值后算子成像结果;(d)横向1∶6粗网格插值后算子成像结果 |
对波数域粗算子进行插值,测试方法中较优的为双线性插值法。用此方法对粗点扩散算子进行插值并与反射系数进行褶积,得到的模拟成像结果干扰最少。基于粗网格构建的粗算子插值模拟成像可很大程度上提高计算效率,但是对于不同复杂程度的模型要具体问题具体分析,选择合适的粗网格在很大程度上减少计算时间的同时也不会偏离获取理论成像结果的初衷。
3 多点布置算子模拟成像 3.1 多点算子布置原则与理论模型测试传统的模拟成像结果是通过在目的层放置散射点,根据观测系统与速度模型构建点扩散算子进行模拟成像。对于散射点附近的局部成像较为准确,却不适合控制整个地下空间的模拟成像。本文提出多算子模拟成像方法,设置多个偏移成像窗并布置多个算子,计算多点处散射向量,构建多点处成像算子还原观测系统对于地下介质成像的全局控制效果。
根据速度模型与成像精度要求设置偏移成像窗的尺寸,成像窗的长、宽比应控制在1~2范围内,尽量保证成像窗中心位置的算子对整个成像窗成像效果的控制。又因为增加新的算子会增加计算量,所以布置算子是应综合考虑计算时间与成像精度要求。
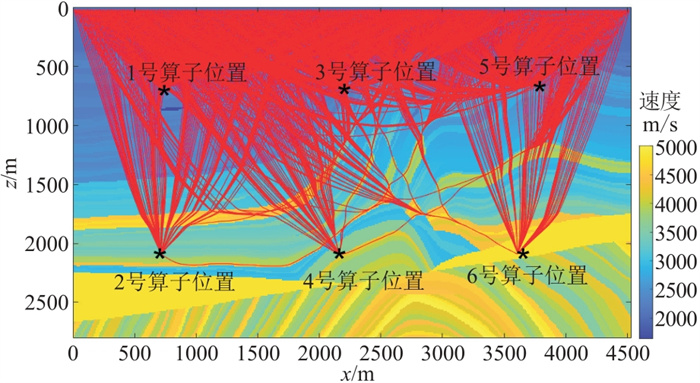
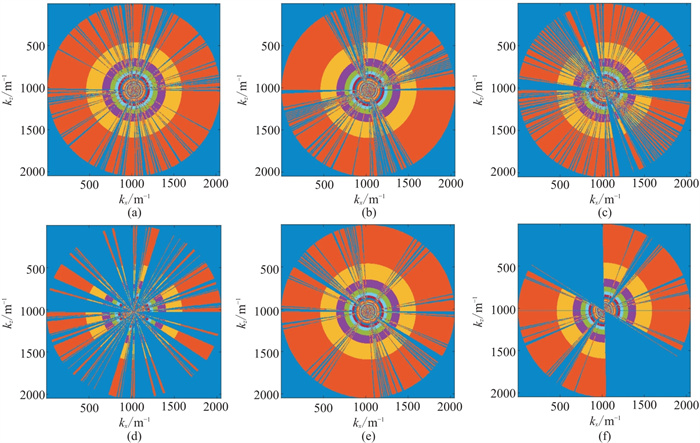
使用1361×561网格的Marmousi模型进行粗网格多算子模拟成像测试。地面均匀激发40炮,每炮227道接收,地震子波为主频30 Hz的Ricker子波,使用横向1∶3、纵向1∶2的粗网格得到一个网格为454×281的新模型。布置3×2个算子,算子位于(1125 m, 700 m)、(1125 m, 2100 m)、(2250 m, 700 m)、(2250 m, 2100 m)、(3375 m, 700 m)和(3375 m, 2100 m)。每个算子控制一个近似正方形的成像区域。为了方便表述,给这些位置赋予1号到6号的位置编号(图 8)。分别构建1~6号位置的点扩散算子(图 9),完成多算子以及单算子模拟成像(图 10)。
|
图 8 多散射点处射线路径(*表示散射点位置) |
|
图 9 多散射点处点扩散算子 (a)~(f)分别为1号位置到6号位置处的点扩散算子。 |
|
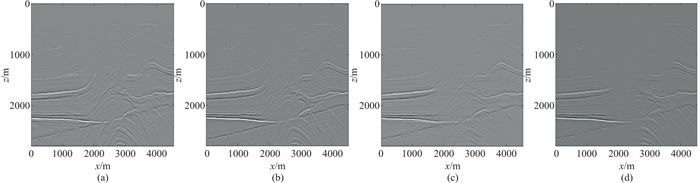
图 10 多算子模拟成像结果与单算子模拟成像结果对比 (a) 多散射点综合模拟成像;(b)2号位置点扩散算子模拟成像结果;(c)4号位置点扩散算子模拟成像结果;(d)6号位置点扩散算子模拟成像结果 |
通过对比不同算子情况的模拟成像结果,发现使用单点扩散算子控制全局的模拟成像得到的仅为单一散射点处照明信息,不适宜用作全局的成像算子(图 10b、图 10c、图 10d)。例如使用4号算子进行插值后模拟成像,其方位信息仅能保证对倾角较小的地层有较好的成像效果,不符合全局理论成像结果(图 10c)。同理,2号算子的方位信息较为完备,也不适宜作用到照明不好的区域进行模拟成像(图 10b)。所以最合适的是使用多散射点进行综合模拟成像。
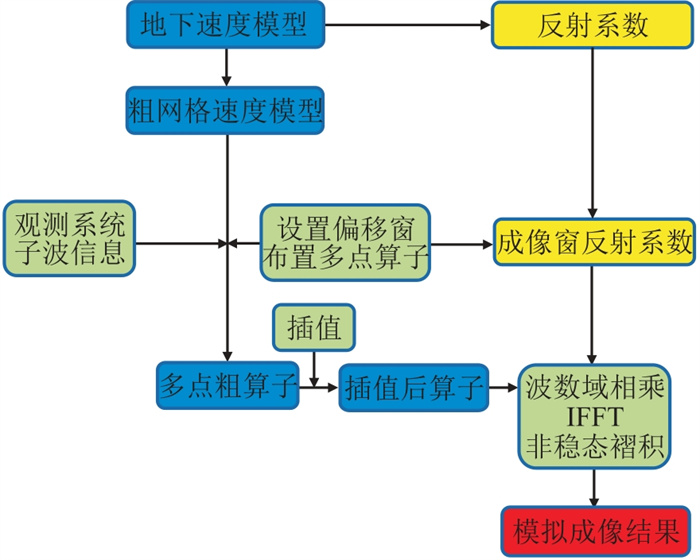
3.2 实际数据测试观测系统信息:地面均匀激发20炮,每炮125道接收,地震子波为30 Hz的Ricker子波。具体成像流程参考图 11。
|
图 11 多点算子模拟成像流程图 |
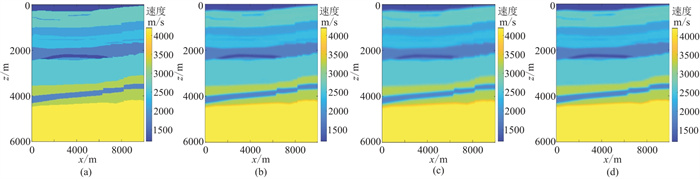
选取网格为2001×1201的纵向速度变化剧烈且夹有一层低速异常的实际速度模型。使用射线类偏移成像中平滑处理方法[31-33]得到不同平滑次数和平滑系数的三种不同平滑程度的速度模型。如图 12b、图 12c为两种简单平滑速度模型,图 12d则使用了纵向更大的平滑系数检测存在速度误差情况的模拟成像结果。
|
图 12 原速度模型与不同程度平滑速度模型 (a)原速度模型;(b)低平滑速度模型;(c)纵向高平滑速度模型;(d)高平滑速度模型 |
对四种模型使用横向1:5、纵向1:4的粗网格进行离散,算子均匀布置在4条平行于x轴的直线z=750、2250、3750、5250 m和5条平行于z轴的直线x=1000、3000、5000、7000、9000 m的20个交点的位置。
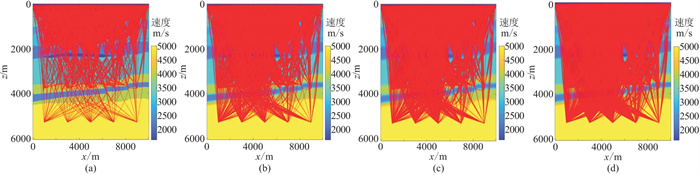
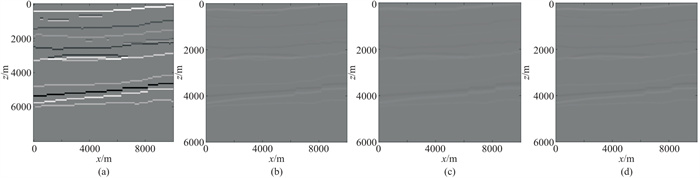
根据每个散射点处的射线路径信息可以构建控制每个成像窗的波数域点扩散算子,并在波数域进行插值(图 13)。因为速度平滑的原因,不同平滑模型的反射系数相较于原模型的反射系数也更模糊,符合实际情况中宏观的深度域地层速度模型,如图 14所示。
|
图 13 不同速度模型射线路径 (a)原速度模型射线路径;(b)低平滑速度模型射线路径;(c)纵向高平滑速度模型射线路径;(d)高平滑速度模型射线路径 |
|
图 14 不同速度模型反射系数 (a)原模型反射系数;(b)低平滑速度模型反射系数;(c)纵向高平滑速度模型反射系数;(d)高平滑速度模型反射系数 |
多算子模拟成像需要使用成像窗内反射系数与算子在波数域相乘;平滑速度模型也符合只能得到宏观的深度域层速度模型;得不到准确的速度反射系数这一实际情况。即使使用适合射线类偏移成像的平滑方法,平滑后的速度模型在射线照明区域上有优势,但是平滑后的反射系数也影响多算子成像效果。
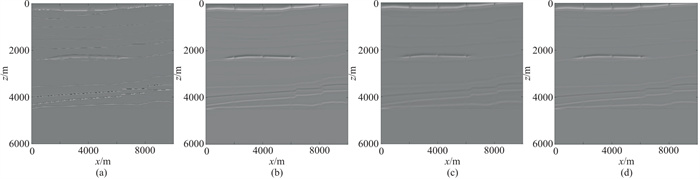
在原模型多算子成像清晰的区域在平滑速度模型多算子成像中也能很好地模拟成像,成像结果也符合平滑后的速度模型。如图 15所示,观测系统无论是对2000 m处的低速异常体还是3500~4500 m处的速度层,其成像控制效果均较好;同样对于成像结果干扰较多的近地表浅层,四个模型的多算子成像也都能体现出观测系统对此区域成像效果的控制不佳。所以对于所提实际数据,如果针对浅层进行地震勘探,需要改进观测系统;若针对深层进行地震勘探,则可以使用此观测系统。因此,可根据目的层具体问题具体分析地设计和优化观测系统。
|
图 15 不同速度模型粗网格多算子模拟成像结果 (a)原速度模型成像结果;(b)低平滑速度模型;(c)纵向高平滑速度模型;(d)高平滑速度模型 |
本文在已有的研究基础上改进了模拟叠前深度域偏移成像方法,提出了粗网格多算子模拟成像,在粗网格的基础上使用多散射点算子综合模拟成像。理论模型和实际数据测试表明:对于不同复杂程度的模型使用不同程度粗网格,并设置合适的局部偏移成像窗,在不影响计算速度与成像效果的前提下可以得到观测系统对全局理论模拟成像结果的控制;此方法使用多算子代替单算子的模拟成像效果,在保持高计算效率的同时,更直观地展示了观测系统对不同区域理论成像结果的控制效果。
| [1] |
FLETCHER R P, ARCHER S, NICHOLS D, et al. Inversion after depth imaging[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [2] |
周东勇, 印兴耀, 宗兆云. 基于褶积理论的深度域地震记录制作方法研究[J]. 物探化探计算技术, 2020, 42(1): 17-23. ZHOU Dongyong, YIN Xingyao, ZONG Zhaoyun. The method for making seismic records in depth domain based on convolution theory[J]. Computing Techniques for Geophysical andGeochemical Exploration, 2020, 42(1): 17-23. |
| [3] |
向晨, 孙敏傲, 白英哲. 基于点扩散函数的快速成像技术附视频[C]. 2022年中国石油物探学术年会论文集(上册), 2022: 486-489. XIANG Chen, SUN Min'ao, BAI Yingzhe. Rapid imaging technique based on point spread function[C]. Proceedings of the 2022 China Petroleum Geophysical Exploration Academic Annual Conference(Volume 1), 2022: 486-489. |
| [4] |
郝洪鉴, 刘俊州, 韩磊, 等. 点扩散函数深度域反演[J]. 矿产与地质, 2023, 37(1): 138-144. HAO Hongjian, LIU Junzhou, HAN Lei, et al. Depth domain inversion of point spread function[J]. Mineral Resources and Geology, 2023, 37(1): 138-144. |
| [5] |
段伟国, 毛伟建, 张庆臣, 等. 基于密度扰动的点扩散函数计算与三维深度域模拟成像[J]. 地球物理学报, 2022, 65(4): 1402-1415. DUAN Weiguo, MAO Weijian, ZHANG Qingchen, et al. Computation of density perturbation based point spread function and simulation of migration image in 3D depth domain[J]. Chinese Journal of Geophysics, 2022, 65(4): 1402-1415. |
| [6] |
张庆臣. 时间域弹性波动方程全波形反演方法研究[D]. 北京: 中国石油大学(北京), 2017. ZHANG Qingchen. Full Waveform Inversion Based on the Time-Domain Elastic Wave Equations[D]. China University of Petroleum(Beijing), Beijing, 2017. |
| [7] |
姚振岸, 孙成禹, 喻志超, 等. 融合点扩散函数的预条件黏声最小二乘逆时偏移[J]. 石油地球物理勘探, 2019, 54(1): 73-83. YAO Zhen'an, SUN Chengyu, YU Zhichao, et al. Preconditioned visco-acoustic least-squares reverse time migration integrated with point spread function[J]. Oil Geophysical Prospecting, 2019, 54(1): 73-83. |
| [8] |
岳玉波, 秦宁, 杨哲, 等. 基于射线理论点扩散函数的成像域最小二乘偏移[J]. 地球物理学报, 2023, 66(2): 774-783. YUE Yubo, QIN Ning, YANG Zhe, et al. Image domain least-squares migrationn based on ray-based point spread function[J]. Chinese Journal of Geophysics, 2023, 66(2): 774-783. |
| [9] |
袁江洋, 孙成禹. 深度域合成地震记录精度分析[C]. 2020年中国地球科学联合学术年会, 2020, 2802-2804. YUAN Jiangyang, SUN Chengyu. Accuracy analysis of synthetic seismic recording in deep domain[C]. 2020 China Earth Science Joint Academic Annual Conference, 2020, 2802-2804. |
| [10] |
GELIUS L J, JOHANSEN I, SPONHEIM N, et al. A generalized diffraction tomography algorithm[J]. The Journal of the Acoustical Society of America, 1991, 89(2): 523-528. |
| [11] |
GELIUS L J, LECOMTE I, TABTI H. Analysis of the resolution function in seismic prestack depth imaging[J]. Geophysical Prospecting, 2002, 50(5): 505-515. |
| [12] |
HAMRAN S E, LECOMTE I. Local plane-wave-number diffraction tomography in heterogeneous back-grounds, Part I: Theory[J]. Journal of Seismic Exploration, 1993, 2(2): 133-146. |
| [13] |
HAMRAN S E, LECOMTE I. Local plane-wave imaging of GPR data[J]. Journal of Environmental and Engineering Geophysics, 2003, 8(2): 9-16. |
| [14] |
徐海, 王光付, 李发有, 等. 一种基于高频噪声定量约束函数的地震高分辨率处理方法[J]. 石油物探, 2024, 63(2): 408-416. XU Hai, WANG Guangfu, LI Fayou, et al. A high-resolution seismic processing method based on quantitative constraint function of high-frequency noises[J]. Geophysical Prospecting for Petroleum, 2024, 63(2): 408-416. |
| [15] |
LECOMTE I, GELIUS L J. Have a look at the resolution of prestack migration for any model, survey and wavefields[C]. SEG Technical Program Expanded Abstracts 1998, 17: 1112-1115.
|
| [16] |
LECOMTE I, HAMRAN S E, TABTI H, et al. New insights in migration through analogies between generalized diffraction tomography and synthetic aperture radar[C]. SEG Technical Program Expanded Abstracts, 2001, 20: 1111-1114.
|
| [17] |
LECOMTE I, GELIUS L J, HAMRAN S E. Local imaging approach and applications[J]. Bulletin of Volcanology, 2002, 71(7): 753-765. |
| [18] |
LECOMTE I. Resolution and illumination analyses in PSDM: a ray-based approach[J]. The Leading Edge, 2008, 27(5): 650-663. |
| [19] |
吴涵. 模拟叠前深度偏移成像的地震正演方法研究[D]. 山东青岛: 中国石油大学(华东), 2021. WU Han. Study on Seismic Forward Modelling of Simulated Prestack Depth Migration[D]. China University of Petroleum(East China), Qingdao, Shangdong, 2021. |
| [20] |
吴涵, 廉西猛, 孙成禹, 等. 叠前深度偏移地震记录直接模拟方法[J]. 石油地球物理勘探, 2020, 55(4): 747-753. WU Han, LIAN Ximeng, SUN Chengyu, et al. Research on direct simulation to seismic record of pre-stack depth migration[J]. Oil Geophysical Prospec-ting, 2020, 55(4): 747-753. |
| [21] |
焦峻峰, 赵爱国, 廉西猛, 等. 基于照明补偿的变"子波"模拟成像方法[J]. 石油地球物理勘探, 2023, 58(4): 883-892. JIAO Junfeng, ZHAO Aiguo, LIAN Ximeng, et al. Variable "wavelet"simulated imaging method based on illumination compensation[J]. Oil Geophysical Prospecting, 2023, 58(4): 883-892. |
| [22] |
STAMNES J J. Waves in Focal Regions: Propagation, Diffraction and Focusing of Light, Sound and Water Waves[M]. Routledge, New York, 1986.
|
| [23] |
BEYLKIN G, ORISTAGLIO M, MILLER D. Spatial resolution of migration algorithms[C]. Proceedings of the 14th International Symposium on Acoustical Image, 1985, 155-167.
|
| [24] |
BEYLIKIN G. Imaging of discontinuities in the inverse scattering problem by inversion of a causal gene-ralized Radon transform[J]. Journal of Mathematical Physics, 1985, 26(1): 99-108. |
| [25] |
VIDALE J. Finite-difference calculation of travel times[J]. Bulletin of the Seismological Society of America, 1988, 78(6): 2062-2076. |
| [26] |
张云, 李夕海, 白超英, 等. 2D/3D起伏地表多震相地震波走时的因式分解程函方程算法[J]. 石油地球物理勘探, 2023, 58(4): 857-871. ZHANG Yun, LI Xihai, BAI Chaoying, et al. Multi-phase seismic traveltime computation in 2D/3D undulated surface model using factored eikonal equation[J]. Oil Geophysical Prospecting, 2023, 58(4): 857-871. |
| [27] |
李天扬. 基于快速行进法射线追踪的反射波走时反演[D]. 吉林长春: 吉林大学, 2021. LI Tianyang. Reclection Travel Time Iinversing Based on Fast Marching RayTracing[D]. Jilin University, Changchun, Jilin, 2021. |
| [28] |
王飞, 曲昕馨, 刘四新, 等. 一种新的基于多模板快速推进算法和最速下降法的射线追踪方法[J]. 石油地球物理勘探, 2014, 49(6): 1106-1114. WANG Fei, QU Xinxin, LIU Sixin, et al. A new ray tracing approach based on both multi-stencils fast marching and the steepest descent[J]. Oil Geophysical Prospecting, 2014, 49(6): 1106-1114. |
| [29] |
辛凯凯. 基于旅行时双线性插值三维地震波场数值模拟[D]. 陕西西安: 长安大学, 2021. XIN Kaikai. Numerical Simulation of 3D Seismic Wavefield Baswd on Traveltime Bilinear Iinterpolation[D]. Chang'an University, Xi'an, Shaanxi, 2021. |
| [30] |
李同宇, 张建中. 地震射线追踪的线性走时扰动插值法[J]. 石油地球物理勘探, 2018, 53(6): 1165-1174. LI Tongyu, ZHANG Jianzhong. A linear traveltime interpolation method for seismic ray tracing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1165-1174. |
| [31] |
韩复兴, 孙建国, 王雪秋. 射线类偏移成像中的模型平滑处理研究[J]. 地球物理学报, 2019, 62(6): 2249-2257. HAN Fuxing, SUN Jianguo, WANG Xueqiu. Research on model smoothing in ray type migration imaging[J]. Chinese Journal of Geophysics, 2019, 62(6): 2249-2257. |
| [32] |
文冉, 樊骐铖, 衡德, 等. 长宁页岩气开发随钻跟踪叠前深度偏移建模方法及应用效果[J]. 石油地球物理勘探, 2022, 57(增刊2): 46-52, 69. WEN Ran, FAN Qicheng, HENG De, et al. Modeling method pfr prestack depth migration and tracking while drilling in shale gas development and its application effect in Changning[J]. Oil Geophysical Prospecting, 2022, 57(S2): 46-52, 69. |
| [33] |
姜晓宇, 宋涛, 甘利灯, 等. 花岗岩潜山裂缝型储层多尺度建模与应用[J]. 石油地球物理勘探, 2023, 58(2): 403-411. JIANG Xiaoyu, SONG Tao, GAN Lideng, et al. Multi-scale modeling of granite buried-hill fractured reservoir and its application[J]. Oil Geophysical Prospecting, 2023, 58(2): 403-411. |



 孙成禹, 山东省青岛市长江西路66号中国石油大学(华东)中国石油大学(华东)地球科学与技术学院,266580。Email:
孙成禹, 山东省青岛市长江西路66号中国石油大学(华东)中国石油大学(华东)地球科学与技术学院,266580。Email: