2. 油气资源与勘探技术教育部重点实验室(长江大学), 湖北武汉 430100;
3. 中石化石油工程地球物理公司国际业务发展中心, 北京 100728
2. Key Laboratory of Exploration Technologies for Oil and Gas Resources(Yangtze University), Ministry of Education, Wuhan, Hubei 430100, China;
3. Sinopec Geophysics Corporation International Business Center, Beijing 100728, China
在各向异性介质中,地震波的传播受多个参数的控制。弹性波波动方程可以模拟地震波的传播过程,但是面临参数多、算法复杂等问题。因为实际地震资料以纵波数据为主[1-6],所以许多学者研究了如何准确描述纵波的传播规律。
Alkhalifah[7-8]从频散关系出发,人为将沿着对称轴方向的qSV波速度设为0,推导了四阶时间—空间域qP波方程以及分裂后的二阶方程组,提出声学近似假设。声学近似假设可以较准确地描述qP波的运动学规律,为各向异性介质纵波勘探提供了理论基础。在此基础上,一些学者开展了关于各向异性介质qP波方程正演方面的研究。Du等[9]、Zhou等[10]以及Hestholm[11]通过简化频散关系,利用不同的降阶处理导出了不同形式的二阶耦合VTI介质qP波方程;吴国忱等[12-13]在空间—频率域推导了VTI介质qP波波动方程;Duveneck等[14]从胡克定律及质点方程出发,基于qSV波速度为0的假设,推导了VTI介质二阶耦合qP波波动方程;Xu等[15-16]基于Alkhalifah的声学近似方程[7],推导了各向异性介质的纯qP波波动方程。
虽然Alkhalifah提出的声学近似方法能够较准确地描述qP波,但直接设定沿对称轴方向qSV波波速为0的方法,并不能保证非对称轴方向的qSV波波速也为0,其余方向的残余会在波场中形成菱形的qSV波伪影[17]。在不改变声学近似原理的基础上,有学者根据菱形伪影产生的原理,在数值求解过程中通过各向异性参数匹配法[8]、波场滤波法[18]和辅助波场法[19]等压制qSV波伪影,但都未能完全消除。而且,声学近似改变了VTI介质原有的弹性介质,只有在Thomsen参数[20]
为了解决上述问题,Xu等[21]将qSV波在各个方向上的波速均设为0,提出一种新声学近似方程。新声学近似方程在理论上可以准确描述纯qP波的传播规律,但形式上却比Alkhalifah的方程更复杂,无法直接用有限差分法求解。Liang等[22]基于新声学近似的纯qP波频散关系提出一种正演方法,将纯qP波频散关系式通过空间近似[15]转化为可以直接用有限差分法求解的时间—空间域纯qP波波动方程。但空间近似是利用传播方向矢量代替波数矢量,与Poynting矢量有着类似的缺点,对复杂模型存在模拟精度低的问题[23]。
本文基于新声学近似的纯qP波频散关系,推导了新的纯qP波波动方程。通过引入中间变量,将频散关系中分数形式的空间—波数域混合算子转化成一个求解中间变量的方程,从而得到时间—空间域纯qP波波动方程组。然后通过有限差分法实现二维VTI介质纯qP波模拟,并与纯qP波等相位面进行对比。数值模拟结果表明新的纯qP波波动方程具有更高的精度。
1 新声学近似二维VTI介质中qP波和qSV波的精确频散关系分别为[24]
| $ {\omega }_{\mathrm{P}}^{2}=\frac{1}{2}\left\{{V}_{\mathrm{P}0}^{2}\left[(1+2ε ){k}_{x}^{2}+{k}_{z}^{2}\right]+\\{V}_{\mathrm{S}0}^{2}\left({k}_{x}^{2}+{k}_{z}^{2}\right)+\sqrt{D}\right\} $ | (1) |
| $ {\omega }_{\mathrm{S}\mathrm{V}}^{2}=\frac{1}{2}\left\{{V}_{\mathrm{P}0}^{2}\left[(1+2ε ){k}_{x}^{2}+{k}_{z}^{2}\right]+\\{V}_{\mathrm{S}0}^{2}\left({k}_{x}^{2}+{k}_{z}^{2}\right)-\sqrt{D}\right\} $ | (2) |
式中:
| $ \begin{array}{l}D={\left\{{V}_{\mathrm{P}0}^{2}\left[(1+2ε ){k}_{x}^{2}-{k}_{z}^{2}\right]-{V}_{\mathrm{S}0}^{2}\left({k}_{x}^{2}-{k}_{z}^{2}\right)\right\}}^{2}+\\ 4\left({V}_{\mathrm{P}0}^{2}-{V}_{\mathrm{S}0}^{2}\right)\left[(1+2\delta ){V}_{\mathrm{P}0}^{2}-{V}_{\mathrm{S}0}^{2}\right]{k}_{x}^{2}{k}_{z}^{2}\end{array} $ | (3) |
Alkhalifah提出的声学近似方法令对称轴方向qSV波速度为0,只能消除对称轴方向的qSV波。为了完全消除各个方向的qSV波,Xu等[21]将qSV波在各个方向的波速都设为0,即式(2)中
| $ {V}_{\mathrm{S}0}^{2}=\frac{-2(ε -\delta ){k}_{x}^{2}{k}_{z}^{2}}{(1+2ε ){k}_{x}^{4}+{k}_{z}^{4}+2(1+\delta ){k}_{x}^{2}{k}_{z}^{2}}{V}_{\mathrm{P}0}^{2} $ | (4) |
然后将式(4)代入式(1),可得到基于新声学近似的纯qP波频散关系
| $ {\omega }_{\mathrm{P}}^{2}={V}_{\mathrm{P}0}^{2}\left[(1+2ε ){k}_{x}^{2}+{k}_{z}^{2}\right]-2(ε -\delta ){V}_{\mathrm{P}0}^{2}G $ | (5) |
式中
| $ G=\frac{{k}_{x}^{2}{k}_{z}^{2}\left({k}_{x}^{2}+{k}_{z}^{2}\right)}{(1+2ε ){k}_{x}^{4}+{k}_{z}^{4}+2(1+\delta ){k}_{x}^{2}{k}_{z}^{2}} $ | (6) |
为分数形式的空间—波数域混合算子,无法通过有限差分法直接求解。
在推导基于新声学近似的纯qP波频散关系方程时,将各个方向上的qSV波波速均设为0,因此推导出的纯qP波频散关系方程中理论上不包含qSV波。
2 基于空间近似的纯qP波波动方程为了用有限差分法求解基于新声学近似的纯qP波波动方程,Liang等[22]构造了波数域标量算子Sk
| $ {S}_{k}=\frac{-2\left(ε -\delta \right){k}_{x}^{2}{k}_{z}^{2}}{\left(1+2ε \right){k}_{x}^{4}+{k}_{z}^{4}+2\left(1+\delta \right){k}_{x}^{2}{k}_{z}^{2}} $ | (7) |
并利用传播方向矢量n代替波数矢量k,即
| $ {S}_{n}=\frac{-2\left(ε -\delta \right){n}_{x}^{2}{n}_{z}^{2}}{\left(1+2ε \right){n}_{x}^{4}+{n}_{z}^{4}+2\left(1+\delta \right){n}_{x}^{2}{n}_{z}^{2}} $ | (8) |
nx和nz的计算采用如下近似
| $ \left\{\begin{array}{l}{n}_{x}=\frac{\frac{\partial U}{\partial x}}{\sqrt{{\left(\frac{\partial U}{\partial x}\right)}^{2}+{\left(\frac{\partial U}{\partial z}\right)}^{2}}}\\ {n}_{z}=\frac{\frac{\partial U}{\partial z}}{\sqrt{{\left(\frac{\partial U}{\partial x}\right)}^{2}+{\left(\frac{\partial U}{\partial z}\right)}^{2}}}\end{array}\right. $ | (9) |
式中U为空间域波场。
将算子Sn利用式(9)的近似方法转化到空间域,并与式(5)结合,得到基于空间近似的时间—空间域qP波波动方程
| $ \left\{\begin{array}{l}\frac{{\partial }^{2}U}{\partial {t}^{2}}={V}_{\mathrm{P}0}^{2}\left[\left(1+2ε \right)+{S}_{n}\right]\frac{{\partial }^{2}U}{\partial {x}^{2}}+{V}_{\mathrm{P}0}^{2}\left(1+{S}_{n}\right)\frac{{\partial }^{2}U}{\partial {z}^{2}}\\ {S}_{n}=\frac{-2\left(ε -\delta \right){\left(\frac{\partial U}{\partial x}\right)}^{2}{\left(\frac{\partial U}{\partial z}\right)}^{2}}{\left(1+2ε \right){\left(\frac{\partial U}{\partial x}\right)}^{4}+{\left(\frac{\partial U}{\partial z}\right)}^{4}+2\left(1+\delta \right){\left(\frac{\partial U}{\partial x}\right)}^{2}{\left(\frac{\partial U}{\partial z}\right)}^{2}}\end{array}\right. $ | (10) |
利用空间近似虽然可以将纯qP波频散关系式转化为可以直接用有限差分法求解的时间—空间域纯qP波波动方程, 但由于其波数矢量是用传播方向矢量代替,而传播方向由空间导数计算,因而与利用Poynting矢量计算波传播方向的缺点相似。对于复杂模型,如果有多个波同时到达空间某点,受限于每个空间点上只能表示一个传播方向的原则,导致正演结果精度降低[23]。
3 新的纯qP波波动方程为了提高基于新声学近似的纯qP波正演的正演精度,本文提出一种新的纯qP波波动方程。首先将式(5)转换到频率―波数域,为
| $ \begin{array}{l}{\omega }^{2}\widetilde{U}={V}_{\mathrm{P}0}^{2}\left[\left(1+2ε \right){k}_{x}^{2}+{k}_{z}^{2}\right]\widetilde{U}-\\ \frac{2\left(ε -\delta \right){V}_{\mathrm{P}0}^{2}\left({k}_{x}^{2}+{k}_{z}^{2}\right){k}_{x}^{2}{k}_{z}^{2}}{\left(1+2ε \right){k}_{x}^{4}+{k}_{z}^{4}+2\left(1+\delta \right){k}_{x}^{2}{k}_{z}^{2}}\widetilde{U}\end{array} $ | (11) |
式中
| $ \widetilde{P}=\frac{{k}_{x}^{2}{k}_{z}^{2}}{\left(1+2ε \right){k}_{x}^{4}+{k}_{z}^{4}+2\left(1+\delta \right){k}_{x}^{2}{k}_{z}^{2}}\widetilde{U} $ | (12) |
则式(11)可表示为
| $ \left\{\begin{array}{l}{\omega }^{2}\widetilde{U}={V}_{\mathrm{P}0}^{2}\left[\left(1+2ε \right){k}_{x}^{2}+{k}_{z}^{2}\right]\widetilde{U}-\\ \begin{array}{cc}& \end{array}2{V}_{\mathrm{P}0}^{2}\left(ε -\delta \right)\left({k}_{x}^{2}+{k}_{z}^{2}\right)\widetilde{P}\\ \widetilde{P}\left[\left(1+2ε \right){k}_{x}^{4}+{k}_{z}^{4}+2\left(1+\delta \right){k}_{x}^{2}{k}_{z}^{2}\right]={k}_{x}^{2}{k}_{z}^{2}\widetilde{U}\end{array}\right. $ | (13) |
转换到时间—空间域,有
| $ \left\{\begin{array}{l}\frac{{\partial }^{2}U}{\partial {t}^{2}}={V}_{\mathrm{P}0}^{2}\left[\left(1+2ε \right)\frac{{\partial }^{2}U}{\partial {x}^{2}}+\frac{{\partial }^{2}U}{\partial {z}^{2}}\right]-2{V}_{\mathrm{P}0}^{2}\left(ε -\delta \right)\left(\frac{{\partial }^{2}P}{\partial {x}^{2}}+\frac{{\partial }^{2}P}{\partial {z}^{2}}\right)\\ \frac{{\partial }^{4}U}{\partial {x}^{2}\partial {z}^{2}}=\left(1+2ε \right)\frac{{\partial }^{4}P}{\partial {x}^{4}}+\frac{{\partial }^{4}P}{\partial {z}^{4}}+2\left(1+\delta \right)\frac{{\partial }^{4}P}{\partial {x}^{2}\partial {z}^{2}}\end{array}\right. $ | (14) |
上式即本文建立的时间—空间域纯qP波波动方程组。与基于空间近似的qP波波动方程(式(10))相比,本文推导过程中未采用任何近似,因此该方程能够精确模拟基于新声学近似的qP波传播规律,理论上具有更高的精度。
采用有限差分法求解式(14)。时间二阶导数采用二阶中心差分格式,空间二阶和四阶导数的有限差分格式为
| $ \left\{\begin{array}{l}\frac{{\partial }^{2}f}{\partial {x}^{2}}\approx \frac{1}{{\left(\mathrm{\Delta }x\right)}^{2}}\left({f}_{i+1,j}-2{f}_{i,j}+{f}_{i-1,j}\right)\\ \frac{{\partial }^{2}f}{\partial {z}^{2}}\approx \frac{1}{{\left(\mathrm{\Delta }z\right)}^{2}}\left({f}_{i,j+1}-2{f}_{i,j}+{f}_{i,j-1}\right)\\ \frac{{\partial }^{4}f}{\partial {x}^{4}}\approx \frac{1}{{\left(\mathrm{\Delta }x\right)}^{4}}\left({f}_{i+2,j}-4{f}_{i+1,j}+6{f}_{i,j}-4{f}_{i-1,j}+{f}_{i-2,j}\right)\\ \frac{{\partial }^{4}f}{\partial {z}^{4}}\approx \frac{1}{{\left(\mathrm{\Delta }z\right)}^{4}}\left({f}_{i,j+2}-4{f}_{i,j+1}+6{f}_{i,j}-4{f}_{i,j-1}+{f}_{i,j-2}\right)\\ \frac{{\partial }^{4}f}{\partial {x}^{2}\partial {z}^{2}}\approx \frac{1}{{\left(\mathrm{\Delta }x\right)}^{2}{\left(\mathrm{\Delta }z\right)}^{2}}\left[4{f}_{i,j}-2\left({f}_{i+1,j}+{f}_{i-1,j}+{f}_{i,j+1}+{f}_{i,j-1}\right)\right.+\left.{f}_{i+1,j+1}+{f}_{i+1,j-1}+{f}_{i-1,j-1}+{f}_{i-1,j+1}\right]\end{array}\right. $ | (15) |
式中:f代表网格点上P或U;Δx和Δz分别是x和z方向的空间采样间隔;i、j分别为两个方向的网格点序号。
式(14)中第二式是求解中间变量P的方程,将其离散后形成一个线性方程组
| $ \boldsymbol{A}\boldsymbol{P}=\boldsymbol{U} $ | (16) |
式中:

|
图 1 系数矩阵A示意图 |
通过求解线性方程可以得到中间变量P,将P代入式(14)中第一个公式,通过有限差分法迭代求解U,可得到qP波正演模拟结果。另外,在正演过程中采用完全匹配层(PML)边界条件[25-26](附录A)。
4 正演数值模拟 4.1 均匀模型试算为了证明新声学近似能有效消除qSV波伪影并解决
|
|
表 1 三个均匀VTI介质模型的各向异性参数 |
图 2为基于Alkhalifah提出的声学近似纯qP波波动方程模拟的三个模型波场快照,可以看出当

|
图 2 不同均匀模型Alkhalifah声学近似qP波波动方程的正演波场快照 (a)模型A;(b)模型B;(c)模型C |
与图 2相比,基于空间近似的纯qP波波动方程模拟的波场快照(图 3)和本文提出的新的纯qP波波动方程模拟的波场快照(图 4)基本消除了qSV波伪影,并且在

|
图 3 不同均匀模型基于空间近似的qP波波动方程正演波场快照 (a)模型A;(b)模型B;(c)模型C;(d)图a的局部放大;(e)图c的局部放大 |

|
图 4 不同均匀模型新的qP波波动方程的正演波场快照 (a)模型A;(b)模型B;(c)模型C;(d)图a的局部放大;(e)图c的局部放大 |
为了比较基于空间近似的qP波波动方程与新的纯qP波波动方程的精度,根据Xu等[21]推出的纯qP波群速度绘出纯qP波的等相位面(图 3、图 4中红线)。由图 3b、图 4b可以看出:当
为了进一步比较三种方法的差异,绘制了均匀介质中检波点处记录的波形,如图 5所示。可以看出:当
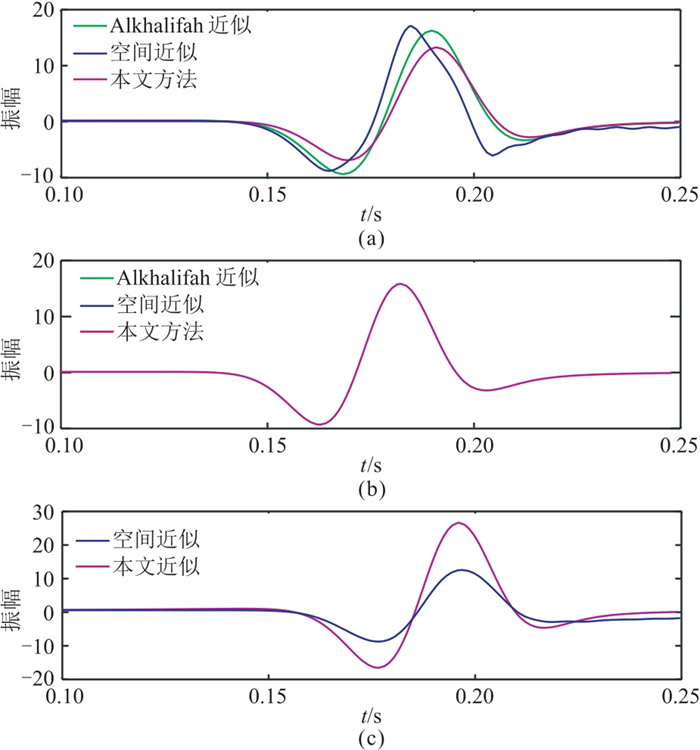
|
图 5 不同均匀模型不同方法模拟记录的波形对比 (a)模型A;(b)模型B;(c)模型C |
应用Sigsbee2a模型和Marmousi-Ⅱ模型对比新的纯qP波波动方程与基于空间近似的纯qP波波动方程对复杂模型的适应能力。将水平和垂直的网格间距均设为10 m,时间采样率为0.1 ms,震源采用主频为15 Hz的Ricker子波,震源位于图 6a的星号处, 并在三角标处设置三个检波点。
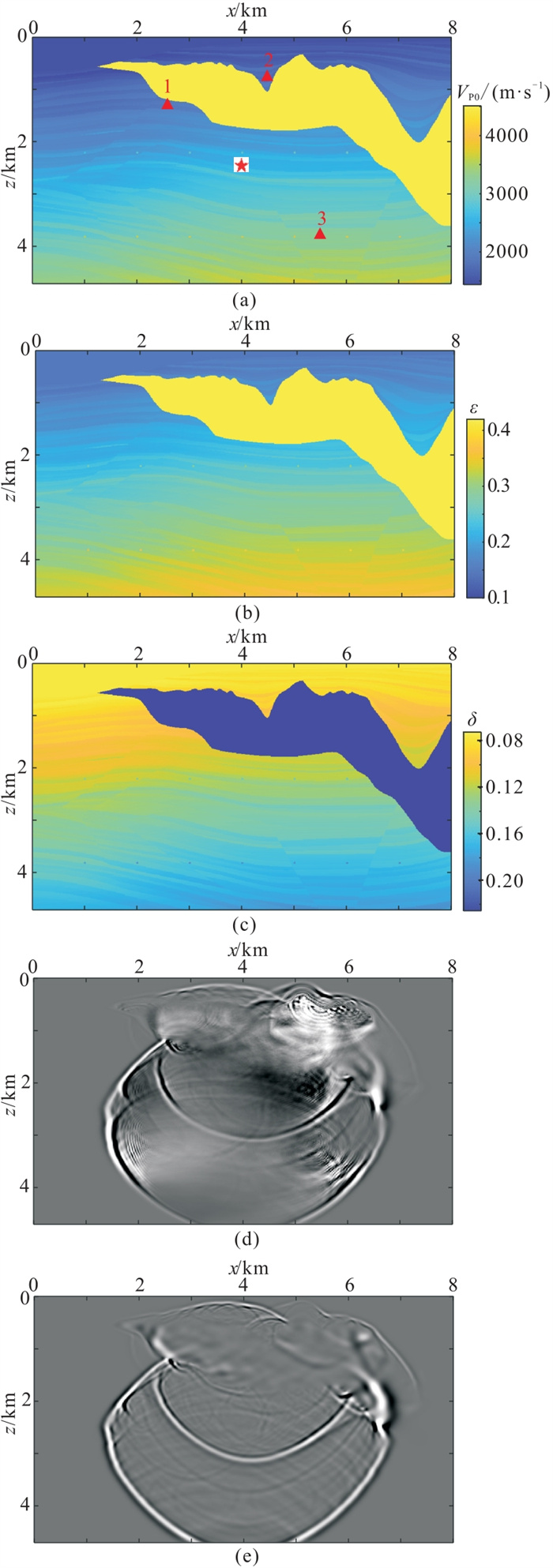
|
图 6 Sigsbee2a模型两种方法的模拟快照对比 (a)VP0模型;(b)ε参数模型;(c)δ模型;(d)基于空间近似的纯qP波波动方程的模拟波场快照(0.9 s);(e)新的纯qP波波动方程的模拟波场快照(0.9 s) |
图 6a~图 6c为Sigsbee2a模型的速度、各向异性参数。在各向异性参数相同的情况下,基于空间近似波动方程模拟的qP波(图 6d)出现了严重的频散,而本文新的波动方程模拟的qP波(图 6e)几乎没有频散。图 7为两种波动方程在三个检波点处记录的波形对比,可以看出空间近似方法模拟的波形振幅与新的方法相比,其振幅变化更大,原因在于:首先,空间近似只能表示一个传播方向,当多个波重叠时,会降低模拟精度[23];其次,空间近似会在一定程度上加重频散现象。而本文新的波动方程在推导过程中没有使用近似,因此对于复杂模型具有更高的模拟精度。
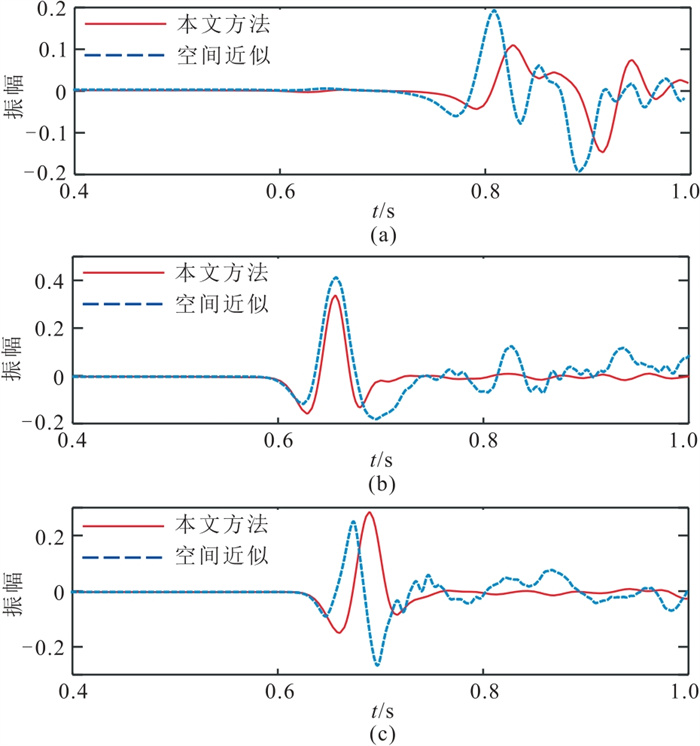
|
图 7 不同检波点Sigsbee2a模型两种方法模拟记录的波形对比 (a)检波点1;(b)检波点2;(c)检波点3 |
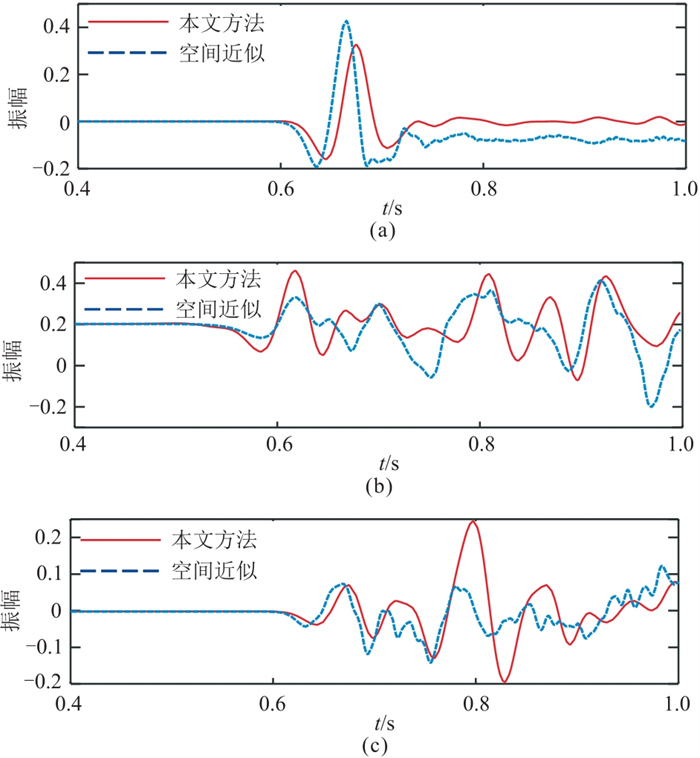
Marmousi-Ⅱ模型的参数如图 8a~图 8c所示。由于受到较为明显的频散干扰,从基于空间近似的纯qP波波动方程模拟的波场快照中(图 8d)无法清晰地观察qP波的传播规律,并且检波点处接收到的波场信息(直达波、反射波)均被频散干扰,使检波点处的记录不够精确(图 9);而本文提出的新波动方程模拟出的波场快照(图 8e)中未发现明显的频散,可以清楚地观察到qP波在复杂介质中的传播规律,检波点处也能够接收到较准确的波场信息(直达波、反射波),由此可进一步说明本文提出的纯qP波方程对稍复杂的模型具有更好的适应性,在正演模拟过程中不容易产生频散,正演模拟结果也更加精确。
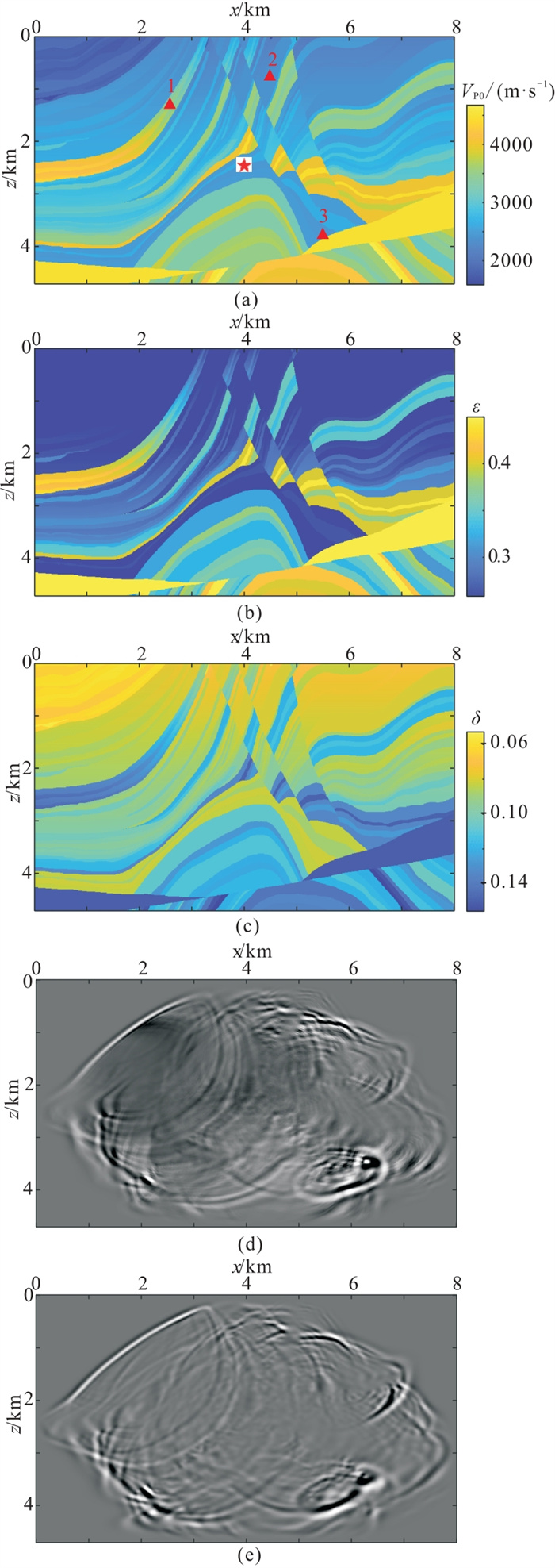
|
图 8 Marmousi-Ⅱ模型及两种方法的模拟快照对比 (a)VP0模型;(b)ε参数模型;(c)δ模型;(d)基于空间近似的纯qP波波动方程的模拟波场快照(0.9 s);(e)新的纯qP波波动方程的模拟波场快照(0.9 s) |
|
图 9 不同检波点Marmousi-Ⅱ两种方法模拟记录的波形对比 (a)检波点1;(b)检波点2;(c)检波点3 |
结合两种模型的各向异性参数的数值分布(图 6b~图 6c、图 8b~图 8c)以及波场快照(图 6d~图 6e、图 8d~图 8e),可以看出波场快照中出现明显频散的地方,其各向异性参数之间的差值
本文基于新声学近似的纯qP波频散关系,通过引入中间变量推导了新的纯qP波波动方程,避免了空间近似带来的误差,从理论上提高了正演结果的精度。
均匀VTI介质模型模拟结果完全消除了qSV波伪影,在
以x方向为例(左、右边界),通过参考复数伸展坐标系[27-28],将新的x方向坐标表示为
| $ \tilde{x}\left(x\right)=x-\frac{\mathrm{i}}{\omega }{\int }_{0}^{x}{d}_{x}\left(s\right)\mathrm{d}s $ | (A-1) |
式中:
| $ {d}_{x}\left(x\right)=\left\{\begin{array}{l}2\mathrm{\pi }\alpha F{\left(\frac{x-{x}_{0}}{{L}_{\mathrm{P}\mathrm{M}\mathrm{L}}}\right)}^{2}\\ 0\end{array}\right. $ | (A-2) |
其中:α为指数常数,通常取1.79;F是子波主频;LPML表示PML吸收层的厚度;x0为边界常数。
对式(A-1)求导可得
| $ \frac{\partial \tilde{x}}{\partial x}=1+\frac{{d}_{x}\left(x\right)}{\mathrm{i}\omega } $ | (A-3) |
记
| $ \frac{\partial }{\partial \tilde{x}}=\frac{\partial }{\partial x}\left(\frac{1}{\xi }\right)=\frac{-\mathrm{i}\omega \cdot {d}_{x}^{\text{'}}\left(x\right)}{{\left[\mathrm{i}\omega +{d}_{x}\left(x\right)\right]}^{2}} $ | (A-4) |
式中
将式(14)中的P和U带入式(A-4)并对其求偏导,可得
| $ \left\{\begin{array}{l}\frac{{\partial }^{2}U}{\partial {\tilde{x}}^{2}}=\frac{{\partial }^{2}U}{\partial {x}^{2}}{\left(\frac{1}{\xi }\right)}^{2}+\frac{\partial U}{\partial x}\frac{1}{\xi }\left[\frac{\partial }{\partial x}\left(\frac{1}{\xi }\right)\right]\\ \frac{{\partial }^{2}U}{\partial {\tilde{z}}^{2}}=\frac{{\partial }^{2}U}{\partial {z}^{2}}{\left(\frac{1}{\xi }\right)}^{2}+\frac{\partial U}{\partial z}\frac{1}{\xi }\left[\frac{\partial }{\partial z}\left(\frac{1}{\xi }\right)\right]\\ \frac{{\partial }^{2}P}{\partial {\tilde{x}}^{2}}=\frac{{\partial }^{2}P}{\partial {x}^{2}}{\left(\frac{1}{\xi }\right)}^{2}+\frac{\partial P}{\partial x}\frac{1}{\xi }\left[\frac{\partial }{\partial x}\left(\frac{1}{\xi }\right)\right]\\ \frac{{\partial }^{2}P}{\partial {\tilde{z}}^{2}}=\frac{{\partial }^{2}P}{\partial {z}^{2}}{\left(\frac{1}{\xi }\right)}^{2}+\frac{\partial P}{\partial z}\frac{1}{\xi }\left[\frac{\partial }{\partial z}\left(\frac{1}{\xi }\right)\right]\end{array}\right. $ | (A-5) |
将波场分裂为
| $ \left\{\begin{array}{l}{\left(\mathrm{i}\omega +{d}_{x}\right)}^{2}{U}_{1}=\left(1+2ε \right)\frac{{\partial }^{2}U}{\partial {x}^{2}}+{Q}_{1}\\ {Q}_{1}=-\left(1+2ε \right)\frac{{d}_{x}^{\text{'}}}{\mathrm{i}\omega +{d}_{x}}\frac{\partial U}{\partial x}\\ {\left(\mathrm{i}\omega \right)}^{2}{U}_{2}=\frac{{\partial }^{2}U}{\partial {z}^{2}}\\ {\left(\mathrm{i}\omega +{d}_{x}\right)}^{2}{P}_{1}=-2\left(ε -\delta \right)\frac{{\partial }^{2}P}{\partial {x}^{2}}+{Q}_{2}\\ {Q}_{2}=2\left(ε -\delta \right)\frac{{d}_{x}^{\text{'}}}{\mathrm{i}\omega +{d}_{x}}\frac{\partial P}{\partial x}\\ {\left(\mathrm{i}\omega \right)}^{2}{P}_{2}=-2\left(ε -\delta \right)\frac{{\partial }^{2}P}{\partial {z}^{2}}\end{array}\right. $ | (A-6) |
则时间域PML吸收边界条件为
| $ \left\{\begin{array}{l}{\left({\partial }_{t}+{d}_{x}\right)}^{2}{U}_{1}=\left(1+2ε \right)\frac{{\partial }^{2}U}{\partial {x}^{2}}+{Q}_{1}\\ \left({\partial }_{t}+{d}_{x}\right){Q}_{1}=-\left(1+2ε \right){d}_{x}^{\text{'}}\frac{\partial U}{\partial x}\\ {\left({\partial }_{t}\right)}^{2}{U}_{2}=\frac{{\partial }^{2}U}{\partial {z}^{2}}\\ {\left({\partial }_{t}+{d}_{x}\right)}^{2}{P}_{1}=-2\left(ε -\delta \right)\frac{{\partial }^{2}P}{\partial {x}^{2}}+{Q}_{2}\\ \left({\partial }_{t}+{d}_{x}\right){Q}_{2}=2\left(ε -\delta \right){d}_{x}^{\text{'}}\frac{\partial P}{\partial x}\\ {\left({\partial }_{t}\right)}^{2}{P}_{2}=-2\left(ε -\delta \right)\frac{{\partial }^{2}P}{\partial {z}^{2}}\end{array}\right. $ | (A-7) |
同理可获得z方向的PML边界条件。
| [1] |
何樵登, 张中杰. 横向各向同性介质中地震波及其数值模拟[M]. 吉林长春: 吉林大学出版社, 1996. HE Qiaodeng, ZHANG Zhongjie. Seismic Waves and Their Modeling in Transversely Isotropic Media[M]. Changchun, Jilin: Jilin University Press, 1996. |
| [2] |
杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移[J]. 地球物理学报, 2009, 52(3): 801-807. DU Qizhen, QIN Tong. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium[J]. Chinese Journal of Geophysics, 2009, 52(3): 801-807. |
| [3] |
ZHANG Q, MCMECHAN G A. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media[J]. Geophysics, 2010, 75(3): D13-D26. |
| [4] |
YAN J, SAVA P. Elastic wave-mode separation for VTI media[J]. Geophysics, 2009, 74(5): WB19-WB32. |
| [5] |
徐世刚, 包乾宗, 任志明. 简化的三维TTI介质黏滞纯声波方程及其数值模拟[J]. 石油地球物理勘探, 2022, 57(2): 331-341. XU Shigang, BAO Qianzong, REN Zhiming. A simplified pure visco-acoustic wave equation for 3D TTI media and its numerical simulation[J]. Oil Geophysical Prospecting, 2022, 57(2): 331-341. |
| [6] |
梁锴, 曹丹平, 孙上饶, 等. 椭球各向异性介质弹性波完全解耦波动方程[J]. 石油地球物理勘探, 2021, 56(6): 1254-1261. LIANG Kai, CAO Danping, SUN Shangrao, et al. The complete decoupled wave equations for ellipsoidal anisotropic media[J]. Oil Geophysical Prospecting, 2021, 56(6): 1254-1261. |
| [7] |
ALKHALIFAH T. Acoustic approximations for processing in transversely isotropic media[J]. Geophysics, 1998, 63(2): 623-631. |
| [8] |
ALKHALIFAH T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4): 1239-1250. |
| [9] |
DU X, BANCROFT J C, LINES L R. Reverse-time migration for titled TI media[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 1930-1933.
|
| [10] |
ZHOU H, BLOOR R, ZHANG G. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 194-198.
|
| [11] |
HESTHOLM S. Acoustic VTI modeling using high-order finite differences[J]. Geophysics, 2009, 74(5): T67-T73. |
| [12] |
吴国忱, 梁锴. VTI介质频率―空间域准P波正演模拟[J]. 石油地球物理勘探, 2005, 40(5): 535-545. WU Guochen, LIANG Kai. Quasi-P wave forward modeling in frequency-space domain in VTI media[J]. Oil Geophysical Prospecting, 2005, 40(5): 535-545. |
| [13] |
吴国忱, 梁锴. VTI介质qP波方程高精度有限差分算子[J]. 地球物理学进展, 2007, 22(3): 896-904. WU Guochen, LIANG Kai. High precision finite difference operators for qP wave equation in VTI media[J]. Progress in Geophysics, 2007, 22(3): 896-904. |
| [14] |
DUVENECK E, MILCIK P, BAKKER P M, et al. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2186-2190.
|
| [15] |
XU S, ZHOU H. Accurate simulations of pure quasi-P‑waves in complex anisotropic media[J]. Geophysics, 2014, 79(6): T341-T348. |
| [16] |
XU S, TANG B, MU J, et al. Quasi-P wave propagation with an elliptic differential operator[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 4380-4384.
|
| [17] |
GRECHKA V, ZHANG L, RECTOR J W. Shear waves in acoustic anisotropic media[J]. Geophysics, 2004, 69(2): 576-582. |
| [18] |
ZHANG H, ZHANG G, ZHANG Y. Removing S-wave noise in TTI reverse time migration[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2849-2853.
|
| [19] |
张岩, 吴国忱. TTI介质qP波逆时偏移中伪横波噪声压制方法[J]. 地球物理学报, 2013, 56(6): 2065-2076. ZHANG Yan, WU Guochen. Methods of removing pseudo SV-wave artifacts in TTI media qP-wave reverse-time migration[J]. Chinese Journal of Geophysics, 2013, 56(6): 2065-2076. |
| [20] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. |
| [21] |
XU S, STOVAS A, ALKHALIFAH T, et al. New acoustic approximation for transversely isotropic media with a vertical symmetry axis[J]. Geophysics, 2020, 85(1): C1-C12. |
| [22] |
LIANG K, CAO D, SUN S, et al. Decoupled wave equation and forward modeling of qP wave in VTI media with the new acoustic approximation[J]. Geophysics, 2023, 88(1): WA335-WA344. |
| [23] |
CHEN T, GEORGE A M. Multidirectional slowness vector for computing angle gathers from reverse time migration[J]. Geophysics, 2016, 81(2): S87-S100. |
| [24] |
LIU F, MORTON S A, JIANG S, et al. Decoupled wave equations for P and SV waves in an acoustic VTI media[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2844-2848.
|
| [25] |
王辉, 何兵寿, 邵祥奇. 一阶速度—胀缩—旋转弹性波方程交错网格数值模拟[J]. 石油地球物理勘探, 2022, 57(6): 1352-1361. WANG Hui, HE Bingshou, SHAO Xiangqi. Numerical simulation of first-order velocity-dilatation-rotation elastic wave equation with staggered grid[J]. Oil Geophysical Prospecting, 2022, 57(6): 1352-1361. |
| [26] |
刘有山, 刘少林, 张美根, 等. 一种改进的二阶弹性波动方程的最佳匹配层吸收边界条件[J]. 地球物理学进展, 2012, 27(5): 2113-2122. LIU Youshan, LIU Shaolin, ZHANG Meigen, et al. An improved perfectly matched layer absorbing boun-dary condition for second order elastic wave equation[J]. Progress in Geophysics, 2012, 27(5): 2113-2122. |
| [27] |
CHEW W, LIU Q. Using perfectly matched layers for elastodynamics[C]. IEEE Antennas and Propagation Society International Symposium, 1996, 366-369.
|
| [28] |
BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. |



 范娜, 湖北省武汉市蔡甸区蔡甸街大学路111号长江大学(武汉校区)地球物理与石油资源学院,430100。Email:
范娜, 湖北省武汉市蔡甸区蔡甸街大学路111号长江大学(武汉校区)地球物理与石油资源学院,430100。Email: