2. 成都工业学院智能制造学院, 四川成都 611730
2. School of Intelligent Manufacturing, Chengdu Technology University, Chengdu, Sichuan 611730, China
地震波初始拾取是地震数据处理的关键问题之一。随着地震数据量的不断增加,人工拾取已难以满足地震监测实时数据处理需求[1],为此研究人员提出了不同自动拾取方法。经典的自动拾取方法大致分为两类:时域类和频域类。时域类方法通常基于信噪比突变原理,常用方法有长短时均值比(STA/LTA)法[2-3]、赤池信息准则(AIC)法[4-7]、分形维数法[8-9]和相关法[10-13]。STA/LTA法通过比较短期和长期时间窗口内的信号能量比值确定地震事件的起始时间。通过改变窗口的选择方式,该方法可拓展为修正能量比法[14-15]、改进Coppens方法[16],这些方法计算简单,但对噪声敏感,拾取准确率不高。AIC法的基本原理是求取地震信号AIC函数的最小值[17],而真实的初至位置可能位于AIC函数的局部最小值点,因此该类方法适于初至大致位置已知的情况。分形曲线具有某种自相似或自仿射形式,通过检测背景噪声与噪声+信号之间分形维数值的变化可确定初至[16],但该方法计算量大,效率较低,不适合于单独拾取初至。相似震源位置及破裂机理的地震事件通常在地震记录上表现出相似的波形特征[18],波形相关法则是利用这一特点,通过高质量的波形模板可以确定其他地震道的初至时间,但此方法对波形与主事件不同的事件不敏感,并且在地震信号受大量噪声干扰时,难以确定合适的参考波形。频域类方法有短时傅里叶变换(STFT)[19]、小波变换(WT)[20-23]、希尔伯特—黄变换(HHT)[24-25]和S变换[26]等。同一窗口下,STFT不能同时拥有高时域分辨率和高频域分辨率。噪声较强时,WT会出现过度分析的问题。HHT部分参数的选择没有统一标准,且需要对输入数据的长度进行控制。S变换有较好的全局分析能力,但无法提供局部时频信息。
上述地震拾取方法都有一定的局限性,没有一种方法适用于所有的情况。为了提高初至拾取的精度和速度,学者们一方面将已有的算法相互结合形成新的算法[27-30],另一方面将人工智能方法引入地震拾取[31-32]。人工智能方法相对于经典自动拾取方法精度更高、速度更快,已经在初至拾取方面取得了很好的效果,本文对此进行总结和分析。
从图 1可以看出相关文献数量逐年增加,初至拾取依旧是地震数据处理的研究热点。本文从传统机器学习和深度机器学习(深度学习)两方面对初至拾取方法进行总结和分析,以期能为地学领域的研究提供参考。
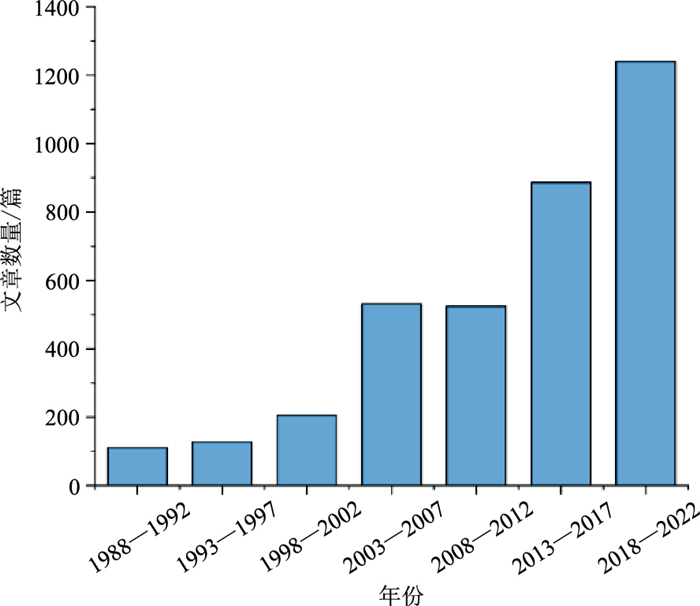
|
图 1 初至拾取研究文献数量(1988—2022年) 统计数据来自谷歌网站。 |
基于传统机器学习的初至拾取方法主要有聚类算法、支持向量机(SVM)和反向传播神经网络(BPNN),这类方法的关键在于选择与初至相关的特征表示和建立适当的目标函数或分类模型。合适的特征主要是以运动学或动力学为基础的地震属性,如振幅、波形、频率、能量、相关、比率等[33]。目标函数或分类模型可依据实际需求设计,根据数据特点调整和优化,以达到较好的初至拾取效果。
2.1 基于聚类算法的初至拾取地震记录中,噪声信号具有相似性,地震事件信号也具有相似性,但两者具有不同的特征,因此聚类算法可实现初至波的拾取。聚类算法属于无监督算法,优势在于使用的数据是没有标记的原始数据。应用于初至拾取的聚类算法主要有K均值聚类、模糊C均值(FCM)聚类、分层聚类(HC)、谱多流形聚类(SMMC)等。本节主要介绍K均值聚类、FCM聚类和其他聚类地震初至拾取方法。
2.1.1 基于K均值聚类的初至拾取K均值聚类属于硬聚类,即每一个数据点只能属于一类,在地震初至拾取中通常演变为二分聚类问题,即K=2,其目标函数为
| $ J=\sum\limits_{{\boldsymbol{x}}_{i}\in {\boldsymbol{C}}_{1}}{‖{\boldsymbol{x}}_{i}-{\boldsymbol{u}}_{1}‖}_{2}^{2}+\sum\limits_{{\boldsymbol{x}}_{i}\in {\boldsymbol{C}}_{2}}{‖{\boldsymbol{x}}_{i}-{\boldsymbol{u}}_{2}‖}_{2}^{2} $ | (1) |
式中:xi是样本的特征向量;C1和C2分别代表初至集群和非初至集群;u1和u2是集群C1和C2中心的特征向量。
Chen[34]利用K均值实现了地面微地震信号的波形检测。该方法的优点在于保留了事件的初至信息(波形分量的第一索引,即初至时刻)和波形特征,能直接反演震源位置。如果直接使用K均值聚类,算法容易陷入局部最优值。针对这个问题,Ma等[35]提出了一种基于局部线性嵌入(LLE)和改进粒子群优化(PSO)的聚类算法,用于微地震三分量数据的初至拾取。该方法在局部线性嵌入降维的同时能够保留高维数据的固有规律。改进的PSO算法通过全局搜索,可从低维数据中选出最优聚类中心,避免K均值聚类陷入局部最优值,提高了聚类的准确率。根据重要程度赋予不同权重的办法也可避免陷入局部最优解的情况。周竹生等[36]采用了这一策略,同时利用相位差自适应时间校正法校正超过阈值的异常地震道。对于地面和井下微地震数据,该算法具有较好的噪声适应性和准确性。但是属性选取过多会造成特征冗余。Li等[37]采用ReliefF算法实现了最优特征的自动选择,相对于未进行特征选择的K均值初至拾取,该算法可消除冗余特征的不利影响,在低信噪比条件下具有更高的计算效率和稳定性。为了提高算法在复杂近地表条件下的性能,需要进一步优化算法,以确保拾取结果的准确性。常用的优化思想是首先确定初至波的大致范围,再准确拾取初至时刻。李康丽等[38]基于此思想,首先进行高维多属性K均值聚类,再通过马尔可夫智能决策(MDP)完成初至时刻的准确拾取。该算法利用了相邻地震道间的相关性,拾取结果具有横向连续性。高磊等[39]进一步完善了此优化策略,所提算法包含四个步骤:①使用K均值聚类选取初至波簇;②使用基于密度的噪声应用空间聚类(DBSCAN)技术实现初至拾取;③利用线性回归补全缺失值;④利用能量比值法调整错误初至。显然,初至拾取后再微调的算法在拾取结果方面优于只拾取、未微调的算法。Zhu等[40]提出了一种时间序列分割聚类(TSSC)算法,用于S波到达时间拾取。这种方法首先用AIC方法得到P波初至时刻,再利用K均值算法确定P波与S波的分界点,即S波初至位置。TSSC方法考虑了P波和S波记录在时间上连续、在空间上彼此独立的特性,该算法计算简单,但S波拾取结果会受P波拾取结果影响。与前面提到的方法相比,TSSC方法不需要迭代计算。基于K均值聚类算法初至拾取的代表性工作如表 1所示。
|
|
表 1 基于K均值聚类算法初至拾取的代表性研究成果 |
模糊C均值聚类算法属于软聚类,即一个样本点可以属于不同的类,以隶属度表示属于每一类的可能性。在微地震拾取中,FCM方法能增强微地震信号的特征,降低噪声影响。相对于K均值方法,FCM对弱信号的检测能力更强,聚类结果也更稳定可靠,其目标函数为
| $ J=\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{Q}{U}_{ij}^{m}{d}_{ij}^{2} $ | (2) |
式中:N是样本数量;Q是集群数量;Uij为隶属度;m是模糊指数;dij表示第i个样本到第j类集群中心的距离。利用FCM算法进行地震拾取的流程见图 2。
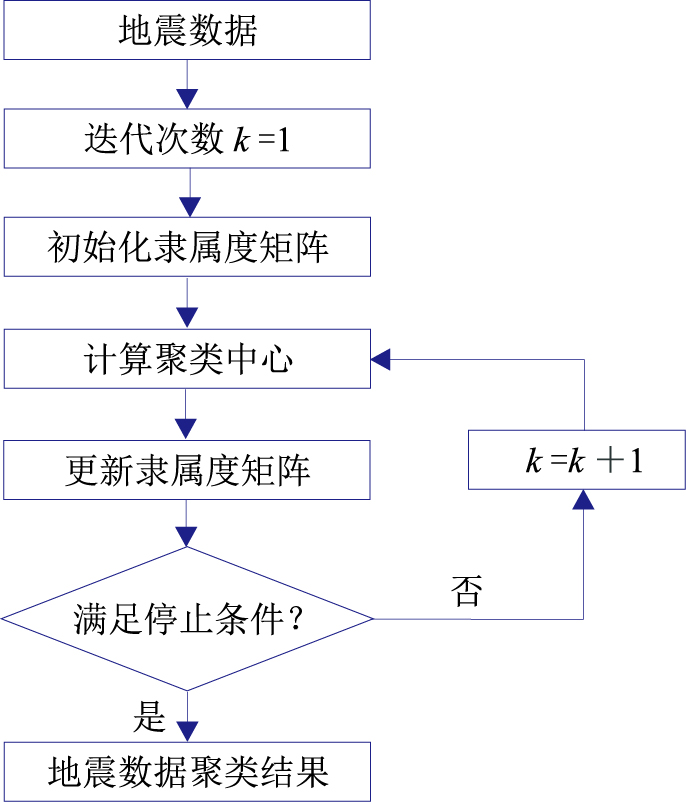
|
图 2 基于FCM聚类的地震拾取流程[46] |
Zhu等[41]首次将FCM算法引入微地震三分量信号分析,通过试验确定模糊指数,算法能有效平衡噪声干扰和弱信号检测,这项关键性研究为后续研究奠定了基础。若FCM聚类初始化选择不合理,对具有高维特征、结构复杂、类别不平衡或存在噪声和异常点的数据集会表现出高敏感性。为了克服这些问题,Pal等[42]提出模了糊可能性C均值算法(FPCM),Saad等[43]利用该算法计算地震信号的到达时间。与FCM方法相比,FPCM算法表现出更高的准确率和更快的速度,可处理低至-10 dB的地震信号,适用于地震预警系统。Gao等[44]提出了一种基于滑动窗口和模糊C均值的初至旅行时提取算法(FPSF),利用垂向窗口确定单道初至范围,利用水平窗口调整相邻初至间隔。基于这两种滑动窗口能减少90%的数据,提高初至拾取的精度。FPSF算法的缺点是窗口大小和最佳结果需要手动选择。为解决这一问题,Gao等[45]又将自适应阈值和空间约束聚类(FASC)应用于初至拾取。空间信息约束提高了算法的抗噪能力,将其应用于新疆和四川的数据集,FASC算法的准确率优于FPSF算法。拾取准确率不仅与算法相关,还受微震信号信噪比的影响,信噪比越高,拾取效果越好。谭家炜等[46]使用超级虚折射干涉(SVI)约束模糊C均值,SVI能在远道极低信噪比情况下增强初至信号,压制随机噪声。早期是通过人工选择固定阈值,挑选困难且不适用于所有场合。为此,Lan等[47]引入了一种自适应选择方法,该方法利用最终标签和隶属度向量之间的相关系数确定最优阈值。相比于固定阈值的FCM算法,基于自适应阈值的FCM在合成数据和地面监测煤矿数据的应用中显示出更高的鲁棒性。为了消减不同背景噪声和不规则近地表带来的影响,Gao等[48]提出了模糊C均值和局部加权回归(FPFR)算法,该算法的实现包括两个子程序:第一个子程序通过FCM和自适应聚类选择得到初步的拾取结果;第二个子程序将鲁棒局部加权回归和遗传算法相结合,解决了算法参数设置敏感的问题,能够纠正初至拾取中的异常点。Cano等[49]和Lan等[50]将FCM方法和AIC方法同时应用于初至拾取。前者利用偏振属性将FCM算法识别的波形间隔分为P波、S波和未识别波,然后通过AIC方法确定初至时间,通过二次函数拟合P、S波的移动曲线对未识别波进行归类;后者未细分震相,但进行了特征及其维度的选择,并直接使用AIC方法对FCM的初选结果进行调整。Cano等[49]提出的方法繁杂,仅适用于事先监测到的事件,在低信噪比情况下表现一般,但其能够处理包含多种初至情况的微地震三分量数据,如某些波形含P波、S波两种初至,有些只含其中一种初至;Lan等[50]提出的方法对-7 dB的高斯白噪声(WGN)数据集和1 dB的真实噪声数据集(RN)可以保证100%精度。多方法结合的初至拾取,精确度会有所提升,但会牺牲计算速度,目前只适合处理离线数据和采样率较低的实时微地震数据。基于FCM聚类初至拾取的代表性研究成果见表 2。
|
|
表 2 基于FCM聚类算法初至拾取的代表性研究成果 |
K均值聚类和FCM聚类在初至拾取中应用最广,还有一些其他聚类算法也在初至拾取中表现出良好性能,如谱多流形聚类、分层聚类。谱多流形聚类是谱聚类的一种变形,通过结构相似性和局部相似性构造亲和矩阵,能够更好地处理非线性和复杂结构的聚类问题。2017年,谱多流形聚类[51]首次应用于三分量P波初至拾取,通过2D流形特征对噪声和信号进行分类。与以地震道为单位进行聚类处理不同,此方法将不同地震道上同一时间的采样数据作为一行数据进行处理。因此,每行中的信号流形特征相对较少,在低信噪比条件下,需要在拾取前对微地震数据进行剩余静校正处理。HC是一个树形结构,树结构中的叶与数据点相对应,树内部节点与层次结构间的聚类相对应。在微地震拾取中,该方法表现为循环度量簇间距离和合并簇,直到只剩下信号簇和非信号簇。Huang[52]利用HC算法进行井下数据拾取时,从能量角度提出两个新的统计指标,能更好地评价聚类或分类中地震信号识别性能。
2.2 基于SVM的初至拾取基于SVM将高维地震信号映射到低维空间,并在低维空间通过处理所有样本点找到最优超平面,将地震数据中所有噪声采样点和所有信号采样点分开,规定噪声和信号之间的跳变点为信号初至。SVM是基于结构风险最小化思想,当地震数据较少时,与基于经验风险最小的神经网络拾取相比,其效果更好,但计算过程复杂,训练时间会随着数据量的增加而增大。
Chen等[53]采用一种加权SVM方法检测经过小波去噪的5道实际地震记录。通过增加信号权重和减小噪声权重解决地震数据样本不均引起的问题。研究证实,在小样本情况下,这种方法优于传统的人工神经网络。Zhao等[54]提取了71个时域和频域特征,用于训练初始模型,其中16个特征被证明是区分噪声与微地震事件的相关特征,并用于训练最终的SVM模型。实验结果表明,基于高斯核函数的SVM在训练时间和预测精度方面都优于基于线性核函数和基于多项式核函数(二次核和三次核)的SVM。只考虑1D特征会损失很多重要信息,因此Qu等[55]在Zhao等[54]研究基础上增加了2D纹理特征,通过单变量特征选择和随机森林进行特征筛选,还提出一种C-SVM模型,通过系数控制误差项容限,该模型能在强烈噪声环境中进行初至拾取。随后,Qu等[56]又对该方法进行扩展,增加了2D纹理特征的数量,与卷积神经网络(CNN)相比,在数据非常有限时表现更好。蒋一然等[57]设计了两种基于SVM的分类器用于识别震相:地震信号探测器(SSD)用于分离噪声和震相;震相分离器(SPS)利用三分量数据的偏振和主频信息区分P波和S波。为了提高震相识别的准确性,学者们进一步运用传统方法和台阵信息对分类进行时空约束,但精确度有待提高。Duan等[58]在常用特征属性的基础上,基于互相关原理引入三个多地震道属性。由于新属性具有空间信息,因此在同一项目中,只需对少量数据进行训练,SVM就可以达到分类要求。王腾[59]提出一种人工蜂群优化支持向量机(ABC-SVM)方法,该方法通过人工蜂群算法优化SVM的参数设计,得到最优分类超平面,对极低信噪比的三分量合成数据和真实微地震数据进行初至点拾取,结果准确且无漏拾取情况。针对训练样本不足和无质量标签的问题,Li等[60]将特征迁移学习(TTL)与蒋一然等[57]提出的两种SVM分类器结合,通过查找源域与目标域的共同特征表示,可以拾取不同环境和地质条件下的地震三分量数据的初始到达点。基于SVM方法初至拾取的代表性研究成果见表 3。
|
|
表 3 基于SVM方法初至拾取的代表性研究成果 |
BPNN由输入层、若干中间隐藏层和输出层相互连接构成[61],学习过程包括信息前向传播和误差反向传播两个步骤(图 3)。基于BPNN的地震初至拾取可以看作模式识别中的分类任务,网络将规定的节点(如波峰、波谷和振幅零点位置等)或片段(如地震波的某个半周期或某几个采样点范围等)判断为初至或者非初至。BPNN能较好地拟合非线性地震数据,具有较高精度和效率。但是,该网络学习速度较慢,容易陷入局部最小值,且地震数据的高维特征不能直接作为网络的输入属性。

|
图 3 BPNN结构图 x0,x1,…表示输入,y0,y1,…表示输出。图 6同。 |
基于BPNN的震相初至拾取研究始于20世纪90年代[62-64],初始网络深度一般为三层或四层,应用于较简单的数据时,拾取速度优于人工。研究发现,节点和隐藏层的几种组合中,隐藏层含10个节点时效果最优[63]。为提高拾取准确率、加快网络收敛和避免代价函数陷入局部最小值,学者们从训练数据、输入特征属性、拾取位置和优化算法四个方面开展研究。在训练数据方面,使用较高和较低频率数据训练网络,能够成功拾取频率变化的波形;当网络应用于比训练数据信噪比更差的数据时,其性能严重下降[64]。在特征属性方面,相比单一的振幅属性,不同的时间序列属性能携带更多的初至信息。McCormack等[64]的研究表明,以二进制像素图像作为输入是一个不错的选择。在拾取位置方面,以多样本点为初至,比拾取单一样本点更稳定,但同时也引入了误差。在优化算法方面,Maity等[65]使用遗传算法进行网络训练,网络可以更好地学习和收敛,提高了模型性能。针对近地表复杂区域地震资料存在假初至、多干扰波的情况,兰金涛等[66]通过分析影响初至波分布的因素,提出用神经网络确定初至的大致范围。对于实际数据,该方法能够隔离初至附近的干扰。宋建国等[67]提出一种基于一个三层BPNN结构的级联相关算法,解决了传统BPNN算法收敛速度慢和传统级联相关网络计算量大的缺点,并且能扩展网络去学习新的样本,但对低品质地震数据的拾取效果不佳。曹晓莉等[68]为提高初至拾取的精度和效率,利用综合动量和可变学习速度改进BPNN的权值更新过程,改进的网络比传统的BPNN拾取误差更小,结构也更稳定。由于BPNN自身的局限性和深度学习的兴起,近年来,该方法逐渐被其他网络取代。
3 基于深度学习的地震拾取随着深度学习的兴起,神经网络结构朝更复杂的方向发展。基于深度学习的方法往往遵循以下五个基本步骤:①收集数据,并将其划分为训练集和测试集,有时还会需要分出一个验证集。训练集用于训练模型,验证集用于调整模型结构和超参数,防止过拟合,测试集用于验证模型性能。②预处理,通过裁剪、清理、特征提取和归一化等,将数据转换为更适合的形式,提高机器学习算法的性能,如初至拾取的准确度、精确度和速度等。③训练模型,根据任务建立的代价函数调整模型参数。④评估模型性能,常用评估标准有准确率、召回率、F1分数、误差平均值等。⑤将训练好的模型用于新数据的产生。
3.1 基于CNN的初至拾取CNN提供了一种有效结构,能够自动学习地震数据特征,包括用专业知识也难以解释的复杂特征,可提高初至拾取的效率和准确性,降低时间成本。CNN结构包括一个输入层、一个输出层和若干中间层,中间层主要由卷积层、池化层和全连接层构成。卷积层通过内核自动提取地震数据的深层特征,池化层可以降低特征的维度和尺度,全连接层将特征空间表示映射到样本标记空间。经过这些处理过程就能够得到地震波初至拾取结果。用于初至拾取的CNN可分为两种类型:一是经典的CNN结构(图 4),模型最后的结构为全连接层;二是模型中没有全连接层的全卷积神经网络(FCN)。
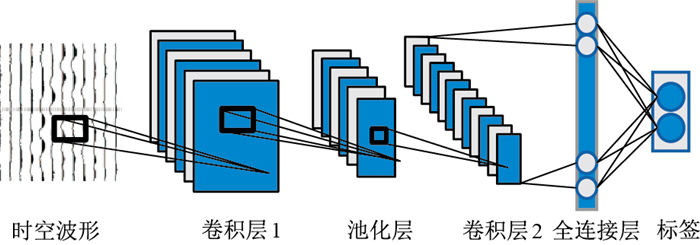
|
图 4 基于CNN的微震初至拾取[69] |
Ross等[70]利用南加州地震台网(SCSN)记录的垂直分量数据训练CNN,该网络包含三个卷积层和两个全连接层。通过回归方法确定P波到达时间。研究表明,在75%的情况下,网络预测的初至时间与人工选择结果的时间差在28 ms以内。随后,Ross等[71]又提出广义相位检测(GPD)算法,它在数百万个三分量地震记录上学习P波、S波和噪声的广义表示,能够可靠地检测低震级事件的P波和S波,在训练集未覆盖的数据上也能得到可接受的结果,这项研究成果填补了模板匹配的空缺。Zhu等[72]将训练数据从数百万个缩减到几千个,训练出一种适用于中、小数据集的相位识别分类器(CPIC),在汶川7.9级余震数据集上的初至拾取准确率大于95%。此项研究的另一个重要贡献是发现分类器具有不同数量全连接层(1层、2层、3层)时,准确率没有明显差异,这一结论可应用于简化网络结构。于子叶等[73]在CNN中加入Inception层构成新的结构,实现了不同尺度特征的提取和训练参数的减少。但因缺乏相关训练数据,对于远震三分量数据,该模型对于P波、S波初至提取的准确率不如人工。李健等[74]提出一种多任务的CNN模型,采用联合损失函数。与首先检测震相再拾取的方法不同,该模型在全连接部分分为两个支路,能同时实现分类(震相识别)和回归(初至拾取)任务。全连接层之前的结构为模型的共享层,可用于迁移学习,提高模型的泛化能力。基于迁移学习理念,Johnson等[75]使用相对较少的采矿地震数据重新训练了Ross等[70]的模型,采用训练后的模型的识别效果与人工识别相当。迁移学习不仅适用于相同类型的数据,也能对不相关的数据进行模型迁移。在ImageNet图像数据集上预训练的三种CNN模型(AlexNet、GoogLeNet和SqueezeNet)经微调后,可用于地震波形的分类。当以地震道连续小波变换(CWT)特征图像作为输入时,三种CNN都获得了比STA/LTA和自适应多波段算法更好的拾取结果[76]。此外,胶囊网络[77]的应用和数据增强[78-79]也可降低CNN对大量标记数据的依赖性。原始胶囊网络没有池化层,可以获取更多的信息,因此基于胶囊单元的模型往往具有更轻量化的结构和更好的泛化能力。Guo等[80]以实验室声发射(AE)数据的波形和高阶统计量作为CNN的输入,这两种输入能使网络获得更丰富的信息。缩小范围进行拾取的方法可以减少负面样本,提升拾取精度和速度。如Li等[81]先用目标检测模型YOLO网络提取微地震波形区域,再用回归方法CNN预测P波和S波的初至时间。
3.1.2 全卷积神经网络(FCN)初至拾取刘佳楠等[82]构建了三种不同深度的FCN用于地震初至半波拾取,其最优网络拾取性能明显优于商业地震处理软件TomoPlus。U-Net[83]是在FCN基础上提出的,由编码器、解码器和跳跃连接三部分组成,可实现端到端的学习。其中,编码器用于缩小尺寸、逐渐提取全局特征;解码器用于恢复尺寸和信息;跳跃连接是编码器和解码器特征融合的媒介。Zhu等[84]使用1D U-Net(PhaseNet,图 5)预测美国北加州地震台网(NCEDC2014)记录的三分量波形数据中P波、S波和噪声的概率分布,并将P波、S波概率分布的峰值作为初至。该方法的重要特点是不受一个时间窗内地震次数的限制。Chai等[85]将PhaseNet迁移到水力压裂的井下三分量数据的初至拾取与人工拾取结果相比,获得较少的P波拾取和更多的S波拾取,二者精度相当。Hu等[86]以2D数据作为U-Net的输入,学习了不同质量的数据集(山地、黄土高原和爆炸震源)时间和空间上的初至到达特征,因此模型能够直接迁移到更简单数据集上。Han等[87]对U-Net在初至拾取上的应用开展了进一步的研究,以3D地震的归一化波形数据和能量表象作为模型输入,通过对合成数据与海底节点数据的测试结果进行对比,表明该网络能够忽略错误的标签。与2D U-Net相比,3D U-Net预测的旅行时更连续,在噪声存在的情况下更加稳健。值得注意的是,2D U-Net和3D U-Net并未进行S波的拾取,且这三种U-Net结构因输入数据的维度不同而有所差别。
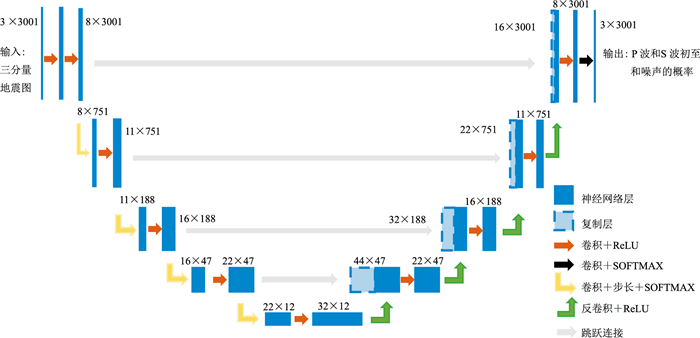
|
图 5 U-Net结构图[84] |
初至拾取还可视为图像分割任务[88]。Wu等[89]应用SegNet分割地震数据,初至时刻将一维图像分为包含和不包含微地震事件的两个部分。当SegNet学习了各种随机缺失迹线的炮集后,即使随机缺失迹线达到50%[90],也可以直接从具有稀疏分布迹线或缺失迹线的炮集拾取初至。与U-Net相比,SegNet不需要学习上采样参数。Pardo等[91]构建了Cospy模型,模型通过霍夫投票模块综合分割和回归两个网络的输出结果,细化了位置预测。为获得更好的分割性能,Yuan等[92]和吴雨鑫[93]分别用Lovasz Loss、Focal Loss代替传统的交叉熵损失,这两种新的损失函数会更加关注困难样本。
网络构架间合理的结合也能获得更好的拾取性能。Wang等[94]开发的PickNet模型由修改的VGG-16和丰富的侧输出残差网络组成,侧输出组合可以使模型对具有各种尺度和纵横比的信号具有鲁棒性。该方法能拾取震中距高达1000 km地震波的初至,这个范围远大于其他模型,其缺点是只能在提供目录的情况下使用[95]。陈德武等[96]提出的U-SegNet结合了U-Net和SegNet的优点,可以在融合特征以及保留图元轮廓信息的同时加快收敛。该方法训练周期短、拾取效率高,在工业化应用方面具有发展前景。陈德武等[97]将残差块引入U-Net的跳跃连接部分,解决了低维特征和高维特征直接融合引起的误差缺陷。
U-Net++是传统U-Net结构的改进和扩展,它综合了长连接和短连接,可视为不同深度U-Net结构的组合,因此在初至拾取时能够通过整合不同层次的特征提升精度[98]。Zhang等[99]在U-Net++最后一个下采样中添加残差块,构造了残差链路嵌套U-Net网络(RLU-Net)。残差块的添加使网络能够获取微地震数据深层特征,模型的鲁棒性和泛化能力得到提高。用于初至拾取的CNN模型的代表性结构和研究成果见表 4。
|
|
表 4 基于CNN初至拾取的代表性研究成果 |
RNN可以处理长度可变的时序数据,能将上一个时间步的信息传递到下一个时间步。在处理地震数据时,RNN模型常采用长短期记忆(LSTM)和门控循环单元(GRU)等变体,这些变体可以决定记忆单元时间状态的去留,所以在处理地震数据时有更大优势。图 6为基于循环神经网络的震相拾取示意图。首先,将地震信号分割成较小的时间窗口;然后,将窗口中的时序特征输入以循环神经网络为主干的初至拾取网络;最后,得到初至拾取结果。
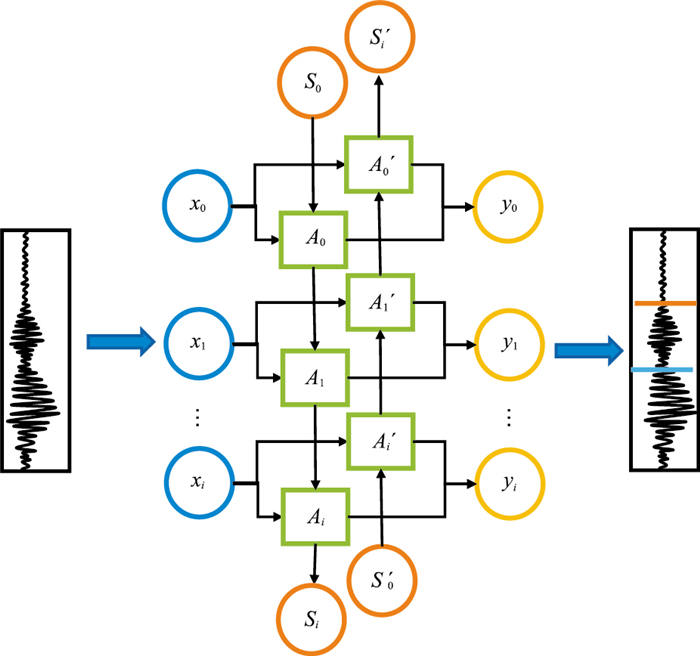
|
图 6 基于RNN的震相拾取 A0,A1,…和A0',A1',…分别表示正向和反向计算网络隐藏层保存的值;S0,S1,…和S0',S1',…分别表示表示正向和反向隐藏层的状态。 |
Zheng等[100]利用煤样岩石力学实验的AE波形数据进行训练并测试了LSTM网络,实验结果表明对于低SNR数据的初至拾取准确度不高。此方法存在两个问题:一是含噪数据太少,导致模型过拟合;二是单向的LSTM使得RNN只能获取前文信息。后续研究主要从两个方面改进模型结构:为获取地震记录上、下文信息,将模型调整为具有双向性的构架;将CNN引入RNN,作为前置处理器,提供有用的特征表示。Birnie等[101]在Zheng等[100]的研究基础上使用两个LSTM单元构成双向结构,仅在合成地震数据集上训练的模型成功运用于陆地井数据和海洋环境微地震记录,突出了网络的稳健性。Zhou等[102]将CNN检测出的地震事件图传递给具有双向GRU的震相拾取网络PpkNet,该算法对汶川地震余震数据的拾取效果良好。Mousavi等[103]开发了一种CNN-RNN地震探测器CRED,在一个残差结构中组合了卷积层和双向LSTM单元,能够利用三分量数据对微地震事件进行可靠监测。当用GRU代替LSTM时,网络具有非常相似的精度和误差。与STA/LTA、模板匹配和FAST算法相比,该方法可提高准确度,同时,在减少误报检测方面表现出更高的性能。随后,Mousavi等[104]又对斯坦福大学地震数据集(STEAD)训练了一个具有分层注意力机制的网络模型EQTransformer,并成功应用于日本地震记录数据的处理。该模型性能优于CRED,拾取P相和S相初至的精确度较高,同时具有更高的效率和灵敏度。针对一些只有1C记录的数据,Zheng等[105]设计了一个由U-Net结合GRU结构的深度神经网络(SC-PSNET),进一步提出通过信号时频分析设计标签向量的宽度。与大部分混合网络相似,SC-PSNET具有震相检测和初至拾取两项功能,相比于PhaseNet,该网络可以提高S相识别和初至拾取精度。Liao等[106]使用中国台湾地区不同震源机制、广泛的深度和震级分布的地震记录来训练和测试ARRU震相拾取器,通过将软注意力门和递归残差卷积单元融合到U-Net架构来抑制地震相位无关波形的响应并增强多个尺度地震图的时间连接,在处理未知数据时表现出较好的泛化能力。近来,学者们还提出了基于阵列的相位拾取方法,该方法是基于地震阵列中不同台站之间地震相位的空间相干性。EdgePhase[107]是一个多站相位拾取模型,该模型集合了边缘卷积模块与EQTranformer。与标准EQTransformer相比,EdgePhase在南加州数据集(SCSN2021)上的查准率和F1分数均提高了5%。此外,研究人员进一步将EdgePhase模型用于检测2020年希腊M7.0地震后的早期余震,与本地地震记录相比,检测到了更多事件,且事件分布更符合平面断层界面特征,表明该方法在实际应用中具有很强的泛化能力。现有的RNN模型难以安装在小型物联网设备上,为此,Lim等[108]基于EQTransformer提出了一个轻量级模型LEQNet,该模型利用深度可分离卷积、循环神经网络和瓶颈结构等模型轻量化技术,在保证性能的同时模型参数量减少了87.68%,模型规模减小了79%。基于RNN拾取的几种混合网络模型性能统计见表 5。
|
|
表 5 基于RNN的混合网络模型拾取性能对比 |
本文叙述了机器学习在解决地震波初至拾取上的应用和趋势。在微地震监测方面,传统机器学习方法较深度神经网络应用更广泛。天然地震的初至拾取情况则与之相反。分析其原因,有如下几点:一是天然地震的数据量远远大于微地震,在需要数据驱动的深度神经网络方面,训练效果更好;二是微地震通常发生在局部范围,能量较小,频率较高,地震波的特征相对简单、清晰,相对容易提取,而天然地震通常具有更大的能量和更广泛的频率范围,其波形特征提取较困难;三是地理位置和计算资源的均衡,深度学习方法通常需要大量的计算资源,需要的存储内存也相对较大,很难在低功耗无线通信设备和小内存现场设备或嵌入式系统中得到应用。因此,如果要将深度学习方法更好地运用于微地震现场数据,可尝试使用一些轻量级的深度学习模型,如MobileNet、SqueezeNet等,或者通过模型裁剪、量化等技术对标准的深度学习模型进行优化和轻量化。
天然地震波与微地震波在波形特征上存在一定的相似性,例如初至波的能量变化、波形持续时间等,这些特征对初至拾取具有指导意义。初至拾取涉及信号处理和特征提取等技术,而这些技术对于天然地震波和微地震波分析具有一定的通用性。因此,天然地震波和微地震波的初至拾取方法在一定层面上可以互相借鉴,迁移学习的成功应用充分证明了这一观点。目前,深度学习在微地震方面的应用还不够深入,今后需要加强对迁移学习的研究。
传统机器学习算法还存在一些问题。一是算法的评价标准不一致,从前文表格的实验结果可以看出,实际情况可能会更复杂。有些学者以偏差判定,有些以准确率判定,有些学者直接用地震图展示匹配情况,判断标准不统一,这不利于各种算法间的对比。二是无监督学习算法在噪声比较大、波形变化较复杂的情况下的性能比较差,对一些极端条件的处理能力有限。
在深度学习方面,除了需要对网络轻量化开展深入研究,还需要加强注意力机制方面的应用。对同一数据集STEAD进行训练时,使用了注意力机制的网络结构EQTranformer比包含卷积和递归单元的模型CRED性能更好[101]。这表明注意力机制对地震信号检测是有益的。所以,后续可开展检验注意力机制与更多网络相结合的实验和分析。
最后,需要考虑不同数据适用于不同的算法。对于来自地面或是井中的数据,其最主要的差异是信噪比。地表数据可能会受到地表噪声和人类活动的影响,这些噪声可通过滤波去掉。井中数据的质量通常较高,因而对于算法的抗噪性能要求相对较低。关于1C和3C数据,前者较后者包含的信息更多,但处理过程也更复杂。3C数据中,垂直分量P波振幅较高,水平分量的S波振幅更强[69],因此,垂直分量常用于P波拾取,而3C数据常用于拾取P波和S波的初至。对于P波初至,算法仅需要考虑信号和噪声的差异。对于S波初至,算法还需要考虑P波与S波的差异。在传统机器学习算法中,可将偏振和主频信息作为深度学习网络的输入属性,利用大量包含P波和S波的数据进行学习。
5 结论与展望本文对基于人工智能的微震拾取技术进行总结和分析,得到以下结论。
(1)收集数据要遵循的原则是高质量和准确性、多样性和代表性、数据量和平衡性。很多学者先后使用合成数据和实测数据进行训练和模型测试。合成数据由理论无噪数据添加高斯白噪声或者真实噪声得到。实测数据最具代表性的是北加州地震数据集、南加州地震数据集、斯坦福全球数据集和汶川余震数据集。
(2)在预处理时,需要对地震数据进行裁剪、清理、特征提取和归一化等处理,当样本数量较少时,还需要通过数据增强的方式扩充数据集。
(3)在训练模型部分,要选择合适的输入、优化方法和代价函数。聚类、SVM、BPNN需要人工选择多种具有代表性的属性(如振幅、长短时窗比值、高阶统计量等),CNN和RNN可选择地震波形(单道、多道和多台站波形)、地震图像和传统代表属性(可根据经验和专业知识得到)中的一类或几类输入进行学习。为了加快收敛和避免陷入局部最优、过拟合等问题,采用了一系列优化方法,如:粒子群优化,人工蜂群优化,随机失活,提前停止等。应用代价函数时要考虑地震数据正、负样本不均的情况,适当使用权重。
(4)综合方法、混合网络以及多步拾取在地震初至拾取中显示出良好性能,尤其是注意力机制的引入显著增强了模型的学习能力。
综合当前基于人工智能初至拾取方法的研究现状,今后相关研究应主要集中在下述几个方面。
(1)当前各种算法的评价函数缺乏统一的标准,尤其是传统机器学习方面。对于算法的性能评价,需制定统一、合理的标准。
(2)进一步研究无监督学习算法在低信噪比数据初至拾取上的应用,主要可以从多模态数据融合、自适应算法设计和损失函数改进等方面入手。
(3)地震的初至拾取方法在实际数据的应用中,需进一步深入研究注意力机制、迁移学习和新型网络结构。过于复杂的网络结构在计算力和存储有限的移动设备上难以实现,因此需要研究一种超轻量级且准确度较高的网络构架,实现工程现场数据的实时处理。
| [1] |
SHENG G, TANG X, XIE K, et al. Hydraulic fracturing microseismic first arrival picking method based on non-subsampled shearlet transform and higher-order-statistics[J]. Journal of Seismic Exploration, 2019, 28(6): 593-618. |
| [2] |
ALLEN R V. Automatic earthquake recognition and timing from single traces[J]. Bulletin of the Seismological Society of America, 1978, 68(5): 1521-1532. DOI:10.1785/BSSA0680051521 |
| [3] |
JONES J P. VAN DER BAAN M. Adaptive STA-LTA with outlier statistics[J]. Bulletin of the Seismological Society of America, 2015, 105(3): 1606-1618. DOI:10.1785/0120140203 |
| [4] |
SLEEMAN R, VAN ECK T. Robust automatic P-phase picking: an on-line implementation in the analysis of broadband seismogram recordings[J]. Physics of the Earth and Planetary Interiors, 1999, 113(1/4): 265-275. |
| [5] |
MAEDA N. A method for reading and checking phase time in auto-processing system of seismic wave data[J]. Zisin (Journal of the Seismological Society of Japan, 2nd ser.), 1985, 38(3): 365-379. DOI:10.4294/zisin1948.38.3_365 |
| [6] |
ZHU M B, WANG L G, LIU X M, et al. Accurate identification of microseismic P-and S-phase arrivals using the multi-step AIC algorithm[J]. Journal of Applied Geophysics, 2018, 150: 284-293. DOI:10.1016/j.jappgeo.2018.01.007 |
| [7] |
LONG Y, LIN J, LI B, et al. Fast-AIC method for automatic first arrivals picking of microseismic event with multitrace energy stacking envelope summation[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(10): 1832-1836. DOI:10.1109/LGRS.2019.2952571 |
| [8] |
BOSCHETTI F, DENTITH M D, LIST R D. A fractal-based algorithm for detecting first arrivals on seismic traces[J]. Geophysics, 1996, 61(4): 1095-1102. DOI:10.1190/1.1444030 |
| [9] |
曹茂森, 任青文, 万林梅, 等. Length分形维算法拾取地震波初至[J]. 石油地球物理勘探, 2004(5): 509-514. CAO Maosen, REN Qingwen, WAN Linmei, et al. Length fractal dimension algorithm to pick up seismic waves for the first time[J]. Oil Geophysical Prospec-ting, 2004(5): 509-514. |
| [10] |
WU H, XIAO W, REN H. Automatic time picking for weak seismic phase in the strong noise and interference environment: an hybrid method based on array similarity[J]. Sensors, 2022, 22(24): 9924. DOI:10.3390/s22249924 |
| [11] |
SEMIN K U, OZEL N M, NECMIOGLU O. Detection and identification of low-magnitude seismic events near Bala, central turkey, using array-based waveform correlation[J]. Seismological Research Letters, 2011, 82(1): 97-103. DOI:10.1785/gssrl.82.1.97 |
| [12] |
AIT LAASRI E H, AKHOUAYRI E S, AGLIZ D, et al. Automatic detection and picking of P-wave arrival in locally stationary noise using cross-correlation[J]. Digital Signal Processing, 2014, 26: 87-100. DOI:10.1016/j.dsp.2013.12.009 |
| [13] |
AKRAM J, EATON D W. Refinement of arrival-time picks using a cross-correlation based workflow[J]. Journal of Applied Geophysics, 2016, 135: 55-66. DOI:10.1016/j.jappgeo.2016.09.024 |
| [14] |
LEE M, BYUN J, KIM D, et al. Improved modified energy ratio method using a multi-window approach for accurate arrival picking[J]. Journal of Applied Geophysics, 2017, 139: 117-130. DOI:10.1016/j.jappgeo.2017.02.019 |
| [15] |
GACI S. The use of wavelet-based denoising techniques to enhance the first-arrival picking on seismic traces[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4558-4563. DOI:10.1109/TGRS.2013.2282422 |
| [16] |
SABBIONE J I, VELIS D. Automatic first-breaks picking: new strategies and algorithms[J]. Geophysics, 2010, 75(4): V67-V76. DOI:10.1190/1.3463703 |
| [17] |
刘劲松, 王赟, 姚振兴. 微地震信号到时自动拾取方法[J]. 地球物理学报, 2013, 56(5): 1660-1666. LIU Jinsong, WANG Yun, YAO Zhenxing. On micro-seismic first arrival identification: A case study[J]. Chinese Journal of Geophysics, 2013, 56(5): 1660-1666. |
| [18] |
魏梦祎, 谭玉阳, 毛中华, 等. 基于波形互相关的微地震事件自动识别及初至拾取[J]. 北京大学学报(自然科学版), 2018, 54(2): 361-372. WEI Mengyi, TAN Yuyang, MAO Zhonghua, et al. Automatic microseismic event detection and arrival picking based on waveform cross-correlation[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2018, 54(2): 361-372. |
| [19] |
严海滔, 周怀来, 牛聪, 等. 同步挤压改进短时傅里叶变换分频相干技术在断裂识别中的应用[J]. 石油地球物理勘探, 2019, 54(4): 860-866. YAN Haitao, ZHOU Huailai, NIU Cong, et al. Application of synchronous squeezing improved short-time Fourier transform split-frequency coherence technique in fracture identification[J]. Oil Geophysical Prospecting, 2019, 54(4): 860-866. |
| [20] |
ZHANG H, THURBER C, ROWE C. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings[J]. Bulletin of the Seismological Society of America, 2003, 93(5): 1904-1912. DOI:10.1785/0120020241 |
| [21] |
HAFEZ A G, RABIE M, KOHDA T. Seismic noise study for accurate P-wave arrival detection via MODWT[J]. Computers & Geosciences, 2013, 54: 148-159. |
| [22] |
HU R Q, WANG Y C. A first arrival detection method for low SNR microseismic signal[J]. Acta Geophysica, 2018, 66(5): 945-957. DOI:10.1007/s11600-018-0193-3 |
| [23] |
HE Z, MA S, WANG L, et al. A novel wavelet selection method for seismic signal intelligent processing[J]. Applied Sciences, 2022, 12(13): 6470. DOI:10.3390/app12136470 |
| [24] |
BARGEES A, AL-SHUHAIL A A. First arrival picking of zero-phase seismic data by Hilbert envelope empirical half window (HEEH) method[J]. Sensors, 2022, 22(19): 7580. DOI:10.3390/s22197580 |
| [25] |
AL-MASHHOR A A, AL-SHUHAIL A A, HANAFY S M, et al. First arrival picking of seismic data based on trace envelope[J]. IEEE Access, 2019, 7: 128806-128815. DOI:10.1109/ACCESS.2019.2939320 |
| [26] |
CHENG Y, LI Y, ZHANG C. First arrival time picking for microseismic data based on shearlet transform[J]. Journal of Geophysics and Engineering, 2017, 14(2): 262-271. DOI:10.1088/1742-2140/aa5777 |
| [27] |
ZHANG J, TANG Y, LI H. STA/LTA fractal dimension algorithm of detecting the P-wave arrival[J]. Bulletin of the Seismological Society of America, 2018, 108(1): 230-237. DOI:10.1785/0120170099 |
| [28] |
马强, 金星, 李山有, 等. 用于地震预警的P波震相到时自动拾取[J]. 地球物理学报, 2013, 56(7): 2313-2321. MA Qiang, JIN Xing, LI Youshan, et al. Automatic P-arrival detection for earthquake early warning[J]. Chinese Journal of Geophysics, 2013, 56(7): 2313-2321. |
| [29] |
DONG L, BI S, ZHANG Y, et al. Arrival-time detection with multiscale wavelet analysis and source location of acoustic emission in rock[J]. IEEE Sensors Journal, 2023, 23(14): 16313-16323. DOI:10.1109/JSEN.2023.3280347 |
| [30] |
ZHANG Y, CHEN Q, LIU X, et al. Adaptive and automatic P-and S-phase pickers based on frequency spectrum variation of sliding time windows[J]. Geophysical Journal International, 2018, 215(3): 2172-2182. |
| [31] |
龚屹, 孟庆利, 蓝加达, 等. 利用聚类算法提高微地震初至拾取的稳定性[J]. 石油地球物理勘探, 2024, 59(1): 110-121. GONG Yi, MENG Qingli, LAN Jiada, et al. Improving the stability of microseismic event detection by clustering algorithm[J]. Oil Geophysical Prospecting, 2024, 59(1): 110-121. |
| [32] |
邓飞, 蒋沛凡, 蒋先艺, 等. 应用图像语义分割网络的微地震事件识别和初至拾取方法[J]. 石油地球物理勘探, 2022, 57(5): 1011-1019. DENG Fei, JIANG Peifan, JIANG Xianyi, et al. Microseismic event recognition and first break picking method based on image semantic segmentation network[J]. Oil Geophysical Prospecting, 2022, 57(5): 1011-1019. |
| [33] |
王永刚, 乐友喜, 张军华. 地震属性分析技术[M]. 山东东营: 中国石油大学出版社, 2007.
|
| [34] |
CHEN Y. Fast waveform detection for microseismic imaging using unsupervised machine learning[J]. Geophysical Journal International, 2018, 215(2): 1185-1199. DOI:10.1093/gji/ggy348 |
| [35] |
MA H T, WANG T, LI Y, et al. A time picking method for microseismic data based on LLE and improved PSO clustering algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(11): 1677-1681. DOI:10.1109/LGRS.2018.2854834 |
| [36] |
周竹生, 曾维祖, 刘思琴, 等. 基于加权K均值聚类的多属性初至拾取方法[J]. 地震学报, 2020, 42(2): 177-186. ZHOU Zhusheng, ZENG Weizu, LIU Siqin, et al. First arrival picking method by seismic multi-attribute based on weighted K-means clustering algorithm[J]. Acta Seismologica Sinica, 2020, 42(2): 177-186. |
| [37] |
LI Y, WANG Z, WANG J, et al. First arrival picking on microseismic signals based on K-means with a relief algorithm[J]. Symmetry, 2021, 13(5): 790. DOI:10.3390/sym13050790 |
| [38] |
李康丽, 冯波, 王华忠. 基于高维多属性决策过程的复杂地表初至波识别与走时检测方法[J]. 石油物探, 2022, 61(4): 599-608. LI Kangli, FENG Bo, WANG Huazhong. Identification and travel time detection method for complex surface first arrivals based on high-dimensional multi-attribute decision-making process[J]. Geophysical Prospecting for Petroleum, 2022, 61(4): 599-608. |
| [39] |
高磊, 罗关凤, 刘荡, 等. 基于聚类和局部线性回归的初至波自动拾取算法[J]. 计算机应用, 2022, 42(2): 655-662. GAO Lei, LUO Guanfeng, LIU Dang, et al. First-arrival automatic picking algorithm based on clustering and local linear regression[J]. Computer Applications, 2022, 42(2): 655-662. |
| [40] |
ZHU X, CHEN B, WANG X, et al. Time series segmentation clustering: a new method for S-phase picking in microseismic data[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [41] |
ZHU D, LI Y, ZHANG C. Automatic time picking for microseismic data based on a fuzzy C-means clustering algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1900-1904. DOI:10.1109/LGRS.2016.2616510 |
| [42] |
PAL N R, PAL K, BEZDEK J C. A mixed c-means clustering model[C]. Proceedings of 6th International Fuzzy Systems Conference, 1997, 11-21.
|
| [43] |
SAAD O M, SHALABY A, SAYED M S. Automatic arrival time detection for earthquakes based on fuzzy possibilistic C-means clustering algorithm[C]. 2017 8th International Conference on Recent Advances in Space Technologies (RAST), 2017, 143-148.
|
| [44] |
GAO L, JIANG Z Y, MIN F. First-arrival travel times picking through sliding windows and fuzzy C-means[J]. Mathematics, 2019, 7(3): 221. DOI:10.3390/math7030221 |
| [45] |
GAO L, JIANG H K, MIN F. Stable first-arrival picking through adaptive threshold determination and spatial constraint clustering[J]. Expert Systems with Applications, 2021, 182(C): 115216. |
| [46] |
谭家炜, 李静, 李飞达, 等. 基于超虚干涉法约束的模糊C均值聚类地震初至自动提取[J]. 石油地球物理勘探, 2020, 55(5): 979-990. TAN Jiawei, LI Jing, LI Feida, et al. Automatic extraction of fuzzy C-mean clustered seismic first arrivals based on super-virtual interferometry constraints[J]. Oil Geophysical Prospecting, 2020, 55(5): 979-990. |
| [47] |
LAN Z, WANG Y, WANG P, et al. An adaptive FCM-based approach of first arrival time picking for microseismic data[C]. 2021 IEEE International Geoscience and Remote Sensing Symposium, 2021, 8404-8407.
|
| [48] |
GAO L, LIU D, LUO G F, et al. First-arrival picking through fuzzy c-means and robust locally weighted regression[J]. Acta Geophysica, 2021, 69(5): 1623-1636. DOI:10.1007/s11600-021-00636-z |
| [49] |
CANO E V, AKRAM J, PETER D B. Automatic seismic phase picking based on unsupervised machine-learning classification and content information analysis[J]. Geophysics, 2021, 86(4): V299-V315. DOI:10.1190/geo2020-0308.1 |
| [50] |
LAN Z Q, GAO P, WANG P, et al. Automatic first arrival time identification using fuzzy C-means and AIC[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-13. |
| [51] |
MENG Y Q, LI Y, ZHANG C, et al. A time picking method based on spectral Multimani fold cluste-ring in microseismic data[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(8): 1273-1277. DOI:10.1109/LGRS.2017.2705703 |
| [52] |
HUANG W. Seismic signal recognition by unsupervised machine learning[J]. Geophysical Journal International, 2019, 219(2): 1163-1180. DOI:10.1093/gji/ggz366 |
| [53] |
CHEN M, LI Y, XIE J. A novel SVM-based method for seismic first-arrival detecting[J]. Applied Mechanics and Materials, 2010, 29-32: 973-978. DOI:10.4028/www.scientific.net/AMM.29-32.973 |
| [54] |
ZHAO Z G, GROSS L. Using supervised machine learning to distinguish microseismic from noise events[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 2918-2923.
|
| [55] |
QU S, VERSCHUUR E, CHEN Y K. Automatic microseismic-event detection via supervised machine learning[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2287-2291.
|
| [56] |
QU S, GUAN Z, VERSCHUUR E, et al. Automatic high-resolution microseismic event detection via supervised machine learning[J]. Geophysical Journal International, 2020, 222(1): 1881-1895. |
| [57] |
蒋一然, 宁杰远. 基于支持向量机的地震体波震相自动识别及到时自动拾取[J]. 地球物理学报, 2019, 62(1): 361-373. JIANG Yiran, NING Jieyuan. Automatic detection of seismic body-wave phases and determination of their arrival times based on support vector machine[J]. Chinese Journal of Geophysics, 2019, 62(1): 361-373. |
| [58] |
DUAN X, ZHANG J. Multi-trace and multi-attribute analysis for first-break picking with the support vector machine[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2559-2563.
|
| [59] |
王腾. 基于LLE-IPSO聚类和ABC-SVM的微地震初至拾取研究[D]. 吉林长春: 吉林大学, 2019. WANG Teng. Research on Automatic Time Picking for Microseismic Data Based on LLE-ISPO Clustering and ABC-SVM Algorithm[D]. Jilin University, Chang-chun, Jilin, 2019. |
| [60] |
LI J H, RAN M K, TONG W K, et al. Transfer-learning-based SVM method for seismic phase picking with insufficient training samples[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [61] |
DAI H C, MACBETH C. Automatic picking of seismic arrivals in local earthquake data using an artificial neural network[J]. Geophysical Journal International, 1995, 120(3): 758-774. DOI:10.1111/j.1365-246X.1995.tb01851.x |
| [62] |
VEEZHINATHAN J, WAGNER D. A neural network approach to first break picking[C]. 1990 International Joint Conference on Neural Networks, 1990, 235-240.
|
| [63] |
MURAT M E, RUDMAN A J. Automated first arrival picking: a neural network approach1[J]. Geophysical Prospecting, 1992, 40(6): 587-604. DOI:10.1111/j.1365-2478.1992.tb00543.x |
| [64] |
MCCORMACK M D, ZAUCHA D E, DUSHEK D W. First-break refraction event picking and seismic data trace editing using neural networks[J]. Geophysics, 1993, 58(1): 67-78. DOI:10.1190/1.1443352 |
| [65] |
MAITY D, AMINZADEH F, KARRENBACH M. Novel hybrid artificial neural network based autopicking workflow for passive seismic data[J]. Geophysical Prospecting, 2014, 62(4): 834-847. DOI:10.1111/1365-2478.12125 |
| [66] |
兰金涛, 张凤军, 王春梅, 等. 基于神经网络算法的可空变初至自动拾取时窗设计[C]. 中国石油学会2017年物探技术研讨会, 2017, 197-200. LAN Jintao, ZHANG Fengjun, WANG Chunmei, et al. Design of automatic pickup time window for nullable initial-to-variable first-arrival based on neural network algorithm[C]. 2017 Geophysical Exploration Technology Seminar of China Petroleum Society, 2017, 197-200. |
| [67] |
宋建国, 李赋真, 徐维秀, 等. 改进的神经网络级联相关算法及其在初至拾取中的应用[J]. 石油地球物理勘探, 2018, 53(1): 8-16. SONG Jianguo, LI Fuzhen, XU Weixiu, et al. Improved neural network cascade correlation algorithm and its application to first-to-first pickup[J]. Oil Geophysical Prospecting, 2018, 53(1): 8-16. |
| [68] |
曹晓莉, 刘斌, 王淑荣, 等. 综合动量法和可变学习速度的BP神经网络地震初至拾取[J]. 石油地球物理勘探, 2020, 55(1): 71-79. CAO Xiaoli, LIU Bin, WANG Shurong, et al. Integrated momentum method and variable learning speed for seismic first-to-earth pickup by BP neural network[J]. Oil Geophysical Prospecting, 2020, 55(1): 71-79. |
| [69] |
YUAN S Y, LIU J W, WANG S X, et al. Seismic waveform classification and First-Break picking using convolution neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(2): 272-276. DOI:10.1109/LGRS.2017.2785834 |
| [70] |
ROSS Z E, MEIER M A, HAUKSSON E. P wave arrival picking and first-motion polarity determination with deep learning[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(6): 5120-5129. DOI:10.1029/2017JB015251 |
| [71] |
ROSS Z E, MEIER M A, HAUKSSON E, et al. Generalized seismic phase detection with deep learning[J]. Bulletin of the Seismological Society of America, 2018, 108(5A): 2894-2901. DOI:10.1785/0120180080 |
| [72] |
ZHU L J, PENG Z G, MCCLELLAN J, et al. Deep learning for seismic phase detection and picking in the aftershock zone of 2008 Mw7.9 Wenchuan Earthquake[J]. Physics of the Earth and Planetary Interiors, 2019, 293: 106261. DOI:10.1016/j.pepi.2019.05.004 |
| [73] |
于子叶, 储日升, 盛敏汉. 深度神经网络拾取地震P和S波到时[J]. 地球物理学报, 2018, 61(12): 4873-4886. YU Ziye, CHU Risheng, SHENG Minhan. Pick onset time of P and S phase by deep neural network[J]. Chinese Journal of Geophysics, 2018, 61(12): 4873-4886. DOI:10.6038/cjg2018L0725 |
| [74] |
李健, 王晓明, 张英海, 等. 基于深度卷积神经网络的地震震相拾取方法研究[J]. 地球物理学报, 2020, 63(4): 1591-1606. LI Jian, WANG Xiaoming, ZHANG Yinghai, et al. Research on the seismic phase picking method based on the deep convolution neural network[J]. Chinese Journal of Geophysics, 2020, 63(4): 1591-1606. |
| [75] |
JOHNSON S W, CHAMBERS D J A, BOLTZ M S, et al. Application of a convolutional neural network for seismic phase picking of mining-induced seismicity[J]. Geophysical Journal International, 2021, 224(1): 230-240. |
| [76] |
LIAO X F, CAO J X, HU J T, et al. First arrival time identification using transfer learning with continuous wavelet transform feature images[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(11): 2002-2006. DOI:10.1109/LGRS.2019.2955950 |
| [77] |
HE Z X, PENG P G, WANG L G, et al. PickCapsNet: capsule network for automatic P-Wave arrival picking[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(4): 617-621. DOI:10.1109/LGRS.2020.2983196 |
| [78] |
李安, 杨建思, 彭朝勇, 等. 基于样本增强的卷积神经网络震相拾取方法[J]. 地震学报, 2020, 42(2): 163-176, 244. LI An, YANG Jiansi, PENG Chaoyong, et al. Seismic phase identification using the convolutional neural networks based on sample enhancement[J]. Acta Seismologica Sinica, 2020, 42(2): 163-176, 244. |
| [79] |
ZHANG X, CHEN H, ZHANG W, et al. Generalized neural network trained with a small amount of base samples: application to event detection and phase picking in downhole microseismic monitoring[J]. Geophysics, 2021, 86(5): KS95-KS108. |
| [80] |
GUO C, ZHU T, GAO Y, et al. AEnet: automatic picking of P-wave first arrivals using deep learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(6): 5293-5303. |
| [81] |
LI J M, LI K Y, TANG S B. Automatic arrival-time picking of P-and S-waves of microseismic events based on object detection and CNN[J]. Soil Dynamics and Earthquake Engineering, 2023, 164: 107560. |
| [82] |
刘佳楠, 武杰. 基于全卷积神经网络的地震初至波拾取[J]. 信息技术与网络安全, 2018, 37(11): 58-63. LIU Jianan, WU Jie. Seismic first arrival picking based on fully convolutional networks[J]. Information Technology and Network Security, 2018, 37(11): 58-63. |
| [83] |
RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutional Networks for Biomedical Image Segmentation[M]//Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015. Cham, Springer, 2015, 234-241.
|
| [84] |
ZHU W, BEROZA G C. PhaseNet: a deep-neural-network-based seismic arrival-time picking method[J]. Geophysical Journal International, 2018, 216(1): 261-273. |
| [85] |
CHAI C, MACEIRA M, SANTOS-VILLALOBOS H J, et al. Using a deep neural network and transfer learning to bridge scales for seismic phase picking[J]. Geophysical Research Letters, 2020, 47(16): e2020GL0-88651. |
| [86] |
HU L, ZHENG X, DUAN Y, et al. First-arrival picking with a U-net convolutional network[J]. Geophysics, 2019, 84(6): U45-U57. |
| [87] |
HAN S, LIU Y J, LI Y B, et al. First arrival traveltime picking through 3-D U-Net[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [88] |
李建平, 张硕伟, 丁仁伟, 等. 面向地震波初至智能拾取的超分辨率深度残差方法研究[J]. 石油地球物理勘探, 2023, 58(2): 251-262. LI Jianping, ZHANG Shuowei, DING Renwei, et al. Research on depth residual method of super-resolution for intelligent seismic wave first arrival pickup[J]. Oil Geophysical Prospecting, 2023, 58(2): 251-262. |
| [89] |
WU H, ZHANG B, LI F, et al. Semiautomatic first-arrival picking of microseismic events by using the pixel-wise convolutional image segmentation method[J]. Geophysics, 2019, 84(3): V143-V155. |
| [90] |
YUAN S Y, ZHAO Y, XIE T, et al. SegNet-based first-break picking via seismic waveform classification directly from shot gathers with sparsely distributed traces[J]. Petroleum Science, 2022, 19(1): 162-179. |
| [91] |
PARDO E, GARFIAS C, MALPICA N. Seismic phase picking using convolutional networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 7086-7092. |
| [92] |
YUAN P Y, HU W Y, WU X Q, et al. First arrival picking using U-net with Lovasz loss and nearest point picking method[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2624-2628.
|
| [93] |
吴雨鑫. 基于U-Net的自动初至拾取方法[D]. 黑龙江哈尔滨: 哈尔滨工业大学, 2020. WU Yuxin. Automatic First-to-First Pickup Method Based on U-Net[D]. Harbin Institute of Technology, Harbin, Heilongjiang, 2020. |
| [94] |
WANG J, XIAO Z W, LIU C, et al. Deep learning for picking seismic arrival times[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(7): 6612-6624. |
| [95] |
ZHANG L, FANG L H, WANG W L, et al. Seismic phase picking in China Seismic Array using a deep convolutional neuron network[J]. Earthquake Science, 2020, 33(2): 72-81. |
| [96] |
陈德武, 杨午阳, 魏新建, 等. 基于混合网络U-SegNet的地震初至自动拾取[J]. 石油地球物理勘探, 2020, 55(6): 1188-1201. CHEN Dewu, YANG Wuyang, WEI Xinjian, et al. Automatic seismic first-arrival pickup based on hybrid network U-SegNet[J]. Oil Geophysical Prospecting, 2020, 55(6): 1188-1201. |
| [97] |
陈德武, 杨午阳, 魏新建, 等. 一种基于改进的U-Net网络的初至自动拾取研究[J]. 地球物理学进展, 2021, 36(4): 1493-1503. CHEN Dewu, YANG Wuyang, WEI Xinjian, et al. Research on first-break automatic picking based on an improved U-Net network[J]. Progress in Geophysics, 2021, 36(4): 1493-1503. |
| [98] |
李薇薇, 龚仁彬, 周相广, 等. 基于深度学习UNet++网络的初至波拾取方法[J]. 地球物理学进展, 2021, 36(1): 187-194. LI Weiwei, GONG Renbin, ZHOU Xiangguang, et al. UNet++: a deep-neural-network-based seismic arrival time picking method[J]. Progress in Geophysics, 2021, 36(1): 187-194. |
| [99] |
ZHANG J L, SHENG G Q. First arrival picking of microseismic signals based on nested U-Net and Wasserstein generative adversarial network[J]. Journal of Petroleum Science and Engineering, 2020, 195: 107527. |
| [100] |
ZHENG J, LU J, PENG S, et al. An automatic microseismic or acoustic emission arrival identification scheme with deep recurrent neural networks[J]. Geophysical Journal International, 2018, 212(2): 1389-1397. |
| [101] |
BIRNIE C, HANSTEEN F. Bidirectional recurrent neural networks for seismic event detection[J]. Geophysics, 2022, 87(3): KS97-KS111. |
| [102] |
ZHOU Y, YUE H, KONG Q, et al. Hybrid event detection and phase-picking algorithm using convolutional and recurrent neural networks[J]. Seismological Research Letters, 2019, 90(3): 1079-1087. |
| [103] |
MOUSAVI S M, ZHU W Q, SHENG Y X, et al. CRED: a deep residual network of convolutional and recurrent units for earthquake signal detection[J]. Scientific Reports, 2019, 9(1): 10267. |
| [104] |
MOUSAVI S M, ELLSWORTH W L, ZHU W Q, et al. Earthquake transformer-an attentive deep-learning model for simultaneous earthquake detection and phase picking[J]. Nature Communications, 2020, 11(1): 3952. |
| [105] |
ZHENG J, HARRIS J M, LI D, et al. SC-PSNET: a deep neural network for automatic P-and S-phase detection and arrival-time picker using 1C recordings[J]. Geophysics, 2020, 85(4): U87-U98. |
| [106] |
LIAO W Y, LEE E J, MU D, et al. ARRU phase picker: attention recurrent-residual U-Net for picking seismic P-and S-phase arrivals[J]. Seismological Research Letters, 2021, 92(4): 2410-2428. |
| [107] |
FENG T, MOHANNA S, MENG L. EdgePhase: a deep learning model for multi-station seismic phase picking[J]. Geochemistry Geophysics Geosystems, 2022, 23(11): e2022GC010453. |
| [108] |
LIM J, JUNG S, JEGAL C, et al. LEQNet: light earthquake deep neural network for earthquake detection and phase picking[J]. Frontiers in Earth Science, 2022, 10: 848237. |



 唐东林,四川省成都市新都区新都大道8号西南石油大学机电工程学院,610500。Email:
唐东林,四川省成都市新都区新都大道8号西南石油大学机电工程学院,610500。Email: