海洋可控源电磁(MCSEM)法勘探是在海底布设源激发电磁场,通过布置在海底的采集站接收电磁场信号,然后进行数据处理和分析,获得地下电阻率分布。众所周知,利用电磁法开展油气勘探的基础是目标与围岩间存在电性差异。海底油气藏(层)具有高阻特征,因此可以通过MCSEM对其进行勘探。早期的海洋电磁勘探以一维为主,其数据的正、反演技术已经发展成熟。早在1983年Chave[1]提出了海洋电磁法理论,实现了海洋可控源电磁数据的一维正演模拟,据此可分析海洋浅部地层的电性特征。Flosadóttir等[2]在此基础上提出了一维快速OCCAM反演,实现了MCSEM数据的反演。Christensen等[3]采用阻尼最小二乘法实现了一维MCSEM数据的反演,对储层参数反演误差的原因进行了分析。Key[4]将一维OCCAM反演推广到MCSEM数据,并深入研究了不同采集参数条件下该方法对海洋油气藏薄电阻层的分辨率。
随着MCSEM法应用的不断深入,得益于计算方法和电子计算机性能的快速提升,MCSEM数据的二维和三维正、反演技术也取得了重要进展。Cai等[5]基于边缘有限元方法开展了三维可控源电磁(CSEM)数据的正、反演,利用多个求解器并行求解方程组,对于多源及大规模电磁建模效果较好。刘颖等[6]采用非结构四面体单元进行三维网格剖分,实现了可控源电磁场三维自适应矢量有限元正演。Ye等[7]在频域使用自适应节点有限元方法,开展了MCSEM数据三维正演。刘玲等[8]利用谱元法进行MCSEM三维电磁场正演模拟,在稀疏网格剖分情况下实现了较准确的正演计算。高妍等[9]提出了一种在频率域基于预条件迭代求解的有限元电磁数值模拟方法,并利用该方法对可燃冰与油气双储层模型的MCSEM正演响应特征进行模拟和分析。张岩等[10]设计了一种可控源电磁法2.5 D观测系统,噪声压制效果较好,获得了精确的地下电性分布。Li等[11]使用自适应有限元方法实现了各向异性三维MCSEM电磁场正演,结果表明MCSEM电磁响应受地下介质各向异性方位的影响较大。Chen等[12]提出了一种新的小波伽辽金方法应用于二维正演建模,该方法在计算时间和内存要求方面优于有限元法和差分方法。
Weitemeyer等[13]使用有限差分算法实现了MCSEM数据的二维反演,并将正演结果与Li等[14]的研究结果进行对比,证明了通过可调节网格的有限差分算法,可在保证计算精度的前提下提高计算效率。Kerry[15]使用自适应非结构网格剖分,开展了具有较高精度和较强灵活性的大地磁测深(MT)数据和CSEM数据的二维各向异性反演。肖俊等[16]对带地形MCSEM数据二维OCCAM反演算法进行了研究,正演采用非结构三角形网格的自适应有限元可模拟具有复杂界面和地形的模型。龙志丹[17]提出了一种适用于六面体网格和四面体网格的粗糙度矩阵计算策略的频率域CSEM三维反演方法,对带地形的海洋油气藏模型进行反演,反演表明,当两个油气藏距离较近时,反演结果无法对其进行准确分辨。为了提高CSEM数据的电阻率反演分辨率,Long等[18]将多元变换函数应用于CSEM数据的三维反演,将模型参数从连续分布空间转换为半步分布的多元空间。
CSEM法通常应用于油气勘探,寻找有利钻探目标区[19]。随着CSEM数据质量的提升和先进处理方法的提出,该方法可应用于精确研究电阻率分布。时移地球物理成像是监测储层内部物性变化的有效手段,其中时移海洋可控电磁法适合于海洋油气藏(层)开展过程的监督。Kong等[20]基于传统MCSEM法,采用井中数据接收方式,成功开展了油气藏开采监测。Wirianto等[21]对复杂三维电阻率模型进行正演模拟,结果表明CSEM法可应用于陆地油气储层开采监测。Shahin等[22]使用2.5D并行自适应有限元算法对三个生产时间步长(0、5、10年)开展时移CSEM数据模拟,可监测到储层电阻率降低20%~60%的过程。Shantsev等[23]为了分析时移CSEM勘探重复性的重要性,对实测CSEM数据进行分析,发现通过反演电阻率体而非原始电磁数据建立时移模型,可大幅度降低对重复性的要求。刘勇等[24]采用MCSEM法对不同环境、不同工作方式下的油气层开采监测过程进行了数值模拟,证明了利用该方法对深海油藏的开采过程进行监测是可行的。
为了更高效地利用时移CSEM技术,本文提出在油藏开采过程中对油气藏进行时移反演成像,目的是检测是否存在勘探初期遗漏的小型油气藏(次油气层)。对油气开采过程进行动态监测,能实时了解当前油气层的开采状态,检测是否存在未发现的次油气层。前人的研究[20-24]表明,利用MCSEM法对油气储层开采过程进行监测效果良好,但对于次油气层探测的应用未见报道。本文首先设计一系列地电模型,模拟油气开采过程中的电磁响应特征;然后,模拟分析次油气层在不同厚度、不同位置及不同埋深等情况下对电磁响应的影响;最后,为了进一步分析次油层的影响,采用OCCAM反演对上述模型的正演数据及复杂地质条件下的油气开采数据进行反演[14]。
1 正、反演原理 1.1 二维正演理论对于一个二维地电模型,沿异常体走向方向设为x轴,时间因子为
| $ \left\{\begin{array}{l}\nabla \times \boldsymbol{E}=\mathrm{i}\omega {\mu }_{0}\boldsymbol{H}\\ \nabla \times \boldsymbol{H}-\sigma \boldsymbol{E}={\boldsymbol{J}}_{\mathbf{s}}\end{array}\right. $ | (1) |
式中:
在笛卡尔坐标系对式(1)的展开式做傅里叶变换
| $ \widehat{F}({k}_{x},y,z)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x,y,z){\mathrm{e}}^{-\mathrm{i}{k}_{x}x}\mathrm{d}x $ | (2) |
式中:
| $ \begin{array}{l}\nabla \cdot \left(\frac{\mathrm{i}\omega {\mu }_{0}}{{\gamma }^{2}}\nabla {\widehat{H}}_{x}\right)-\mathrm{i}\omega {\mu }_{0}{\widehat{H}}_{x}-\frac{\partial }{\partial y}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{E}}_{x}}{\partial z}\right)+\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial }{\partial z}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{E}}_{x}}{\partial y}\right)=-\frac{\partial }{\partial y}\frac{\mathrm{i}\omega {\mu }_{0}{J}_{z}{\delta }_{\mathrm{s}}}{{\gamma }^{2}}+\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial }{\partial z}\frac{\mathrm{i}\omega {\mu }_{0}{J}_{y}\delta \mathrm{s}}{{\gamma }^{2}}\end{array} $ | (3) |
| $ \begin{array}{l}\nabla \cdot \left(\frac{\sigma }{{\gamma }^{2}}\nabla {\widehat{E}}_{x}\right)-\sigma {\widehat{E}}_{x}-\frac{\partial }{\partial y}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{H}}_{x}}{\partial z}\right)+\frac{\partial }{\partial z}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{H}}_{x}}{\partial y}\right)\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =-\frac{\partial }{\partial y}\frac{\mathrm{i}{k}_{x}{J}_{y}{\delta }_{\mathrm{s}}}{{\gamma }^{2}}-\frac{\partial }{\partial z}\frac{\mathrm{i}{k}_{x}{J}_{z}{\delta }_{\mathrm{s}}}{{\gamma }^{2}}+{J}_{x}{\delta }_{\mathrm{s}}\end{array} $ | (4) |
式中:
利用加权余量法将式(3)和式(4)改写为积分方程的形式,并在区域
| $ \begin{array}{l}{\int }_{\varOmega }\frac{\sigma }{{\gamma }^{2}}\nabla {\widehat{E}}_{x}\cdot \nabla \delta {\widehat{E}}_{x}\mathrm{d}\varOmega +{\int }_{\varOmega }\sigma {\widehat{E}}_{x}\delta {\widehat{E}}_{x}\mathrm{d}\varOmega -\\\ \ \ \ {\int }_{\varOmega }\left[\frac{\partial \delta {\widehat{E}}_{x}}{\partial y}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{H}}_{x}}{\partial z}\right)-\frac{\partial \delta {\widehat{E}}_{x}}{\partial z}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{H}}_{x}}{\partial y}\right)\right]\mathrm{d}\varOmega \\ =-{\oint }_{\varGamma }^{}\delta {\widehat{E}}_{x}{\widehat{H}}_{t}\mathrm{d}\varGamma -{\int }_{\varOmega }\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\left(\frac{\partial \delta {\widehat{E}}_{x}}{\partial y}{J}_{y}{\delta }_{\mathrm{s}}+\right.\\ \ \ \ \ \left.\frac{\partial \delta {\widehat{E}}_{x}}{\partial z}{J}_{z}{\delta }_{\mathrm{s}}\right)\mathrm{d}\varOmega -{\int }_{\varOmega }\delta {\widehat{E}}_{x}{J}_{x}{\delta }_{\mathrm{s}}\mathrm{d}\varOmega \end{array} $ | (5) |
| $ \begin{array}{l}-{\int }_{\varOmega }\frac{\mathrm{i}\omega {\mu }_{0}}{{\gamma }^{2}}\nabla {\widehat{H}}_{x}\cdot \nabla \delta {\widehat{H}}_{x}\mathrm{d}\varOmega -{\int }_{\varOmega }i\omega {\mu }_{0}{\widehat{H}}_{x}\delta {\widehat{H}}_{x}\mathrm{d}\varOmega +\\\ \ \ \ {\int }_{\varOmega }\left[\frac{\partial \delta {\widehat{H}}_{x}}{\partial y}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{E}}_{x}}{\partial z}\right)-\frac{\partial \delta {\widehat{H}}_{x}}{\partial z}\left(\frac{\mathrm{i}{k}_{x}}{{\gamma }^{2}}\frac{\partial {\widehat{E}}_{x}}{\partial y}\right)\right]\mathrm{d}\varOmega \\ ={\int }_{\varOmega }\frac{\mathrm{i}\omega {\mu }_{0}}{{\gamma }^{2}}\left({J}_{z}{\delta }_{\mathrm{s}}\frac{\partial \delta {\widehat{H}}_{x}}{\partial y}-{J}_{y}{\delta }_{\mathrm{s}}\frac{\partial \delta {\widehat{H}}_{x}}{\partial z}\right)\mathrm{d}\varOmega +\\\ \ \ \ {\oint }_{\varGamma }^{}\delta {\widehat{H}}_{x}{\widehat{E}}_{\mathrm{t}}\mathrm{d}\varGamma \end{array} $ | (6) |
式中:
对式(5)和式(6)的所有方程组求和,得到线性方程组
| $ \boldsymbol{K}\boldsymbol{U}=\boldsymbol{S} $ | (7) |
式中:
正则化MCSEM数据的反演目标函数为
| $ \begin{array}{l}{\boldsymbol{U}}_{\boldsymbol{m}}={‖\boldsymbol{R}\boldsymbol{m}‖}^{2}+{‖\boldsymbol{P}(\boldsymbol{m}-{\boldsymbol{m}}_{\boldsymbol{*}})‖}^{2}+\\\ \ \ \ \ \ \ \ \ \ \ {\mu }^{-1}{‖\boldsymbol{w}\left[\boldsymbol{d}-{\boldsymbol{F}}_{\boldsymbol{m}}\left(\boldsymbol{m}\right)\right]‖}^{2}\end{array} $ | (8) |
式中:
采用OCCAM方法进行迭代,实现模型m的最小化,其模型更新迭代公式为
| $ \begin{array}{l}{\boldsymbol{m}}_{K+1}=\left[\lambda \right({\boldsymbol{R}}^{\mathrm{T}}\boldsymbol{R}+{\boldsymbol{P}}^{\mathrm{T}}\boldsymbol{P})+(\boldsymbol{W}{\boldsymbol{J}}_{K}{)}^{\mathrm{T}}\boldsymbol{W}{\boldsymbol{J}}_{K}{]}^{-1}\times \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[\right(\boldsymbol{W}{\boldsymbol{J}}_{K}{)}^{\mathrm{T}}\boldsymbol{W}\widehat{\boldsymbol{d}}+{\boldsymbol{P}}^{\mathrm{T}}\boldsymbol{P}{\boldsymbol{m}}_{\boldsymbol{*}}]\end{array} $ | (9) |
式中: K表示迭代次数; λ为正则化因子。修改后的数据向量满足
| $ \widehat{\boldsymbol{d}}=\boldsymbol{d}-{\boldsymbol{F}}_{\boldsymbol{m}}\left({\boldsymbol{m}}_{K}\right)+{\boldsymbol{J}}_{K}{\boldsymbol{m}}_{K} $ | (10) |
式中
| $ {\boldsymbol{m}}_{K+1}^{\mathrm{\text{'}}}=\alpha {{\boldsymbol{m}}_{K}}_{+1}+(1-\alpha ){\boldsymbol{m}}_{K} $ | (11) |
式中α表示迭代步长。首先设置
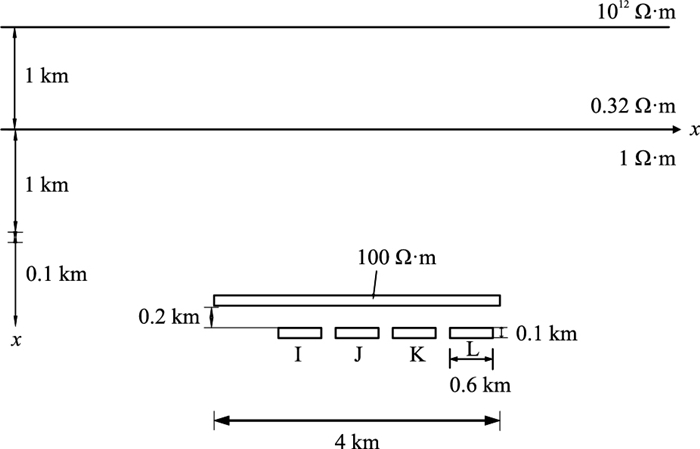
对图 1所示二维海洋地电模型进行模拟。油气模型包括两部分:主油气层和次油气层。在海底-4~4 km范围内等间隔放置9个接收站,间隔为1 km。发射源沿接收站上方50 m高度拖曳前进,行进范围为-6~6 km,每隔200 m激发一次。发射频率为0.25 Hz,电流为1 A,电极长度为1 m。主油气层从右向左开采,每次开采20%。油气开采完后储层电阻率降为1 Ω·m(即与围岩电阻率相等)。
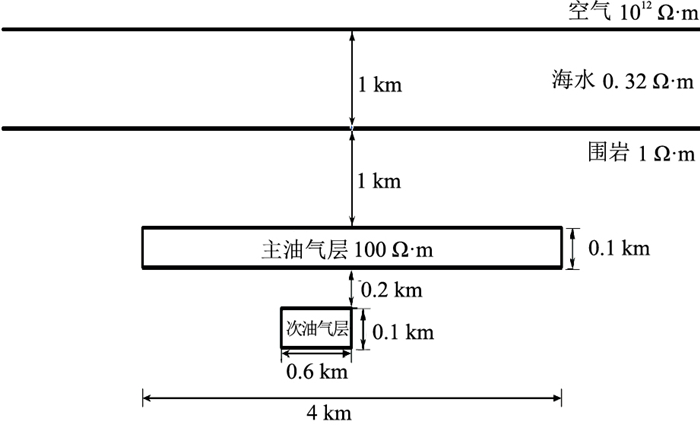
|
图 1 二维海洋地电模型 |
对该二维海洋地电模型建立初始网格。采用自适应有限元方法,对网格逐步细化,每次细化会增加约5%的网格数,最终得到满足精度要求的细网格。同时,电磁响应采用分组并行计算,将一定数量的发射位置和接收位置组合为一组,因而最终的正演网格大小会有所不同。
本文以使用归一化振幅及含有和不含次油气层的归一化振幅之间的差异(归一化振幅差异)作为判断正演效果的参数。以电场为例,归一化振幅为
| $ {E}_{\mathrm{g}}=\frac{E}{{E}_{\mathrm{b}}} $ | (12) |
式中:
| $ {E}_{\mathrm{d}}=\frac{{E}_{\mathrm{g}}^{\mathrm{\text{'}}}}{{E}_{\mathrm{g}}} \times 100\mathrm{\%} $ | (13) |
式中
为了探究油气开采时,次油气层对MCSEM正演响应的影响,分别设计有、无次油层的模型进行仿真模拟。对于图 1所示的含次油气层的模型,不同开采程度下的电场分量Ey模拟结果见图 2a。对于不存在次油气层的模型,模拟的MCSEM电场分量Ey见图 2b。有、无次油气层模型在主油气层不同开采程度下的MCSEM电场分量Ey的归一化振幅曲线见图 3a,归一化振幅差异见图 3b。可以看出,当主油气藏未开采时,含有次油气层和不含有次油气层模型的归一化振幅差异极小;当主油气层的含油量剩余40%时,两者开始出现较大差异,最高差异值约为7%。因此,利用MCSEM法在油气开采过程中对次油气层进行探测是可行的。
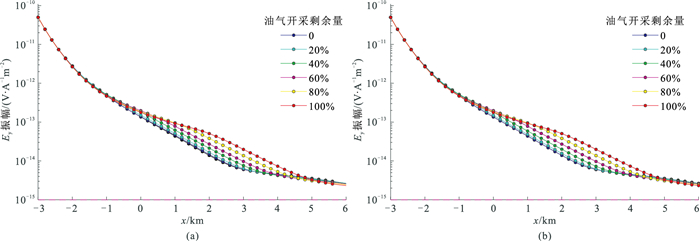
|
图 2 不同开采程度下含次油气层(a)和无次油气层(b)模型的电场分量Ey振幅 图中离散点对应模型值,曲线对应背景值。 |
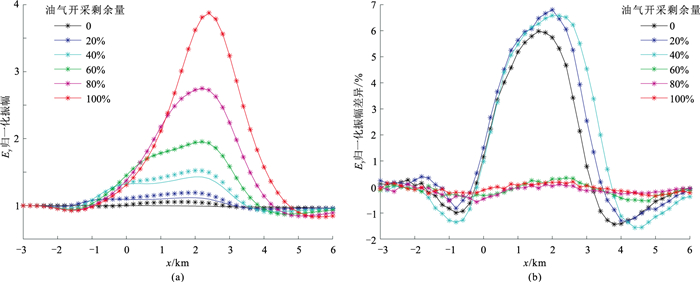
|
图 3 有、无次油气层模型的电场分量Ey归一化振幅曲线(a)及归一化振幅差异(b) 图a中的离散点对应有次油气层的模型,曲线对应无次油气层的模型。 |
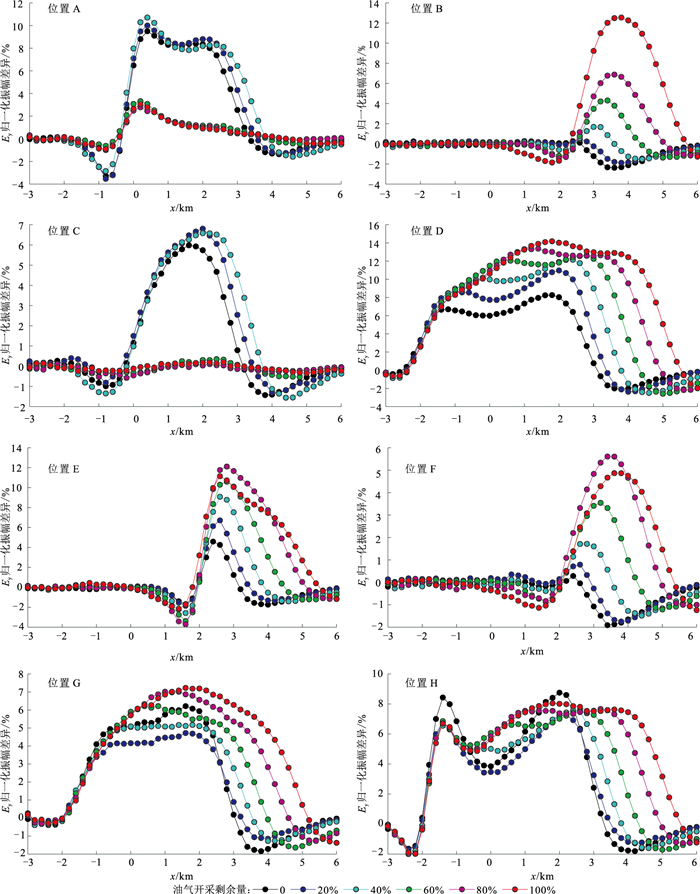
考虑实际生产中的开采方向与次油气层深度这两个因素,设计一个复杂油气模型(图 4)。假设次油气层分别位于图 4中的A~H处(A~D位于上下左右等“正”方向,E~H位于“斜”方向),分别模拟其电磁响应,据此分析次油气层位置对主油气层MCSEM响应的影响。
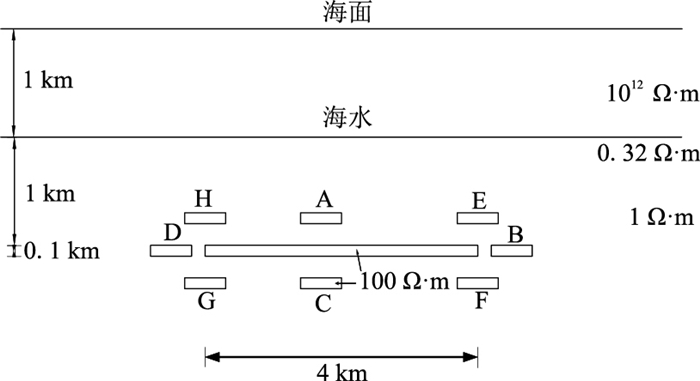
|
图 4 次油气层位于不同位置(相对于主油气层)示意图 A~H分别代表次油气层的不同位置。次油气层长度为600 m,厚度为100 m。在水平或垂直方向上与主油气层的距离均为200 m。斜向时次油气层的中心在主油气层垂直边界所在直线上,与主油气层边界相距250 m。 |
数值模拟时,源的发射频率为0.25 Hz,每次模拟时只涉及一个次油气层。电磁信号记录仪置于海底。图 4模型的归一化Ey振幅差异见图 5。从图 5可见,次油气层在主油气层上方(位置A)和下方(位置C)时,油气开采前(开采剩余量100%)电场Ey归一化差值很小;在其余位置(位置B、D、E、F)时,电场Ey归一化差值在开采前、后均表现出较大差异,其中次油气层位于位置B时,Ey归一化差异约14%,达到最大值;在位置C时达到最小值,约为5%。在主油气层未开采(剩余量100%)时,若次油气层位于主油藏上方,则次油气层对电场的影响约为2%;若位于主油藏的下方,对电场几乎没有影响。
|
图 5 图 4模型不同主油气层开采情况下的Ey归一化振幅差异曲线 |
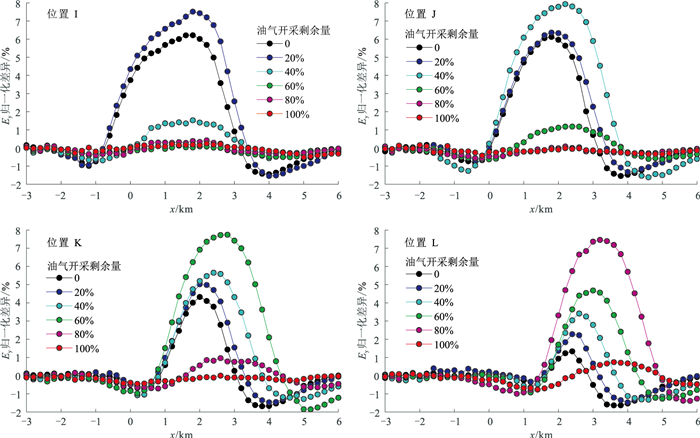
当次油气层位于主油气层下方不同水平位置时,其电磁特征也不同。为此,设计一组次油气层位于主油气层下方不同位置的模型(图 6),讨论分析整个开采过程中的电磁响应特征。归一化Ey振幅差异见图 7。可以看出,当次油气层上方的主油气层被完全开采(图中剩余开采量为0)后,次油气层产生的电磁响应非常明显;次油气层越接近主油气层的初始开采区域(右侧),开采过程中可更早地监测到次油气层的存在。
|
图 6 次油气层位于主油气层下方不同位置的模型 I~L分别代表次油气层所在位置编号。 |
|
图 7 图 6模型MCSEM电磁分量归一化Ey振幅差异曲线 |
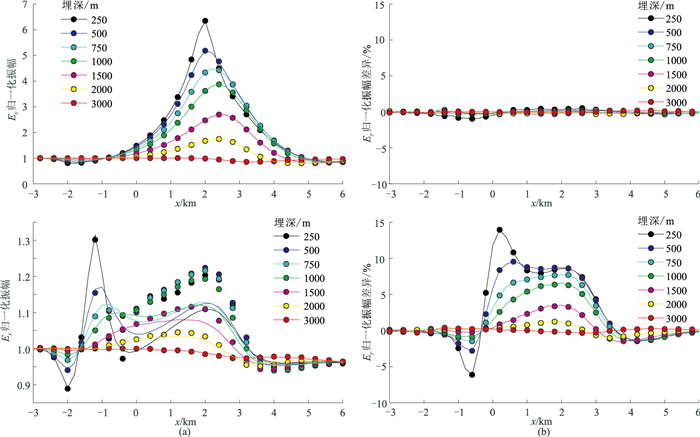
为了探究主油气层埋深对次油气层探测结果的影响,设计一组主油气层位于不同深度(250~3000 m,间隔250 m)的油气层模型(图 8),分别计算开采前和开采至剩余量为20%时的电磁响应。源的发射频率为0.25 Hz,电磁信号采集站置于海底x=-4 km处。图 9为主油气层开采前和油气开采剩余量为20%时的Ey归一化振幅和归一化振幅差异曲线,可见: 主油气层位于不同深度时,主油藏开采前,次油气层对主油气层的电磁响应的影响微乎其微,影响最大的情况是主油气层位于250 m深度的模型,但其影响程度也不及1%;当油气开采剩余20%时,次油气层对主油气层电磁响应的影响增强,主油气层埋深越小,影响越大,250 m埋深情况下Ey振幅差最大可达约17%。
|
图 8 主油气层埋深变化模型示意图 |
|
图 9 主油层位于不同深度时次油气层对电场分量Ey的影响 (a)Ey归一化振幅曲线;(b)Ey归一化振幅差异。上:主油气层未开采;下:主油气层开采剩余量为20%。 图a中的离散点对应有次油气层的模型,曲线对应无次油气层的模型。 |
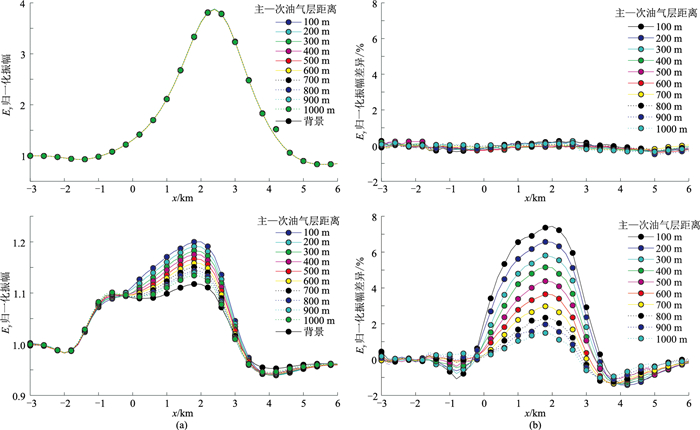
为了探究主—次油气层间距对次油气层探测结果的影响,设计一组不同间距的油气层模型(参考图 8模型)。次油气层位于主油气层正下方,两者距离为100~1000 m,每隔100 m取一个值,分别计算不同主油气层和次油气层间距的模型在主油气层开采前和开采至剩余量20%的电磁响应。源频率为0.25 Hz,电磁数据采集站置于海底x=-4 km处。图 10为模拟计算结果, 由图可见: 主油气层开采前,对于主、次油气层间距不同的情况,次油气层对主油气层电磁响应的影响微乎其微,影响最大的是间距为100 m的模型,影响最大不足1%; 当主油气层开采至剩余量为20%时,次油气层对主油气层电磁响应的影响大幅提高,且主、次油气层间距越小,次油气层对主油气层电磁响应的影响越大,在间距为1000 m情况下,最大产生约10%的差异。
|
图 10 主—次油气层不同距离条件下模型电场分量Ey归一化振幅(左)及其差异(右) (a)主油气层未开采;(b)主油气层开采剩余量为20% |
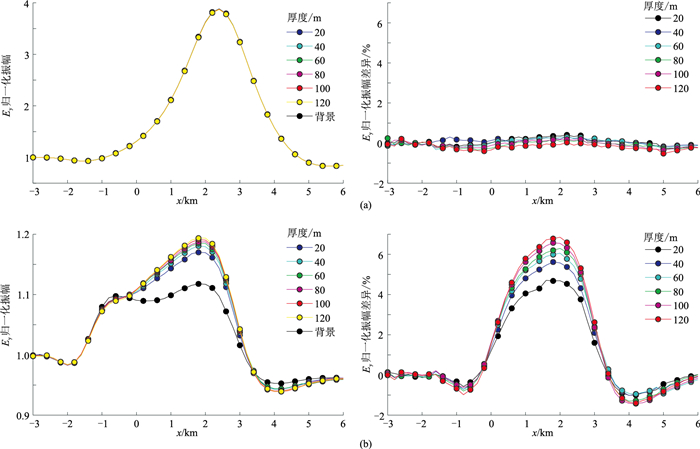
为了分析次油气层在不同厚度情况下的电磁响应特征,设计一组次油气层厚度变化(厚度20~120 m,每隔20 m取一个值)的模型(基本参数同图 8),分别计算该模型在主油气层开采前和开采剩余量为20%时的电场响应。源频率为0.25 Hz,电磁数据采集站置于海底x=-4 km处。图 11为模拟计算结果,可以看出,主油层开采前,不同厚度的次油气层对主油气层的电磁响应的影响微乎其微,差异最大的情况出现在厚度为120 m的模型,最大值不到1%;当主油气层开采量达到80%(剩余量20%)时,次油气层对主油气层电磁响应的影响大幅增强,次油气层厚度越大,该影响越大,厚度为120 m的情况下,最大产生约7%的差异。
|
图 11 次油气层厚度不同时模型电场分量Ey归一化振幅(左)及其差异(右) (a)主油气层未开采;(b)主油气层开采至剩余量20% |
从上述正演结果可以发现,不同模型的正演响应是有区别的,但这些差异都很小。因此,仅从正演结果是很难分辨是否存在次油气层,也无法判断次油层的位置及其他信息。为此,需进一步开展电阻率反演。
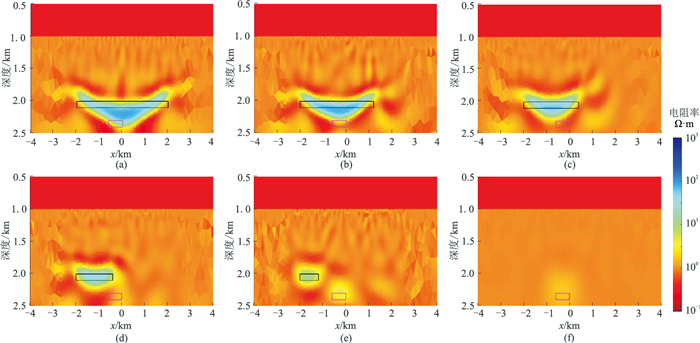
3.1 主油气层不同开采程度模型反演对图 1所示主油气层不同开采程度模型的正演数据进行电阻率反演,结果见图 12。由图可见:当主油气层剩余量大于40%(图 12a~图 12c)时,反演电阻率剖面上无法明显观察到次油气层引起的异常,但次油气的存在对反演结果的影响是可以观察到的,即高阻区向下凹陷;当主油气层剩余量小于或等于40%(图 12d~图 12f)时,次油气层的电阻率异常不甚明显,主油气层剩余量为40%(图 12d)时,次油气层的水平投影开始出现;当主油气层的油气剩余量只有20%(图 12e)时,可以明显观测到次油气层的存在。从图 3可见:主油气层剩余量为0、20%、40%模型的Ey归一化振幅曲线上都出现了较大差异;主油气层剩余量从40%降至20%时,主油气层和次油气层在水平方向上的投影出现分离现象,电阻率反演剖面上次油气层的特征更明显,说明MCSEM法对高阻油气藏的水平边界检测效果较好。
|
图 12 基于主油气层不同开采剩余量模型正演数据的电阻率反演剖面 (a)100%;(b)80%;(c)60%;(d)40%;(e)20%;(f)0。图中长方形表示油气层。 |
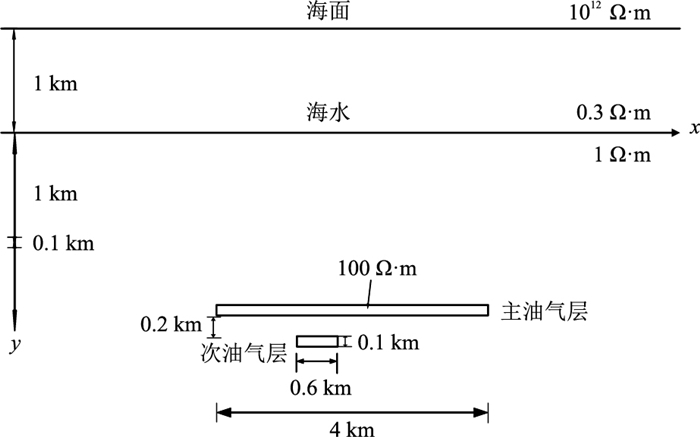
为了研究复杂地质条件下利用MCSEM法进行油气层开采监测的效果,设计图 13a所示复杂地电模型。图中高阻区域即为油气层,其中位于上方的高阻区(蓝色区域)为主油气层,下方的高阻区(蓝色区域)为次油气层。该模型的电阻率反演结果见图 13b。可以看出:油气开采前,次油气层的存在使得主油气层反演电阻率整体呈现下凹特征;随着油气开采的进行,当主油气层的油气剩余量为20%时,剖面上出现两个次高阻区域(图 13中方框内的黄色区域),这两个次高阻区即是主油气层和次油气层的反映,且主、次油气层分界线明显。该复杂模型的电阻率反演结果表明利用MCSEM监测海底油气开采过程、探测次油气层是可行的。
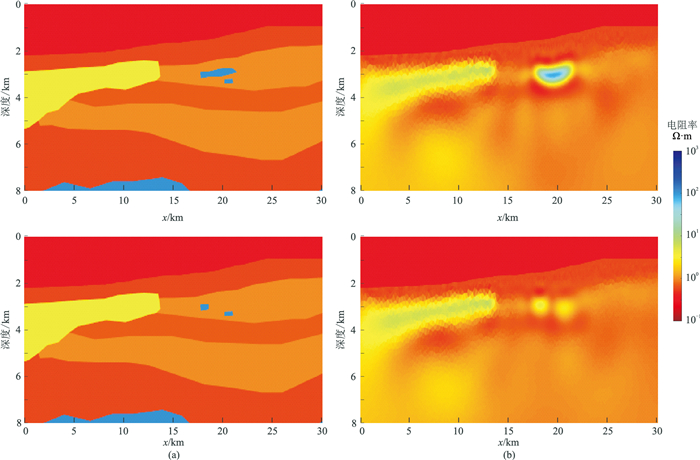
|
图 13 复杂地电模型(a)及电阻率反演剖面(b) 上:未开采模型;下:主油气层油气开采剩余量为20%。图a中方框内部高阻区表示油气分布区。 |
本文利用MCSEM法对油气开发过程进行检测,通过模拟、分析油气开采过程中电磁响应特征的变化,判断次油气层是否存在。得到以下结论。
(1) 对MCSEM电磁响应进行电阻率反演,根据电阻率分布特征可判断次油气层是否存在。
(2) 油田开采过程中MCSEM响应仿真模拟结果表明:次油气层越接近初始开采区(主油气层),越容易观测到电磁差异;主油层埋深越小、主—次油气层间距越小、次油气层厚度越大,次油气层对观测结果的影响越大,越容易探测到次油气层。
(3) 利用正演归一化结果进行电阻率反演,可据此对次油气层进行探测。对复杂地质条件下的油气模型开采过程进行反演实验,结果表明在油气开采监测过程中利用MCSEM法探测次油气层是可行的和可靠的。
| [1] |
CHAVE A D. On the theory of electromagnetic induction in the Earth by ocean currents[J]. Journal of Geophysical Research: Solid Earth, 1983, 88(B4): 3531-3542. DOI:10.1029/JB088iB04p03531 |
| [2] |
FLOSADÓTTIR Á H, CONSTABLE S. Marine controlled-source electromagnetic sounding: 1. Modeling and experimental design[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B3): 5507-5517. DOI:10.1029/95JB03739 |
| [3] |
CHRISTENSEN N B, DODDS K. 1D inversion and resolution analysis of marine CSEM data[J]. Geophysics, 2007, 72(2): WA27-WA38. DOI:10.1190/1.2437092 |
| [4] |
KEY K. 1D inversion of multicomponent, multifrequency marine CSEM data: methodology and synthetic studies for resolving thin resistive layers[J]. Geophysics, 2009, 74(2): F9-F20. DOI:10.1190/1.3058434 |
| [5] |
CAI H Z, HU X Y, LI J H, et al. Parallelized 3D CSEM modeling using edge-based finite element with total field formulation and unstructured mesh[J]. Computers & Geosciences, 2017, 99: 125-134. |
| [6] |
刘颖, 李予国, 韩波. 可控源电磁场三维自适应矢量有限元正演模拟[J]. 地球物理学报, 2017, 60(12): 4874-4886. LIU Ying, LI Yuguo, HAN Bo. Adaptive edge finite element modeling of the 3D CSEM field on unstructured grids[J]. Chinese Journal of Geophysics, 2017, 60(12): 4874-4886. DOI:10.6038/cjg20171227 |
| [7] |
YE Y X, LI Y G, LI G, et al. 3-D adaptive finite-element modeling of Marine controlled-source electromagnetics with seafloor topography based on secondary potentials[J]. Pure and Applied Geophysics, 2018, 175(12): 4449-4463. DOI:10.1007/s00024-018-1921-y |
| [8] |
刘玲, 殷长春, 刘云鹤, 等. 基于谱元法的频率域三维海洋可控源电磁正演模拟[J]. 地球物理学报, 2018, 61(2): 756-766. LIU Ling, YIN Changchun, LIU Yunhe, et al. Spectral element method for 3D frequency-domain marine controlled-source electromagnetic forward modeling[J]. Chinese Journal of Geophysics, 2018, 61(2): 756-766. |
| [9] |
高妍, 马超, 张向宇. 可燃冰与油气双储层模型的海洋可控源电磁响应特征模拟分析[J]. 石油地球物理勘探, 2022, 57(4): 950-962. GAO Yan, MA Chao, ZHANG Xiangyu. Characteristics of simulated marine controlled-source electromagnetic responses of coupled gas hydrate and petroleum reservoir models[J]. Oil Geophysical Prospecting, 2022, 57(4): 950-962. |
| [10] |
张岩, 戴世坤, 张钱江, 等. 一种可控源电磁法2.5维观测系统设计[J]. 中国科技信息, 2020(14): 86-89. ZHANG Yan, DAI Shikun, ZHANG Qianjiang, et al. Design of a 2.5-dimensional observation system using controllable source electromagnetic method[J]. China Science and Technology Information, 2020(14): 86-89. |
| [11] |
LI J K, LI Y G, LIU Y, et al. 3-D Marine CSEM forward modeling with general anisotropy using an adaptive Finite-Element method[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(11): 1936-1940. DOI:10.1109/LGRS.2020.3011743 |
| [12] |
CHNE H B, XIONG B, HAN Y. An effective algorithm for 2D marine CSEM modeling in anisotropic media using a wavelet Galerkin method[J]. Minerals, 2022, 12(2): 124. DOI:10.3390/min12020124 |
| [13] |
WEITEMEYER K, GAO G, CONSTABLE S, et al. The practical application of 2D inversion to marine controlled-source electromagnetic data[J]. Geophysics, 2010, 75(6): F199-F211. DOI:10.1190/1.3506004 |
| [14] |
LI Y, KEY K. 2D marine controlled-source electromagnetic modeling: part 1-an adaptive finite-element algorithm[J]. Geophysics, 2007, 72(2): WA51-WA62. DOI:10.1190/1.2432262 |
| [15] |
KERRY K. MARE2DEM: a 2-D inversion code for controlled-source electromagnetic and magnetotelluric data[J]. Geophysical Journal International, 2016, 207(1): 571-588. DOI:10.1093/gji/ggw290 |
| [16] |
肖俊, 叶益信, 薛海军, 等. 基于非结构有限元的带地形海洋可控源电磁法二维Occam反演[J]. 工程地球物理学报, 2020, 17(2): 217-224. XIAO Jun, YE Yixin, XUE Haijun, et al. Two-dimensional Occam inversion of marine controlled-source electromagnetic method in terrain based on unstructured finite element method[J]. Chinese Journal of Engineering Geophysics, 2020, 17(2): 217-224. |
| [17] |
龙志丹. 基于矢量有限元的频率域可控源电磁法三维反演研究[D]. 北京: 中国地质大学(武汉), 2021.
|
| [18] |
LONG Z D, HU X Y, SHAO O Y, et al. 3-D inversion of CSEM data with hexahedral mesh in the multinary model space[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. |
| [19] |
LØSETH L O, WIIK T, OLSEN P A, et al. Detecting skrugard by CSEM-prewell prediction and postwell evaluation[J]. Interpretation, 2014, 2(3): SH67-SH78. DOI:10.1190/INT-2013-0152.1 |
| [20] |
KONG F N, ROTH F, OLSEN P A, et al. Casing effects in the sea-to-borehole electromagnetic method[J]. Geophysics, 2009, 74(5): F77-F87. DOI:10.1190/1.3173807 |
| [21] |
WIRIANTO M, MULDER W A, SLOB E C. A feasibility study of land CSEM reservoir monitoring in a complex 3-D model[J]. Geophysical Journal International, 2010, 181(2): 741-755. |
| [22] |
SHAHIN A, KEY K, STOFFA P, et al. Petro-electric modeling for CSEM reservoir characterization and monitoring[J]. Geophysics, 2012, 77(1): E9-E20. |
| [23] |
SHANTSEV D V, NERLAND E A, GELIUS L J. Time-lapse CSEM: how important is survey repeatability?[J]. Geophysical Journal International, 2020, 223(3): 2133-2147. |
| [24] |
刘勇, 李文彬, 邓方顺, 等. 海洋可控源电磁法深海油藏开采监测仿真[J]. 石油地球物理勘探, 2022, 57(1): 237-244. LIU Yong, LI Wenbin, DENG Fangshun, et al. Monitoring and simulation of deep-sea reservoir exploitation by marine controlled source electromagnetic method[J]. Oil Geophysical Prospecting, 2022, 57(1): 237-244. |
| [25] |
刘颖. 海洋可控源电磁法二维有限元正演及反演[D]. 山东青岛: 中国海洋大学, 2014.
|



 刘颖,山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email:
刘颖,山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email: