2. 中国石油勘探开发研究院西北分院, 甘肃兰州 730020;
3. 中海石油(中国)有限公司上海分公司, 上海 200335;
4. 中石油西南油气田公司勘探开发研究院, 四川成都 610041
2. Northwest Branch of China Petroleum Exploration and Development Research Institute, Lanzhou, Gansu 730020, China;
3. CNOOC (China) Co., Ltd., Shanghai Branch, Shanghai 200335, China;
4. Exploration and Development Research Institute of PetroChina Southwest Oil and Gas Field Company, Chengdu, Sichuan 610041, China
页岩储层作为重要的非常规储层,近年来一直是学者们研究的重点,在学者们的探究下,页岩储层的流体性质预测技术得到不断推进。页岩气储层水平层理较发育,呈现明显的VTI(Transverse Isotropy with a Vertical Axis of Symmetry)介质特征,对地震反射特征产生了显著的改变[1]。在反演时按各向同性介质模型进行分析,会造成极大误差[2]。研究基于VTI介质的弹性参数和各向异性参数反演方法,在反演过程中考虑到各向异性因素,对更精确地识别页岩气储层的位置和分布范围、预测储层各向异性程度和页岩气储层的勘探、开发具有重要意义。在探索地下储层中的流体时,选择合适的流体因子是关键一环。早期基于各向同性假设,Smith等[3]定义了流体因子的概念,之后通过众多学者的探索,发现了多种适用于不同储层的识别流体位置与类型的参数[4-6],如Russell等[7]提出的表征流体的模量、Gassmnn流体项等,作为经典的孔隙流体因子,这些参数可区分流体类型,识别储层中流体位置。
研究发现,地震波在地下传播时,储层的各向异性对振幅与速度的影响不容忽视[8-14]。韩建光等[15]针对水平层状VTI介质模型,分析了各向异性参数ε和δ对高斯束叠前深度偏移的影响,发现当忽略各向异性影响时,模型界面附近存在较大的噪声干扰,页岩层的弯曲底界面成像不准确,而且在弯曲界面处存在明显的能量发散。Jamali等[16]利用三分量VSP数据集研究了两种分析策略的各向异性模型,探索了VTI介质中弹性模量随流体含量的变化规律,发现如果将各向同性状态假设为各向异性状态,则计算得到的剪切模量将比实际值低8%~10%。Dande等[17]在室内研究了孔隙流体和岩石结构对三维VTI岩石模型地震速度和各向异性的影响,发现流体饱和度与流体黏度的变化会对岩石各向异性产生影响。Li[18]探索了物理建模和孔隙弹性模型在VTI介质流体检测中的应用,结果表明,有效流体因子的应用大大提高了VTI介质中地震流体探测的解释分辨率。刘瑞合等[19]为解决因地下介质的各向异性对大炮检距数据影响较大而导致成像精度降低的问题,提出了针对VTI介质的各向异性参数层析反演策略。忽略各向异性带来的影响,将会在一定程度上影响流体识别的准确性。
对于较强各向异性的储层(如页岩储层),在反演时应特别注意各向异性的影响,避免因假设与实际不符造成的较大误差。建立基于各向异性介质弹性参数与地震反射特征之间的定量关系是地震反演的重要基石。针对VTI介质,在基于各向同性假设的Zoeppritz方程基础上,Garebner[20]推导了平面波在VTI介质中的反射、透射精确传播方程。精确传播方程虽计算精度高,但方程为非线性,用于反演过程时计算效率低、稳定性差。学者们针对此问题开展了一系列近似方程的推导工作,并基于推导的近似方程实现了稳定、有效的弹性参数预测。Rüger[21]推导了VTI介质的P-P和P-SV反射波近似反射系数公式。Mavko等[22]推导出沿横向各向同性(HTI)介质对称轴传播的地震波各向异性流体替代方程的近似形式,实验证明近似流体替代方程适用于任何弱各向异性的VTI介质,能够得到更精确的反演结果。Cui等[23]将各向异性参数和HTI介质方位角引入流体识别因子方程。在分析各向异性介质中识别因子变化的同时,通过引入方位角极大地扩展了流体识别因子的应用范围,实现了HTI介质各向异性参数与流体的预测。陈怀震等[24]利用裂缝参数与储层流体的关系,考虑了裂缝引起的各向异性,通过方位弹性阻抗反演和地震AVAZ反演实现了储层流体的识别。侯栋甲等[25]基于Rüger近似公式实现了基于贝叶斯理论的VTI介质多波叠前联合反演。印兴耀等[26]基于Russell的近似公式推导了以流体因子F、拉梅常数
考虑到各向异性的影响,针对由水平层理引起的VTI介质,将Russell流体因子F和杨氏模量
根据弱各向异性假设条件,Rüger[21]推导了VTI介质纵波反射系数近似方程
| $ {R}_{\mathrm{P}\mathrm{P}}^{}={R}_{\mathrm{P}\mathrm{P}}^{\mathrm{i}\mathrm{s}\mathrm{o}}+{R}_{\mathrm{P}\mathrm{P}}^{\mathrm{a}\mathrm{n}\mathrm{i}} $ | (1) |
其中
| $ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}^{\mathrm{i}\mathrm{s}\mathrm{o}}=\frac{1}{2}\frac{\mathrm{\Delta }Z}{\stackrel{-}{Z}}+\frac{1}{2}\left[\frac{\mathrm{\Delta }{V}_{\mathrm{p}}}{\overline{{V}_{\mathrm{p}}}}-{\left(2\frac{\overline{{V}_{\mathrm{s}}}}{\overline{{V}_{\mathrm{p}}}}\right)}^{2}\cdot \frac{\mathrm{\Delta }G}{\stackrel{-}{G}}\right]\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\\ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2}\frac{\mathrm{\Delta }{V}_{\mathrm{p}}}{\overline{{V}_{\mathrm{p}}}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \end{array} $ | (2) |
| $ {R}_{\mathrm{P}\mathrm{P}}^{\mathrm{a}\mathrm{n}\mathrm{i}}=\frac{1}{2}\mathrm{\Delta }\varepsilon \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta +\frac{1}{2}\mathrm{\Delta }\delta \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (3) |
式中:
Russell等[7]提出的流体因子为
| $ F=(\rho {V}_{\mathrm{P}}{)}^{2}-c(\rho {V}_{\mathrm{S}}{)}^{2} $ | (4) |
式中c表示干岩石的纵横波速度比的平方。杨氏模量E与储层脆性具有较强的相关性,将E放到方程中,可以实现地质甜点与工程甜点的同时预测。E可用纵、横波速度表示为
| $ E=\rho {{V}_{\mathrm{S}}}^{2}\frac{3{{V}_{\mathrm{P}}}^{2}-4{{V}_{\mathrm{S}}}^{2}}{{{V}_{\mathrm{P}}}^{2}-{{V}_{\mathrm{S}}}^{2}} $ | (5) |
为了使各向异性参数反演更稳定,将
| $ \left\{\begin{array}{l}{\varepsilon }_{\mathrm{r}}=\frac{\varepsilon +1-\overline{\varepsilon }}{1-\overline{\varepsilon }}\\ {\delta }_{\mathrm{r}}=\frac{\delta +1-\overline{\delta }}{1-\overline{\delta }}\\ \mathrm{\Delta }\varepsilon =\frac{\mathrm{\Delta }{\varepsilon }_{\mathrm{r}}}{\overline{{\varepsilon }_{\mathrm{r}}}}\\ \mathrm{\Delta }\delta =\frac{\mathrm{\Delta }{\delta }_{\mathrm{r}}}{\overline{{\delta }_{\mathrm{r}}}}\end{array}\right. $ | (6) |
式中:
将式(4)~式(6)代入式(1),可得到
| $ \begin{aligned}{R}_{\mathrm{P}\mathrm{P}}\left(\theta \right)=&\left[\frac{(1-cg)(4{g}^{2}-8g+3)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{\chi }+\right.\\ &\left.\frac{8{g}^{2}(1-cg)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }F}{\overline{F}}+\\& \left[\frac{cg(3-4g)(1-g)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{\chi }-\right.\\& \left.\frac{8g(3-4g)(1-g)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }E}{\overline{E}}+\\& \frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{\varepsilon }_{\mathrm{r}}}{\overline{{\varepsilon }_{\mathrm{r}}}}+\frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{\delta }_{\mathrm{r}}}{\overline{{\delta }_{\mathrm{r}}}}\end{aligned} $ | (7) |
式中:
首先选用Rüger模型[30]和Thomsen模型[30]验证、分析式(7)的精度,模型参数如表 1所示。在Rüger模型中,上层为强VTI各向异性的页岩,下层为各向同性围岩;在Thomsen模型中,上、下层均为VTI各向异性砂岩和泥岩,该界面两侧阻抗差异较大。
|
|
表 1 VTI介质模型参数 |
图 1为VTI各向异性模型的
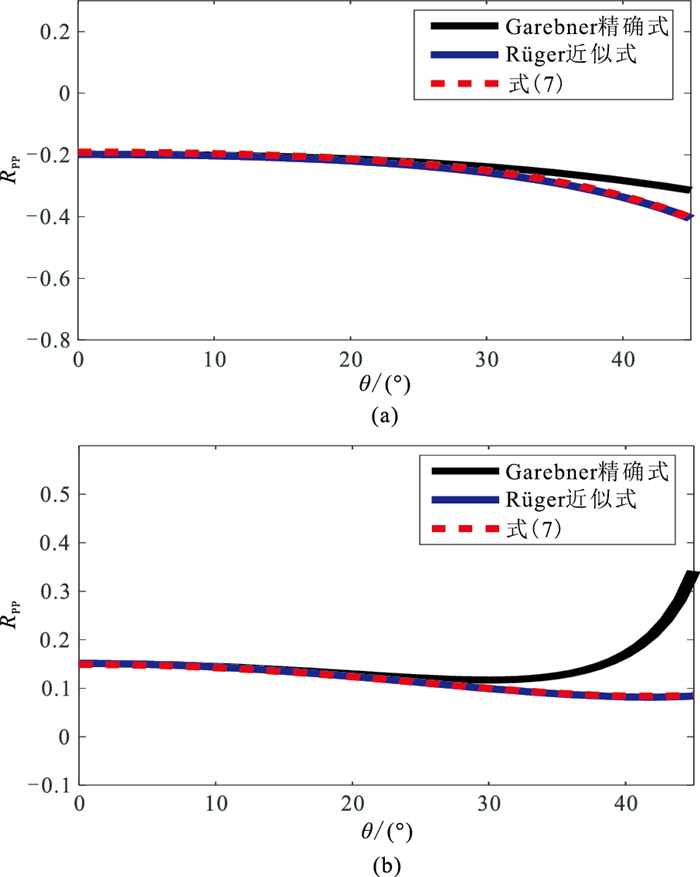
|
图 1 VTI各向异性模型的 |
根据Connolly[31]对弹性阻抗的定义,式(7)可写为
| $ \begin{aligned}{R}_{\mathrm{P}\mathrm{P}}\left(\theta \right)&\approx \frac{1}{2}\frac{\mathrm{\Delta }\mathrm{E}\mathrm{I}\left(\theta \right)}{\overline{\mathrm{E}\mathrm{I}\left(\theta \right)}}\\ &=\left[\frac{(1-cg)(4{g}^{2}-8g+3)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{\chi }+\right.\\&\ \ \left.\frac{8{g}^{2}(1-cg)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }F}{\overline{F}}+\\&\ \ \left[\frac{cg(3-4g)(1-g)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{\chi }-\right.\\&\ \ \left.\frac{8g(3-4g)(1-g)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }E}{\overline{E}}+\\ &\ \ \frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{\varepsilon }_{r}}{\overline{{\varepsilon }_{\mathrm{r}}}}+\frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{\delta }_{r}}{\overline{{\delta }_{\mathrm{r}}}}\end{aligned} $ | (8) |
式中
| $ \mathrm{E}\mathrm{I}\left(\theta \right)=\mathrm{E}{\mathrm{I}}_{0}\left[{\left(\frac{F}{\overline{F}}\right)}^{a\left(\theta \right)}{\left(\frac{E}{\overline{E}}\right)}^{b\left(\theta \right)}{\left(\frac{{\varepsilon }_{\mathrm{r}}}{\overline{{\varepsilon }_{\mathrm{r}}}}\right)}^{c\left(\theta \right)}{\left(\frac{{\delta }_{\mathrm{r}}}{\overline{{\delta }_{\mathrm{r}}}}\right)}^{d\left(\theta \right)}\right] $ | (9) |
| $ \left\{\begin{array}{l}a\left(\theta \right)=\frac{(1-cg)(8{g}^{2}-16g+6)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{\chi }+\\\ \ \ \ \ \ \ \ \ \ \ \ \frac{16{g}^{2}(1-cg)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\\ b\left(\theta \right)=\frac{2cg(3-4g)(1-g)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{\chi }-\\\ \ \ \ \ \ \ \ \ \ \ \ \frac{16g(3-4g)(1-g)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\\ c\left(\theta \right)=\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \\ d\left(\theta \right)=\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \end{array}\right. $ | (10) |
式中
采用基于模型先验约束的阻尼最小二乘反演方法[32],由地震数据求解模型参数。VTI介质
(1) 对已有的叠前地震数据分别做角度叠加,得到多个入射角道集;
(2) 提取相应的地震子波(不同
(3) 以测井数据和岩石物理模型估测结果计算测井曲线的
(4) 分别对角度叠加道集做波阻抗反演,得到不同
通过反演得到
对式(9)两边取对数
| $ \begin{array}{l}\mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{i}\right)}{\mathrm{E}{\mathrm{I}}_{0}}=a\left({\theta }_{i}\right)\mathrm{l}\mathrm{n}\frac{F}{{F}_{0}}+b\left({\theta }_{i}\right)\mathrm{l}\mathrm{n}\frac{E}{{E}_{0}}+\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ c\left({\theta }_{i}\right)\mathrm{l}\mathrm{n}\frac{{\varepsilon }_{\mathrm{r}}}{{\varepsilon }_{\mathrm{r}0}}+d\left({\theta }_{i}\right)\mathrm{l}\mathrm{n}\frac{{\delta }_{\mathrm{r}}}{{\delta }_{\mathrm{r}0}}\end{array} $ | (11) |
式中:
| $ \boldsymbol{d}=\boldsymbol{G}\boldsymbol{X} $ | (12) |
其中
| $ \left\{\begin{array}{l}\boldsymbol{d}=\left[\begin{array}{l}\mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{1}\right)}{\mathrm{E}{\mathrm{I}}_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{2}\right)}{\mathrm{E}{\mathrm{I}}_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{3}\right)}{\mathrm{E}{\mathrm{I}}_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{4}\right)}{\mathrm{E}{\mathrm{I}}_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{5}\right)}{\mathrm{E}{\mathrm{I}}_{0}}\end{array}\right]\\ \boldsymbol{G}=\left[\begin{array}{l}a\left({\theta }_{1}\right)b\left({\theta }_{1}\right)c\left({\theta }_{1}\right)d\left({\theta }_{1}\right)\\ a\left({\theta }_{2}\right)b\left({\theta }_{2}\right)c\left({\theta }_{2}\right)d\left({\theta }_{2}\right)\\ a\left({\theta }_{3}\right)b\left({\theta }_{3}\right)c\left({\theta }_{3}\right)d\left({\theta }_{3}\right)\\ a\left({\theta }_{4}\right)b\left({\theta }_{4}\right)c\left({\theta }_{4}\right)d\left({\theta }_{4}\right)\\ a\left({\theta }_{5}\right)b\left({\theta }_{5}\right)c\left({\theta }_{5}\right)d\left({\theta }_{5}\right)\end{array}\right]\\ \boldsymbol{X}=\left[\begin{array}{l}\mathrm{l}\mathrm{n}\frac{F}{{F}_{0}}\\ \mathrm{l}\mathrm{n}\frac{E}{{E}_{0}}\\ \mathrm{l}\mathrm{n}\frac{{\varepsilon }_{r}}{{\varepsilon }_{r0}}\\ \mathrm{l}\mathrm{n}\frac{{\delta }_{r}}{{\delta }_{r0}}\end{array}\right]\end{array}\right. $ | (13) |
式中:
建立一个三层水平层状VTI介质模型(图 2),开展流体因子在不同程度的各向异性影响下的反演精度试验和分析,中间层段为含气页岩,上、下围岩均为泥岩。对原始合成地震记录添加有用信号功率的1/2的高斯白噪声,然后分别对加噪前、后的合成地震记录(图 3)进行反演,结果如图 4所示。由图可见:随着各向异性参数的增大,相对误差增大;未考虑各向异性时的F反演结果的相对误差大于考虑各向异性。在无噪的情况下,当
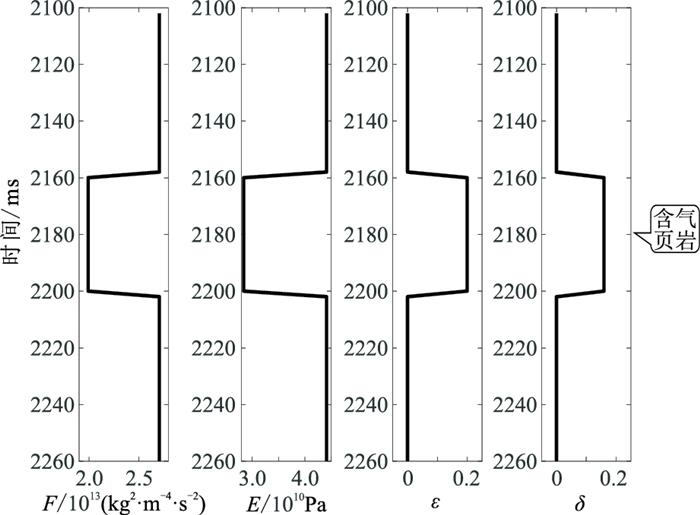
|
图 2 模型数据 |
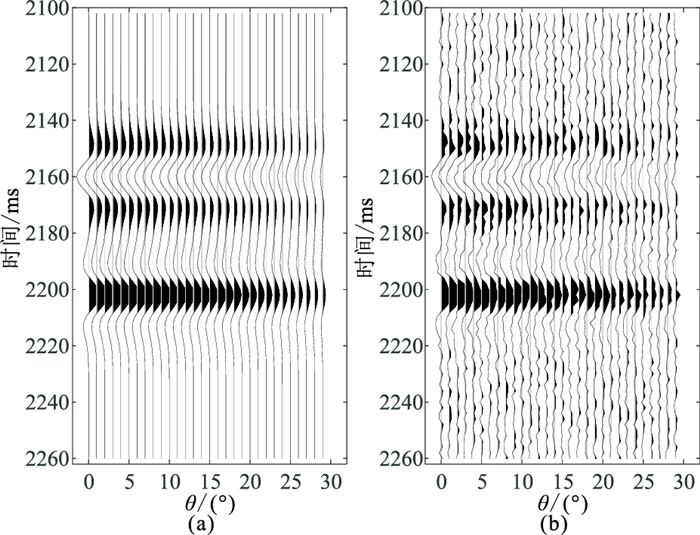
|
图 3 加噪前(a)、后(b)的合成地震记录 |
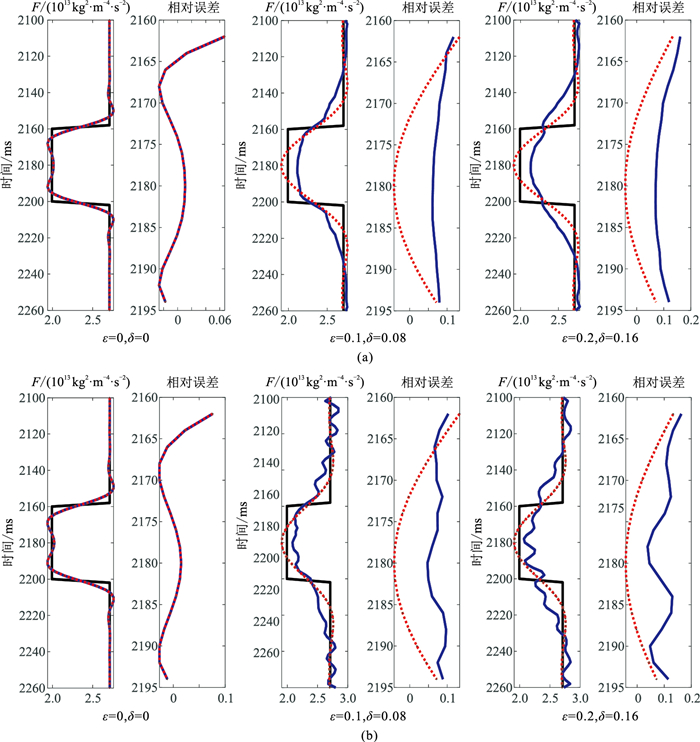
|
图 4 无噪(a)和加噪(b)的模型参数反演结果对比 黑色代表真实模型,蓝色和红色分别代表未考虑和考虑各向异性时的反演结果。 |
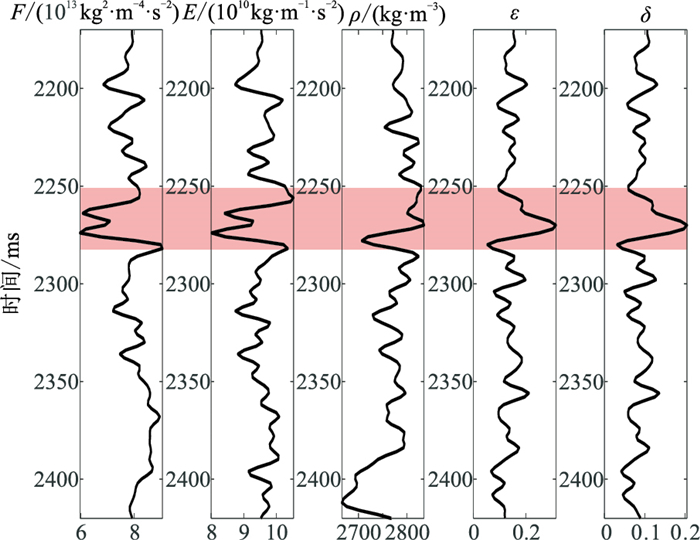
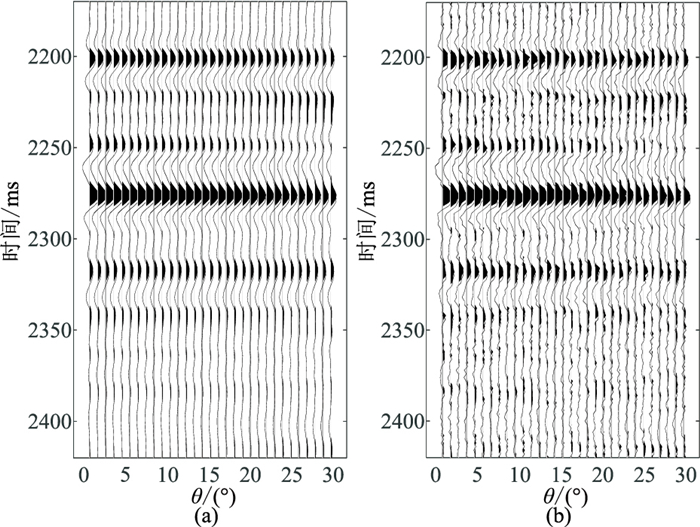
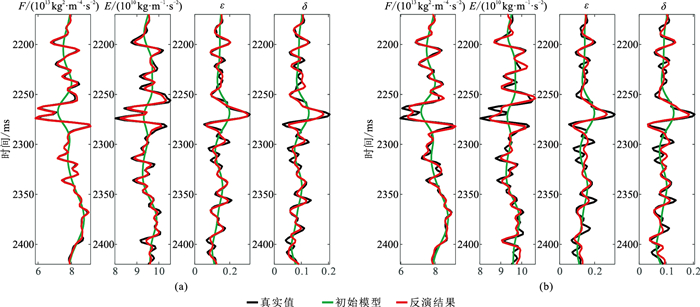
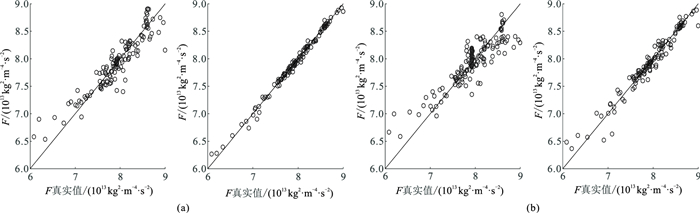
选取某工区实际井数据开展模型测试,以测试所提方法的效果。A井数据如图 5所示,其中红色区域对应储层位置。将图 5井数据与主频为35 Hz的Ricker子波褶积得到合成地震记录(图 6a),在合成地震记录上添加信噪比为2的高斯白噪(图 6b)。图 7展示了无噪和有噪时反演的F、E和
|
图 5 A井数据 |
|
图 6 无噪(a)和有噪(b)合成地震记录 |
|
图 7 加噪前(a)、后(b)模型参数反演结果 |
|
图 8 加噪前(a)、后(b)考虑(左)和不考虑(右)各向异性时模型参数反演结果与真实值交会图 |
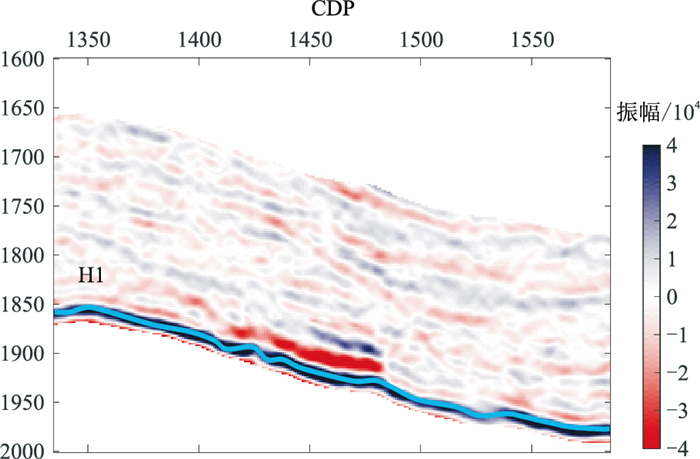
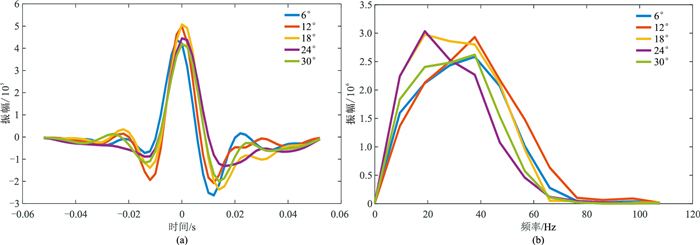
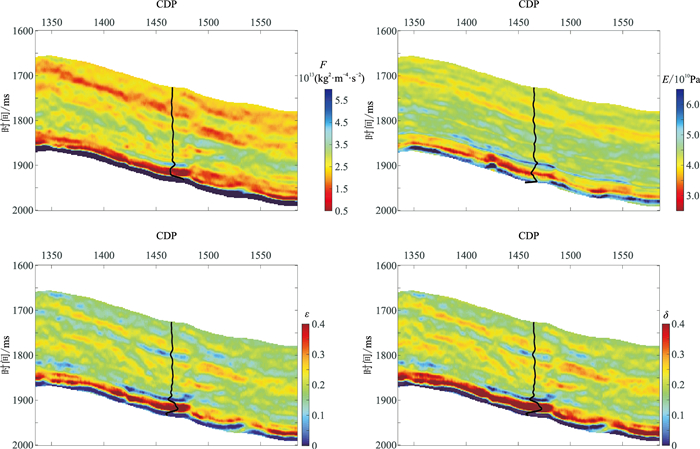
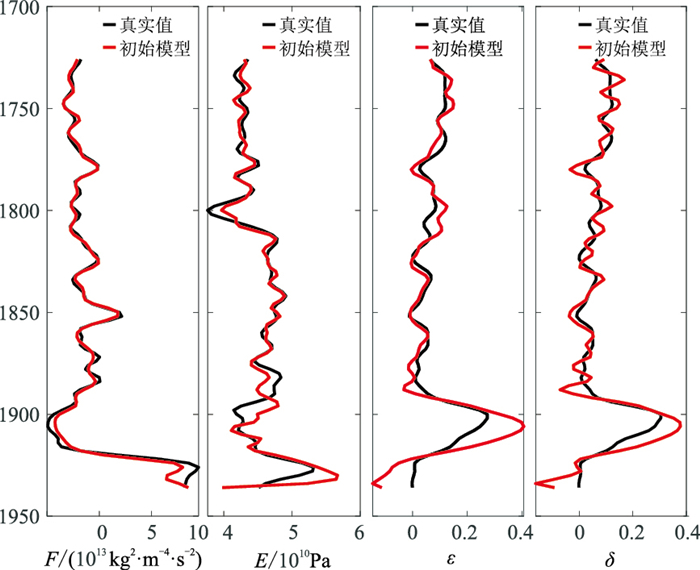
研究工区页岩储层厚度大、品质优、压力系数高、构造相对简单,叠加剖面如图 9所示,其中页岩储层位于H1层位之上。选取5个角度(6°、12°、18°、24°、30°)并从对应分角度道集叠加数据中提取地震子波(图 10),由图 10可见,随着入射角增大,子波频带变窄。EI反演结果如图 11所示,提取的F、E和Thomsen各向异性参数如图 12所示。由图 11和图 12可见,反演结果与测井曲线(图 12中黑色曲线)吻合较好,清晰地显示了储层范围。反演的F、E在储层位置均表现为相对低值,而反演的各向异性参数在储层位置表现为相对高值,表明储层位置层理较为丰富,与地质认识一致。提取工区C井井旁道的反演结果与测井曲线(图 13)进行对比发现,井旁道反演的F、E以及各向异性参数均与测井曲线较为吻合,验证了所提方法在实际应用中的可行性。
|
图 9 全角度叠后地震剖面 |
|
图 10 不同入射角对应的叠加数据中提取的地震子波(a)和频谱(b) |

|
图 11 入射角为6°(a)、12°(b)、18°(c)、24°(d)、30°(e)对应的EI反演结果 |
|
图 12 流体因子、杨氏模量及各向异性参数反演结果 |
|
图 13 C井井旁道预测结果与测井曲线对比 |
页岩储层发育水平层理时会呈现VTI特征。本文主要研究了基于VTI介质的页岩储层流体因子的弹性阻抗反演方法,通过推导包含目标流体因子的VTI介质纵波反射系数近似公式,并在此基础上推导出弹性阻抗方程,实现流体因子和各向异性参数的反演。对比发现,以各向异性背景为前提进行反演得到的流体因子、杨氏模量精确度更高。应用表明,利用本文方法预测的流体因子和杨氏模量与井数据较为吻合,且反演剖面具有较好的横向连续性,有助于对流体与有利压裂区域的横向识别。
在实际页岩储层预测时,还要考虑分离储层中水平层理与水平裂缝的各向异性的影响,这也是后续研究的主要内容。
附录A 纵波反射系数近似方程对式(4)、式(5)两边做差分计算可得式(A-1)~式(A-4),由式(A-2)、式(A-4)可得关系矩阵(A-5),对式(A-5)取逆,得到式(A-6),进而得到式(A-7)。式(2)中:
| $ \mathrm{\Delta }F=2{\overline{\rho }}^{2}\overline{{V}_{\mathrm{P}}}\mathrm{\Delta }{V}_{\mathrm{P}}-2c{\overline{\rho }}^{2}\overline{{V}_{\mathrm{S}}}\mathrm{\Delta }{V}_{\mathrm{S}}+2\overline{\rho }({\overline{{V}_{\mathrm{P}}}}^{2}-c{\overline{{V}_{\mathrm{S}}}}^{2})\mathrm{\Delta }\rho $ | (A-1) |
| $ \frac{\mathrm{\Delta }F}{\overline{F}}=\frac{2}{1-cg}\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}-\frac{2cg}{1-cg}\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}+2\frac{\mathrm{\Delta }\rho }{\overline{\rho }} $ | (A-2) |
| $ \mathrm{\Delta }E=\frac{2\overline{\rho }\overline{{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{S}}}}^{4}}{{\left({\overline{{V}_{\mathrm{P}}}}^{2}-{\overline{{V}_{\mathrm{S}}}}^{2}\right)}^{2}}\mathrm{\Delta }{V}_{\mathrm{P}}+\frac{2\overline{\rho }\overline{{V}_{\mathrm{S}}}\left(3{\overline{{V}_{\mathrm{P}}}}^{4}-8{\overline{{V}_{\mathrm{P}}}}^{2}{\overline{{V}_{\mathrm{S}}}}^{2}+4{\overline{{V}_{\mathrm{S}}}}^{4}\right)}{{\left({\overline{{V}_{\mathrm{P}}}}^{2}-{\overline{{V}_{\mathrm{S}}}}^{2}\right)}^{2}}\mathrm{\Delta }{V}_{\mathrm{S}}+\frac{{\overline{{V}_{\mathrm{S}}}}^{2}\left(3{\overline{{V}_{\mathrm{P}}}}^{2}-4{\overline{{V}_{\mathrm{S}}}}^{2}\right)}{{\overline{{V}_{\mathrm{P}}}}^{2}-{\overline{{V}_{\mathrm{S}}}}^{2}}\mathrm{\Delta }\rho $ | (A-3) |
| $ \frac{\mathrm{\Delta }E}{\overline{E}}=\frac{2g}{(3-4g)(1-g)}\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}+\frac{8{g}^{2}-16g+6}{(3-4g)(1-g)}\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}+\frac{\mathrm{\Delta }\rho }{\overline{\rho }} $ | (A-4) |
| $ \left[\begin{array}{l}\frac{\mathrm{\Delta }F}{\overline{F}}\\ \frac{\mathrm{\Delta }E}{\overline{E}}\\ \frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array}\right]=\left[\begin{array}{ccc}\frac{2}{1-cg}& -\frac{2cg}{1-cg}& 2\\ \frac{2g}{(3-4g)(1-g)}& \frac{8{g}^{2}-16g+6}{(3-4g)(1-g)}& 1\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}\\ \frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}\\ \frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array}\right] $ | (A-5) |
| $ \left[\begin{array}{ccc}\frac{(8{g}^{2}-16g+6)(1-cg)}{\chi }& \frac{2cg(3-4g)(1-g)}{\chi }& \frac{8c{g}^{3}-18c{g}^{2}+6cg-16{g}^{2}+32g-12}{\chi }\\ \frac{-2g(1-cg)}{\chi }& \frac{2(3-4g)(1-g)}{\chi }& \frac{-8{g}^{2}+18g-6-4c{g}^{2}}{\chi }\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}\frac{\mathrm{\Delta }F}{\overline{F}}\\ \frac{\mathrm{\Delta }E}{\overline{E}}\\ \frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array}\right]=\left[\begin{array}{l}\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}\\ \frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}\\ \frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array}\right] $ | (A-6) |
| $ \left\{\begin{array}{l}\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}=\frac{(8{g}^{2}-16g+6)(1-cg)}{\chi }\frac{\mathrm{\Delta }F}{\overline{F}}+\frac{2cg(3-4g)(1-g)}{\chi }\frac{\mathrm{\Delta }E}{\overline{E}}+\frac{8c{g}^{3}-18c{g}^{2}+6cg-16{g}^{2}+32g-12}{\chi }\frac{\mathrm{\Delta }\rho }{\overline{\rho }}\\ \frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}=\frac{-2g(1-cg)}{\chi }\frac{\mathrm{\Delta }F}{\overline{F}}+\frac{2(3-4g)(1-g)}{\chi }\frac{\mathrm{\Delta }E}{\overline{E}}+\frac{-8{g}^{2}+18g-6-4c{g}^{2}}{\chi }\frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array}\right. $ | (A-7) |
| $ \begin{aligned}{R}_{\mathrm{P}\mathrm{P}}\left(\theta \right)=&\left[\frac{(1-cg)(4{g}^{2}-8g+3)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta +8{g}^{2}(1-cg)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }F}{\overline{F}}+\\& \left[\frac{(4c{g}^{3}-9c{g}^{2}+3cg-8{g}^{2}+16g-6)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta +(32{g}^{3}-72{g}^{2}+24g+16c{g}^{3})\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }+\right.\\ &\left.\frac{1}{2}(1-4g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta )\right]\frac{\mathrm{\Delta }\rho }{\overline{\rho }}+\frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \mathrm{\Delta }\varepsilon +\frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{\Delta }\delta \end{aligned} $ | (A-8) |
| $ \begin{aligned}{R}_{\mathrm{P}\mathrm{P}}\left(\theta \right)=&\left[\frac{(1-cg)(4{g}^{2}-8g+3)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta +8{g}^{2}(1-cg)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }F}{\overline{F}}+\\& \left[\frac{cg(3-4g)(1-g)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -8g(3-4g)(1-g)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }E}{\overline{E}}+\\& \left[\frac{cg(3-4g)(1-g)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -8g(3-4g)(1-g)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\chi }\right]\frac{\mathrm{\Delta }E}{\overline{E}}+\\ &\frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{\varepsilon }_{r}}{\overline{{\varepsilon }_{r}}}+\frac{1}{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{\delta }_{r}}{\overline{{\delta }_{r}}} \end{aligned} $ | (A-9) |
致谢
Geosoftware公司为本论文的研究提供了软件支持,在此表示感谢。
| [1] |
THOMSEN L. Understanding Seismic Anisotropy in Exploration and Exploitation[M]. Society of Exploration Geophysicists, 2014.
|
| [2] |
BAYUK I O. Why anisotropy is important for location of microearthquake events in shale?[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 1632-1636.
|
| [3] |
SMITH G C, GIDLOW P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophysical Prospecting, 1987, 35(9): 993-1014. DOI:10.1111/j.1365-2478.1987.tb00856.x |
| [4] |
SCHOENBERG M, SAYERS C M. Seismic anisotropy of fractured rock[J]. Geophysics, 1995, 60(1): 204-211. DOI:10.1190/1.1443748 |
| [5] |
李春宁. 多波联合AVA属性提取与油气预测[D]. 山东青岛: 中国石油大学(华东), 2014. LI Chunning. Multi-wave Joint Attributes Extraction and Hydrocarbon Prediction[D]. China University of Petroleum, Qingdao, Shandong, 2014. |
| [6] |
MA Z, YIN X, ZONG Z, et al. Sequential Bayesian seismic inversion for fracture parameters and fluid indicator in tilted transversely isotropic media[J]. Geophysics, 2023, 88(3): R355-R371. DOI:10.1190/geo2022-0439.1 |
| [7] |
RUSSELL B H, HEDLIN K, HILTERMAN F J, et al. Fluid-property discrimination with AVO: A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [8] |
WRIGHT J. The effects of transverse isotropy on reflection amplitude versus offset[J]. Geophysics, 1987, 52(4): 564-567. DOI:10.1190/1.1442325 |
| [9] |
KIM K Y, WROLSTAD K H, AMINZADEH F. Effects of transverse isotropy on P-wave AVO for gas sands[J]. Geophysics, 1993, 58(6): 883-888. DOI:10.1190/1.1443472 |
| [10] |
李振春, 黄金强, 黄建平, 等. 基于平面波加速的VTI介质最小二乘逆时偏移[J]. 地球物理学报, 2017, 60(1): 240-257. LI Zhenchun, HUANG Jinqiang, HUANG Jianping, et al. Fast least-squares reverse time migration based on plane-wave encoding for VTI media[J]. Chinese Journal of Geophysics, 2017, 60(1): 240-257. |
| [11] |
周城, 杨宇勇, 周怀来, 等. 基于HTI介质走时反演的各向异性参数建模与AVAZ反演[J]. 石油地球物理勘探, 2023, 58(4): 949-960, 969. ZHOU Cheng, YANG Yuyong, ZHOU Huailai, et al. Modeling of anisotropic parameters based on HTI medium travel-time inversion and AV AZ inversion[J]. Oil Geophysical Prospecting, 2023, 58(4): 949-960, 969. |
| [12] |
梁锴, 陈浩然, 孙上饶, 等. VTI介质改进声学近似qP波交错网格正演模拟[J]. 石油地球物理勘探, 2024, 59(1): 89-97. LIANG Kai, CHEN Haoran, SUN Shangrao, et al. Staggered-grid forward modeling of qP wave in VTI media with improved acoustic approximation[J]. Oil Geophysical Prospecting, 2024, 59(1): 89-97. |
| [13] |
魏建, 孙祥娥. 计算水平层状VTI介质中P波旅行时的近似公式[J]. 石油地球物理勘探, 2023, 58(4): 812-817. WEI Jian, SUN Xiange. Approximate equation for calculating P-wave traveltime in horizontally layered VTI media[J]. Oil Geophysical Prospecting, 2023, 58(4): 812-817. |
| [14] |
李映艳, 张乐乐, 陈刚, 等. 基于P/S波解耦和上下行波分离的二维VTI介质弹性波逆时偏移[J]. 石油地球物理勘探, 2023, 58(03): 651-659. LI Yingyan, ZHANG Lele, CHEN Gang, et al. Elastic reverse time migration in VTI medium based on P/S wave-mode decoupling and upgoing/downgoing wavefield decomposition[J]. Oil Geophysical Prospecting, 2023, 58(03): 651-659. |
| [15] |
韩建光, 王赟, 张晓波, 等. VTI介质高斯束叠前深度偏移[J]. 石油地球物理勘探, 2015, 50(2): 267-273. HAN Jianguang, WANG Yun, ZHANG Xiaobo, et al. Gaussian beam prestack depth migration in VTI media[J]. Oil Geophysical Prospecting, 2015, 50(2): 267-273. |
| [16] |
JAMALI J, JAVAHERIAN A, WANG Y H, et al. The behavior of elastic moduli with fluid content in the VTI media[J]. Journal of Petroleum Science and Engineering, 2022, 208(Part A): 109308. |
| [17] |
DANDE S, STEWART R R, DYAUR N. The effect of fluids and their viscosity on the elastic-wave velocity and anisotropy of 3D-printed VTI rock models[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 347-350.
|
| [18] |
LI S. Physical modelling and the poroelastic model with application to fluid detection in a VTI medium[J]. Journal of Geophysics and Engineering, 2013, 10(5): 054005. DOI:10.1088/1742-2132/10/5/054005 |
| [19] |
刘瑞合, 赵金玉, 印兴耀, 等. VTI介质各向异性参数层析反演策略与应用[J]. 石油地球物理勘探, 2017, 52(3): 484-490. LIU Ruihe, ZHAO Jinyu, YIN Xingyao, et al. Strategy of anisotropic parameter tomography inversion in VTI medium[J]. Oil Geophysical Prospecting, 2017, 52(3): 484-490. |
| [20] |
GRAEBNER M. Plane-wave reflection and transmission coefficients for a transversely isotropic solid[J]. Geophysics, 1992, 57(11): 1512-1519. DOI:10.1190/1.1443219 |
| [21] |
RÜGER A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[M]. Society of Exploration Geophysicists, 2002.
|
| [22] |
MAVKO G, BANDYOPADHYAY K. Approximate fluid substitution for vertical velocities in weakly anisotropic VTI rocks[J]. Geophysics, 2009, 74(1): D1-D6. DOI:10.1190/1.3026552 |
| [23] |
CUI J, HAN L G, LIU Q K, et al. P-SV wave elastic impedance and fluid identification factor in weakly anisotropic media[J]. Applied Geophysics, 2010, 7(2): 135-142. DOI:10.1007/s11770-010-0237-1 |
| [24] |
陈怀震, 印兴耀, 高成国, 等. 基于各向异性岩石物理的缝隙流体因子AVA反演[J]. 地球物理学报, 2014, 57(3): 968-978. CHEN Huaizhen, YIN Xingyao, GAO Chengguo, et al. AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory[J]. Chinese Journal of Geophysics, 2014, 57(3): 968-978. |
| [25] |
侯栋甲, 刘洋, 任志明, 等. 基于贝叶斯理论的VTI介质多波叠前联合反演[J]. 石油物探, 2014, 53(3): 294-303. HOU Dongjia, LIU Yang, REN Zhiming, et al. Multi-wave prestack joint inversion in VTI media based on Bayesian theory[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 294-303. |
| [26] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. |
| [27] |
陈勇, 孙振涛, 许凯. 面向页岩气储层的叠前多参数地震反演方法研究[J]. 石油物探, 2022, 61(6): 1016-1027. CHEN Yong, SUN Zhentao, XU Kai. Pre-stack multi-parameter seismic inversion in shale-gas reservoirs[J]. Geophysical Prospecting for Petroleum, 2022, 61(6): 1016-1027. |
| [28] |
王波, 张峰, 代福材, 等. VTI介质SH-SH波地震反演方法研究[J]. 地球物理学报, 2023, 66(5): 2112-2122. WANG Bo, ZHANG Feng, DAI Fucai, et al. Study on seismic inversion method of SH-SH wave in VTI media[J]. Chinese Journal of Geophysics, 2023, 66(5): 2112-2122. |
| [29] |
高刚, 贺振华, 曹俊兴, 等. 两项式弹性波阻抗反演方法在深层碳酸盐岩储层预测中的应用[J]. 石油地球物理勘探, 2013, 48(3): 450-457. GAO Gang, HE Zhenhua, CAO Junxing, et al. The new two-term elastic impedance inversion and its application to predict deep gas-bearing carbonate reserviors[J]. Oil Geophysical Prospecting, 2013, 48(3): 450-457. |
| [30] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. |
| [31] |
CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. |
| [32] |
TARANTOLA A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Society for Industrial and Applied Mathematics, Philadelphia, PA, 2005.
|



 张广智,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
张广智,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: