近年来,各种分类或聚类算法应用于地球物理资料处理和反演,主要包括模糊C均值(FCM)聚类[1]、支持向量机(SVM)[2-3]和神经网络(NN)[4-5]等。其中,SVM和NN算法均属于监督学习分类方法,需要足够数量的样本维持结果的稳定性;而FCM聚类算法是一种无监督学习方法,具有样本量需求少的优势[6-7],更适用于地球物理方法联合反演。Paasche等[8]运用FCM聚类技术开展基于井间地震、地质雷达和地面地震等多种数据的物性预测,论证了FCM聚类算法对于不同物性数据聚类的实用性。Orfanos等[9]通过密度和电阻率二维反演开展裂缝预测,在优化模型的过程中同步分析了FCM聚类算法的有效性。Ward等[10]利用FCM聚类算法对小范围矿区的三维电阻率反演结果开展聚类分析,以确定地层的年代属性,提出了将结果偏差纳入FCM加权项以进一步指导聚类的思想。刘佳成等[11]在地震走时反演中应用FCM聚类算法有效提升了反演效果。为了更有效地利用先验信息优化聚类结果,Pedrycz[12]提出了一种部分监督的模糊聚类算法。Bensaid等[13]提出了一种半监督模糊聚类算法。Noordam等[14]在FCM聚类算法中加入了先验空间域几何信息以提高图像分割效果。Sun等[15-16]在反演中引入了模型约束机制,使反演结果更接近实际地下地质体和背景值。
但是,目前基于FCM聚类算法的地质属性解释主要针对单一反演结果,不能克服多解性。随着地球物理联合反演技术的发展,反演结果的不确定性得以降低[17-21],而利用多元地球物理信息进行综合定量解释方面尚缺乏相关的技术方法。因此,本文将引导FCM聚类方法应用于分析、评价地球物理联合反演结果,以获得一个更科学的综合解释结果,进而形成一套适用于多元地球物理反演信息的地质综合定量解释技术。
1 方法原理FCM聚类是一种无监督的聚类技术,可以将一组对象自动分为几个子集。在FCM聚类算法中,聚类中心仅取决于数据对象之间的距离关系和初始类别的数量,因此所获取的聚类中心很难与地下真实的物性相匹配。上述问题可以通过对FCM聚类算法引入先验信息得到解决。Sun等[15]提出了一种将统计岩石物理数据纳入地球物理反演的方法,从反演目标函数中提取引导FCM聚类目标函数,进而将引导FCM聚类用于反演结果联合解释。引导FCM聚类目标函数可以表达为
| $ \begin{aligned}{\varPhi }_{\mathrm{F}\mathrm{C}\mathrm{M}}\left({u}_{i,k},{\boldsymbol{p}}_{k}\right)=&\sum\limits_{i=1}^{M}\sum\limits_{k=1}^{C}{u}_{i,k}^{m}{‖{\boldsymbol{x}}_{i}-{\boldsymbol{p}}_{k}‖}_{2}^{2}+\\& \sum\limits_{i=1}^{M}{\gamma }_{i}\left(1-\sum\limits_{k=1}^{C}{u}_{i,k}\right)+\\& \eta \sum\limits_{k=1}^{C}{‖{\boldsymbol{p}}_{k}-{\boldsymbol{t}}_{k}‖}_{2}^{2}\end{aligned} $ | (1) |
式中:M为待聚类的目标个数;C为待发现类型的数量;
在目标函数最小化过程中,
| $ \begin{aligned}{\varPhi }_{\mathrm{F}\mathrm{C}\mathrm{M}}\left({u}_{i,k},{\boldsymbol{p}}_{k}\right)=&\sum\limits_{i=1}^{M}\sum\limits_{k=1}^{C}{u}_{i,k}^{m}{‖{\boldsymbol{x}}_{i}-{\boldsymbol{p}}_{k}‖}_{2}^{2}+\\& \eta \sum\limits_{k=1}^{C}{‖{\boldsymbol{p}}_{k}-{\boldsymbol{t}}_{k}‖}_{2}^{2}\end{aligned} $ | (2) |
式中最后一项称为引导项,即
| $ {\varPhi }_{pt}\left({\boldsymbol{p}}_{k},{\boldsymbol{t}}_{k}\right)=\eta \sum\limits_{k=1}^{C}{‖{\boldsymbol{p}}_{k}-{\boldsymbol{t}}_{k}‖}_{2}^{2} $ | (3) |
更新后的聚类中心pk可以表达为
| $ {\boldsymbol{p}}_{k}=\frac{\sum\limits_{i=1}^{M}{u}_{i,k}^{m}{\boldsymbol{x}}_{i}+\eta {\boldsymbol{t}}_{k}}{\sum\limits_{i=1}^{M}{u}_{i,k}^{m}+\eta } $ | (4) |
根据式(4),聚类中心pk受η和tk控制。当η趋向于0时,tk不起作用,算法回归为传统FCM聚类算法;当η趋向于无穷大时,tk成为影响聚类中心的主要因素,这种情况下需要首先明确聚类值。在式(2)中,选取适当的η值可以将等式右侧的两项调整为相同的量级。本文由L曲线法选取适当的η值[22]。
上述推导仅针对单一物性参数,当存在多种物性参数时,式(2)可以写为
| $ \begin{aligned}{\varPhi }_{\mathrm{m}\mathrm{F}\mathrm{C}\mathrm{M}}\left({u}_{i,k},{\boldsymbol{p}}_{k}\right)=&\sum\limits_{i=1}^{M}\sum\limits_{k=1}^{C}{u}_{i,k}^{m}{‖{\boldsymbol{x}}_{i}-{\boldsymbol{p}}_{k}‖}_{2}^{2}+\\ &\eta \sum\limits_{k=1}^{C}{‖{\boldsymbol{p}}_{k}-{\boldsymbol{t}}_{k}‖}_{2}^{2}\end{aligned} $ | (5) |
式中:
聚类精度由解释结果的均方根误差定量描述
| $ \mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}{\mathrm{l}}_{\mathrm{R}\mathrm{M}\mathrm{S}}=\sqrt{\frac{\sum\limits_{l=1}^{{N}_{m}}({m}_{i}^{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}-{m}_{i}^{\mathrm{c}\mathrm{a}\mathrm{l}}{)}^{2}}{{N}_{m}}} $ | (6) |
式中:
设计一个二维模型(图 1)验证本文方法的效果。
|
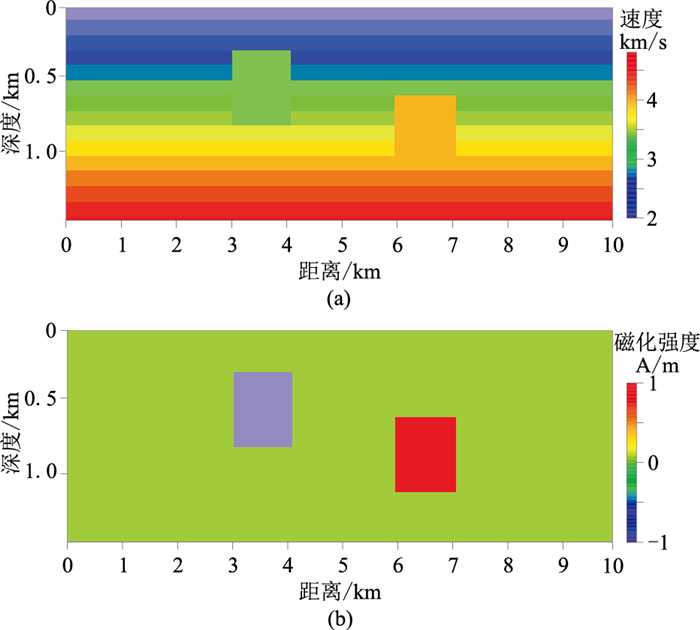
图 1 速度(a)和磁化强度(b)二维模型 |
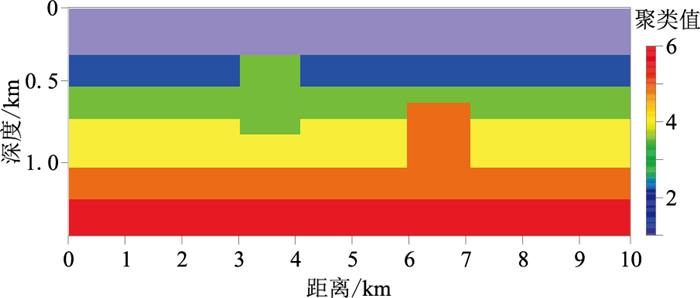
首先,进行单一物性参数的引导聚类实验。以图 1a为例,模型速度呈梯度变化,可以划分为四个聚类中心,其值分别为2.3、3.0、3.8和4.5,而矩形异常体的聚类中心值分别为3.0和4.0。速度模型的引导FCM聚类结果见图 2所示。由图可见,异常体和速度背景不能完全区分,存在部分聚类结果不准确的问题,因此引导FCM聚类算法在单一物性参数中的应用效果并不明显。
|
图 2 速度模型引导FCM聚类结果 模型横向尺度为10 km,纵向尺度为1.4 km,网格数为100×14,横向和纵向网格间距均为100 m。模型中设置两个矩形异常体:左侧异常体的速度为3.0 km/s,右侧异常体的速度为4.0 km/s,背景速度由浅到深线性增大(2.0~4.8 km/s)(图 1a);左侧异常体的磁化强度为-1.0 A/m,右侧异常体的磁化强度为1.0 A/m,背景磁化强度设置为0(图 1b)。 |
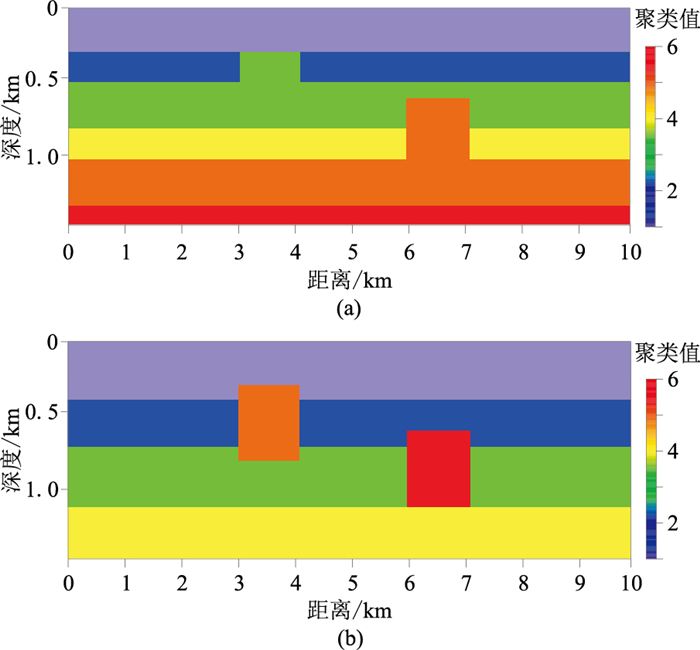
其次,进行两种物性参数的引导聚类实验。将速度模型数据和磁化强度模型数据集成后分为六层,分别利用传统FCM算法和引导FCM算法计算聚类结果(图 3)。由图 3可见,传统FCM聚类算法在加入磁化强度属性后,效果依然不理想,异常体和背景不能完全区分,仍然存在聚类不准确的问题(图 3a)。在引导FCM聚类结果中,背景和异常体能够清晰地区分,说明两种物性参数的引导FCM结果对异常体的识别能力较强(图 3b)。
|
图 3 速度和磁化强度模型不同算法聚类结果 (a)传统FCM;(b)引导FCM |
按照速度、磁化强度两种物性参数计算了两种聚类算法的模型聚类中心值。由表 1可见,以速度为例,两种物性参数引导FCM聚类结果与模型参数最接近,且聚类结果优于单一物性参数。
|
|
表 1 简单速度模型不同聚类方法的聚类中心值 |
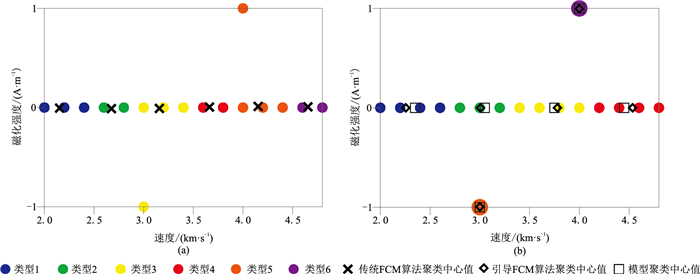
最后,绘制速度、磁化强度两种物性参数聚类结果的交会图(图 4)。由图可见,引导FCM聚类算法得到的各层聚类数比传统FCM聚类算法更接近真实值,可以有效地识别并区分两个矩形异常体。
|
图 4 速度和磁化强度不同聚类方法结果交会图 (a)传统FCM;(b)引导FCM |
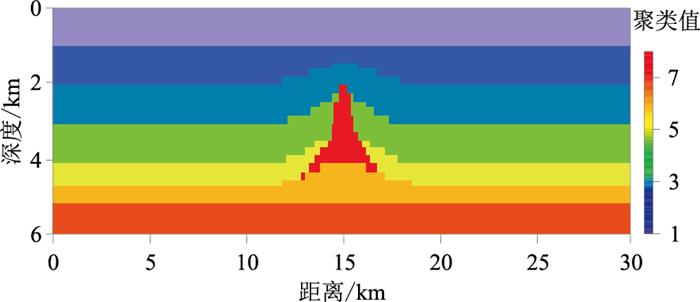
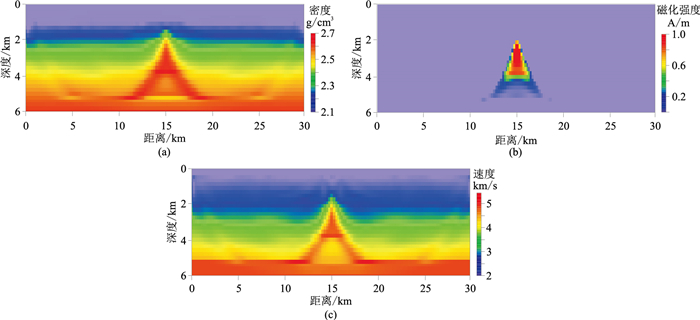
通过复杂多层模型(图 5)进一步对比传统FCM聚类算法和引导FCM聚类算法的效果。模型来源于前人的反演研究成果[19],模型物性参数见表 2。三种物性参数反演结果见图 6所示。根据三种物性参数的反演结果开展聚类分析,恢复真实的地下模型。
|
图 5 复杂模型 横向尺度为30 km、纵向尺度为6 km,网格数为150×30,纵向和横向网格间距均为0.2 km。模型中央设置一个三角形异常体,物性特征为高密度、高磁化强度、高速度。 |
|
|
表 2 复杂模型的物性参数表 |
|
图 6 复杂模型不同物性参数反演结果 (a)密度;(b)磁化强度;(c)速度 |
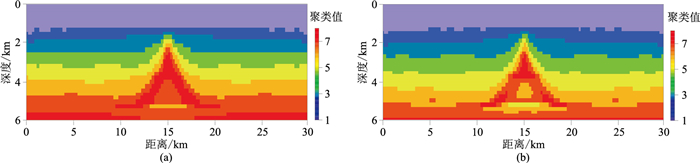
设置先验约束聚类中心的值与模型物性一致(表 2),将模型分为8个层。首先,对单一密度反演结果开展聚类分析(图 7),相应的先验约束聚类中心值、FCM聚类中心值和引导FCM聚类中心值见表 3所示。随深度增加,引导FCM的结果逐渐向模型(先验聚类中心)靠近,说明先验地质信息起到了引导聚类的作用。
|
图 7 密度反演的不同方法聚类结果 (a)传统FCM;(b)引导FCM |
|
|
表 3 复杂模型单一密度参数不同算法的聚类中心值 |
由图 7可见,三角形异常体出现在模型底部,同时其下部产生部分异常值,水平层界面也出现较大起伏。
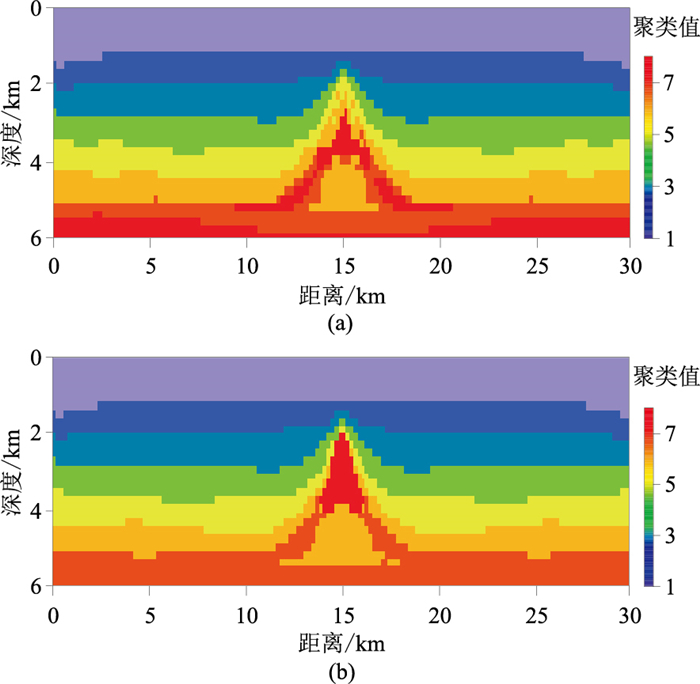
根据式(5),将密度、速度和磁化强度反演结果集成后开展聚类分析,分别得到两种聚类算法的结果(图 8)及聚类中心值(表 4)。
|
图 8 三种物性参数反演结果的不同聚类结果 (a)传统FCM;(b)引导FCM |
|
|
表 4 复杂模型三参数同时聚类下不同算法的聚类中心值 |
由图 8可见,每层的厚度、深度在引导FCM聚类结果中与真实模型更相近。在传统FCM聚类结果中,第七层与异常体之间、异常体与第六层之间均存在不同程度的错误聚类(图 8a);在引导FCM聚类结果中,各地层的边界划分效果更好,高速异常体的形状与真实模型间仅存在轻微的偏差,第七层的区分度更高,高速异常体轮廓与真实模型高度相似(图 8b)。由表 4可知,与块状模型类似,随着深度逐渐增加,引导FCM的结果逐渐向模型(先验聚类中心)靠近,说明先验地质信息起到了引导聚类的作用,深层更明显。
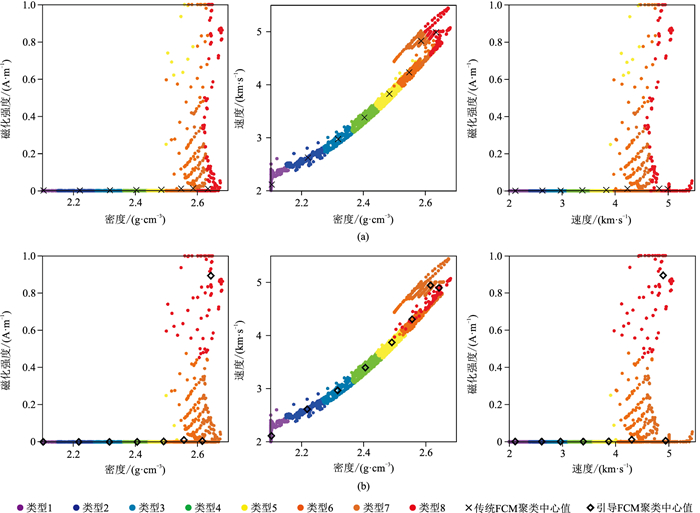
由图 9可见,两种算法的物性统计结果均表现出较强的正态性。相比之下,引导FCM聚类算法中每一层的物性统计结果都更接近于真实物性值,更符合真实模型(图 9b)。这证明了在反演结果的解释中,引导FCM聚类算法比传统FCM聚类算法效果更好。
|
图 9 三种物性参数不同聚类方法结果交会图 (a)传统FCM;(b)引导FCM |
进一步分析不同物性数据的两种聚类结果的均方根误差。单一密度的聚类结果为:传统FCM的均方根误差为0.886,而引导FCM的均方根误差为0.621;三种物性参数的聚类结果为:传统FCM的均方根误差为0.604,而引导FCM的均方根误差为0.478。因此,多物性参数聚类结果明显优于单一物性,而引导FCM聚类的结果也明显优于传统FCM,即多物性参数的引导FCM聚类是相对最优的一种解释方案,其结果最接近实际模型。
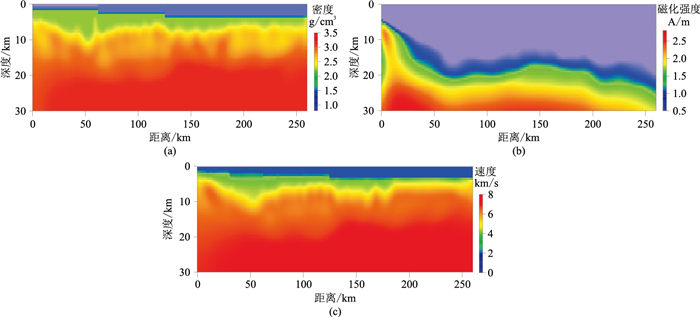
4 实际数据分析实际数据选自于南海珠江口盆地白云凹陷的一条二维测线。在前人岩石密度、速度和磁性特征相关成果[23-24]的基础上,统计研究区岩石密度和速度数据(表 5),指导建立密度、速度和磁化强度三种参数初始模型,通过基于区域模型余弦相似度耦合方式的联合反演方法[19]得到了密度、磁化强度和速度的反演结果(图 10)。根据表 5确定重力、地震联合反演结果的先验约束聚类中心(考虑到目标区磁性规律研究程度略低,磁化强度先验约束聚类中心值为人为给定的参考值),开展聚类分析并提取结果聚类中心值(表 6)。由表 6可见,加入先验信息后,聚类中心值明显表现出以先验值为目标的导向性。
|
|
表 5 白云凹陷地层密度和速度统计结果 |
|
图 10 二维测线不同物性的反演结果 (a)密度;(b)磁化强度;(c)速度 |
|
|
表 6 二维剖面不同物性参数的不同算法聚类中心值 |
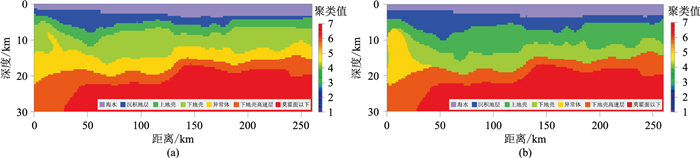
图 11为两种算法的聚类效果。由图可见,在传统FCM聚类结果中,测线左侧的块状异常体被聚类为层状,上部地壳的厚度仅为2 km,而下部地壳整体被抬升了5~12 km(图 11a);在引导FCM聚类结果中各地层的边界划分结果更准确,上部地壳的厚度约为7~8 km,下部地壳的深度范围约为12~20 km,且异常体的形态更加清晰(图 11b)。由于实际应用中无法获得真实的地下信息,仅参考前人对靶区的认识对结果进行评价。据庞雄等[25]的研究成果,在白云凹陷北部,莫霍面深度约为30 km,至测线末端莫霍面深度抬升至19 km,表现出地壳的快速减薄和莫霍面的剧烈抬升特征,且上地壳平均厚度大于下地壳平均厚度,这与引导FCM聚类结果一致。
|
图 11 二维测线密度、速度、磁化强度联合反演结果的不同聚类结果 (a)传统FCM;(b)引导FCM |
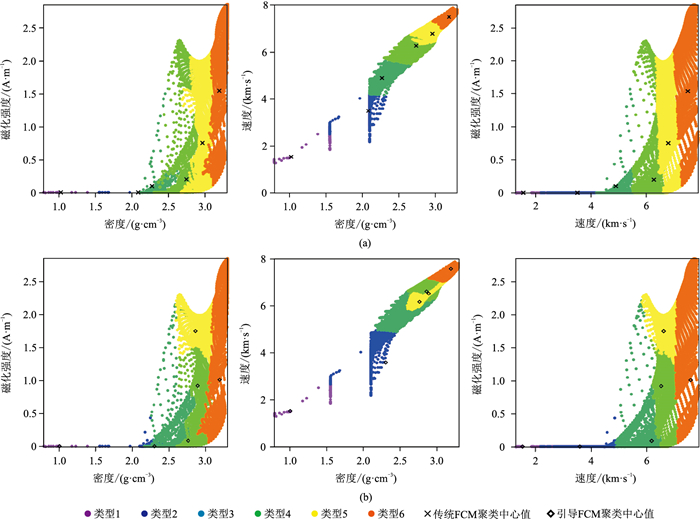
进一步绘制三种物性参数聚类结果的交会图(图 12)。由图可见,与理论模型结果类似,使用先验约束信息引导的FCM聚类算法使每一层的聚类结果更接近相应的聚类中心,这表明先验约束对聚类结果具有引导作用,可准确认识地下结构。进一步证实了引导FCM聚类算法的精度高于传统FCM聚类算法。
|
图 12 三种物性的不同聚类方法结果交会图 (a)传统FCM;(b)引导FCM |
(1) 本文在传统FCM聚类方法的基础上,通过加入先验约束信息,提出了引导FCM聚类算法,并应用于理论模型和实际数据的地球物理联合反演。定量化模型实验证明,对于单一物性参数而言,引导FCM聚类结果较传统FCM聚类结果的提升有限;而在多物性参数反演结果情况下,引导FCM聚类算法表现出了更出色的边界划分能力,说明随着样本类型的丰富,引导FCM聚类算法的精度提升更明显。
(2) 实际二维剖面联合反演结果表明,引导FCM聚类算法能够为复杂地球物理数据的解释提供更加准确、客观的结果。
(3) 所提方法在地球物理反演综合解释领域具有较好的参考意义。
| [1] |
PAASCHE H, TRONICKE J. Cooperative inversion of 2D geophysical data sets: a zonal approach based on fuzzy c-means cluster analysis[J]. Geophysics, 2007, 72(3): A35-A39. DOI:10.1190/1.2670341 |
| [2] |
HAMMER B, VILLMANN T. Generalized relevance learning vector quantization[J]. Neural Networks, 2002, 15(8/9): 1059-1068. |
| [3] |
邹华胜, 宁书年, 杨峰, 等. 支持向量机在储层厚度预测和计算中的应用[J]. 地球物理学进展, 2007, 22(5): 1597-1601. ZOU Huasheng, NING Shunian, YANG Feng, et al. Application of support vector machine to forecasting and calculating reservoir thickness[J]. Progress in Geophysics, 2007, 22(5): 1597-1601. DOI:10.3969/j.issn.1004-2903.2007.05.039 |
| [4] |
马国庆, 王泽坤, 李丽丽. 基于自注意力机制深度学习的重磁数据网格化和滤波方法[J]. 石油地球物理勘探, 2022, 57(1): 34-42. MA Guoqing, WANG Zekun, LI Lili. Gridding and filtering method of gravity and magnetic data besed on self-attention deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 34-42. |
| [5] |
王迪, 张益明, 张繁昌, 等. 利用先验信息约束的深度学习方法定量预测致密砂岩"甜点"[J]. 石油地球物理勘探, 2023, 58(1): 65-74. WANG Di, ZHANG Yiming, ZHANG Fanchang, et al. Quantitative prediction of tight sandstone sweet spots based on deep learning method with prior information constraints[J]. Oil Geophysical Prospecting, 2023, 58(1): 65-74. |
| [6] |
BEZDEK J C, EHRLICH R, FULL W. FCM: the fuzzy c-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2/3): 191-203. |
| [7] |
BEZDEK J C, HATHAWAY R J, SABIN M J, et al. Convergence theory for fuzzy c-means: Counterexamples and repairs[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1987, 17(5): 873-877. DOI:10.1109/TSMC.1987.6499296 |
| [8] |
PAASCHE H, TRONICKE J, HOLLIGER K, et al. Integration of diverse physical-property models: subsurface zonation and petrophysical parameter estimation based on fuzzy c-means cluster analyses[J]. Geophysics, 2006, 71(3): H33-H44. DOI:10.1190/1.2192927 |
| [9] |
ORFANOS C, APOSTOLOPOULOS G. Multiparameter analysis of geophysical methods for target detection: the unified geophysical model approach[J]. Geophysics, 2013, 78(6): IM1-IM13. DOI:10.1190/geo2012-0285.1 |
| [10] |
WARD W O C, WILKINSON P B, CHAMBERS J E, et al. Distribution-based fuzzy clustering of electrical resistivity tomography images for interface detection[J]. Geophysical Journal International, 2014, 197(1): 310-321. DOI:10.1093/gji/ggu006 |
| [11] |
刘佳成, 张志勇, 周钦渊, 等. 基于FCM聚类模型约束的二维初至旅行时反演[J]. 石油地球物理勘探, 2023, 58(5): 1115-1123. LIU Jiacheng, ZHANG Zhiyong, ZHOU Qinyuan, et al. 2D inversion of seismic first-arrival traveltime based on FCM clustering model constraint[J]. Oil Geophysical Prospecting, 2023, 58(5): 1115-1123. |
| [12] |
PEDRYCZ W. Algorithms of fuzzy clustering with partial supervision[J]. Pattern Recognition Letters, 1985, 3(1): 13-20. DOI:10.1016/0167-8655(85)90037-6 |
| [13] |
BENSAID A M, HALL L O, BEZDEK J C, et al. Partially supervised clustering for image segmentation[J]. Pattern Recognition, 1996, 29(5): 859-871. DOI:10.1016/0031-3203(95)00120-4 |
| [14] |
NOORDAM J C, VAN DEN BROEK W H A M. Multivariate image segmentation based on geometrically guided fuzzy C-means clustering[J]. Journal of Chemometrics, 2002, 16(1): 1-11. DOI:10.1002/cem.656 |
| [15] |
SUN J, LI Y. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering[J]. Geophysics, 2015, 80(4): ID1-ID18. DOI:10.1190/geo2014-0049.1 |
| [16] |
SUN J, LI Y. Joint inversion of multiple geophysical data using guided fuzzy c-means clustering[J]. Geophysics, 2016, 81(3): ID37-ID57. DOI:10.1190/geo2015-0457.1 |
| [17] |
CARCIONE J M, URSIN B, NORDSKAG J I. Cross-property relations between electrical conductivity and the seismic velocity of rocks[J]. Geophysics, 2007, 72(5): E193-E204. DOI:10.1190/1.2762224 |
| [18] |
MICHAEL S Z, ALEXANDER G, GLENN W. Generalized joint inversion of multimodal geophysical data using Gramian constraints[J]. Geophysical Research Letters, 2012, 39(9): L09301. |
| [19] |
SHI B, YU P, ZHAO C, et al. Linear correlation constrained joint inversion using squared cosine similarity of regional residual model vectors[J]. Geophysical Journal International, 2018, 215(2): 1291-1307. |
| [20] |
胡祖志, 刘雪军, 王志刚, 等. 时频电磁与大地电磁数据联合反演[J]. 石油地球物理勘探, 2023, 58(3): 720-727. HU Zuzhi, LIU Xuejun, WANG Zhigang, et al. Joint inversion of time-frequency electromagnetic and magnetotelluric data[J]. Oil Geophysical Prospecting, 2023, 58(3): 720-727. |
| [21] |
张志勇, 易柯, 谢尚平, 等. 基于模糊C均值聚类的二维直流电阻率与射频大地电磁联合反演[J]. 同济大学学报(自然科学版), 2023, 51(1): 135-144. ZHANG Zhiyong, YI Ke, XIE Shangping, et al. Joint inversion of two-dimensional direct current resistivity and radio-magnetotelluric data based on fuzzy c-means clustering model constraint[J]. Journal of Tongji University(Natural Science), 2023, 51(1): 135-144. |
| [22] |
VOGEL C R. Non-convergence of the L-curve regularization parameter selection method[J]. Inverse Problems, 1996, 12(4): 535. |
| [23] |
黄春菊, 周蒂, 陈长民, 等. 深反射地震剖面所揭示的白云凹陷的深部地壳结构[J]. 科学通报, 2005, 50(10): 1024-1031. HUANG Chunju, ZHOU Di, CHEN Changmin, et al. Deep crustal structure of Baiyun Sag, northern South China Sea as interpreted from deep seismic reflection profile[J]. Chinese Science Bulletin, 2005, 50(10): 1024-1031. |
| [24] |
鲁宝亮, 孙晓猛, 张功成, 等. 南海北部盆地基底岩性地震—重磁响应特征与识别[J]. 地球物理学报, 2011, 54(2): 563-572. LU Baoliang, SUN Xiaomeng, ZHANG Gongcheng, et al. Seismic-potential field response characteristics and identification of basement lithology of the northern South China Sea basin[J]. Chinese Journal of Geophysics, 2011, 54(2): 563-572. |
| [25] |
庞雄, 任建业, 郑金云, 等. 陆缘地壳强烈拆离薄化作用下的油气地质特征——以南海北部陆缘深水区白云凹陷为例[J]. 石油勘探与开发, 2018, 45(1): 27-39. PANG Xiong, REN Jianye, ZHENG Jinyun, et al. Petroleum geology controlled by extensive detachment thinning of continental margin crust: a case study of Baiyun sag in the deep-water area of northern South China Sea[J]. Petroleum Exploration and Development, 2018, 45(1): 27-39. |



 陈易周,上海市长宁区通协路388号中海油大厦A540室,200335。Email:
陈易周,上海市长宁区通协路388号中海油大厦A540室,200335。Email: