叠前反演主要通过计算地震AVO(Amplitude Versus Offset)信息获得地下岩层的弹性参数(纵波速度VP、横波速度VS、密度ρ以及其他相关参数),方法的理论较成熟、应用效果较好,是储层预测和含气性检测的主流方法[1-5]。叠前反演的核心环节是建立符合地层岩性背景的弹性模型(包括横波模型、纵波模型、ρ模型——由于其频带较低,也称低频模型),通过低频模型约束地质条件可提高反演结果的可靠性。在不同地区采用不同的建模方法[6-7],如在地质条件较简单的地区,依据速度场和钻井数据插值建立低频模型。而在地质条件较复杂的地区,如在海洋深水地区,虽然基于海洋常规拖缆地震数据采集及处理可提供精细的VP场和纵波低频模型,并通过深度学习、全波形反演等方法建立更复杂的纵波模型[8-11],但由于缺少横波资料,目前无法获得精细的横波模型,该问题一直是深水区开展叠前反演的研究重点。
研究表明,通过纵波和横波联合约束可显著提高岩性和含气性的预测能力[12-15],横波信息对储层预测和含气性检测非常重要。珠江口盆地中浅层主要为泥岩,岩石速度变化主要受埋深影响。测井纵、横波数据的统计关系表明,VP和VS一般为线性关系[14, 16]。通过上述线性关系可将纵波模型转换为横波模型,但获得的纵、横波信息特征基本一致,无法精细表征地层的岩性变化,因此该方法适用于地层岩性单一的局部地区。当研究区范围较大、层系较多时,通过分层段、分区域、分岩性等相控约束,采用不同的线性转换关系建立横波模型,可提高表征地层岩性变化的能力[17-19],但实现过程受人为因素影响较大,难以推广。
为改善目前横波建模方法的局限性对储层预测的影响,本文结合生产需求,基于远道地震数据提取三维空间的泊松比信息,作为纵、横波模型之间的转换关系,进而获得泊松比约束的横波低频模型。文中将新方法用于白云深水区,以验证方法的效果。结果表明,新方法建立的模型包含的地层岩性信息更丰富,建模过程受人为影响较小,可靠性高,实用性强,储层预测结果更可靠。
1 技术原理及方法 1.1 岩性背景表征参数叠前反演AVO理论表明,随着入射角增大,横波对反射系数的影响也增大,因此远道地震数据包含了更丰富的横波信息。为了从地震数据中提取相关的横波信息,需要构建一个参数,同时满足包含纵横波信息、可区分岩性、满足地震标定、可通过地震反演求解等条件,并以该参数作为获得横波模型的桥梁。
岩石物理分析表明,常见的岩性识别参数包括VP/VS、LMR(
弹性阻抗(EI)理论基于经典Aki-Richards近似公式发展而来[20]。基于该理论可评估不同入射角的地震数据表征岩性、物性、含气性的能力。因此,可针对特定反演目标优选入射角[21-23]。EI为
| $ \mathrm{E}\mathrm{I}\left(\theta \right)={{V}_{\mathrm{P}}}^{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{}^{}{{V}_{\mathrm{S}}}^{-8K\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{}^{}{\rho }^{1-4K\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{}^{} $ | (1) |
式中:θ为入射角;
式(1)中EI的值域随
| $ \mathrm{E}\mathrm{I}\left(0°\right)={V}_{\mathrm{P}}\rho $ | (2) |
为更好地对比不同角度的EI曲线与阻抗参数,需要统一值域。为此,Whitcombe等[24]将式(1)改写为
| $ \begin{array}{l} \mathrm{E}\mathrm{I}\left(\theta \right)=\\ {{V}_{\mathrm{P}}}_{0}{\rho }_{0}\left[{\left(\frac{{V}_{\mathrm{P}}}{{{V}_{\mathrm{P}}}_{0}}\right)}^{1+\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{}^{}{\left(\frac{V\mathrm{s}}{V{\mathrm{s}}_{0}}\right)}^{-8K\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{}^{}{\left(\frac{\rho }{{\rho }_{0}}\right)}^{1-4K\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{}^{}\right] \end{array} $ | (3) |
式中VP0,VS0,ρ0为各弹性参数在目的段的平均值。
由于
| $ {\left(\frac{{V}_{\mathrm{S}}}{{V}_{\mathrm{P}}}\right)}^{2}=\frac{1-2\delta }{2\left(1-\delta \right)} $ | (4) |
令参数
| $ \mathrm{P}\mathrm{E}\mathrm{I}\left(\theta \right)={{V}_{\mathrm{P}}}_{0}{\rho }_{0}{\left(\frac{{V}_{\mathrm{P}}}{{{V}_{\mathrm{P}}}_{0}}\right)}^{a}{\left(\frac{p}{{p}_{0}}\right)}^{b}{\left(\frac{\rho }{{\rho }_{0}}\right)}^{c} $ | (5) |
其中
| $ a=\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -8{\left(\frac{{V}_{\mathrm{S}}}{{V}_{\mathrm{P}}}\right)}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (6) |
| $ b=4\left[{\left(\frac{{V}_{\mathrm{S}}}{{V}_{\mathrm{P}}}\right)}^{2}-1\right]\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (7) |
| $ c=1-4{\left(\frac{{V}_{\mathrm{S}}}{{V}_{\mathrm{P}}}\right)}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (8) |
由式(5)可知,当θ=0°时,
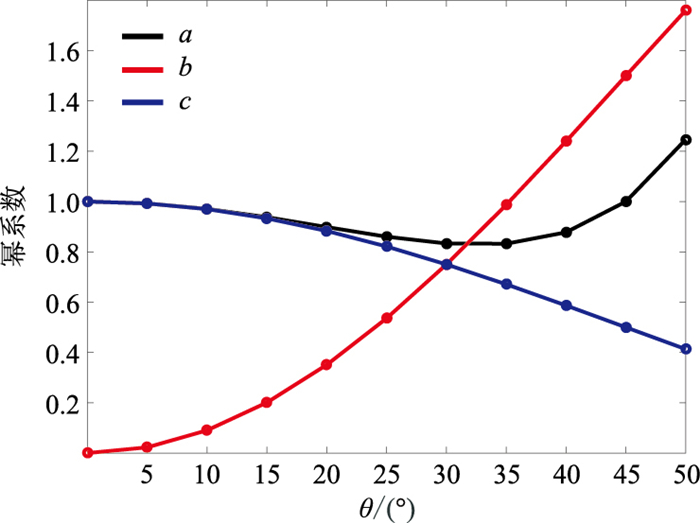
|
图 1 a、b、c随θ的变化趋势 |
为基于远道地震数据提取δ信息提高模型表征岩性的能力,需评估地震数据对岩性敏感的入射角范围。不同深度目的层的地震波入射角和资料信噪比不同,因此一般需优选一个入射角范围提高地震资料品质。另外,还需综合考量PEI对岩性敏感的入射角范围。综合上述分析得到对岩性敏感的PEI曲线和地震资料,进而由叠后反演获取三维PEI体。
基于白云深水区测井声波及密度数据计算不同入射角的PEI曲线,并与δ曲线(投影)对比(图 2)。可见,在30°~45°范围内,PEI曲线与δ曲线呈较强的正相关(图 2c~图 2f),并较好地刻画了岩性变化。另外,由于PEI的量纲与ZP一致,因此可通过合成记录检验由远道地震数据反演PEI的可行性。从标定结果来看,相比近道(图 3d)、中道(图 3e)叠加地震数据,远道叠加地震数据(图 3b)与PEI曲线合成地震数据(图 3c)的相位和能量(2.7、2.84、2.88 s)更一致,相关性最强。因此,选择30°~45°叠加地震数据作为提取PEI参数的基础资料。
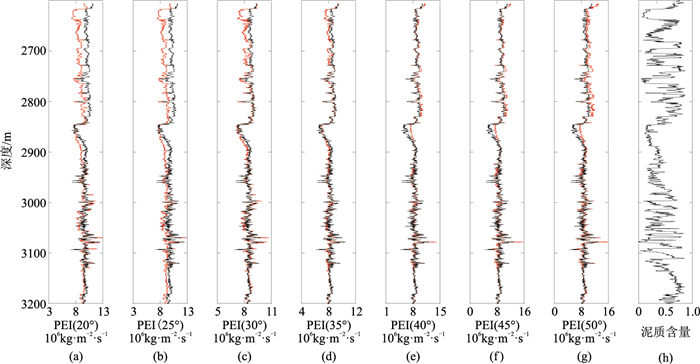
|
图 2 不同入射角的PEI、δ及岩性曲线 (a)~(g)依次为20°、25°、30°、35°、40°、45°、50°的PEI曲线(红色)及投影的δ曲线(黑色);(h)泥质含量曲线 |
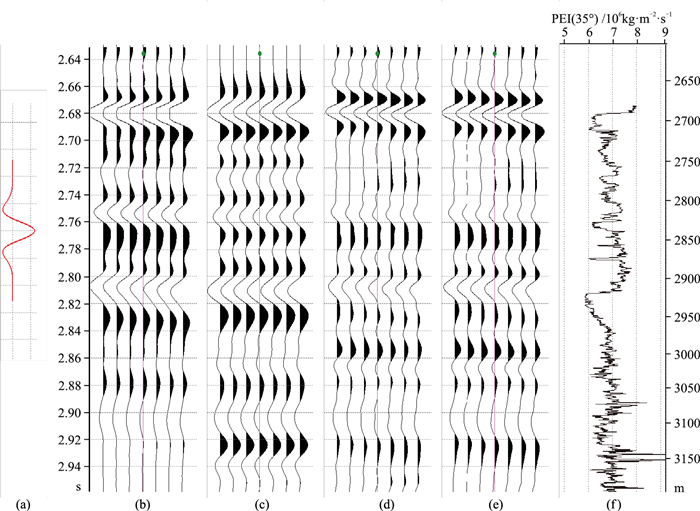
|
图 3 PEI曲线合成地震数据与不同角度的叠加地震数据 (a)子波;(b)远道(30°~45°)叠加地震数据;(c)PEI曲线合成地震数据;(d)近道(0°~12°)叠加地震数据;(e)中道(13°~23°)叠加地震数据;(f)PEI曲线 |
基于PEI曲线和远道地震数据,通过叠后反演得到PEI体。在深水区,钻井数据少是反演面临的一大难点。为测试井约束数量和远道地震数据对PEI反演结果的影响,测试了三种井约束方案(研究区内共有L1、L2、L3、L4四口井):①仅用L1井约束;②采用L1、L2两口井约束;③采用L1、L2、L3、L4四口井约束。分别通过井插值建模,获得PEI初始模型(图 4a、图 4c、图 4e),并由叠后反演得到PEI属性体。最后通过PEI与δ的拟合关系式
| $ \delta =6.4198\times {10}^{-8}\times \mathrm{P}\mathrm{E}\mathrm{I}-0.1778 $ | (9) |
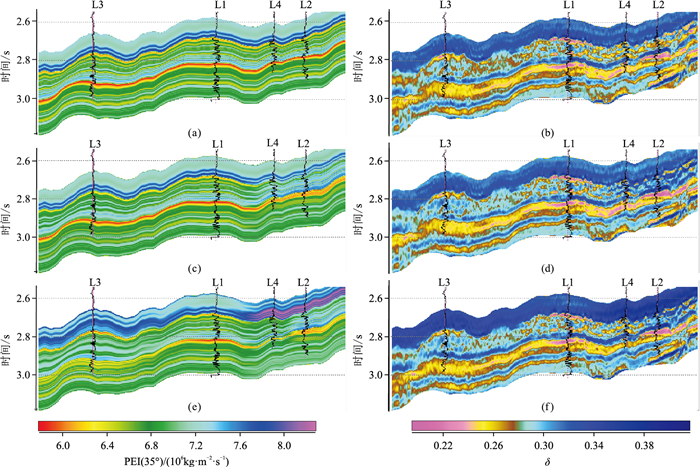
|
图 4 不同井约束方案的PEI初始模型及δ结果 (a)方案①PEI插值模型;(b)基于图a的反演结果;(c)方案②PEI插值模型;(d)基于图c的反演结果;(e)方案③PEI插值模型;(f)基于图e的反演结果井点处投影曲线为GR曲线。 |
将反演PEI属性体转换为δ体(图 4b、图 4d、图 4f)。可见,采用不同方案得到的δ体基本类似,与钻井信息及地层背景较吻合,说明图 4b、图 4d、图 4f主要来自地震数据,与井约束数量无关。图 4表明,基于远道地震数据提取δ参数的方法是可靠的。由于不受井数量约束的影响,该方法在深水区是适用的。
2.3 横波低频模型对比常规建模主要基于低频模型和测井曲线插值共同约束完成。如前文所述,通常基于VP与VS之间的线性关系将纵波模型转换为横波低频模型,再与井插值模型在频率域融合形成用于叠前反演的初始模型,在井资料丰富的地区可较精细地表征地层变化。而在深水区,钻井密度普遍较低,且部分层段没有测井声波数据约束,因此常规方法在大范围区域存在较大不确定性。本文基于图 4f将纵波阻抗模型(图 5a)转换为横波阻抗模型(图 5d),并与常规的横波建模结果(图 5c)进行对比。可见,线性转换横波阻抗(图 5b)和井插值阻抗的融合模型(图 5c)与图 5d的主要特征基本相似,这说明新方法可以保持井数据的低频特点,但图 5d的地层细节更丰富(GR较低的层段对应富砂层段),地层的层次也更分明,因此图 5d更好地反映了地层的岩性背景。

|
图 5 线性转换横波模型与新横波模型对比 (a)纵波阻抗模型;(b)线性转换横波阻抗模型;(c)图b和井插值阻抗的融合模型;(d)本文方法建立的横波阻抗模型井点处投影曲线为GR曲线。 |
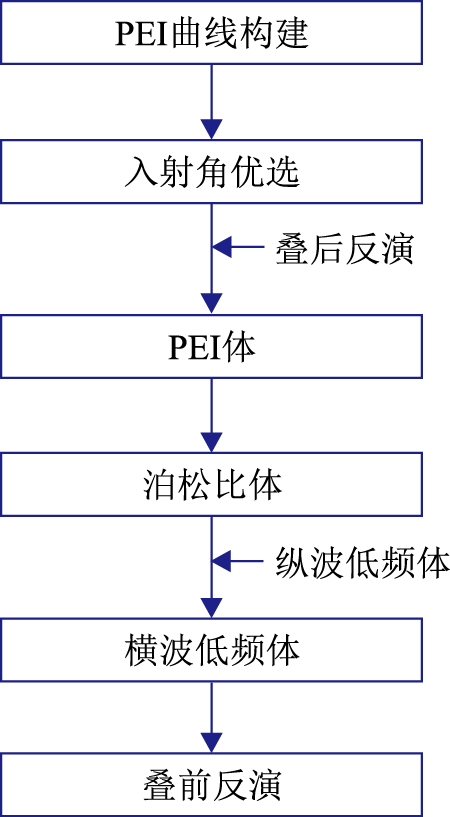
综上所述,总结了基于地震的横波低频模型建立流程(图 6)。
|
图 6 横波低频模型建立流程 |
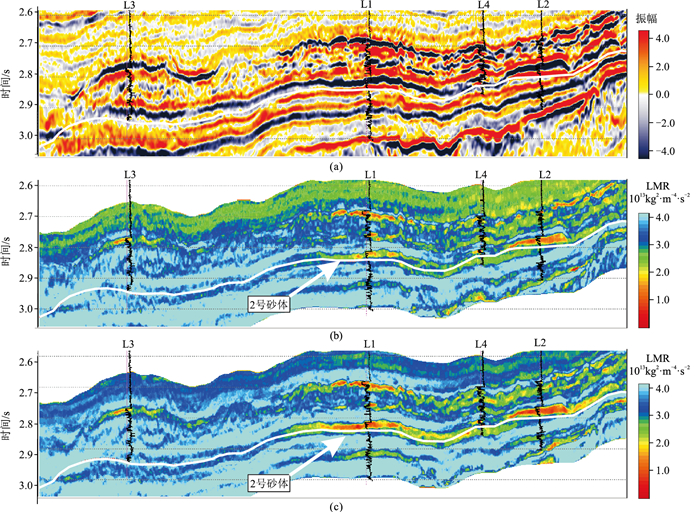
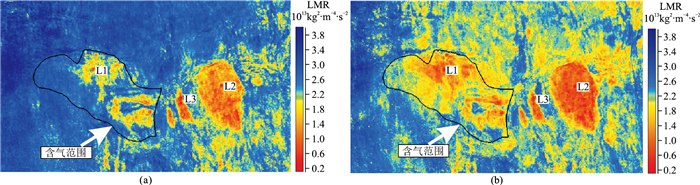
珠江口盆地白云深水区珠江组是南海北部天然气勘探的主要领域,重力流水道及朵叶砂体是主要储层相带[27]。但由于水道摆动迁移以及朵叶展布规律不明显,储层识别和含气性检测面临较大挑战[28]。一般采用LMR表征储层和含气性,LMR值越小,表示储层品质越好、含气性越高。研究区多口井均钻遇2号厚层砂体(图 7白色层位),2号砂体主要为重力流朵叶体,厚度为40~80 m,平面分布广泛、稳定,L1井钻遇2号砂体厚度为40 m。常规建模方法的储层预测结果表明,属性异常分布较局限(图 7b、图 8a),在图 7b的2.7 s以上(绿色区域)存在异常值,与实际地质情况差异较大。本文方法的反演结果(图 7c、图 8b)表明,由于初始模型更好地反映了地层岩性背景(图 5d),反演结果的异常值也减少(图 7c),2号砂体的平面分布与气/水边界一致(图 7c、图 8b),如L1井处的2号砂体(2.85 s)预测厚度较大,平面分布较稳定,反演结果与实钻结果吻合。本文方法反演结果落实了储层分布,扩大了天然气探明储量,取得了较好的经济效益。
|
图 7 本文方法和传统建模方法的反演LMR剖面 (a)地震数据;(b)传统建模方法反演结果;(c)本文方法反演结果井点处投影曲线为密度曲线。 |
|
图 8 传统建模方法(a)和本文方法(b)的2号砂体LMR平面图 |
海洋深水区钻井少、地层岩性变化快,通过叠前反演预测储层和含气性对提高勘探成效十分重要,其中初始模型对地层岩性背景的刻画精度直接影响预测结果的可靠性。目前由常规地震资料处理仅能获取较精细的纵波信息,无法获得横波信息。常规方法是基于纵、横波速度之间的线性关系将纵波模型转换为横波模型,无法精细表征地层的岩性变化。本文结合海洋地区资料特点以及泊松比弹性阻抗相关原理,基于远道地震数据提取泊松比信息,并转换为横波模型。所提方法通过泊松比参数丰富了初始模型的地层岩性信息,提高了横波模型精度及反演结果的可靠性。在白云深水区的勘探实践证明所提方法可行,具有借鉴意义。
| [1] |
张卫卫. 利用叠前反演技术规避地震振幅异常陷阱[J]. 石油天然气学报, 2013, 35(1): 67-72. ZHANG Weiwei. Avoiding the trap of seismic amplitude abnormality by using pre-stack inversion technique[J]. Journal of Oil and Gas Technology, 2013, 35(1): 67-72. |
| [2] |
李建华, 刘百红, 张延庆, 等. 叠前AVO反演在储层含油气性预测中的应用[J]. 石油地球物理勘探, 2016, 51(6): 1180-1186. LI Jianhua, LIU Baihong, ZHANG Yanqing, et al. Oil-bearing reservoir prediction with prestack AVO inversion[J]. Oil Geophysical Prospecting, 2016, 51(6): 1180-1186. |
| [3] |
周林, 廖建平, 李景叶, 等. 基于精确Zoeppritz方程的储层含油气性预测方法[J]. 地球物理学报, 2021, 64(10): 3788-3806. ZHOU Lin, LIAO Jianping, LI Jingye, et al. Prediction method of reservoir oil-gas potential based on exact Zoeppritz equations[J]. Chinese Journal of Geophysics, 2021, 64(10): 3788-3806. DOI:10.6038/cjg2021P0099 |
| [4] |
韩刚, 高红艳, 龙凡, 等. 叠前反演在西湖凹陷致密砂岩储层"甜点"预测中的应用[J]. 石油物探, 2021, 60(3): 471-478. HAN Gang, GAO Hongyan, LONG Fan, et al. Prestack elastic inversion for sweet-spot prediction in tight reservoirs in Xihu Sag[J]. Geophysical Prospec-ting for Petroleum, 2021, 60(3): 471-478. |
| [5] |
胡鑫, 王国权, 刘俊洲, 等. 基于Zoeppritz方程的纵横波联合反演方法及应用[J]. 石油科学通报, 2022, 7(4): 515-531. HU Xin, WANG Guoquan, LIU Junzhou, et al. The joint PP-and PS-wave inversion method based on the Zoeppritz equations and its application[J]. Petroleum Science Bulletin, 2022, 7(4): 515-531. |
| [6] |
马良涛, 范廷恩, 王宗俊, 等. 不同地质条件下反演低频模型构建方法分析[J]. 地球物理学进展, 2021, 36(2): 625-635. MA Liangtao, FAN Tingen, WANG Zongjun, et al. Analysis on construction method of inversion low frequency model under different geological conditions[J]. Progress in Geophysics, 2021, 36(2): 625-635. |
| [7] |
黄诚, 李鹏飞, 陈元勇, 等. 山前复杂岩性地区低频模型的构建方法[J]. 重庆大学学报, 2018, 41(12): 30-35. HUANG Cheng, LI Pengfei, CHEN Yuanyong, et al. The establishment of low frequency mode in piedmont complex lithology area[J]. Journal of Chongqing University, 2018, 41(12): 30-35. |
| [8] |
高云峰, 乐靖, 范洪军, 等. 基于地震信息的相控建模方法优化[J]. 长江大学学报(自科版), 2016, 13(31): 1-4. GAO Yunfeng, LE Jing, FAN Hongjun, et al. The optimizing method for facies controlled modeling based on seismic data[J]. Journal of Yangtze University(Nat Sci Edit), 2016, 13(31): 1-4. |
| [9] |
李冀蜀, 李志刚, 吴建鲁. 基于反射能量约束全波形反演初始速度场建立研究[J]. 地球物理学进展, 2019, 34(4): 1453-1459. LI Jishu, LI Zhigang, WU Jianlu. Establishment of initial velocity field for full waveform inversion based on reflective energy constraints[J]. Progress in Geophysics, 2019, 34(4): 1453-1459. |
| [10] |
汪生好, 李黎, 董政, 等. 基于深度学习的古近系复杂沉积地区低频模型构建方法——以珠江口盆地LA油田为例[J]. 天然气与石油, 2022, 40(3): 90-97. WANG Shenghao, LI Li, DONG Zheng, et al. Development of low frequency model with multi-source information in complex sedimentary strata based on deep learning method: Taking LA oilfield as an example[J]. Natural Gas and Oil, 2022, 40(3): 90-97. |
| [11] |
刘尧均, 官大勇, 王志萍, 等. 湖底扇水道相控建模技术及应用[J]. 海洋地质前沿, 2020, 36(11): 59-68. LIU Yaojun, GUAN Dayong, WANG Zhipin, et al. Modeling technology for facies controlled sublacustrine fan channel system and its application[J]. Marine Geology Frontiers, 2020, 36(11): 59-68. |
| [12] |
刘军, 刘杰, 曹均, 等. 基于岩石物理试验的储层与孔隙流体敏感参数特征——以珠江口盆地东部中—深层碎屑岩储层为例[J]. 石油学报, 2019, 40(1): 197-205. LIU Jun, LIU Jie, CAO Jun, et al. Characteristics of reservoir and pore fluid sensitivity parameters based on rock physical experiment: a case study of the middle-deep clastic rock reservoirs in the eastern Pearl River Mouth Basin[J]. Acta Petrolei Sinica, 2019, 40(1): 197-205. |
| [13] |
周路, 钟斐艳, 闫佳琛, 等. 四川盆地大猫坪地区二叠系长兴组生物礁气层叠前反演识别[J]. 石油勘探与开发, 2020, 47(1): 86-97. ZHOU Lu, ZHONG Feiyan, YAN Jiachen, et al. Prestack inversion identification of organic reef gas reservoirs of Permian Changxing Formation in Damaoping area, Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2020, 47(1): 86-97. |
| [14] |
刘军, 文晓涛, 张雨强, 等. 火成岩储层物性参数叠前地震反演[J]. 地球物理学进展, 2022, 37(5): 1985-1992. LIU Jun, WEN Xiaotao, ZHANG Yuqiang, et al. Prestack seismic inversion of igneous reservoir physical property parameters[J]. Progress in Geophysics, 2022, 37(5): 1985-1992. |
| [15] |
张卫卫, 刘军, 刘力辉, 等. 珠江口盆地番禺4洼古近系文昌组岩性预测技术及应用[J]. 岩性油气藏, 2022, 34(6): 118-125. ZHANG Weiwei, LIU Jun, LIU Lihui, et al. Lithology prediction technology and its application of Paleogene Wenchang Formation in Panyu 4 depression, Pearl River Mouth Basin[J]. Lithologic Reservoirs, 2022, 34(6): 118-125. |
| [16] |
印兴耀, 刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探, 2016, 55(3): 309-325. YIN Xingyao, LIU Xinxin. Research status and progress of the seismic rock-physics modeling methods[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 309-325. |
| [17] |
刘宝鸿, 郭彦民, 田志, 等. 利用地震相控反演预测辽河坳陷兴隆台潜山中生界致密砂砾岩优质储层[J]. 石油地球物理勘探, 2022, 57(增刊2): 100-109. LIU Baohong, GUO Yanmin, TIAN Zhi, et al. Prediction of high-quality tight sandy conglomerate reservoirs in Mesozoic of Xinglongtai buried hill, Liaohe Depression by seismic facies-controlled inversion[J]. Oil Geophysical Prospecting, 2022, 57(S2): 100-109. |
| [18] |
凌东明, 杜启振, 田军, 等. 基于岩相约束的Xu-White模型线性化近似与反演[J]. 石油地球物理勘探, 2019, 54(3): 577-586. LING Dongming, DU Qizhen, TIAN Jun, et al. The Xu-White model linearized approximation and inversion based on lithofacies constraint[J]. Oil Geophysical Prospecting, 2019, 54(3): 577-586. |
| [19] |
王朋, 徐立恒, 杨会东, 等. 相控叠前地质统计学反演在剩余油预测中的应用[J]. 石油地球物理勘探, 2023, 58(5): 1192-1201. WANG Peng, XU Liheng, YANG Huidong, et al. Application of facies-controlled pre-stack geostatistical inversion in residual oil prediction[J]. Oil Geophysical Prospecting, 2023, 58(5): 1192-1201. |
| [20] |
CONNOLLY P A. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. |
| [21] |
周义军, 李喜瑞. 敏感角度弹性阻抗在流体预测中的应用[J]. 石油地球物理勘探, 2010, 45(5): 710-713. ZHOU Yijun, LI Xirui. Application of sensitive angle elastic impedance in fluid prediction[J]. Oil Geophysical Prospecting, 2010, 45(5): 710-713. |
| [22] |
李超, 印兴耀, 张广智, 等. 基于入射角的两项流体阻抗反演方法[J]. 地球物理学报, 2014, 57(10): 3442-3452. LI Chao, YIN Xingyao, ZHANG Guangzhi, et al. Two-term elastic impedance inversion based on the incidentangle approximation[J]. Chinese Journal of Geophysics, 2014, 57(10): 3442-3452. |
| [23] |
马辉, 郭继茹, 孙星, 等. 优势角度叠加数据在阿联酋陆海一区块油气检测中的应用[J]. 石油地球物理勘探, 2022, 57(增刊1): 223-228. MA Hui, GUO Jiru, SUN Xing, et al. Application of superior-angle stack data in oil and gas detection in Land and Sea Block 1, United Arab Emirates[J]. Oil Geophysical Prospecting, 2022, 57(S1): 223-228. |
| [24] |
WHITCOMBE D N, CONNOLLY P A, REAGAN R L, et al. Extended elastic impedance for fluid and lithology prediction[J]. Geophysics, 2002, 67(1): 63-67. |
| [25] |
桂金咏, 印兴耀, 曹丹平. 基于弹性阻抗反演理论的泊松比反演方法研究[J]. 石油物探, 2011, 50(5): 463-469. GUI Jinyong, YIN Xingyao, CAO Danping. Poisson's ratio inversion method on elastic impedance inversion theory[J]. Geophysical Prospecting for Petroleum, 2011, 50(5): 463-469. |
| [26] |
SHUEY R T. A simplification of the Zoeppritzequations[J]. Geophysics, 1985, 50(4): 609-614. |
| [27] |
陈亮, 庞雄, 刘军, 等. 珠江口盆地白云凹陷深水重力流优质砂岩储集层特征及识别方法[J]. 石油勘探与开发, 2015, 42(4): 463-471. CHEN Liang, PANG Xiong, LIU Jun, et al. Characteristics and identification of high quality deep-water gravity flow sandstone reservoirs in Baiyun sag, Pearl River Mouth Basin, South China Sea[J]. Petroleum Exploration and Development, 2015, 42(4): 463-471. |
| [28] |
朱焱辉, 张向涛, 刘立峰, 等. 白云凹陷深水区河道砂体分布预测[J]. 石油物探, 2022, 61(5): 888-897. ZHU Yanhui, ZHANG Xiangtao, LIU Lifeng, et al. Prediction of channel sand body distribution in deep water area of Baiyun sag[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 888-897. |



 敖威,深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座1806,518054。Email:
敖威,深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座1806,518054。Email: