0 引言

地震波阻抗反演是获取地下介质信息的有效途径，反演结果可以反映地下介质的岩性变化，是储层预测的一项关键技术^[1-2]。地震波阻抗具有高分辨率、地质信息丰富的特点，叠后地震波阻抗反演在储层预测中具有重要意义^[3-5]。然而，由于地震数据的频带限制以及数据噪声等影响，地震波阻抗反演问题是一个不适定问题。

为了获取较稳定和精确的反演结果，可以使用正则化方法约束反演过程，从而获取高精度反演结果^[6]。目前有平滑约束和块约束两种典型的正则化地震反演方法^[7-9]。平滑约束有Tikhonov^[10]提出的L₂范数约束反演参数的方法，通过低频初始模型得到平滑反演结果。然而平滑约束会模糊边界和断层信息，并不能有效提高反演结果的分辨率。为此，王宁等^[11]提出数据驱动的块排列正则化方法，利用叠后地震数据高信噪比的特点，通过提取一个块排列的矩阵记录地下构造信息，利用地震数据局部相似性记录相邻采样点的位置，通过构造地震道的块排列正则项有效提高了反演结果的分辨率。然而，上述方法是逐道进行的，忽略了地层构造信息的空间连续性，使单道反演结果的横向连续性较差^[12-14]。

现阶段地震波阻抗反演问题可以转化为常规的单道反演，单道反演的计算效率高、稳定性强^[15-16]。由于单道反演只考虑当前道的地震响应，缺乏相邻道的横向约束，从而不易控制反演结果的横向连续性^[17]。因此，有人尝试将单道地震波阻抗反演转变为多道反演。Gholami^[18]利用全变分约束多道非线性波阻抗反演，反演结果具有块状特征，增强了空间连续性。Hamid等^[5]将所有地震道连成一道数据，并在水平方向平滑约束相邻道反演结果；但是当真实情况与假设前提不一致时，不能得到准确的反演结果。随后，人们发展了数据驱动的多道地震反演方法，如Hamid等^[19]利用观测数据计算地震同相轴的局部倾角，并将倾角信息和测井数据引入地震反演，提高了反演结果的横向连续性。Huang等^[20]根据地震数据估算斜率属性，并引入全变分正则化反演，获得了高分辨率反演结果。印兴耀等^[21]提出了地震数据互相关驱动的多道反演方法，通过计算地震数据的相关性描述地震结构特征，并作为地震反演的一个约束项，该方法极大地提高了反演结果的横向连续性。

目前提高反演横向连续性的主要手段仍是基于模型参数先验信息假设的正则化方法，当先验信息与实际情况矛盾时，正则化方法会出现问题^[22]。为此，文中基于多道反演理论和方法，提出一种自适应时窗多道相关的叠后地震波阻抗反演方法。首先，利用主动学习的思想^[23]，通过查询原始地震数据筛选地震数据关键特征的位置；其次，根据上述位置将地震数据划分为不同尺度的时窗，有助于断层信息保护以及异常体边界识别；再次，根据点乘计算自适应时窗内地震道之间的相关性；最后，通过“加权求和”地震道得到重构地震道——反演目标泛函的约束条件。所提方法借助主动学习以及地震数据局部相关的思想，较好地反映了自适应时窗内的多道间的相关性，并且可并行化处理。文中利用模型和实际数据测试了所提方法的效果。

1 方法原理

所提方法在计算地震道相关性时根据数据特征变化确定参与计算的地震道，而不是人为选取地震道。鉴于此，采用主动学习（Active Learning）^[23]的整体思想自动选取地震道，主要利用机器学习算法查询地震数据并筛选地震数据关键特征的位置，通过上述位置划分地震数据，得到一系列不同道数的地震数据，由此计算地震数据的相关性更符合地质变化规律，从而获得多道时窗自适应效果。所提方法避免了固定时窗导致的断层以及异常体边界信息的破坏。

由于地震数据可以视为一种序列信息，并且地震道之间具有一定相关性，因此可以计算时窗内的每一道与所有道的相关性，从而得到每一道占所有道的权重，通过不同权重的“加权求和”得到重构地震道。重构地震道包含了其他道的信息，即权重越小的道包含的信息越少，权重越大的道包含的信息越多。

1.1 自适应时窗的创建

为更好地保护断层、异常体等边界信息，采用查询算法得到地震数据的关键特征位置，并利用该位置划分地震数据，从而识别关键地质构造并实现自适应时窗多道相关。

首先，建立机器学习模型。利用已知地震数据和测井波阻抗数据预训练径向基函数（RBF）神经网络得到一个初始模型。其次，加入查询算法。采用机器学习的最小置信度算法查询地震数据，即

$ \begin{array}{l}{x}_{\mathrm{L}\mathrm{C}}^{\mathrm{*}}=\arg\max_{x}[1-{p}_{\boldsymbol \theta }(\widehat{y}\left|x\right)]\\ \ \ \ \ \ \ =\arg\min_{x}{p}_{\boldsymbol \theta }\left(\widehat{y}\right|x)\end{array} $

(1)

式中：$ \widehat{y} $为对于给定的地震数据样本$ x $，通过模型预测得到概率最大的波阻抗数据；$ {p}_{\boldsymbol \theta }(\cdot ) $为在模型参数为$ \boldsymbol \theta $时计算的概率值；$ \arg\max(\cdot ) $为最大概率值的位置；$ \arg\min(\cdot ) $为最小概率值的位置；$ {x}_{\mathrm{L}\mathrm{C}}^{\mathrm{*}} $为$ x $中最小置信度值位置的地震数据。

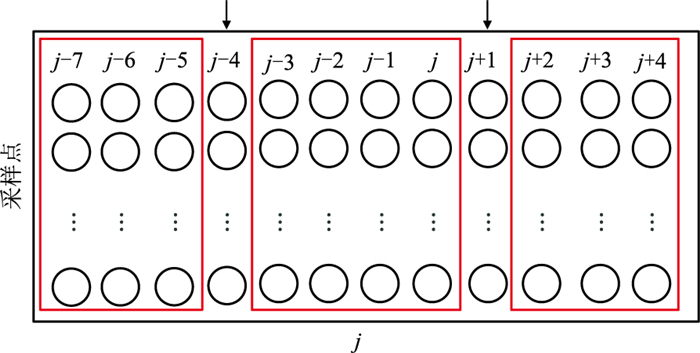
通过上述算法可以找到关键地震特征的位置，利用该位置即可将原始地震数据划分为不同尺度的时窗（图 1）。

1.2 地震数据相关性计算

计算任一时窗地震数据的相关性的步骤分述如下。

（1）将时窗内的地震数据排序，得到$ \mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{1}, $$ \mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{2},\cdots ,\mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{j},\cdots ,\mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{n} $，j=1, 2, …, n, n为总CDP数。

（2）设置单位矩阵$ {\boldsymbol{W}}^{Q}\mathrm{、}{\boldsymbol{W}}^{K}\mathrm{、}{\boldsymbol{W}}^{V} $作为求取权重的基础矩阵，然后将时窗内的每道数据$ \mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{j} $分别与$ {\boldsymbol{W}}^{Q}\mathrm{、}{\boldsymbol{W}}^{K}\mathrm{、}{\boldsymbol{W}}^{V} $相乘得到$ {\boldsymbol q}_{j}\mathrm{、}{\boldsymbol k}_{j}\mathrm{、}{\boldsymbol v}_{j} $，即通过

$ {\boldsymbol q}_{j}={\boldsymbol{W}}^{Q}\mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{j} $

(2)

$ {\boldsymbol{k}}_{j}={\boldsymbol{W}}^{K}\mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{j} $

(3)

$ {\boldsymbol v}_{j}={\boldsymbol{W}}^{V}\mathrm{s}\mathrm{e}\mathrm{i}{\mathrm{s}}_{j} $

(4)

初始化矩阵。$ {\boldsymbol{W}}^{Q}\mathrm{、}{\boldsymbol{W}}^{K}\mathrm{、}{\boldsymbol{W}}^{V} $是单位矩阵，主要利用$ {\boldsymbol{W}}^{Q}\mathrm{、}{\boldsymbol{W}}^{K} $求取时窗内每一道与其他道的权重系数，$ {\boldsymbol{W}}^{V} $主要用于“加权求和”。设置三个单位矩阵可以确保并行化计算。

（3）求解每一道与其他道的相关性，即

$ {A}_{ji}=\frac{{\boldsymbol{q}}_{j}^{\mathrm{T}}\cdot {\boldsymbol{k}}_{i}}{\sqrt{{d}_{}}} $

(5)

式中$ d $为$ {\boldsymbol{q}}_{j}^{\mathrm{T}}\cdot {\boldsymbol{k}}_{i} $的维度，目的是使$ {\boldsymbol{q}}_{j}^{\mathrm{T}}\cdot {\boldsymbol{k}}_{i} $的结果满足期望为0、方差为1的正态分布，类似归一化操作。通过$ {\boldsymbol{q}}_{j}^{\mathrm{T}} $查询j道与第i（i≠j）道的相关性，即求取每一道与其他道的相关性并Softmax归一化，可以得到权重矩阵

$ \boldsymbol A=\left[\begin{array}{cccc}{A}_{11}& {A}_{12}& \cdots & {A}_{1n}\\ {A}_{21}& {A}_{22}& \cdots & {A}_{2n}\\ & & ⋮& \\ {A}_{n1}& {A}_{n2}& \cdots & {A}_{nn}\end{array}\right] $

(6)

该权重矩阵元素的数值范围为0~1，以进行加权求和。

（4）将步骤（2）得到的$ {\boldsymbol v}_{j} $转换为

$ \boldsymbol V=[{\boldsymbol v}_{1},{\boldsymbol v}_{2},\cdots ,{\boldsymbol v}_{n}] $

(7)

将$ \boldsymbol A $与$ \boldsymbol V $相乘重构一个具有相邻地震道信息的多道地震数据，即

$ {\boldsymbol A}_{\mathrm{s}\mathrm{e}\mathrm{i}\mathrm{s}}=\boldsymbol A{\boldsymbol V}^{\mathrm{T}} $

(8)

通过多道信息约束可保证地震波阻抗反演结果的横向连续性。

通过上述步骤即可实现自适应时窗的多道相关性计算。

1.3 自适应时窗多道相关的叠后地震反演目标函数构建

观测地震数据$ \boldsymbol d $是由反射系数r与震源产生的带限子波w褶积而成^[24]，即

$ \boldsymbol d=\boldsymbol{w}\boldsymbol{r}+\boldsymbol n $

(9)

式中n为随机噪声。

常规单道地震反演的目标函数为

$ f\left(\boldsymbol{r}\right)=\left|\right|\boldsymbol d-\boldsymbol{w}\boldsymbol{r}|{|}_{2}^{2} $

(10)

基于式(10)的解，可以得到r，进一步通过递推公式

$ Z\left(u\right)=Z\left(0\right)\mathrm{e}\mathrm{x}\mathrm{p}\left[2\sum\limits_{u=0}^{U}r\left(u\right)\right] $

(11)

估计波阻抗$ Z\left(u\right) $。式中：$ Z\left(0\right) $为第一层波阻抗；r(u)为r的离散形式，u=1，2，…，U，U为地层层数。

为了充分利用各种先验地质信息提高反演精度，在宽带约束反演（BCI，Broadband Constrained Inversion）方法的基础上，笔者提出自适应时窗多道相关的叠后地震波阻抗反演方法。该方法通过查询将地震数据划分为不同尺度的时窗，分别计算每个时窗内地震道之间的相关性，并重构地震道作为反演约束条件，构建了基于多道相关的目标函数

$ \begin{array}{l}f\left(\boldsymbol Z\right)=\min\left\{\right||{\boldsymbol A}_{\mathrm{s}\mathrm{e}\mathrm{i}\mathrm{s}}-\boldsymbol {GZ}|{|}_{2}^{2}+\lambda \left|\right|\boldsymbol D-\boldsymbol {GZ}|{|}_{2}^{2}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\mu \left|\right|{\boldsymbol Z}_{\mathrm{p}\mathrm{i}\mathrm{o}\mathrm{r}}-\boldsymbol Z\left|{|}_{2}^{2}\right\}\end{array} $

(12)

式中：$ \boldsymbol Z $为Z的矩阵形式；$ \boldsymbol G $为地震子波时移矩阵与一阶差分矩阵的乘积；$ \boldsymbol D $为原始地震数据；$ \lambda $为正则化参数；$ {\boldsymbol Z}_{\mathrm{p}\mathrm{i}\mathrm{o}\mathrm{r}} $为通过测井资料沿层内插、外推建立的先验波阻抗模型；$ \mu $为模型正则化参数，可控制$ {\boldsymbol Z}_{\mathrm{p}\mathrm{i}\mathrm{o}\mathrm{r}} $对反演的贡献率。

2 模型测试 2.1 无噪模型测试

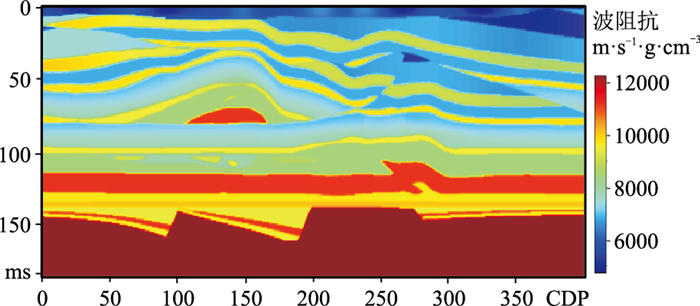
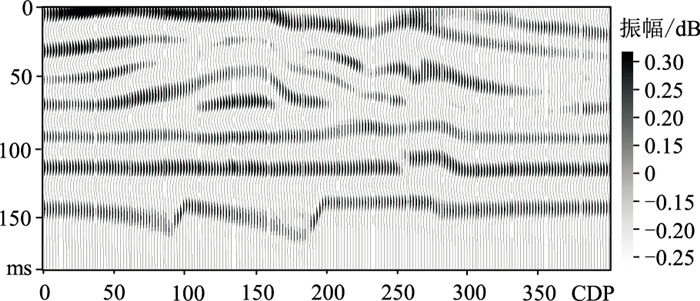
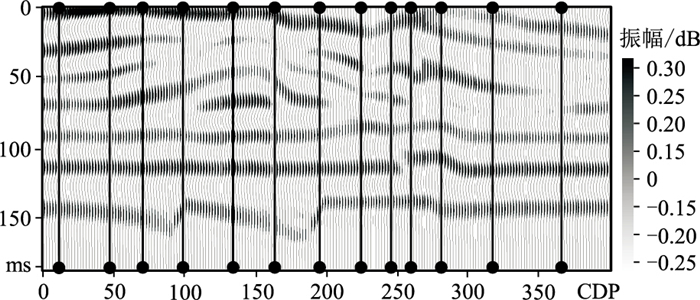
采用Overthrust模型（图 2）^[25]测试所提方法的可行性。利用主频为30 Hz的Ricker子波与图 2褶积得到正演记录（图 3）。由于地震数据频带限制，反演缺少低频成分，因此将图 2进行0~5 Hz的低通滤波得到低频初始阻抗模型，以补充反演结果的低频成分。设置主动学习模型的初始样本集为图 2中CDP 50、CDP 75、CDP 150、CDP 200、CDP 225、CDP 275、CDP 300、CDP 350、CDP 400处的地震道及其波阻抗。选取初始样本集的原则为：对于模型数据而言，选取地震数据中差异大的区域中的一个代表性样本；对于实际数据，选取井位置的地震数据和阻抗（井数据的差异明显）。根据初始样本集查询的自适应时窗如图 4所示。

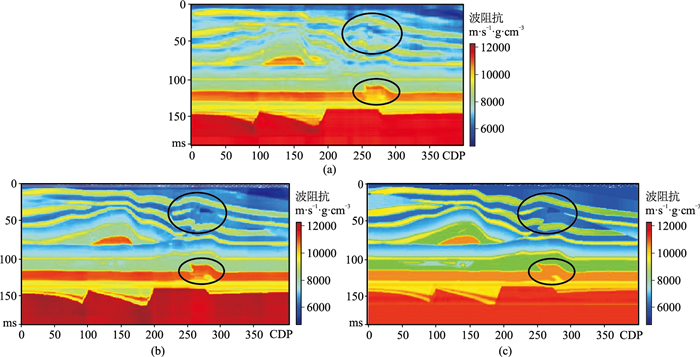
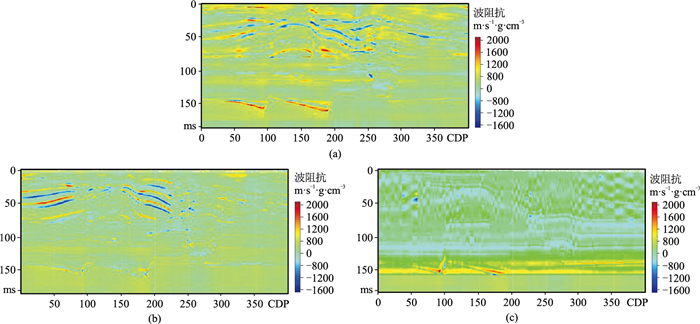
图 5、图 6分别为模型不加噪反演结果、残差。由图 5可见：相对于单道宽带约束反演结果（图 5a），固定时窗多道相关（图 5b）和自适应时窗多道相关（图 5c）反演结果在一定程度上提高了横向连续性；图 5b断层边界模糊，也未能较好地识别异常体，图 5c断层边界清晰，且较好地识别了异常体。因此，自适应时窗多道相关反演不仅可以提高反演结果的横向连续性，还能刻画断层边界和异常地质体边界。由图 6可见，自适应时窗多道相关反演的残差（图 6c）明显小于固定时窗多道相关（图 6b）以及单道宽带约束反演（图 6a），反演结果精度较高，但也存在一定局限性，如在深层高速体位置（150 ms）存在一定误差。文中采用皮尔逊相关系数（PearsonCorrelation Coefficient，PCC）、决定系数（Coefficient of Determination，R²）和均方误差（Mean Squared Error，MSE）定量分析反演结果（表 1）。PCC反映了两个量之间的相关程度，越接近1相关程度越高；R²表示回归分析中自变量对因变量的解释，越接近1解释效果越好；MSE反映了预测值与真实值之间的差异程度，越接近0预测精度越高。可见，自适应时窗多道相关反演的精度高于单道宽带约束反演和固定时窗多道相关反演（表 1），但计算效率较低（表 2），主要原因是计算过程涉及大量矩阵存储和计算。

2.2 加噪模型测试

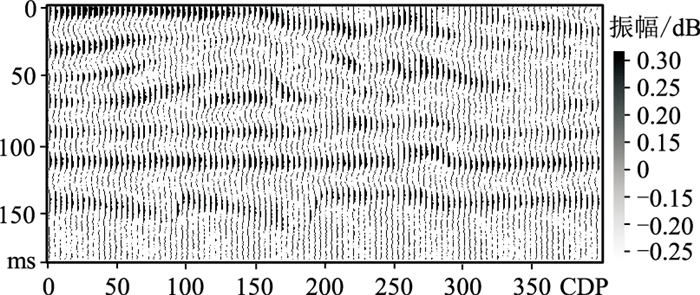
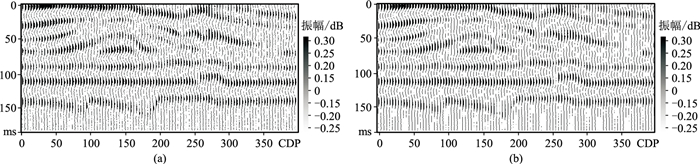
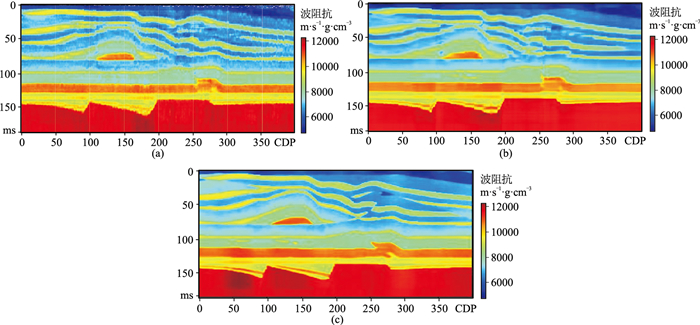
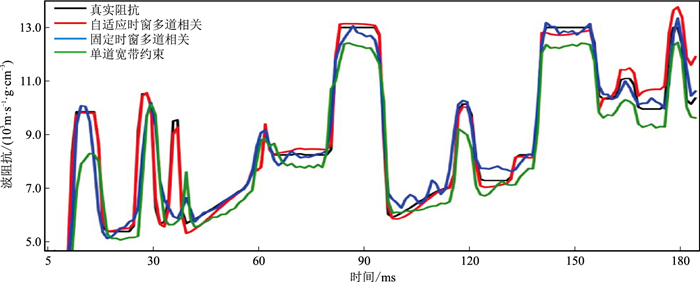
对图 3添加10%、20%和30%的高斯噪声（表 3），结果表明所提方法具有一定抗噪性，但随着噪声增加，抗噪性能下降。为了更直观地了解自适应时窗多道相关反演方法的抗噪性，分析加入30%高斯噪声正演记录（图 7）的反演结果。图 8为图 7的重构合成记录，图 9为图 8的反演结果。由图可见，自适应时窗多道相关反演结果（图 9c）的横向连续性强于单道宽带约束反演结果（图 9a），并且对复杂构造的识别效果好于固定时窗多道相关反演结果（图 9b）。图 10为CDP 150处的单道反演结果。由图可见，自适应时窗多道相关反演结果更接近真实阻抗，具有一定的抗噪性。上述模型测试结果表明：单道宽带约束反演运行效率高，但反演结果的横向连续性差，仅适用于地层结构较平滑地区；固定时窗多道相关反演结果的横向连续性较好，但难以兼顾特殊构造（断层、异常体等）信息，适用于无特殊构造、横向连续性较差的地区；自适应时窗多道相关反演结果的横向连续性较好，可以兼顾特殊构造信息，但计算效率较低，且在浅、深层速度差异较大的区域存在一定局限性（图 6c），适用于具有特殊构造的狭小地区。

3 实际资料处理

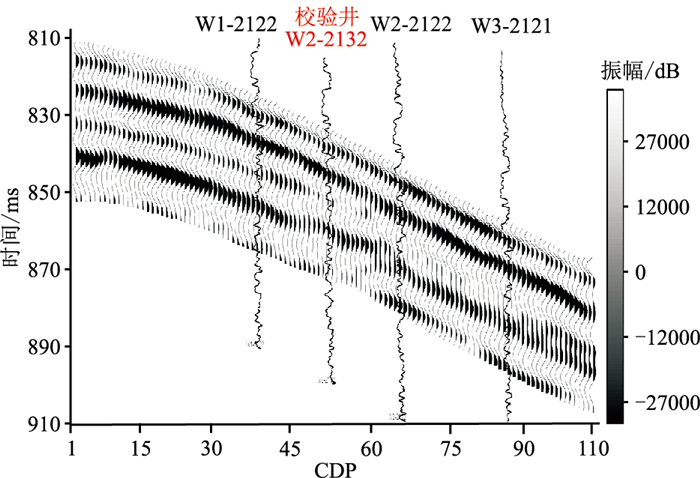
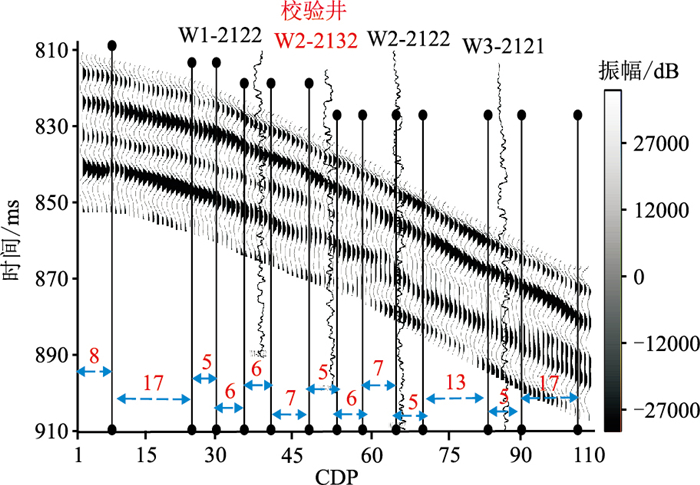
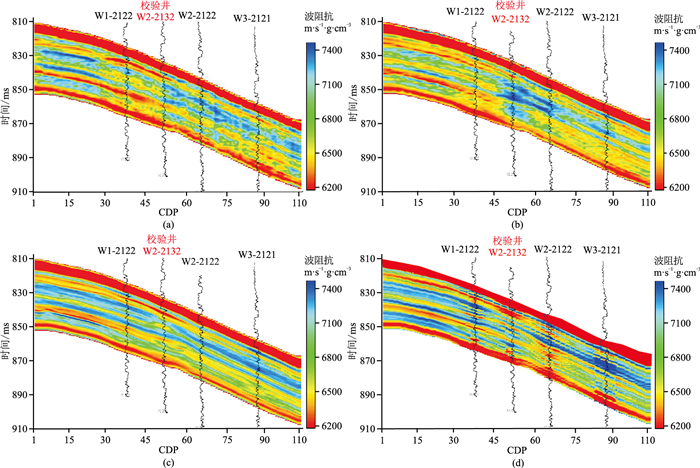
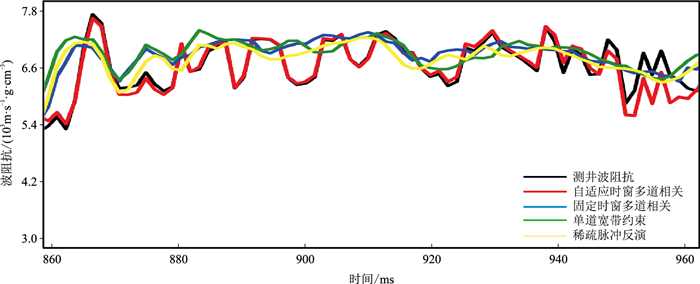
A区现有30口井的声波、密度测井资料。图 11为A区地震剖面，通过主动学习得到自适应时窗（图 12）。图 13为不同方法的反演结果。由图可见，自适应时窗多道相关反演结果（图 13d）的横向连续性优于单道宽带约束(图 13a)、固定时窗多道相关(图 13b) 及稀疏脉冲(图 13c)反演结果。井震标定结果表明，图 13d与测井资料吻合程度更好，并且与测井波阻抗的相关系数为0.85，且能提高反演的纵向分辨率。图 14为单道反演结果。由图可见，自适应时窗多道相关反演结果与测井曲线基本吻合，验证了方法的可行性和有效性。

4 结束语

本文提出了一种自适应时窗多道相关的叠后地震波阻抗反演方法。该方法不仅考虑地震道之间的相关性，还同时兼顾特殊构造信息，使反演结果更合理。模型测试和实际数据测试表明，该方法反演结果的横向连续性较好，且可以兼顾特殊构造信息，但计算效率较低，且在浅、深层速度差异较大的区域存在一定局限性，适用于具有特殊构造的狭小地区。