0 引言

振幅随角度变化（AVA）反演方法通过利用角度信息获取地下地质体的弹性参数估计，这在储层含气性预测中起着至关重要的作用^[1-3]。偏移后的地震数据可以通过偏移速度转换为角度域数据，即AVA数据。将AVA数据进行部分角度叠加即可获得用于AVA反演的部分叠加角度数据^[4]。Zoeppritz方程是AVA反演的基础，但Zoeppritz方程对于反演计算来说过于复杂，因此常使用AVA线性近似构建反演算法中的正演矩阵^[5]。反演获得的纵波速度、横波速度和密度等参数会被转换为含气指示因子，从而用于储层含气性预测^[6-8]。

利用AVA技术进行含气性预测时，通常存在两个方面的问题。

第一个方面是关于AVA线性近似式的选择和部分叠加策略的选择。前人^[1-2]一般专注于改进反演过程，包括目标函数的求解方法、降低非唯一性的约束等，但对AVA线性近似式与部分叠加策略的研究略少，未形成针对性的有效方法。实际上，叠前道集质量、AVA线性近似式与部分叠加策略的选择非常关键^{[4, 9]}。基于AVA反演的含气性预测会将反演的参数转换为储层或含气性指示因子用于指导油气勘探。因此，结合目标区的含气性指示因子，选择相应的AVA近似公式，可以减少参数变换的累积误差，增强反演的稳定性^{[6, 10]}。考虑到目标区域的采集因素（信噪比、最大入射角等），如何生成部分叠加角度数据、最大程度地利用已有数据信息也比较关键。一个好的部分叠加策略可以在充分利用AVA特征的同时，还可为反演提供高信噪比数据。

第二个方面是关于AVA反演的先验约束。最常用的AVA反演方法是在贝叶斯框架下，采用先验约束，以后验概率（先验函数与似然函数的组合）的最大化作为估计参数的标准^[11-12]。其中，似然函数表示观测数据的匹配度。似然函数通常通过假设高斯噪声来构造，具有足够的有效性^[13]。然而，先验的选择多种多样，对于平滑边界，高斯先验是理想的选择；Cauchy分布等长尾先验因其稀疏性和良好的边界刻画能力受到关注^[14-15]。然而，无论是高斯先验还是稀疏先验都受固定参数控制（如高斯先验的固定参数是均值和方差）。在反演过程中，固定参数不会随着地震数据变化，这意味着估计参数的趋势将被迫趋于同质化，储层性质的横向变化引起的参数变化将变得模糊^[16-17]。前人为了缓解这种固化参数，在构造目标函数时，将先验的固定参数改写为权重参数，并采用自适应变化的权重参数^[18]，在一定程度上改善了反演效果。

综上所述，本文提出了基于ARD-AVA反演的含气性预测技术，将包含超参数的自动相关判别（ARD）先验信息作为约束引入到叠前AVA反演方法中。先验信息中的超参数被视为从不同的地震道中估计出的特定值，而不是固定参数（如高斯先验、柯西先验等）。超参数随着不同地震道变化的自适应估计可以使反演结果与地质特征的横向变化具有更好的相关性，且具有稀疏性^{[16, 19-20]}。此外，基于AVA正演矩阵的灵敏度和条件数参数，讨论了AVA线性近似式和部分叠加策略的选择，形成了有效的方法。实际资料应用效果证实了技术的可行性和优势。

1 ARD-AVA叠前反演方法

采用Fatti两项式^[21]作为构建方法的基本公式

$ {\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left(\theta \right)=\left[\begin{array}{cc}\boldsymbol{A}\left(\theta \right)& \boldsymbol{B}\left(\theta \right)\end{array}\right]{\left[\begin{array}{cc}{\boldsymbol{R}}_{\mathrm{I}\mathrm{P}}& {\boldsymbol{R}}_{\mathrm{I}\mathrm{S}}\end{array}\right]}^{\mathrm{T}} $

(1)

式中：$ {\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left(\theta \right) $为随角度变化的反射系数，θ是入射角；$ \boldsymbol{A}\left(\theta \right)=\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta /2 $；$ \boldsymbol{B}\left(\theta \right)=-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $，γ为横纵波速度比；$ {\boldsymbol{R}}_{\mathrm{I}\mathrm{P}} $、$ {\boldsymbol{R}}_{\mathrm{I}\mathrm{S}} $分别为纵波阻抗、横波阻抗的参数反射系数。

令对应不同入射角的部分叠加数据为N个，则

$ \left[\begin{array}{c}{\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left({\theta }_{1}\right)\\ ⋮\\ {\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left({\theta }_{N}\right)\end{array}\right]=\left[\left[\begin{array}{cc}\boldsymbol{A}\left({\theta }_{1}\right)& \boldsymbol{B}\left({\theta }_{1}\right)\\ ⋮& ⋮\\ \boldsymbol{A}\left({\theta }_{N}\right)& \boldsymbol{B}\left({\theta }_{N}\right)\end{array}\right]\right]\left[\begin{array}{c}{\boldsymbol{R}}_{\mathrm{I}\mathrm{P}}\\ {\boldsymbol{R}}_{\mathrm{I}\mathrm{S}}\end{array}\right] +n $

(2)

其中

$ \left(\begin{array}{l}\boldsymbol{A}\left(\theta \right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\begin{array}{cccc}A\left({t}_{1}, \theta \right)& A\left({t}_{2}, \theta \right)& ...& A\left({t}_{K}, \theta \right)\end{array}\right]\\ \boldsymbol{B}\left(\theta \right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\begin{array}{cccc}B\left({t}_{1}, \theta \right)& B\left({t}_{2}, \theta \right)& ...& B\left({t}_{K}, \theta \right)\end{array}\right]\\ {\boldsymbol{R}}_{\mathrm{I}\mathrm{P}}={\left[\begin{array}{cccc}{R}_{\mathrm{I}\mathrm{P}}\left({t}_{1}\right)& {R}_{\mathrm{I}\mathrm{P}}\left({t}_{2}\right)& ...& {R}_{\mathrm{I}\mathrm{P}}\left({t}_{K}\right)\end{array}\right]}^{\mathrm{T}}\\ {\boldsymbol{R}}_{\mathrm{I}\mathrm{S}}={\left[\begin{array}{cccc}{R}_{\mathrm{I}\mathrm{S}}\left({t}_{1}\right)& {R}_{\mathrm{I}\mathrm{S}}\left({t}_{2}\right)& ...& {R}_{\mathrm{I}\mathrm{S}}\left({t}_{K}\right)\end{array}\right]}^{\mathrm{T}}\end{array}\right. $

(3)

上述式中：$ \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[...\right] $代表对角矩阵；$ {t}_{K} $为采样点时间，K为时间采样点总数；n为噪声。为了提升稳定性增加低频趋势约束^[22]，则

$ \left[\begin{array}{c}{\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left({\theta }_{1}\right)\\ ⋮\\ {\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left({\theta }_{N}\right)\\ \mathbf{L}\mathbf{o}\mathbf{w}\mathbf{I}\mathbf{P}\\ \mathbf{L}\mathbf{o}\mathbf{w}\mathbf{I}\mathbf{S}\end{array}\right]=\left[\begin{array}{c}\left[\begin{array}{cc}\boldsymbol{A}\left({\theta }_{1}\right)& \boldsymbol{B}\left({\theta }_{1}\right)\\ ⋮& ⋮\\ \boldsymbol{A}\left({\theta }_{N}\right)& \boldsymbol{B}\left({\theta }_{N}\right)\end{array}\right]\\ \begin{array}{cc}\boldsymbol{\varPsi }& \mathit{0}\\ \mathit{0}& \boldsymbol{\varPsi }\end{array}\end{array}\right]\left[\begin{array}{c}{\boldsymbol{R}}_{\mathrm{I}\mathrm{P}}\\ {\boldsymbol{R}}_{\mathrm{I}\mathrm{S}}\end{array}\right] +n $

(4)

式中：$ \boldsymbol{\varPsi } $为低频提取矩阵^[22]；LowIP和LowIS分别为纵、横波阻抗低频模型矩阵。将上述矩阵进行简化，可得

$ {\boldsymbol{d}}_{N\times K+2K}={\boldsymbol{G}}_{\left(N\times K+2K\right)\times 2K}{\boldsymbol{m}}_{2K}+\boldsymbol{n} $

(5)

$ 式中：\boldsymbol{d}=\left[\begin{array}{c}{\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left({\theta }_{1}\right)\\ ⋮\\ {\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left({\theta }_{N}\right)\\ \mathbf{L}\mathbf{o}\mathbf{w}\mathbf{I}\mathbf{P}\\ \mathbf{L}\mathbf{o}\mathbf{w}\mathbf{I}\mathbf{S}\end{array}\right] ; \boldsymbol{G}=\left[\begin{array}{c}\left[\begin{array}{cc}\boldsymbol{A}\left({\theta }_{1}\right)& \boldsymbol{B}\left({\theta }_{1}\right)\\ ⋮& ⋮\\ \boldsymbol{A}\left({\theta }_{N}\right)& \boldsymbol{B}\left({\theta }_{N}\right)\end{array}\right]\\ \begin{array}{cc}\boldsymbol{\varPsi }& \mathit{0}\\ \mathit{0}& \boldsymbol{\varPsi }\end{array}\end{array}\right] ; \boldsymbol{m}=\left[\begin{array}{c}{\boldsymbol{R}}_{\mathrm{I}\mathrm{P}}\\ {\boldsymbol{R}}_{\mathrm{I}\mathrm{S}}\end{array}\right] 。$

假设采用均值为0、方差为$ {\sigma }^{2} $的高斯噪声，似然函数为^[23]

$ p\left(\boldsymbol{d}\right|\boldsymbol{m}, {\sigma }^{2}, \theta )={\left(2\mathrm{\pi }{\sigma }^{2}\right)}^{-K\times N}\mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{-{\left(\boldsymbol{d}-\boldsymbol{G}\boldsymbol{m}\right)}^{\mathrm{T}}\left(\boldsymbol{d}-\boldsymbol{G}\boldsymbol{m}\right)}{2{\sigma }^{2}}\right] $

(6)

ARD先验信息为

$ p\left(\boldsymbol{m}\right|\boldsymbol{h})={\left(2\mathrm{\pi }\right)}^{-K}\prod\limits_{k=1}^{2K}{h}_{k}^{\frac{1}{2}}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-{h}_{k}{m}_{k}^{2}}{2}\right) $

(7)

式中h为超参数矩阵，包含2K个独立参数^[24]。根据贝叶斯公式，后验概率为

$ p\left(\boldsymbol{m}\right|\boldsymbol{d}, \boldsymbol{h}, {\sigma }^{2}, \theta )=|\boldsymbol{\varSigma }{|}^{-\frac{1}{2}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{\left(\boldsymbol{m}-\boldsymbol{\mu }\right)}^{\mathrm{T}}{\boldsymbol{\varSigma }}^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu }\right)}{2}\right] $

(8)

式中：$ \boldsymbol{\mu }={\sigma }^{-2}\boldsymbol{\varSigma }{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{d} $；$ \boldsymbol{\varSigma }={\left(\boldsymbol{H}+{\sigma }^{-2}{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{G}\right)}^{-1} $, 其中H为超参数组成的对角矩阵，类似于柯西分布或高斯分布等常用先验约束中的阻尼系数矩阵，每一个超参数的值都对应一个反演时窗内的采样点的反射系数幅值。利用第二型最大似然估计算法可以获得超参数的估计，进而决定参数反射系数的大小，将最终确定的超参数代入$ \boldsymbol{\mu }={\sigma }^{-2}\boldsymbol{\varSigma }{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{d} $，即可获得参数反射系数的估计^{[19-20, 24]}。

从似然函数（式(6)）中可知，超参数在求解过程中与地震数据的残差相关，即该参数会随不同地震道数据的特点自适应变化。同时，每个参数均以自己的分布作为约束，进而实现待估计参数横向特征的保持^{[11, 24]}。获得了参数反射系数的估计后，再通过道积分可获得纵波阻抗和横波阻抗的估计^[22]。

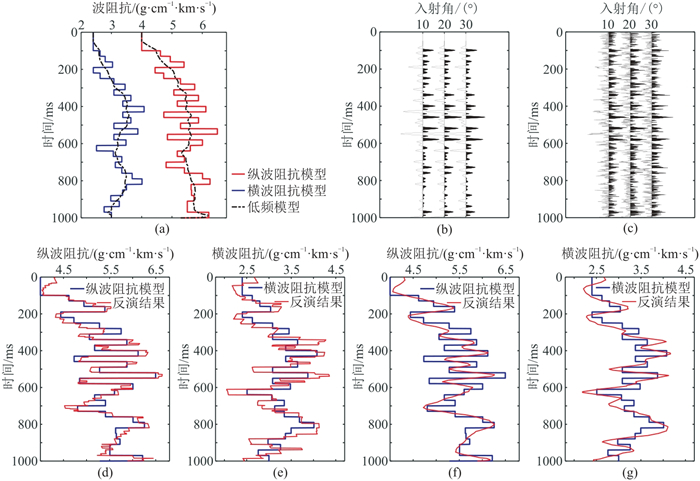
利用模拟数据证实本文方法的可行性。图 1a~图 1c分别展示了模型及合成数据。合成数据采用30 Hz雷克子波和1 ms的采样间隔。从含噪声数据的纵波阻抗（图 1d）、横波阻抗（图 1e）反演结果可以看出，在较低的信噪比情况下，本文反演算法仍然取得了合理的结果。图 1f、图 1g展示了常规高斯先验约束的反演结果。由图可见，高斯先验属于光滑约束，模型边界刻画能力不足；同时，横波阻抗的反演结果更易受到噪声的影响。

2 AVA近似式分析与部分叠加策略分析

可以根据参数灵敏度（不同参数偏导数）分析预期结果，以正演矩阵的条件数分析部分角叠加数据的叠加策略效果，即最小角度、最大角度和角度间隔如何影响反演结果。

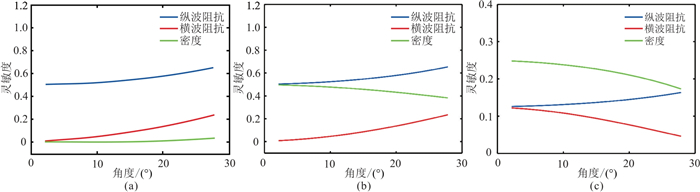
本文选取了常用的三种AVA近似式^{[21, 25-26]}（图 2）的不同参数的敏感性。灵敏度越高表示该参数的变化对反演过程的影响越大，预期反演效果越好。

从图 2a可见，Fatti近似式的第三项（密度）灵敏度较低，符合常理^[21]。同时，纵波阻抗和横波阻抗的第一项和第二项灵敏度随着角度变化的趋势一致性较好，表明上述两参数预期的反演效果相当。

从图 2b可见，Aki & Richards近似式中的密度项比横波速度项具有更高的灵敏度。由于密度项的反演对可利用角度范围要求高，因此不稳定的密度反演结果会对横波速度项产生不利影响。

从图 2c可见，对于Gray近似式而言，每个参数都具有相近的、较低的灵敏度。因此，当需要直接获取拉梅参数避免转换误差时，才可采用该近似式。

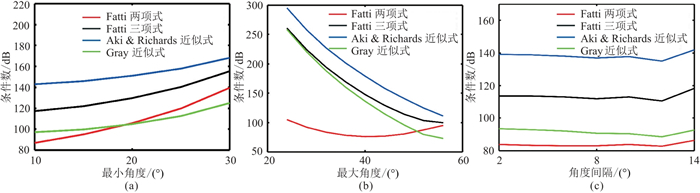
图 3展示了部分叠加策略对反演稳定性的影响。图 3a给出了最小角度对不同近似式的影响，可见各近似式都随着最小角度的变大而变得不稳定，因此在近偏数据质量较好的时候，最小角度越小反演越稳定。由图 3b可见，Fatti两项式由于不考虑密度项，在角度超过37°时稳定性变差，这符合常理。图 3c给出了不同角度间隔的稳定性分析，相对来说，角度间隔在12°左右时，条件数最小，稳定性最好。

3 实际资料应用

川西地区侏罗系浅层河道砂岩储层横向窄，变化快；纵向上多层叠置，垂直厚度为10~40 m。不同河道或同一河道不同部位天然气富集程度差异明显，具有普遍含气、局部富集的特点。近年来，天然气富集“甜点”的准确预测和含气、水储层的区分成为制约勘探的一个难点。

研究区缺乏大的入射角度数据，最大入射角度小于30°，且含气性指示因子为$ \lambda \rho ={{I}_{\mathrm{P}}}^{2}-2\times {{I}_{\mathrm{S}}}^{2} $（$ \lambda $为拉梅系数，$ \rho $为密度，$ {I}_{\mathrm{P}} $为纵波阻抗，$ {I}_{\mathrm{S}} $为横波阻抗），因此选用Fatti近似式。结合最小角度、最大角度和角度间隔的特征（图 3），数据部分叠加策略方案为1°~13°(7°)、13°~25°(19°)和25°~37°(31°)。

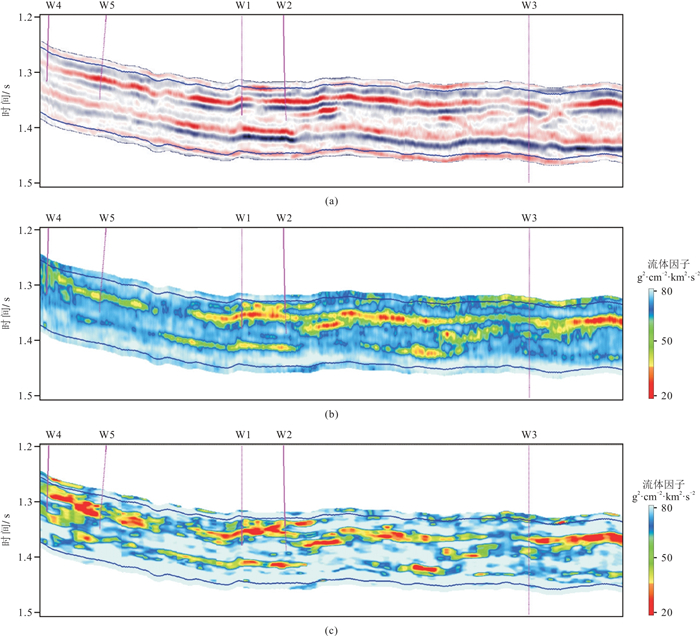
图 4a为一条过5口井（W1~W5井）的地震剖面，各井河道储层的日产气能力相当。图 4b和4c分别为使用传统高斯先验方法和ARD-AVA方法获得的含气性指示因子反演剖面。由图可见，ARD-AVA方法的结果优于传统方法，5口井均钻遇含气储层，而传统方法只有W1井和W2井钻遇含气储层。

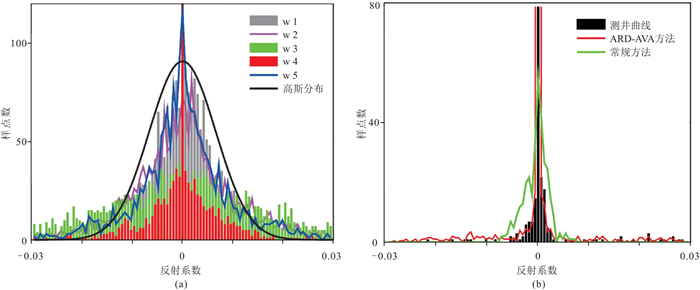
5口井河道储层的纵波阻抗反射系数分布如图 5a所示。由图可见，不同钻井的反射系数分布明显不同。高斯先验约束中的固定参数在反演过程中将模糊这种差异，导致反演结果不够理想。图 5b为常规方法和ARD-AVA方法反演获得的参数反射系数分布，与传统方法相比，可见ARD-AVA方法得到的参数反射系数分布与测井统计结果一致性更好。

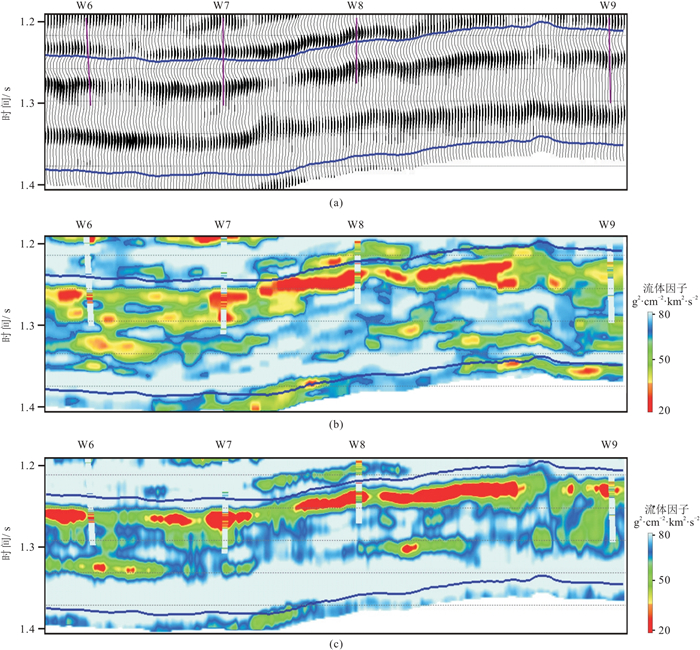
图 6a为过4口井（W6~W9）的地震剖面。测井解释结论认为，4口井均钻遇同一河道储层，但含气性不同。W9井产水，W6、W7、W8井均为高产气井。ARD-AVA方法反演结果（图 6b）很好地展示出了该河道的含气性变化特征，即流体因子小值（红色）表征了“甜点”分布，W6、W7、W8井处于“甜点”区，且含气特征在河道储层内部的变化清晰可见，而W9井处含气特征不明显。但常规技术预测的结果（图 6c）认为4口井均钻遇“甜点”，与实际不符。据此，可知本文方法反演结果更准确。

4 结论

（1）提出了基于ARD-AVA反演的含气性预测方法，并给出了AVA近似式和部分叠加策略方案。该方法用于川西地区侏罗系浅层河道储层的含气性预测，获得了较好的效果。

（2）自适应相关判别先验的引入提高了基于AVA反演技术的含气性预测的横向准确性。

（3）提出的AVA近似式和部分叠加策略将有助于针对性地选择目标参数及叠加策略进行反演。