2. 中海石油(中国)有限公司, 北京 100005;
3. 东方地球物理公司研究院大港分院, 天津 300280
2. China National Offshore Oil Corporation, Beijing 100005, China;
3. GRI Dagang Branch, BGP, CNPC, Tianjin 300280, China
火山岩指高温熔融的岩浆在地下或喷出地表后冷凝而成的岩石[1]。火山岩和火山碎屑岩在各时代地层中都有广泛分布,已陆续发现一些以其为储集层的油气田[2]。
长期以来,火山岩及下伏地层的成像问题一直是火山岩发育区地震资料处理的巨大挑战。火山岩主要在两方面影响地震资料处理:一是受火山岩屏蔽的影响,火山岩下伏地层反射能量弱,噪声淹没了有效信号,难以有效识别地层真实的反射特征;二是火山岩发育区速度的剧烈变化导致地震波场复杂、时间域构造成像畸变,使速度建模和成像极为困难[3]。地球物理工作者针对上述两方面挑战进行了长期探索。黎书琴等[4]通过高精度三维观测系统优化设计和低频检波器的应用,提高了火山岩地区地震数据品质。彭浩天等[5]通过低频补偿和Q偏移技术,以提高火山岩成像质量。韩站一等[6]从Zoeppritz方程出发,分析了火成岩地层中地震波的透射损失,通过模型正演揭示了火成岩非均质性对透射能量的衰减作用,认为火成岩对下伏地层的影响因素除了高速屏蔽外还有介质非均质性导致的散射问题。姜岩等[7]根据广义O'Doherty-Anstey公式,探索了一种利用声波曲线求取透射系数的方法, 以补偿强波阻抗界面对下伏地层反射振幅的影响。张涛等[8-9]根据火山岩特殊的地质特征,利用VSP测井信息为约束条件,解决三维网格层析反演速度建模的多解性问题。郭树祥[10]根据火山岩的波场特征,正演模拟了火山岩地震波场频散以及低通滤波效应。王兴等[11]利用全区的声波测井速度平滑插值得到初始速度模型,以减小火山岩速度误差。梁海龙等[12]基于高密度地震数据,尝试利用Q叠前深度偏移技术提高火山岩地层的成像精度。这些研究成果大多依赖原始资料和钻井资料的品质,在工区钻井资料不足或火山岩空间分布较复杂时,仍然难以有效解决火山岩及下伏地层的成像问题。
本文依托EP地区地震采集资料研究火山岩发育区的成像处理技术。针对长期困扰该地区的火山岩及下伏构造成像瓶颈问题,在火山岩多次波压制、火山岩下弱信号恢复、火山岩速度精细刻画三方面进行了新的探索,有效改善了火山岩及下伏地层成像质量。
1 研究区概况EP地区处于阳江—一统断裂带,资源潜力大,且发育有大量构造圈闭,是油气勘探有利的战略接替区。该地区古近系及上覆地层发育多期火山岩,且形态复杂,明显屏蔽地震信号;火山岩多次波对火山岩下伏地层反射的干扰作用强;同时,不同层系、不同类型火山岩速度差异大。而且,工区位于水深50~90 m的浅海地区,反射波在水层中反复振荡产生极强能量的多次波,掩盖了火山岩下伏地层真实的反射特征。另外,工区地震数据为常规的窄方位拖缆数据,目前仅有的一口探井也未在火山岩区域。
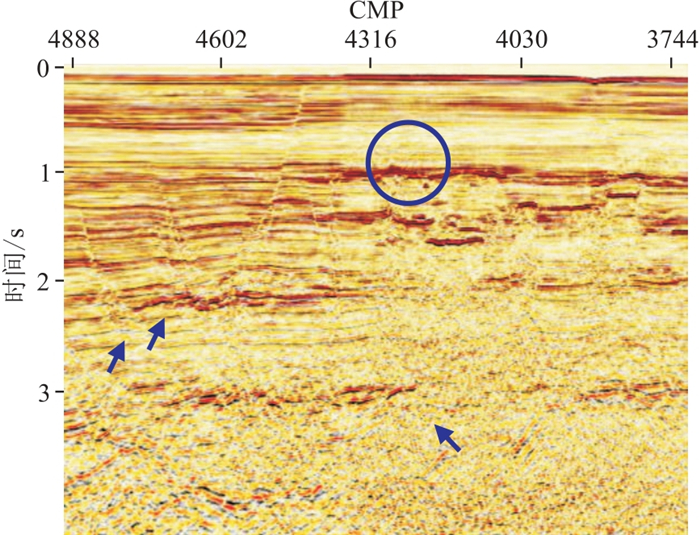
火山岩对地震数据的影响导致该地区地震成像品质差,严重制约了油气勘探、开发工作的进程。图 1为工区以往叠前深度偏移成果的时间域剖面。在750~3000 ms的时间范围内,可见明显的不同层系火山岩强振幅特征,但在蓝色圆圈区域,复杂火山岩体的边界不清楚;在火山岩下,箭头所示位置地层和控洼断裂成像不清楚,导致地层产状难以落实,深部疑似半地堑的凹陷结构难以识别。
|
图 1 EP地区重处理前叠前偏移剖面 |
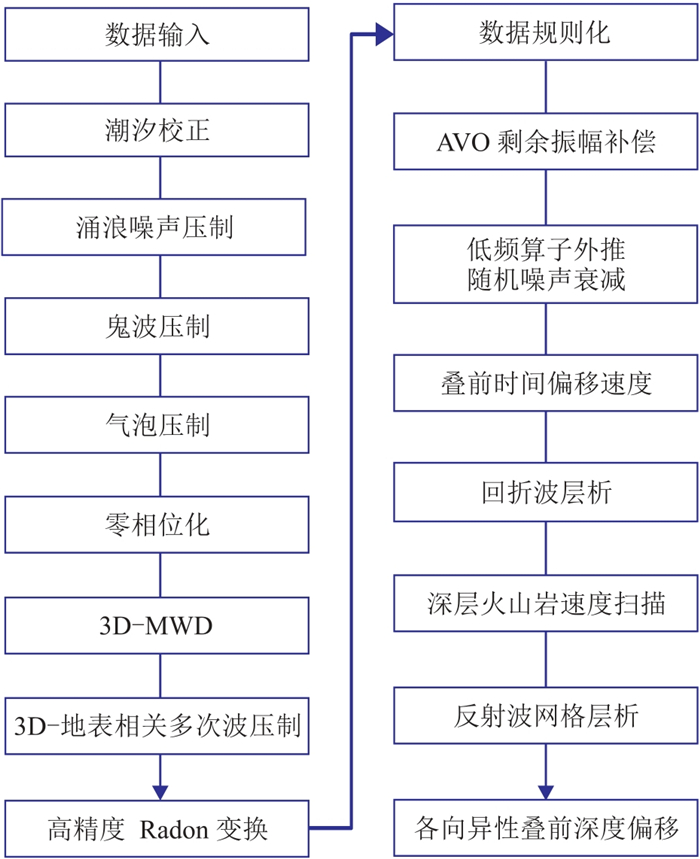
本文在针对拖缆地震数据特点完成涌浪噪声压制等基本的前置处理后,根据EP火山岩发育区的地震资料特点,针对制约地震成像的关键问题,制定了图 2所示的地震成像处理技术方案。首先采用三维MWD(Model based Water-layer related Demultiple)技术提高火山岩微屈多次波预测效果;然后,通过AVO剩余振幅补偿及低频算子外推随机噪声衰减技术合理补偿地震波的透射损失,并提高火山岩下伏地层信噪比;最后,综合应用回折波层析反演和反射波网格层析,精细刻画火山岩导致的速度纵、横向变化,为叠前深度偏移成像奠定了基础。
|
图 2 火山岩发育区地震成像处理技术流程 |
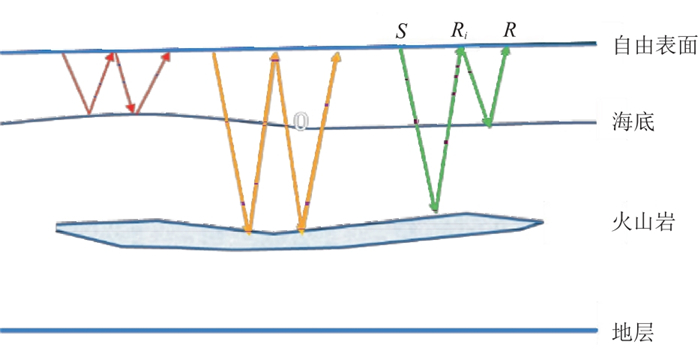
EP地区水深为50~90 m,自由表面(海水面)、海底、火山岩顶是工区最主要的三个强反射界面。与这三个强反射界面对应的三种多次波(图 3):第一种传播路径如红色箭头所示,海底反射波在水层中反复振荡形成海底的水层多次波;第二种为黄色箭头所示的火山岩全程多次波;第三种为绿色箭头所示,火山岩一次反射在海水层反复振荡,形成与火山岩和水层相关的火山岩微屈多次波。其中,火山岩全程多次波由于反射周期长,多次波旅行时大于目的层的一次波旅行时,反射能量大多位于主要目的层以下,对地震成像的影响较小。而且,由于多次波仅与火山岩和海水面相关,与海底反射无关,SRME(Surface Related Multiple Elimination)等自由表面多次波预测技术可以较好地构建多次波模型。而海底的水层多次波和火山岩微屈多次波是一次波在海底与自由表面之间的水层反复振荡产生的多次反射,当海底反射缺失时,SRME等依赖地震数据褶积预测多次波的方法难以发挥作用,需要采用新的方法预测多次波模型。
|
图 3 工区主要多次波类型 S为激发点,R为接收点 |
三种多次波全部和自由表面相关,理论上可以采用SRME等数据驱动的自由表面多次波预测方法预测多次波模型。然而,在水深非常浅的海域,SRME的应用效果往往不理想。首先,海洋拖缆采集的最小炮检距一般在200 m左右,因为缺少近炮检距数据,大部分水底反射信号缺失,接收到的信息主要来自临界角之外的水底反射能量,对较小炮检距的水层多次波没有贡献;其次,由于观测到的一次水底反射被直达波干扰,因而不能正确重构水底一次波[13]。
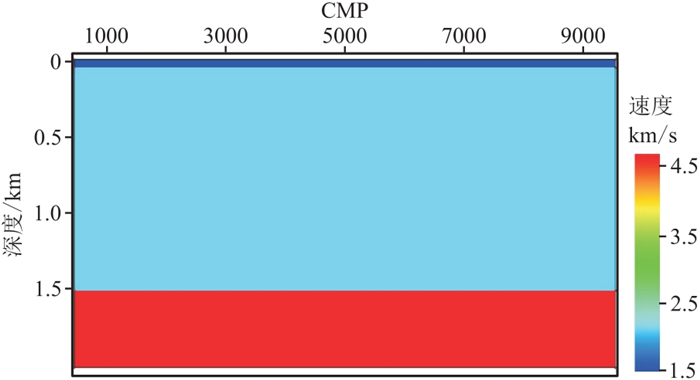
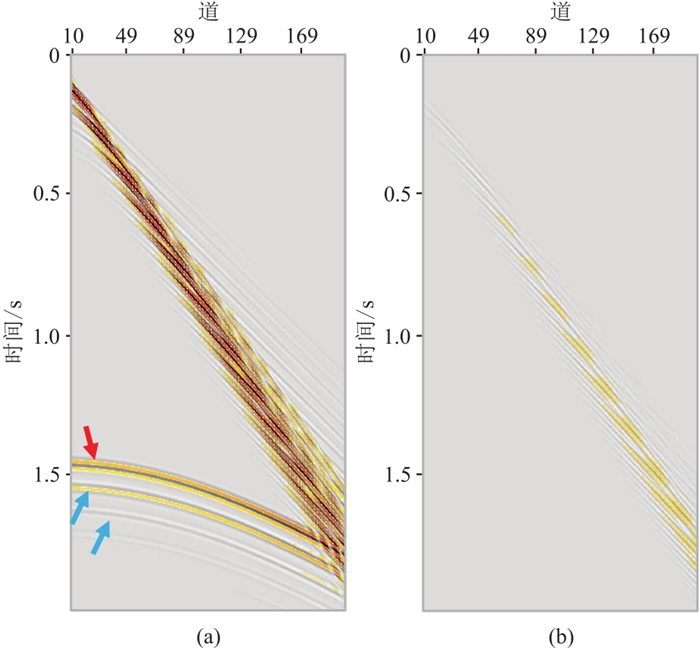
正演记录能够揭示近道水底反射信号缺失对SRME多次波预测的影响。选择一个二维正演模拟观测系统建立多次波正演模型(图 4)。从图 5a的正演记录可以发现,在火山岩一次反射(红色箭头)下,存在明显的火山岩反射在水层反复振荡形成的短周期多次波(蓝色箭头),而海底近道反射信息的缺失严重制约了SRME对火山岩多次波的预测效果(图 5b)。为弥补SRME技术在浅水区多次波预测的不足,本文采用模型驱动的三维MWD多次波预测方法预测火山岩微屈多次波。
|
图 4 多次波正演模型 观测系统的炮间距为20 m,道间距为10 m,最小炮检距为200 m,最大炮检距为2000 m。模型由三层介质组成:第一层为水层,厚度为60 m,地震波速度为1500 m/s;第二层为低速反射层,地震波速度为2000 m/s;地层最大埋深1500 m以下为高速火山岩地层,地震波速度为4500 m/s。 |
|
图 5 多次波正演记录(a)及SRME预测多次波模型(b) |
MWD是一种模型驱动的水层相关多次波预测技术,首先利用已知的海底曲面模型构建海底的格林函数,然后将接收地震记录与格林函数褶积,恢复浅水环境的多次波信息。
理论上,如图 3所示的火山岩微屈多次波S→R可以通过地震数据与水层一次反射的褶积得到[14]
| $ M\left(S, R, \omega \right)=\int D(S, {R}_{i}, \omega )P(R, \omega )\mathrm{d}{R}_{i} $ | (1) |
式中:M是多次波模型;D为地震数据;P为海底一次反射,具有多次波预测算子的作用;
为解决浅水区因海底近道反射缺失导致的多次波预测问题,可以利用海底测深信息计算水层格林函数,用格林函数代替水层的一次反射预测多次波
| $ M(S, R, \omega )=\sum\limits_{\varOmega }{D}_{r}(S, {R}_{i}, \omega )G(R, {R}_{i}, \omega ) $ | (2) |
式中:G为水层的格林函数;Ω为多次波预测孔径。
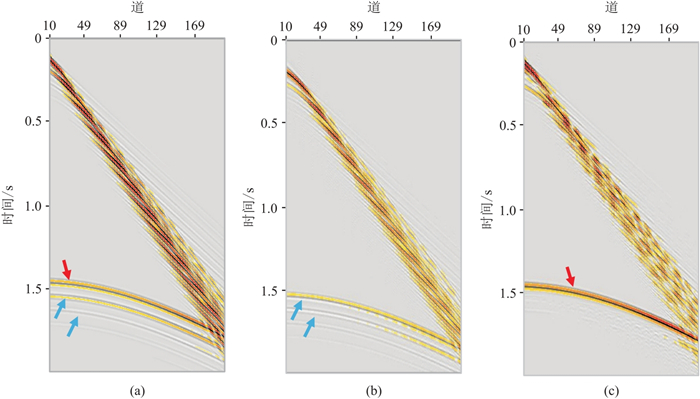
由于利用格林函数代替海底一次反射和地震数据褶积,MWD摆脱了对海底反射的依赖,从而解决了浅水区海底近道反射信息缺失导致的多次波预测问题。图 6的正演记录显示了MWD在浅水区预测多次波的优势。对于最小炮检距为200 m的正演记录(图 6a),MWD获得的火山岩多次波模型(图 6b)和正演记录的多次波(图 6a)反射特征非常相似。
|
图 6 正演记录(a)、MWD多次波模型(b)及去多次波后记录(c) |
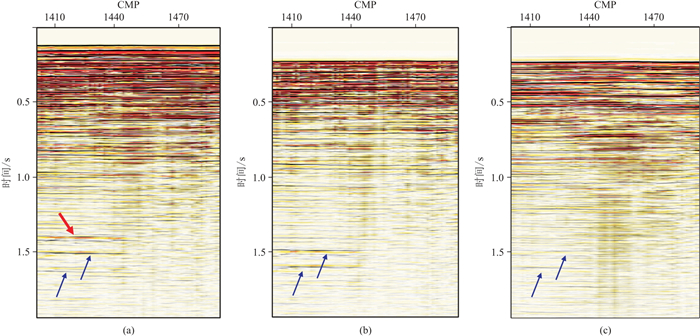
图 7为EP地区SRME与MWD多次波预测获得的多次波模型对比。在原始叠加剖面上(图 7a),红色箭头指示火山岩反射层,蓝色箭头处可见明显的火山岩微屈多次波。MWD预测的火山岩多次波模型(图 7b)较SRME(图 7c)更接近真实的多次波反射特征。
|
图 7 EP地区叠加剖面(a)、MWD多次波模型(b)、SRME多次波模型(c) |
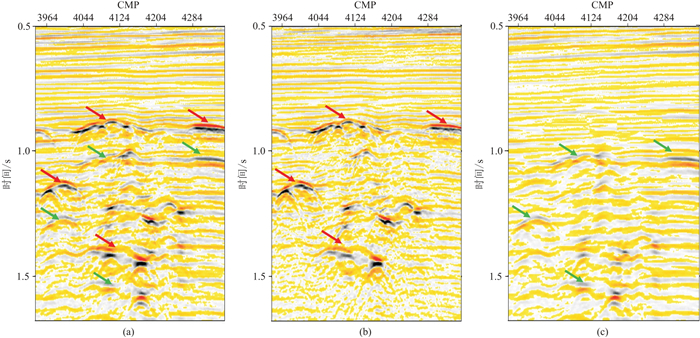
MWD的技术原理决定了其难以预测与水层无关的火山岩全程多次波。由于火山岩全程多次波可以由火山岩一次反射褶积得到,不需要海底反射信息,因此,SRME能够得到较好的多次波模型。根据EP火山岩发育区多次波的特点,本文分别采用MWD和SRME进行多次波预测,然后利用多模型同时自适应相减技术[15],在最小平方意义下完成MWD和SRME多次波模型与地震数据的最佳匹配,并从地震数据中减去多次波数据。图 8为自适应相减前、后的叠加剖面及差剖面。由图可见,自适应相减后,不仅海底及正常反射层的多次波得到有效压制,火山岩的强多次波能量也得到很好的衰减(图 8b)。
|
图 8 EP地区多次波压制前(a)、后(b)的叠加剖面及差值剖面(c) 红色箭头为火山岩一次反射,绿色箭头为火山岩微屈多次波。 |
当地震纵波从一种介质进入相互密接的另一种介质时,会发生地震波的反射和透射。反射和透射系数可以用Zoeoppritz方程表示
| $ \left(\begin{array}{cccc}\mathrm{s}\mathrm{i}\mathrm{n}\alpha & \mathrm{c}\mathrm{o}\mathrm{s}\beta & -\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }^{\mathrm{\text{'}}}& \mathrm{c}\mathrm{o}\mathrm{s}{\beta }^{\mathrm{\text{'}}}\\ \mathrm{c}\mathrm{o}\mathrm{s}\alpha & -\mathrm{s}\mathrm{i}\mathrm{n}\beta & \mathrm{c}\mathrm{o}\mathrm{s}{\alpha }^{\mathrm{\text{'}}}& \mathrm{s}\mathrm{i}\mathrm{n}{\beta }^{\mathrm{\text{'}}}\\ \mathrm{c}\mathrm{o}\mathrm{s}2\beta & -\frac{{v}_{\mathrm{S}1}}{{v}_{\mathrm{P}1}}\mathrm{s}\mathrm{i}\mathrm{n}2\beta & -\frac{{\rho }_{2}{v}_{\mathrm{P}2}}{{\rho }_{1}{v}_{\mathrm{P}1}}\mathrm{c}\mathrm{o}\mathrm{s}2{\beta }^{\mathrm{\text{'}}}& -\frac{{\rho }_{2}{v}_{\mathrm{S}2}}{{\rho }_{1}{v}_{\mathrm{P}1}}\mathrm{s}\mathrm{i}\mathrm{n}2{\beta }^{\mathrm{\text{'}}}\\ \mathrm{s}\mathrm{i}\mathrm{n}2\alpha & \frac{{v}_{\mathrm{P}1}}{{v}_{\mathrm{S}1}}& \frac{{\rho }_{2}{v}_{\mathrm{P}1}{{v}_{\mathrm{S}2}}^{2}}{{\rho }_{1}{v}_{\mathrm{P}2}{{v}_{\mathrm{S}1}}^{2}}\mathrm{c}\mathrm{o}\mathrm{s}2{\alpha }^{\mathrm{\text{'}}}& -\frac{{\rho }_{2}{v}_{\mathrm{P}1}{v}_{\mathrm{S}2}}{{\rho }_{1}{v}_{\mathrm{S}1}}\mathrm{s}\mathrm{i}\mathrm{n}2{\beta }^{\mathrm{\text{'}}}\end{array}\right)\left(\begin{array}{c}{R}_{\mathrm{P}\mathrm{P}}\\ {R}_{\mathrm{P}\mathrm{S}}\\ {T}_{\mathrm{P}\mathrm{P}}\\ {T}_{\mathrm{P}\mathrm{S}}\end{array}\right)=\left(\begin{array}{c}-\mathrm{s}\mathrm{i}\mathrm{n}\alpha \\ \mathrm{c}\mathrm{o}\mathrm{s}\alpha \\ -\mathrm{c}\mathrm{o}\mathrm{s}2\beta \\ \mathrm{s}\mathrm{i}\mathrm{n}2\alpha \end{array}\right) $ | (3) |
式中:α为纵波入射角或反射角;β为P-SV波反射角;
当地震波垂直入射时,即
| $ \left\{\begin{array}{l}({R}_{\mathrm{P}\mathrm{P}}{)}_{0}=\frac{{\rho }_{2}{v}_{\mathrm{P}2}-{\rho }_{1}{v}_{\mathrm{P}1}}{{\rho }_{2}{v}_{\mathrm{P}2}+{\rho }_{1}{v}_{\mathrm{P}1}}\\ ({R}_{\mathrm{P}\mathrm{S}}{)}_{0}=0\\ ({T}_{\mathrm{P}\mathrm{P}}{)}_{0}=\frac{2{\rho }_{1}{v}_{\mathrm{P}1}}{{\rho }_{2}{v}_{\mathrm{P}2}+{\rho }_{1}{v}_{\mathrm{P}1}}\\ ({T}_{\mathrm{P}\mathrm{S}}{)}_{0}=0\end{array}\right. $ | (4) |
从式(4)可知,上覆地层与下伏地层的波阻抗差异越大,反射波能量越强,而透射波能量越小。由于火山岩和围岩在速度、密度上存在明显差异,导致地震波穿过火山岩时透射损失增大,即使前期进行了球面扩散补偿等一系列振幅恢复处理,火山岩下伏地层仍然存在振幅补偿不足的问题。在多次波等噪声得到有效压制后, 通过剩余振幅补偿进一步增强火山岩下弱信号能量,改善地震数据纵、横向能量的一致性是提高地震资料品质的重要一步。
2.2.2 AVO剩余振幅补偿在地震勘探中,地震波是非垂直入射的,理论上求取叠前地震数据的透射损失需要求解式(3)。但由于式(3)涉及的地球物理参数较多,地震资料处理中又难以获得准确的参数信息,因此,透射系数的求取非常困难。剩余振幅补偿是基于统计地震数据补偿地震波能量损失的一种方法,不需要地层反射系数等先验信息。在完成球面扩散补偿等的基础上,通过剩余振幅补偿可以较好补偿透射损失等因素导致的前期振幅恢复不足部分。
AVO剩余振幅补偿是在分时窗统计振幅随炮检距变化的基础上补偿振幅的一种方式,该方法在地震资料处理中分两步实施。
第一步为剩余振幅补偿函数的计算。首先按等间距划分成若干个炮检距组,分别对每个炮检距组沿时间方向滑动时窗,统计全部输入CMP的地震道振幅绝对值,计算叠前数据的AVO剩余振幅补偿函数。
第n个炮检距组、第k个时窗的剩余振幅补偿函数为
| $ {F}_{n}({x}_{n}, k)=\frac{1}{\sum\limits_{m=1}^{M}\left\{\sum\limits_{i=1}^{I}\left[\sum\limits_{j=1}^{J}\left|\frac{{A}_{n}(m, i, j)}{P}\right|\right]\right\}} $ | (5) |
式中:M为输入的总CMP数;I为总地震道数;J为第k个时窗内的总样点数;xn为第n个剩余振幅补偿函数的参考炮检距;An(m, i, j)为第m个CMP、第n个炮检距组、第i道、第k个时窗的第j个样点的地震道振幅值;P为常数。利用式(5)可以计算不同时窗、不同炮检距分组的剩余补偿函数。
第二步为剩余振幅补偿函数的平滑应用。先对计算出的补偿函数沿炮检距组和时间方向进行多点平滑,消除局部异常;然后将补偿函数应用于对应的地震道。
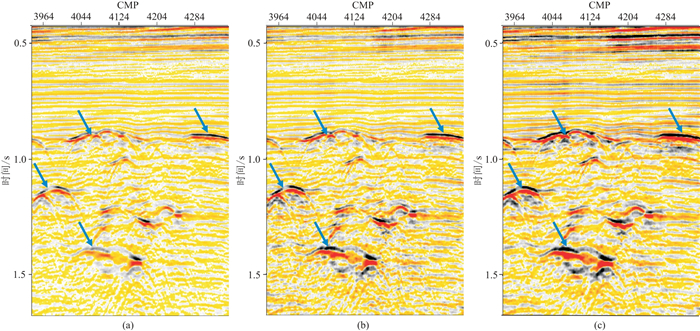
由于AVO剩余振幅补偿在横向上按指定的炮检距分组,纵向上按指定的时窗长度进行振幅统计,最终计算出不同时窗、不同炮检距分组的补偿函数,因此在增加振幅横向一致性的同时,对透射引起的纵向能量损失有一定的补偿作用。从图 9所示剩余振幅补偿前(图 9a)、后(图 9b)叠加剖面可以发现,后者火山岩下的反射信号能量得到进一步补偿,地震数据能量的纵、横向一致性得到进一步改善。
|
图 9 剩余振幅补偿前(a)、后(b)及随机噪声衰减后(c)叠加剖面对比 |
AVO剩余振幅补偿在恢复弱信号振幅的同时,会导致随机噪声能量的同步放大。具有低频算子外推功能的随机噪声衰减技术能够利用低频优势频段预测地震信号,有利于提高火山岩下地震数据的噪声压制效果。
本文采用的低频算子外推随机噪声衰减方法将常规RNA(Randon Noise Attenuation)方法扩展到四维空间,即将三维叠前地震数据视为一个拟四维数据体,四个维度分别为线号、CMP号、CMP内的炮检距、记录时间,沿时间方向进行傅里叶变换后,利用频率—空间域预测理论求取每一个频率成分的预测算子,把预测算子应用于三维叠前地震数据,达到衰减三维叠前随机噪声的目的。另外,该方法具有低频算子外推的功能,其基本技术原理表述为:一组道间时差为Δt1的地震波W1(t),经过傅氏变换后,各道的地震数据可以用一个复数序列表示
| $ {w}_{1}\left(f\right), {w}_{1}\left(f\right){\mathrm{e}}^{-\mathrm{i}2\mathrm{\pi }f\mathrm{\Delta }{t}_{1}}\cdot {w}_{1}\left(f\right){\mathrm{e}}^{-\mathrm{i}2\mathrm{\pi }f2\mathrm{\Delta }{t}_{1}}, \cdots $ | (6) |
预测算子
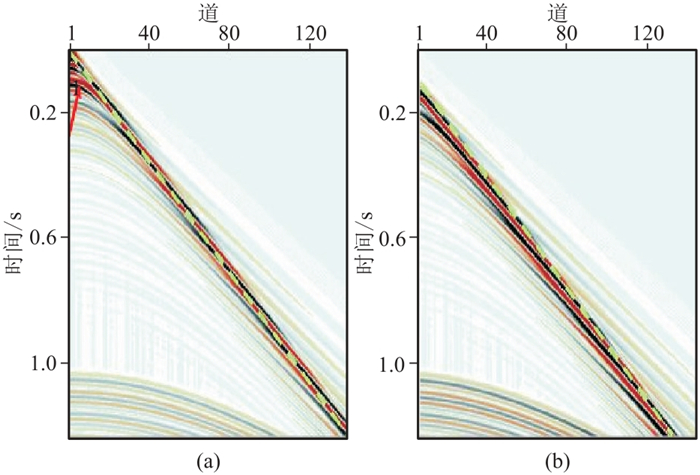
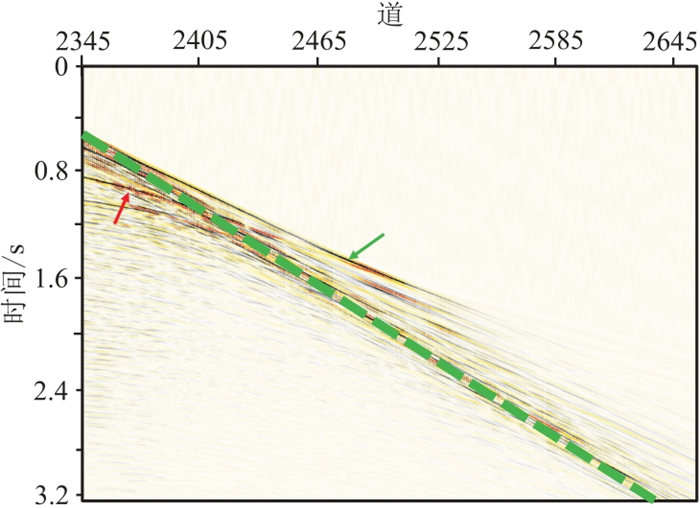
准确的火山岩速度模型是提高火山岩及下伏构造成像质量的必要前提。EP工区位于水深不足100 m的浅水区,地震资料采集的最小炮检距为200 m。图 10所示的正演记录展示了相似地震采集条件下地震数据的波场特征,在最小炮检距为0时,图中红色箭头所示近道位置可见海底双曲线反射;当最小炮检距增大到200 m时,由于出射角超过临界角,海底一次反射无法被检波器所接收,仅在绿线以外区域记录了明显的回折波信息。从图 11所示实际炮集记录上同样可以发现,红色箭头所示浅层火山岩及上覆地层的反射波信息相对不足,而在绿线以外的远炮检距区域,浅部地层的回折波信息丰富,绿色箭头所示的初至波位置可见明显的火山岩高速、强振幅特征。
|
图 10 最小炮检距为0(a)、200 m(b)的正演记录对比 |
|
图 11 EP地区叠前炮集 |
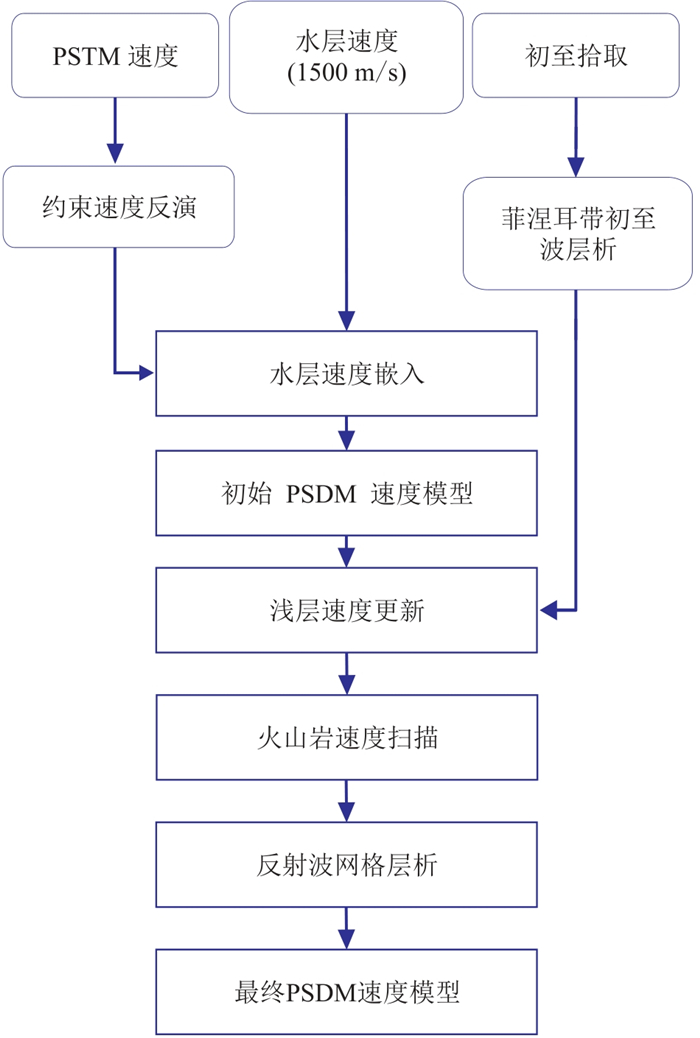
考虑EP火山岩发育区的地震波场特点,采用如图 12所示的技术流程开展叠前深度偏移速度建模。
|
图 12 速度建模流程 |
技术流程划分为三个阶段。
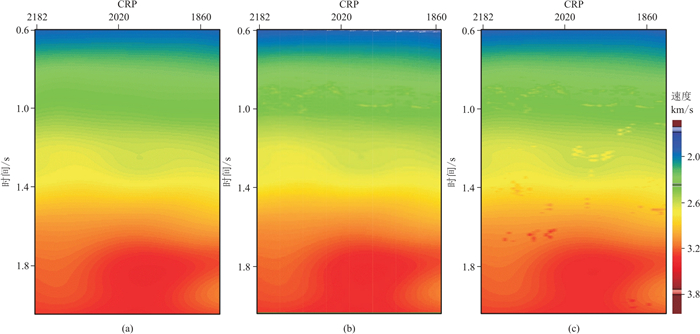
(1) 建立初始PSDM速度模型。用多次波压制、火山岩弱信号恢复处理后的地震数据开展PSTM速度分析,建立PSTM速度模型并通过约束速度反演将其转化为深度域层速度模型;利用海底测深文件将海水层速度嵌入PSTM深度域速度模型中,形成如图 13a所示的初始PSDM速度模型。
|
图 13 初始(a)、初至波层析(b)、反射波层析(c)速度模型对比 |
(2) 浅层速度模型更新。拾取单炮初至后,通过菲涅耳带初至波层析反演,利用中浅层火山岩及上覆地层的走时信息更新浅层速度,形成如图 13b所示的速度模型。
(3) 深层速度模型更新。由于初至波层析反演的有效深度受排列长度限制,而且理论上初至波层析反演也难以准确反演高速层下低速地质体的速度,因此,需要利用反射波层析反演进一步优化浅层火山岩以下深部地层的速度。首先通过速度扫描确定深层火山岩相对准确的速度范围,更新火山岩速度,减小火山岩的速度误差;然后利用反射波网格层析,精确刻画深部火山岩及火山岩下伏地层的速度变化,形成如图 13c所示的最终叠前深度偏移速度模型。
2.3.2 初至波层析速度建模和传统的基于最小走时的初至波层析相比,本文采用的初至波层析技术是一种基于菲涅耳带初至波走时运算的网格层析技术。
由于地震波是有限带宽的,地震波主要能量不只沿着最小走时路径传播,也在包含最小走时路径的第一菲涅耳带内传播。检波器接收到的初至波是第一菲涅耳带内介质的综合效应。
对于EP地区而言,由于一条菲涅耳带覆盖的网格数远大于一条最小走时射线,菲涅耳带射线形成的射线密度远大于最小走时射线。因此,一些由于火山岩等速度异常体引起的射线阴影区,在菲涅耳射线下可能不复存在,有助于提高浅层速度模型的精度。
2.3.3 反射波网格层析速度建模反射波网格层析技术的有效反演深度不受排列长度限制,能够有效提高深层速度模型的精度。同时,可以自动拾取地震反射倾角和反射同相轴,对反演过程进行约束,减少网格层析速度的多解性[6]。层析方程可简单表示为
| $ \boldsymbol{D}\mathrm{\Delta }\boldsymbol{S}=\mathrm{\Delta }\boldsymbol{t} $ | (7) |
式中:D为给定反演网格的射线追踪矩阵;ΔS为慢度误差矩阵;Δt为剩余残差。实际地震资料处理中首先拾取全局剩余延迟,建立剩余旅行时残差矩阵,然后通过最小平方算法求解最终剩余速度。
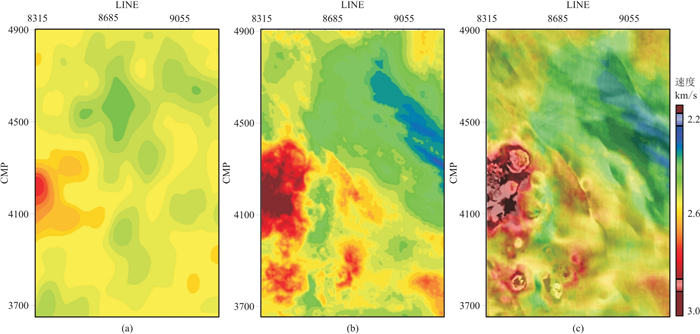
初至波和反射波层析联合应用的速度建模方案充分利用了火山岩发育区的地震波场信息,提高了速度精度和速度模型准确性。图 14为速度模型切片对比,在最终速度模型上,速度的空间变化与构造的空间展布吻合较好,火山岩的高速异常也被精确刻画(图 14c)。
|
图 14 初始速度模型切片(a)、最终速度模型切片(b)、最终速度与叠前偏移切片叠合(c)显示 |
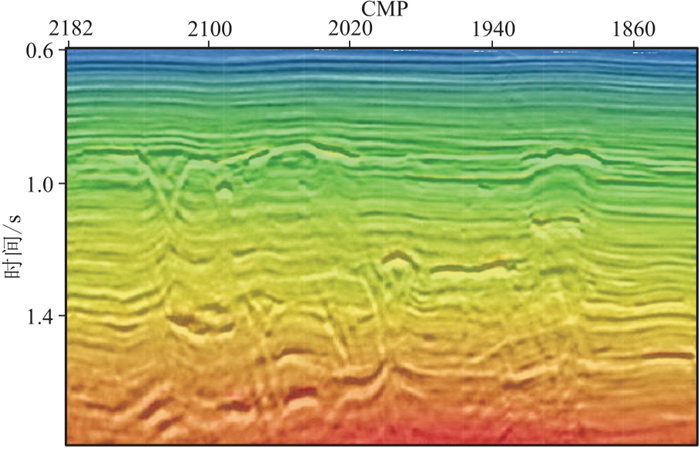
图 15是最终速度模型与偏移剖面的叠合显示,速度模型由浅至深与构造及火山岩分布吻合较好。高精度的速度模型为改善火山岩及下伏构造成像质量奠定了基础。
|
图 15 速度模型与偏移剖面叠合显示 |
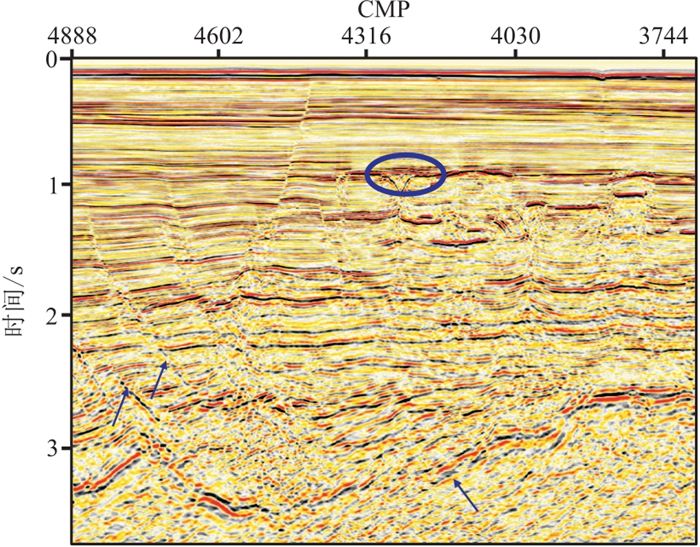
本文围绕EP地区火山岩及下伏地层的成像问题,在工区以往叠前深度偏移处理方案的基础上针对性地优化了成像处理技术。首先通过MWD技术有效提高了火山岩多次波的压制效果,克服了以往处理方案单纯依赖SRME存在的问题;其次,在流程中增加了AVO剩余振幅补偿和低频算子外推随机噪声压制处理,有效补偿了火山岩下伏地层反射信号的能量,提高了地震数据信噪比;最后,通过初至波和反射波层析技术的联合应用,克服了以往单纯依赖反射波层析进行速度建模的不足,综合利用回折波和反射波信息有效提高了火山岩发育区速度模型精度,叠前深度偏移成像质量有了显著改善。图 16是本次PSDM重处理成果的时间域剖面,和图 1相比,在火山岩反射层以下,控洼断裂成像更清晰,断面干脆,复式半地堑结构更容易被识别,洼陷内波组特征清楚,小、微断裂成像有一定程度改善;受火山岩屏蔽的地层成像得到较好恢复;基于重处理资料可以相对更准确地落实火山岩下构造形态及规模。
|
图 16 重处理后叠前偏移剖面 |
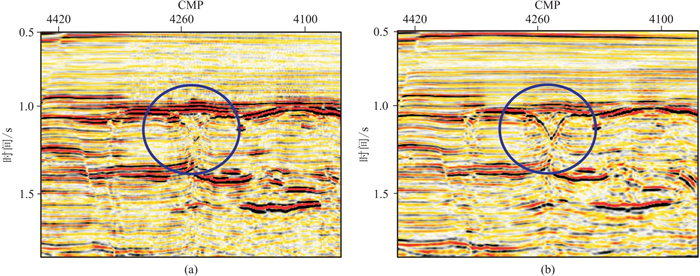
图 17是重处理前、后偏移成果的局部放大显示,在蓝色椭圆所示位置,火山岩体的边界成像有了明显改善(圆圈所示),有利于准确落实火山岩及正常沉积地层的分布范围,降低了勘探、开发风险。
|
图 17 重处理前(a)、后(b)叠前偏移剖面 |
本文采用多次波压制、信号恢复等一系列技术重新处理了EP地区火山岩发育区的地震资料,得出以下结论。
(1) 在浅水火山岩发育区,由于海底反射的缺失,SRME等数据驱动的多次波预测技术难以预测火山岩微屈多次波。MWD是一种以海底测深为先验信息的模型驱动的多次波预测技术,在浅水火山岩微屈多次波以及其他与水层相关多次波的预测方面更具优势。
(2) 在测井资料不足的情况下,基于振幅统计的AVO剩余振幅补偿技术是补偿火山岩下伏地层反射能量不足的一种适用方法;在恢复弱振幅的基础上,应用具有低频算子外推功能的随机噪声衰减技术,可以进一步压制火山岩下伏地层的随机噪声,提高资料信噪比。
(3) 浅水火山岩发育区回折波发育,初至波层析可以较准确地刻画浅层火山岩速度变化;以准确的浅层速度模型为基础,进一步开展反射波网格层析迭代,能够明显提高整体速度模型的准确性和模型精度,为获得高品质的叠前深度偏移成果奠定基础。
| [1] |
徐夕生, 邱检生. 火成岩岩石学[M]. 北京: 科学出版社, 2010. XU Xisheng, QIU Jiansheng. Igneous Petrology[M]. Beijing: Science Press, 2010. |
| [2] |
赵澄林, 朱筱敏. 沉积岩石学[M]. 北京: 石油工业出版社, 2001. ZHAO Chenglin, ZHU Xiaomin. Sedimentary Petrology[M]. Beijing: Petroleum Iindustry Press, 2001. |
| [3] |
熊翥. 复杂地区地震数据处理思路[M]. 北京: 石油工业出版社, 2002. XIONG Zhu. Processing Ideas for Seismic Data in Complex Areas[M]. Beijing: Petroleum Industry Press, 2002. |
| [4] |
黎书琴, 王晓阳, 张孟, 等. 川西地区二叠系火山岩地震采集关键技术应用及效果[J]. 石油地球物理勘探, 2022, 57(1): 62-73. LI Shuqin, WANG Xiaoyang, ZHANG Meng, et al. Application and effect of key seismic acquisition technologies for permian volcanic rocks in western Sichuan basin[J]. Oil Geophysical Prospecting, 2022, 57(1): 62-73. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.007 |
| [5] |
彭浩天, 冉崎, 陈康, 等. GeoEast系统在四川盆地JY地区二叠系火山岩地震资料处理中的应用[J]. 石油地球物理勘探, 2022, 57(增刊1): 6-15. PENG Haotian, RAN Qi, CHEN Kang, et al. Application of GeoEast system in seismic data processing of Permian volcanic rocks in JY area of Sichuan Basin[J]. Oil Geophysical Prospecting, 2022, 57(S1): 6-15. DOI:10.13810/j.cnki.issn.1000-7210.2022.S1.002 |
| [6] |
韩站一, 尚新民, 孙成禹, 等. 火成岩下伏地层地震反射波场特征研究[J]. 石油物探, 2009, 48(3): 226-231. HAN Zhanyi, SHANG Xinmin, SUN Chengyu, et al. Study on seismic reflection wave field characteristics of formations below igneous rock[J]. Geophysical Prospecting for Petroleum, 2009, 48(3): 226-231. |
| [7] |
姜岩, 李文艳, 徐仲达, 等. 地震传播的透射损失补偿方法及正演模拟分析[J]. 大庆石油地质与开发, 2007(3): 132-134. JIANG Yan, LI Wenyan, XU Zhongda, et al. Transmission dissipation method and forward simulation analysis of seismic propagation[J]. Petroleum Geology & Oilfield Development in Daqing, 2007(3): 132-134. |
| [8] |
张涛, 王小卫, 田彦灿, 等. 火成岩速度—深度模型建立方法研究[J]. 石油地球物理勘探, 2015, 50(3): 431-435. ZHANG Tao, WANG Xiaowei, TIAN Yancan, et al. Igneous velocity-depth model building[J]. Oil Geophysical Prospecting, 2015, 50(3): 431-435. DOI:10.13810/j.cnki.issn.1000-7210.2015.03.007 |
| [9] |
张涛, 王小卫, 王孝, 等. 特殊岩性体的速度—深度建模方法[J]. 石油地球物理勘探, 2020, 55(增刊1): 49-55. ZHANG Tao, WANG Xiaowei, WANG Xiao, et al. The velocity-depth modeling method of special litho-logic bodies[J]. Oil Geophysical Prospecting, 2020, 55(S1): 49-55. DOI:10.13810/j.cnki.issn.1000-7210.2020.S.008 |
| [10] |
郭树祥. 火山岩发育区地震处理技术及需求分析——以胜利油田济阳拗陷探区为例[J]. 石油地球物理勘探, 2013, 48(2): 228-238. GUO Shuxiang. Processing technology of seismic data acquired in igneous rock area: example of Jiyang depression in Shengli oilfiled[J]. Oil Geophysical Prospecting, 2013, 48(2): 228-238. DOI:10.13810/j.cnki.issn.1000-7210.2013.02.019 |
| [11] |
王兴, 曾同生, 宋雅莹, 等. 滴西火山岩区地震成像关键技术[J]. 石油地球物理勘探, 2017, 52(增刊1): 47-54. WANG Xing, ZENG Tongsheng, SONG Yaying, et al. Key techniques for volcanic reservoir imaging in the Dixi area[J]. Oil Geophysical Prospecting, 2017, 52(S1): 47-54. DOI:10.13810/j.cnki.issn.1000-7210.2017.S1.008 |
| [12] |
梁海龙, 陈志德. 利用高密度地震技术精细刻画叠置火山岩[J]. 石油地球物理勘探, 2021, 56(4): 833-844. LIANG Hailong, CHEN Zhide. Depiction of superimposed volcanic edifices in detail by high-density seismic technique[J]. Oil Geophysical Prospecting, 2021, 56(4): 833-844. DOI:10.13810/j.cnki.issn.1000-7210.2021.04.017 |
| [13] |
弗斯丘尔著; 陈浩林, 张保庆, 等译. 地震多次波去除技术的过去、现在和未来[M]. 北京: 石油工业出版社, 2010.
|
| [14] |
SUN W, WANG H. Model-based water-layer-related demultiple with sparse constraints[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 4152-4156.
|
| [15] |
BARNES S R, HEGGE R F. Improved shallow water demultiple with 3D multi-model subtraction[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 4460-4464.
|



 张卫卫,广东省深圳市南山区后海滨路(深圳湾段)3168号中海石油(中国)有限公司深圳分公司南海东部石油研究院,518000。Email:
张卫卫,广东省深圳市南山区后海滨路(深圳湾段)3168号中海石油(中国)有限公司深圳分公司南海东部石油研究院,518000。Email: