2. 海洋地质国家重点实验室, 上海 200092
2. State Key Laboratory of Marine Geology, Shanghai 200092, China
海洋油气勘探开发主要包括浅海(水深小于500 m)、深水(水深超过500 m)和超深水(水深大于1500 m)三大领域,其中深水、超深水油气约占海洋油气资源总量的2/5[1]。为了满足全球能源市场的需求,在油气地质理论和勘探开发技术的推动下,深水—超深水区域已经成为油气勘探开发的重点领域[2]。中国海域总面积约3×106 km2,平均水深约为1210 m,最深可达5567 m[1]。深水沉积盆地主要分布在南海传统疆域和东海冲绳海槽,油气勘探开发集中在南海北部,其他深水海域仅实施了初步的地质调查和地震勘探。
中国南海深水—超深水油气勘探程度低、钻井数量少、勘探风险非常高,高效勘探与经济开发须充分发挥地球物理资料尤其是地震数据的作用。受海面、崎岖海底、海洋动力环境以及地下复杂地质构造的综合影响,许多探区目的层地震资料品质较低,常规数据处理方法对深部沉积层和基底的成像质量较差[3]。近年来,利用宽方位拖缆、富低频震源和海底多分量等新型采集技术,实现大孔径照明、高次数覆盖和宽频带信号的采集,对压制鬼波和表面多次波、改善潜山内幕与断层阴影区成像起到了一定效果[4-5]。数十年勘探实践表明大部分探区深层介质复杂,发育多期、多向断层或微断裂系统[5]。在超深水条件下的地震成像难以达到深层复杂油气圈闭精准定位与精细描述的要求,原因在于地震波在巨厚海水层中的传播时间长、能量衰减快,有限炮检距观测的折射波和回转波等大角度信号穿透深度小,崎岖海底及其下伏地层速度的剧烈变化使有效波和干扰波的运动学、动力学特征复杂化。巨厚水层不仅大幅增加旅行时计算或波场延拓的成本,而且降低了速度分析的精度,不利于全波形反演(FWI)、逆时偏移(RTM)等建模和成像技术的应用。
超深水区地震成像亟需新型数据处理技术。对于拖缆地震数据而言,消除巨厚水层影响对深度域速度建模非常重要。在起伏海底情况下,简单时移静校正无法准确消除地震波随炮检距变化的异常时差。Berryhill[6]提出用波动方程的Kirchhoff积分解,实施针对海水层的基准面延拓,改善了有效信号的品质;杨锴等[7]采用有限差分单程波传播算子实现起伏面观测数据的基准面校正,提高了速度分析和深度偏移精度;金丹等[8]、王祥春等[9]先后将Kirchhoff基准面延拓用于提高南海浅水、深水区的叠加速度精度;Arnulf等[10]将基准面延拓与射线旅行时层析相结合,提升了拖缆地震数据的洋壳速度建模能力。
相较于射线旅行时层析,基于波动方程的FWI具有高分辨率建模优势。然而,常规拖缆地震数据一般缺少有效的低频(小于3 Hz)信号,有限的炮检距也很难采集到穿透深层的回转波、折射波等大角度信号,致使经典FWI的有效建模深度仅有最大炮检距的1/3左右[11-12]。为此,只能改造FWI方法以强化其反射层析功能[13],或者发展反射旅行时—波形反演(RTI-RWI)方法,以便有效地捕捉速度结构的长波长和中波长分量[14-18]。在超深水条件下,巨厚水层严重加大了顺时波场和逆时波场模拟的计算负担,给基于波动方程的FWI、反射旅行时反演(RTI)、反射波形反演(RWI)以及RTM等先进技术的大规模应用带来挑战。为此,本文借鉴前人的研究,提出基准面延拓驱动的反射波形反演技术,目的是尽可能降低巨厚水层的影响,减小数据规模和压缩模型空间,使超深水区高效、高精度速度建模和成像的计算成为可能。文中首先简要回顾波动方程基准面延拓和反射波形反演的方法原理,然后建立基准面延拓驱动的反射波形反演、成像的技术流程,最后通过数值试验考察其有效性。
1 波动方程基准面延拓针对超深水区拖缆地震数据,可利用波场延拓克服巨厚水层的影响。当海底高程变化不太剧烈时,基准面可设在水层接近海底的某个深度。根据相对恒定的水层波速构建高精度的基准面延拓算子,进而消除地震波在上覆水层中的传播效应(图 1)。
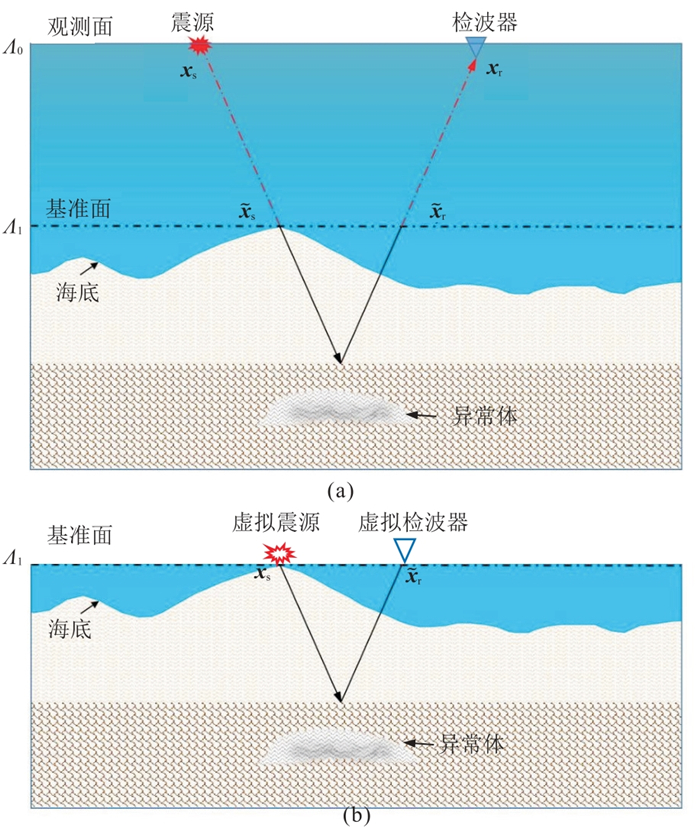
|
图 1 海洋拖揽地震数据基准面延拓示意图 (a)实际观测;(b)虚拟观测 |
基准面延拓需建立实际观测数据
| $ d=W{d}_{\mathrm{v}} $ | (1) |
式中:
| $ \begin{array}{l}d\left({\boldsymbol{x}}_{\mathrm{s}}, {\boldsymbol{x}}_{\mathrm{r}};\omega \right)={\int }_{{\varLambda }_{1}}{\int }_{{\varLambda }_{1}}{G}^{-}\left({\boldsymbol{x}}_{\mathrm{r}}, {\tilde{\boldsymbol{x}}}_{\mathrm{r}};\omega \right)\times \\ \begin{array}{cc}& \end{array}{d}_{\mathrm{v}}\left({\tilde{\boldsymbol{x}}}_{\mathrm{r}}, {\tilde{\boldsymbol{x}}}_{\mathrm{s}};\omega \right){G}^{+}\left({\tilde{\boldsymbol{x}}}_{\mathrm{s}}, {\boldsymbol{x}}_{\mathrm{s}};\omega \right)\mathrm{d}{\tilde{\boldsymbol{x}}}_{\mathrm{r}}\mathrm{d}{\tilde{\boldsymbol{x}}}_{\mathrm{s}}\end{array} $ | (2) |
式中:
从理论上讲,通过对观测数据施加上覆介质传播算子的逆运算才能求取虚拟观测数据。对于实际反射地震数据,为了避免对大型传播矩阵的求逆计算,通常采用W的伴随算子近似逆算子,即
| $ \begin{array}{l}{d}_{\mathrm{v}}\left({\tilde{\boldsymbol{x}}}_{\mathrm{r}}, {\tilde{\boldsymbol{x}}}_{\mathrm{s}}\right)={\int }_{{\varLambda }_{0}}{\int }_{{\varLambda }_{0}}{\left[{G}^{+}\left({\tilde{\boldsymbol{x}}}_{\mathrm{s}}, {\boldsymbol{x}}_{\mathrm{s}};\omega \right)I\left(\omega \right)\right]}^{\mathrm{*}}\times \\ \begin{array}{cc}& \end{array}\left[{G}^{-\mathrm{*}}\left({\tilde{\boldsymbol{x}}}_{\mathrm{r}}, {\boldsymbol{x}}_{\mathrm{r}};\omega \right)d\left({\boldsymbol{x}}_{\mathrm{r}}, {\boldsymbol{x}}_{\mathrm{s}};\omega \right)\right]\mathrm{d}{\boldsymbol{x}}_{\mathrm{s}}\mathrm{d}{\boldsymbol{x}}_{\mathrm{r}}\end{array} $ | (3) |
式中:
在水层中传播的格林函数(场)对应单位脉冲源情况下标量声波方程的解。假定海水的密度相对均匀,且水速为c,则从水中任意一点x到另外一点
| $ G\left(\tilde{\boldsymbol{x}}, \boldsymbol{x};\omega \right)=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{\mathrm{i}\omega \left|\tilde{\boldsymbol{x}}-\boldsymbol{x}\right|}{c}\right]}{4\mathrm{\pi }{\left|\tilde{\boldsymbol{x}}-\boldsymbol{x}\right|}^{2}} $ | (4) |
格林函数伴随算子与逆算子的运动学特征是一致的,二者在动力学上的偏差源于对几何扩散的处理方法不同,逆算子需进行与传播距离相关的振幅补偿,而伴随算子仍然是按几何扩散衰减振幅的。在相对均匀的水层中,伴随算子振幅随炮检距变化的相对关系与逆算子是一致的,反射波形反演只需要振幅相对关系正确即可,因此可以用伴随算子代替逆算子进行后续的反射波走时与波形反演进行速度建模。当然,若要修正水层中伴随格林函数的振幅,将式(4)的振幅因子
就拖缆地震数据而言,在其有限的炮检距范围内观测不到穿透较深的回转波与折射波,深层速度建模只能依靠反射波或背向散射波信号。以地震波长为参照,地下介质非均匀的波速结构可分解到不同尺度,其中长波长和中波长部分构成光滑的“宏观速度模型”,短波长部分构成震荡的“扰动速度模型”或“反射率模型”。深度域层速度建模主要依靠基于共成像点道集剩余时差的反射旅行时层析,而扰动速度或反射率模型通常由真振幅偏移或最小平方偏移获得。为了提升深层速度建模能力,本文选择波动方程RWI方法。经典RWI由嵌套在一起的两个“子反演”交替求解宏观速度和扰动速度。程玖兵等[20]详细给出了这两个“子反演”的泛函梯度与海森算子,揭示了基于海森算子的二阶优化方法在提高模型分辨率与反演收敛性方面的优势。已有大量文献讨论如何由真振幅偏移[21]或最小平方逆时偏移(LSRTM)[22-24]构建扰动速度模型或反射率图像。本文只介绍宏观速度的局部优化反演方法。
采用频率域的常密度声波方程描述标量纵波的传播过程,即
| $ L\left(\boldsymbol{x}, \omega \right)u\left(\boldsymbol{x}, \omega \right)=f\left({\boldsymbol{x}}_{\mathrm{s}}, \omega \right) $ | (5) |
式中:
| $ \left\{\begin{array}{l}{L}_{0}\left(\boldsymbol{x}, \omega \right){u}_{0}\left(\boldsymbol{x}, \omega \right)=f\left({\boldsymbol{x}}_{\mathrm{s}}, \omega \right)\\ {L}_{0}\left(\boldsymbol{x}, \omega \right){u}_{1}\left(\boldsymbol{x}, \omega \right)={\omega }^{2}{M}_{1}\left(\boldsymbol{x}\right){u}_{0}\left(\boldsymbol{x}, \omega \right)\end{array}\right. $ | (6) |
式中:
假定
| $ {\boldsymbol{m}}_{0}^{\mathrm{*}}=\mathrm{a}\mathrm{r}\mathrm{g}\,\mathrm{m}\mathrm{i}\mathrm{n}\;C\left({\boldsymbol{m}}_{0}\right)=\frac{1}{2}{‖S{u}_{1}-d‖}_{2}^{2} $ | (7) |
式中:
| $ {\boldsymbol{m}}_{0}^{\left(i+1\right)}\approx {\boldsymbol{m}}_{0}^{\left(i\right)}+{\beta }^{\left(i\right)}\mathrm{\Delta }{\boldsymbol{m}}_{0}^{\left(i\right)} $ | (8) |
式中
| $ \mathrm{\Delta }{{\boldsymbol{m}}_{0}}^{(i+1)}=-\epsilon \boldsymbol{g}+\mathrm{\Delta }{{\boldsymbol{m}}_{0}}^{\left(i\right)} $ | (9) |
式中ε为预条件因子[25]。由伴随状态法[18]可导出泛函梯度
| $ \boldsymbol{g}=\mathfrak{R}\left[{\omega }^{2}\left({\boldsymbol{U}}_{0}^{†}{\widehat{u}}_{1}+{\boldsymbol{U}}_{1}^{†}{\widehat{u}}_{0}\right)\right] $ | (10) |
式中:
| $ \left\{\begin{array}{l}{L}_{0}^{†}\left(\boldsymbol{x}, \omega \right){\widehat{u}}_{0}\left(\boldsymbol{x}, \omega \right)=-{S}^{†}\mathrm{\Delta }d\left({\boldsymbol{x}}_{\mathrm{r}}, \omega \right)\\ {L}_{0}^{†}\left(\boldsymbol{x}, \omega \right){\widehat{u}}_{1}\left(\boldsymbol{x}, \omega \right)={\omega }^{2}{M}_{1}\left(\boldsymbol{x}\right){\widehat{u}}_{0}\left(\boldsymbol{x}, \omega \right)\end{array}\right. $ | (11) |
式中
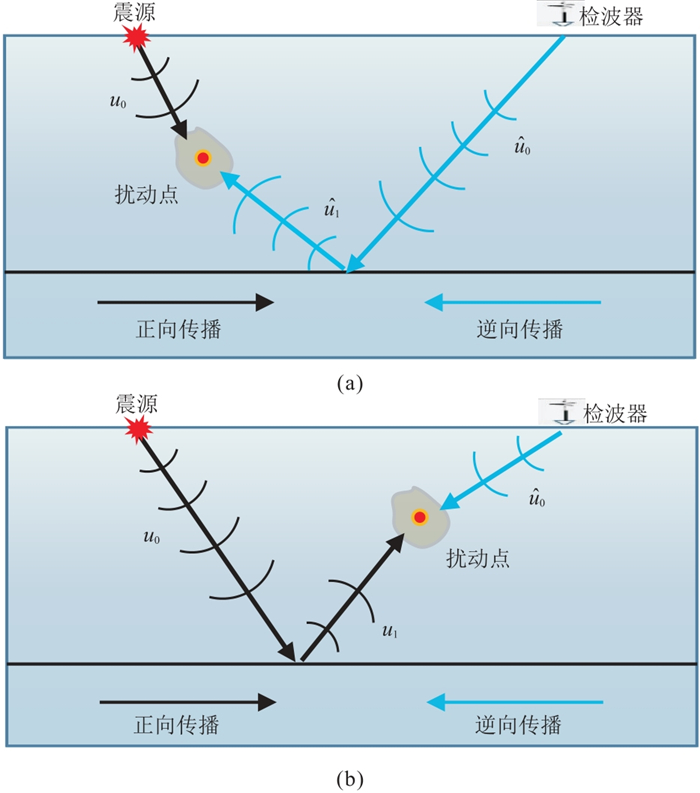
|
图 2 源端(a)和接收端(b)反射波形反演泛函梯度计算涉及的波场示意图 |
当初始速度模型精度不够时,波形反演易受“周波跳跃”问题困扰。为了降低对初始模型的依赖,在模型更新初始阶段一般用旅行时残差代替波形残差[16]。针对任一炮集,采用局部互相关算法估计反射旅行时残差,然后将其用于修正式(11)中的伴随源[26]。从上述理论推导可知,RTI-RWI与LSRTM嵌套的反演算法都是基于Born近似,都只能利用小于临界角的反射或背向散射信号。因此,输入的叠前地震数据需提前切除直达波、折射波以及过临界反射波信号。
3 基准面延拓驱动的速度建模与偏移成像波动方程反射波形反演迭代过程中最耗时的是计算泛函梯度,需利用式(6)描述的Born模拟获得从震源正向传播的入射场与散射场,以及由式(11)模拟从观测面注入伴随源后逆时传播的伴随入射场和散射场。为了避免在巨厚水层中的波场延拓消耗大量计算资源并降低超深水区速度建模的精度,本文提出了基准面延拓驱动的RWI建模和RTM成像技术流程(图 3)。首先,由基准面延拓将实际拖缆观测数据“沉降”到海底附近的基准面,获得规模大幅缩小的虚拟观测数据;其次,籍此逐级重构速度模型的长波长与中波长分量,有效构建宏观速度模型;最后,由RTM完成地质构造高精度成像。
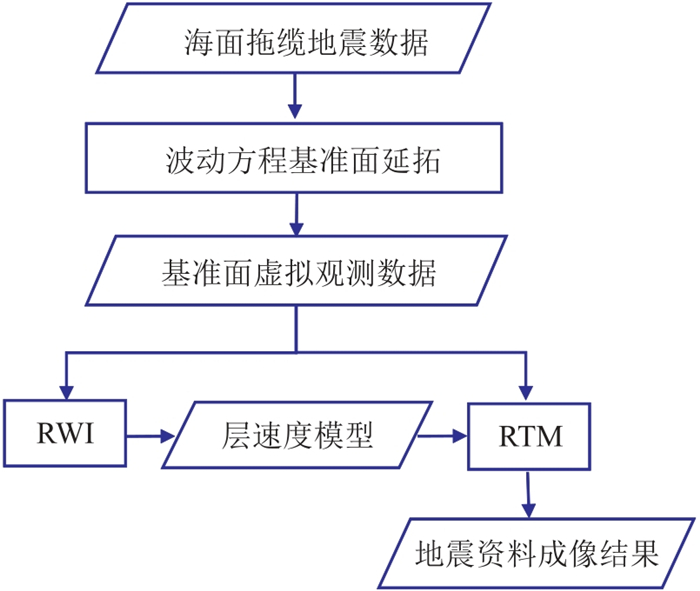
|
图 3 基准面延拓驱动的速度建模与偏移成像技术流程 |
为了保证RWI建模过程的稳定性,本文采用多尺度策略。首先,基于当前已知的宏观速度模型利用小炮检距数据的LSRTM估计扰动速度模型;然后,由基于共轭梯度优化算法的RWI更新宏观速度模型。以上过程交替进行,直到RWI波形残差下降趋于稳定。在模型更新的初始阶段采用旅行时匹配准则,主要更新速度模型的长波长成分。当旅行时残差下降趋于稳定后,切换为波形匹配准则, 进一步更新速度模型的中波长成分。随着炮检距增大,反射波数据对宏观速度模型的误差更敏感,故随迭代次数的增加逐步扩展炮检距范围。此外,从低频到高频的多尺度策略也能提高反演的稳定性。
4 数值实验通过理论模型合成数据与实际地震资料检验本文技术流程的有效性。基准面设置在水层紧靠海底的深度,速度更新只发生在海底之下的模型空间。依次分两个频带(起始频率为0,截止频率分别取10、20 Hz)进行多尺度RWI建模,利用合理的数据和梯度预条件克服深层反射波照明不足问题,通过构造倾角约束的梯度平滑提高反演的稳定性,最后通过逆时偏移成像与共成像点道集验证模型更新的有效性。
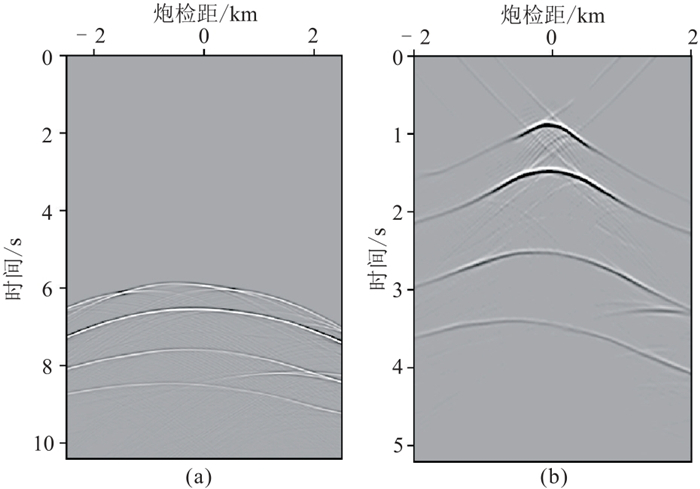
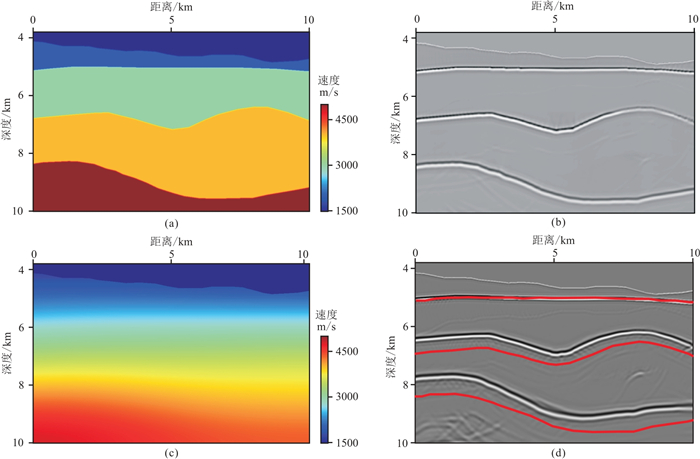
4.1 理论模型合成数据图 4为深水区层状速度模型,平均水深约为4.5 km。通过声波方程高阶有限差分算法合成350炮拖缆观测数据,最大炮检距为5 km,道距为20 m,炮点距为40 m,记录时长为10.4 s,时间采样间隔为4 ms。为了简化数据处理,在海平面采用吸收边界避免多次波干扰。实验中将基准面设置在3.8 km深度(图 4中红色虚线)。虚拟观测系统最大炮检距为4 km,道距为20 m,炮点距为80 m。基准面延拓获得了176炮虚拟数据。图 5显示了实际和虚拟震源横坐标相同的一炮原始数据和虚拟数据。可见基准面延拓缩短了有效记录时长、缩小了炮检距范围。将真实速度模型(图 6a)进行半径为1 km的大尺度高斯平滑,获得如图 6c所示的初始速度模型。由于与真实速度模型偏差较大,其相应的RTM成像(图 6d)与真实速度模型RTM成像(图 6b)结果相差甚远(图 6d红线表示图 6b中的反射界面投影)。
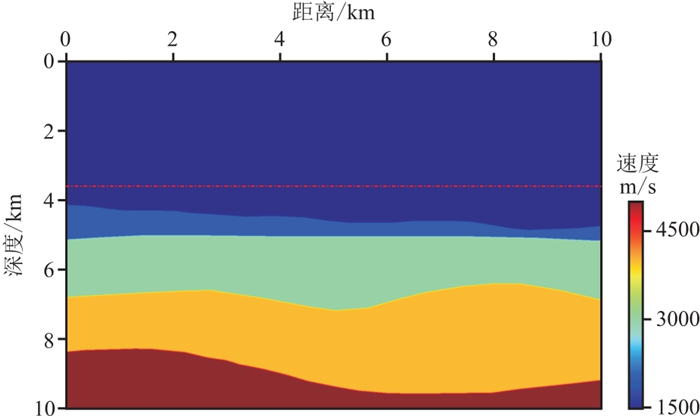
|
图 4 理论模型 |
|
图 5 合成的拖缆单炮记录(a)与基准面延拓重构的虚拟炮记录(b)的对比 |
|
图 6 真实(a)与初始(b)速度模型及其逆时偏移结果(b、d)对比 |
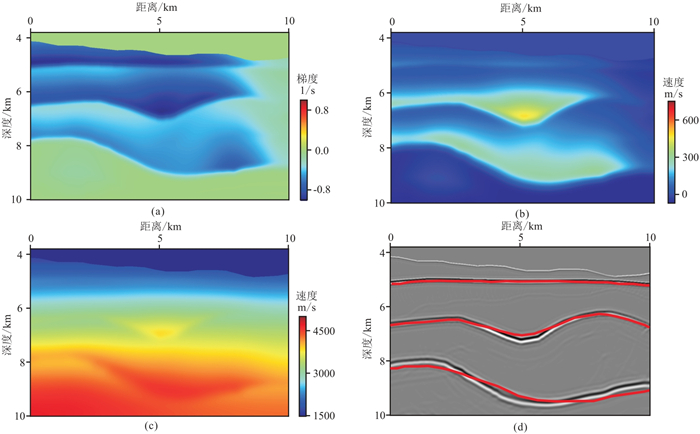
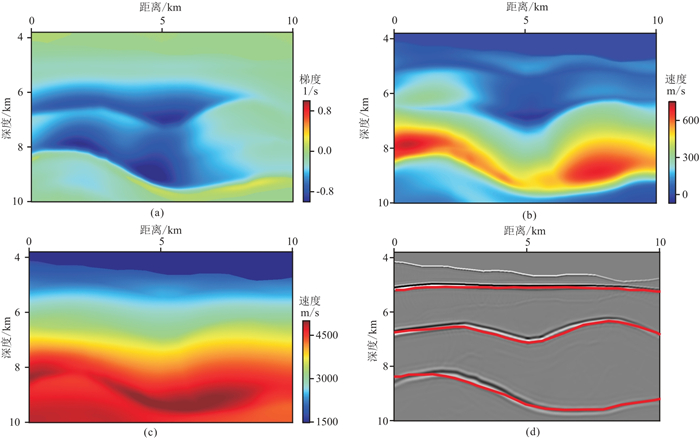
对比原始数据和虚拟数据的多尺度RWI建模结果。首先,基于海面拖缆数据进行全局RWI建模。如图 7所示,虽然泛函梯度反映的更新方向(负梯度方向,图 7a)和多次迭代累加的速度更新量(图 7b)总体上是合理的,但中、深层速度更新幅度偏小,导致RTM成像剖面(图 7d)中深部界面的形态与位置与真实速度模型RTM成像结果(图中红线)仍有一定差距。然后,基于基准面虚拟数据进行RWI建模。得益于基准面延拓的数据预条件和在基准面下伏模型空间的梯度预条件处理,此时的泛函梯度在浅、中、深层都比较均衡,代表了更合理的更新方向(图 8a),进而估计出更准确的速度更新量(图 8b)。基准面延拓驱动的RWI建模从运动学上保证了能获得与真实速度模型基本一致的结果,既减小了图 8d中第二个界面凹陷部位的深度误差,又使图 8d中第三个界面的成像定位更加准确。基准面延拓使虚拟数据的规模减小到原始数据的1/5,也使RWI可以在较小的模型空间进行波场延拓与泛函梯度计算,最终使计算成本降低了75%左右。
|
图 7 海面拖缆数据全局RWI建模与成像结果(局部) (a)第1次迭代的泛函梯度;(b)速度总更新量;(c)更新后速度模型;(d)基于更新后模型的RTM成像剖面 |
|
图 8 基准面虚拟数据RWI建模与成像结果(局部) (a)第1次迭代的泛函梯度;(b)速度总更新量;(c)更新后速度模型;(d)基于更新后模型的RTM成像剖面 |
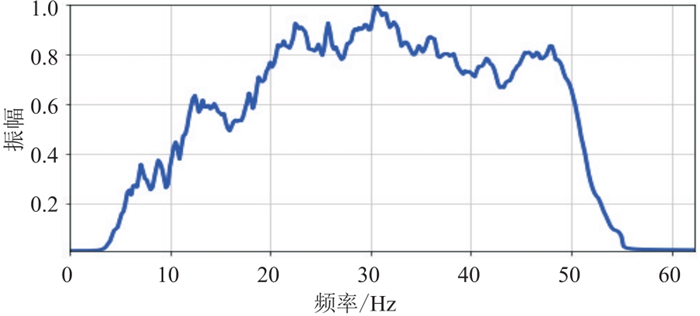
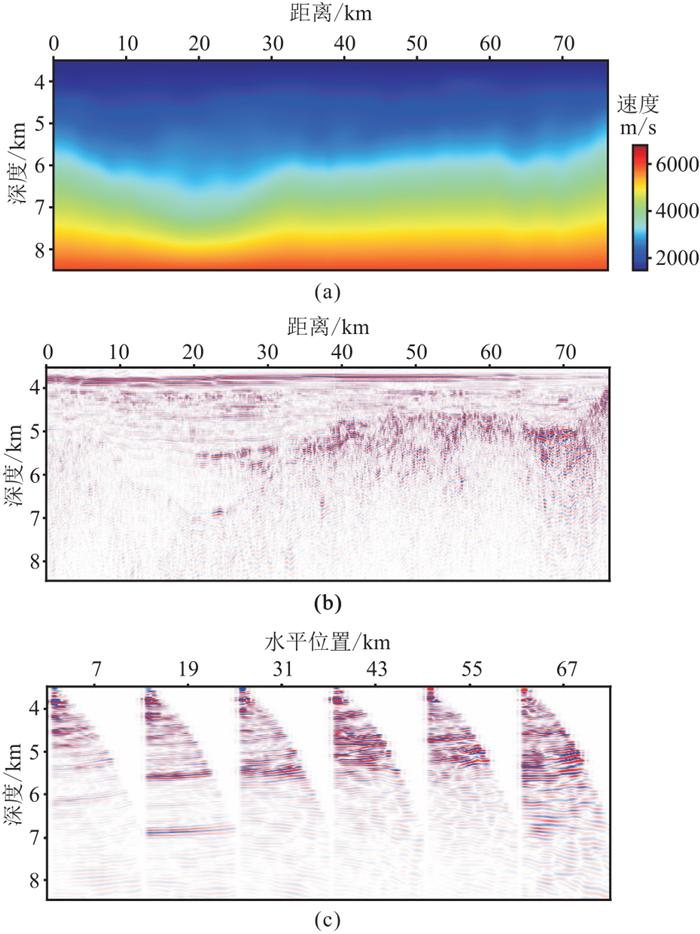
应用南海A区块采集的拖缆地震数据检验本文技术流程的实用性。实验选取的1560炮数据水深超过3.5 km,炮点距为50 m,拖缆长度为6 km,道距为6.25 m,时间采样率为2 ms,记录时长为10 s。前期处理已消除涌浪噪声和海面多次波干扰。从图 9展示的共炮检距剖面(炮检距为300 m)可知,由于地震波在巨厚水层中的双程传播,有效反射信号出现在5 s之后。频谱分析(图 10)表明主频约为30 Hz,有效频带为5~85 Hz。深度域初始层速度模型由叠加速度转换而成(图 11a)。由基于初始层速度模型的RTM成像剖面(图 11b)与共成像点道集(图 11c)可见,速度值整体偏小,主要沉积界面和盆地基底的成像效果都很差。

|
图 9 近炮检距剖面 |
|
图 10 典型炮集频谱分析 |
|
图 11 实际深海地震数据的初始层速度模型及RTM结果 (a)初始速度模型;(b)RTM成像剖面;(c)共成像点道集 |
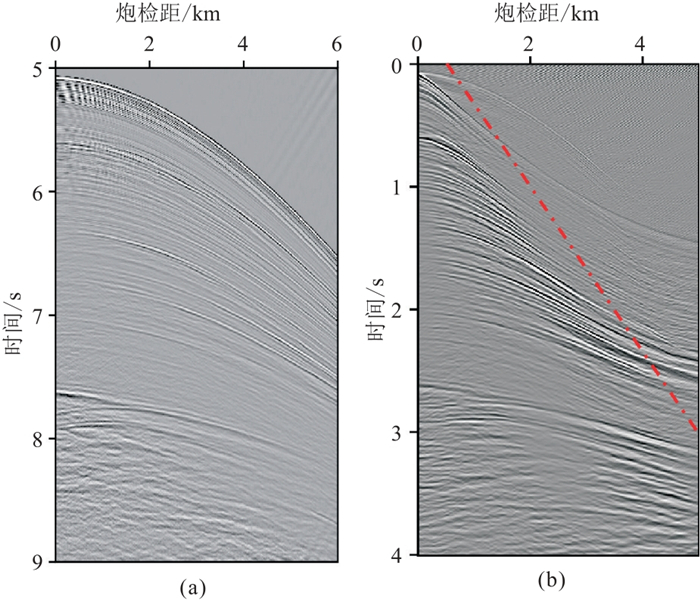
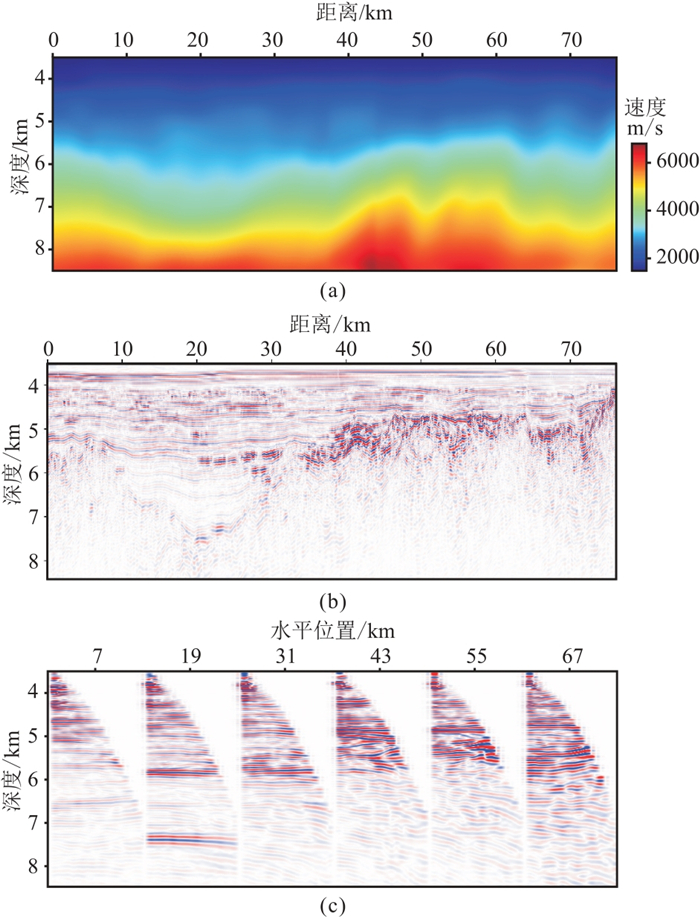
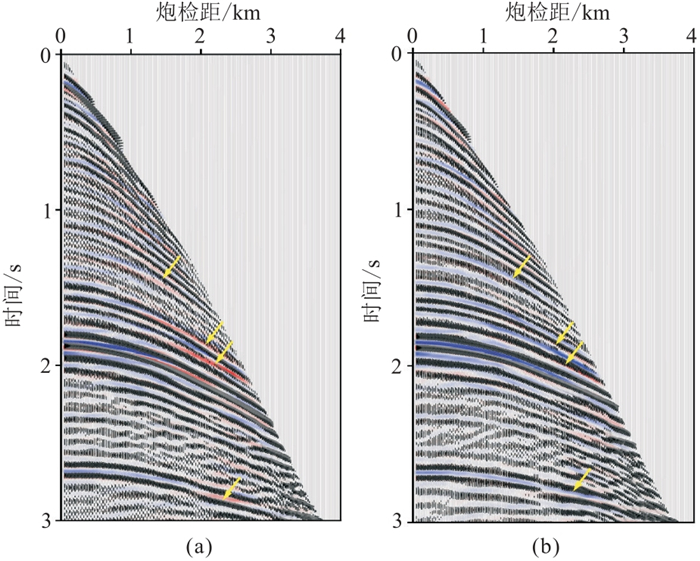
采用基准面延拓驱动的RWI建模技术对初始速度模型进行更新。基准面设置在水深3.5 km处,虚拟观测系统仍包含1560炮,虚拟震源、虚拟检波器的间隔分别为50和6.25 m,最大炮检距为4 km,时间记录长度为4 s。图 12显示震源横坐标一致的实际与虚拟观测炮集,其主要反射同相轴在运动学上有很好的对应关系。因海面拖缆观测的孔径限制,虚拟炮集在远炮检距会引入假信号,需在RTI-RWI之前加以切除(图 12b红色虚线)。虚拟数据多尺度RWI更新的速度模型如图 13a,从共成像点道集(图 13c)上可以看出,同相轴基本拉平,说明该速度模型更接近真实地层速度。从RTM成像剖面(图 13b)可以看出同相轴更连续,同时由浅及深从新近系到古近系主要沉积地层界面和起伏的洋壳基底也更清晰。此外,图 14是基准面虚拟观测数据与Born模拟数据拟合分析。当合成数据与观测数据同相时,黑色波形会盖住红色波形。图 14b中显露出的红色波形明显少于图 14a,表明速度更新后其偏移后共成像点道集的波形匹配度更高,黄色箭头处波形拟合效果明显得到改善。
|
图 12 实际拖缆观测数据与基准面延拓重构数据 (a)海面拖缆炮记录(局部显示);(b)基准面虚拟炮记录 |
|
图 13 虚拟数据RWI构建的速度模型与RTM成像结果 (a)更新后速度模型;(b)RTM成像剖面;(c)共成像点道集 |
|
图 14 基准面虚拟观测数据与Born模拟数据拟合分析 (a)初始模型合成数据与虚拟观测数据匹配;(b)更新模型合成数据与虚拟观测数据匹配。红色波形对应合成数据,黑色波形对应观测数据。 |
如图 15所示,对于海底崎岖且横向速度变化剧烈的超深水情况,为了克服巨厚水层和海底附近复杂波场效应对速度建模与地震资料成像的影响,建议对基准面延拓驱动的速度建模技术进行适当的拓展。例如可依次延拓到两个不同深度的基准面上,分阶段实施基于虚拟观测数据的RWI建模:首先,把基准面设置在水层临近海底的深度,借助延拓到该基准面的虚拟数据反演,获得海底附近可靠的宏观速度模型;然后,把基准面设置在崎岖海底之下,并基于延拓到该深度的虚拟数据反演中、深层的宏观速度模型。后一阶段可采用Zhu等[19]提出的双参数最小平方基准面延拓方法,通过迭代反演消除崎岖海底附近波场效应带来的串扰,高精度重构中深层的反射或背向散射响应。这是今后值得尝试的研究。

|
图 15 超深水崎岖海底情况下基准面设置示意图 |
针对超深水探区速度建模与深层成像面临的困难,本文提出了基准面延拓驱动的波动方程反射波形反演成像技术。该技术通过有效剥离巨厚水层的影响,极大地压缩了观测数据的规模与波场延拓的模型空间,从而使反射波形反演更有效地构建中深层的宏观速度模型,用以支撑叠前逆时偏移的高精度成像。合成数据实验证实,针对海底附近虚拟观测数据的RWI建模,不仅大幅降低计算成本,而且提升了模型更新与偏移成像的精度;在南海A区块的成功应用表明该技术值得在超深水探区推广应用。
| [1] |
王陆新, 潘继平, 杨丽丽. 全球深水油气勘探开发现状与前景展望[J]. 石油科技论坛, 2020, 39(2): 31-37. WANG Luxin, PAN Jiping, YANG Lili. Present conditions and prospect of global deep-water oil and gas exploration and development[J]. Petroleum Science and Technology Forum, 2020, 39(2): 31-37. |
| [2] |
张功成, 屈红军, 张凤廉, 等. 全球深水油气重大新发现及启示[J]. 石油学报, 2019, 40(1): 1-34, 55. ZHANG Gongcheng, QU Hongjun, ZHANG Fenglian, et al. Major new discoveries of oil and gas in global deepwaters and enlightenment[J]. Acta Petrolei Sinica, 2019, 40(1): 1-34, 55. |
| [3] |
邓盾, 邓勇, 马光克, 等. 双方位地震资料联合成像处理技术在深水崎岖海底区的应用[J]. 石油地球物理勘探, 2019, 54(6): 1293-1301. DENG Dun, DENG Yong, MA Guangke, et al. Two-azimuth deep water seismic data combined imaging in rugged seabed areas[J]. Oil Geophysical Prospecting, 2019, 54(6): 1293-1301. DOI:10.13810/j.cnki.issn.1000-7210.2019.06.012 |
| [4] |
杜向东. 中国海上地震勘探技术新进展[J]. 石油物探, 2018, 57(3): 321-331. DU Xiangdong. Progress of seismic exploration technology in offshore China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 321-331. |
| [5] |
谢玉洪, 袁全社. 中国近海深水深层油气地球物理勘探实践与展望[J]. 石油物探, 2023, 62(2): 183-193. XIE Yuhong, YUAN Quanshe. Practice and prospects of deep-water and deep-formation geophysical exploration[J]. Geophysical Prospecting for Petroleum, 2023, 62(2): 183-193. |
| [6] |
BERRYHILL J R. Wave-equation datuming before stack[J]. Geophysics, 1984, 49(11): 1942-2156. |
| [7] |
杨锴, 王华忠, 程玖兵, 等. 非水平观测面有限差分法叠前波动方程基准面校正[J]. 石油地球物理勘探, 2002, 37(2): 154-162. YANG Kai, WANG Huazhong, CHENG Jiubing, et al. Pre-stack wave equation datum correction from non-flat surface with finite-difference scheme[J]. Oil Geophysical Prospecting, 2002, 37(2): 154-162. DOI:10.13810/j.cnki.issn.1000-7210.2002.02.014 |
| [8] |
金丹, 阎贫, 唐群署, 等. Kirchhoff波场延拓在OBC记录海水层基准面校正中的应用[J]. 热带海洋学报, 2011, 30(6): 84-89. JIN Dan, YAN Pin, TANG Qunshu, et al. Application of Kirchhoff integral wave field extrapolation to water layer datuming for OBC record[J]. Journal of Tropical Oceanography, 2011, 30(6): 84-89. |
| [9] |
王祥春, 王延峰, 夏常亮, 等. Kirchhoff积分法OBS数据地震波场延拓[J]. 现代地质, 2012, 26(6): 1231-1236. WANG Xiangchun, WANG Yanfeng, XIA Changliang, et al. Extrapolating the OBS data using the Kirchhoff integral method[J]. Geoscience, 2012, 26(6): 1231-1236. |
| [10] |
ARNULF A F, SINGH S C, HARDING A J, et al. Strong seismic heterogeneity in layer 2A near hydrothermal vents at the Mid‐Atlantic Ridge[J]. Geophysical Research Letters, 2011, 38(13): L13320. |
| [11] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [12] |
VIGH D, MOLDOVEANU N, JIAO K, et al. Ultralong-offset data acquisition can complement full-waveform inversion and lead to improved subsalt imaging[J]. The Leading Edge, 2013, 32(9): 1116-1122. DOI:10.1190/tle32091116.1 |
| [13] |
ALKHALIFAH T. Scattering-angle based filtering of the waveform inversion gradients[J]. Geophysical Journal International, 2015, 200(1): 363-373. |
| [14] |
WANG Y, RAO Y. Reflection seismic waveform tomography[J]. Journal of Geophysical Research, 2009, 114(B3): 1-12. |
| [15] |
XU S, WANG D, CHEN F. et al. Inversion on reflected seismic wave[C]. SEG Technical Program Expanded Abstracts 2012, 2012, 31: 1052-3812.
|
| [16] |
MA Y, HALE D. Wave-equation reflection traveltime inversion with dynamic warping and full-waveform inversion[J]. Geophysics, 2013, 78(6): 1ND-Z204. DOI:10.1190/2013-1009-TIOGEO.1 |
| [17] |
姚刚, 吴迪. 反射波全波形反演[J]. 中国科学: 地球科学, 2017, 47(10): 1220-1232. YAO Gang, WU Di. Reflection full waveform inversion[J]. Scientia Sinica(Terrae), 2017, 47(10): 1220-1232. |
| [18] |
WANG T, CHENG J, GENG J. Reflection full wave-form inversion with second-order optimization using the adjoint-state method[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(8): e2021JB022135. DOI:10.1029/2021JB022135 |
| [19] |
ZHU F, CHENG J B. An extension of least-squares redatuming: simultaneous reconstruction of overburden reflectivities and virtual data[J]. Journal of Computational Physics, 2022, 461: 111159. DOI:10.1016/j.jcp.2022.111159 |
| [20] |
程玖兵, 王腾飞, 徐文才. 地震反射波反演二阶优化方法及其应用[J]. 地球物理学报, 2021, 64(10): 3685-3700. CHENG Jiubing, WANG Tengfei, XU Wencai. Second-order optimization of seismic reflection waveform inversion and its application[J]. Chinese Journal of Geophysics, 2021, 64(10): 3685-3700. |
| [21] |
ZHANG Y, ZHANG G, BLEISTEIN N. Theory of true-amplitude one-way wave equations and true-amplitude common-shot migration[J]. Geophysics, 2005, 70: E1-E10. DOI:10.1190/1.1988182 |
| [22] |
DAI W, SCHUSTER J. Least-squares migration of simultaneous sources data with a deblurring filter[J]. SEG Technical Program Expanded Abstracts, 2009, 28: 4338. |
| [23] |
郭振波, 李振春. 最小平方逆时偏移真振幅成像[J]. 石油地球物理勘探, 2014, 49(1): 113-120, 303. GUO Zhenbo, LI Zhenchun. True amplitude imaging based on least-squares reverse-time migration[J]. Oil Geophysical Prospecting, 2014, 49(1): 113-120, 303. DOI:10.13810/j.cnki.issn.1000-7210.2014.01.014 |
| [24] |
周华敏, 陈生昌, 任浩然, 等. 基于照明补偿的单程波最小二乘偏移[J]. 地球物理学报, 2014, 57(8): 2644-2655. ZHOU Huamin, CHEN Shengchang, REN Haoran, et al. One-way wave equation least-squares migration based on illumination compensation[J]. Chinese Journal of Geophysics, 2014, 57(8): 2644-2655. |
| [25] |
NOCEDAL J, WRIGHT S J. Numerical Optimization[M]. New York: Springer, 2006.
|
| [26] |
WANG T, CHENG J, GENG J. Reflection-based travel-time and waveform inversion with second-order optimization[J]. Petroleum Science, 2022, 19(4): 1582-1591. DOI:10.1016/j.petsci.2022.02.003 |
| [27] |
赵钊, 赵志刚, 沈怀磊, 等. 南海北部超深水区双峰盆地构造演化与油气地质条件[J]. 石油学报, 2016, 37(增刊1): 47-57. ZHAO Zhao, ZHAO Zhigang, SHEN Huailei, et al. Tectonic evolution and hydrocarbon geological conditions of Shuangfeng Basin in the ultra-deep water area of the northern South China Sea[J]. Acta Petrolei Sinica, 2016, 37(S1): 47-57. |



 程玖兵,上海市杨浦区四平路1239号同济大学海洋楼403室,200092。Email:
程玖兵,上海市杨浦区四平路1239号同济大学海洋楼403室,200092。Email: