2. 河北地质大学河北省战略性关键矿产资源重点实验室, 河北石家庄 050031;
3. 河北地质大学数理教学部, 河北石家庄 050031;
4. 河北地质大学地球科学学院, 河北石家庄 050031;
5. 中国矿业大学(北京)地球科学与测绘工程学院, 北京 100083;
6. 河北省煤田地质局物测地质队, 河北邢台 054000
2. Hebei Key Laboratory of Strategic Critical Mineral Resources, Hebei GEO University, Shijiazhuang, Hebei 050031, China;
3. School of Mathematics and Science, Hebei GEO University, Shijiazhuang, Hebei 050031, China;
4. School of Earth Sciences, Hebei GEO University, Shijiazhuang, Hebei 050031, China;
5. College of Geoscience and Surveying Engineering, China University of Mining and Technology⁃Beijing, Beijing 100083, China;
6. Geophysical Exploration Team, Hebei Coal Field Geology Bureau, Xingtai, Hebei 054000, China
地震绕射波成像是油气资源勘探的重要方法之一,在小尺度地质体探测中具有重要应用前景。以塔河油田为例,应用该技术能提取溶洞的“串珠状”信号,在缝洞型储层的预测方面获得了较好的应用效果[1]。除此之外,在其他油气富集地区也应用绕射波成像解决了断裂识别[2]和潜山裂缝储层预测[3]等难题。
绕射波分离是实现绕射波成像的前提。由于绕射波较反射波能量弱1~2个量级[4],通常掩盖于反射波场中,现有的做法是通过压制反射能量以保留绕射波信息。基于Radon变换的绕射波分离方法是一种常用的绕射波分离手段,其主要思想是图像中的直线变换到Radon域后会在对应位置产生极值,这就期望在特定的道集内反射波呈线性形态且绕射波与之有较大的形态差异。Klokov等[4]在倾角域共成像点道集上利用混合域Radon变换消除反射波、保留绕射波。罗腾腾等[5]提出了应用迭代收缩高分辨率Radon变换的绕射波分离方法,解决了绕射波场分离效果不理想和计算效率低的问题。在共炮检距道集,Chen等[6]提出了双稀疏变换绕射波分离法,其做法是利用线性高分辨率Radon变换提取反射信号,通过曲波变换提取绕射信号,从而实现绕射波和反射波的高质量分离。应用Radon变换分离绕射波要求输入数据具有较高的信噪比,分离结果会受到噪声的影响。
平面波分解(PWD)也是一种常用的反射和绕射波分离方法。在平面波域反射波、绕射波时距曲线分别呈拟线性和双曲型,通过PWD滤波器可以单独提取出绕射信息。朱生旺等[7]在平面波分解剖面上采用预测反演方法分离出低倾角绕射信息,弥补了局部倾角估计的不足;孔雪等[8]利用PWD滤波器关于反射同相轴局部倾角估计表现较好的特性提取绕射波;刘斌等[9]将PWD滤波器应用于倾角域共成像点道集成功分离出绕射波场。在叠后域或共炮检距域分离绕射波会导致叠前信息丢失,且对数据质量要求严苛。Lin等[10]基于PWD工作流程将平面波分解的应用扩展到叠前;Wang等[11]用PWD方法压制反射波,采用双稀疏字典法提取绕射波进而提升了绕射信号的信噪比。赵惊涛等[12]提出基于曲波变换和平面波分解的多参数稀疏化绕射分离方法,提升了地震波场相切或相交时分离的绕射波完整性。由于PWD是一种基于波动方程的方法,计算复杂,不便于推广和实际应用。
近年来基于人工智能的绕射波分离方法逐渐成为新的研究方向。Serfaty等[13]在方位角道集采用主成分分析(PCA)和卷积神经网络分离和归类反射波与绕射波;Lowney等[14]采用生成对抗网络(GAN)由叠前数据分离绕射信息,其运行效率优于传统PWD方法;Lowney等[15]还提出了多域有监督深度学习方法将地震信号自动分类成反射、绕射和噪声三部分,该方法具有用时少、比PWD方法计算成本低的优势,但提取绕射波的表现能力相似;盛同杰等[16]利用基于编码—解码框架下的U-net网络和注意力机制分离绕射波,克服了传统方法难以去除陡倾角反射波的局限;马铭等[17]提出基于深度神经网络(DNN)的复杂异常体绕射波分离技术,通过引入空洞卷积降低算法复杂度并增大感受野,同时引进深度可分离卷积在保持相同特征图数量的条件下减少运算步骤。由于深度学习中使用的训练数据大多源自物理或数学模型,以此产生的数据在噪声、振幅、频率等方面缺乏多样性,会导致模型的泛化能力较差。
基于秩约束类的方法也被广泛用于绕射波分离,其理论基础来源于地震信号的稀疏性假设——地震道的缺失或数据中的噪声均会增加矩阵的秩。秩约束类的方法目前可采用两种手段实现,一种是根据反射波和绕射波的相干性对数据直接做奇异值分解(SVD),反射波对应大的奇异值、绕射波对应于小的奇异值,选择合适的奇异值个数后再做逆SVD变换,这一方法关键步骤在于奇异值的截断。魏巍等[18]利用奇异值重建了绕射波场,但奇异值序列的截断是通过试验或人为给定,结果受主观因素较多。Chen等[19]提出的基于Cook距离的SVD方法则实现了奇异值自动截断,奇异值重建绕射波场摆脱了主观因素的束缚。另一种秩约束方法则是基于多道奇异谱分析(MSSA)类的方法,该类方法先将数据在频率域内做Hankel变换,再对变换结果做SVD分解并奇异值截断,可以有效提取数据中的反射波场,通过与原波场相减从而得到绕射波场。
目前MSSA在反射波场提取的应用存在两方面问题。第一,在反射波去噪应用方面存在分离出的噪声中有反射能量残余。Huang等[20]通过引入阻尼因子以抑制反射能量残留,最终形成了阻尼多道奇异谱分析(DMSSA)算法。第二,无论MSSA或DMSSA算法,提取反射波场都依赖人工试验以确定秩,这并不适用于大规模地震数据处理,需要解决反射波场秩的自动求解问题。为此朱跃飞等[21]、曹静杰等[22]分别提出了不同的秩计算方法以满足自动化处理的需要。Lin等[23]将MSSA算法应用于反射和绕射波分离问题。该类方法分离绕射波要重点关注分离出的绕射波场,对秩的选取精准度提出了更高的要求。
本文采用DMSSA算法在共炮检距域或叠后域进行绕射波和反射波分离。为了克服DMSSA方法人工选择秩的问题,本文提出采用Cook距离自动确定奇异值个数,设定Cook阈值为3倍的Cook距离均值并对数据进行分块处理。通过模拟和实际数据验证了基于Cook距离的DMSSA算法对于绕射波场分离的有效性和适用性。
1 方法原理 1.1 DMSSA算法DMSSA是MSSA的改进算法,二者在数据处理流程上基本一致。DMSSA分离绕射波的流程如下。
共炮检距道集时间域二维地震数据可表示为矩阵形式
| $ \boldsymbol{s}=\left[\begin{array}{cccc}{s}_{\mathrm{1, 1}}& {s}_{\mathrm{1, 2}}& \cdots & {s}_{1, m}\\ {s}_{\mathrm{2, 1}}& {s}_{\mathrm{2, 2}}& \cdots & {s}_{2, m}\\ & & \vdots & \\ {s}_{n, 1}& {s}_{n, 2}& \cdots & {s}_{n, m}\end{array}\right] $ | (1) |
式中m和n分别为道数和样点数。
第1步:将时间域地震数据通过Fourier变换到频率域
| $ \boldsymbol{S}=\left[\begin{array}{cccc}{S}_{\mathrm{1, 1}}& {S}_{\mathrm{1, 2}}& \cdots & {S}_{1, m}\\ {S}_{\mathrm{2, 1}}& {S}_{\mathrm{2, 2}}& \cdots & {S}_{2, m}\\ & & \vdots & \\ {S}_{n, 1}& {S}_{n, 2}& \cdots & {S}_{n, m}\end{array}\right] $ | (2) |
写成行向量的形式
| $ \boldsymbol{S}=\left[\begin{array}{c}{\boldsymbol{S}}_{1}\\ {\boldsymbol{S}}_{2}\\ \vdots \\ {\boldsymbol{S}}_{n}\end{array}\right] $ | (3) |
式中Si为第i个频率分量,有
| $ {\boldsymbol{S}}_{i}=\left[{S}_{i, 1}, {S}_{i, 2}, \cdots , {S}_{i, m}\right] $ | (4) |
第2步:将Si排列成Hankel矩阵形式
| $ \boldsymbol{H}=\left[\begin{array}{cccc}{S}_{i, 1}& {S}_{i, 2}& \cdots & {S}_{i, m-g+1}\\ {S}_{i, 2}& {S}_{i, 3}& \cdots & {S}_{i, m-g+2}\\ & & \vdots & \\ {S}_{i, g}& {S}_{i, g+1}& \cdots & {S}_{i, m}\end{array}\right] $ | (5) |
式中
第3步:对矩阵H做SVD分解,即
| $ \boldsymbol{H}=\boldsymbol{U}\left[\begin{array}{cc}\boldsymbol{\varSigma }& 0\\ 0& 0\end{array}\right]{\boldsymbol{V}}^{\mathrm{H}}=\boldsymbol{U}\boldsymbol{R}{\boldsymbol{V}}^{\mathrm{H}} $ | (6) |
式中:上标“H”表示共轭转置;U是H左奇异向量矩阵,为g阶正交方阵;V是H右奇异向量矩阵,为m-g+1阶正交方阵;
| $ \boldsymbol{\varSigma }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\sigma }_{1}, {\sigma }_{2}, \cdots , {\sigma }_{r}) $ | (7) |
其中:r为H的秩;σj为H的第j个奇异值,且
| $ {\sigma }_{1}\ge {\sigma }_{2}\ge \cdots \ge {\sigma }_{r}>0 $ | (8) |
能量强的反射波通常对应着数值较大的奇异值,能量弱的绕射波通常对应着数值较小的奇异值。
第4步:加入阻尼算子D削弱反射波对绕射信号的影响
| $ \boldsymbol{H}=\boldsymbol{U}\left[\begin{array}{cc}\boldsymbol{D}\left(\boldsymbol{\varSigma }\right)& 0\\ 0& 0\end{array}\right]{\boldsymbol{V}}^{\mathrm{H}} $ | (9) |
阻尼算子作用于对角矩阵
| $ D\left({\sigma }_{i}\right)={\sigma }_{i}-\frac{{\sigma }_{N+1}^{K}}{{\sigma }_{i}^{K-1}} $ | (10) |
式中:K为阻尼因子;N表示待保留的反射波奇异值的个数。
第5步:截断奇异值(TSVD)——只保留反射波所对应的奇异值部分。式(9)还可以表示为
| $ \boldsymbol{H}=\left[\begin{array}{cc}{\boldsymbol{U}}^{\mathrm{r}}& {\boldsymbol{U}}^{\mathrm{d}}\end{array}\right]\left[\begin{array}{cc}\boldsymbol{D}\left({\boldsymbol{\varSigma }}^{\mathrm{r}}\right)& 0\\ 0& \boldsymbol{D}\left({\boldsymbol{\varSigma }}^{\mathrm{d}}\right)\end{array}\right]\left[\begin{array}{c}{\left({\boldsymbol{V}}^{\mathrm{r}}\right)}^{\mathrm{H}}\\ {\left({\boldsymbol{V}}^{\mathrm{d}}\right)}^{\mathrm{H}}\end{array}\right] $ | (11) |
式中上标“r、d”分别代表反射波和绕射波。令
第6步:TSVD后的数据按照Hankel矩阵的构造方式还原成初始形态。
第7步:将所有频率域的数据逆Fourier变换到时间域并构成了反射波场sr,用原始波场减去反射波场即为绕射波场
| $ {\boldsymbol{s}}^{\mathrm{d}}=\boldsymbol{s}-{\boldsymbol{s}}^{\mathrm{r}} $ | (12) |
TSVD的目的是为了截取反射波所对应的奇异值,从而将式(9)中反射与绕射波分别变换到彼此正交的子空间。在引入Cook距离之前,需要了解奇异值曲线的特征。式(8)中的奇异值序列按大小可以划分成Xr和Xd两部分
| $ {\boldsymbol{X}}^{\mathrm{r}}=\left\{{\sigma }_{1}, {\sigma }_{2}, \cdots , {\sigma }_{N}\right\} $ | (13) |
| $ {\boldsymbol{X}}^{\mathrm{d}}=\left\{{\sigma }_{N+1}, {\sigma }_{N+2}, \cdots , {\sigma }_{r}\right\} $ | (14) |
Xr包含的元素数值较大,个数占比较小。Xd是数值较小的绕射波奇异值序列。因绕射波的能量远低于反射波能量,该部分元素个数占整个奇异值序列的大多数。在理想状态下,反射波奇异值的个数和原始数据中反射波同相轴的条数相匹配[24],基于该假设,绕射波和反射波的分离问题就转换为反射波奇异值个数的判定问题。
1.3 基于Cook距离分离绕射波Cook[25]将学生化(Studentized)残差和残差的方差估计结合起来构成新的评价指标以增强线性回归模型评价的可靠性。利用Cook距离确定反射波奇异值个数的原理如下。
对于一个给定的线性回归模型
| $ \boldsymbol{y}=\boldsymbol{x}\boldsymbol{\beta }+\boldsymbol{\varepsilon } $ | (15) |
式中:y为q维列向量,表示待预测向量;x是q×p维已知满秩矩阵,是线性回归模型的自变量;β是p维列向量,包含模型的回归系数;ε是期望值为0的随机误差向量。参数β的最小二乘估计为
| $ \widehat{\boldsymbol{\beta }}={\left({\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{x}\right)}^{-1}{\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{y} $ | (16) |
则估计残差为
| $ \boldsymbol{e}=\boldsymbol{y}-\widehat{\boldsymbol{y}}=\boldsymbol{y}-\boldsymbol{x}\widehat{\boldsymbol{\beta }}=\left[\boldsymbol{I}-\boldsymbol{x}{\left({\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{x}\right)}^{-1}{\boldsymbol{x}}^{\mathrm{T}}\right]\boldsymbol{y} $ | (17) |
模型的均方误差为
| $ {E}^{2}={\boldsymbol{e}}^{\mathrm{T}}\boldsymbol{e}/\left(q-p\right) $ | (18) |
记
| $ {d}_{i}=\frac{{\left[\widehat{\boldsymbol{\beta }}-{\widehat{\boldsymbol{\beta }}}_{\left(-i\right)}\right]}^{\mathrm{T}}{\boldsymbol{x}}^{\mathrm{T}}\boldsymbol{x}\left[\widehat{\boldsymbol{\beta }}-{\widehat{\boldsymbol{\beta }}}_{\left(-i\right)}\right]}{p{E}^{2}} $ | (19) |
Cook距离的含义是衡量删除第i个观测值对整个线性回归模型的影响,第i个观测值越突出,di就越大,从而越有可能作为回归模型中的异常值。进一步地说,需要设置合理的Cook距离阈值判定di是否异常。现有的文献对Cook距离阈值并未形成统一的观点。Cook[25]将阈值确定为一个F分布——
Hankel矩阵(式(5))奇异值分解得到奇异值序列(式(7))作为观测数据构成(y,x),其中
式(13)和式(14)指出奇异值序列可分成Xr和Xd两个部分。由于反射地震信号的稀疏性,反射波奇异值的个数只占少数,故Xr与拟合直线间会存在较大的残差,会对线性回归模型的参数估计产生较大的影响,反映到Cook距离就表现为di较大。在设定阈值T之后,满足di>T的σi就成为了(y,x)的异常值。式(10)中待求的参数N为y中满足di>T的观测总数。
本文采用3倍Cook距离均值作为阈值的方案。该阈值的定义为
| $ T=3\sum\limits_{i=1}^{q}\frac{{d}_{i}}{q} $ | (20) |
应用单断层模型和多断层模型模拟数据验证本文方法的绕射波分离有效性。
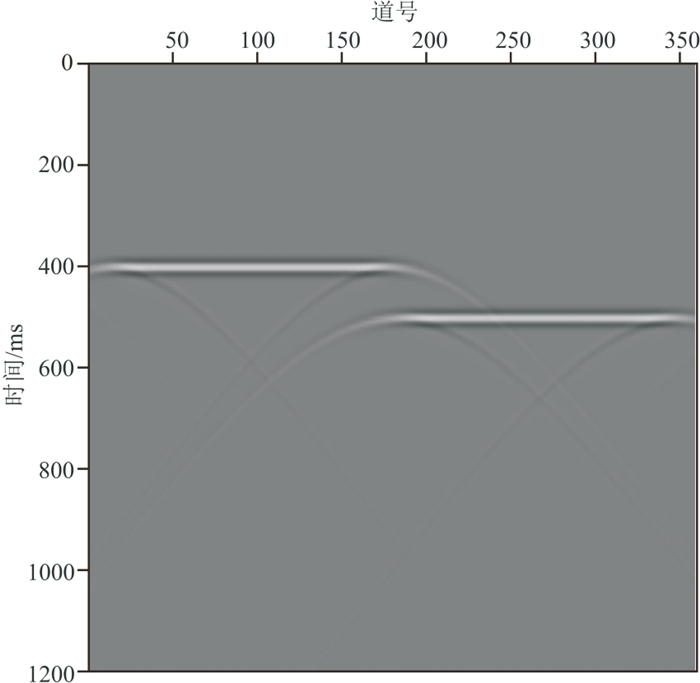
图 1是用主频为30 Hz的Ricker子波通过单程波动方程正演模拟的单断层模型的共炮检距道集,共360道、1200个样点,采样间隔为1 ms,包含2条线性同相轴及断点绕射。能量较强的反射波同相轴为图中明亮的直线,能量较弱的绕射波同相轴为较暗的拟双曲线。
|
图 1 单断层模型的共炮检距道集 |
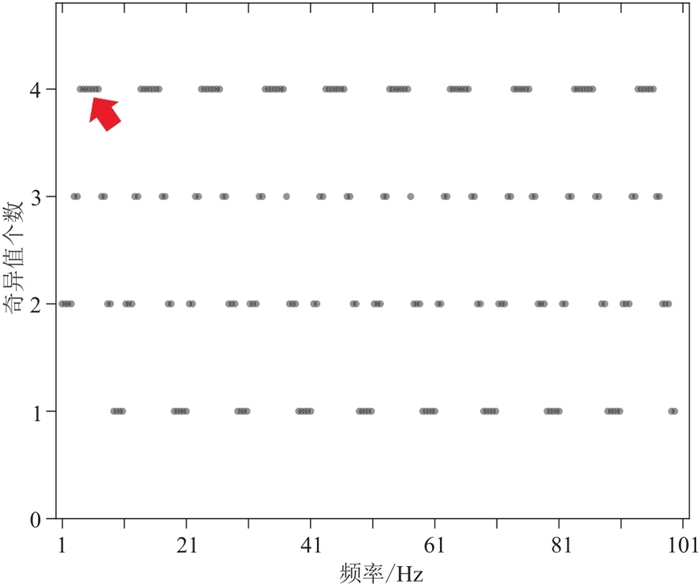
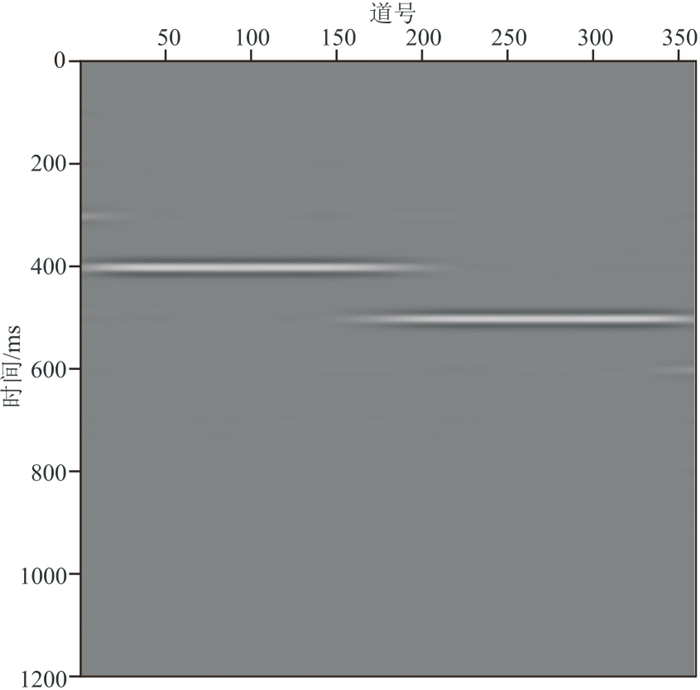
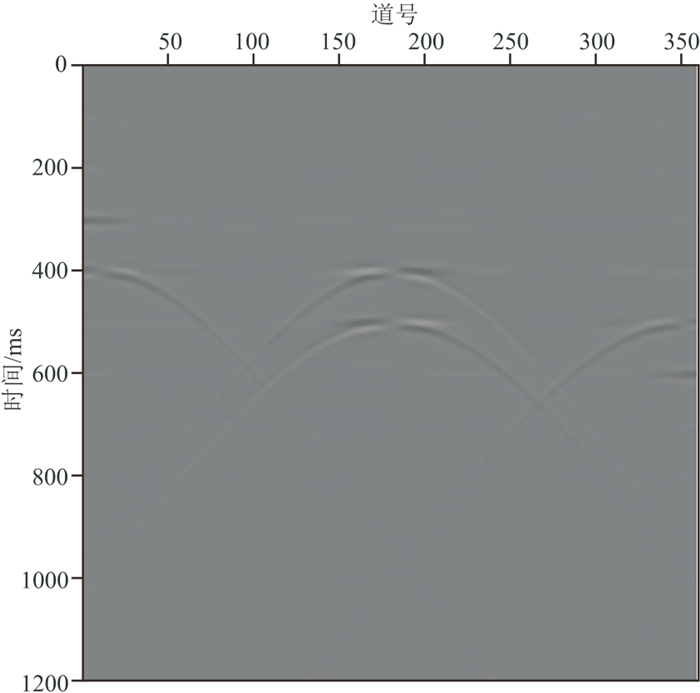
在信号有效频带1~100 Hz的每个频率上,Cook距离检测出来的反射波奇异值个数如图 2的散点图所示,最大值为4(红色箭头所示)。将1~100 Hz频率段的反射波奇异值个数设置为4并完成奇异值截断。图 3和图 4分别是本文算法针对该模型分离出的反射波场和绕射波场。分离后的反射波场中已观察不到拟双曲线的绕射波,绕射波场中也不存在能量强的反射波,且双曲型的绕射波同相轴清晰。在图 3、图 4边缘处存在能量极弱的同相轴,为波场分离时产生的轻微假象,不会影响对反射波和绕射波的判断。
|
图 2 单断层模型数据的奇异值个数散点图 |
|
图 3 单断层模型数据分离的反射波场 |
|
图 4 单断层模型数据分离的绕射波场 |
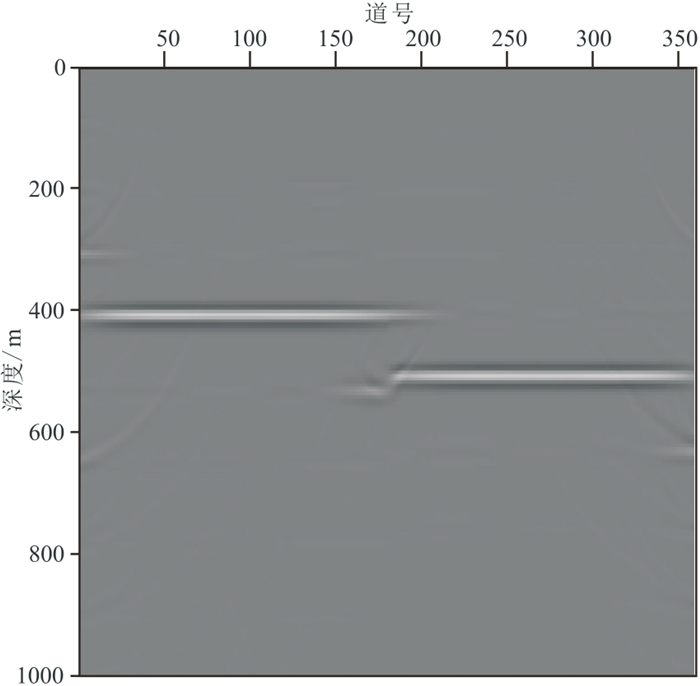
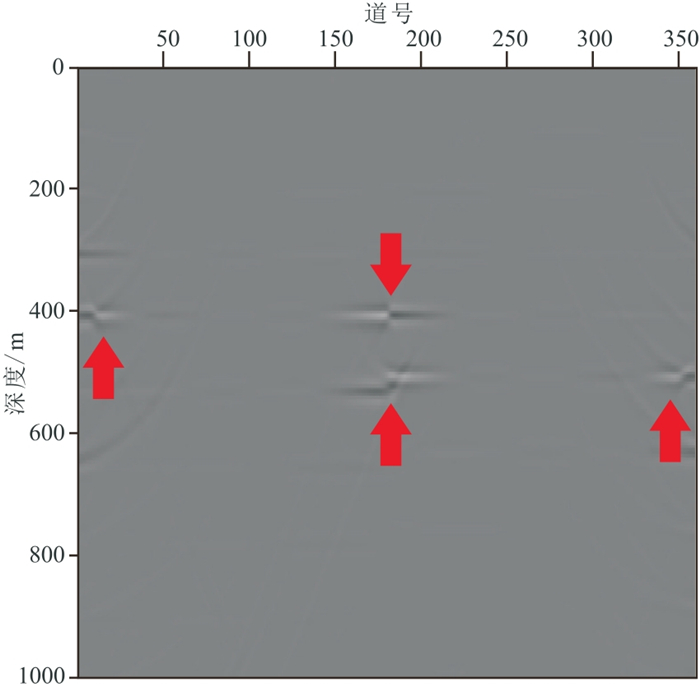
图 5~图 7分别是图 1、图 3和图 4的深度偏移成像结果。偏移后的反射波波场(图 6)同相轴清晰,绕射波经过偏移处理后收敛归位(图 7红色箭头所示),绕射点清晰地刻画了反射界面的边缘,揭示了断层所在位置。

|
图 5 单断层模型的全波场深度偏移结果 |
|
图 6 单断层模型的反射波场深度偏移结果 |
|
图 7 单断层模型数据的绕射波场深度偏移结果 |
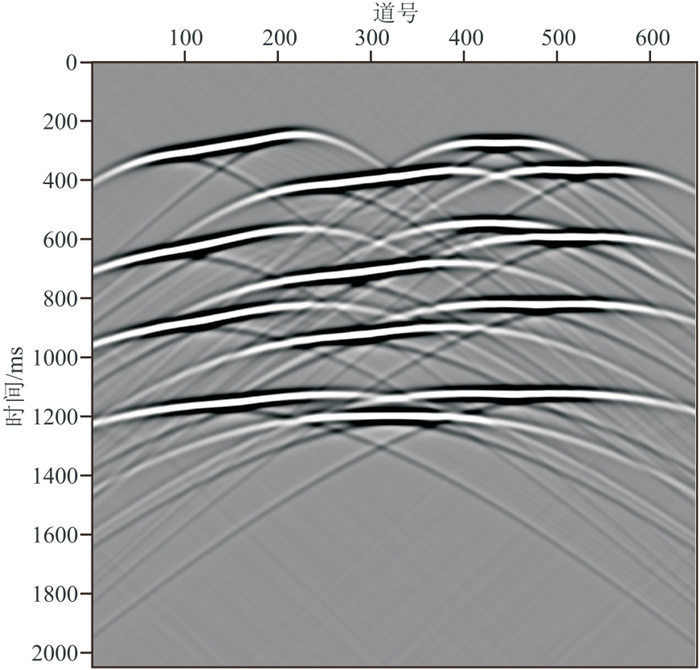
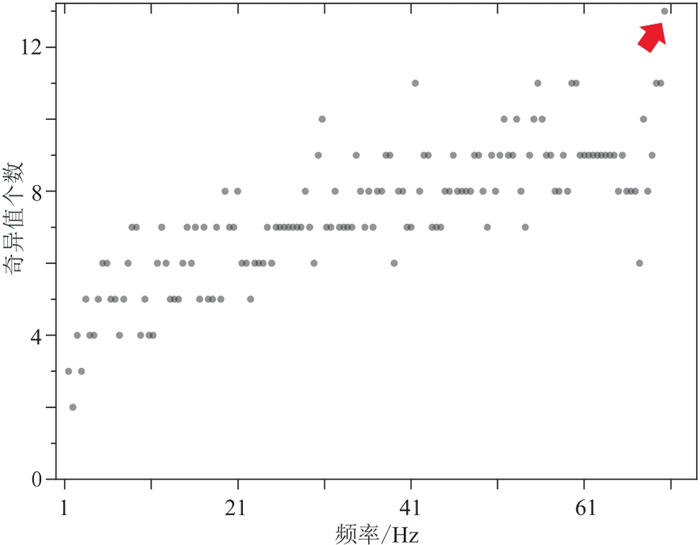
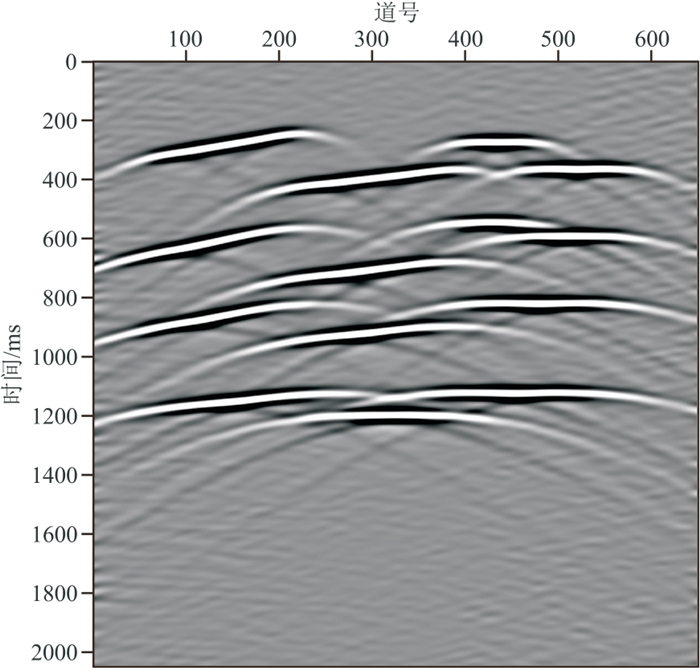
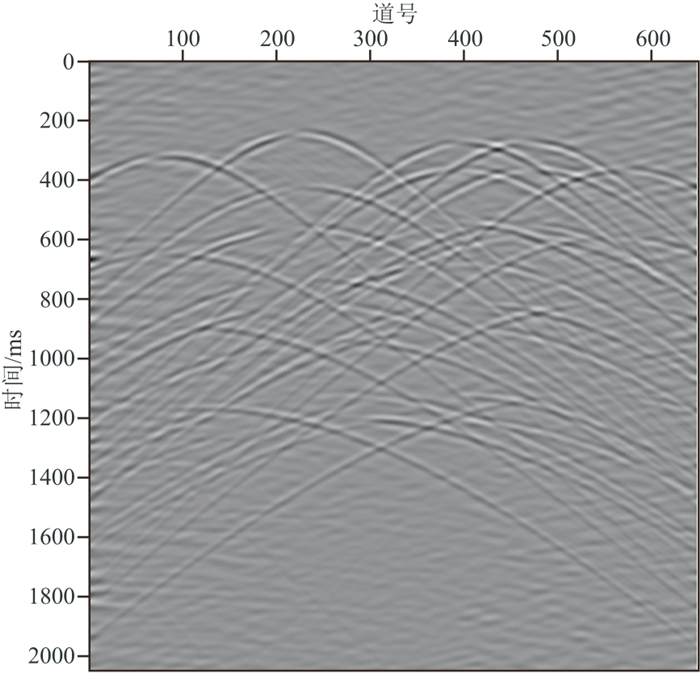
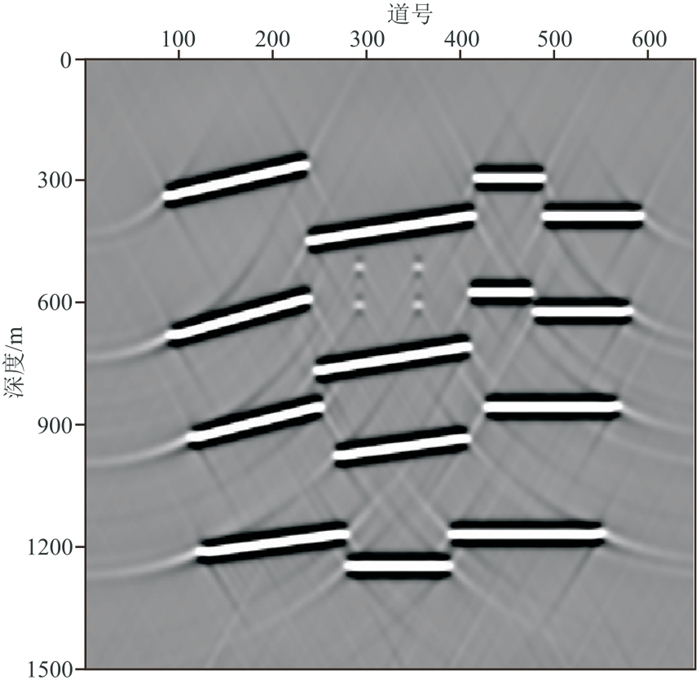
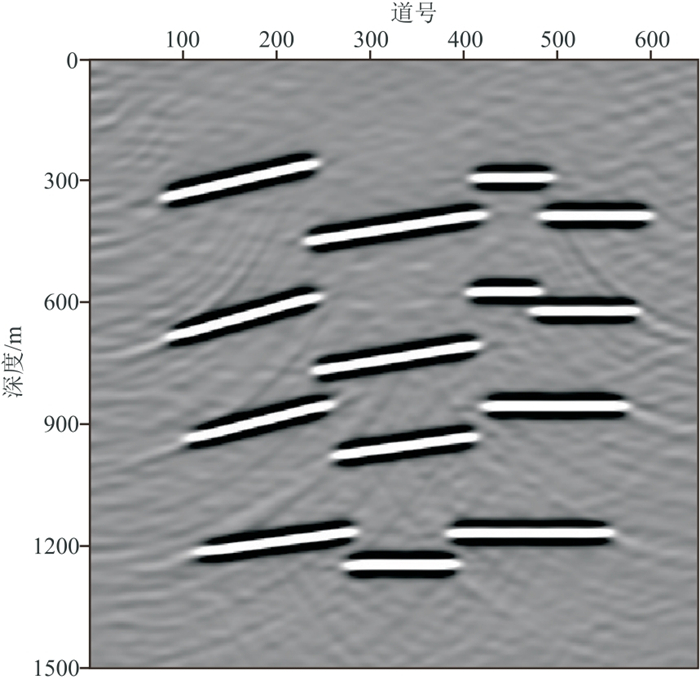
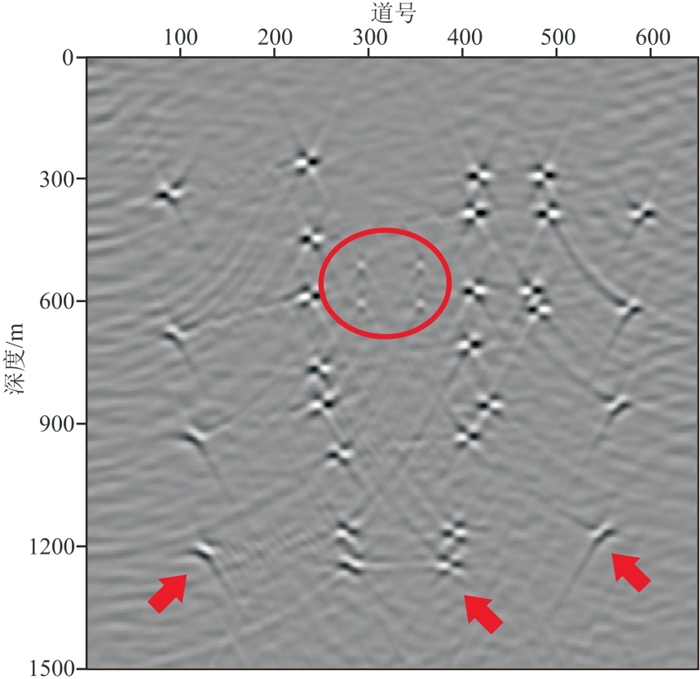
图 8是主频为20 Hz的Ricker子波通过单程波动方程正演模拟的多断层模型的共炮检距道集,共650道,每道2048个样点,采样间隔为1 ms,包含14条反射同相轴、3条断层的断点绕射及4个绕射点的绕射。直线为反射波同相轴,拟双曲线为绕射波同相轴。Cook距离在该模型的信号有效频带1~70 Hz内每个频率上检测出的反射波奇异值个数如图 9所示,红色箭头所指处为奇异值个数的最大值,即13个。在1~70 Hz频段上设定反射波奇异值个数为13,完成奇异值截断。图 10为本文算法分离出的反射波场,同相轴清晰,波场中残余的绕射能量水平较低。图 11是分离的绕射波场,同相轴完整,没有反射能量残留。图 12~图 14分别为图 8、图 10和图 11的深度偏移成像结果。反射波偏移结果同相轴清晰,准确刻画了界面位置。在绕射波偏移结果中,断点绕射波收敛,清晰地刻画了反射界面的边缘(图 14红色箭头所指),揭示了断层位置;四个绕射点同样收敛到真实位置(图 14中红色圆圈处),与全波场偏移结果相近。
|
图 8 多断层模型数据全波场正演模拟结果 |
|
图 9 多断层模型数据奇异值个数散点图 |
|
图 10 多断层模型分离的反射波场 |
|
图 11 多断层模型分离的绕射波场 |
|
图 12 多断层模型的全波场深度偏移结果 |
|
图 13 多断层模型的反射波深度偏移结果 |
|
图 14 多断层模型绕射波场深度偏移结果 |
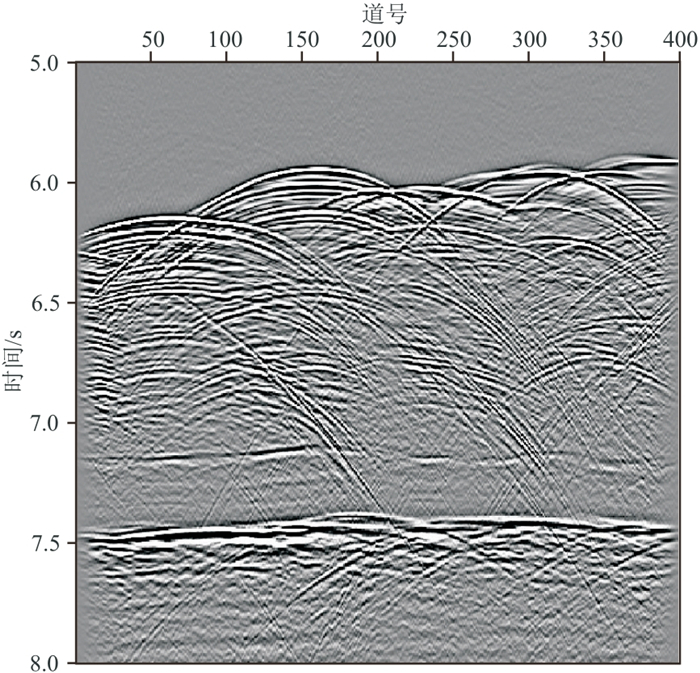
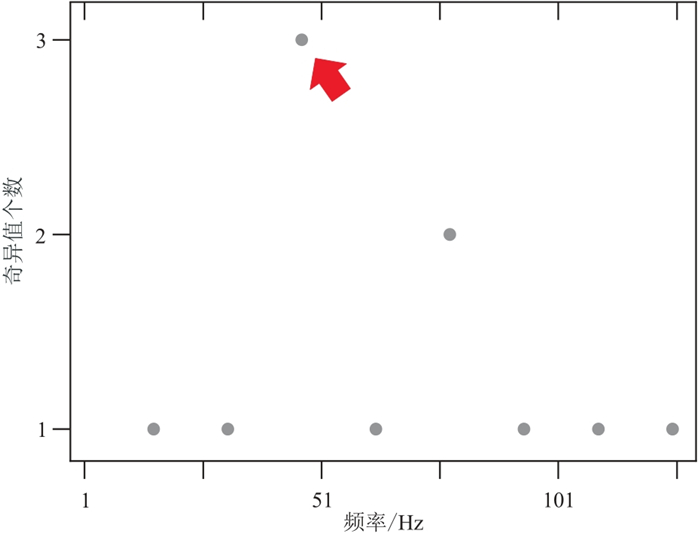
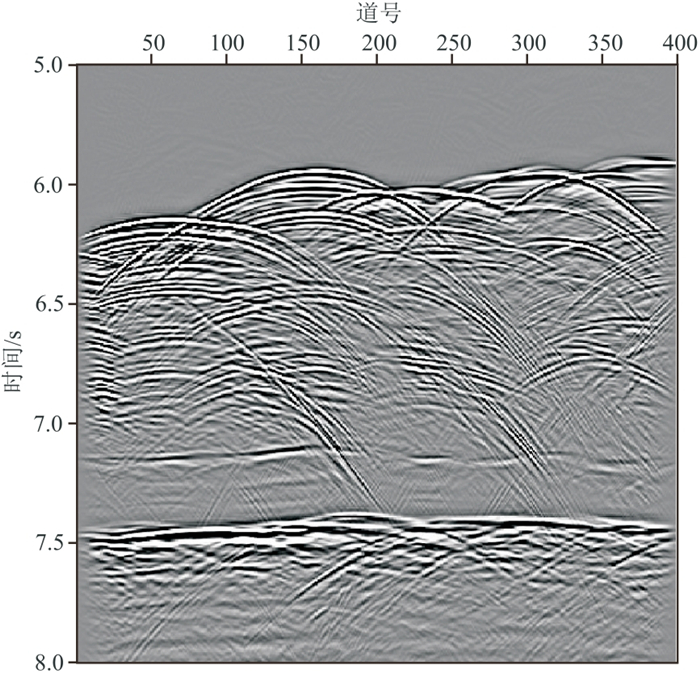
叠后实际数据来源于日本南海海槽俯冲带(Madagascar软件的开源数据),图 15截取了该数据中深水NT62-8二维测线[29]的一部分,共400道。由于实际数据较复杂,在分离反射和绕射波时采用分块处理的方式,经过多次实验确定的块的大小为12样点×24道。实际数据的频带为1~124 Hz,在该频段内由Cook距离识别出一个数据块的反射波奇异值个数由图 16所示,红色箭头所指处标明奇异值个数的最大值为3(奇异值的个数与分块的横向尺寸有关),从而每个频率上保留3个反射波奇异值,同时将全部数据块内的奇异值均设置为3。实际数据的复杂程度远比模拟数据高,特别是图 15中6.0~6.5 s存在大量的反射波和绕射波,二者均呈拟双曲线型态,对算法的分离能力提出了更高的要求。图 17和图 18是本文算法从叠后实际数据中分离出的反射波场和绕射波场。图 19~图 21分别为图 15、图 17和图 18的叠后时间偏移成像结果。
|
图 15 日本南海叠后DMO实际数据 |
|
图 16 实际数据的奇异值个数散点图 |
|
图 17 实际数据分离的反射波场 |
|
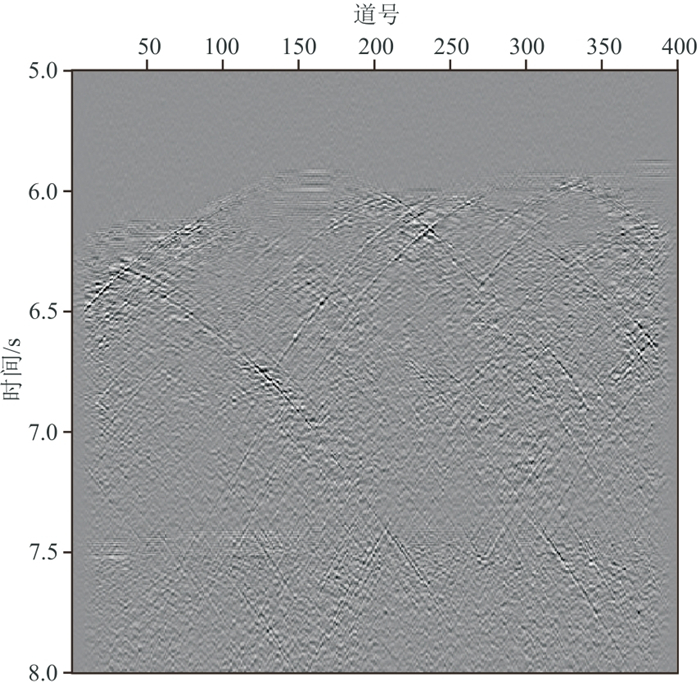
图 18 实际数据分离的绕射波场 |
|
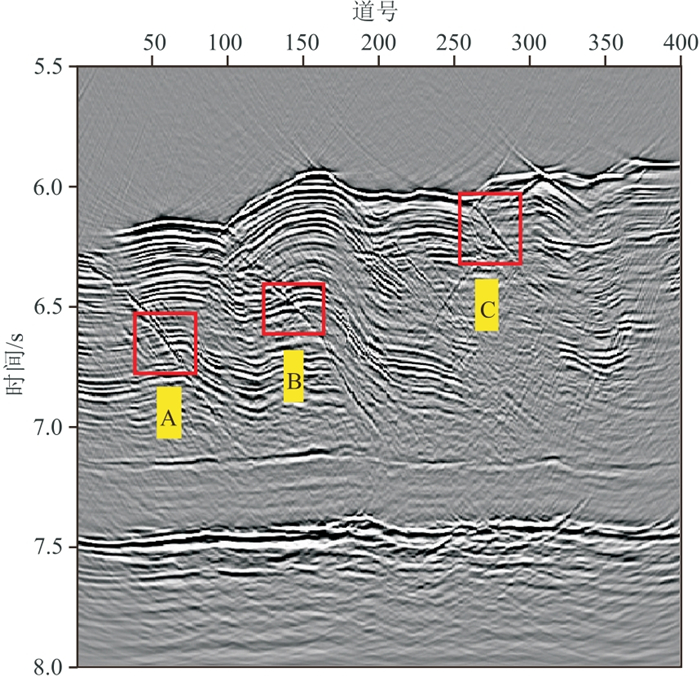
图 19 实际数据全波场的时间偏移结果 |
|
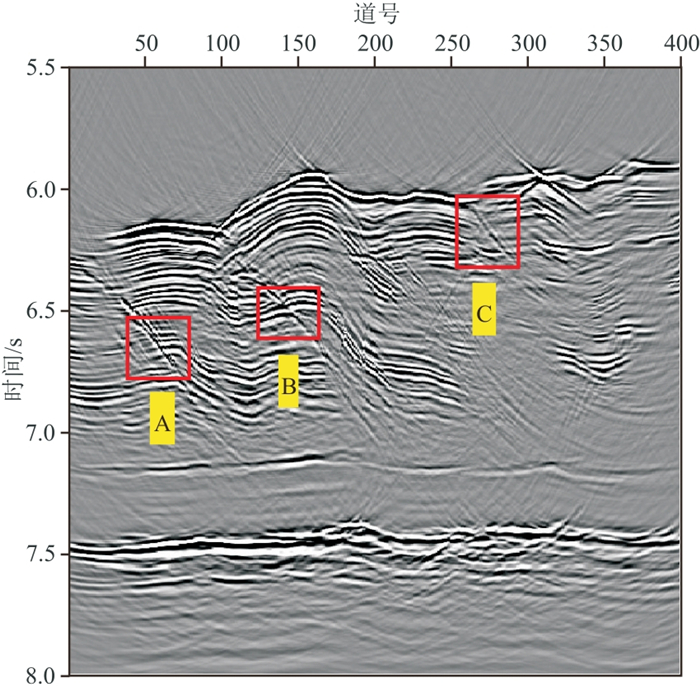
图 20 实际数据分离的反射波场偏移结果 |
|
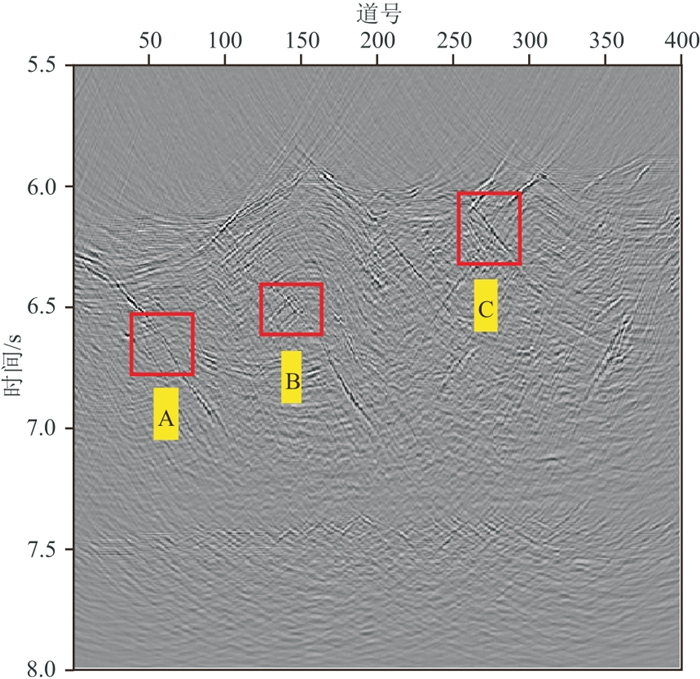
图 21 实际数据分离的绕射波场偏移结果 |
图 17分离出的反射波在7.2 s处的水平同相轴清晰可见。图 18中基本只含能量弱的绕射波,反射波基本被消除,仅有少量的反射能量残留。偏移处理后的反射波场中同相轴清晰且连续(图 20),但断层处清晰度较全波场偏移结果有所下降(对比图 19和图 20红色方框处)。绕射波偏移结果凸显了断层所在位置(图 21)。对全波场、反射波场和绕射波场偏移结果在三条断层处进行放大对比,如图 22所示,可以发现,绕射波偏移结果中断层位置更突出、刻画得更清晰,体现了绕射波对不连续地质体成像分辨率更高的优势。
综合以上分析可知,本文算法可以有效地从全波场数据中分离出反射波场和绕射波场。实验结果表明,分离出的绕射波场经过偏移后给予了断层、绕射点等小尺度地质异常体充足的照明度,获得了更加精细的成像结果。
4 讨论地震数据中一般会含有噪声,包括相干噪声和随机噪声。本文的方法将较大的奇异值对应成反射波,较小的奇异值对应成绕射波,因此在分离前需要消除相干和随机噪声。
阻尼因子的取值对于本文的分离结果有一定的影响。在数值实验中,处理不同的数据时使用的阻尼因子各不相同。阻尼效果在因子取值为1时最强,数值远离1时效果逐渐减弱,本文在处理过程中所获得的经验是通过试验的方式选择比1稍大的数值,才有可能获得良好的反射、绕射分离结果。
5 结论传统的MSSA绕射和反射波分离算法,其核心原理在于反射地震信号的低秩特性,通过截断反射波奇异值以实现波场分离。这种方法分离出的绕射波场中存在反射能量残留的现象,并且算法在计算过程中,奇异值的截断需要人工调参,不能适应大规模数据计算的需求。为此,本文采用MSSA的改进算法DMSSA作为绕射和反射波分离的框架,引入了阻尼因子以提升分离效果。为了解决反射波奇异值自动截断问题,本文采用Cook距离作为反射波奇异值识别的方法,并将这一方法嵌入到DMSSA框架中以实现自动分离绕射波场和反射波场。模拟和实际数据结果表明,使用本文方法提取的绕射波能清晰刻画诸如断层、绕射点等小尺度地质体。
| [1] |
陈明政, 邓光校, 朱生旺, 等. 绕射波分离成像技术在塔河油田碳酸盐岩地震弱反射储层预测中的应用[J]. 石油物探, 2015, 54(2): 234-240. CHENG Mingzheng, DENG Guangxiao, ZHU Shengwang, et al. Application of diffraction wave separation and imaging technique in weak seismic reflection of carbonate reservoir prediction in Tahe Oilfield[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 234-240. |
| [2] |
肖曦, 周鹏, 张益明, 等. 基于绕射信息提取技术的断裂识别方法及应用[J]. 石油地球物理勘探, 2021, 56(5): 1130-1136, 1179. XIAO Xi, ZHOU Peng, ZHANG Yiming, et al. Research and application of fracture identification method based on diffraction information extraction technology[J]. Oil Geophysical Prospecting, 2021, 56(5): 1130-1136, 1179. DOI:10.13810/j.cnki.issn.1000-7210.2021.05.019 |
| [3] |
肖广锐, 李尧, 张羽茹, 等. 绕射波成像在潜山裂缝储层预测中的应用——以渤中A气田为例[J]. 石油物探, 2022, 61(5): 812-820. XIAO Guangrui, LI Yao, ZHANG Yuru, et al. Application of diffraction wave imaging for fractured reservoir prediction of buried hill: A case study of BZ-A Oilfield[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 812-820. |
| [4] |
KLOKOV A, BAINA R, LANDA E, et al. Diffraction imaging for fracture detection: Synthetic case study[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3354-3358.
|
| [5] |
罗腾腾, 徐基祥, 孙夕平. 应用迭代收缩高分辨率Radon变换的绕射波分离与成像方法[J]. 石油地球物理勘探, 2021, 56(2): 313-322. LUO Tengteng, XU Jixiang, SUN Xiping. Diffraction wave separation and imaging based on high-resolution Radon transform on an iterative model shrinking approach[J]. Oil Geophysical Prospecting, 2021, 56(2): 313-322. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.013 |
| [6] |
CHEN X, CAO J J, YANG H L, et al. Diffraction separation and imaging based on double sparse transforms[J]. Petroleum Science, 2022, 19(2): 534-542. DOI:10.1016/j.petsci.2021.12.002 |
| [7] |
朱生旺, 李佩, 宁俊瑞. 局部倾角滤波和预测反演联合分离绕射波[J]. 地球物理学报, 2013, 56(1): 280-288. ZHU Shengwang, LI Pei, NING Junrui. Reflection/diffraction separation with a hybrid method of local dip filter and prediction inversion[J]. Chinese Journal of Geophysics, 2013, 56(1): 280-288. |
| [8] |
孔雪, 李振春, 黄建平, 等. 基于平面波记录的绕射目标成像方法研究[J]. 石油地球物理勘探, 2012, 47(4): 674-682. KONG Xue, LI Zhenchun, HUANG Jianping, et al. Diffracting objective imaging based on plane wave record[J]. Oil Geophysical Prospecting, 2012, 47(4): 674-682. DOI:10.13810/j.cnki.issn.1000-7210.2012.04.014 |
| [9] |
刘斌, 邸志新, 李晓峰, 等. 一种基于局部倾角估计的倾角域绕射波分离与成像方法[J]. 地球物理学进展, 2014, 29(5): 2204-2210. LIU Bin, DI Zhixin, LI Xiaofeng, et al. Separation and imaging method of diffraction based on local dip estimation in the dip-angle domain[J]. Progress in Geophysics, 2014, 29(5): 2204-2210. |
| [10] |
LIN P, PENG S P, HUANG X G, et al. Plane-wave destruction‑based workflow for prestack diffraction separation in the shot domain[J]. Pure and Applied Geophysics, 2022, 179(6-7): 2215-2229. DOI:10.1007/s00024-022-03034-8 |
| [11] |
WANG T, PENG S P, LIN P, et al. Diffraction enhancement using the double sparse dictionary method[J]. Acta Geophysica, 2023, 71(3): 1259-1271. |
| [12] |
赵惊涛, 彭苏萍, 陈宗南, 等. 煤矿隐蔽致灾地质体地震绕射波探测方法[J]. 矿业科学学报, 2022, 7(1): 1-8. ZHAO Jingtao, PENG Suping, CHEN Zongnan, et al. Seismic diffraction detection method for geological hidden disasters in coal mining[J]. Journal of Mining Science and Technology, 2022, 7(1): 1-8. |
| [13] |
SERFATY Y, ITAN L, CHASE D, et al. Wavefield separation via principle component analysis and deep learning in the local angle domain[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 991-995.
|
| [14] |
LOWNEY B, LOKMER I, O̓ BRIEN G, et al. Pre-migration diffraction separation using generative adversarial networks[J]. Geophysical Prospecting, 2021, 69(5): 949-967. DOI:10.1111/1365-2478.13086 |
| [15] |
LOWNEY B, LOKMER I, O'BRIEN G. Multi-domain diffraction identification: A supervised deep learning technique for seismic diffraction classification[J]. Computers and Geosciences, 2021, 155(3): 104845-104861. |
| [16] |
盛同杰, 赵惊涛, 彭苏萍. 地震绕射波弱信号U-net网络提取方法[J]. 地球物理学报, 2023, 66(3): 1192-1204. SHENG Tongjie, ZHAO Jingtao, PENG Suping. Seismic diffraction extraction method using U-net for weak signals[J]. Chinese Journal of Geophysics, 2023, 66(3): 1192-1204. |
| [17] |
马铭, 包乾宗. 利用Encoder-Decoder框架的深度学习网络实现绕射波分离及成像[J]. 石油地球物理勘探, 2023, 58(1): 56-64. MA Ming, BAO Qianzong. Diffraction wave separation and imaging with deep learning network based on encoder-decoder framework[J]. Oil Geophysical Prospecting, 2023, 58(1): 56-64. DOI:10.13810/j.cnki.issn.1000-7210.2023.01.005 |
| [18] |
魏巍, 高鸿, 刘忠岩. 奇异值分解技术在绕射波分离成像中的应用研究[J]. 石油物探, 2020, 59(2): 236-241. WEI Wei, GAO Hong, LIU Zhongyan. Separation and imaging of seismic diffractions using singular value decomposition[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 236-241. |
| [19] |
CHEN Z N, ZHAO J T, PENG S P, et al. Separating seismic diffractions by an improved Cook-distance singular value decomposition method[J]. Geophysics, 2023, 88(1): WA377-WA386. DOI:10.1190/geo2022-0284.1 |
| [20] |
HUANG W L, WANG R Q, CHEN Y K, et al. Damped multichannel singular spectrum analysis for 3D random noise attenuation[J]. Geophysics, 2016, 81(4): V261-V270. DOI:10.1190/geo2015-0264.1 |
| [21] |
朱跃飞, 曹静杰, 殷晗钧. 一种自动判定保留的奇异值个数的地震随机噪声压制算法[J]. 石油地球物理勘探, 2022, 57(3): 570-581. ZHU Yuefei, CAO Jingjie, YIN Hanjun. Seismic random noise suppression algorithm with automatic determination of the number of retained singular values[J]. Oil Geophysical Prospecting, 2022, 57(3): 570-581. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.008 |
| [22] |
曹静杰, 许昌昊, 朱跃飞. 基于层次聚类多道奇异谱分析的地震数据同时重建与去噪方法[J]. 石油地球物理勘探, 2023, 58(4): 818-829. CAO Jingjie, XU Changhao, ZHU Yuefei. Simultaneous reconstruction and denoising of seismic data using multi‑channel singular spectrum analysis based on hierarchical clustering[J]. Oil Geophysical Prospecting, 2023, 58(4): 818-829. DOI:10.13810/j.cnki.issn.1000-7210.2023.04.007 |
| [23] |
LIN P, ZHAO J T, PENG S P, et al. A robust adaptive rank‑reduction method for 3D diffraction separation and imaging[J]. Pure and Applied Geophysics, 2021, 178(8): 2917-2931. DOI:10.1007/s00024-021-02778-z |
| [24] |
黄建平, 李闯, 李国磊, 等. 基于奇异谱分析的联合去噪及规则化方法[J]. 地球物理学进展, 2014, 29(4): 1666-1671. HUANG Jianping, LI Chuang, LI Guolei, et al. Simultaneous seismic data de‑noising and regularization method based on singular spectrum analysis[J]. Progress in Geophysics, 2014, 29(4): 1666-1671. |
| [25] |
COOK R D. Detection of influential observation in linear regression[J]. Technometrics, 2000, 42(1): 65-68. DOI:10.1080/00401706.2000.10485981 |
| [26] |
ALGUR S, BIRADAR J. Cooks distance and Mahanabolis distance outlier detection methods to identify review spam[J]. International Journal of Engineering and Computer Science, 2017, 6(6): 21638-21649. |
| [27] |
JIANG J G, SUN L, FAN Z Y, et al. Outlier detection and sequence reconstruction in continuous time series of ocean observation data based on difference analysis and the Dixon criterion[J]. Limnology and Oceanography-Methods, 2017, 15(11): 916-927. DOI:10.1002/lom3.10212 |
| [28] |
Pinho L G B, Nobre J S, Singer J M. Cook's distance for generalized linear mixed models[J]. Computational Statistics & Data Analysis, 2015, 82: 126-136. |
| [29] |
MOORE G, SHIPLEY T, STOFFA P, et al. Structure of the Nankai Trough Accretionary Zone from multichannel seismic reflection data[J]. Journal of Geophysical Research: Solid Earth, 1990, 95(B6): 8753-8765. DOI:10.1029/JB095iB06p08753 |



 曹静杰,河北省石家庄市槐安东路136号河北地质大学地球科学学院,050031。Email:
曹静杰,河北省石家庄市槐安东路136号河北地质大学地球科学学院,050031。Email:
