2. 海洋油气勘探国家工程研究中心, 北京 100028;
3. 自然资源部矿山地质灾害成灾机理与防控重点实验室, 陕西西安 710054
2. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China;
3. Key Laboratory of Geological Disaster Mechanism and Prevention, Ministry of Natural Resources, Xi'an, Shaanxi 710054, China
高分辨率的地震数据更有利于进行地震解释、储层预测和属性分析[1]。地震高分辨率处理的目的是希望获得更精确的反射系数或弹性参数模型,反褶积则是通过压缩地震子波提高地震数据纵向分辨率的有效方案[2]。常规的反褶积方法大多建立在褶积模型上,即认为地震子波在地下传播过程中始终不变。而地震子波的提取依据反射系数是否已知可分为确定性方法和统计性方法。确定性方法主要有线性反演法、维纳滤波法、谱除法、贝叶斯法等,统计性方法主要有自相关法、地震记录谱平滑法、Z变换法、基于分形的方法、复赛谱法、高阶统计量法等[3-5]。前者需要通过测井资料计算反射系数序列,在井资料匮乏的地区难以广泛应用;后者不需要测井资料,而是假设地震子波和反射系数满足一定的条件,从地震记录的统计信息中提取子波。但上述的方法都假设地震记录为稳态,只能在有限的频带范围内压缩地震子波。由于地层的黏滞性和非均质性,实际地震子波在地下传播过程中受到地层吸收的影响,其振幅、相位、频率等都会发生变化,地震子波为最小相位的假设条件与实际情况并不相符,往往更接近于混合相位。这使得传统稳态反褶积方法在处理非稳态的地震数据时得到的反射系数不准确,影响后续的地震解释和储层预测[6]。
基于此,地球物理工作者对地层的吸收机制做了一系列研究,并提出了许多针对非稳态地震数据的处理方法和技术。一方面是从地震数据中提取时变子波,可以分为两类,一类是基于分段的时变子波估计,另一类是基于时频域谱模拟的时变子波估计。冯晅等[7]提出人工划分时窗估计地震子波;高静怀等[8]给出了变子波模型的近似表达式,运用Gabor变换分窗将地震记录近似划分为具有稳态特性的地震记录段,有效地提高了地震资料的分辨率;Van der Baan等[9-10]利用最大峰度估计时变子波;Economou等[11]通过使用分段提取的地震子波校正相位失真;张漫漫等[12]提出一种基于时频谱模拟的时变子波估计方法;戴永寿等[13]提出了基于自适应分段的时变混合相位子波估计,在自适应分段的基础上,利用高阶累计量双谱法估计各个段内的振幅谱以及相位谱,从而实现对混合相位子波的准确估计。时频域谱模拟的子波提取方法在估计子波相位谱时一般基于子波最小相位或者零相位的假设,这与实际地震子波一般是混合相位的事实不符,从而影响了反褶积的效果。分时窗的时变子波提取方法通过地震记录的分段处理,将每段视为近似平稳地震记录提取子波,相比于传统常规的稳态子波提取方法精度有所提高,但其忽略了地震子波在传播过程中变化的连续性,并没有实现真正意义上的针对各个采样点的地震子波估计。
另一方面是对非稳态地震记录进行补偿校正,使其近似成为稳态地震记录,再利用传统的方法提取子波。反Q滤波作为补偿地层吸收衰减的有效手段之一,该方法可以校正相位畸变和补偿振幅衰减,前提是Q值的分布为已知[14-16]。因此,地层Q值的估计变得尤为重要。现有的Q值的估计方法按照数据域的不同可以划分为时间域、频率域和时频域三大类。时间域方法主要有振幅衰减法、上升时间法、子波模拟法和解析信号法等;频率域中估计Q值的方法有谱比法、匹配法和谱模拟法等。相比于时间域,频率域信息受噪声影响较小,所以频率域方法稳定性大多优于时间域方法[5-6]。然而频率域的方法需要选取时窗并做傅里叶变换,时窗函数及长度的选择是个难题,并且信号频谱反应的是整体信号的平均效应,这些都会降低Q值估计的精度。为此,许多学者尝试在时频域求取Q值[6]。Wang[17]通过Gabor变换将叠后地震数据从时间域转换到时频域求取Q值;Reine等[18]比较了四种时频域中谱比法的Q值估计结果,认为变窗口的时频变换法更稳定、更精确;刘国昌等[19]利用整形正则化改进谱比法中的除法运算,在S变换的基础上提出了稳定的Q值估计方法;刘洋等[20]和刘喜恒等[21]都在局部时频分解的基础上估计Q值。
由于地震子波传播的时变性,地震数据为地震时变子波与反射系数的褶积,也有学者针对非稳态反褶积方法开展研究[22-23],其主要思想是通过平面波传播理论和褶积模型构建反演方程,加入相应的稳定约束,最终得到反射系数模型。Margrave等[24]考虑到地层的吸收效应,提出非稳态褶积模型和非稳态Gabor反褶积方法,实现了高分辨率地震反褶积;Yuan等[25]推导了一种非线性时变褶积模型,并提出了一种基于稀疏贝叶斯学习的时变反褶积方法提高分辨率。然而无论是时变反褶积还是非稳态反射系数反演方法,时变子波和Q模型已知的假设条件在一定程度上不可避免,而Q值或子波的误差均会影响最终的高分辨率处理结果[23]。不准确的子波相位也会导致反褶积结果变差[26],Wang等[27]提出一种基于蚁群优化算法的子波相位估计方法,结果表明混合相位子波反褶积能展示更多的细节信息。
综上所述,为了保证高分辨率处理结果的相对振幅关系以及适应地震数据的非稳态特征,本文通过联合子波提取与Q值估计,将能够表征衰减特性的品质因子Q引入到褶积模型中,构造时变子波矩阵,实现了基于非稳态褶积模型的时变反褶积。应用遗传算法可以快速得到混合相位地震子波和地层品质因子Q。理论数据和实际数据的试算结果证实了方法的有效性。
1 方法原理 1.1 子波的Z变换子波相位谱与频率密切相关,对子波进行Z变换求根,可通过根变换的方式实现子波相位的变化。假设子波w(t)的离散形式为(w0, w1, …, wn),根据Z变换可以将子波表示为
| $ \begin{array}{l}w\left(t\right)={\mathrm{Z}}^{-1}\left[{w}_{n}(z-{a}_{1})(z-{a}_{2})\cdots (z-{a}_{n})\right]\\ \begin{array}{cc}& \end{array}={w}_{n}(-{a}_{1}, 1)\mathrm{*}(-{a}_{2}, 1)\mathrm{*}\cdots \mathrm{*}(-{a}_{n}, 1)\end{array} $ | (1) |
式中:Z-1表示逆Z变换;(a1, a2, …, an)为子波w(t)在Z变换域的根;
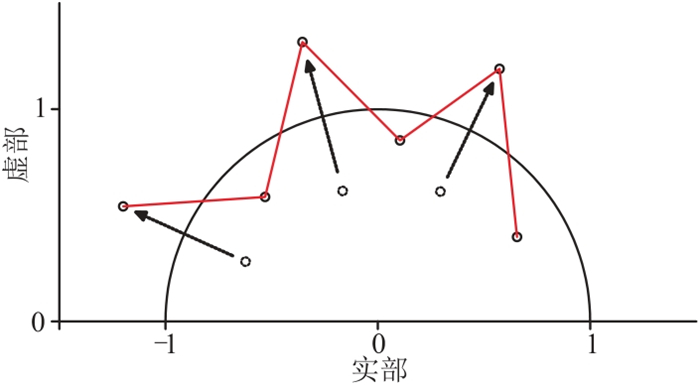
|
图 1 根变换示意图 |
根据衰减传播理论,没有进行振幅补偿和相位校正的叠后地震信号可以表示为[24]
| $ s\left(t\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}r\left(\tau \right)\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }W\left(\omega \right)b(\tau , \omega ){\mathrm{e}}^{\mathrm{i}\omega t}\mathrm{d}\omega \mathrm{d}\tau $ | (2) |
式中:W(ω)为初始子波w(t)的频谱;r(τ)是反射系数序列;b(τ, ω)为衰减函数。假设品质因子Q与频率无关,利用Kjartansson Q模型[28]构建衰减函数b(τ, ω)
| $ b(\tau , \omega )=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\omega \tau {\left(\frac{\omega }{{\omega }_{\mathrm{c}}}\right)}^{\gamma }\left(\mathrm{i}+\frac{1}{2Q}\right)\right] $ | (3) |
式中:ωc是参考角频率;γ=―1/(πQ)。根据式(2)和传播过程中地震子波在水平方向上保持不变的假设,可以将非稳态地震记录简化为初始地震子波、Q模型和反射系数序列的矩阵乘积
| $ \boldsymbol{s}=\frac{1}{n}{\mathbf{F}}^{-1}\boldsymbol{W}\boldsymbol{B}\boldsymbol{r}+\boldsymbol{\varepsilon } $ | (4) |
式中:s为单道地震记录;F-1表示逆傅里叶变换;W为子波矩阵;B为衰减函数矩阵;r为反射系数序列;ε为噪声。
传统反射系数反演或者非稳态反褶积方法都假设子波和Q值已知,而本文通过测井数据获取真实地层反射系数r,并用于地震子波和Q模型的估计。首先根据井旁地震记录拟合得到子波w(t)的振幅谱,然后利用Z变换域的根变换策略不断改变子波的相位谱,并通过合成地震记录与井旁道记录匹配估计出子波的唯一相位,同时得到精确的地层Q模型的估计结果。因其计算量巨大,本文通过引入遗传算法减小计算量,并最大化目标函数,即相关系数
| $ C=\frac{\sum\limits_{t}s\left(t\right){s}^{\text{'}}\left(t\right)}{\sum\limits_{t}{\left[s\left(t\right)\right]}^{2}{\left[{s}^{\text{'}}\left(t\right)\right]}^{2}} $ | (5) |
作为遗传算法的适应度函数。式中:s(t)是井旁地震记录;
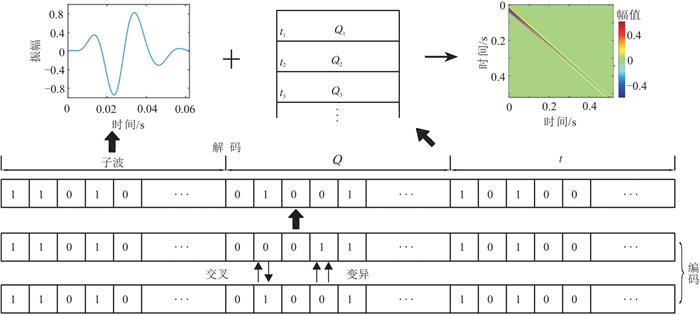
|
图 2 子波和Q模型的编码、解码变换示意图 编码链条的前端1和0表示子波是否进行移根,编码链条的后端可以转化为Q模型的十进制值。 |
图 3给出了地震子波及Q值估计的算法流程。首先利用自相关估计出子波的振幅谱,进而估计出最小相位子波。将该子波作为初始子波,计算其Z变换的根,确定Q模型参数的取值范围,进行子波移根和Q模型的二进制编码。然后按照遗传算法的进化策略生成子波移根和Q模型的编码集合作为初始种群,对子波移根和Q模型编码集合进行解码,计算适应度函数值,即井震匹配相关系数,如果当前迭代的相关系数极大值满足所设值或者进化代数达到所设代数,则进化终止。否则,利用遗传算法的选择、交叉、变异等操作生成子代,重复以上步骤,直到满足条件为止,最终输出最佳地震子波和Q模型估计结果。
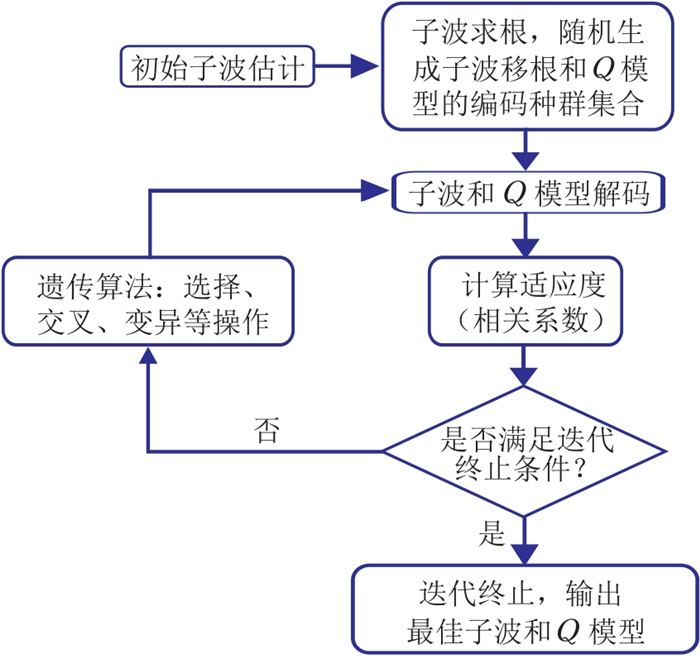
|
图 3 地震子波及Q值估计算法流程 |
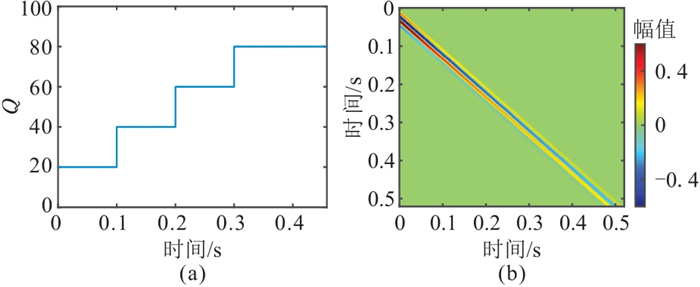
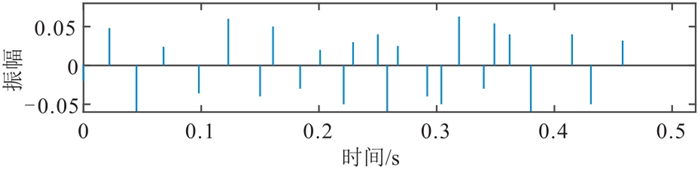
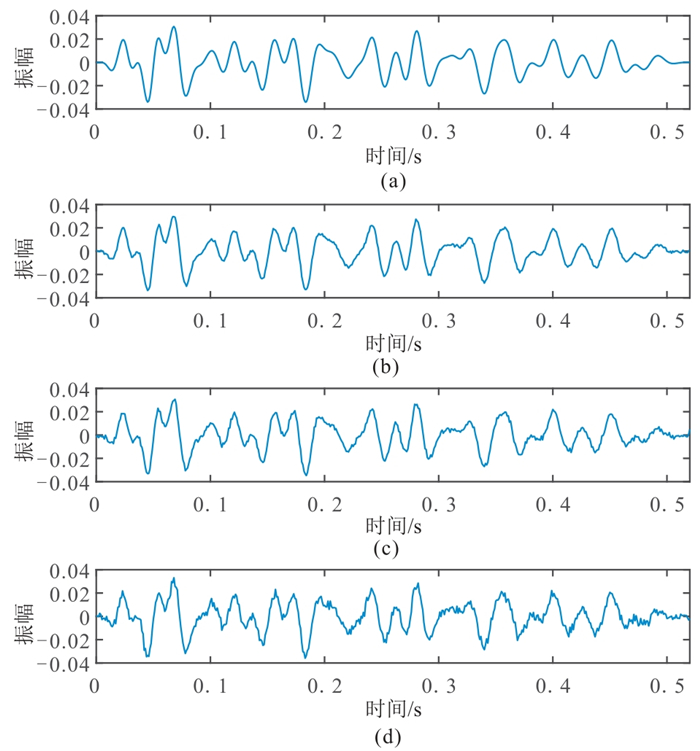
应用理论合成数据验证本文方法的可行性及稳定性。理论混合相位初始地震子波的主频为30 Hz,如图 4a所示, 其Z变换根的分布如图 4b所示,可以看出混合相位子波在单位圆内外均有根。4层理论Q模型的每一层Q值为常数(图 5a)。图 5b是利用式(4)中F-1WB计算得到的时变子波矩阵,可见,随着时间的推移,子波幅值减小,波形拉伸,反映了地层吸收对子波的影响。利用式(4)和稀疏反射系数序列(图 6)合成不同信噪比(SNR)的非稳态地震数据(图 7)。本文方法假设未知参量为地震子波相位、Q及Q变化的时间位置t。本文测试给定遗传算法的种群数为50,进化代数为500,交叉概率为0.8,变异概率为0.2,目标函数截止变化量为1×10-7,即当迭代次数达到500或者目标函数变化值小于1×10-7时,停止迭代。
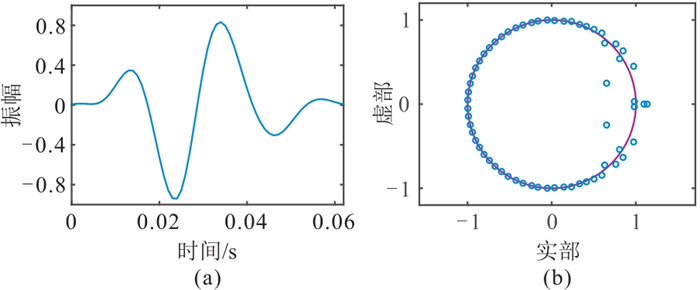
|
图 4 真实混合相位子波(a)及Z变换根的分布(b) |
|
图 5 理论Q模型(a)及子波矩阵(b) |
|
图 6 理论反射系数序列 |
|
图 7 合成的不同噪声水平非稳态地震记录 (a)无噪;(b)SNR=25 dB;(c)SNR=20 dB;(d)SNR=15 dB |
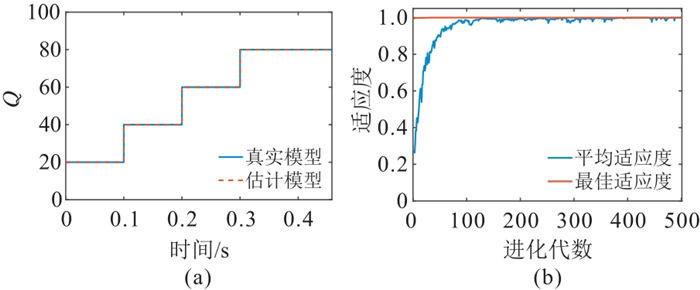
在无噪条件下,本文方法最终输出的混合相位地震子波及其Z变换根的分布如图 8所示,可见,估计子波与真实子波完全吻合,同时二者的Z变换根的分布也完全重合。估计的Q模型与真实模型也完全匹配(图 9a)。图 9b为目标函数值随进化代数的变化曲线,其中平均适应度为当前迭代中所有个体的适应度函数(相关系数)的平均值,最佳适应度为当前代中所有个体的适应度函数的最大值,可以看到在种群进化过程中,平均适应度和最佳适应度逐渐增大,平均适应度逐渐向最佳适应度靠近,并且最佳适应度值达到了1,即合成地震记录与真实地震记录相关系数为1,即获得了最优解。

|
图 8 无噪条件下本文方法估计的混合相位子波(a)及其Z变换根的分布(b)与真实子波的对比 |
|
图 9 无噪条件下本文方法估计的Q模型与真实模型的对比(a)及目标函数值的变化曲线(b) |
图 10a~图 10c为由图 7b~图 7d不同噪声水平记录估计的子波,图 11左为估计的Q模型。对比可以看出:在不同噪声条件下估计的子波与真实子波基本吻合,对应Z变换根的分布也基本吻合;同时估计Q模型与真实Q模型基本匹配;虽然随着噪声水平的增加,估计与真实Q模型的误差在逐渐增大,但均保持在较小范围内。同样,图 11右为不同噪声水平下算法的进化曲线,平均适应度逐渐向最优适应度靠拢,并且最优适应度均达到了0.95以上,这表明该方法具有较强的抗随机干扰能力。
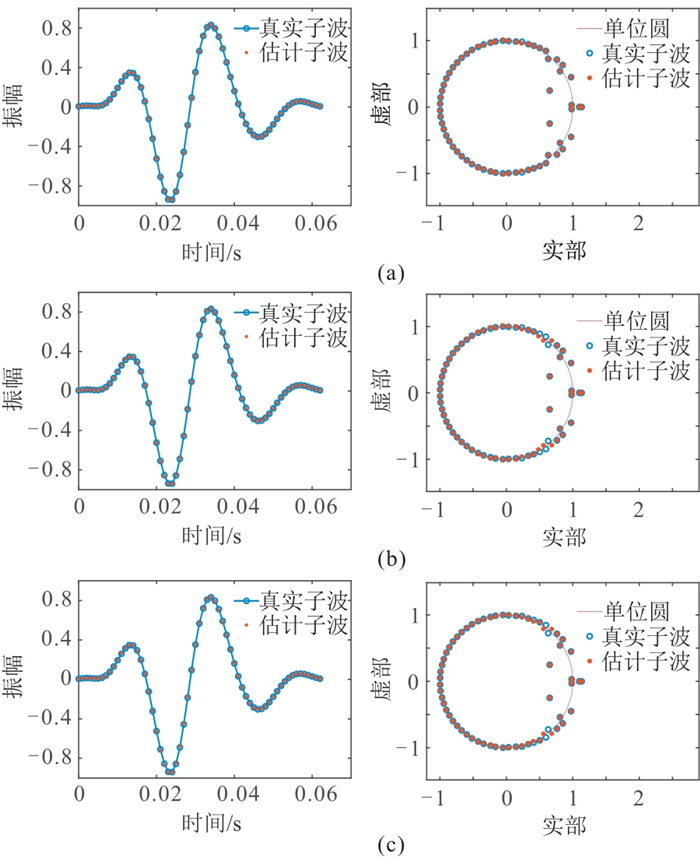
|
图 10 不同噪声水平时本文方法估计的混合相位子波(左)及其Z变换根的分布(右)与真实子波的对比 (a)SNR=25 dB;(b)SNR=20 dB;(c)SNR=15 dB |
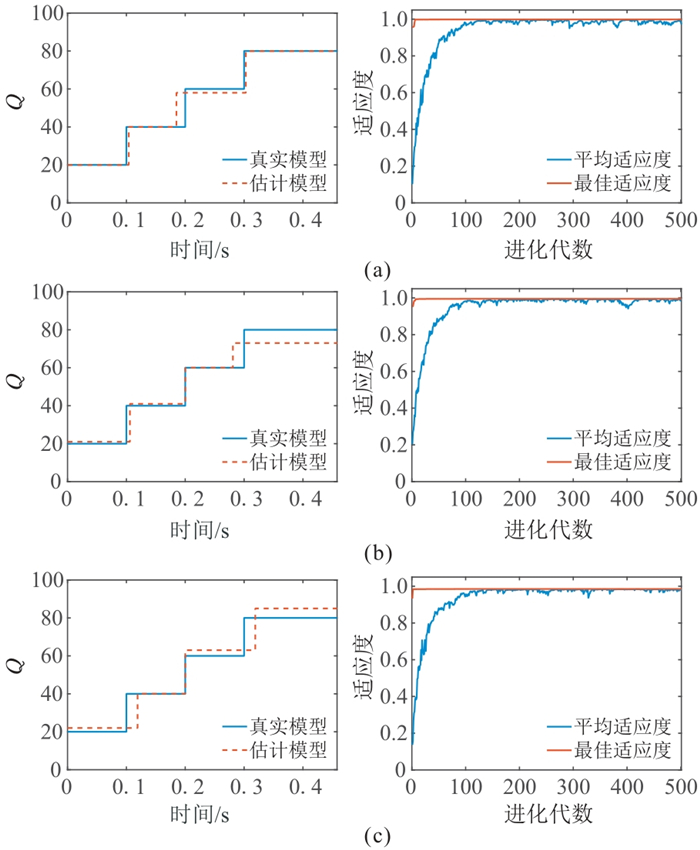
|
图 11 不同噪声水平时本文方法估计的Q模型与真实模型的对比(左)及目标函数的变化曲线(右) (a)SNR=25 dB;(b)SNR=20 dB;(c)SNR=15 dB |
选择一条实际过井地震剖面(图 12)测试本文方法的实用性。该剖面共900道,采样间隔为1 ms。在该条剖面上布有天然气探井,井位于第76和第760道。
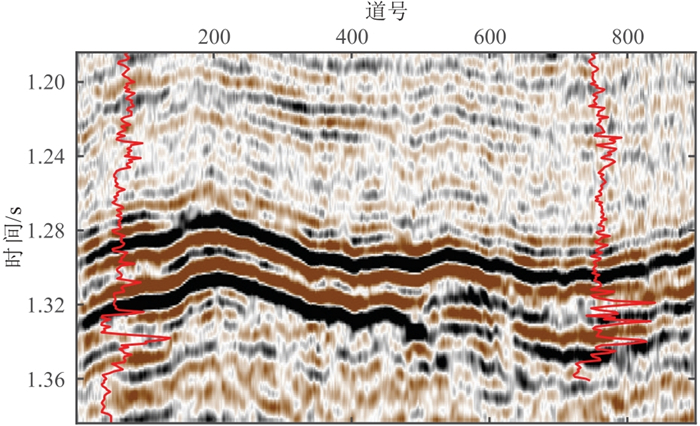
|
图 12 实际地震剖面 红色实线为井的声波时差曲线投影。 |
根据第76道对应的测井数据计算得到地层反射系数,应用新方法进行混合相位子波提取和Q值估计,为了减少问题的多解性并提升求解效率,针对该数据能量分布的特点,将其划分为4个部分,即假设为4层的等效Q模型,算法设定种群规模为80,进化代数为600,交叉概率为0.8,变异概率为0.2。
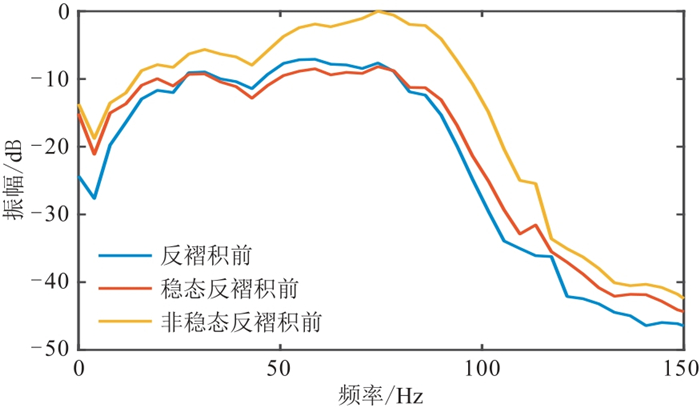
图 13a为混合相位初始子波估计结果,其中最小相位子波是通过井旁地震记录拟合得到的,混合相位子波是本文方法估计的。图 13b为输出的Q模型曲线,可以看出,随着时间的增加,Q值整体上呈增大的趋势,只是在1.335~1.384 s之间有所减小。与原始地震剖面对比可见,在Q值较小的区段,信号能量相对较弱。图 13c为遗传算法进化曲线,目标函数值在进化过程中逐渐增大,平均适应度与最佳适应度同时提高,初始平均适应度为0.41,最终最佳适应度值达到了0.62,这表明了方法的收敛性。最小相位子波合成记录与原始记录的匹配度为0.57,而估计子波合成记录与原始记录的匹配度为0.62,即经过子波相位和Q值自适应调整,井震匹配程度有所提高。为了说明新方法相较于传统方法在子波和Q模型输出方面的准确性,利用估计得到的混合相位子波对地震记录分别进行稳态反褶积和非稳态反褶积处理,结果如图 14所示,可以看出:混合相位子波稳态反褶积相比于原始记录分辨率略有提高;利用本文方法得到的子波及Q模型进行反褶积处理后的资料整体能量得到了补偿,视分辨率明显提高,同相轴连续性增强,波形更为自然,丰富了细节信息,地层结构与测井曲线基本吻合,效果明显优于稳态反褶积。图 15为反褶积后与原始剖面的振幅谱对比。反褶积前的频带为15~90 Hz,而非稳态反褶积后的频带为10~100 Hz,提高了主频、拓宽了频带。

|
图 13 实际地震数据子波(a)和Q模型(b)的估计结果及目标函数的进化曲线(c) |
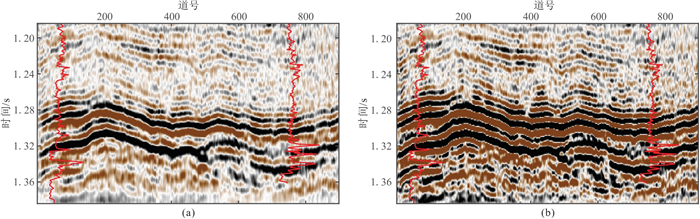
|
图 14 实际地震剖面混合相位子波稳态(a)与非稳态(b)反褶积结果对比 |
|
图 15 实际地震剖面反褶积前、后振幅谱对比 |
本文以合成地震记录与井旁道记录的互相关系数为适应度函数,将子波提取与Q值估计问题有效结合起来,提出了基于全局优化策略的非稳态地震数据混合相位子波和地层Q模型同时估计的方法。本文方法不仅可以输出更接近实际传播情况的混合相位子波,而且实现了对地层Q模型有效估计。理论数据测试说明了方法有较强的实用性和抗噪能力。实际数据处理结果井震匹配度进一步提升,从而验证了方法的实用性。利用估计的地震子波和Q模型进行非稳态反褶积处理,能够拓宽地震剖面频带、提高分辨率,同时能够补偿深部弱能量。
| [1] |
刘汉卿, 罗明, 孙辉, 等. 应用匹配追踪算法的高分辨率处理方法[J]. 石油地球物理勘探, 2022, 57(6): 1325-1331. LIU Hanqing, LUO Ming, SUN Hui, et al. High-resolution processing method based on matching pursuit algorithm[J]. Oil Geophysical Prospecting, 2022, 57(6): 1325-1331. DOI:10.13810/j.cnki.issn.1000-7210.2022.06.007 |
| [2] |
卫泽, 潘树林, 程祎, 等. 自适应变分模态分解同态反褶积方法[J]. 石油地球物理勘探, 2023, 58(1): 105-113. WEI Ze, PAN Shulin, CHENG Yi, et al. Homomorphic deconvolution method based on adaptive variational mode decomposition[J]. Oil Geophysical Prospecting, 2023, 58(1): 105-113. DOI:10.13810/j.cnki.issn.1000-7210.2023.01.011 |
| [3] |
高少武, 赵波, 贺振华, 等. 地震子波提取方法研究进展[J]. 地球物理学进展, 2009, 24(4): 1384-1391. GAO Shaowu, ZHAO Bo, HE Zhenhua, et al. Research progress of seismic wavelet extraction[J]. Progress in Geophysics, 2009, 24(4): 1384-1391. |
| [4] |
杨培杰, 印兴耀. 地震子波提取方法综述[J]. 石油地球物理勘探, 2008, 43(1): 123-128. YANG Peijie, YIN Xingyao. Summary of seismic wavelet pick‑up[J]. Oil Geophysical Prospecting, 2008, 43(1): 123-128. DOI:10.13810/j.cnki.issn.1000-7210.2008.01.02 |
| [5] |
于永才. 地震子波估计与地震波吸收衰减参数估计方法研究[D]. 北京: 中国石油大学(北京), 2012.
|
| [6] |
王青晗. 非平稳地震数据高分辨率处理关键技术研究[D]. 吉林长春: 吉林大学, 2022.
|
| [7] |
冯晅, 刘财, 杨宝俊, 等. 分时窗提取地震子波及在合成地震记录中的应用[J]. 地球物理学进展, 2002, 17(1): 71-77. FENG Xuan, LIU Cai, YANG Baojun, et al. The extractive method of seismic wavelet in different time window and the application in synthetic seismogram[J]. Progress in Geophysics, 2002, 17(1): 71-77. |
| [8] |
高静怀, 汪玲玲, 赵伟. 基于反射地震记录变子波模型提高地震记录分辨率[J]. 地球物理学报, 2009, 52(5): 1289-1300. GAO Jinghuai, WANG Lingling, ZHAO Wei. Enhancing resolution of seismic traces based on the chan- ging wavelet model of the seismogram[J]. Chinese Journal of Geophysics, 2009, 52(5): 1289-1300. |
| [9] |
VAN DER BAAN M. Time-varying wavelet estimation and deconvolution by kurtosis maximization[J]. Geophysics, 2008, 73(2): V11-V18. DOI:10.1190/1.2831936 |
| [10] |
VAN DER BAAN M, Fomel S. Nonstationary phase estimation using regularized local kurtosis maximization[J]. Geophysics, 2009, 74(6): A75-A80. DOI:10.1190/1.3213533 |
| [11] |
ECONOMOU N, VAFIDIS A. GPR data time varying deconvolution by Kurtosis maximization[J]. Journal of Applied Geophysics, 2012, 81: 117-121. DOI:10.1016/j.jappgeo.2011.09.004 |
| [12] |
张漫漫, 戴永寿, 张亚南, 等. 基于时频域谱模拟的时变子波估计方法[J]. 石油物探, 2014, 53(6): 675-682. ZHANG Manman, DAI Yongshou, ZHANG Yanan. Time-variant seismic wavelet estimation method based on spectral modeling in time‑frequency domain[J]. Geophysical Prospecting for Petroleum, 2014, 53(6): 675-682. |
| [13] |
戴永寿, 王晓波, 丁进杰, 等. 自适应分段的时变子波估计方法[J]. 石油地球物理勘探, 2015, 50(4): 607-612. DAI Yongshou, WANG Xiaobo, DING Jinjie, et al. Time‑variant wavelet estimation based on adaptive segmentation[J]. Oil Geophysical Prospecting, 2015, 50(4): 607-612. DOI:10.13810/j.cnki.issn.1000-7210.2015.04.005 |
| [14] |
WANG Y H. Quantifying the effectiveness of stabilized inverse Q filtering[J]. Geophysics, 2003, 68(1): 337-345. DOI:10.1190/1.1543219 |
| [15] |
WANG Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [16] |
WANG Y H. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. DOI:10.1190/1.2192912 |
| [17] |
WANG Y H. Q analysis on reflection seismic data[J]. Geophysical Research Letters, 2004, 31(17): L17606. |
| [18] |
REINE C, VAN DER BAAN M, CLARK R. The robustness of seismic attenuation measurements using fixed‑ and variable‑window time‑frequency transforms[J]. Geophysics, 2009, 74(2): WA123-WA135. DOI:10.1190/1.3043726 |
| [19] |
刘国昌, 陈小宏, 杜婧, 等. 基于整形正则化和S变换的Q值估计方法[J]. 石油地球物理勘探, 2011, 46(3): 417-422. LIU Guochang, CHEN Xiaohong, DU Jing, et al. Seismic Q estimation using S-transform with regulari- zed inversion[J]. Oil Geophysical Prospecting, 2011, 46(3): 417-422. DOI:10.13810/j.cnki.issn.1000-7210.2011.03.008 |
| [20] |
刘洋, 李炳秀, 刘财, 等. 局部时频变换域地震波吸收衰减补偿方法[J]. 吉林大学学报(地球科学版), 2016, 46(2): 594-602. LIU Yang, LI Bingxiu, LIU Cai, et al. Attenuation compensation method of seismic wave in the local time- frequency transform domain[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(2): 594-602. |
| [21] |
刘喜恒, 刘国昌, 崔永谦, 等. 局部时频变换横向约束Q值估计方法[J]. 石油地球物理勘探, 2016, 51(5): 868-874. LIU Xiheng, LIU Guochang, CUI Yongqian, et al. Q estimation with lateral constraint based on local time-frequency transform[J]. Oil Geophysical Prospecting, 2016, 51(5): 868-874. DOI:10.13810/j.cnki.issn.1000-7210.2016.05.004 |
| [22] |
柴新涛. 非稳态地震数据反射系数反演方法研究与应用[D]. 北京: 中国石油大学(北京), 2016.
|
| [23] |
马铭. 自适应评价空间关系的稀疏贝叶斯学习反射系数反演方法研究[D]. 北京: 中国石油大学(北京), 2018.
|
| [24] |
MARGRAVE G F, LAMOUREUX M P, HENLEY D C. Gabor deconvolution: Estimating reflectivity by nonstationary deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. DOI:10.1190/1.3560167 |
| [25] |
YUAN S Y, WANG S X, MA M, et al. Sparse Baye- sian learning‑based time‑variant deconvolution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(11): 6182-6194. DOI:10.1109/TGRS.2017.2722223 |
| [26] |
YUAN S Y, WANG S X. Influence of inaccurate wavelet phase estimation on seismic inversion[J]. Applied Geophysics, 2011, 8(1): 48-59. DOI:10.1007/s11770-011-0273-5 |
| [27] |
WANG S X, YUAN S Y, MA M, et al. Wavelet phase estimation using ant colony optimization algorithm[J]. Journal of Applied Geophysics, 2015, 122: 159-166. DOI:10.1016/j.jappgeo.2015.09.013 |
| [28] |
KJARTANSSON E. Constant Q-wave propagation and attenuation[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |



 包乾宗,陕西省西安市雁塔区大雁塔街道雁塔路南段126号长安大学地质工程与测绘学院,710054。Email:
包乾宗,陕西省西安市雁塔区大雁塔街道雁塔路南段126号长安大学地质工程与测绘学院,710054。Email: