0 引言

拖缆是海洋地震勘探的主要采集方式，因海平面这个强反射界面产生的虚反射是拖缆数据中最严重干扰之一，造成地震数据频谱出现严重的陷波畸变，常规的数学处理方法难以恢复被陷波畸变了的频率成分。海底节点（OBN）采集技术将特性不同的水、陆两种检波器同时放置海底进行记录。水检记录的是压力波场，陆检垂直分量记录的是垂直速度波场，两种波场反射信号极性相同，虚反射和鸣震干扰极性相反。通过适当的数据合并与组合，物理上可有效消除虚反射和海水鸣震的影响。其关键是水检和陆检两种数据在振幅、相位等方面要尽量保持一致^[1-6]。

上、下行波场分离技术是水陆检数据处理的基础和桥梁。高少武等^[7-25]开展了海洋水陆检数据处理方法和技术的系统研究，首次提出了基于水检数据平均均方根振幅、陆检数据平均均方根振幅、标定因子、海水深度、海底反射系数、海平面反射系数、海水速度七个参数的上行波场分离公式，创立了七参数水陆检数据合并处理方法与技术^[7-10]；首次提出了基于水检数据上、下行波场贡献因子和陆检数据上、下行波场贡献因子四个波场分离贡献因子参数的上、下行波场分离公式，创立了四参数水陆检数据上、下行波场分离方法与技术^[20-23]；创造性提出了基于相位特征方程的相位匹配方法、匹配滤波器算子的滤波器匹配方法、最大方差模方程分子分母系数特征方程的标定因子匹配方法三大技术系列，组成了水陆检数据相位匹配、滤波器匹配、均方根振幅匹配和标定因子匹配的水陆检数据匹配方法与技术^[10-13]。这些方法都是基于常数标定，不能满足水、陆检数据处理需要。

Amundsen^[26]最早提出了频率—波数域水陆检数据上、下行波场分离计算公式。随后，Day等^[27]、Amundsen等^[28]和Caprioli等^[29]相继发展了一系列频率—波数域水陆检数据标定和上、下行波场分离理论方法和技术，但都是使用直达波之下的水陆检数据进行标定因子计算。由于直达波之下水陆检数据信噪比低，特别是陆检数据中包含着较强的噪声，计算的标定因子存在误差，造成上、下行波场分离不彻底，上行波场中包含少量下行波场，下行波场中包含少量上行波场，无法满足水陆检数据处理需要^[30-32]。

水陆检数据直达波部分信噪比高，为此，充分利用直达波部分数据，在频率—波数域直接计算水陆检数据标定因子，然后进行水陆检数据标定和上、下行波场处理，可实现频率—波数域水陆检数据上、下行波场分离，为双检数据的后续处理奠定良好的基础^[33]。

1 方法原理

根据文献[26]，标定陆检数据之后，频率—波数域海底之上的上、下行波场数据可以表示为

$\begin{aligned} \boldsymbol{U}(k, m)= & \frac{1}{2} \boldsymbol{H}(k, m)- \\ & \frac{1}{2} C_z(k) \boldsymbol{A}(k, m) \boldsymbol{G}(k, m)\end{aligned}$

(1)

$\begin{aligned} \boldsymbol{D}(k, m)= & \frac{1}{2} \boldsymbol{H}(k, m)+ \\ & \frac{1}{2} C_z(k) \boldsymbol{A}(k, m) \boldsymbol{G}(k, m)\end{aligned}$

(2)

$ \boldsymbol{A}\left(k, m\right)=\frac{{\rho }_{\mathrm{w}}{c}_{\mathrm{w}}}{\sqrt{1-\frac{{c}_{\mathrm{w}}^{2}{k}_{{x}_{m}}^{2}}{{\omega }_{k}^{2}}}} $

(3)

式中：$ \boldsymbol{H}\left(k, m\right) $为水检数据；$ \boldsymbol{G}\left(k, m\right) $为陆检数据；$ {C}_{z}^{}\left(k\right) $为频率域标定滤波因子，$ k=\mathrm{1, 2}, \cdots , \mathrm{N}\mathrm{T} $，$ \mathrm{N}\mathrm{T} $是频率采样点总个数；$ \boldsymbol{U}_{}^{}\left(k, m\right) $为标定处理后频率—波数域海底之上的上行波场；$ \boldsymbol{D}\left(k, m\right) $是标定处理后频率—波数域海底之上的下行波场，$ m=\mathrm{1, 2}, \cdots , \mathrm{N}\mathrm{X} $，$ \mathrm{N}\mathrm{X} $是波数采样点总个数；$ {\omega }_{k} $是第$ k $个频率样点处的圆频率；$ {k}_{{x}_{m}} $是第$ m $个波数样点处空间方向圆波数；$ {\rho }_{\mathrm{w}}^{} $为海水密度；$ {c}_{\mathrm{w}}^{} $是海水速度。

使用切除函数切除水陆检数据中直达波场数据。切除直达波场数据之后频率—波数域海底之上水陆检数据为

$ \boldsymbol{H}_{\mathrm{r}}^{}\left(k, m\right)=\boldsymbol{W}_{\mathrm{d}}^{}\left(k, m\right)\boldsymbol{H}\left(k, m\right) $

(4)

$ \boldsymbol{G}_{\mathrm{r}}^{}\left(k, m\right)=\boldsymbol{W}_{\mathrm{d}}^{}\left(k, m\right)\boldsymbol{G}\left(k, m\right) $

(5)

式中：$ \boldsymbol{W}_{\mathrm{d}}^{}\left(k, m\right) $为频率—波数域切除函数，用于从频率—波数域水检数据和陆检数据中去除直达波场数据；$ \boldsymbol{H}_{\mathrm{r}}^{}\left(k, m\right) $是切除直达波场之后频率—波数域水检数据；$ \boldsymbol{G}_{\mathrm{r}}^{}\left(k, m\right) $是切除直达波之后频率—波数域陆检数据。

切除直达波之后频率—波数域下行波场为

$\begin{aligned} \boldsymbol{D}_{\mathrm{r}}^{}\left(k, m\right)= & \frac{1}{2}\boldsymbol{H}_{\mathrm{r}}^{}\left(k, m\right)+\\&\frac{1}{2}{C}_{z}^{}\left(k\right)\boldsymbol{A}\left(k, m\right)\boldsymbol{G}_{\mathrm{r}}^{}\left(k, m\right) \end{aligned}$

(6)

建立下列目标函数

$ Q=\sum\limits_{k=1}^{\mathrm{N}\mathrm{T}}\sum\limits_{m=1}^{\mathrm{N}\mathrm{X}}\left[{\left|\boldsymbol{U}\left(k, m\right)\right|}^{2}-{\left|\boldsymbol{D}_{\mathrm{r}}^{}\left(k, m\right)\right|}^{2}\right] $

(7)

式（7）两边对频率域标定滤波因子$ {C}_{z}^{}\left[k\right] $求导，并令导数为零，简化整理得

$ {C}_{z}^{}\left(k\right)=\frac{{F}_{z}^{}\left(k\right)}{{B}_{z}^{}\left(k\right)} $

(8)

其中

$ {F}_{z}^{}\left(k\right)=\sum\limits_{m=1}^{NX}\left[\boldsymbol{f}_{1}^{*}\left(k, m\right)+\boldsymbol{f}_{2}^{*}\left(k, m\right)\right] $

(9)

$ {B}_{z}^{}\left(k\right)=\sum\limits_{m=1}^{NX}\left[\boldsymbol{b}_{1}^{}\left(k, m\right)-\boldsymbol{b}_{2}^{}\left(k, m\right)\right] $

(10)

$ \boldsymbol{b}_{1}^{}\left(k, m\right)=\frac{1}{4}{\boldsymbol{A}}_{}^{2}\left(k, m\right){\boldsymbol{G}}_{}^{}\left(k, m\right){\boldsymbol{G}}_{}^{\mathrm{*}}\left(k, m\right) $

(11)

$ \boldsymbol{f}_{1}^{}\left(k, m\right)=\frac{1}{4}\boldsymbol{A}\left(k, m\right)\boldsymbol{G}\left(k, m\right){\boldsymbol{H}}_{}^{\mathrm{*}}\left(k, m\right) $

(12)

$ \boldsymbol{b}_{2}^{}\left(k, m\right)=\frac{1}{4}{\boldsymbol{A}}_{}^{2}\left(k, m\right){\boldsymbol{G}}_{\mathrm{r}}^{}\left(k, m\right){\boldsymbol{G}}_{\mathrm{r}}^{\mathrm{*}}\left(k, m\right) $

(13)

$ \boldsymbol{f}_{2}^{}\left(k, m\right)=\frac{1}{4}\boldsymbol{A}\left(k, m\right){\boldsymbol{G}}_{\mathrm{r}}^{}\left(k, m\right){\boldsymbol{H}}_{\mathrm{r}}^{\mathrm{*}}\left(k, m\right) $

(14)

式中上标“*”表示复共轭运算。

为了增加式（8）的稳定性，式（8）右边分子和分母乘以共轭因子$ {B}_{z}^{\mathrm{*}}\left[k\right] $，则频率域标定滤波因子计算公式为

$ {C}_{z}^{}\left(k\right)=\frac{{B}_{z}^{\mathrm{*}}\left(k\right){F}_{z}^{}\left(k\right)}{{B}_{z}^{\mathrm{*}}\left(k\right){B}_{z}^{}\left(k\right)+\varepsilon } $

(15)

式中$ \varepsilon $是一个非常小的正数（例如0.00000001），防止被零除产生的不稳定和数值溢出。详细推导过程见文献[30]。

2 模型数据处理

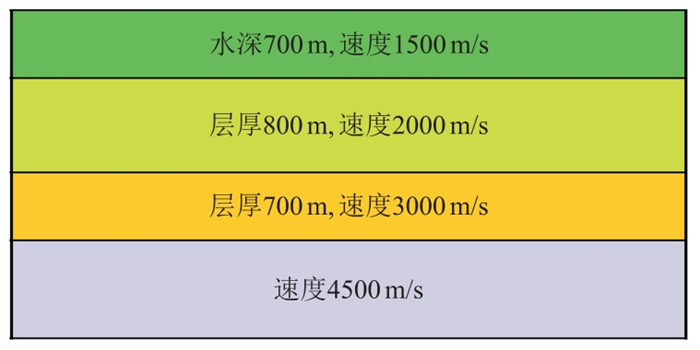
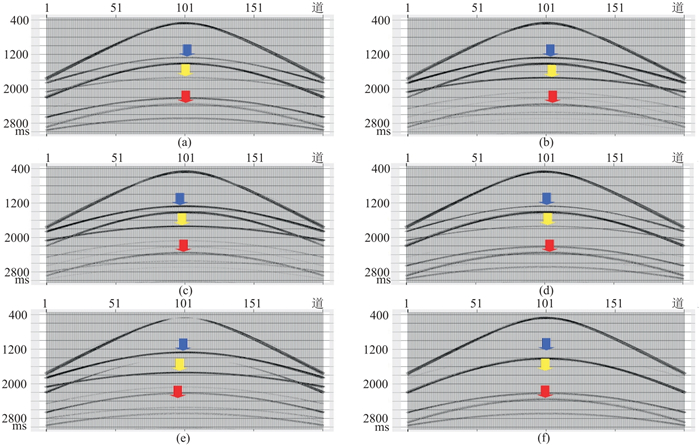
图 1是水平层状深度—速度模型，炮点沉放深度为7.5 m，炮点间距为25 m；检波点沉放海底，检波点间距为25 m。图 1模型合成水陆检共检波点道集数据如图 2a、图 2b。对比合成数据不同方法的处理结果可以看出：对于上行波场，常规方法（图 2c）和本文方法（图 2e）分离效果基本相当，但是常规方法结果中还包含少量下行波场（图 2c中红色箭头所示）；常规方法分离的下行波场中（图 2d）仍包含着较强的上行波场（图中蓝色和黄色箭头所示），而对应本文方法结果（图 2f）中几乎看不到上行波场残留。说明本文方法处理后，上行波场和下行波场完全分离开来，特别是下行波场，几乎看不到上行波场残余。

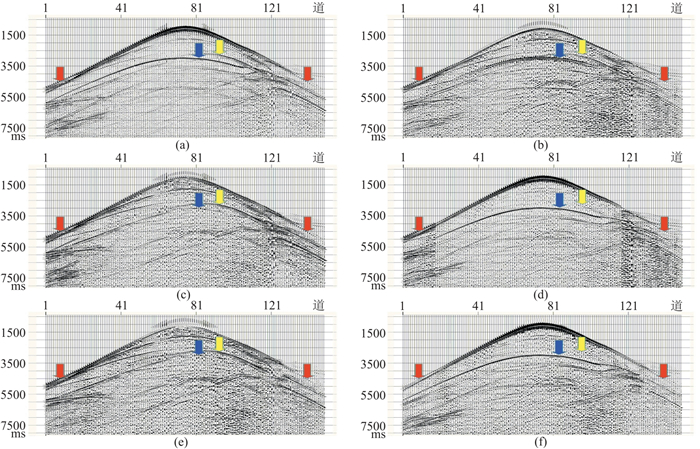
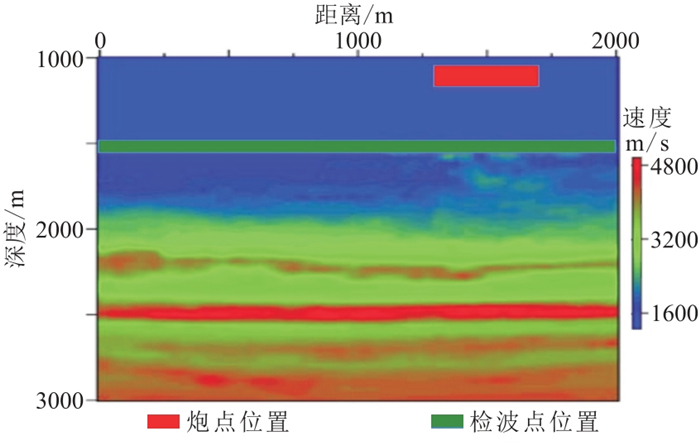
图 3是SEAM速度—深度模型，检波点位于海底1500 m处，检波点间距为10 m，分布范围如图中绿色方框所示；炮点位于水深15 m处，炮点间距为10 m，分布范围如图中红色方框所示。数据是SEG发布的标准海洋海底节点四分量模拟数据，水、陆检共炮点道集数据分别如图 4a和图 4b。本文方法与主流商业软件处理SEAM数据的结果对比显示：对于远炮检距数据，由于处理是在共检波点道集上进行，当共检波点道集数据道数较少时，主流商业软件不进行处理，直接将水检数据输出到上行波场，陆检数据输出到下行波场中，而本文方法使用相邻共检波点道集算子进行标定并进行上、下行波场分离处理（如图 4红色箭头所示）；对于近炮检距数据，主流商业软件方法与本文方法分离效果总体相当，仅局部稍有差别；对于上行波场，主流商业软件方法（图 4c）中还包含少量下行波场，而对应本文方法结果（图 4e）中几乎看不到下行波场残留（图中蓝色箭头所示）；对于下行波场，主流商业软件方法（图 4d）分离的下行波场中还包含着少量的上行波场，而对应本方法处理结果（图 4f）中几乎看不到上行波场残留（图中黄色箭头所示）。说明本文方法处理后，上行波场和下行波场完全分离开来，不含剩余上、下行波场。

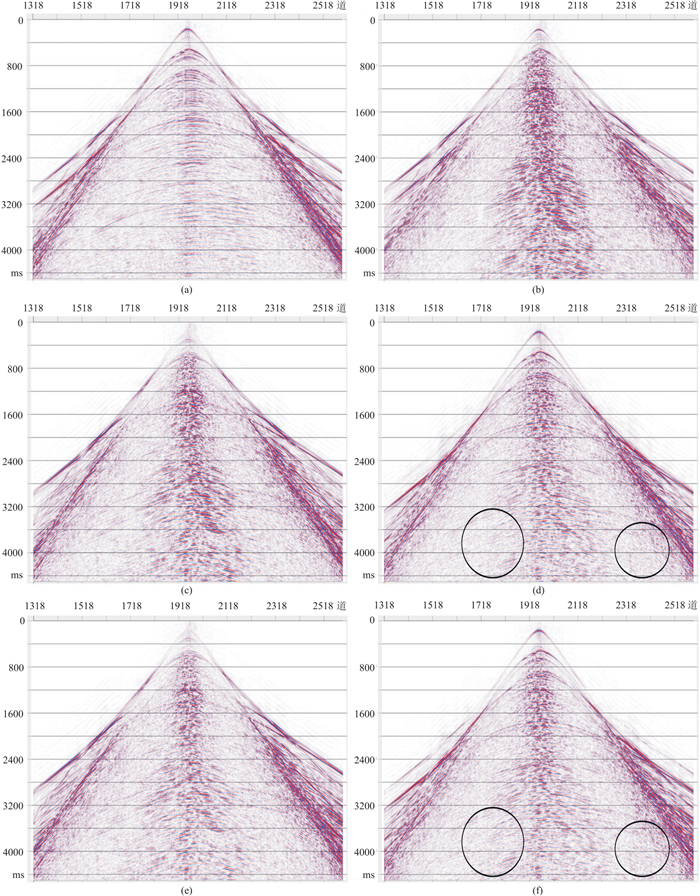
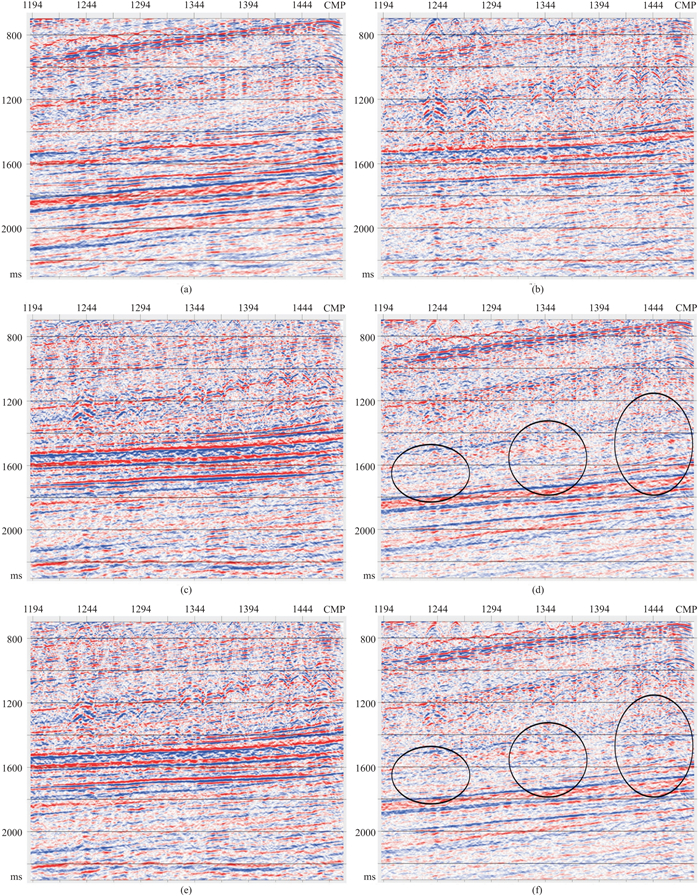
图 5是实际水陆检共炮点道集数据本文方法与主流商业软件方法处理结果对比，图 6是实际水陆检叠后数据本文方法与主流商业软件方法处理结果对比。两种方法分离效果总体相当，但本文方法局部细节优于主流商业软件方法，如图 6中圆圈区所示。

3 结束语

本文提出的频率—波数域水陆检数据上、下行波场分离方法，通过计算频率—波数域陆检数据加权自相关、频率—波数域水陆检数据加权互相关、切除直达波后频率—波数域陆检数据加权自相关、切除直达波后频率—波数域水陆检数据加权互相关，直接计算频率域水陆检数据标定滤波因子，实现水陆检数据上行波场与下行波场的分离处理，消除地震数据中海水多次波干扰影响，提高地震数据信噪比和分辨率，为后续联合反褶积和偏移成像处理提供高保真的上行波场与下行波场数据。模型数据和实际数据处理结果表明：

（1）本文方法直接计算频率域标定滤波因子，可实现水检数据上、下行波场的波场能量匹配和波场分离，是水陆检数据上、下行波场分离的有效方法；

（2）本文方法的水陆检数据上、下行波场的波场分离处理结果，上行波场有效地压制了虚反射多次波干扰，提高了反射数据的信噪比和分辨率；

（3）使用频率—波数域水陆检数据和切除直达波后频率—波数域水陆检数据，直接计算频率域标定滤波因子，使得频率域标定滤波因子参数的计算更加稳定和准确。