2. 河北地质大学河北省战略性关键矿产资源重点实验室, 河北石家庄 050031;
3. 河北地质大学地球科学学院, 河北石家庄 050031;
4. 东方地球物理公司采集技术中心, 河北涿州 072751;
5. 中国矿业大学(北京)地球科学与测量工程学院, 北京 100083
2. Hebei Key Laboratory of Strategic Critical Mineral Resources, Hebei GEO University, Shijiazhuang, Hebei 050031, China;
3. School of Earth Sciences, Hebei GEO University, Shijiazhuang, Hebei, 050031, China;
4. Acquisition Technology Institute, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China;
5. College of Geoscience and Surveying Engineering, China University of Mining and Technology(Beijing), Beijing 100083, China
野外地震施工过程受设备、环境等各种因素的影响,采集的数据经常混杂着各种噪声,影响了后续数据处理的保真度、分辨率和信噪比,甚至地震资料解释的准确性[1]。地震资料去噪是提高地震数据质量的重要手段[2],也是地震信号处理的重要环节。
目前已经存在多类去噪方法。第一类为滤波类方法,基本原理是根据地震信号的频率特性,设计合适的滤波器对信号滤波和去噪。这类方法包括自适应滤波[3]、非局部均值滤波[4]、K-L变换滤波[5]、F-X域预测滤波[6]、时间—频率峰滤波[7]、径向预测滤波[8]、倾角导向中值滤波[9-10]等。第二类方法是基于变换的方法,通过对地震数据进行数学变换,将信号从时域转换到变换域(如频率域或小波域),再利用变换域中信号和噪声的差异进行信噪分离,最后再变换回时间域。常用的变换包括Fourier变换[11]、小波变换[12-13]、Randon变换[14]、Curvelet变换[15-16]、S变换[17]等。除此之外还有稀疏字典学习[18]和局部正交压制[19]等方法。这些方法虽然都取得了不错的效果,但是方法的应用均基于某种假设条件[20]。
此外,近年来基于人工神经网络的深度学习[21]发展迅速,其主要特点是可以处理大规模和高维度的数据。深度学习的基本思想是通过构建多层神经网络模型实现对数据的高层次抽象和表示。与传统的浅层学习相比,深度学习模型通常具有更多的神经网络层和参数,可以更准确地表达和模拟数据中的复杂结构和规律。随着层数的增加,神经网络可以学习更复杂的特征和模式,从而实现对数据的分类、回归、聚类等任务。在地球物理反演中,祁锐等[22]基于LinkNet网络和残差块结构构建网络,实现重力异常反演;张岩等[23]提出一种基于特征强化U-Net的地震速度反演方法,提高了精度。深度学习方法已逐渐应用到地震数据去噪领域,如:Si等[24]将去噪卷积神经网络(Denoising Convolutional Neural Network,DnCNN)用于去除随机噪声;韩卫雪等[25]将深度学习卷积神经网络应用于实际叠前海上数据、叠后陆地数据的随机噪声压制;Zhang等[26]将基于残差学习的DnCNN用于地震数据去噪,效果好于传统方法;李海山等[27]提出将一种深度残差网络应用于叠前地震数据随机噪声压制;王钰清等[28]提出一种基于数据增广和U-Net的地震随机噪声压制方法,该方法基于实际数据制作标签,可以有效去除地震数据中的随机噪声;罗仁泽等[29]提出一种基于残差U型网络(RU-Net)去除随机噪声的方法,与其他常见的去噪方法相比,该方法具有更好的去噪效果和更高的鲁棒性;吴学峰等[30]提出基于循环一致性生成对抗网络(CycleGAN)的地震数据随机噪声压制方法,该方法在真实数据中能够有效地压制随机噪声;陈天等[31]使用深度卷积神经网络(Deep Convolutional Neural Network,DCNN)模型学习地震数据的噪声特征,能够有效地抑制地震数据中的随机噪声;张岩等[32]介绍了一种基于联合深度学习的地震数据随机噪声压制方法,提高了地震信号的质量和可解释性。彭海龙等[33]提出一种改进的生成式对抗神经网络方法,并在地震数据去噪中取得了良好效果。
人类在面对复杂信息时,往往会选择性地关注某些特定的信息,而忽略其他无关的信息。这种选择性关注和集中注意力的能力被称为注意力机制(Attention Mechanism,AM),目前已广泛应用到自然语言处理、计算机视觉和语音识别等领域。在地震数据中有些区域的有效信号较强、特征较复杂,有些区域特征较简单,而U-Net网络无法对较复杂的特征予以更多关注,因而无法充分学习到复杂的特征,导致结果受到影响。
本文在U-Net网络结构中添加AM模块,搭建了一种具有注意力功能的U-Net网络(AU-Net)。AU-Net在处理数据时自动关注输入有效信号不同强、弱部分,从而提高网络的表现力和效率。在训练时,为了避免边界效应,使用膨胀填充的方法对数据进行切分。分别采用U-Net和AU-Net对模拟数据、真实数据进行去噪实验,对比了去噪处理效果,并通过迁移学习验证了AU-Net去噪方法的可行性。
1 方法原理一般地,含有随机噪声的地震数据可表示为
| $\boldsymbol x=\boldsymbol y+\boldsymbol n $ | (1) |
式中:
深度学习的思想可以概括为在
| $ \overline{\boldsymbol y}=\mathrm{N}\mathrm{e}\mathrm{t}(\boldsymbol x, \boldsymbol \theta ) $ | (2) |
式中:
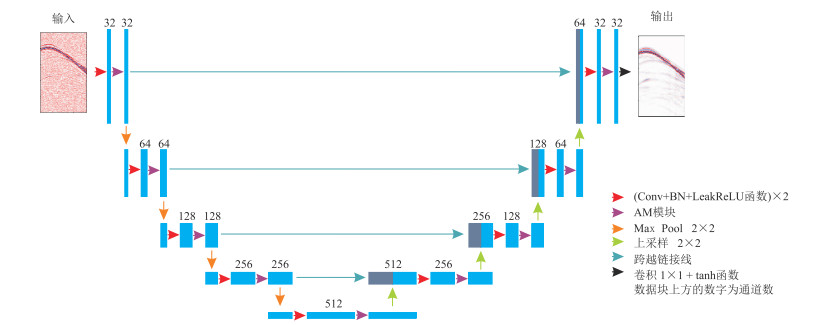
U-Net在图像分割领域取得了成功,同时也应用到地震数据去噪问题上。U-Net因数据特征的复杂程度不同会导致特征学习不充分的问题,为此,本文基于U-Net结构,在每个双卷积模块(连续两次卷积)后添加AM模块,构建了AU-Net(图 1)。AU-Net的结构可以分为四个部分:编码器、解码器、跳跃连接(Skip Connection)模块和AM模块。编码器主要分为卷积(Conv)、AM和下采样三部分,具体过程为:①将64×64的含噪数据输入网络后,经过两次卷积将数据编码为64×64×32的特征信息,卷积核设置为3×3。卷积过程还包含批归一化(BN)层和激活层。BN层可加速模型训练,提高模型的泛化能力并且减小梯度消失的问题,这里利用BN将数据归一化到(-1, 1)。激活函数用Leaky_Relu,可以在一定程度上缓解梯度消失或梯度爆炸的现象。②在AM模块中对特征做通道和高、宽维度的重塑并保持数据大小不变。后面紧跟一个2×2的最大池化层(Max Pool),使特征图的大小变为原来的1/2,然后经过两次卷积使特征图的通道变为原来的2倍。
|
图 1 AU-Net网络结构图 |
解码部分具体过程为:①编码得到的数据每经过一次上采样,特征图的大小会翻倍、数量减半。然后通过两次卷积,通道减半,再经过一次AM模块则完成了一次上采样的操作。②在最后一层通过一个1×1的卷积还原输出,再用tanh函数将其激活,得到最终的输出数据。
跳跃连接模块是指将下采样过程中的特征图与上采样过程中相同维度的特征图直接在通道上连接起来,从而保留了更多的低层次特征信息,它可帮助模型更好地利用低层次特征信息,提高分割精度和鲁棒性。同时,跳跃连接模块还可以缓解梯度消失问题,有助于提高模型的学习效率和泛化能力。
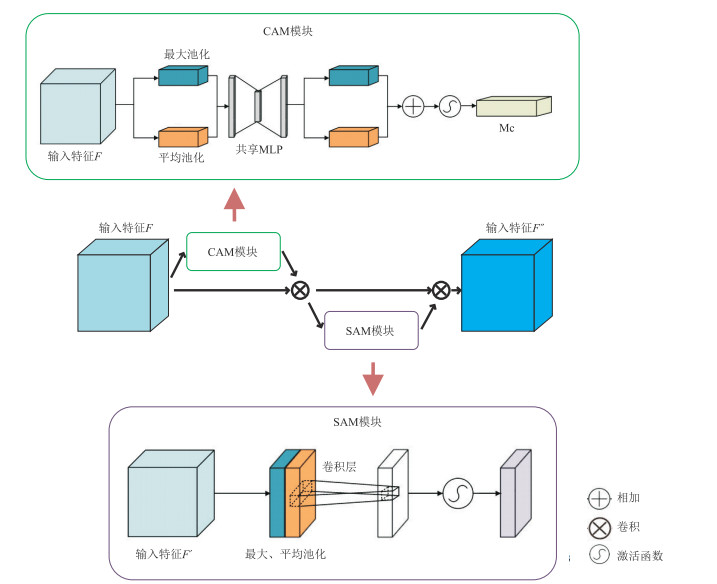
AM的本质是对于输入数据进行加权处理,根据输入数据的重要性对其进行不同程度的关注,从而帮助深度学习模型更好地理解和处理输入数据。本文使用的AM包含两个独立的模块,分别是通道注意力模块(Channel Attention Module,CAM)和空间注意力模块(Spatial Attention Module,SAM)。AM结构如图 2所示。
|
图 2 AM结构图 |
CAM的输入是特征图,维度设为H×W×C,其中H、W分别指特征图的高度和宽度,C指通道数。具体流程是:首先对输入的特征图分别进行全局最大池化和全局平均池化(在空间维度进行池化,压缩空间尺寸,便于后面学习通道的特征)处理,得到两个1×1×C的特征图,将它们送入多层感知机(MLP)中学习(基于MLP学习通道维度的特征和各个通道的重要性);然后将MLP输出的结果进行“加”操作,再经过Sigmoid函数激活处理,得到最终的“通道注意力值(Mc)”[34]。
SAM的输入是CAM处理输出的特征图。具体流程是:首先对输入的特征图进行全局最大池化和全局平均池化(在通道维度进行池化,压缩通道大小,便于后面学习空间的特征)处理;然后将全局池化和平均池化的结果在通道维度拼接,得到维度为H×W×2的特征图;其次对拼接结果进行卷积操作,得到特征图的维度(H×W×1);最后通过激活函数Sigmoid处理,得到“空间注意力值(Ms)”[35]。
将输入CAM的特征图F和Mc做乘法操作,得到输入SAM的特征图F′,再将F′和SAM输出的Ms做乘法操作,得到最终生成的特征F″。
1.2 损失函数优化和评价指标为了取得较好的去噪结果,需将网络参数优化至最佳,通过求解以下损失函数实现参数的优化
| $ L\left(\boldsymbol \theta \right)=\frac{1}{2N}\sum\limits_{i=1}^{N}{‖\mathrm{N}\mathrm{e}\mathrm{t}({x}_{i};\boldsymbol \theta )-{y}_{i}‖}_{\mathrm{F}}^{2} $ | (3) |
式中:
为了衡量神经网络的去噪性能,使用峰值信噪比(Peak Signal to Noise Ratio,PSNR)和信噪比(Signal to Noise Ratio,SNR)作为评价指标
| $ \mathrm{P}\mathrm{S}\mathrm{N}\mathrm{R}=10\mathrm{l}\mathrm{g}\frac{\mathrm{m}\mathrm{a}\mathrm{x}{‖\boldsymbol{y}‖}^{2}M}{{‖\boldsymbol{y}-{\boldsymbol{x}}_{n}‖}_{2}^{2}} $ | (4) |
| $ \mathrm{S}\mathrm{N}\mathrm{R}=10\mathrm{l}\mathrm{g}\frac{{‖\boldsymbol{y}‖}^{2}}{{‖\boldsymbol{y}-{\boldsymbol{x}}_{n}‖}_{2}^{2}} $ | (5) |
式中:xn为含有随机噪声的地震数据;M为地震数据采样点数。PSNR和SNR的单位均为dB,其数值越大表示去噪效果越好。
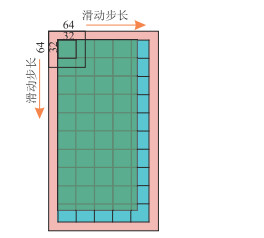
1.3 AU-Net的数据切分在地震数据处理的过程中,边界效应是一个普遍存在的问题。边界效应也称为边缘效应,是指在地震数据处理中,由于采样率、滤波器设计等因素的限制,数据在边缘处出现异常变化的现象。具体表现为靠近数据边缘的部分信号和噪声被过滤或平滑处理,导致数据在边缘处出现失真、偏移或振铃等现象,从而影响地震数据的准确性和可靠性。在深度学习的方法中,如果直接用数据进行去噪,去噪效果往往不理想,所以通常将数据切成小方块。但是神经网络在去噪过程中也会存在边界效应的影响,即数据块的中心去噪效果较好,而数据块的边缘去噪效果较差。为解决此问题,本文采用以下膨胀填充的方式进行切分(图 3):
|
图 3 数据切分示意图 |
(1) 在原始数据块(Ⅰ)的右边和下边进行填充,使其在横向和纵向均可被64整除,使数据可以恰好被切为若干个64×64的Patch,得到填充后的数据块(Ⅱ);
(2) 将Ⅱ向四周再次填充16个单位,得到新的数据块(Ⅲ);
(3) 对Ⅲ进行x和y方向步长均为32的切分,将数据块切分为大小为64×64的Patch,并用于网络训练;
(4) 将网络输出的64×64的数据块,只取中间32×32的部分,并且按照顺序拼接起来就可以得到和Ⅰ尺寸相同的数据。
2 模型的训练及测试本文使用SEG-C3数据进行训练,该数据由45个炮集组成,每炮可以获得201个625×201的二维地震记录。首先选取前9炮的数据,在每个二维记录中添加20%~40%的随机噪声。通过数据切分得到40725份64×64的数据,其中32625份作为训练集,4050份作为验证集,4050份作为测试集。模型训练的迭代次数(Epoch)为100,批次大小(Batch Size)为32。每遍历训练集一次就要计算一次损失函数,并且对测试集做去噪处理,计算去噪后的PSNR。学习率(Learning Rate,LR)为1×10-3,采用固定步长方式衰减,间距为5,衰减系数为0.8。选择Pytorch框架搭建网络,硬件使用Nvidia RTX3090显卡加快计算速度,其中运用的损失函数为均方误差,其数学表达式为
| $ E=\frac{1}{2}\sum\limits_{i=1}^{N}{\left({y}_{i}-{t}_{i}\right)}^{2} $ | (6) |
式中
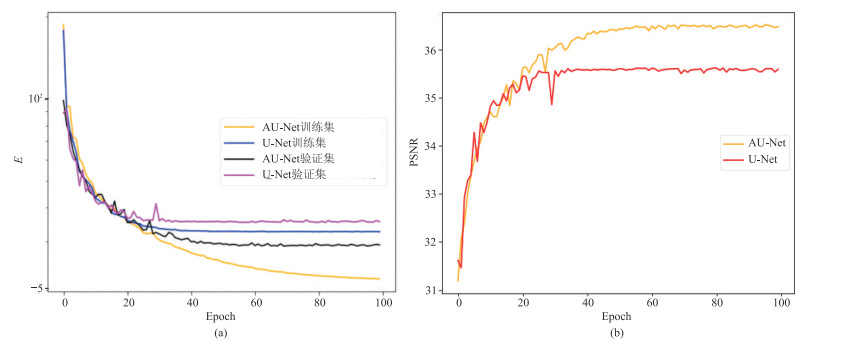
|
图 4 AU-Net和U-Net训练和测试曲线 (a)训练集和测试集的损失曲线;(b)验证集的PSNR曲线 |
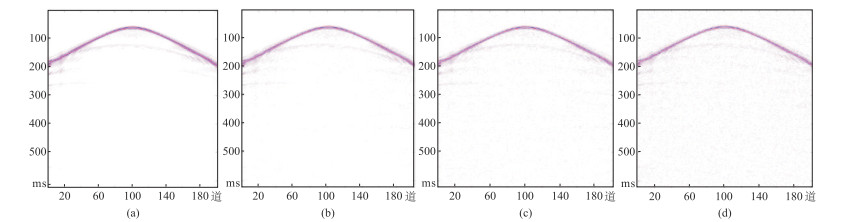
基于前文的膨胀填充的数据切分方式,对SEG-C3数据的其他的炮中随机抽取一炮进行去噪试验,炮数据大小为625×201。在干净数据中分别加入20%、25%、30%的随机噪声(图 5),然后分别使用U-Net和AU-Net去噪。
|
图 5 干净数据(a)和含20%(b)、25%(c)、30%(d)的噪声数据 |
表 1为去噪效果。可见:在加入20%随机噪声的情况下,AU-Net的评价指标较U-Net高约4 dB;随着噪声能量的增加,AU-Net依然能够保持4 dB左右的优势。由此可见,AU-Net的去噪效果明显好于U-Net,且随着含噪比例的增大依然能够保持良好的效果。
|
|
表 1 地震数据去噪结果PSNR和SNR对比 |
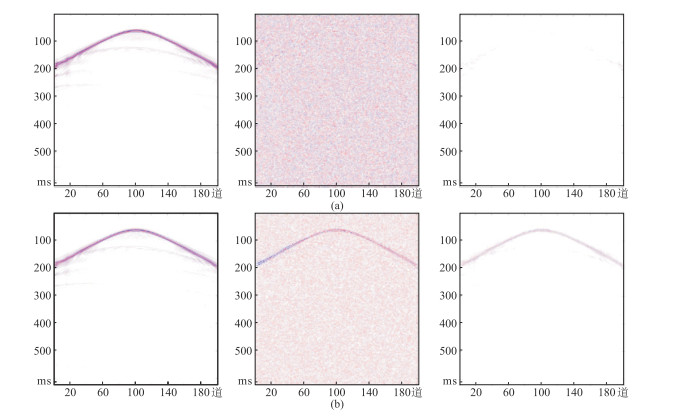
图 6~图 8是使用两种网络去噪方法,分别对随机加噪20%、25%和30%的地震数据进行去噪的试验结果和误差。由图 6可见:AU-Net的去噪效果较好(图 6a左),有效信号较完整,去除的噪声也较干净(图 6a中);U-Net的去噪效果相对较差(图 6b左),去除的噪声中含有明显的有效信号(图 6a中),信噪比较低。由图 7可见,AU-Net去噪效果良好(图 7a左),但U-Net噪声剖面中强轴依然存在,除此之外,不能很好地保留较弱的有效信号(图 7a中)。由图 8可见,AU-Net去噪效果整体较好(图 8a左),U-Net网络中上述的两个问题愈发明显(图 8b)。
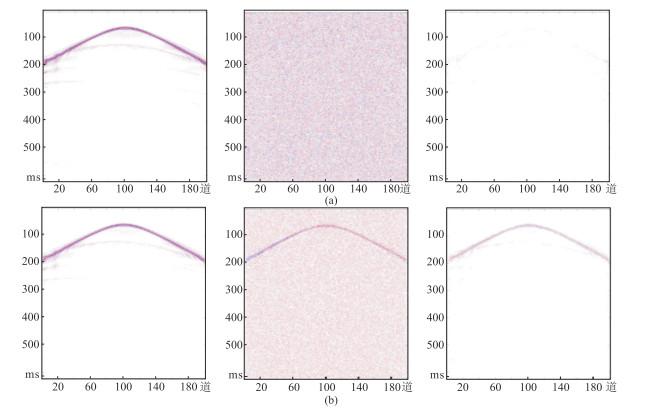
|
图 7 AU-Net(a)和U-Net(b)对含25%噪声数据的去噪效果对比 |
|
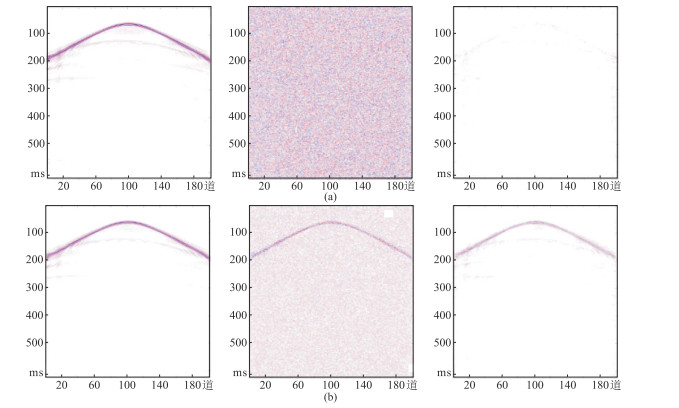
图 8 AU-Net(a)和U-Net(b)对含30%噪声数据的去噪效果对比 |
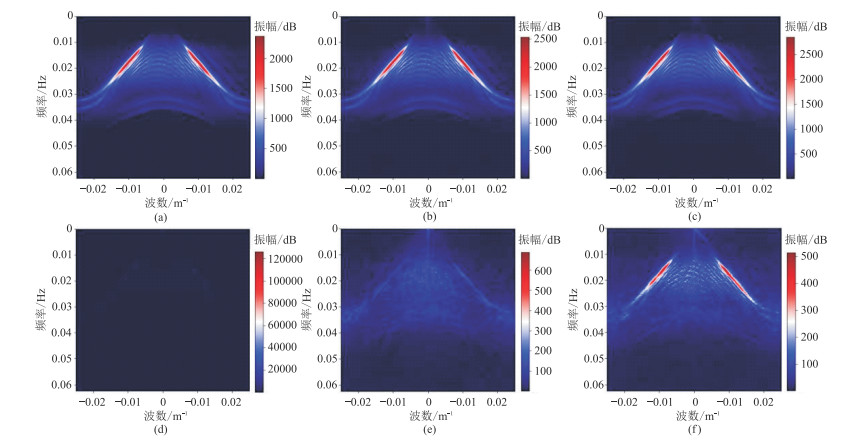
综上所述,U-Net网络可能将较弱或过强的有效信号当作噪声去除,所以会造成强轴被去除而较弱的有效信号得不到保留。而AU-Net由于添加了AM,会根据信号的强、弱对不同的区域有不同的关注度,所以不会存在此类问题。在两种方法的三种噪声比例的残差剖面中可以明显看出:U-Net残差剖面(图 6b右、图 7b右、图 8b右)中整体误差较大,且信号强轴部分的误差十分明显,有效信号损失较大;AU-Net去噪结果的残差(图 6a右、图 7a右、图 8a右)明显小于U-Net。图 9a、图 9b和图 9c分别为图 5a、图 8a左和图 8b左对应的F-K谱,由图可见,两种方法都具有较好的去噪效果,均没有空间假频的现象。图 9d、图 9e和图 9f分别为图 5d、图 8a右和图 8b右对应的F-K谱,通过误差谱可以明显看出:U-Net还残留较多能量,未对去噪数据进行合适的能量补偿;AU-Net中的AM模块则能够关注到信号的能量差异,更适合实际情况。
2.2 模型的泛化能力模型的泛化能力是指模型在未训练过的数据上的表现能力,具体而言,是指模型在某个训练数据中学到的模式和规律的基础上,对新的、未知的数据进行准确预测或分类的能力。一个具有良好泛化能力的模型能够在面对新的数据时保持较低的误差。这意味着模型能够捕捉到数据中的一般特征和规律,而不是只记住训练数据的具体样本。相反,一个过拟合的模型在训练数据上表现良好,但在新的数据上表现较差,因为它过度适应了训练数据中的噪声和细节。
在深度学习领域,一个长期以来的研究重点和难点是如何提升模型的通用性。当使用某一地区的数据训练网络时,直接将该模型应用于另一个地区的数据处理往往效果不佳。不同地区之间的地震数据既具有共性又存在差异性,通过迁移学习可以在了解了一些数据的共同特点后,快速掌握数据间的某些差异信息。因此,可以利用待处理地区的一部分数据进行迁移学习,以提高不同地区数据模型的性能。为验证本文所提AU-Net模型的泛化能力,将新的模拟数据添加20%~40%的随机噪声后,切分为64×64的数据块,并以8∶1∶1的比例划分训练集、验证集和测试集。模型训练的超参数和网络训练以及测试方式与前文保持一致。对于本次数据集,分别使用已经完成训练和未经训练的AU-Net进行训练。
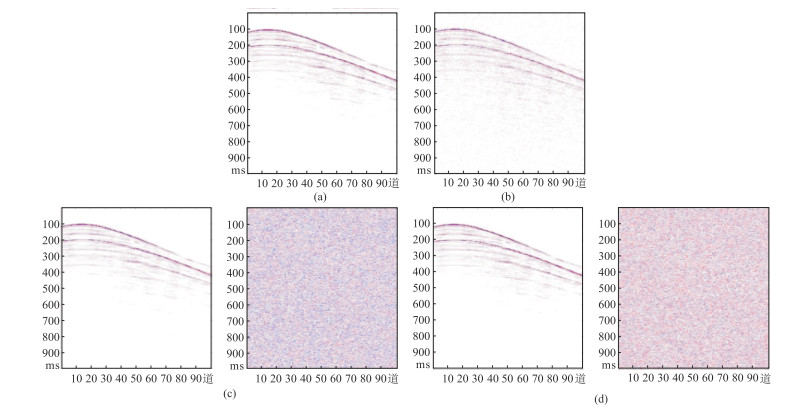
随机抽取一个二维剖面(图 10a),添加30%随机噪声(如图 10b),SNR为2.4172 dB。分别使用迁移学习和直接训练的方法对其进行处理。迁移学习的去噪结果(图 10c左),SNR为14.0769 dB;未使用迁移学习的结果(图 10d左)的SNR为12.2998 dB。图 10c右和图 10d右展示了上述两种方法去除的噪声。在直接学习去除的噪声中仍还有少量有效信号(图 10d右),而通过迁移学习可以有效地改善这一问题(图 10c右)。
|
图 10 AU-Net迁移学习(c)和直接训练(d)的去噪效果对比 (a)干净数据;(b)加30%随机噪声数据;图c和图d中左图、右图分别为去噪结果和去除的噪声。 |
选用F地区真实数据进行测试,数据为276×831的地震剖面,在其中添加一定量的噪声后切分为96份64×64的数据切片,并以8∶1∶1的比例划分训练集、验证集和测试集。在训练模型时,超参数的设置和网络的训练以及测试方式与前文保持一致。分别使用AU-Net和U-Net对数据集进行训练并对比试验结果。
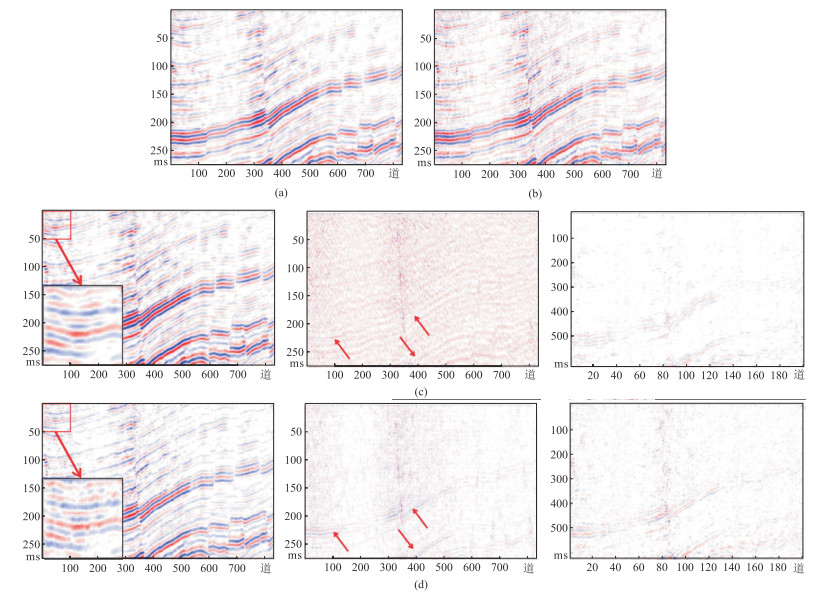
原始地震剖面如图 11a所示,图 11b为含噪地震剖面,其SNR为7.8250 dB(以图 11a为基准),PSNR为20.1968 dB,分别用两种网络训练好的模型进行去噪。图 11c为AU-Net网络的去噪结果,左图SNR为12.5289 dB,PSNR为24.9006 dB。图 11d为U-Net网络的处理结果,SNR为9.9881 dB,PSNR为22.3559 dB。图 11c和图 11d的中图为两种方法去除的噪声,图 11c和图 11d为图 11b与两种方法去噪结果的误差。由图 11c和图 11d左图可见AU-Net网络去噪效果更好,而U-Net网络去噪效果较差,整张剖面上都存在一定的噪声残留。在去除的噪声剖面(图 11d中)上,U-Net去除掉的噪声中含有几处明显的有效信号,且随机噪声较少,而AU-Net网络去除的噪声剖面图中,随机噪声分布较为均匀,说明AU-Net在压制随机噪声的同时,有效信息也得到了最大程度的保留。由此可见,AU-Net网络相较于U-Net在真实数据去噪上有一定的优势。然而在误差剖面(图 11c和图 11d右)中,虽然AU-Net网络的误差剖面和U-Net相比较为干净,但也存在着一些有效信号,效果并不是特别理想,这是由于真实数据的量比较小,用于训练的切片较少,造成去噪效果并不像模拟数据那样好。
|
图 11 AU-Net(c)和U-Net(d)真实地震数据去噪效果对比 (a)真实地震数据;(b)加入30%随机噪声后的真实地震数据;图c、图d中左、中、右图分别为去噪结果、去除的噪声和去噪误差。 |
深度学习是基于数据驱动的方法,它可以学习地震数据中的特征,自适应地去除各种类型的噪声,且能够在一定程度上处理数据中的缺失、异常和噪声等问题,具有更强的鲁棒性。原始U-Net网络方法无法根据不同区域的噪声密度给予不同的关注,针对其在特征提取方面的局限性,本文基于原始U-Net网络并结合AM,提出一种具有注意力功能的网络架构(AU-Net),并将其应用于地震数据去噪问题。通过在U-Net网络中添加AM模块,使其有效地对噪声进行合理取舍。为解决边界效应,使用了膨胀填充的数据切分方法进行数据切分和拼接。
基于AU-Net和原始U-Net分别对模拟数据、真实数据进行随机噪声压制试验,试验结果证明了本文所提AU-Net去噪效果有明显提升,网络的去噪能力增强,且时间上仅增加了约10%。针对地震数据在不同地区之间既存在差异又具有共性的特点,采用AU-Net迁移学习的策略,可以快速适应不同地震数据之间的差异,从而使该方法更加具有灵活性和适应性。
| [1] |
王琪琪, 汤井田, 张良, 等. 利用多层感知机的地震数据去噪[J]. 石油地球物理勘探, 2020, 55(2): 272-281. WANG Qiqi, TANG Jingtian, ZHANG Liang, et al. Seismic data denoising based on multi-layer perceptron[J]. Oil Geophysical Prospecting, 2020, 55(2): 272-281. |
| [2] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法综合评述[J]. 地球物理学进展, 2005, 20(4): 1083-1091. ZHANG Junhua, LYU Ning, TIAN Lianyu, et al. An overview of the methods and techniques for seismic data noise attenuation[J]. Progress in Geophysics, 2005, 20(4): 1083-1091. DOI:10.3969/j.issn.1004-2903.2005.04.032 |
| [3] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136, 1187. CAO Pengtao, ZHANG Min, LI Zhenchun. An adaptive filtering denoising method based on generalized S-transform and Gaussian smoothing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1128-1136, 1187. |
| [4] |
BUADES A, COLL B, MOREL J M. Nonlocal image and movie denoising[J]. International Journal of Computer Vision, 2008, 76(2): 123-139. DOI:10.1007/s11263-007-0052-1 |
| [5] |
JONES I F, LEVY S. Signal-to-noise ratio enhancement in multichannel seismic data via the Karhunen-Loéve transform[J]. Geophysical Prospecting, 1987, 35(1): 12-32. DOI:10.1111/j.1365-2478.1987.tb00800.x |
| [6] |
HARRIS P E, WHITE R E. Improving the performance of f-x prediction filtering at low signal-to-noise ratios[J]. Geophysical Prospecting, 1997, 45(2): 269-302. DOI:10.1046/j.1365-2478.1997.00347.x |
| [7] |
LIN H B, LI Y, MA H T, et al. Matching-pursuit-based spatial-trace time-frequency peak filtering for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2): 394-398. DOI:10.1109/LGRS.2014.2344020 |
| [8] |
夏洪瑞, 陈德刚, 周开明. 地震资料处理中随机干扰消除方法分析[J]. 石油物探, 2003, 42(1): 93-96. XIA Hongrui, CHEN Degang, ZHOU Kaiming. Random noise elimination in seismic data processing[J]. Geophysical Prospecting for Petroleum, 2003, 42(1): 93-96. DOI:10.3969/j.issn.1000-1441.2003.01.021 |
| [9] |
王伟, 高静怀, 陈文超, 等. 基于结构自适应中值滤波器的随机噪声衰减方法[J]. 地球物理学报, 2012, 55(5): 1732-1741. WANG Wei, GAO Jinghuai, CHEN Wenchao, et al. Random seismic noise suppression via structure-adaptive median filter[J]. Chinese Journal of Geophy- sics, 2012, 55(5): 1732-1741. |
| [10] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. SUN Zhe, WANG Jianfeng, WANG Jing, et al. Random noise elimination based on the time space va-riant median filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [11] |
ALSORFK D. Noise reduction in seismic data using Fourier correlation coefficient filtering[J]. Geophysics, 1997, 62(5): 1617-1627. DOI:10.1190/1.1444264 |
| [12] |
CAO S Y, CHEN X P. The second-generation wavelet transform and its application in denoising of seismic data[J]. Applied Geophysics, 2005, 2(2): 70-74. DOI:10.1007/s11770-005-0034-4 |
| [13] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 254-260. |
| [14] |
WANG Y. Antialiasing conditions in the delay-time Radon transform[J]. Geophysical Prospecting, 2002, 50(6): 665-672. DOI:10.1046/j.1365-2478.2002.00340.x |
| [15] |
齐少华, 刘启元, 陈九辉, 等. 接收函数的曲波变换去噪[J]. 地球物理学报, 2016, 59(3): 884-896. QI Shaohua, LIU Qiyuan, CHEN Jiuhui, et al. Attenuation of noise in receiver functions using curvelet transform[J]. Chinese Journal of Geophysics, 2016, 59(3): 884-896. |
| [16] |
张华, 刁塑, 温建亮, 等. 应用二维非均匀曲波变换压制地震随机噪声[J]. 石油地球物理勘探, 2019, 54(1): 16-23. ZHANG Hua, DIAO Su, WEN Jianliang, et al. A random noise suppression with 2D non-uniform curvelet transform[J]. Oil Geophysical Prospecting, 2019, 54(1): 16-23. |
| [17] |
赵淑红, 朱光明. S变换时频滤波去噪方法[J]. 石油地球物理勘探, 2007, 42(4): 402-406. ZHAO Shuhong, ZHU Guangming. Time-frequency filtering to denoise by S transform[J]. Oil Geophysical Prospecting, 2007, 42(4): 402-406. DOI:10.3321/j.issn:1000-7210.2007.04.008 |
| [18] |
张岩, 任伟建, 唐国维. 应用结构聚类字典学习压制地震数据随机噪声[J]. 石油地球物理勘探, 2018, 53(6): 1119-1127. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression on seismic data based on structured-clustering dictionary learning[J]. Oil Geophysical Prospecting, 2018, 53(6): 1119-1127. |
| [19] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. A local orthogonalization for seismic random noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [20] |
钟铁, 李月, 杨宝俊, 等. 陆地地震勘探随机噪声统计特性[J]. 地球物理学报, 2017, 60(2): 655-664. ZHONG Tie, LI Yue, YANG Baojun, et al. Statistical features of the random noise in land seismic prospecting[J]. Chinese Journal of Geophysics, 2017, 60(2): 655-664. |
| [21] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [22] |
祁锐, 李厚朴, 胡佳心, 等. 基于U-Rnet的重力全张量梯度数据反演[J]. 石油地球物理勘探, 2024, 59(2): 331-342. QI Rui, LI Houpiao, HU Jiaxin, et al. Inversion of gravity full tensor gradient data based on U-Rnet network[J]. Oil Geophysical Prospecting, 2024, 59(2): 331-342. |
| [23] |
张岩, 孟德聪, 宋利伟, 等. 基于特征强化U-Net的地震速度反演方法[J]. 石油地球物理勘探, 2024, 59(2): 185-194. ZHANG Yan, MENG Decong, SONG Liwei, et al. Seismic velocity inversion method based on feature enhancement U-Net[J]. Oil Geophysical Prospecting, 2024, 59(2): 185-194. |
| [24] |
SI X, YUAN Y. Random noise attenuation based on residual learning of deep convolutional neural network[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 1986-1990.
|
| [25] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869, 877. HAN Weixue, ZHOU Yatong, CHI Yue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869, 877. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [26] |
ZHANG K, ZUO W, CHEN Y, et al. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [27] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [28] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [29] |
罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59. LUO Renze, LI Yangyang. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59. |
| [30] |
吴学锋, 张会星. 基于循环一致性生成对抗网络的地震数据随机噪声压制方法[J]. 石油地球物理勘探, 2021, 56(5): 958-968. WU Xuefeng, ZHANG Huixing. Random noise suppression method of seismic data based on CycleGAN[J]. Oil Geophysical Prospecting, 2021, 56(5): 958-968. |
| [31] |
陈天, 易远元. 基于深度卷积神经网络的地震数据随机噪声压制[J]. 地震学报, 2021, 43(4): 474-482. CHEN Tian, YI Yuanyuan. Random noise suppression of seismic data based on deep convolution neural network[J]. Acta Seismologica Sinica, 2021, 43(4): 474-482. |
| [32] |
张岩, 李新月, 王斌, 等. 基于联合深度学习的地震数据随机噪声压制[J]. 石油地球物理勘探, 2021, 56(1): 9-25, 56. ZHANG Yan, LI Xinyue, WANG Bin, et al. Random noise suppression of seismic data based on joint deep learning[J]. Oil Geophysical Prospecting, 2021, 56(1): 9-25, 56. |
| [33] |
彭海龙, 李明, 孙文钊, 等. 生成式对抗神经网络的改进及其在地震数据压噪中的应用[J]. 石油物探, 2024, 63(1): 104-115, 128. PENG Hailong, LI Ming, SUN Wenzhao, et al. Seismic data denoising based on improved generative adversarial network[J]. Geophysical Prospecting for Petroleum, 2024, 63(1): 104-115, 128. |
| [34] |
HU J, SHEN L, SUN G. Squeeze-and-Excitation networks[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, 7132-7141.
|
| [35] |
JADERBERG M, SIMONYAN K, ZISSERMAN A, et al. Spatial transformer networks[C]. 28th International Conference on Neural Information Processing Systems-Volume 2, 2015, 2017-2025.
|



 曹静杰, 河北省石家庄市槐安东路136号河北地质大学地球科学学院,050031。Email:
曹静杰, 河北省石家庄市槐安东路136号河北地质大学地球科学学院,050031。Email: