2. 东北石油大学人工智能能源研究院, 黑龙江大庆 163318;
3. 黑龙江省网络与智能控制重点实验室, 黑龙江大庆 163318;
4. 东北石油大学物理与电子工程学院, 黑龙江大庆 163318
2. Artificial Intelligence Energy Research Institute, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
3. Key Laboratory of Networking and Intelligent Control of Heilongjiang Province, Daqing, Heilongjiang 163318, China;
4. School of Physics and Electronic Engineering, Northeast Petroleum University, Daqing, Heilongjiang 163318, China
在地震资料采集过程中,由于环境干扰和采集条件的限制,地震数据通常会受到随机噪声的干扰。此外,由于经济和地形等条件的限制,采集的地震数据通常采样不足,会出现欠采样或不规则采样等现象。当前地震数据的处理与解释对数据的信噪比和规则性有很高的要求,所以研究高效的地震数据重建和去噪算法对提高数据处理的精度具有重要意义。
近些年,学者们提出了一些地震数据重建和去噪的方法,从实现机理上大致上可分为传统方法和基于深度学习的方法两类。
传统的地震数据重建和去噪算法大多基于地震波的传播特性和数字信号处理技术。主要可分为四类:预测滤波器、波动方程、数学变换和矩阵降秩。基于预测滤波方法主要是利用线性同相轴在F-X域的可预测性,对混叠的高频地震数据进行重建。同样也可以通过设计特定的算法对噪声进行压制,但是此类方法仅适用于规则采样的地震数据[1]。基于波动方程的方法[2]需要地下介质的先验参数,但在实践中难以准确获得,并且太过耗时。基于数学变换的方法利用有效信号和缺失信号及噪声在变换域中分布差异进行重建与去噪,如傅里叶变换、Curvelet变换[3]等。相比于基于波动方程的方法,计算成本小,对先验知识的依赖少。基于矩阵降秩的方法[4]原理是假设地震数据存在较强的时空相关性,无噪声、完整的地震数据可以通过低秩矩阵描述,含有噪声或缺失道的地震数据会增加矩阵的秩。但是由于在降秩中的块Hankel矩阵远大于对应切片的频率数量,因此处理过程中计算量较大,而且对数据存储量的要求较高。
目前,深度学习方法已经被应用到地震数据处理[5]、地震波形分类[6]、速度模型建立[7-8]、地震数据解释[9]等多个领域。Si等[10]使用去噪卷积神经网络(Denoising Convolutional Neural Networks, DnCNN)模型实现了地震数据的去噪,并且对实际地震数据取得了较好效果;Wang等[11]利用残差网络对规则缺失的地震数据进行重建;Chai等[12]利用U-Net对不规则缺失的地震数据进行重建;Zhong等[13]提出一种基于残差结构的U-Net,通过学习地震数据的多尺度特征区分信号和随机噪声,达到去噪的目的。
上述方法仅关注单一去噪或重建问题,对具有缺失并含噪地震数据大多分步处理。这样的处理方式不仅会引入额外噪声,还会导致地震数据处理质量下降,降低运算效率。针对这一问题,学者们基于深度学习提出了能够同时重建和去噪的方法。Wang等[14]基于残差网络提出了一种多尺度、端到端的网络,分别使用去噪网络和插值网络同时对地震数据进行处理,进而完成地震数据重建和去噪的任务;Jiang等[15]提出了一种改进的卷积自编码器方法实现地震数据的同时重建和去噪;Mandelli等[16]提出一种基于卷积神经网络(Convolutional Neural Networks,CNN)的同时重建与去噪方法,选用网络输出与标签数据间的均方误差作为损失函数,调整网络结构实现地震数据的重建与去噪。
作为近年来研究的热点,生成对抗网络(Generative Adversarial Networks,GAN)有着广泛的应用。GAN是由Goodfellow等[17]于2014年提出的网络模型,主要灵感来源于博弈论中的零和博弈思想。相较于其他深度学习方法,GAN通过生成器(Ge-nerator)和判别器(Discriminator)的不断博弈,使得生成器学习并生成与目标数据相似的概率分布。原始的GAN使用KL(Kullback-Leibler)散度和JS(Jensen-Shannon)散度计算目标数据和生成数据之间的距离,由于二者做损失函数时会出现局部不连续的情况,容易出现梯度消失和模式崩溃等问题。因此,有学者们试图寻找新的目标函数计算目标数据和生成数据之间的距离。Mao等[18]在判别器中使用最小二乘损失函数改进了网络,提高了生成图像的质量,并且训练过程更加稳定。Arjovsky等[19]提出了韦氏生成对抗网络(Wasserstein Generative Adversarial Networks, WGAN),由于韦氏距离具有优越的平滑特性,理论上能够解决梯度消失的问题,能够提高生成图像的质量。
目前,GAN在地震数据处理方面的应用逐渐受到关注。GAN使用判别器引导生成器的梯度方向,通过判别器识别整体的地震数据并引入全局信息,因此更适合用于缺失地震数据的重建和去噪。Oliveira等[20]使用条件生成对抗网络(condition Ge-nerative Adversarial Networks,cGAN)的损失函数训练网络,用于重建叠后地震数据。Wei等[21]基于cGAN将对抗性损失函数改进为韦氏损失函数,对常规缺失地震数据进行插值以消除空间假频,并实现了多达35条连续地震道缺失的二维插值。
综上所述,传统重建和去噪方法具有较强的可解释性,但由于依赖地震数据的先验性假设,模型参数受人工经验因素影响大,导致通用性降低。基于深度学习的重建和去噪方法可以自动提取地震数据的主要特征,在一定程度上提高了适应性。GAN通过生成器与判别器相互博弈,具有更强的学习能力,有利于提高对包含缺失道与噪声地震数据的特征提取能力。但普通GAN生成的地震数据具有随机性,在逼近理想地震数据的过程中容易产生较大的误差,而且训练过程中会出现梯度消失、模式崩塌等问题从而导致生成的地震数据较为模糊、在同向轴连续性和波阻特征等方面与理想数据差距较大。
因此,本文将cWGAN引入到地震数据同时重建和去噪,并在模型中加入一体化损失函数引导生成器梯度优化的方向提高重建数据的质量。首先,以U-Net为基准构建生成器模型,充分利用网络结构的特点,分级提取地震数据同相轴特征,并通过跳跃连接加强特征的融合,提高生成器在缺失道和随机噪声干扰下对地震数据特征的提取能力;在判别器中引入条件约束,引导生成器优化梯度方向,使重建的地震数据更加逼近理想地震数据。然后,提出同时重建和去噪一体化损失函数,使网络模型能够兼顾地震数据的重建和去噪两个方面,并可以根据权重系数进行调整,提高重建和去噪效果。本文提出的网络模型在缺失道和噪声的干扰下具有更强的特征提取能力,可以对不同采样方式、不同采样比例以及含不同强度随机噪声的地震数据同时进行重建和去噪。经过合成数据和实际数据的测试,证明了本文提出的网络模型恢复出的地震数据信噪比更高,且具有一定的鲁棒性。
1 条件韦氏生成对抗网络GAN由生成器和判别器两部分组成,其中生成器通过学习拟合目标数据的概率分布,使学习到的概率分布能够充分接近目标数据的概率分布。判别器则用于判别生成器生成的数据是否符合目标数据的概率分布。模型在训练过程中,生成器和判别器二者相互对抗,通过不断地优化,最终达到纳什均衡。
cGAN是GAN的拓展[22],二者结构与训练过程基本相同,差异在于cGAN将有着对应关系的缺失含噪地震数据和理想地震数据的数据对作为标签输入到判别器中进行条件约束,引导生成器的优化方向,使得生成器生成的数据接近理想地震数据。cGAN的损失函数可以描述为
| $ \begin{array}{l}\underset{\boldsymbol{G}}{\mathrm{m}\mathrm{i}\mathrm{n}}\underset{{\boldsymbol{D}}_{\mathrm{K}}}{\mathrm{m}\mathrm{a}\mathrm{x}}{L}_{\mathrm{c}\mathrm{G}\mathrm{A}\mathrm{N}}={E}_{\boldsymbol{x} \sim {\boldsymbol{P}}_{\mathrm{r}}\left(\boldsymbol{x}\right)}\left[\mathrm{l}\mathrm{n}{D}_{\mathrm{K}}\right(\boldsymbol{x}, \boldsymbol{y}\left)\right]+\\ {E}_{\boldsymbol{x} \sim {\boldsymbol{P}}_{\mathrm{g}}\left(\boldsymbol{x}\right)}\left\{\mathrm{l}\mathrm{n}\left[1-{D}_{\mathrm{K}}(\boldsymbol{x}, G(\boldsymbol{x}\left)\right)\right]\right\}\end{array} $ | (1) |
式中:x为缺失含噪的地震数据;y为理想的地震数据;G(x)为通过生成器生成的地震数据;
包括cGAN在内的传统GAN都使用KL散度和JS散度计算理想地震数据和生成地震数据之间的距离,在生成的地震数据概率分布与理想地震数据概率分布没有重叠或者重叠较少的情况下,JS散度为常数,KL散度会产生无意义的值,无法提供训练所需的梯度,会出现模式崩塌和梯度消失等问题。
为解决cGAN中出现的这些问题,cWGAN使用韦氏距离作为损失函数计算目标数据和生成数据之间的距离。韦氏距离又称作地球移动器(Earth-Mover)距离,被定义为从生成的数据分布收敛到目标数据的最小成本,具有对称性。韦氏距离作为损失函数的优点在于即使在生成的数据分布与目标数据分布没有重叠或者重叠较少的情况下,依然能够反映距离的远近,引导训练优化的方向。根据Rüschendorf[23]的理论,可以将韦氏距离描述为
| $ W({P}_{\mathrm{r}}, {P}_{\mathrm{g}})=\underset{\gamma \sim \boldsymbol{\varPi }({P}_{\mathrm{r}}, {P}_{\mathrm{g}})}{\mathrm{i}\mathrm{n}\mathrm{f}}\left\{{\boldsymbol{{E}}}_{(\boldsymbol{x}, \boldsymbol{y})\sim \gamma }\left[{‖\boldsymbol{G}\left(\boldsymbol{x}\right)-\boldsymbol{y}‖}_{1}\right]\right\} $ | (2) |
式中:Π(Pr, Pg)表示生成地震数据概率分布Pr和理想地震数据概率分布Pg的所有可能联合概率分布的集合;γ为Pr和Pg的所有可能联合分布的集合的样本;inf函数是计算所有符合条件的集合下的最大下界。由于
| $ W({P}_{\mathrm{r}}, {P}_{\mathrm{g}})=\frac{1}{K}\underset{{‖f‖}_{\mathrm{L}}\le K}{\mathrm{s}\mathrm{u}\mathrm{p}}\left\{{E}_{\boldsymbol{x} \sim {\boldsymbol{P}}_{\mathrm{r}}}\left[f\left(\boldsymbol{x}\right)\right]-{E}_{\boldsymbol{x} \sim {\boldsymbol{P}}_{\mathrm{g}}}\left[f\left(\boldsymbol{x}\right)\right]\right\} $ | (3) |
式中:
| $ \begin{array}{l}\underset{\boldsymbol{G}}{\mathrm{m}\mathrm{i}\mathrm{n}}\underset{{D}_{\mathrm{W}}\in {\boldsymbol{D}}_{\mathrm{L}}}{\mathrm{m}\mathrm{a}\mathrm{x}}{L}_{\mathrm{c}\mathrm{W}\mathrm{G}\mathrm{A}\mathrm{N}}={E}_{\boldsymbol{x} \sim {P}_{\mathrm{r}}\left(\boldsymbol{x}\right)}\left[{D}_{\mathrm{W}}\right(\boldsymbol{x}, \boldsymbol{y}\left)\right]-\\ {E}_{\boldsymbol{x} \sim {P}_{\mathrm{g}}\left(\boldsymbol{x}\right)}\left\{{D}_{\mathrm{W}}\left[\boldsymbol{x}, \boldsymbol{G}\left(\boldsymbol{x}\right)\right]\right\}\end{array} $ | (4) |
式中
| $ \left|{D}_{\mathrm{W}}\right({\boldsymbol{x}}_{1}, {\boldsymbol{y}}_{1})-{D}_{\mathrm{W}}({\boldsymbol{x}}_{2}, {\boldsymbol{y}}_{2}\left)\right|\le |{\boldsymbol{x}}_{1}-{\boldsymbol{x}}_{2}| $ | (5) |
此时判别器不再执行分类功能,而是测量理想地震数据概率分布与生成地震数据概率分布之间的距离,判别器中使用权重裁剪实现1-Lipschitz条件。
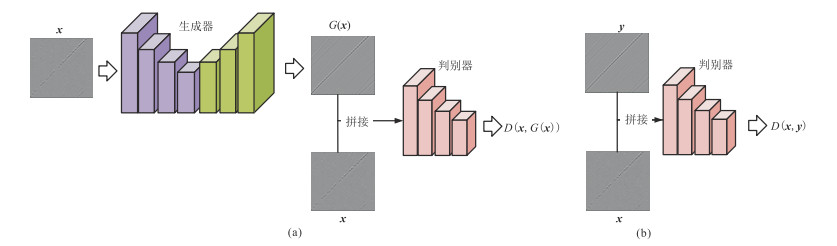
2 模型设计 2.1 重建和去噪一体化cWGAN设计针对GAN网络训练过程中容易出现的梯度消失和模式崩塌等问题,引出了使用韦氏距离作为损失函数的WGAN模型,它可以通过权重裁剪方法处理以满足Lipschitz连续。又因为WGAN网络模型生成的地震数据具有较强的随机性,其细节纹理部分和理想地震数据仍有一定差距。为了在重建和去噪一体化任务中更精确地拟合理想地震数据,在WGAN网络模型中添加缺失含噪地震数据和对应的理想地震数据构成的数据对作为标签对其进行条件约束构建cWGAN网络模型。本文网络的简要结构如图 1所示。
|
图 1 cWGAN的简要结构 (a)生成器数据流向图;(b)判别器数据流向图 |
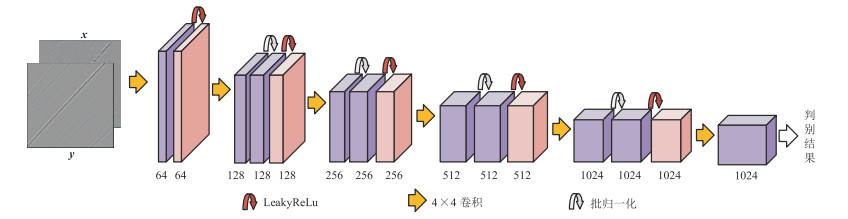
判别器网络结构如图 2所示。为获取地震数据更大邻域中的信息,增大深度神经网络中感受野,判别器中的卷积层使用尺寸为4×4、步长为2的卷积核。由于平均池化会模糊边界,最大池化会丢弃掉有些位置的像素值,采用卷积操作来代替池化让网络自适应学习下采样操作。为在反向传播过程中,对激活函数输出小于0的部分依旧可以产生梯度支持训练,判别器使用LeakyReLu激活函数。本文添加的条件约束,是将理想地震数据作为标签与对应的缺失含噪地震数据一同输入到判别器中,以引导生成器的优化方向,使得生成器生成的地震数据更接近理想地震数据。
|
图 2 判别器的结构示意图 紫色块表示卷积和归一化得到的特征图;粉色块表示经过激活函数后的特征图;图下的数字代表特征图的通道数,图 3同。 |
生成器网络结构如图 3所示。基于U-Net网络架构使得生成器能够分级提取地震数据同相轴特征,并通过跳跃连接的结构加强特征的融合,进而提高生成器在缺失道和随机噪声干扰下对地震数据特征的提取能力;在卷积层与激活函数层中间添加批归一化层(Batch Normalization,BN)进行归一化操作,能够减少内部协变量偏移,使每一层神经网络的输入相对稳定,训练过程中更易学习到地震数据的特征,提高网络模型收敛效率,有效地防止过拟合。

|
图 3 生成器的结构示意图 |
本文网络模型的总体损失函数为
| $ L={L}_{\mathrm{c}\mathrm{W}\mathrm{G}\mathrm{A}\mathrm{N}}+\lambda {L}_{\mathrm{S}\mathrm{E}} $ | (6) |
式中:LcWGAN为cWGAN网络模型的对抗损失函数;LSE为评价地震数据重建和去噪效果的一体化损失函数;λ为LSE的权重系数,以保持LcWGAN和LSE在同一数量级上。
为了提高生成数据的质量,借鉴内容损失函数的思想,由于缺失含噪地震数据中的缺失的地震道中不存在噪声,在重建缺失的地震道时无需考虑噪声,只需要对缺失道的重建效果进行评估;同样,在没有缺失的地震道中只需要对去噪效果进行评估。基于上述特点,设计一种新的用于评估重建和去噪效果的一体化损失函数,即
| $ {L}_{\mathrm{S}\mathrm{E}}={L}_{\mathrm{D}\mathrm{N}}+\mu {L}_{\mathrm{R}\mathrm{C}} $ | (7) |
式中:LDN为评估非缺失部分去噪效果的损失函数;LRC为评估缺失部分重建效果的损失函数;μ为用来保持两者在同一量级上的参数。LDN和LRC表达式分别为
| $ {L}_{\mathrm{D}\mathrm{N}}=\frac{1}{N}\sum\limits _{i=1}^{N}{\left[\boldsymbol{M}\odot \boldsymbol{G}\left({\boldsymbol{x}}_{i}\right)-\boldsymbol{M}\odot {\boldsymbol{y}}_{i}\right]}^{2} $ | (8) |
| $ {L}_{\mathrm{R}\mathrm{C}}=\frac{1}{N}\sum\limits _{i=1}^{N}{\left[\stackrel{-}{\boldsymbol{M}}\odot \boldsymbol{G}\left({\boldsymbol{x}}_{i}\right)-\stackrel{-}{\boldsymbol{M}}\odot {\boldsymbol{y}}_{i}\right]}^{2} $ | (9) |
式中:N为批量大小;
应用合成数据集验证本文网络模型重建和去噪的效果。首先,应用BP2004模型数据集进行实验,分析可能影响地震数据重建去噪效果的因素。然后,使用Marmousi模型数据对比与其他主流网络模型的重建和去噪效果,分析算法的优缺点。本文使用信噪比(SNR)
| $ \mathrm{S}\mathrm{N}\mathrm{R}=10\times \mathrm{l}\mathrm{g}\frac{{‖\boldsymbol{y}‖}_{2}^{2}}{{‖\boldsymbol{y}-\boldsymbol{G}\left(\boldsymbol{x}\right)‖}_{2}^{2}} $ | (10) |
评估重建和去噪后的地震数据质量。
3.1 BP2004合成数据集及训练策略BP2004数据集[24]共包括1340炮,雷克子波主频为27 Hz,采样间隔为6 ms。从1340炮数据中抽取300炮1920×1152(1920为样点数,1152为道数)的剖面,并将其切分成128×128的切片,共10000片,作为训练数据。并在切片数据中分别加入噪声强度等级l (噪声的标准差与地震数据的标准差比值)为0.03、0.06和0.10的噪声,并进行采样比例为0.5和0.8的随机采样以仿真包含噪声和缺失的数据,将数据集按照80%、10%、10%的比例分别划分为训练集、验证集和测试集。实验批量大小设置为20,初始判别器和生成器学习率都为2×10-3,λ为100,μ为1。使用Adam优化器训练网络,训练期间判别器每更新5次,生成器更新1次,最大训练轮次设置为300,网络输入、输出尺寸均为128×128的切片数据。实验使用Ubuntu 18.04 LTS系统,环境为RTX3080GPU,平台为PyTorch。
3.2 BP2004模型数据实验对比首先,应用BP2004模型数据对比cGAN、WGAN和cWGAN的训练过程。cGAN采用KL散度计算理想地震数据概率分布与生成器生成的地震数据概率分布之间的距离,WGAN和cWGAN均采用韦氏距离计算理想地震数据概率分布与生成器生成的地震数据概率分布之间的距离。WGAN的输入与cGAN和cWGAN不同,其余训练步骤与参数均相同。WGAN只将生成器生成的地震数据或者理想地震数据输入到判别器中,cGAN和cWGAN输入到判别器中的是缺失含噪的地震数据和对应的理想地震数据对或者是缺失含噪的地震数据和生成的地震数据对。
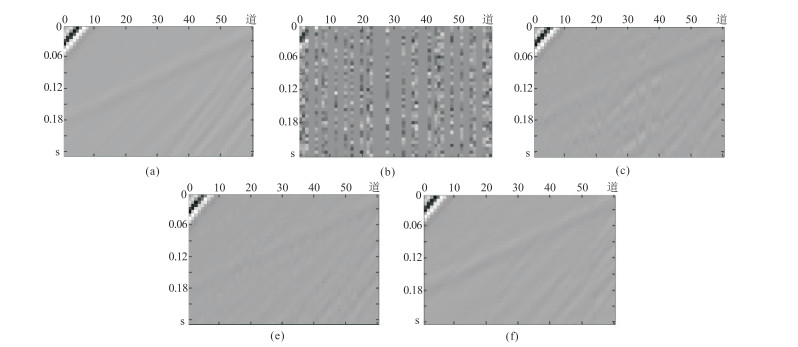
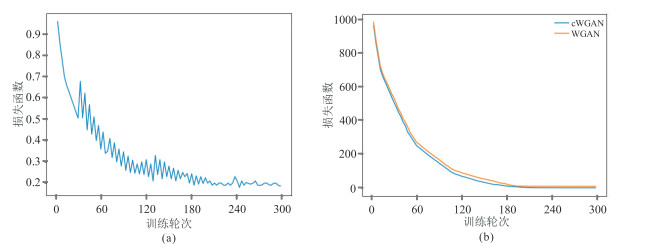
训练结束后,随机选取测试集的样本,使用训练好的cGAN、WGAN和cWGAN的模型对其进行重建及去噪,结果如图 4所示。其中图 4b是噪声强度为0.1、缺失比例为0.5的随机缺失含噪地震数据部分区域放大图。对比图 4c与图 4a可见,cGAN网络恢复得到的地震数据同相轴不连续,残存噪声较多,细节部分与理想数据差距较大。对比图 4d与图 4a可见,WGAN网络恢复得到的地震数据同相轴少部分不连续,噪声残存较少,细节部分与理想数据还有一定差距。对比图 4e与图 4a可知,cWGAN网络恢复得到的地震数据同相轴光滑连续,噪声基本去除,细节部分也与理想数据基本一致。由图 5a可知,cGAN训练过程中损失函数出现较为剧烈的抖动现象说明该方法稳定性较差。由图 5b可知WGAN收敛时其损失略高于cWGAN。所以相较于KL散度,韦氏距离作为计算理想地震数据概率分布与生成器生成的地震数据概率分布之间的距离指标,使训练过程更稳定,而且重建和去噪后的地震数据比其他模型更逼近理想地震数据;加入约束条件的网络模型重建的地震数据在数据的概率分布相差较小的情况下也能更好地引导生成器优化梯度方向,从而提高生成器生成的地震数据的质量。
|
图 4 三种网络模型的重建和去噪结果的放大对比 (a) 理想地震数据;(b)缺失含噪地震数据;(c)cGAN模型,SNR为15.1 dB;(d)WGAN模型,SNR为16.4 dB;(e)cWGAN模型,SNR为17.5 dB |
|
图 5 三种网络模型的训练损失函数曲线对比(a)cGAN;(b)WGAN和cWGAN |
其次,应用BP2004模型数据对比cWGAN使用L1损失函数、MSE损失函数和本文的一体化损失函数作为约束条件的效果。L1、MSE损失函数的具体形式分别为
| $ {L}_{1}={E}_{\boldsymbol{x}, \boldsymbol{y} \sim {P}_{\mathrm{r}}(\boldsymbol{x}, \boldsymbol{y})}\left[{‖\boldsymbol{y}-\boldsymbol{G}\left(\boldsymbol{x}\right)‖}_{1}\right] $ | (11) |
| $ \mathrm{M}\mathrm{S}\mathrm{E}={E}_{\boldsymbol{x}, \boldsymbol{y} \sim {P}_{\mathrm{r}}(\boldsymbol{x}, \boldsymbol{y})}\left[{‖\boldsymbol{y}-\boldsymbol{G}\left(\boldsymbol{x}\right)‖}_{2}^{2}\right] $ | (12) |
图 6b为噪声强度l为0.1、随机采样比例为0.5的切片。从图 6c可以看出无损失函数约束的处理结果同相轴不连续,有明显的道缺失,残存噪声也较多,重建和去噪均较差;L1损失函数约束的处理结果(图 6d)同相轴较光滑、连续,但残存噪声较多;MSE损失函数约束的处理结果(图 6e)残存噪声较少,但同相轴连续性较差,有较明显的道缺失;本文一体化损失函数约束的处理结果(图 6f)同相轴光滑、连续,噪声基本消除,其SNR比其他两种损失函数均高。可见,本文一体化损失函数能够同时兼顾缺失道的重建和非缺失道的去噪两个方面的任务,而L1损失函数和MSE损失函数则只能针对性的评价重建或去噪的单方面任务,在引导生成器梯度方向时会侧重其中一方面而忽略另外一方面。

|
图 6 BP2004模型数据应用不同损失函数的处理结果对比 (a) 理想地震数据;(b)缺失含噪地震数据,SNR为-2.7 dB;(c)无损失函数约束,SNR为14.6 dB;(d)L1损失函数,SNR为15.4 dB;(e)MSE损失函数,SNR为15.3 dB;(f)一体化损失函数,SNR为16.4 dB |
Marmousi是由Institut Français du Pétrole (IFP)生成的二维合成数据集,采样间隔4 ms。从Marmousi模型数据中抽取300炮1920×1152的剖面,然后截取成10000个250×160的切片数据。将数据集按照80%、10%、10%的比例分别划分为训练集、验证集和测试集。训练过程中l设置为0.03、0.06和0.10,采样比例设为0.5和0.8,其他实验参数与BP2004模型数据相同。
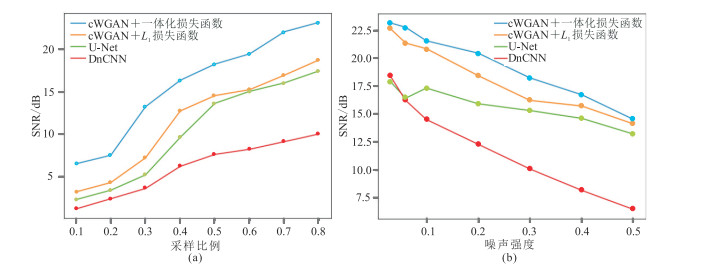
当噪声强度固定为0.03,cWGAN与U-Net及DnCNN的重建SNR随采样比例的变化曲线如图 7a所示。当采样比例固定为0.8,四个网络模型的重建SNR随噪声强度的变化曲线如图 7b所示。由图可看出:cWGAN网络模型的重建SNR明显高于其他网络模型;与使用L1损失函数约束相比,使用本文一体化损失函数约束的cWGAN,无论是在低采样比例条件下还是在高噪声干扰情况下,重建结果的SNR均较高。由此可见,本文提出的生成对抗网络结构相较于一般的网络模型有着更强的特征提取能力和重建能力。通过一体化损失函数对重建和去噪任务分别进行约束,可以更加逼近于理想的地震数据,提高重建地震数据的质量。
|
图 7 四种网络模型重建、去噪地震数据的SNR随采样比例(a)、噪声强度(b)的变化曲线对比 |
除此之外,本文还对均匀采样和局部采样的地震数据进行了实验,结果如表 1和表 2所示。分析可知,在均匀采样和局部采样时,本文模型对不同噪声强度和不同程度缺失的地震数据均有着较好的重建效果。相较于其他网络模型,在强噪声和低采样比例的条件下,本文网络模型的重建质量均较高。
|
|
表 1 均匀采样方式下、不同采样比例和噪声强度时三种网络重建结果的SNR对比 |
|
|
表 2 局部采样方式下、不同采样比例和噪声强度时三种网络重建结果的SNR对比 |
应用实际地震数据验证本文网络模型在不同噪声强度、不同采样比例条件下对实际地震数据的处理效果。
实际地震数据共60炮(采样点数为7000,道数为14400),采样间隔4 ms。从实际地震数据集中截取300张1920×1152(采样点数为1920,道数为1152)的地震剖面,然后截取成10000个250×160的切片。实际数据处理方法及参数设置与Marmousi模型相同。
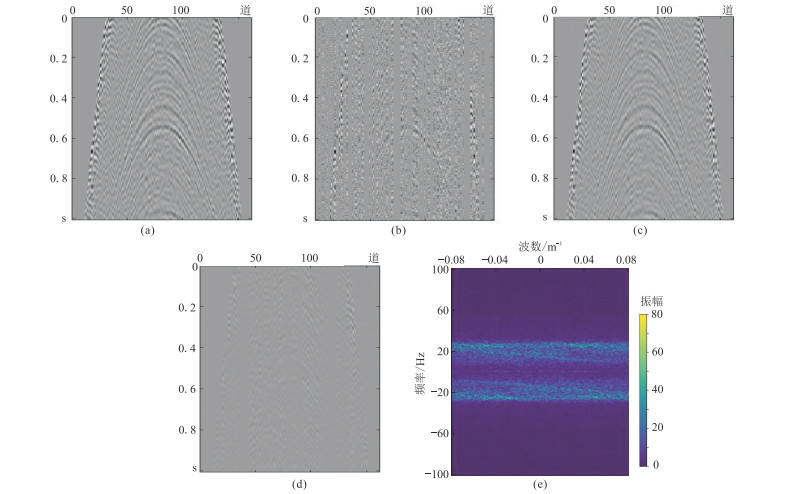
应用本文模型对噪声强度l为0.1、采样比例为0.5的地震数据处理结果如图 8所示。处理后的图片结果清晰,同相轴光滑、连续,只有少部分细节纹理丢失。由残差剖面及频谱可见,残留信息能量较低,说明处理后地震数据质量较高。由表 3可知,本文算法对实际地震数据集依然有较好的处理效果。在较强噪声干扰和地震道较大程度缺失的情况下,本文网络模型恢复出的地震数据同相轴光滑、连续,信噪比较高,其波阻特征与实际地震数据相似,有利于后续的处理和解释。
|
图 8 实际地震数据本文模型重建去噪结果 (a)理想地震数据;(b)缺道、含噪地震数据;(c)本文模型重建+去噪结果;(d)残差剖面;(e)残差剖面的频谱 |
|
|
表 3 本文模型对不同采样比例、不同强度噪声实际地震数据的重建前、后的SNR对比 |
针对当前基于深度神经网络的同时重建和去噪算法,在较强噪声等级、地震道较大程度缺失的情况下,无法同时有效恢复地震数据的高频轮廓信息和低频同相轴信息的问题,本文提出了基于生成对抗网络的重建与去噪一体化方法。经过合成和实际地震数据集测试,得到如下结论:
(1) 生成器采用U-Net为基础结构分级提取特征,并通过跳跃连接进行高、低频信息的融合,能够提高生成器在缺失道与随机噪声干扰下对地震数据特征的提取能力;
(2) 在判别器结构中引入条件约束引导生成器训练,生成器恢复的地震数据会更逼近于理想的地震数据;
(3) 重建与去噪一体化损失函数能够在缺失道和噪声的干扰下,提高重建和去噪效果;
(4) 相较于其他深度学习方法,本文网络模型均可以在地震道较大程度缺失和较强的噪声干扰下有效学习地震数据的特征,恢复出质量较高的地震数据,具有较强的鲁棒性。
| [1] |
SPITZ S. Seismic trace interpolation in the F‑X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [2] |
FOMEL S. Seismic reflection data interpolation with differential offset and shot continuation[J]. Geophysics, 2003, 68(2): 733-744. DOI:10.1190/1.1567243 |
| [3] |
NAGHIZADEH M, SACCHI M D. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J]. Geophysics, 2010, 75(6): WB189-WB202. DOI:10.1190/1.3509468 |
| [4] |
MA J. Three-dimensional irregular seismic data reconstruction via low‑rank matrix completion[J]. Geophysics, 2013, 78(5): V181-V192. DOI:10.1190/geo2012-0465.1 |
| [5] |
冯永基, 陈学华. 融合部分卷积和注意力机制对抗网络模型的地震数据重建[J]. 石油地球物理勘探, 2023, 58(1): 21-30. FENG Yongji, CHEN Xuehua. Seismic data reconstruction based on partial convolution and attentional mechanism adversarial network model[J]. Oil Geophysical Prospecting, 2023, 58(1): 21-30. |
| [6] |
张明, 张昕, 梁菁, 等. 多分量地震在致密气储层精细描述中的应用[J]. 石油地球物理勘探, 2023, 58(6): 1454-1462. ZHANG Ming, ZHANG Xin, LIANG Jing, et al. Application of multi-component seismic technology in fine description of tight gas reservoirs[J]. Oil Geophysical Prospecting, 2023, 58(6): 1454-1462. |
| [7] |
张岩, 孟德聪, 宋利伟, 等. 基于特征强化U-Net的地震速度反演方法[J]. 石油地球物理勘探, 2024, 59(2): 185-194. ZHANG Yan, MENG Decong, SONG Liwei, et al. Seismic velocity inversion method based on feature enhancement U‑Net[J]. Oil Geophysical Prospecting, 2024, 59(2): 185-194. |
| [8] |
ZHANG Y, MENG D C, ZHOU Y F, et al. Seismic velocity inversion based on physically constrained neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 1-17. |
| [9] |
王静, 张军华, 芦凤明, 等. 构建三维深度监督网络的断层检测方法[J]. 石油地球物理勘探, 2021, 56(5): 947-957. WANG Jing, ZHANG Junhua, LU Fengming, et al. Research on fault detection method based on 3D deeply supervised network[J]. Oil Geophysical Prospecting, 2021, 56(5): 947-957. |
| [10] |
SI X, YUAN Y, SI T, et al. Attenuation of random noise using denoising convolutional neural networks[J]. Interpretation, 2019, 7(3): SE269-SE280. |
| [11] |
WANG F, CHEN S. Residual learning of deep convolutional neural network for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1314-1318. |
| [12] |
CHAI X, GU H, LI F, et al. Deep learning for irregularly and regularly missing data reconstruction[J]. Scientific Reports, 2020, 10(1): 3302. |
| [13] |
ZHONG T, CHENG M, DONG X, et al. Seismic random noise suppression by using deep residual U-Net[J]. Journal of Petroleum Science and Engineering, 2022, 209(2): 109901. |
| [14] |
WANG Q, LI H. Multi-scale residual network for seismic data denoising and reconstruction[C]. 2020 15th IEEE International Conference on Signal Proces-sing (ICSP), 2020: 333-336.
|
| [15] |
JIANG J, REN H, ZHANG M. A convolutional autoencoder method for simultaneous seismic data reconstruction and denoising[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [16] |
MANDELLI S, LIPARI V, BESTAGINI P. Interpolation and denoising of seismic data using convolutional neural networks[DB/OL]. https://arxiv.org/abs/1901.07927.
|
| [17] |
GOODFELLOW I, POUGET A J, MIRZA M, et al. Generative adversarial nets[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems, 2014, 2672-2680.
|
| [18] |
MAO X, LI Q, XIE H, et al. Least squares generative adversarial networks[C]. 2017 IEEE International Conference on Computer Vision (ICCV), 2017, 2813-2821.
|
| [19] |
ARJOVSKY M, CHINTALA S, BOTTOU L. Wasserstein generative adversarial networks[C]. Proceedings of the 34th International Conference on Machine Learning, 2017, 214-223.
|
| [20] |
OLIVEIRA D A B, FERREIRA R S, SILVA R, et al. Interpolating seismic data with conditional generative adversarial networks[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(12): 1952-1956. |
| [21] |
WEI Q, LI X, SONG M. De-aliased seismic data interpolation using conditional Wasserstein generative adversarial networks[J]. Computers & Geosciences, 2021, 154: 104801. |
| [22] |
MIRZA M, OSINDERO S. Conditional generative adversarial nets[DB/OL]. https://arxiv.org/abs/1411.1784.
|
| [23] |
RÜSCHENDORF L. The Wasserstein distance and approximation theorems[J]. Probability Theory and Related Fields, 1985, 70(1): 117-129. |
| [24] |
BILLETTE F J, BRANDSBERG-DAHL S. The 2004 BP velocity benchmark[C]. Extended Abstracts of 67th EAGE Conference & Exhibition, 2005, cp-1-00513.
|



 董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email:
董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email: