2. 西安交通大学电子与信息学部, 陕西西安 710064
2. Faculty of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an, Shaanxi 710064, China
利用地震勘探技术获得的宽频带地震数据通常蕴含十分重要的地层信息[1],因此高分辨率地震数据对于精细地震解释意义重大。然而,地震波受地层吸收等因素影响,地震采集的原始数据分辨率较低。此外,随着勘探区域地质构造复杂度和勘探深度的增加,勘探难度增大。尽管地震勘探野外采集技术有了很大的进步,原始地震数据的质量明显优于以住,但仍不满足精细解释勘探目标的需求[2]。为了得到高分辨率地震资料并为后续地震解释提供可靠依据,必须进一步发展和应用高分辨率地震资料处理技术[3]。
传统常用的提高地震资料分辨率方法有反褶积法、反Q滤波法、时频分析法(时频变换法)以及谱白化法。其中,反褶积法通过压缩子波提高地震资料分辨率[4-7];反Q滤波法是一种对地层吸收导致的地震子波能量衰减进行补偿的技术,通过补偿地震波振幅、频率提高分辨率[8-11];时频分析法首先利用数学变换对地震资料实施分解,然后根据分解得到的不同尺度分量的时频信息进行高分辨处理[12],常见的变换有短时傅里叶变换[13]、小波变换[14-17]、广义S变换[18-19]等;谱白化法是通过在有效频带内拉平地震记录的振幅谱以补偿高频损失,实现提高地震资料分辨率的目的[20-23]。应用传统方法实现提高地震资料分辨率时需要满足一些假设条件,例如反Q滤波法假设地层是一个常Q模型,难以反映地下介质的真实情况;反褶积法假设反射系数序列谱为高斯分布且是最小相位子波;谱白化法假设反射系数序列的谱是白的。然而,实际地震资料往往不能满足这些假设,导致传统方法处理效果受到影响。
近年来,深度学习(Deep Learning)发展迅猛,被广泛应用到很多领域并取得了显著效果。作为深度学习的典型算法之一,卷积神经网络(Convolutional Neural Networks,CNN)表现十分亮眼,在许多领域取得了突破性的成果,如计算机视觉、语音识别等。CNN通过“学习”输入与输出之间的复杂映射函数在地震数据处理中显现出巨大的潜力,目前,基于CNN的地震数据处理主要集中在噪声压制[24-28]、盐体识别[29]、断层检测[30]、超分辨[31-35]等方向,并且在不断扩充、发展。
有监督深度学习方法在地震数据提高分辨率方面也有相应的应用。Choi等[31]使用U-Net基于有监督学习实现了单道地震数据的高分辨率处理,通过学习原始地震数据到高分辨率地震数据的映射,一定程度上恢复了单道地震数据的高频信息;Chen等[32]使用预训练的深度神经网络(DNN)实现解卷积过程,通过反复迭代、同时优化子波和反射系数,实现地震记录解卷积;Zhang等[33]将生成对抗网络引入地震数据提高分辨率处理中,获得了与常规方法相当的结果,甚至恢复了比常规方法更细微、连续的反射;蔡涵鹏等[34]设计了优化的生成对抗网络架构,用于实现稀疏地震数据的超分辨率重建,该方法使用Wasserstein损失加梯度惩罚项作为损失函数,克服了传统生成对抗网络在训练过程中会出现训练梯度不稳定和模式崩溃等问题,获得了比传统插值方法更好的结果;Li等[35]提出一种同时实现地震图像的超分辨率重建和去噪的DNN,在合成地震数据和实际地震数据上应用都有很好的效果;Chen等[36]提出了一种优化启发的深度学习方法用于快速求解各种地震子波的盲高分辨率(Blind High-Resolution Inverse,BHRI)反演问题,该方法将传统BHRI算法展开为一个深层神经网络并学习近端映射,能够在训练中学习BHRI算法的所有参数,克服了正则化方法需要设置所有参数的缺点,应用于模型及实际资料的处理结果验证了方法的有效性。
从以上文献不难看出,对CNN提高地震资料分辨率方向的研究处于快速发展阶段,如何有效设计网络结构和损失函数是众多学者关注的热点。本文提出一种基于强监督学习的提高地震资料分辨率方法:①利用地下结构的空间连续性,借鉴图像超分辨率重建的思想,设计了一种生成对抗网络结构;②为了提高网络感知质量,采用一种结合L1损失和多尺度结构相似性(Multi-scale Structural Simila- rity,MS-SSIM))损失的损失函数用于提高处理效果;③以连续小波域自适应频谱扩展方法处理得到的高分辨率地震数据作为标签,通过网络训练实现端到端的地震资料提高分辨率方法。合成数据和实际地震数据的应用结果表明,本文算法明显优于常规的均方误差损失(Mean Squared Error,MSE)和VGG(Visual Geometry Group)损失结合的同类算法,验证了本文方法的有效性。
1 基本原理 1.1 强监督学习强监督学习是有监督深度学习的一种,即所有的训练数据都要有一一对应且完全正确的标签。强监督学习被广泛应用在图像超分辨领域,所谓超分辨是指通过各种方法将低分辨率图像恢复为高分辨率图像。目前,基于强监督学习的单幅图像超分辨率重建网络主要有SRCNN[37]、FSRCNN[38]、ESPCN[39]、VDSR[40]、DRCN[41]、SRDenseNet[42]等。
单幅图像超分辨率重建的研究任务是设法从细节模糊的下采样图像中恢复原始尺寸的高分辨率图像。超分辨率重建的主要思想是:由于图像本身具有冗余性,相邻像素点具有很强的相似性,因此可以结合先验条件,从周围像素点推测缺失部分的像素值,而该过程与CNN中二维卷积算子的特征恰好相符。与图像信号类似,地震信号本身也具有冗余性,相邻地震道波形结构相似,因此同样可以结合地震子波等先验信息,借助周围波形特点恢复当前位置地震信号的真实值。同时,二维CNN的结构也适用于地震信号高分辨处理问题,可以将图像超分辨率网络用于提高地震资料的分辨率。
1.2 网络模型设计生成对抗网络是近几年应用前景最好的深度学习算法之一,它是由Goodfellow等[43]在2014年首次提出。该网络的基本思想是判断和博弈,训练过程就是博弈双方在不断对抗中学习并实现各自能力的提升。将博弈双方视为两个不同的网络,并被分别命名为生成器和判别器,生成器的主要任务是学习真实数据所具有的特征,并且生成器的输出能够被判别器判别为真;判别器的主要任务是判断它的输入是真实的数据还是来自生成器的输出,如果判定为真则输出1,判定为假则输出0。生成器和判别器在训练过程中会不断提高自身能力以战胜对方,直到达到一个纳什均衡,此时生成器输出的数据与真实数据几乎完全相同,判别器无法正确辨别真假。
研究者发现使用生成对抗网络模型可以获得比传统方法或其他图像超分辨网络更好的效果。SRGAN[43]是首次用于处理图像超分辨率任务的生成对抗网络,网络训练时如果采用MSE作为损失函数,这种逐像素计算方式未考虑人类视觉感知系统,恢复的图像虽然具有较高的峰值信噪比,但往往丢失了一些高频细节信息,导致恢复图像的视觉体验效果不佳。本文提出感知损失的概念增强了恢复图片的真实感,得到的结果虽然峰值信噪比不是最高,但视觉体验更好,图片更逼真。
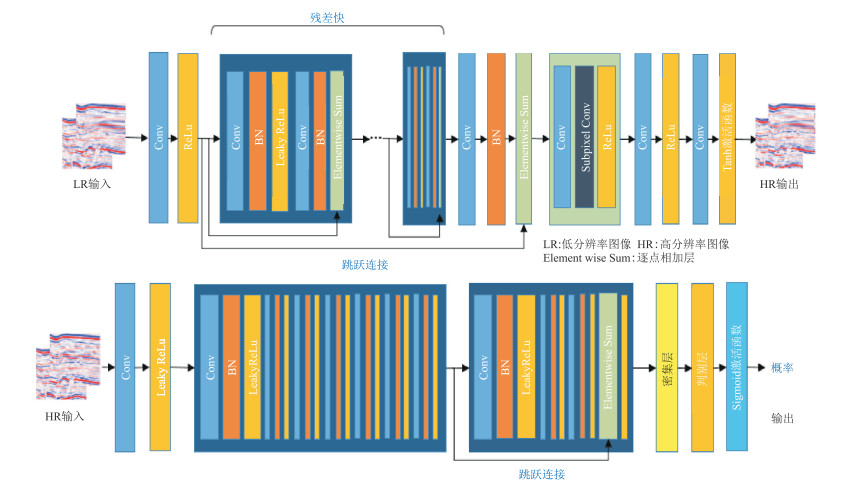
1.2.1 网络结构本文在SRGAN的基础上加以改进,得到适用于处理地震资料的VGG19网络结构。如图 1所示,生成器网络用来学习低分辨率地震数据到高分辨率地震数据的映射,共包含22个卷积(Conv)层,具有以下特点:①不包含池化层,避免了有效信息的损伤;②使用多个残差单元和批归一化(BN)层加速网络收敛,并且避免出现梯度消失或爆炸的现象,在一定程度上解决了网络过拟合问题;③使用亚像素卷积(Sub-pixel Conv)层,其功能类似于反卷积,通过增加通道数放大图像的尺寸并实现上采样,提供了更大的感受野,能够提取更丰富的上、下文信息,有利于生成更真实的图像细节。由于亚像素卷积层有放大图像尺寸的作用,因此在其后增加了步长为2的卷积层缩小尺寸,以保证输入、输出图像尺寸始终一致。
|
图 1 生成器(上)和判别器(下)结构 |
判别器的网络结构相对简单,包含12个卷积层,使用LeakyRelu(α)作为激活层的激活函数,其中α=0.2。判别器网络完成一个判别任务,需判断输入数据是来自真实的高分辨率地震数据还是生成器生成的地震数据。
1.2.2 生成器预训练在生成对抗网络中,生成器需要学习一个由低分辨率地震数据到高分辨率地震数据的映射,而判别器只需要完成一个二分类任务。由于分类任务相较于生成任务容易得多,在刚开始训练时,生成器的能力远低于判别器,这种由于能力不匹配导致的网络难以收敛是生成对抗网络比较常见的问题。为此,首先对生成器进行预训练,即在正式训练前预先对生成器训练一定的轮数(具体的预训练轮数由训练过程中的测试效果决定),使生成器获得一定的学习能力之后再与判别器抗衡。
1.2.3 损失函数在深度学习中,损失函数的选取直接影响网络最终的训练效果。通过最小化损失函数,使模型收敛并减小预测误差。生成对抗网络的损失函数包括两部分,分别为生成器损失和判别器损失。本文采用两种类型的损失函数对生成器进行训练,一种是结合了MSE损失和VGG损失的常规损失函数;另一种是为了提高网络感知质量而采用的结合了L1损失和MS-SSIM损失的本文方法损失函数。
生成器预训练时,采用MSE损失作为损失函数,即
| $ {l}_{\mathrm{M}\mathrm{S}\mathrm{E}}=\frac{1}{NP}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{P}{\left[{G}_{{\theta }_{\mathrm{G}}}\left({I}_{ij}^{\mathrm{L}\mathrm{R}}\right)-{I}_{ij}^{\mathrm{H}\mathrm{R}}\right]}^{2} $ | (1) |
式中:N为训练样本数,即批处理大小(Batch);P为每个分块(Patch)中总的数据点数(对应图像块总的像素点数);
正式训练时,生成器的损失函数采用内容损失与对抗损失加权组合的形式,即
| $ {l}_{\mathrm{G}\mathrm{e}\mathrm{n}}={l}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}}+{10}^{-3}{l}_{\mathrm{a}\mathrm{d}\mathrm{v}} $ | (2) |
式中:
| $ {l}_{\mathrm{a}\mathrm{d}\mathrm{v}}=\frac{1}{N}\sum\limits_{i=1}^{N}-\mathrm{l}\mathrm{g}{D}_{{\theta }_{\mathrm{D}}}\left[{G}_{{\theta }_{\mathrm{G}}}\left({I}_{i}^{\mathrm{L}\mathrm{R}}\right)\right] $ | (3) |
式中:
内容损失按照不同损失组合分为以下两种。
(1) 常规损失函数,其内容损失采用MSE损失和VGG损失的加权组合,即
| $ {l}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}}={\alpha }_{1}{l}_{\mathrm{M}\mathrm{S}\mathrm{E}}+{\alpha }_{2}{l}_{\mathrm{V}\mathrm{G}\mathrm{G}} $ | (4) |
式中:
VGG损失是将生成器生成的伪高分辨率地震数据和高分辨率标签数据输入VGG19网络进行特征提取,然后计算出的两个特征图的MSE误差。VGG损失定义为
| $ {l}_{\mathrm{V}\mathrm{G}\mathrm{G}}=\frac{1}{NP}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{P}{\left\{{\phi }_{\mathrm{5, 4}}\left[{G}_{{\theta }_{\mathrm{G}}}\left({I}_{ij}^{\mathrm{L}\mathrm{R}}\right)\right]-{\phi }_{\mathrm{5, 4}}\left({I}_{ij}^{\mathrm{H}\mathrm{R}}\right)\right\}}^{2} $ | (5) |
式中:
(2) 本文方法损失函数,其内容损失为L1损失和MS-SSIM损失的加权组合,即
| $ {l}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}}={\alpha }_{3}{l}_{1}+(1-{\alpha }_{3}){l}_{\mathrm{M}\mathrm{S}\mathrm{⁃}\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}} $ | (6) |
式中:
L1损失表达式为
| $ {l}_{1}=\frac{1}{N}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{P}\left|{G}_{{\theta }_{\mathrm{G}}}\left({I}_{ij}^{\mathrm{L}\mathrm{R}}\right)-{I}_{ij}^{\mathrm{H}\mathrm{R}}\right| $ | (7) |
MS-SSIM算法是一种对局部结构变化敏感的图像质量评估方法,可定义为
| $ \begin{array}{l}\mathrm{M}\mathrm{S}\mathrm{⁃}\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}(x, y)={\left[{b}_{M}(x, y)\right]}^{{\alpha }_{M}}\times \\ \prod \limits_{m=1}^{M}{\left[{c}_{m}(x, y)\right]}^{{\beta }_{m}}{\left[{s}_{m}(x, y)\right]}^{{\gamma }_{m}}\end{array} $ | (8) |
式中:M表示分辨率尺度;
数学上,MS-SSIM损失表达式为
| $ {l}_{\mathrm{M}\mathrm{S}\mathrm{⁃}\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}=\frac{1}{N}\sum\limits_{i=1}^{N}\left\{1-\mathrm{M}\mathrm{S}\mathrm{⁃}\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}\left[{G}_{{\theta }_{G}}\left({I}_{i}^{LR}\right), {I}_{i}^{HR}\right]\right\} $ | (9) |
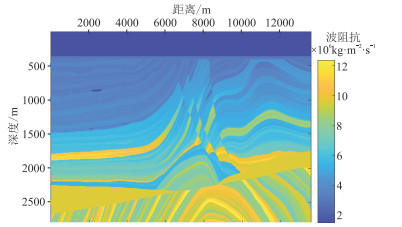
本文利用Marmousi2模型构建合成地震数据。首先利用纵波(P波)速度和密度得到反射系数,然后与子波卷积得到二维合成地震数据。图 2为构建合成数据所使用的波阻抗模型。
|
图 2 波阻抗模型 |
选择的子波类型为带通子波。带通子波也称为Ormshy小波,其定义如下
| $ \begin{array}{l}w\left(t\right)=\left[\frac{(\mathrm{\pi }{f}_{\mathrm{H}2}{)}^{2}}{\mathrm{\pi }({f}_{\mathrm{H}2}-{f}_{\mathrm{H}1})}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(\mathrm{\pi }{f}_{\mathrm{H}2}{t)}^{2}-\frac{(\mathrm{\pi }{f}_{\mathrm{H}1}{)}^{2}}{\mathrm{\pi }({f}_{\mathrm{H}2}-{f}_{\mathrm{H}1})}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(\mathrm{\pi }{f}_{\mathrm{H}1}{t)}^{2}\right]-\\ \left[\frac{(\mathrm{\pi }{f}_{\mathrm{L}2}{)}^{2}}{\mathrm{\pi }({f}_{\mathrm{L}2}-{f}_{\mathrm{L}1})}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(\mathrm{\pi }{f}_{\mathrm{L}2}{t)}^{2}-\frac{(\mathrm{\pi }{f}_{\mathrm{L}1}{)}^{2}}{\mathrm{\pi }({f}_{\mathrm{L}2}-{f}_{\mathrm{L}1})}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(\mathrm{\pi }{f}_{\mathrm{L}1}{t)}^{2}\right]\end{array} $ | (10) |
式中
最后,将反射系数序列和指定
| $ {d}_{n}={c}_{n}\mathrm{*}w\left(t\right), n=\mathrm{1, 2}, \cdots , q $ | (11) |
式中
由
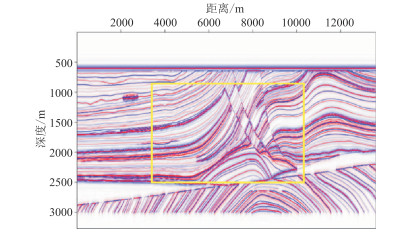
在训练开始前,分别对合成的低、高分辨率地震数据进行归一化预处理,以保证不同位置信号的相对能量保持不变。如图 3所示,选择黄色矩形框区域作为训练区域,其余部分作为测试区域,训练区域尺寸为1676 m×6801 m,约占总数据的25%。
|
图 3 合成地震数据 |
本次合成数据实验使用Adam优化器进行网络训练,优化器参数β1=0.9,训练时的相关参数设置见表 1。需要指出的是,这里衰减周期的轮数并非传统意义上的轮数。在训练时不是将训练样本对一次性全部取出,而是每次从训练区域以随机抽取的方式(均匀分布的随机采样)取出100个训练样本对输入网络中进行训练,一轮训练结束后,下一轮又在训练区域中重新抽取100个新的样本对。
|
|
表 1 合成数据训练相关参数 |
衡量地震资料高分辨率处理效果的重要指标,是在不破坏低频有效信息的前提下,能够拓展原始地震信号的有效频宽,提升高频有效信息。通过两组对比示例剖面(图 4、图 5)以及多道平均振幅谱(图 6)展示了合成数据的处理效果。

|
图 4 合成数据处理结果剖面对比示例1 (a)合成的低分辨率数据;(b)合成的高分辨率数据(标签);(c)常规损失函数处理结果;(d)本文方法损失函数处理结果 |
|
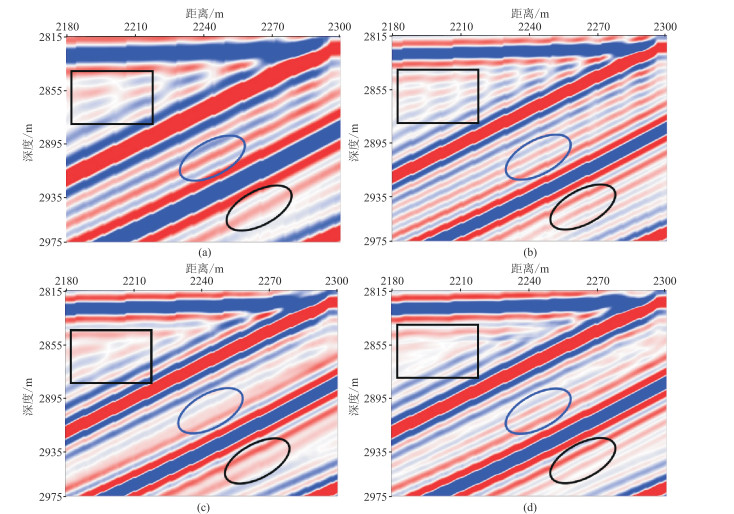
图 5 合成数据处理结果剖面对比示例2 (a)合成的低分辨率数据;(b)合成的高分辨率数据(标签);(c)常规损失函数处理结果;(d)本文方法损失函数处理结果 |
|
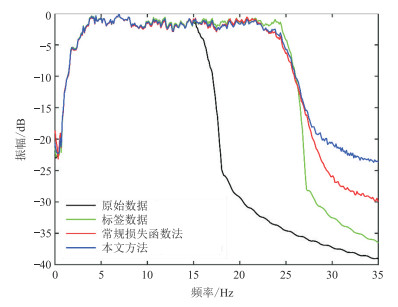
图 6 合成数据的多道平均振幅谱对比 |
从图 4、图 5剖面对比结果可以看出,采用两种损失函数处理都显著提高了合成低分辨率地震数据的分辨率,获得了与标签数据十分接近的结果。
进一步对比图 4矩形框区域可以看出,结合了L1损失和MS-SSIM损失的本文方法损失函数的处理结果相比常规损失函数得到的结果分辨率更高,与标签数据结构更相似。对比图中箭头所示区域可以看出,本文方法损失函数得到的处理结果同相轴更清晰且能量较强。
对比图 5中矩形框内的复杂构造区域可以看出,两种损失函数得到的处理结果比两个标签数据分辨率略低;对比图 5中椭圆所示区域可以看出,采用常规损失函数处理得到的结果无法区分薄层,而本文方法损失函数得到的处理结果分辨率更高,更接近高分辨率标签数据。
图 6展示了合成地震数据的多道平均振幅谱对比。可以看出,采用两种损失函数处理得到的资料振幅谱在低频段均与标签数据基本重合,极大地扩展了合成低分辨率地震数据的有效频宽,并且扩展的范围和程度基本相同,在不损伤数据低频有效信息的同时增强了高频信息。在高频段,与常规损失函数处理得到的结果相比,本文方法损失函数的处理结果对高频能量的抬升效果更佳。
3 实际数据应用 3.1 数据说明实际地震数据是来自西部某工区的三维叠后地震数据,该工区共有1941条测线,每条测线共有1124道数据,目标层时窗范围为800~3000 ms,采样频率为500 Hz,受各类因素的影响,原始数据的分辨率较低。在实验开始前,首先采用传统方法对该数据进行处理,得到的高分辨率结果作为本次网络训练的标签数据。传统方法选用连续小波域自适应频谱拓展的方法将数据分解到连续小波域,通过改变小波系数的大小,增强地震数据中高、低频成分的占比,从而拓宽地震数据有效频宽,达到提高分辨率的目的。该方法主要参数为高、低频调谐频率,本文使用的高频调谐频率为50 Hz、低频为20 Hz。在得到配对的低分辨率数据和高分辨率标签后,对这两块数据进行归一化预处理,之后选择中心部分区域作为训练区域,然后再对整块数据进行测试。
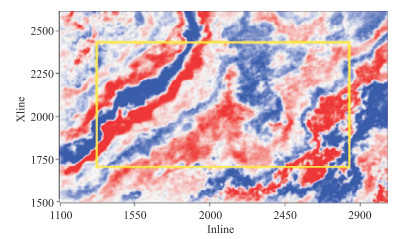
如图 7所示,黄色矩形框所示为数据训练区域,约占工区总面积的51%,训练区域的时间窗为900~1400 ms。对于三维地震数据,位于中心域的数据信噪比高,因此只选择数据中心的一个小空间范围进行训练,之后将其应用到整个工区目的层段完成测试。
|
图 7 实际数据的训练区域展示 |
实际地震数据实验的网络优化器仍选择Adam优化算法,优化器参数设置与合成数据实验相同。训练时的相关参数设置见表 2。
|
|
表 2 实际数据训练相关参数 |
为了衡量本文方法在实际地震数据中的应用效果,从剖面、时间切片和多道平均振幅谱三个方面展示最终的处理结果。图 8和图 9为剖面效果对比,可以看出实验的两种损失函数都显著提高了实际低分辨率地震数据的分辨率,获得了与传统方法(本文标签数据)十分接近的结果,说明常规损失函数和本文方法损失函数处理确实能在一定程度上提高原始地震数据的分辨率。
|
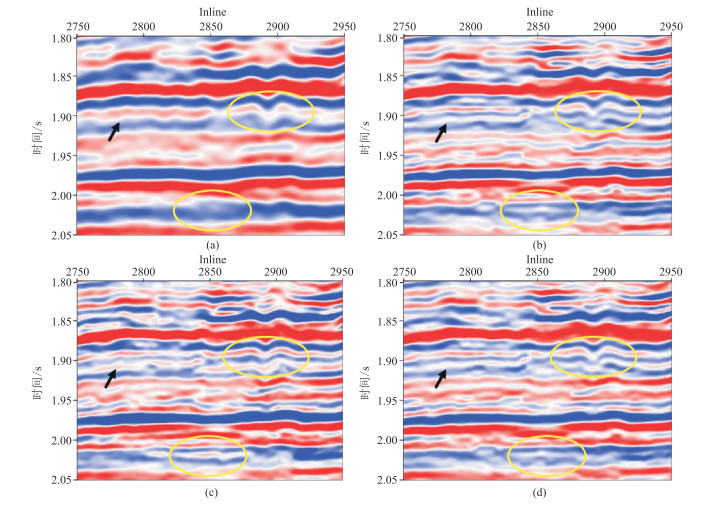
图 8 实际地震数据处理结果剖面对比 (a)原始低分辨率数据;(b)传统方法处理结果(高分辨率数据标签);(c)常规损失函数处理结果;(d)本文方法损失函数处理结果 |
|
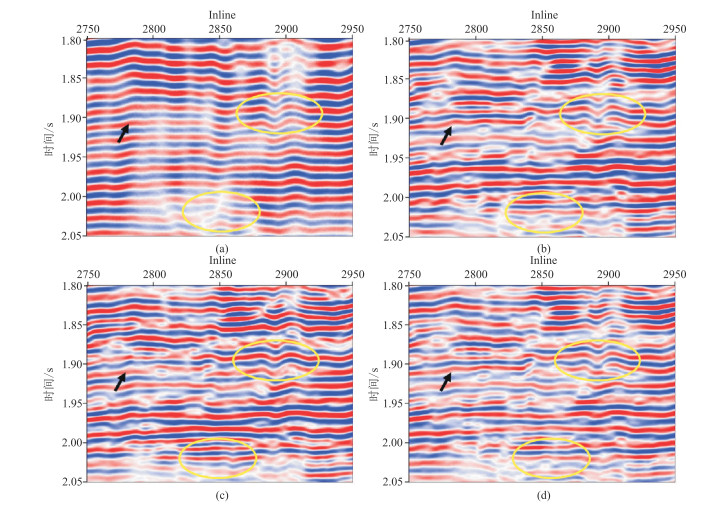
图 9 高通滤波后实际地震数据处理结果剖面对比 (a)原始低分辨率数据;(b)传统方法处理结果(高分辨率数据标签);(c)常规损失函数处理结果;(d)本文方法损失函数处理结果 |
对比图 8中椭圆区域可以看出,两种损失函数都改善了标签数据中同相轴的连续性,增加了一些细节信息。为了判断增加的这部分信息的真实性,需要进一步对比高通滤波结果;此外,对比图 8中箭头指示区域可以看出,本文方法损失函数处理结果中同相轴的形态特征更接近标签数据。
图 9为图 8经高通滤波后的结果(滤波截止频率为50 Hz),可以看到,高通滤波后标签数据中某些同相轴由不连续变得连续,表明采用的两种损失函数确实能够改善同相轴的连续性。此外,可以看到处理结果中增加的细节信息在高通滤波后依旧存在,这表明采用的两种损失函数确实能够提高原始地震数据的分辨率,甚至能够获得比标签数据更高的分辨率以及更多的高频细节信息。
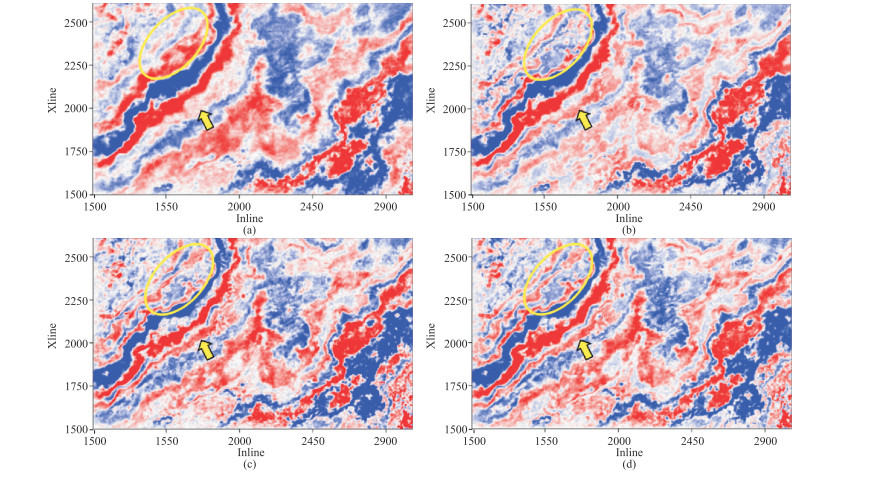
图 10展示了目标层等时切片对比结果。可以看出,两种损失函数处理均在很大程度提高了原始地震数据的分辨率,获得了与标签数据非常接近的结果。对比图中黄色椭圆所示区域可以看出,两种损失函数处理均获得了比标签数据(传统方法获得)分辨率更高的结果,恢复出了更多有效信息;对比图中黄色箭头指示处可以看出,两种损失函数处理结果同相轴更清晰、能量更高。相比常规损失函数,本文方法损失函数处理结果同相轴的延展走向更清晰、分辨率更高。
|
图 10 实际地震数据处理结果时间切片对比 (a)原始低分辨率数据;(b)传统方法处理结果(高分辨率数据标签);(c)常规损失函数处理结果;(d)本文方法损失函数处理结果 |
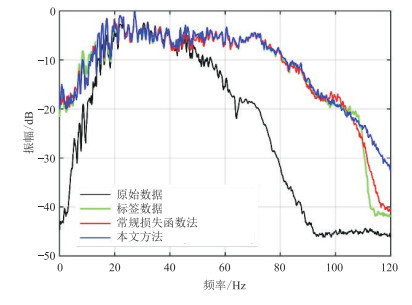
图 11展示了实际数据多道平均振幅谱结果。对比振幅谱可以看出,采用的两种损失函数处理结果均明显扩展了原始地震数据的有效频宽,且带宽拓展的范围和程度基本相同,在抬升高频信息的同时均未损伤原始地震数据的低频信息。两种损失函数的振幅谱与标签数据(传统方法获得)的振幅谱形态走势十分相似,其中,本文方法损失函数处理结果对高频部分的振幅谱能量抬升更高,说明结合L1损失和MS-SSIM损失对高频能量影响更明显。
|
图 11 实际地震数据多道平均振幅谱对比 |
本次实验是在搭载NVIDIA 1080TI GPU的计算平台上进行,网络训练时间约为12 h,测试时间仅为10 min。尽管深度学习模型在训练阶段需要用较长的时间调整参数,但在测试阶段,将训练好的模型应用到测试数据上时,网络运算十分高效,说明本文模型在处理大规模地震数据方面具有实用性。
值得说明的是,如果单纯对比与标签的相似性,采用结合L1损失和MS-SSIM损失的损失函数的处理效果更好一些,因为它不仅提高了原始地震数据的分辨率,改善了同相轴的连续性,还能很好地保持与标签数据几乎完全一致的结构信息。然而从传统意义上讲,网络学习效果很难超越标签数据,本文应用两种损失函数在某些区域的处理结果优于标签,缘于标签数据是采用传统的连续小波域自适应频谱拓展处理方法得到的。传统方法是基于局部优化的策略,而网络是基于全局优化的策略(具有更大的优势),为了降低损失函数,网络必须从高阶层的视角准确识别和提取各种复杂的特征,因而网络训练后能获得比标签数据更好的结果。
4 结束语利用地震数据结构上的连续性和空间上的冗余性,借鉴图像超分辨率重建的思想,本文提出并实现了一种基于强监督学习的地震资料高分辨率处理方法。该方法设计了一种生成对抗网络结构,采用结合L1损失和MS-SSIM损失的损失函数进行提高地震资料分辨率处理。合成地震数据和实际地震数据的应用结果表明,所提方法可行且有效。实验对比认为两种损失函数都能提高地震数据的分辨率,获得十分接近标签数据的结果,改善了剖面同相轴的连续性,增加了地震资料高频细节信息。相比结合MSE损失和VGG损失的常规损失函数,采用本文方法损失函数的处理效果更佳,在某些区域甚至能获得比标签数据更好的结果。
目前,不少探区将不同年代采集的数据进行连片处理,如果连片数据中某局部数据为高分辨率采集、处理结果,该数据即可作为连片数据的训练样本,采用本文方法处理后有可能获得整个连片区域高分辨率成果。不仅如此,通过合理设置正则化项,使之与待处理问题相适配,也可以凸显深度学习方法在处理复杂地质结构地震资料时所具备的优势。
| [1] |
周文辉, 石敏, 朱登明, 等. 基于残差注意力网络的地震数据超分辨率方法[J]. 计算机科学, 2021, 48(8): 24-31. ZHOU Wenhui, SHI Min, ZHU Dengming, et al. Seismic data super-resolution method based on residual attention network[J]. Computer Science, 2021, 48(8): 24-31. |
| [2] |
李曙光, 唐建明, 徐天吉, 等. 几种提高地震资料分辨率的方法及效果分析[J]. 勘探地球物理进展, 2010, 33(5): 323-327. LI Shuguang, TANG Jianming, XU Tianji, et al. Methods for improving seismic data resolution[J]. Progress in Exploration Geophysics, 2010, 33(5): 323-327. |
| [3] |
袁红军, 吴时国, 王箭波, 等. 拓频处理技术在大牛地气田勘探开发中的应用[J]. 石油地球物理勘探, 2008, 43(1): 69-75. YUAN Hongjun, WU Shiguo, WANG Jianbo, et al. Application of frequency-broadening processing technique in exploration and development of Daniudi gas-field[J]. Oil Geophysical Prospecting, 2008, 43(1): 69-75. |
| [4] |
ROBINSON E A. Predictive decomposition of seismic traces[J]. Geophysics, 1957, 22(4): 767-778. DOI:10.1190/1.1438415 |
| [5] |
BERKHOUT A J. Least-squares inverse filtering and wavelet deconvolution[J]. Geophysics, 1977, 42(7): 1369-1383. DOI:10.1190/1.1440798 |
| [6] |
王锐, 孙成禹, 尚新民. 有限熵反褶积[J]. 石油地球物理勘探, 2005, 40(6): 637-641. WANG Rui, SUN Chengyu, SHANG Xinmin. Li- mited entropy deconvolution[J]. Oil Geophysical Prospecting, 2005, 40(6): 637-641. DOI:10.3321/j.issn:1000-7210.2005.06.006 |
| [7] |
李振春, 阿力甫江, 王德营, 等. 时频域时变反褶积方法[J]. 地球物理学进展, 2015, 30(6): 2698-2705. LI Zhenchun, Alifujiang, WANG Deying, et al. Time-varying deconvolution method based on time-frequency domain[J]. Progress in Geophysics, 2015, 30(6): 2698-2705. |
| [8] |
HALE D. Q and adaptive prediction error filters[R]. Stanford Exploration Project Report, 1981, 28: 209-231.
|
| [9] |
BICKEL S H, NATARAJAN R R. Plane-wave Q deconvolution[J]. Geophysics, 1985, 50(9): 1426-1439. DOI:10.1190/1.1442011 |
| [10] |
赵建勋. 反Q滤波的应用[J]. 石油地球物理勘探, 1986, 21(4): 410-421, 447. ZHAO Jianxun. The application of inverse Q filter[J]. Oil Geophysical Prospecting, 1986, 21(4): 410-421, 447. |
| [11] |
张固澜, 林进, 王熙明, 等. 一种自适应增益限的反Q滤波[J]. 地球物理学报, 2015, 58(7): 2525-2535. ZHANG Gulan, LIN Jin, WANG Ximing, et al. A self-adaptive approach for inverse Q-filtering[J]. Chinese Journal of Geophysics, 2015, 58(7): 2525-2535. |
| [12] |
颜中辉, 方刚, 徐华宁, 等. 希尔伯特谱白化方法在海洋地震资料高分辨率处理中的应用[J]. 海洋地质与第四纪地质, 2018, 38(4): 212-220. YAN Zhonghui, FANG Gang, XU Huaning, et al. The application of Hilbert spectral whitening method to high resolution processing of Marine seismic data[J]. Marine Geology & Quaternary Geology, 2018, 38(4): 212-220. |
| [13] |
白桦, 李鲲鹏. 基于时频分析的地层吸收补偿[J]. 石油地球物理勘探, 1999, 34(6): 642-648. BAI Hua, LI Kunpeng. Stratigraphic absorption compensation based on time-frequency analysis[J]. Oil Geophysical Prospecting, 1999, 34(6): 642-648. DOI:10.3321/j.issn:1000-7210.1999.06.005 |
| [14] |
李鲲鹏, 李衍达, 张学工. 基于小波包分解的地层吸收补偿[J]. 地球物理学报, 2000, 43(4): 542-549. LI Kunpeng, LI Yanda, ZHANG Xuegong. A method to compensate earth filtering based on wavelet packet[J]. Chinese Journal of Geophysics, 2000, 43(4): 542-549. DOI:10.3321/j.issn:0001-5733.2000.04.015 |
| [15] |
赵淑红, 朱光明. 用小波变换谱均衡法提高地震资料的分辨率[J]. 西安科技大学学报, 2007, 27(2): 255-259. ZHAO Shuhong, ZHU Guangming. Using combined method of wavelet transform and spectrum equalization to improve seismic data resolution[J]. Journal of Xi'an University of Science and Technology, 2007, 27(2): 255-259. DOI:10.3969/j.issn.1672-9315.2007.02.021 |
| [16] |
SMITH M, PERRY G, STEIN J, et al. Extending seismic bandwidth using the continuous wavelet transform[J]. First Break, 2008, 26(6): 97-102. |
| [17] |
陈文超, 王伟, 李瑞萍. 连续小波域地震信号自适应频谱拓展方法[C]. 中国石油学会2015年物探技术研讨会论文集, 2015, 649-652. CHEN Wenchao, WANG Wei, LI Ruiping. Adaptive spectrum extension method for seismic signal in continuous wavelet domain[C]. Proceedings of the 2015 Geophysical Exploration Technology Symposium of China Petroleum Society, 2015, 649-652. |
| [18] |
刘喜武, 年静波, 刘洪. 基于广义S变换的吸收衰减补偿方法[J]. 石油物探, 2006, 45(1): 9-14. LIU Xiwu, NIAN Jingbo, LIU Hong. Generalized S-transform based compensation for stratigraphic absorption of seismic attenuation[J]. Geophysical Prospec-ting for Petroleum, 2006, 45(1): 9-14. |
| [19] |
黄捍东, 冯娜, 王彦超, 等. 广义S变换地震高分辨率处理方法研究[J]. 石油地球物理勘探, 2014, 49(1): 82-88. HUANG Handong, FENG Na, WANG Yanchao, et al. High-resolution seismic processing based on genera- lized S transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 82-88. |
| [20] |
高静怀, 朱光明, 汪文秉, 等. 小波变换与地震资料谱白化[J]. 煤田地质与勘探, 1997, 25(3): 49-54. GAO Jinghuai, ZHU Guangming, WANG Wenbing, et al. Wavelet transform and spectrum whitening of seismogram[J]. Coal Geology & Exploration, 1997, 25(3): 49-54. |
| [21] |
边国柱, 张立群. 地震数据的谱白化处理[J]. 石油物探, 1986, 25(2): 26-33. BIAN Guozhu, ZHANG Liqun. Spectral whitening of seismic data[J]. Geophysical Prospecting for Petroleum, 1986, 25(2): 26-33. |
| [22] |
高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 2006, 49(4): 1155-1163. GAO Jinghuai, MAO Jian, MAN Weishi, et al. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese Journal of Geophysics, 2006, 49(4): 1155-1163. |
| [23] |
陆文凯, 丁文龙, 张善文, 等. 基于信号子空间分解的三维地震资料高分辨率处理方法[J]. 地球物理学报, 2005, 48(4): 896-901. LU Wenkai, DING Wenlong, ZHANG Shanwen, et al. A high-resolution processing technique for 3-D seismic data based on signal sub-space decomposition[J]. Chinese Journal of Geophysics, 2005, 48(4): 896-901. |
| [24] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869, 877. HAN Weixue, ZHOU Yatong, CHI Yue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869, 877. |
| [25] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Yuqing, LU Wenkai, LIU Jinlin, et ai. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [26] |
俞若水, 张勇, 周创. 基于深度卷积生成对抗网络的瑞雷波信号随机噪声去除[J]. 地球物理学进展, 2020, 35(6): 2276-2283. YU Ruoshui, ZHANG Yong, ZHOU Chuang. Deep convolutional generative adversarial network for random noise attenuation in Rayleigh wave signal[J]. Progress in Geophysics, 2020, 35(6): 2276-2283. |
| [27] |
于四伟, 杨午阳, 李海山, 等. 基于深度学习的地震散射面波智能压制方法[J]. 科学通报, 2021, 66(18): 2343-2354. YU Siwei, YANG Wuyang, LI Haishan, et al. Scattered ground roll intelligent attenuation based on deep learning[J]. Chinese Science Bulletin, 2021, 66(18): 2343-2354. |
| [28] |
钟铁, 陈云, 卢绍平, 等. 基于DMFF-Net的地震随机噪声压制新技术[J]. 地球物理学报, 2022, 65(11): 4418-4432. ZHONG Tie, CHEN Yun, LU Shaoping, et al. New technology of seismic random noise suppression based on DMFF-Net[J]. Chinese Journal of Geophy- sics, 2022, 65(11): 4418-4432. |
| [29] |
张玉玺, 刘洋, 张浩然, 等. 基于深度学习的多属性盐丘自动识别方法[J]. 石油地球物理勘探, 2020, 55(3): 475-483. ZHANG Yuxi, LIU Yang, ZHANG Haoran, et al. Multi-attribute automatic interpretation of salt domes based on deep learning[J]. Oil Geophysical Prospec- ting, 2020, 55(3): 475-483. |
| [30] |
王子健, 伍新明, 杜玉山, 等. 基于深度学习的地震断层检测与断面组合[J]. 油气地质与采收率, 2022, 29(1): 69-79. WANG Zijan, WU Xinming, DU Yushan, et al. Deep learning-based seismic fault detection and surface combination[J]. Petroleum Geology and Recovery Efficiency, 2022, 29(1): 69-79. |
| [31] |
CHOI Y, SEOL S J, BYUN J, et al. Vertical resolution enhancement of seismic data with convolutional U-net[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2388-2392.
|
| [32] |
CHEN D Y, GAO J H, HOU Y P, et al. High resolution inversion of seismic wavelet and reflectivity using iterative deep neural networks[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2538-2542.
|
| [33] |
ZHANG H J, WANG W, WANG X K, et al. An implementation of the seismic resolution enhancing network based on GAN[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2478-2482.
|
| [34] |
蔡涵鹏, 李会强, 秦情, 等. 基于生成对抗网络地震数据超分辨率重建方法[C]. 中国石油学会2019年物探技术研讨会论文集, 2019, 1547-1550.
|
| [35] |
LI J T, WU X M, HU Z X. Deep learning for simultaneous seismic image super-resolution and denoising[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 1661-1665.
|
| [36] |
CHEN H L, GAO J H, JIANG X D, et al. Optimization-inspired deep learning high-resolution inversion for seismic data[J]. Geophysics, 2021, 86(3): R265-R276. |
| [37] |
DONG C, LOY C C, HE K M, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307. |
| [38] |
DONG C, LOY C C, TANG X O. Accelerating the Super-resolution convolutional neural network[C]. Computer Vision-ECCV 2016, 2016, 391-407.
|
| [39] |
SHI W Z, CABALLERO J, HUSZÁR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 1874-1883.
|
| [40] |
KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 1646-1654.
|
| [41] |
KIM J, LEE J K, LEE K M. Deeply-Recursive convolutional network for image super-resolution[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 1637-1645.
|
| [42] |
TONG T, LI G, LIU X J, et al. Image super-resolution using dense skip connections[C]. 2017 IEEE International Conference on Computer Vision (ICCV), 2017, 4809-4817.
|
| [43] |
GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems-Volume 2, 2014, 2672-2680.
|



 刘达伟, 陕西省西安市咸宁西路28号西安交通大学电子与信息学部,710064。Email:
刘达伟, 陕西省西安市咸宁西路28号西安交通大学电子与信息学部,710064。Email: