2. 中国石油大庆油田有限责任公司勘探开发研究院, 黑龙江大庆 163712
2. Research Instituteof Exploration and Development, PetroChina Daqing Oilfield Co., Ltd., Daqing, Heilongjiang 163712, China
精细的油藏描述是复杂油气藏开发的关键,而建立定量的油藏地质模型是油藏描述、数值模拟、油藏工程等研究工作的基础[1]。
油藏地质建模分为确定性建模和随机性建模,这两种方式都需要求取变差函数,传统方法是通过拟合实验变差函数获取理论变差函数。主要的拟合算法有遗传算法[2]、混沌粒子群算法[3]、群搜索优化算法[4]、改进量子粒子群算法[5]、傅里叶积分法[6]等,但当井较少、井距较大时,传统方法得到的平面变差函数不理想。为了解决这一问题,前人提出利用地质统计学反演预测变差函数[7-8]:通过统计井点数据求取纵向变程;通过统计、分析已开发区矿体规模和矿点含矿性求取横向变程;在多尺度变差函数适用性分析基础上,利用测井、地震资料获取的平面变差函数模拟不同尺度储层的特征[9]。以上方法对变差函数的求取具有指导意义,但仍然存在一些不足,如要求勘探程度高且钻井多,需要井网分布完善的先验信息和三维地震资料丰富的横向信息,因而方法实施成本较高、资料收集困难。当井点数据过少时,实验变差函数不易拟合。
目前,人工智能深度学习方法已应用于石油工程多个研究领域[10-12]。在油气藏开发过程中,前人将人工智能与地质建模技术进行融合,形成了智能化地质建模技术,并成功开展了测井解释、地震储层预测[13-15]等。为了降低传统方法实验变差函数建模的主观性,最大限度地利用空间数据,本文提出一种基于U-Net和卷积神经网络(Convolutional Neural Network,CNN)求取变差函数参数的新方法。
1 属性建模基本原理 1.1 属性建模过程储层物性模型描述了孔隙度、渗透率等储层物性在空间的变化特征。Petrel软件中确定性建模方法有近点取值、移动平均、函数插值和克里金算法;随机模拟一般采用序贯高斯模拟(SGS)算法。克里金法和随机模拟方法可以直接应用数据分析得到的参数统计特征及变差函数。在测井曲线粗化、数据转换和变差函数分析后,采用SGS建立储层物性模型,该属性模型的参数分布很大程度上依赖于变差函数中的参数(主变程Rm、主次变程比Ar、主变程方位角θ)。
1.2 变差函数变差函数是对区域化变量空间变异性的一种度量,反映空间变异程度随距离而变化的特征[16]。设变差函数
| $ \begin{array}{l}\gamma \left(h\right)=\frac{1}{2}E\left[Z\left(x\right)-Z\left(x+h\right)\right]\\ =\frac{1}{2N\left(h\right)}\sum\limits_{i=1}^{N\left(h\right)}{\left[{Z}_{i}\left(x\right)-{Z}_{i}\left(x+h\right)\right]}^{2}\end{array} $ | (1) |
式中:h称为滞后距;E表示求
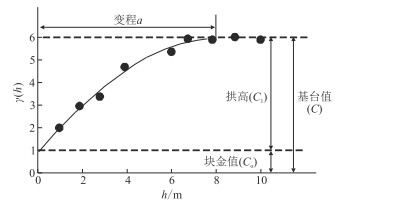
以h为自变量、γ(h)为因变量,得到如图 1所示变差函数曲线。图中变程a是γ(h)达到平稳后的h值,映射样本点在空间上的最大相关距离;C0为块金值,表示变量的空间随机性;C1为拱高,表示局部内变量结构性的强弱;C=C0+C1为基台值。
|
图 1 变差函数示意图 |
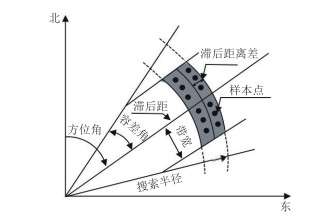
传统方法求取实验变差函数过程中需要利用方位角、搜索半径、容差角、带宽、滞后距、滞后距离差等参数(图 2),实验变差函数所用数据点比较离散,通过拟合理论变差函数曲线可以更好地分析数据的空间结构。常见的理论变差函数模型有球状模型、指数模型、高斯模型等,本文选用球状模型,其表达式为
| $ \gamma \left(h\right)=\left\{\begin{array}{l}0h=0\\ {C}_{o}+C\left(\frac{3h}{2a}-\frac{3{h}^{3}}{2{a}^{3}}\right)0\le h\le a\\ {C}_{o}+Ch > a\end{array}\right. $ | (2) |
|
图 2 楔形搜索域示意图 |
通过数据拟合可得到实验变差函数,常用的拟合方法有最小二乘法、遗传算法等。然而当井点数据过少时,实验变差函数的拟合过程比较困难。因此,本文提出一种不依赖于实验变差函数而基于深度学习求取变差函数的新方法。
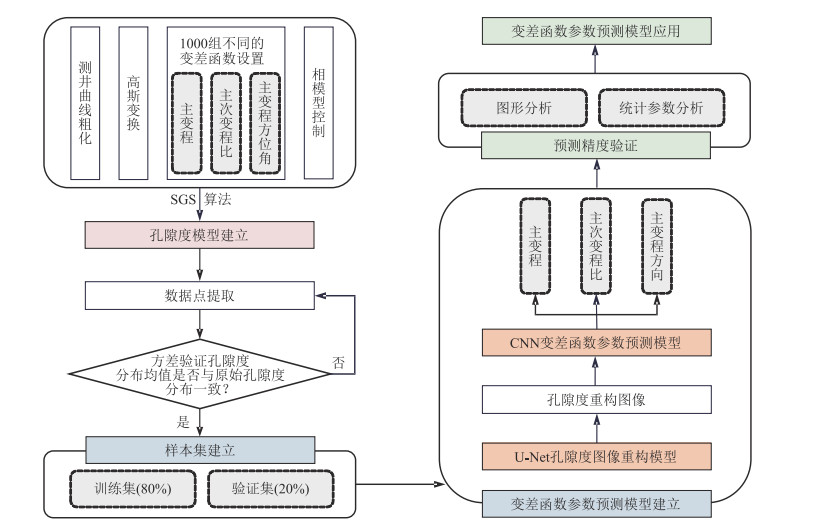
2 变差函数参数求取基本原理基于U-Net和CNN深度学习求取变差函数的方法原理如下(以孔隙度属性建模为例)。①由孔隙度测井解释曲线粗化得到井点属性数据(硬数据),以此为基础,通过设置不同的变差函数参数(主变程、主次变程比、主变程方位角)并选用球状理论模型,利用SGS算法模拟生成多组孔隙度模型。②从这些模型中抽取建模时使用的硬数据(井点数据)并加上一定数量的软数据(模拟得到的孔隙度),构成样本集。软数据数量的选取原则是能提高模型的训练效率以及更好地挖掘参数信息。③对样本集进行深度学习,第一步通过U-Net网络对抽取所得孔隙度点进行模型重构,第二步采用CNN网络对重构的孔隙度模型进行深度学习,建立求取变差函数的预测模型,进而得到变量参数。具体步骤如图 3所示。
|
图 3 U-Net和CNN深度学习模型求取变差函数结构框架 |
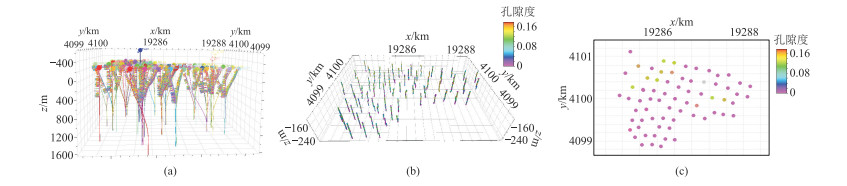
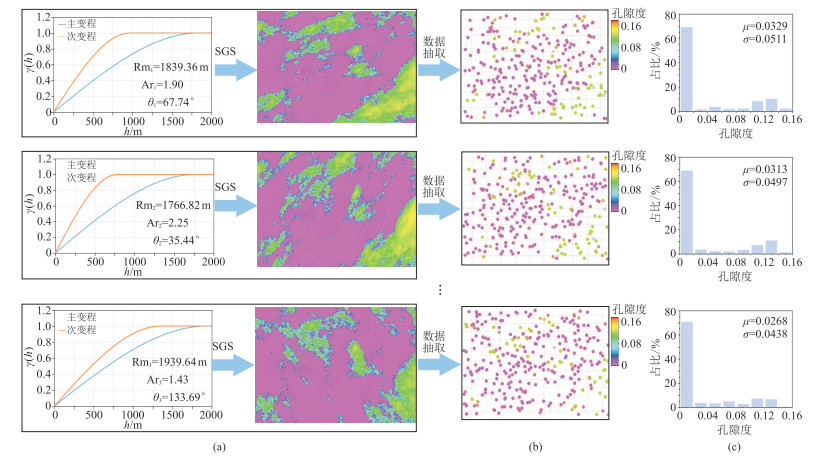
以M油田的X油藏为研究对象,通过地震解释建立了区块地质模型。设置平面网格间距为20 m×20 m,网格总数为294×244=71736。以相模型作为约束,通过测井曲线粗化、数据转换和变差函数分析,采用SGS算法建立了原始孔隙度模型(图 4),从中抽取井点孔隙度数据。通过改变主变程、主次变程比、主变程方位角等变差函数参数的变量范围(见表 1),得到1000组模拟孔隙度模型(图 5a)。基于上述模型构建样本集,依据软数据选取原则,确定实验的软数据数量为硬数据的2倍,即从每一组孔隙度模型中抽取硬数据70个、软数据140个,进而组成深度学习样本集(图 5b)。另外,选取样本集中80%的样本作为训练集,20%的样本为验证集。如图 5c所示,样本集的孔隙度分布均值(
|
图 4 X油藏初始孔隙度模型 (a)测井曲线;(b)孔隙度曲线粗化;(c)原始孔隙度井点数据分布 |
|
|
表 1 变差函数参数变量范围 |
|
图 5 孔隙度数据样本集准备(从上至下分别为第1,2,…,1000组) (a)不同变差函数生成不同孔隙度模型;(b)抽取的孔隙度数据分布;(c)孔隙度分布直方图 |
Ronneberger等[17]于2015年提出的U-Net网格结构最初应用于医学领域的图像分割[18-20],因具有独特的前传结构,基于U-Net的图像重构方法得到了广泛关注[21-22]。U-Net是一种U型结构的全卷积神经网络,U型结构左侧包含4层结构,每层有3个卷积(Conv)层和最大池化(Max Pool)层,通过向下采样实现收缩路径;右侧也包含4层结构,每层有2个卷积层和池化层,通过向上反卷积实现扩展路径。将U型结构左、右两侧大小一致的特征图拼接在一起,可以获取更多细节信息。
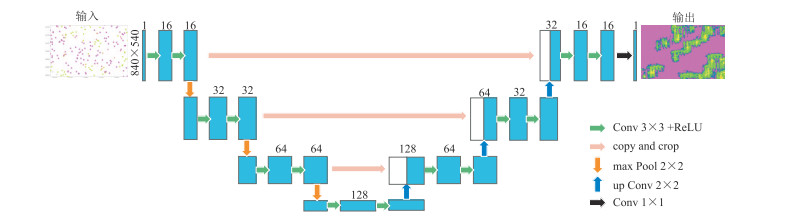
本文选用U-Net网络进行模型重构,以抽取的孔隙度训练样本点作为模型输入,孔隙度重构图像作为模型输出。通常随着网络深度增加,提取图像的信息量和特征也越充足,更便于图像的重构,但是网络层数过多会导致梯度消失、爆炸现象的发生[23]。为此,本文在U-Net的基础上将4层下采样结构减少至3层,其网络结构如图 6所示,在U型结构左侧为主干特征提取部分,卷积核的尺寸为3×3,激活函数为ReLU,通过该部分可获得4个初步有效特征层;U型结构右侧为加强特征提取部分,利用上采样加堆叠的方式,将4个初步有效特征层进行特征融合,最后通过1×1的卷积操作输出图像。
|
图 6 U-Net的平面孔隙度模型重构网络结构 |
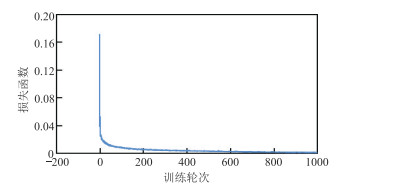
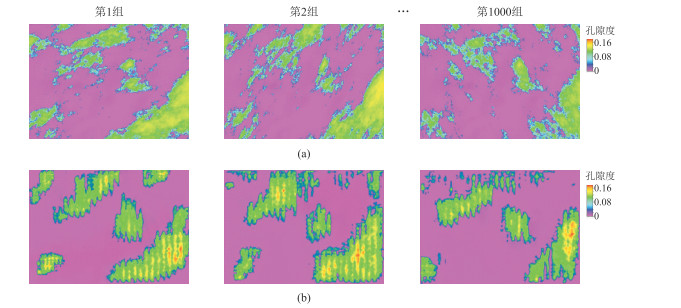
在网络模型中,利用损失函数可以检测网络模型训练的准确性和稳定性,如图 7所示,损失函数曲线随着训练次数的增加迅速下降,迭代100次后逐渐稳定。孔隙度重构结果如图 8所示,可以看出,U-Net重构图像与SGS模拟的原始图像的平面趋势大致相同,能够表示出孔隙度分布的空间相关性,同时也起到一定的降维作用,更有利于特征提取。
|
图 7 U-Net网络训练损失函数曲线 |
|
图 8 孔隙度重构结果 (a)SGS模拟的原始图像;(b)U-Net重构图像 |
CNN是一种前馈神经网络,通过卷积、池化和非线性激活函数将神经元的输入映射到输出端,经过一系列操作的逐层堆砌,将高层语义信息(如图像所表达的对象、行为、场景或感情色彩)逐层从原始数据输入层中提取出来,再逐层地抽象,这一过程便是前馈运算[24]。CNN具有很好的图像特征提取能力,并且可以处理大量的数据集,目前已经在石油行业广泛应用[25-27]。CNN结构通常由若干个卷积层、池化层和全连接(Fully-Connected)层构成。输入图像经由卷积、池化层组成的多个卷积组逐层提取特征之后,由全连接层实现特征与输出目标之间的映射(分类、回归等),最终从输出层得到三参数预测结果。
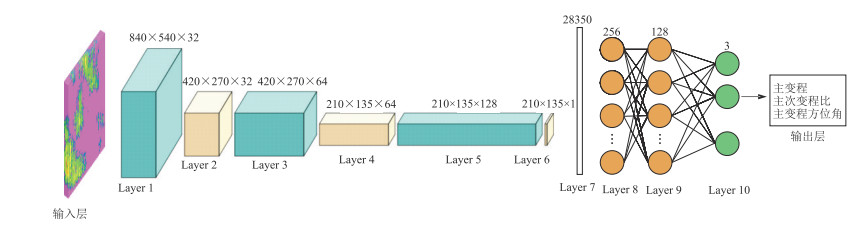
将U-Net重构的孔隙度图像作为输入层导入CNN,经由三层卷积层、三层池化层进行特征提取,最后通过全连接层得到主变程、主次变程比、主变程方位角等变差函数参数。网络参数见表 2, 网络结构如图 9所示。
|
|
表 2 CNN网络参数 |
|
图 9 求取变差函数参数所用CNN网络结构 |
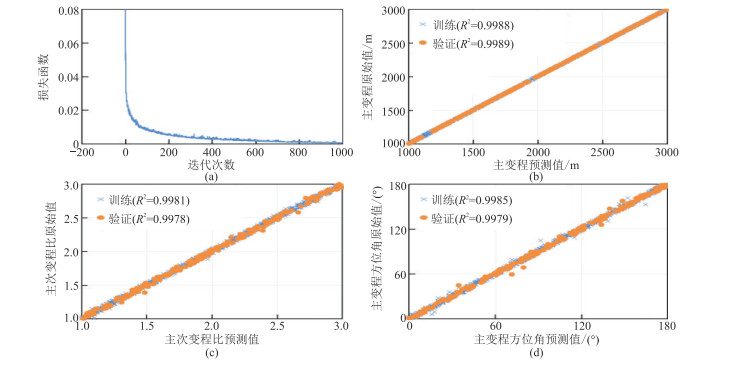
CNN模型迭代训练获得的损失函数曲线如图 10a所示。由图可见,1000次迭代后最终损失函数曲线趋近于0,且曲线平缓,模型表现理想。由三个变量参数的预测值与实测值的对比(图 10b~图 10d)可以看出,三参数的训练集与验证集模型预测结果基本一致,偏离1∶1线的离散数据点较少、回归偏差较小。此外,通过统计参数误差可以更精确地分析模型的预测精度(表 3),均方误差(MSE)、平均绝对误差(MAE)、均方根误差(RMSE)、相关系数(R2)的统计结果表明,三个变量的预测R2均大于0.99,而MSE、MAE、RMSE均较小,证实模型预测精度较高。
|
图 10 CNN模型迭代训练与三参数预测精度验证 (a)损失函数变化曲线;(b)主变程;(c)主次变程比;(d)主变程方位角 |
|
|
表 3 三参数误差统计表 |
综上可知,U-Net和CNN模型具备较高预测精度,可以作为X油藏的变差函数预测模型。对油藏新区(滚动开发)进行地质建模时,在井点较少、难以求取实验变差函数的情况下,可将井点数据输入该模型并求得变差函数三参数。
2.4 训练样本数对参数预测的影响分别选取200、500、800、1000、1200、1500组样本进行训练。对比不同训练样本数所得三参数的RMSE可知,随训练样本数的增加RMSE逐渐减少;当样本数达到1000组以后,RMSE基本趋于稳定(表 4)。
|
|
表 4 不同训练样本数的三参数RMSE统计 |
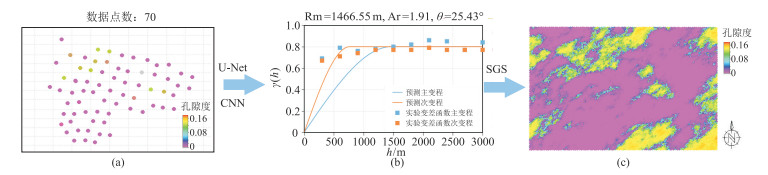
以X油藏研究区内70口井的孔隙度井点数据(图 11a)作为模型输入,运用建立的U-Net和CNN模型求取变差函数参数,求得主变程为1466.55 m,主次变程比为1.91,主变程方位角为25.43°。由图 11b可见,模型预测的主变程和次变程与对应的实验变差函数均较符合,随后利用SGS算法建立了孔隙度模型(图 11c)。
|
图 11 模型预测结果 (a)原始孔隙度空间分布;(b)预测变差函数与实验变差函数对比;(c)通过预测参数建立的孔隙度模型 |
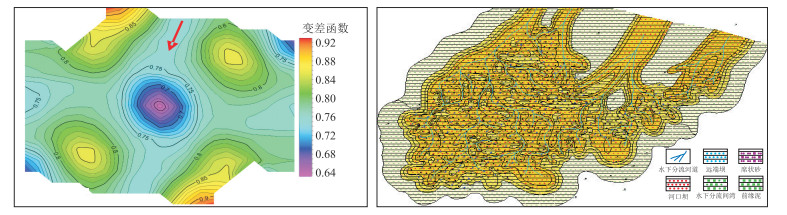
同时,通过对X油藏孔隙度数据分析获得了实验变差函数地图(图 12左),进而确定实验变差函数的主变程方位角为23.91°,该方向与沉积微相(图 12右)所示的砂体展布方向一致,表明确定的主变程方位角符合地质分布规律。相比运用U-Net和CNN模型预测的主变程方位角仅相差1.52°,表明本文方法计算结果可靠。
|
图 12 变差函数地图(左)与沉积微相平面展布图(右) |
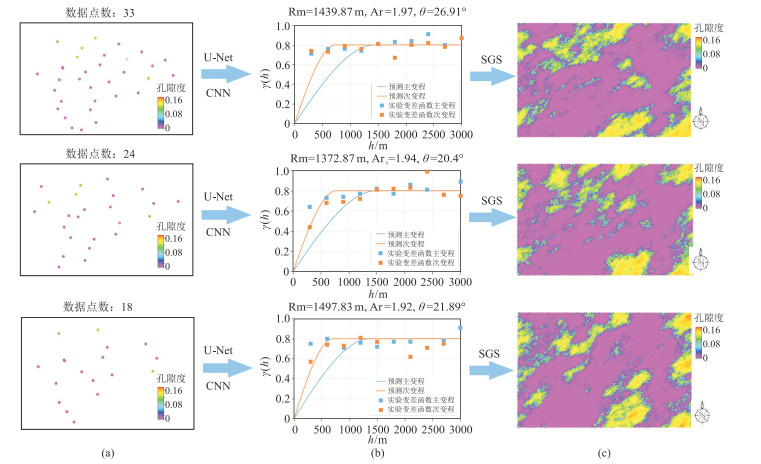
为检验研究区内硬数据数量对模型预测效果的影响,分别将硬数据减少至33、24、18,利用U-Net和CNN模型求取变差函数,然后采用SGS算法进行孔隙度模拟。由图 13可见,当硬数据点减少时,求取实验变差函数的原始孔隙度点空间分布较少(图 13a),采用传统的函数拟合方法获取理论变差函数更加困难,而采用U-Net和CNN模型获取的理论变差函数参数变化较小(图 13b),通过预测参数建立的孔隙度模型具有较好的稳定性(图 13c)。
|
图 13 不同硬数据的模型预测结果 (a)原始孔隙度空间分布;(b)预测变差函数与实验变差函数对比;(c)通过预测参数建立的孔隙度模型 |
由表 5统计结果可知,虽然硬数据点数量减少,但求取的三个变量参数变化较小,即变差函数预测模型依然可以求取相对稳定的变差函数。因此,本文方法解决了当数据点较少时,通过函数拟合方式获取理论变差函数质量较差的问题,减少了数据拟合带来的误差,降低了建模对研究区硬数据的依赖性。
|
|
表 5 不同硬数据点求取的变差函数参数 |
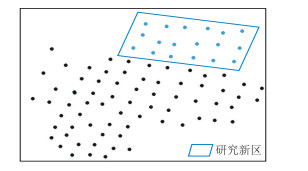
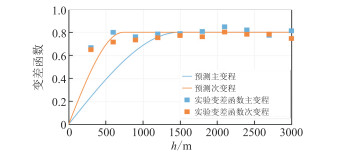
将图 14所示X油藏研究新区的井点孔隙度数据输入训练好的模型,得到该新区的变差函数三参数:主变程为1485.74 m,主次变程比为2.02,主变程方位角为25.43°。由图 15可以看出,模型预测的主变程、次变程与实验变差函数吻合度较高,并且预测的主变程方位角符合砂体展布方向(图 12右)。由图 16对比看出,基于预测变差函数与实验变差函数建模的孔隙度分布基本一致,表明本文建模方法在新区应用亦有效。
|
图 14 研究新区井点分布 |
|
图 15 预测变差函数与实验变差函数对比 |

|
图 16 预测(上)与实验(下)变差函数孔隙度建模对比 |
(1) 采用改进的U-Net模型进行孔隙度图像重构,重构图像与原始图像趋势一致。改进的网络结构既能降低数据维度又能保留数据特征。
(2) 采用CNN模型对U-Net重构图像进行深度学习。经验证,模型计算精度较高,变差函数三参数的相关系数均超过0.99。
(3) 基于U-Net和CNN模型预测参数求取的变差函数与拟合实验变差函数进行对比,二者相差较小,建立的孔隙度模型分布基本一致。
(4) U-Net和CNN模型在硬数据较少时仍然可以求取稳定的变差函数参数,减少了以往拟合实验变差函数带来的误差,降低了建模对硬数据的依赖。
基于U-Net和CNN深度学习的变差函数预测模型为变差函数的求取提供了一种新的思路,减少了以往拟合实验变差函数过程中出现的不确定性,可以在新区油藏建模中推广应用。
| [1] |
贾爱林. 精细油藏描述与地质建模技术[M]. 北京: 石油工业出版社, 2010. JIA Ailin. Fine Reservoir Description and Geological Modeling Technology[M]. Beijing: Petroleum Industry Press, 2010. |
| [2] |
冯国庆, 周涌沂, 李允, 等. 利用遗传算法拟合实验变差函数[J]. 西南石油学院学报, 2005, 27(5): 33-35. FENG Guoqing, ZHOU Yongyi, LI Yun, et al. Application of genetic algorithm to match theoretical va-riogram[J]. Journal of Southwest Petroleum Institute, 2005, 27(5): 33-35. DOI:10.3863/j.issn.1674-5086.2005.05.009 |
| [3] |
陈学工, 陈婷, 肖晓芳. 混沌粒子群算法自动拟合理论变差函数[J]. 计算机工程与应用, 2012, 48(4): 37-39. CHEN Xuegong, CHEN Ting, XIAO Xiaofang. Chaos particle swarm optimization algorithm to match theoretical variogram automatically[J]. Computer Engineering and Applications, 2012, 48(4): 37-39. DOI:10.3778/j.issn.1002-8331.2012.04.010 |
| [4] |
陈华, 张艺丹, 葛新民. 基于改进群搜索优化算法的变差函数拟合[J]. 物探化探计算技术, 2016, 38(4): 566-570. CHEN Hua, ZHANG Yidan, GE Xinmin. The optimal fit of the variational function based on improved group search optimizer algorithm[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2016, 38(4): 566-570. DOI:10.3969/j.issn.1001-1749.2016.04.20 |
| [5] |
谢源, 李琼, 陈杰, 等. 基于改进的量子粒子群算法的变差函数拟合方法及应用[J]. 成都理工大学学报(自然科学版), 2018, 45(3): 379-385. XIE Yuan, LI Qiong, CHEN Jie, et al. Research on variogram fitting method and its application based on the improved quantum particle swarm algorithm[J]. Journal of Chengdu University of Technology(Science & Technology Edition), 2018, 45(3): 379-385. DOI:10.3969/j.issn.1671-9727.2018.03.13 |
| [6] |
DE CARVALHO P R M, DA COSTA J F C L. Automatic variogram model fitting of a variogram map based on the Fourier integral method[J]. Computers & Geosciences, 2021, 156: 104891. |
| [7] |
LAUZON D, MARCOTTE D. Statistical comparison of variogram-based inversion methods for conditioning to indirect data[J]. Computers & Geosciences, 2022, 160: 105032. |
| [8] |
魏达, 孙章庆. 利用地质统计学反演预测砂岩型铀矿体的变差函数求取方法[J]. 石油地球物理勘探, 2021, 56(6): 1381-1390. WEI Da, SUN Zhangqing. Calculation method of variation function for predicting sandstone-type Uranium ore bady by geostatistical inversion[J]. Oil Geophysical Prospecting, 2021, 56(6): 1381-1390. |
| [9] |
陈文浩, 王志章, 刘月田, 等. 储层随机模拟中的多尺度变差函数估算方法[J]. 石油地球物理勘探, 2019, 54(1): 154-163, 174. CHEN Wenhao, WANG Zhizhang, LIU Yuetian, et al. Multi-scale horizontal variogram estimation in reservoir stochastic simulation[J]. Oil Geophysical Prospecting, 2019, 54(1): 154-163, 174. |
| [10] |
GUL S, VAN OORT E. A machine learning approach to filtrate loss determination and test automation for drilling and completion fluids[J]. Journal of Petroleum Science and Engineering, 2020, 186: 106727. DOI:10.1016/j.petrol.2019.106727 |
| [11] |
NIU W, LU J, SUN Y. An improved empirical model for rapid and accurate production prediction of shale gas wells[J]. Journal of Petroleum Science and Engineering, 2022, 208, Part E: 109800.
|
| [12] |
YUAN Z, HUANG H, JIANG Y, et al. Hybrid deep neural networks for reservoir production prediction[J]. Journal of Petroleum Science and Enginee-ring, 2021, 197: 108111. DOI:10.1016/j.petrol.2020.108111 |
| [13] |
SERGEY A, ADRIAN A, NAZANIN J H, et al. Sequential multi-realization probabilistic interpretation of well Logs and geological prediction by a deep-Learning method[C]. SPWLA 63rd Annual Logging Symposium, 2022, SPWLA-2022-0112.
|
| [14] |
KUMAR T, SEELAM N K, RAO G S. Lithology prediction from well log data using machine learning techniques: A case study from Talcher coalfield, Eastern India[J]. Journal of Applied Geophysics, 2022, 199: 104605. DOI:10.1016/j.jappgeo.2022.104605 |
| [15] |
付超, 林年添, 张栋, 等. 多波地震深度学习的油气储层分布预测案例[J]. 地球物理学报, 2018, 61(1): 293-303. FU Chao, LIN Niantian, ZHANG Dong, et al. Prediction of reservoirs using multi-component seismic data and the deep learning method[J]. Chinese Journal of Geophysics, 2018, 61(1): 293-303. |
| [16] |
欧成华, 冯国庆, 李波. 油气藏开发地质建模[M]. 北京: 石油工业出版社, 2018. OU Chenghua, FENG Guoqing, LI Bo. Geological Modeling for Oil and Gas Reservoir Development[M]. Beijing: Petroleum Industry Press, 2018. |
| [17] |
RONNEBERGER O, FISCHER P, BROX T. U-Net: convolutional networks for biomedical image segmentation[DB/OL]. (2015-05-18)[2023-12-10]. https://arxiv.org/abs/1505.04597.
|
| [18] |
YUAN L, SONG J, FAN Y. FM-Unet: biomedical image segmentation based on feedback mechanism Unet[J]. Mathematical Biosciences and Engineering, 2023, 20(7): 12039-12055. DOI:10.3934/mbe.2023535 |
| [19] |
YANG Y, DASMAHAPATRA S, MAHMOODI S. ADS_Unet: A nested U-Net for histopathology image segmentation[J]. Expert Systems with Applications, 2023, 226: 120128. DOI:10.1016/j.eswa.2023.120128 |
| [20] |
XIAO Z, DU M, LIU J, et al. EA-Unet based segmentation method for OCT image of uterine cavity[J]. Photonics, 2023, 10(1): 73. DOI:10.3390/photonics10010073 |
| [21] |
宋蓓蓓, 马穗娜, 何帆, 等. Res2-Unet深度学习网络的RGB-高光谱图像重建[J]. 光学精密工程, 2022, 30(13): 1606-1619. SONG Beibei, MA Suina, HE Fan, et al. Hyperspectral reconstruction from RGB images based on Res2-Unet deep learning network[J]. Optics and Precision Engineering, 2022, 30(13): 1606-1619. |
| [22] |
张文倩, 冯金超, 李哲, 等. 基于Unet的切连科夫激发的荧光扫描断层重建[J]. 中国激光, 2021, 48(17): 129-140. ZHANG Wenqian, FENG Jinchao, LI Zhe, et al. Reconstruction for Cherenkov-Excited luminescence scanned tomography based on Unet network[J]. Chinese Journal of Lasers, 2021, 48(17): 129-140. |
| [23] |
张艳娇, 乔志伟. 基于多残差Unet的CT图像高精度稀疏重建[J]. 计算机应用, 2021, 41(10): 2964-2969. ZHANG Yanjiao, QIAO Zhiwei. High-precision sparse reconstruction of CT images based on multiply residual Unet[J]. Journal of Computer Applications, 2021, 41(10): 2964-2969. DOI:10.11772/j.issn.1001-9081.2020121985 |
| [24] |
LIU Y, LIAO G, XIAO L, et al. Automatic fracture segmentation and detection from image logging using mask R-CNN[C]. SPWLA 63rd Annual Logging Symposium, 2022, SPWLA-2022-0115.
|
| [25] |
SUN J, YANG J, LI Z, et al. Reflection and diffraction separation in the dip-angle common-image gathers using convolutional neural network[J]. Geophysics, 2023, 88(1): WA281-WA291. DOI:10.1190/geo2022-0157.1 |
| [26] |
ZHANG Z, HE X, ALSINAN M, et al. Deep lear-ning model for CO2 leakage detection using pressure measurements[C]. SPE Annual Technical Conference and Exhibition, 2022, SPE-209959-MS.
|
| [27] |
杨博雄. 深度学习理论与实践[M]. 北京: 北京邮电大学出版社, 2020. YANG Boxiong. Deep Learning Theory and Practice[M]. Beijing: Beijing University of Posts and Telecommunications Press, 2020. |



 莫海帅, 四川省成都市新都区新都大道8号西南石油大学石油与天然气工程学院,610500。Email:
莫海帅, 四川省成都市新都区新都大道8号西南石油大学石油与天然气工程学院,610500。Email: