2. 长江大学地球物理与石油资源学院, 湖北武汉 430100;
3. 中国石化西北油田分公司石油工程监督中心, 新疆轮台 841600;
4. 东方地球物理公司国际部, 河北涿州 072751;
5. 中国石油新疆油田公司准东采油厂, 新疆阜康 831511
2. School of Geophysics and Oil Resources, Yangtze University, Wuhan, Hubei 430100, China;
3. Petroleum Engineering Supervision Center, SINOPEC Northwest Oilfield Company, Luntai, Xinjiang 841600, China;
4. BGP International, CNPC, Zhuozhou, Hebei 072751, China;
5. Xinjiang Oilfield Zhundong Oil Production Plant, PetroChina, Fukang, Xinjiang 831511, China
高信噪比、高分辨率和高保真度是地震数据处理追求的三大目标。随着石油勘探开发的不断深入,油气勘探目标以构造勘探为主逐渐进入以岩性勘探为主。岩性圈闭的勘探难度大,对地震数据的分辨率提出了更高的要求。
为提高地震数据的分辨率,前人发展了多种高分辨率处理方法,例如反褶积方法、反Q滤波方法和基于井控的处理方法等,曹思远等[1]对部分方法做了分析与评价。在反褶积方面,Robinson[2-3]首先提出了预测反褶积方法,为反褶积的发展奠定了基础。反褶积通过压缩地震子波达到提高地震资料分辨率的目的,目前常用的有脉冲反褶积[4]、预测反褶积[5]、同态反褶积[6]等。在反Q滤波方面,Hale[7]提出基于Futterman模型的反Q滤波方法,即采用预测误差滤波方法估算Q值,并通过级数展开补偿高频成分。反Q滤波通过补偿深层地震资料的高频振幅能量提高分辨率,但存在不稳定的问题。Wang[8]提出一种基于波场延拓的反Q滤波算法,克服了常规反Q滤波方法的不稳定性问题,并引入Gabor变换提高运算效率。但是在抗噪性方面,常规稳定的反Q滤波方法效果并不理想。Zhao等[9]在稳定反Q滤波方法的基础上,引入一种变稳定因子,有效提高了反Q滤波的抗噪性能,提高了反Q滤波结果的信噪比;Yuan等[10]通过多道变换域稀疏约束和反演策略,提出了稳定的同时多道反Q滤波方法,能够保持空间连续性和补偿弱信号;Tian等[11]通过在稳定因子中引入信噪比信息,提出了一种新的变稳定因子,使反Q滤波方法对噪声的压制更加精准。在基于井控处理方面,孙哲等[12]通过VSP资料提取反褶积算子,并将其用于叠后地面地震资料以提高分辨率;于茜[13]从VSP资料中提取子波,然后将地面地震资料中提取的子波与VSP子波进行匹配,通过子波替换提高地震资料的分辨率;严红勇等[14]和陈双全等[15]从VSP下行波数据中提取较精确的Q值,然后结合稳定的反Q滤波提高地震资料的分辨率。
近年来,深度学习技术在图像超分辨率处理领域取得了显著进展,部分地球物理学者将超分辨率算法引入地震数据的高分辨处理。按照不同网络类型,大概可分为三类。第一类为生成对抗网络:Halpert[16]将低频地震数据输入到生成对抗网络,输出高频地震数据,提高了分辨率;蔡涵鹏等[17]提出一种基于生成对抗网络地震数据超分辨率重建方法,在超分辨重建过程中能压制稀疏地震数据中的噪声;Chen等[18]则更进一步,在使用生成对抗网络进行高分辨处理时,输入低频地震数据,直接输出反射系数。第二类为卷积神经网络:Yuan等[19]将卷积神经网络(CNN)引入地震数据的高分辨率处理,提出一种序列卷积神经网络模型(SCNN);Li等[20]在CNN基础上开发了一种深度卷积神经网络,可以同时实现高分辨率处理和噪声压制,并用理论数据和实际数据进行了验证,取得了理想的效果;周文辉等[21]在卷积神经网络中加入残差块,利用残差神经网络提高地震数据的分辨率。第三类为全卷积神经网络,其中具有代表性的就是U-net:孙永壮等[22]将U-net模型用于地震数据的高分辨率处理,并提出利用伪反射系数模型生成训练样本和标签数据;Jo等[23]同样使用U-net进行高分辨率处理,但是在训练样本中考虑了子波的非平稳性;李子航等[24]提出一种基于S变换和复值U-net的地震数据高分辨处理方法,可以同时考虑到地震数据的时域和频域信息。另外,部分学者将U-net和其他网络相结合,如Choi等[25]将U-net与超分辨率卷积神经网络(SRCNN)相结合,获得了较好的应用效果;陈志明等[26]将U-net与长短时记忆神经网络(LSTM)相结合,有效解决了其在捕捉数据空间特征的能力不足问题。
近年来,随着深度学习技术的不断发展,注意力机制在神经网络中的应用也逐渐流行。注意力机制是一种用于提高深度学习性能的技术,由Bahdanau等[27]提出。它允许模型在处理输入数据时能够集中注意力处理最相关的信息,从而提高模型的性能。李学贵等[28]提出在神经网络中加入双注意力机制提高模型性能。本文提出了一种基于自适应注意力的U-net,通过自适应注意力机制动态调整注意力的分配,提高模型的性能。本文网络模型在理论合成数据和真实数据上的预测精度都比原始U-net网络高,能有效提高地震数据分辨率。
1 网络结构 1.1 自适应注意力机制U-net的网络结构U-net是一种用于图像分割的深度学习模型,它由Ronneberger等 [29]在2015年提出。U-net的结构包括编码器和解码器两部分,其中编码器用于提取图像特征,解码器用于将这些特征映射为原始图像的分辨率。U-net的特点是使用了“跳跃连接”的思想,即将编码器中的一些特征图与解码器中相应的特征图直接连接起来,可以使解码器在还原图像时更容易恢复细节信息。
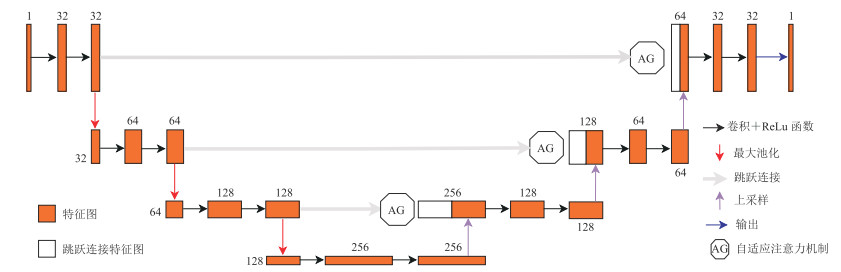
本文提出的AAU-net(Adapt Attention U-net)是在U-net中加入了自适应注意力机制,网络结构如图 1所示。该网络采用编码—解码结构,其中下采样路径负责从输入数据中提取特征并减小尺寸,而上采样路径负责恢复输入数据的尺寸。下采样路径包括三个卷积块,每个卷积块包含两个卷积层和一个最大池化层。卷积层的输出通过ReLU激活函数进行处理,使网络能够学习到数据中的非线性关系。每个卷积层的卷积核尺寸为3,填充为1以保持尺寸不变。这些卷积层逐步减小了特征图的尺寸,并通过“跳跃连接”将它们与在上采样路径对应层的特征图相结合。上采样路径也包括三个卷积块,每个卷积块包含两个卷积层,一个反卷积层(即转置卷积层)和一个自适应注意力机制。反卷积层通过将输入的每个像素插值到其四个相邻像素中从而将特征图的尺寸加倍。与下采样路径类似,每个卷积层输出也通过ReLU激活函数进行处理,使网络能够学习到数据中的非线性关系。每个卷积层的卷积核尺寸为3,填充为1以保持尺寸不变。自适应注意力机制通过将注意力权重与输入张量逐元素相乘,使得模型可以根据注意力权重动态地调整输入张量中每个位置的权重,进而实现了自适应的注意力分配。最后的卷积层将网络的输出通道数设置为1,保持与输入数据一致,以输出最终数据。
|
图 1 AAU-net的网络结构 块上数字表示特征图的通道数,块的大小表示特征图的尺寸变化。 |
本文网络与常规U-net主要区别为在上采样的过程中加入了自适应注意力机制,在处理不同深度和位置的地震数据时,能够在不同位置之间建立长距离依赖关系,提升模型对关键特征的识别和利用能力,在高分辨率处理中能够恢复更多的细节信息并达到更加稳定的效果,从而获得比常规U-net更优的性能。
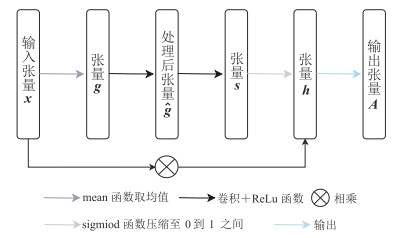
1.2 自适应注意力机制在自适应注意力机制结构中,通过两个卷积块构建网络的基本结构,如图 2所示,具体实现过程分为三个阶段。首先,通过对输入张量x在一维维度上使用mean函数取平均值,得到张量g,代表了包含全局上、下信息的特征张量。然后,将张量g输入到第一个卷积块进行卷积变换和非线性激活,将处理后的张量
|
图 2 自适应注意力机制结构图 |
在深度学习中,数据集是用于训练和评估深度学习模型的基础,数据集的质量和数量都会直接影响深度学习模型的性能和泛化能力。
在本文实验中,首先使用褶积模型进行正演,即分别利用低频雷克子波和高频雷克子波与随机生成的反射系数褶积得到合成地震记录。本文分别用主频为30 Hz和50 Hz雷克子波与反射系数进行褶积,得到训练数据与标签数据。
雷克子波表达式[30]为
| $ w\left(t\right)=(1-2{\mathrm{\pi }}^{2}{f}^{2}{t}^{2})\mathrm{e}\mathrm{x}\mathrm{p}(-{\mathrm{\pi }}^{2}{f}^{2}{t}^{2}) $ | (1) |
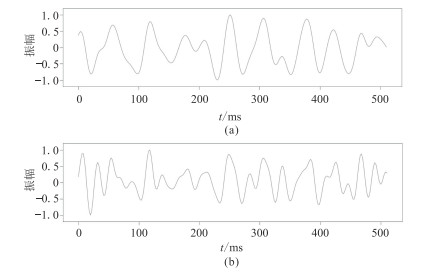
式中:f表示雷克子波的主频;t为时间。通过与不同的反射系数褶积,可以得到不同的数据(图 3)。
|
图 3 合成数据 (a)低频样本数据;(b)高频标签数据 |
本文对目前在高分辨处理中比较常用的结构相似性(SSIM)损失函数、SSIM+L1组合损失函数和均方误差(MSE)损失函数进行测试。
SSIM损失函数[31]是一种比较两个图形之间结构相似性的损失函数,定义为
| $ {F}_{1}(\boldsymbol{x}, \boldsymbol{y})=\sum\limits_{i=1}^{m}\frac{(2+{C}_{1})(2{\sigma }_{\boldsymbol{x}, i}{\sigma }_{\boldsymbol{y}, i}+{C}_{2})}{\left({\mu }_{\boldsymbol{x}, i}^{2}+{\mu }_{\boldsymbol{y}, i}^{2}+{C}_{1}\right)\left({\sigma }_{\boldsymbol{x}, i}^{2}+{\sigma }_{\boldsymbol{y}, i}^{2}+{C}_{2}\right)} $ | (2) |
式中:m为样本个数;x表示真实样本;y表示模型预测样本;μx, i和μy, i表示第i个样本的均值;σx, i和σy, i表示第i个样本的标准差;σx, iσy, i表示第i个样本的协方差;C1、C2为两个常数,用于提高计算的稳定性。
SSIM+L1组合损失函数的定义为
| $ {F}_{2}(\boldsymbol{x}, \boldsymbol{y})=\lambda {F}_{1}(\boldsymbol{x}, \boldsymbol{y})+(1-\lambda ){L}_{1}(\boldsymbol{x}, \boldsymbol{y}) $ | (3) |
式中:λ是一个在0和1之间的权重因子,用于平衡SSIM和L1损失的相对贡献;L1损失函数又称为平均绝对误差,可表示为
| $ {L}_{1}(\boldsymbol{x}, \boldsymbol{y})=\frac{1}{m}\sum\limits_{i=1}^{m}{‖{\boldsymbol{y}}_{i}-{\boldsymbol{x}}_{i}‖}_{1} $ | (4) |
MSE损失函数是指模型预测值与样本真实值之间距离平方的平均值,表达式为
| $ {F}_{3}(\boldsymbol{x}, \boldsymbol{y})=\frac{1}{m}\sum\limits_{i=1}^{m}{‖{\boldsymbol{y}}_{i}-{\boldsymbol{x}}_{i}‖}_{2}^{2} $ | (5) |
MSE损失函数便于使用梯度下降算法,并且随着误差的减小,梯度也在减小,有利于模型的收敛。
使用Person相关系数以及回归任务中常用的三种评价指标MSE、平均绝对误差(MAE)、均方根误差(RMSE)对使用三种损失函数的网络进行预训练并进行评估,如表 1所示。可以看出,在四个评价指标中,MSE损失函数对应的评价指标在整体效果上比其他两个损失函数更优,说明并不是越复杂的损失函数效果越好,要根据网络模型结构以及数据集的特点选择合适的损失函数。因此选择MSE为本文网络的损失函数。
|
|
表 1 不同损失函数的四个评价指标对比 |
按照前述方法生成了8000组数据(每一组数据包含低频训练数据和高频标签数据),并将8000组数据按8:1:1划分为训练集、验证集和测试集。在模型验证的过程中发现模型的样本数据、激活函数、超参数和损失函数等因素都对模型的预测效果有一定的影响。经过测试发现,模型的样本数据类型对模型的整体效果影响最大,使用更具有代表性的样本数据,会使模型的泛化能力更强。在数据预处理方面,由于地震数据的非平稳性,振幅值存在较大的差异,因此需要将数据归一化到[-1, 1]之间。其中模型的超参数以及激活函数可以根据模型的训练情况进行适应性的调整。
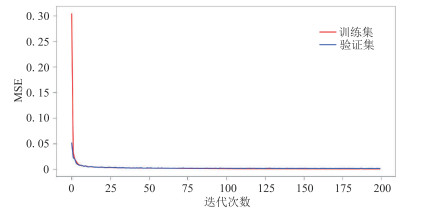
通过预训练得到的初步结果,对模型参数进行优化调整后,在显存为6 GB的GPU-GTX1060中对AAU-net模型进行正式训练。选择pytorch作为基础框架,Adam作为优化器,其中批大小为16,总迭代次数设为200。在迭代过程中训练集和验证集损失函数都逐渐收敛达到一个稳定值(图 4),表示模型已经训练到最优。
|
图 4 模型训练集和验证集损失函数变化曲线 |
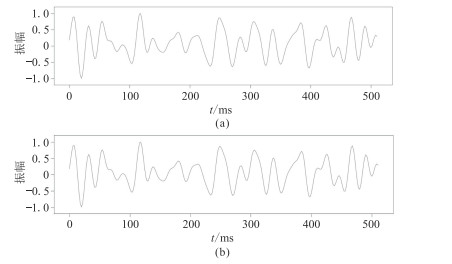
为了测试模型的泛化性能,使用测试集的低频样本数据作为输入,最终输出模型预测的高频数据。从整体上看,预测数据与标签数据具有较高的相似度(图 5),验证了本文网络模型的有效性。
|
图 5 AAU-net预测结果(a)与标签数据(b)的对比 |
为进一步验证AAU-net网络的效果,在只改变网络结构这一变量,其他参数不变的情况下,设计了与U-net网络的对比实验。
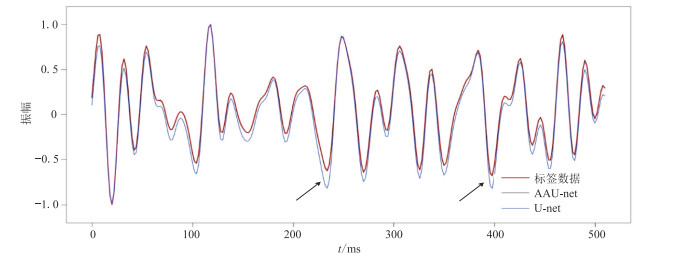
针对前述的测试集,分别使用AAU-net和U-net进行测试,并从预测结果中抽取一道数据与标签数据进行对比(图 6)。
|
图 6 AAU-net和U-net预测结果与标签数据的对比 |
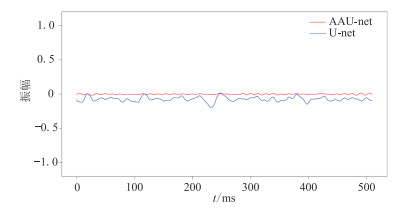
从整体上看,AAU-net和U-net预测结果的轮廓相似,对地震数据的分辨率都有一定的提升。但从细节上看,AAU-net比U-net效果更佳,如图中箭头所指,AAU-net的预测振幅更准确,与标签数据的吻合度更高。同时,为突出两种网络预测结果的差异性,计算其预测残差如图 7所示,可见,AAU-net预测误差更小、效果更好。
|
图 7 两种网络预测残差对比 |
整个测试集两种网络的预测评价指标如表 2所示,可以看出,AAU-net的四种评价指标均优于U-net,说明加入自适应注意机制后,网络的细节处理及泛化能力更强。
|
|
表 2 两种网络的测试集评价指标对比 |
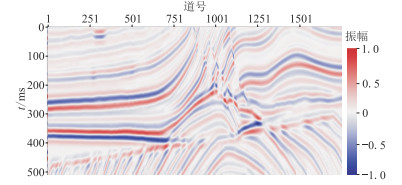
进一步将前述训练得到的模型应用于Marmousi模型进行验证。Marmousi模型合成的理论低频和高频地震记录如图 8、图 9所示。分别使用U-net和AAU-net对低频合成地震记录进行预测,结果如图 10和图 11所示。可以看出,AAU-net的预测结果与理论高频记录的相似度更高。U-net和AAU-net的预测结果与理论高频合成地震记录差值剖面分别如图 12和图 13所示,可以看出,AAU-net预测残差剖面更“干净”,误差更小、效果更好。
|
图 8 Marmousi模型的低频合成地震记录 |

|
图 9 Marmousi模型的高频合成地震记录 |

|
图 10 Marmousi模型数据U-net的预测结果 |

|
图 11 Marmousi模型数据AAU-net的预测结果 |
|
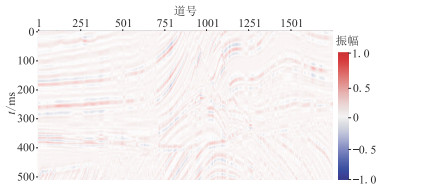
图 12 Marmousi模型数据U-net预测结果的残差剖面 |

|
图 13 Marmousi模型数据AAU-net预测结果的残差剖面 |
用实际地震资料测试本文方法实用性。借鉴陈志明等[26]给出的实际数据训练集和测试集的制作思路和方法,本文用25口井的波阻抗数据制作训练集,3口井的波阻抗数据制作测试集。具体过程如下:①利用井中波阻抗数据计算得到反射系数;②对目的层地震数据进行频谱分析,可知地震数据的主频为40 Hz;③分别利用主频为40 Hz和50 Hz的子波与反射系数进行褶积,得到低分辨率和高分辨率地震数据;④通过滑动窗口采样方法实现数据增广,共生成了含有300对数据的训练集和60对数据的验证集。
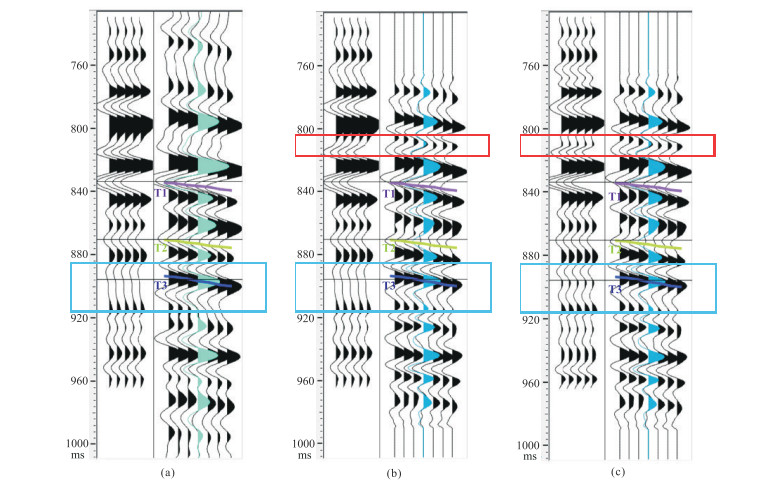
利用训练集对AAU-net进行训练,得到了对应的网络模型。将原始三维地震数据体输入到网络中,通过模型预测得到高分辨率地震数据体。选取一口未参与训练的井对预测的数据进行验证,具体过程如下。①利用主频为40 Hz的子波与反射系数褶积得到合成地震记录,并与原始地震数据的井旁地震道对比,如图 14a所示。由图可见,二者具有较高的相关性,但是在T3层位处相关性较差(蓝色矩形框内)。②利用主频为40 Hz的子波与反射系数褶积得到合成地震记录,并与预测得到的高分辨率地震数据井旁地震道做对比,如图 14b所示,二者的相关性降低,特别是在T1层位上方和T3层位处(红色矩形框和蓝色矩形框内)。③利用主频为50 Hz的子波与反射系数褶积得到合成地震记录,并与预测得到的高分辨率地震数据井旁地震道对比,如图 14c所示,二者的相关性增高,特别是T1层位上方和T3层位处(红色矩形框和蓝色矩形框内)。
|
图 14 合成地震记录与地震数据井旁地震道标定对比 (a)40 Hz合成地震记录与原始井旁道的标定;(b)40 Hz合成地震记录与预测的高分辨率井旁道的标定;(c)50 Hz合成地震记录与预测的高分辨率井旁道的标定 |
由此可知,本文方法预测得到的高分辨率地震记录与井位处的高分辨率合成地震记录具有较高的一致性,证明了本文方法预测得到的高分辨率地震数据具有较高的可靠性。
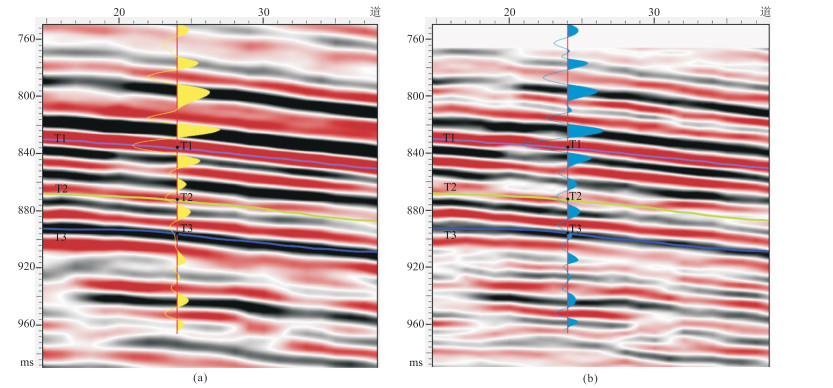
将合成地震记录投影到过井的地震剖面上。图 15a为40 Hz子波合成地震记录在原始地震剖面上的投影;图 15b为50 Hz的子波合成记录在预测的高分辨率地震剖面上的投影。对比可见,预测的地震剖面分辨率明显优于原始剖面,且与高分辨率合成地震记录高度吻合,相关系数为0.7106,验证了本文方法的实用性。
|
图 15 合成地震记录在过井地震剖面投影的对比 (a)40 Hz合成地震记录和原始地震剖面;(b)50 Hz合成地震记录和预测的高分辨率地震剖面 |
本文基于U-Net网络模型,通过引入自适应注意力机制,构建了一个新的AAU-net模型,并对地震数据进行高分辨处理。实验结果表明,加入自适应注意力机制的U-net比常规的U-net模型精度更高,可有效提高地震数据的分辨率。实际地震数据的应用结果显示,模型预测结果具有较高的可靠性。另外,研究中发现,模型的泛化能力容易受数据集的影响,可以考虑采用更具代表性的数据训练网络模型,同时对模型的参数进行一定的优化,可提升模型的性能和泛化能力。
| [1] |
曹思远, 孙耀光, 陈思远. 地震勘探高分辨率资料处理的挑战与对策[J]. 煤田地质与勘探, 2023, 51(1): 277-288. CAO Siyuan, SUN Yaoguang, CHEN Siyuan. Challenges and solutions to high-resolution data processing for seismic exploration[J]. Coal Geology & Exploration, 2023, 51(1): 277-288. |
| [2] |
ROBINSON E A. Predictive decomposition of seismic traces[J]. Geophysics, 1957, 22(4): 767-778. DOI:10.1190/1.1438415 |
| [3] |
ROBINSON E A. Predictive decomposition of time series with application to seismic exploration[J]. Geophysics, 1967, 32(3): 418-484. DOI:10.1190/1.1439873 |
| [4] |
潘树林, 闫柯, 李凌云, 等. 自适应步长FISTA算法稀疏脉冲反褶积[J]. 石油地球物理勘探, 2019, 54(4): 737-743. PAN Shulin, YAN Ke, LI Lingyun, et al. Sparse-spike deconvolution based on adaptive step FISTA algorithm[J]. Oil Geophysical Prospecting, 2019, 54(4): 737-743. |
| [5] |
PEACOCK K L, TREITEL S. Predictive deconvolution: Theory and practice[J]. Geophysics, 1969, 34(2): 155-169. DOI:10.1190/1.1440003 |
| [6] |
卫泽, 潘树林, 程祎等. 自适应变分模态分解同态反褶积方法[J]. 石油地球物理勘探, 2023, 58(1): 105-113. WEI Ze, PAN Shulin, CHENG Yi, et al. Homomorphic deconvolution method based on adaptive variational mode decomposition[J]. Oil Geophysical Prospecting, 2023, 58(1): 105-113. |
| [7] |
HALE D. Q and adaptive prediction error filters[R]. Stanford Exploration Project Report, 1981, 28: 209-231.
|
| [8] |
WANG Y. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. DOI:10.1190/1.2192912 |
| [9] |
ZHAO Y, MAO N. An inverse Q filtering approach based on a varying stabilization factor[J]. Journal of Geophysics and Engineering, 2018, 15(4): 1269-1279. DOI:10.1088/1742-2140/aaae90 |
| [10] |
YUAN S, WANG S, TIAN N, et al. Stable inversion-based multitrace deabsorption method for spatial continuity preservation and weak signal compensation[J]. Geophysics, 2016, 81(3): V199-V212. DOI:10.1190/geo2015-0247.1 |
| [11] |
TIAN G, ZHAO Y, ZHANG W, et al. The inverse Q filtering method based on a novel variable stability factor[J]. Geophysics, 2023, 88(3): V207-V214. DOI:10.1190/geo2022-0088.1 |
| [12] |
孙哲, 刘洋, 王静, 等. VSP优化预测反褶积与VSP子波替换法反褶积[J]. 石油地球物理勘探, 2009, 44(5): 569-573. SUN Zhe, LIU Yang, WANG Jing, et al. VSP optimized predictive deconvolution and VSP wavelet switchover deconvolution[J]. Oil Geophysical Prospecting, 2009, 44(5): 569-573. DOI:10.3321/j.issn:1000-7210.2009.05.009 |
| [13] |
于茜. 利用VSP子波替换提高地面地震资料的分辨率[J]. 物探与化探, 2010, 34(4): 546-548. YU Qian. The enhancement of the resolution of surface seismic data by using wavelet of VSP replacement method[J]. Geophysical and Geochemical Exploration, 2010, 34(4): 546-548. |
| [14] |
严红勇, 刘洋, 于茜. 利用VSP提高地面地震资料的分辨率[J]. 石油天然气学报, 2010, 32(3): 65-68. YAN Hongyong, LIU Yang, YU Qian. Improving the resolution of poststack surface seismic data by VSP[J]. Journal of Oil and Gas Technology, 2010, 32(3): 65-68. DOI:10.3969/j.issn.1000-9752.2010.03.014 |
| [15] |
陈双全, 李向阳. 联合垂直地震剖面资料提高地面地震资料分辨率的应用研究[J]. 中国石油大学学报(自然科学版), 2012, 36(3): 65-68, 75. CHEN Shuangquan, LI Xiangyang. Application of improving surface seismic resolution using vertical-seismic-profile data[J]. Journal of China University of Petroleum(Edition of Natural Science), 2012, 36(3): 65-68, 75. DOI:10.3969/j.issn.1673-5005.2012.03.010 |
| [16] |
HALPERT A D. Deep learning‑enabled seismic image enhancement[C]. SEG Technixal Program Expanded Abstracts, 2018, 37: 2081-2085.
|
| [17] |
蔡涵鹏, 李会强, 秦情, 等. 基于生成对抗网络地震数据超分辨率重建方法[C]. 中国石油学会2019年物探技术研讨会论文集, 2019, 1547-1550.
|
| [18] |
CHEN D, GAO J, GAO Z, et al. Reflectivity-GAN: A data-driven method for seismic deconvolution[C]. Extended Abstracts of 81st EAGE Conference & Exhibition, 2020, 1-5.
|
| [19] |
YUAN Z, JIANG Y, HUANG H, et al. Improving seismic resolution by a sequential convolutional neural network[C]. Extended Abstracts of 82nd EAGE Conference & Exhibition, 2021, 1-5.
|
| [20] |
LI J, WU X, HU Z. Deep learning for simultaneous seismic image super‑resolution and denoising[J]. IEEE Transactions on Geoscience and Remote Sen-sing, 2022, 60: 1-11. |
| [21] |
周文辉, 石敏, 朱登明, 等. 基于残差注意力网络的地震数据超分辨率方法[J]. 计算机科学, 2021, 48(8): 24-31. ZHOU Wenhui, SHI Min, ZHU Dengming, et al. Seismic data super‑resolution method based on residual attention network[J]. Computer Science, 2021, 48(8): 24-31. |
| [22] |
孙永壮, 黄鋆, 俞伟哲, 等. 基于U-Net网络的端到端地震高分辨率处理技术[J]. 地球物理学进展, 2021, 36(3): 1297-1305. SUN Yongzhuang, HUANG Yun, YU Weizhe, et al. End-to-end high-resolution seismic processing method based on U-Net network[J]. Progress in Geophysics, 2021, 36(3): 1297-1305. |
| [23] |
JO Y, CHOI Y, SEOL S J, et al. Machine learning-based vertical resolution enhancement considering the seismic attenuation[J]. Journal of Petroleum Science and Engineering, 2022, 208: 109657. DOI:10.1016/j.petrol.2021.109657 |
| [24] |
李子航, 陈小宏, 李景叶, 等. 基于S变换与复值U-Net网络的地震资料高分辨率处理方法[J]. 石油物探, 2023, 62(3): 406-418. LI Zihang, CHEN Xiaohong, LI Jingye, et al. High-resolution seismic data processing method based on S transform and complex‑valued U‑Net network[J]. Geophysical Prospecting for Petroleum, 2023, 62(3): 406-418. |
| [25] |
CHOI Y, SEOL S J, BYUN J, et al. Vertical resolution enhancement of seismic data with convolutional U‑net[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2388-2392.
|
| [26] |
陈志明, 刘洋, 张浩然. 基于U-Net网络的地震资料高分辨率处理[C]. 中国石油学会2021年物探技术研讨会论文集, 2021, 988-991.
|
| [27] |
BAHDANAU D, CHO K, BENGIO Y. Neural machine translation by jointly learning to align and translate[J]. arXiv preprint arXiv: 1409.0473, 2014.
|
| [28] |
李学贵, 周英杰, 董宏丽等. 基于双注意力U-Net网络的提高地震分辨率方法[J]. 石油地球物理勘探, 2023, 58(3): 507-517. LI Xuegui, ZHOU Yingjie, DONG Hongli, et al. Seismic resolution improvement method based on dual-attention U-Net network[J]. Oil Geophysical Prospec-ting, 2023, 58(3): 507-517. |
| [29] |
RONNEBERGER O, FISCHER P, BROX T. U-net: Convolutional networks for biomedical image segmentation[C]. Medical Image Computing and Computer-Assisted Intervention‑MICCAI 2015, 2015, 234-241.
|
| [30] |
RICKER N. The form and laws of propagation of seismic wavelets[J]. Geophysics, 1953, 18(1): 10-40. DOI:10.1190/1.1437843 |
| [31] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Proces-sing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |



 赵岩, 湖北省武汉市蔡甸区大学路111号长江大学地球物理与石油资源学院,430100。Email:
赵岩, 湖北省武汉市蔡甸区大学路111号长江大学地球物理与石油资源学院,430100。Email: