2. 西南石油大学智能油气实验室, 四川成都 610500;
3. 油气藏地质及开发工程国家重点实验室(西南石油大学), 四川成都 610500
2. Intelligent Oil and Gas Laboratory, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University), Chengdu, Sichuan 610500, China
随着油气资源的持续开发,地震勘探目标逐步从简单地质构造转向复杂地质构造。地震多次波的存在会降低地震资料信噪比,严重影响地震资料的正确解释。多次波根据其产生的地层或者水层界面位置,可以分为自由表面多次波与层间多次波。自由表面多次波是指在地表面或者海面发生两次或两次以上的下行反射,常表现出能量强、周期明显等特征;层间多次波是指在地下的层面发生多次下行反射的地震波,其与一次波的时差小,通常很难压制。由于多次波和某一深层的一次波的形态、能量很相近,二者具有相同的旅行时和同相轴,容易把地震数据中的多次波误认为深层界面中的一次波[1]。因此,对多次波进行有效压制在地震资料的处理过程中既是重点也是难点。为了消除地震多次波对一次波信息的干扰,确保对地震资料的准确解释,众多学者对多次波的压制问题进行了全面探究并提出了许多有效的方法。最典型的方法包括基于信号分析的滤波方法与基于波动理论的预测相减法,这些技术的目标是通过信号处理方法,抑制或减小多次波在地震记录中的干扰,使地震数据更具解释性和分辨力[2-7]。
随着深度学习的不断发展,越来越多的学者将各自的研究领域与深度学习相结合。近年来,地震勘探领域的科研工作者逐步将深度学习应用到地震多次波的压制问题中。基于数据驱动的多次波压制技术避免了对先验地质构造信息的依赖和昂贵的计算成本,深度神经网络可以自动从训练数据中提取多次波特征,一旦网络训练成功,就具有极高的数据处理效率。
Siahkoohi等[8]首次将卷积神经网络(CNN)用于多次波压制,使用生成对抗网络(Generative Adversarial Networks, GAN)对多次波进行压制,实验结果表明GAN对叠前地震数据处理和复杂反演建模任务有效。随后,Siahkoohi等[9]又使用EPSI获得一次波与多次波,将全波场数据与一次波数据作为网络的输入—输出训练对,利用GAN对自由表面相关多次波进行压制,取得了不错的效果。Yu等[10]将全波场数据与一次波数据作为网络的输入—输出对训练CNN,合成数据与真实数据应用结果表明深度学习在多次波衰减方面有潜在作用。Li等[11]提出基于CNN的自适应多次波特征提取,利用预测的多次波作为网络输入,全波场数据作为输出,实验证明该方法比传统方法能更好地保留一次波与压制多次波。Liu等[12]提出基于CNN的自适应自由表面相关多次波的压制方法,比传统方法有更好的压制效果且耗时较少。2021年,Li等[13]提出基于UNet的多次波自适应压制法,将一次波与全波场图像切分成小块分别作为网络的输入和标签进行训练,虽然压制精度较高,但耗时较大。宋欢等[14]提出基于深层神经网络压制多次波,该网络属于UNet的一种变形,对于全波场数据中的多次波有一定的压制效果,并且多次波压制效率较高,泛化能力也较好。王坤喜等[15]对地震数据进行了增广,再将增广后的数据输入改进的UNet进行训练,将全波场数据与多次波数据同时作为网络的输入,一次波数据作为标签,实验表明该网络对地震多次波的压制具有一定的有效性、稳定性和泛化能力。张猛[16]将自注意力机制引入类似UNet的神经网络中,使用卷积自编码器对多次波进行压制。自注意力机制能够提升网络性能,为多次波的压制提供了一个高效方法。刘小舟等[17]提出了使用数据增广的编解码卷积网络对地震层间多次波进行压制,增广的地震数据能提升网络的泛化能力和抗噪能力,将去噪CNN与UNet相结合,使网络学习数据特征的能力更强,该方法提高了压制层间多次波的效率。
目前,不同结构的GAN已广泛应用于地球物理勘探领域中的数据增强、处理和解释。其中pix2pix GAN是运用条件生成式对抗网络(Conditional Generative Adversarial Networks, CGAN) 实现图像到图像转换的鼻祖,本文在经典的pix2pix GAN的基础上进行改进并应用于地震多次波压制。由于地震剖面中多次波与一次波形态相似,需要用更深层的网络提取更多的特征,为了避免深层网络可能引起的梯度消失或梯度爆炸现象,改进网络的生成器将残差网络加入UNet。为了能提取更多的细节特征,在生成器中加入SE注意力机制。使用多尺度判别器代替单尺度判别器,以提高多次波压制的精度。最后将改进的网络应用在两个简单地质模型数据集和一个开放的Sigbee2B复杂地质模型数据集中,并对各网络的多次波压制效果进行对比。结果表明,改进后的网络模型对多次波的压制精度更高,能在更好地压制多次波的同时保护一次波。
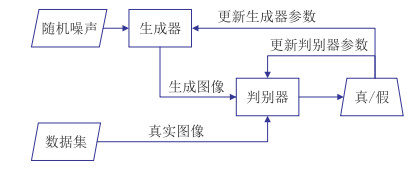
1 方法 1.1 GAN模型2014年,Goodfellow等[18]首次提出GAN模型,该模型当前广泛使用且不断改进,模型通过无监督学习训练数据的概率分布特征,并生成与真实数据非常接近的虚假样本。GAN模型结构如图 1所示,其网络由生成器和判别器构成,它们作为两个网络分别被训练。从使用随机输入的基本模型或使用指定数据集的变换开始,生成器学习生成新的数据实例,旨在产生与真实数据无法区分的数据。将真实数据和生成的虚假数据同时输入网络,判别器致力于对输入数据的真实性进行评估,区分真实数据与虚假数据。经过不断的训练,生成器学习创造更多可信的(尽管是假的)输出,判别器学习更好地识别虚假数据。就它们各自的目标而言,它们是对手,但在训练过程中,它们也是一种合作关系,即生成器会更新与判别器有关的信息。如果生成器生成的数据能够骗过判别器,它就会得到改进;如果判别器能够正确区分真实数据集与生成数据集,它就会得到改进。在整个过程中,如果判别器改进得太快,生成器可能永远追不上;如果判别器改进得太慢,生成器将不断生成质量差的数据。如果二者能够调整它们的改进速度并保持平衡,生成器将成功地在与判别器的激烈竞争中生存下来,最后生成的图像将非常接近真实图像。
|
图 1 经典GAN模型 |
GAN的计算如下
| $ \mathrm{m}\mathrm{i}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{x}V(G, D)={E}_{\boldsymbol{x} \sim p\left(\boldsymbol{x}\right)}\left[\mathrm{l}\mathrm{g}D\left(\boldsymbol{x}\right)\right]+\\ \quad\quad \quad\quad\quad\quad\quad\quad{E}_{\boldsymbol{z} \sim p\left(\boldsymbol{z}\right)}\left\{\mathrm{l}\mathrm{g}\left[1-D\left(G\right(\boldsymbol{z})\right]\right\} $ | (1) |
式中:p(x)表示真实数据集的数据分布,x表示输入网络的真实数据;p(z)表示简单先验分布,z表示输入网络的噪声;D(x)表示输入判别器的数据被认作是真实数据的概率;G(z)表示由生成器生成的虚假数据。生成器把从p(z)的噪声向量z中的随机采样作为输入,尝试生成与真实数据相似的样本G(z),判别器接收从p(x)中抽取的真实数据样本x或者虚假数据样本G(z),并尝试将它们正确地分为真实数据或虚假数据。生成器的目的是让判别器无法正确区分真/假数据,所以D[G(z)]要尽可能小,即minG。判别器的目的是正确区分真假数据,所以D(x)要尽可能大,即maxD,利用最小—最大博弈,使两个神经网络平衡,即D(x)=D[G(z)]=0.5。
GAN自提出以来,就在图像生成、图像处理、目标检测以及视频使用等领域广泛应用,但原始GAN的最小—最大博弈过程存在随机且不可控的缺陷,导致该网络难以收敛。近年来,许多学者对GAN进行了深入的探索,并逐步研究出各种训练更稳定、速度更快、效果更好的网络。
1.2 改进的网络结构本文的网络结构在CGAN基础上进行改进,pix2pix GAN是Isola等[19]为解决图像转换到图像的通用性问题而设计的CGAN,该网络使用UNet模型作为生成器,使用卷积“PatchGAN”结构作为判别器。该生成器包括编码和解码两部分,每个编码块和解码块之间以跳跃连接(Skip Connection)的方式进行串联。网络总层数为n,其中,第i层与第n-i层连接。跳跃连接将下采样过程提取的低层图像特征传递给上采样层进行特征融合。该网络的判别器将输入网络的每张图像分成多个图像块(Patch),独立地对每一个Patch进行真/假判断,然后对所有计算得到的值进行平均,以获得最终的输出值。使用Patch的方式可以有效减少参数量和计算量,使网络训练速度更快,并能运用在任意大的图像中,能有效缓解训练地震多次波压制网络时速度过慢的问题。
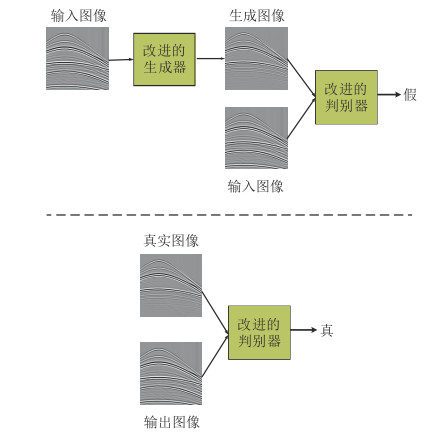
本文网络的训练原理如图 2所示,将全波场数据作为条件输入改进的生成器,生成器根据其分布特征生成虚假地震图像,然后根据判别器的反馈对生成器进行参数调整,以生成与真实图像(不含自由表面多次波的地震剖面图像)更相似的虚假图像。将输入图像(全波场)分别与真实图像和生成图像进行拼接,再将拼接后的图像输入改进的判别器中进行训练,判别器通过比较生成图像与真实图像的相似程度,对生成图像进行真/假判断。改进的生成器与判别器相互学习,经过多次训练后,该网络能够生成与真实图像极为相似的虚假图像。
|
图 2 改进的CGAN的训练原理 |
当图像特征差异较大时,使用简单的神经网络结构就能较好地压制多次波。而对多次波和一次波特征相似性较高的情况,需要设计更深层且效果较好的网络模型。通常情况下,网络越深则网络模型输出结果越好,然而,由于激活函数是非线性的,当网络很深时,可能会出现梯度消失或者梯度爆炸现象,从而难以提高精度,甚至可能降低精度。
pix2pix GAN的生成器是一个UNet。2016年,Quan等[20]将ResNet结构引入UNet,提出了FusionNet网络结构。该网络在UNet的主网络中引入了基于求和的跳跃连接,加入了残差块以及长跳+短跳连接,在更深层的网络上取得不错的网络输出。其中,残差连接是FusionNet内部模块之间使用的一种连接方法,这样的连接结构可以让浅层的图像特征到达网络的深层,可以有效训练深层网络。
本文采用的生成器模型如图 3所示。在编码阶段,使用4个下采样,绿色的块代表一个包括激活函数(ReLU)和批归一化(BN)规则的卷积层(Conv),蓝色的块表示残差层,每一个残差块包含三个卷积块和一个残差跳跃连接,深紫色块表示最大池化层,在编码阶段用于进行下采样,实现特征的压缩。在解码阶段,进行4次上采样,深红色块表示反卷积层,在解码路径中对输入数据进行上采样,使用插值对图像大小进行复原。残差块中的连接为短跳连接,实现编码或者解码路径中与前一层的连接,UNet中只通过长跳连接进行不同层的特征连接,FusionNet将UNet中的长跳连接替换成长跳连接与编码路径中同一级别的特征映射,这样能有效解决深层网络梯度消失的问题。另外,短跳连接和长跳连接的混合使用,能够实现信息在网络层中的跨层流动。为了提高对重要信息的关注,在该生成器中引入了SE注意力机制[21],以降低对特征图中除地震波波形之外的其他干扰的关注,提高了模型的准确率。

|
图 3 改进的生成器模型框架 |
神经网络中的注意力机制源自于人脑长期生存进化而来的信号处理机制。人脑注意力通常集中在感兴趣或信息显著的部分,那些不太重要的部分就会被分配较少的注意力或者被忽视,有助于提升信息处理效率[21]。在图像处理领域,无论是图像识别、分类、分割还是生成,添加注意力机制均有助于提高信息处理的准确性。由于地震波在传播过程中具有动态时域关联性,本文将SE注意力机制加入网络中,提高模型的准确率。
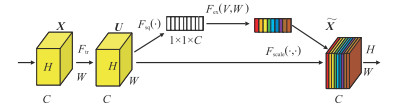
在传统卷积池化过程中,特征图各通道中信息的重要性被认为相同,然而在实际中,各特征图不同通道信息的重要性有一定差异,传统的卷积池化操作会导致结果有损失。SE注意力机制解决了该问题,它通过一个权重矩阵,从通道域的角度给予图像不同位置不同权重,获得对当前任务来说更重要的特征信息。该模块结构如图 4所示,主要包含压缩(Squeeze)、激励(Excitation)和还原(Scale)三个过程,其中压缩过程将每个通道的二维信息通过全局平均池化压缩成一个值,即将大小为H×W×C的特征图经过全局平均生成一个1×1×C的向量,其中H表示高度,W表示宽度,C表示总的通道数,其计算公式为
| $ {z}_{c}={F}_{\mathrm{s}\mathrm{q}}\left({\boldsymbol{u}}_{c}\right)=\frac{1}{H\times W}\sum\limits_{i=1}^{H}\sum\limits_{j=1}^{W}{u}_{c}(i, j) $ | (2) |
|
图 4 SE注意力机制模块 |
式中:
激励过程执行两个全连接(FullyConnected,FC)操作,利用权重W生成所需的权重信息
| $ s={F}_{\mathrm{e}\mathrm{x}}(\boldsymbol{V}, \boldsymbol{W})=\sigma (\boldsymbol{V}, \boldsymbol{W})=\sigma \left[{W}_{2}\delta \left({W}_{1}\boldsymbol{V}\right)\right] $ | (3) |
式中:
还原过程是把激励过程生成的权重向量用于对特征图U进行权重赋值,获得所需的特征图
| $ {\tilde{x}}_{c}={F}_{\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}}({\boldsymbol{u}}_{c}, {s}_{c}) $ | (4) |
式中:
本文改进网络的生成器将ResNet与UNet相结合,引入SE注意力机制,
在地震多次波压制问题中,如果想要提升判别器区分真实图像与生成图像的能力,就需判别器对更精细的波形信息进行正确判别,所以判别器需有一个更大的感知区域。提升判别器感知区域的方法主要包括训练一个更深层次的网络模型或使用更大的卷积核进行特征提取,但这两种方法都会使网络容量增加,导致判别器网络变得十分复杂,训练时的计算量也随之增加,这将消耗更大的内存以及GPU计算资源,在现实中较难实现,并且由于计算量的增加,生成图像的速度也将有所降低,同时还容易出现过拟合现象。
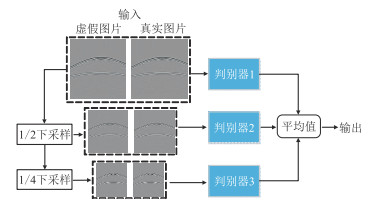
pix2pix GAN使用多尺度判别器对生成图像进行真/假判断,该网络使用三个判别器,为方便描述,下文将这些判别器分别称为Discriminator1、Discriminator2、Discriminator3,它们具有完全相同的网络结构[22]。Quan等[20]仅仅在不同的尺度上进行判别,分别将真实图像和生成图像进行2倍下采样和4倍下采样。在最大的图像尺度上训练的判别器具有最大的感受野、最全局的视野,在提取图像特征时,相同的卷积核能获取更大范围内的特征,具有更好的全局特征辨别能力,并且可以指导生成器生成全局一致的图像。与之相反,在最小图像尺度上运行的判别器拥有的感受野范围最小,更聚焦于局部信息,其提取的特征属于图像的局部纹理特征,辅助生成器产生更精细的图像细节特征和纹理。最后,综合各个判别器的评判结果,对三个不同尺度判别器的输出结果取平均值得到最终结果。由于三个判别器的不同之处仅在于输入图像的尺度不同,所以不必重新训练三个判别器,只需添加对尺度的判断就可训练不同尺度的判别器,这让网络训练变得更容易,如果重新开始训练网络会占用更多不必要的资源和时间。多尺度判别器网络结构如图 5所示。
|
图 5 改进的判别器模型框架 |
网络训练中的损失函数是评价网络输出的预测数据与真实标签数据之间的相似度,能够衡量模型预测的好坏。对于地震自由表面多次波的压制这一任务,CNN需要预测输出数据每个采样点的值,所以多次波压制问题属于回归问题,故本文将平均绝对误差(MAE)作为网络的损失函数
| $ \mathrm{M}\mathrm{A}\mathrm{E}(\boldsymbol{y}, {\boldsymbol{y}}^{\text{'}})=\frac{1}{N}\sum\limits_{k=1}^{N}\left|\right|{y}_{k}-{y}_{k}^{\text{'}}\left|\right| $ | (5) |
式中:yk表示标签数据矩阵y中第k个元素的值;N为y的长度;
CPU采用AMD Ryzen 9 3900X 12Core Processor,GPU采用NVIDIA GeForce RTX3090。操作系统为Ubuntu18.04LTS,GPU开发环境为CUDA10.2,深度学习框架为Pytorch1.10.1。
2.2 数据集准备地震数据通常具有平稳变化的特征,目前还没有适合用于CNN训练的开放数据集,现有的数据集来源主要有两种:一是直接利用一次波与多次波形成原理而合成的数据;二是通过现有的传统多次波压制方法处理获得。本文设计了两个简单地质模型数据以及一个开放地质模型数据(Sigsbee2B模型)验证该网络算法的效果。
对于模拟数据,本文使用Tesseral2D正演模拟软件对数据进行合成。模型训练需要大量的数据集,通过在同一地层模型中的不同位置放置炮点,通过改变震源的位置来获取不同的地震数据。
2.3 评价指标为了更客观地评价本文方法的有效性,使用信噪比(Signal to Noise Ratio,SNR)、结构相似性测量(Structure Similarity Index Measure,SSIM)、峰值信噪比(Peak Signal to Noise Ratio,PSNR)、均方误差(Mean Square Error,MSE)四种定量评价指标比较四种网络对多次波的压制效果。
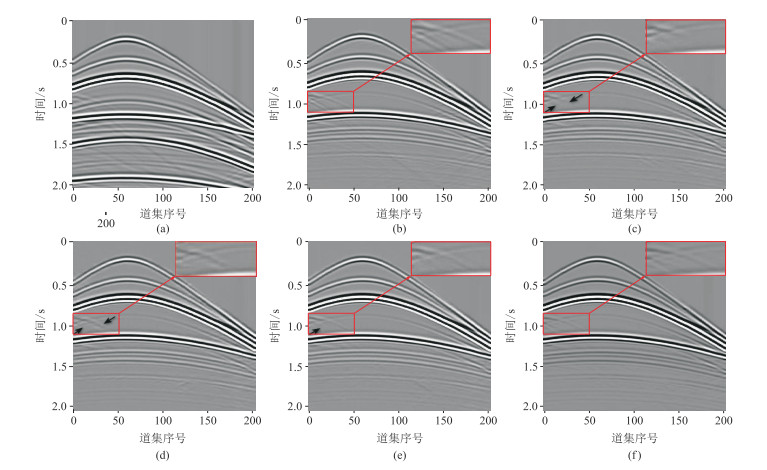
3 模型试算 3.1 模型一模型一如图 6所示,Tesseral软件通过声波方程的有限差分法合成含有一次波与多次波的全波场数据以及不含自由表面多次波的数据。具体模拟参数为:检波器水平间距为10 m;接收道数为201;采用主频30 Hz的Ricker子波作为正演子波。通过移动震源的位置, 共生成200组二维单炮记录,每一组单炮记录包含一个含有自由表面多次波的数据和一个不含自由表面多次波的数据,分别作为网络的输入与标签。采集的每个单炮记录中共有201个地震道数据,每一道地震数据包含985个采样点,采样间隔为2 ms,采样总时长为1.97 s。

|
图 6 简单速度模型 |
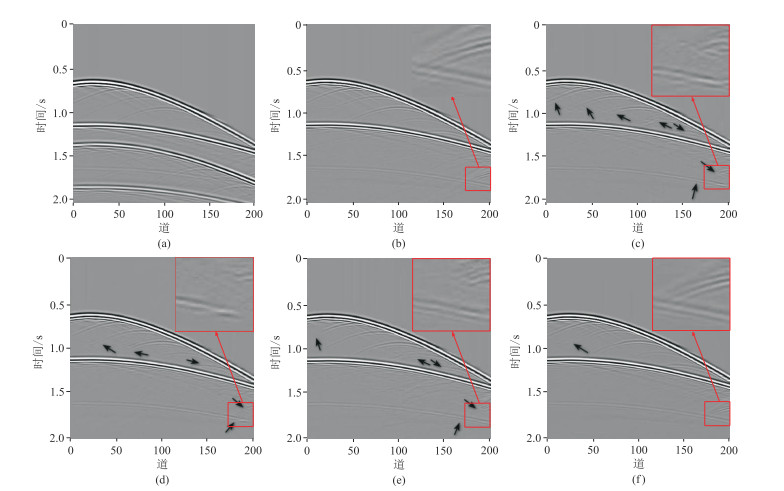
对200组数据集中的全波场数据添加不同强度的高斯噪声,网络优化算法的初始学习率为1×10-4。各种网络的输出结果如图 7所示:图 7a为全波场数据;图 7b为不含自由表面多次波的标签数据;pix2pix GAN网络的输出结果如图 7c所示,其中较明显的多次波被压制,较明显的一次波被保留,但是对浅显细小纹理波形的处理效果不好,如黑色箭头所示,对该处的波形保留效果差;利用TAO等[23]提出的CAESAGAN网络对多次波进行压制,结果如图 7d所示,其多次波压制效果略优于pix2pix GAN,黑色箭头所指的波形保留效果较差;为方便描述,仅对pix2pix GAN的生成器进行修改后的网络命名为FusionNetSEpix2pix,其输出结果如图 7e所示,效果略优于前两个网络,对多次波的去除、一次波的保留效果较好,对细节纹理信息的处理有所改进,但对部分浅显波形的保留依然不完全(图中黑色箭头所示);将本文改进网络命名为FusionNetSEMultipix2pix,其输出结果如图 7f所示,该网络输出结果明显优于前三种网络的输出结果(图中黑色箭头所示),只存在极少处的波形未被保留。对相同位置的局部区域进行放大,如红色框所示前三种网络对该处波形保留效果差,本文网络对细微波形的处理能力明显优于其他网络。
|
图 7 不同网络对简单模型一地震数据中的多次波压制效果对比 (a)全波场数据;(b)标签数据;(c)pix2pixGAN;(d)CAESAGAN;(e)FusionNetSEpix2pix;(f)本文方法 |
使用SNR、SSIM、PSNR和MSE四种评价指标定量地比较四种网络的输出结果。由表 1可见,本文所提方法在各项指标中均为最好。
|
|
表 1 模型一的网络评价指标 |
模型二如图 8所示,Tesseral软件利用有限差分正演的原理,合成含有一次波与自由表面多次波的全波场数据以及不含自由表面多次波的标签数据。具体模拟参数如下:模型大小2000 m×1250 m,整体为七个水平层状介质地质模型;检波器水平间距为10 m;每炮有201道接收。采用主频30 Hz的Ricker子波作为正演子波,通过移动震源位置, 一共生成200组二维单炮记录,每一组单炮记录包含一个含有自由表面多次波的数据和一个不含自由表面多次波的数据,分别作为网络的输入与标签。采集的每个单炮记录中共有201个地震道数据,每一道地震数据包含1220个采样点,采样间隔为1 ms,采样总时长为1.22 s。
|
图 8 简单速度模型二 |
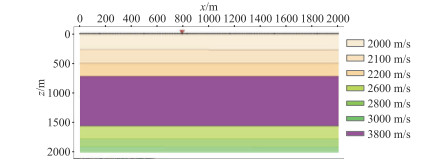
对200组数据集中的全波场数据添加不同强度的高斯噪声和椒盐噪声,数据集增加为600组,网络优化算法的初始学习率为1×10-4。各网络的输出结果如图 9所示:图 9a为全波场数据;图 9b为不含自由表面多次波的标签数据;pix2pix GAN网络输出结果如图 9c所示,较明显的多次波基本被压制,较明显的一次波被保留,但是对浅显细小纹理的波形处理效果不好(图中黑色箭头所示),对该处波形保留效果差;CAESAGAN网络多次波压制结果如图 9d所示,其结果比pix2pix GAN效果略好,但对黑色箭头所指波形的保留效果依然较差;FusionNetSEpix2pix网络输出结果如图 9e所示,结果优于前两种网络,但依然无法清晰地保留细小波形;FusionNetSEMultipix2pix网络的输出结果如图 9f所示,其效果明显好于前三种网络,虽然对黑色箭头所指波形的保留效果有所改进,但与标签相比,依然存在细微差异。
|
图 9 不同网络对简单模型二地震数据中的多次波压制效果对比 (a)全波场数据;(b)标签数据;(c)pix2pixGAN;(d)CAESAGAN;(e)FusionNetSEpix2pix;(f)本文方法 |
对局部区域进行放大,经观察发现,本文改进的网络对纹理较浅的波形保留效果优于其他网络。使用SNR、SSIM、PSNR、MSE四种方法定量地比较四种网络的输出结果,从表 2可以看出,本文提出的方法在各项指标中均为最好。
|
|
表 2 简单模型二的网络评价指标 |
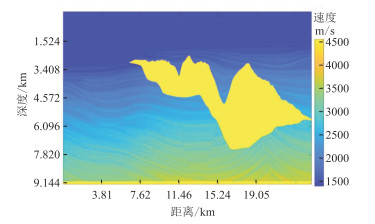
模型三为开放的Sigsbee2B模型(图 10),该模型是由国际SMAART协会提供的用于研究自由表面多次波的标准模型,其盐体的几何形状复杂,包括大量的正断层和逆冲断层,水底、顶部和底部盐丘界面的速度变化使该模型具有很强的水底界面多次波与盐丘顶界面多次波。该模型采用多炮正演模拟,其炮点与检波器排列范围均为3330~25962 m,该模型共包含496个炮点,第1~142个炮点的接收道数从65道逐渐增加到347道,每一炮增加2道,剩余炮点每炮348道检波器接收,道间距为22.86 m,每一道包含1499个采样点,采样间隔为8 ms,采样总时长为11.992 s,采用主频为20 Hz的Ricker子波作为正演子波,最后使用303组全波场数据——不含自由表面多次波数据对作为网络的输入与标签。
|
图 10 Sigsbee2B速度模型 |
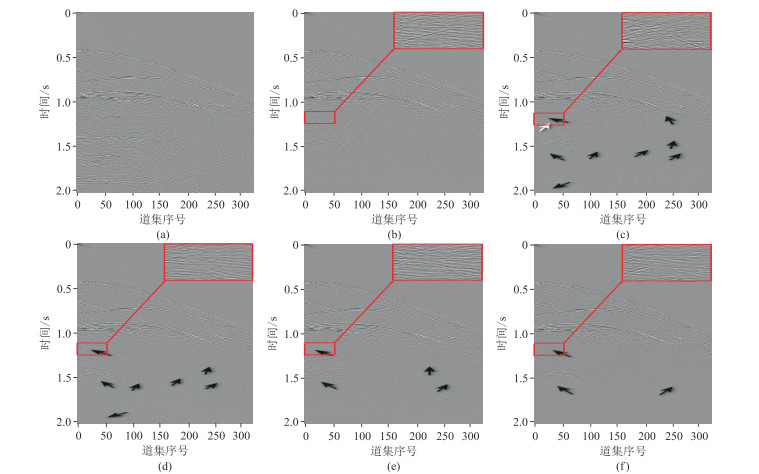
对303组数据集中的全波场数据添加不同强度的高斯噪声和椒盐噪声,将数据集增加为909组,网络优化算法的初始学习率为1×10-4。各网络的输出结果如图 11所示:图 11a为全波场数据;图 11b为不含自由表面多次波的标签数据;pix2pix GAN网络的输出结果如图 11c所示,白色箭头所指的多次波未被压制,黑色箭头所指的一次波未被很好的保留,尤其是对时间更大处(检波器9 s后接收的地震波)的波形处理效果较差;CAESAGAN网络压制多次波的结果如图 11d所示,相比于pix2pix GAN,该网络对多次波的压制效果有一定改进,但其效果依然较差;FusionNetSEpix2pix网络的输出结果如图 11e所示,黑色箭头所指的一次波未被有效保护,时间更大处的波形依然未被很好地处理;FusionNetSEMultipix2pix网络的输出结果如图 11f所示,相比于前三种网络,该网络对更多的细节波形处理效果更好,对于深层的明显波形,该网络的处理效果较好,但是对于更细节的信息处理结果,与标签依然存在差异。为了更好地比较各网络对多次波的压制效果,对标签图像与各网络输出图像相同位置的局部区域进行放大,经观察发现,尽管各网络的输出结果与标签均存在一定差异,但本文网络对多次波的压制效果以及对一次波的保留效果更好,输出图像与标签更接近。
|
图 11 不同网络对Sigbee2B模型数据中的多次波压制效果对比 (a)全波场数据;(b)标签数据;(c)pix2pixGAN;(d)CAESAGAN;(e)FusionNetSE-pix2pix;(f)本文方法 |
使用SNR、SSIM、PSNR、MSE四种评价指标定量地比较四种网络的输出结果。由表 3可见,本文方法与FusionNetSEMultipix2pix网络的MSE相同,并均优于pix2pix与CAESAGAN网络,在SSIM、SNR、PSNR指标中,本文方法的表现均为最好。
|
|
表 3 模型三的网络评价指标 |
本文在pix2pix GAN网络的基础上进行改进,相比于原始网络使用UNet作为网络生成器,本文改进的网络通过使用FusionNet作为生成器,同时引入SE注意力机制,提高了网络对细节纹理信息的生成能力,从而提高了生成器生成图像的精度;相比于原始网络使用“PatchGAN”结构作为判别器,本文方法使用多尺度判别器提高全局特征辨别能力以及局部纹理特征辨别能力,可更精确地区分真实图像和生成图像。
为了确保所提网络模型的可行性,本文使用三个模型数据对其进行验证,将全波场数据作为网络输入,不含自由表面多次波的数据作为网络标签,通过将网络输出结果与标签数据进行比较,表明该网络对多次波压制效果较好。通过比较多种网络的性能指标,所提网络的指标均最好。本文改进网络对多次波的压制、对一次波的保留以及对细节信息的处理效果更好。
| [1] |
秦宁, 王常波, 梁鸿贤, 等. 一次波和层间多次波联合成像方法[J]. 石油地球物理勘探, 2022, 57(6): 1375-1383. QIN Ning, WANG Changbo, LIANG Hongxian, et al. Joint imaging method of primaries and internal multiples[J]. Oil Geophysical Prospecting, 2022, 57(6): 1375-1383. |
| [2] |
LU W. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophysics, 2013, 78(4): V147-V155. DOI:10.1190/geo2012-0439.1 |
| [3] |
SUN W, LI Z, QU Y, et al. Multiple attenuation using λ-f domain high-order and high-resolution Radon transform based on SL0 norm[J]. Applied Geophy-sics, 2019, 16: 473-482. DOI:10.1007/s11770-019-0795-9 |
| [4] |
薛亚茹, 郭蒙军, 冯璐瑜, 等. 应用加权迭代软阈值算法的高分辨率Radon变换[J]. 石油地球物理勘探, 2021, 56(4): 736-744, 757. XUE Yaru, GUO Mengjun, FENG Luyu, et al. High resolution Radon transform based on the reweighted-iterative soft threshold algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4): 736-744, 757. |
| [5] |
马继涛, 刘仕友, 廖震. 三维高精度保幅Radon变换多次波压制方法[J]. 石油地球物理勘探, 2022, 57(3): 582-592. MA Jitao, LIU Shiyou, LIAO Zhen. Research on multiple attenuation using 3D high precision amplitude preserving Radon transform[J]. Oil Geophysical Prospecting, 2022, 57(3): 582-592. |
| [6] |
张全, 林柏栎, 杨勃, 等. CPU-GPU异构平台的抛物线Radon变换并行算法[J]. 石油地球物理勘探, 2020, 55(6): 1263-1270. ZHANG Quan, LIN Baili, YANG Bo, et al. Parabolic Radon transform parallel algorithm for CPU-GPU heterogeneous platform[J]. Oil Geophysical Prospec- ting, 2020, 55(6): 1263-1270. |
| [7] |
WEGLEIN A B. Multiple attenuation: an overview of recent advances and the road ahead (1999)[J]. The Leading Edge, 1999, 18(1): 40-44. |
| [8] |
SIAHKOOHI A, LOUBOUTIN M, KUMAR R, et al. Deep-convolutional neural networks in prestack seismic: two exploratory examples[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2196-2200.
|
| [9] |
SIAHKOOHI A, VERSCHUUR D J, HERRMANN F J. Surface-related multiple elimination with deep learning[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 4629-4634.
|
| [10] |
YU S, MA J, WANG W. Deep learning for denoi-sing[J]. Geophysics, 2019, 84(6): V333-V350. |
| [11] |
LI Z X, GAO H T. Feature extraction based on the convolutional neural network for adaptive multiple subtraction[J]. Marine Geophysical Research, 2020, 41(2): 10. DOI:10.1007/s11001-020-09409-7 |
| [12] |
LIU L C, HU T Y, HUANG J D, et al. Adaptive surface-related multiple subtraction based on convolutional neural network[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [13] |
LI Z X, SUN N N, GAO H T, et al. Adaptive subtraction based on U-net for removing seismic multiples[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(11): 9796-9812. DOI:10.1109/TGRS.2021.3051303 |
| [14] |
宋欢, 毛伟建, 唐欢欢. 基于深层神经网络压制多次波[J]. 地球物理学报, 2021, 64(8): 2795-2808. SONG Huan, MAO Weijian, TANG Huanhuan. Application of deep neural networks for multiples attenuation[J]. Chinese Journal of Geophysics, 2021, 64(8): 2795-2808. |
| [15] |
王坤喜, 胡天跃, 刘小舟, 等. 基于数据增广训练的深度神经网络方法压制地震多次波[J]. 地球物理学报, 2021, 64(11): 4196-4214. WANG Kunxi, HU Tianyue, LIU Xiaozhou, et al. Suppressing seismic multiples based on the deep neural network method with data augmentation training[J]. Chinese Journal of Geophysics, 2021, 64(11): 4196-4214. DOI:10.6038/cjg2021O0517 |
| [16] |
张猛. 基于自注意力机制的卷积自编码器多次波压制方法[J]. 石油物探, 2022, 61(3): 454-462. ZHANG Meng. A multiple suppression method based on self-attention convolutional auto-encoder[J]. Geophysical Prospecting for Petroleum, 2022, 61(3): 454-462. DOI:10.3969/j.issn.1000-1441.2022.03.007 |
| [17] |
刘小舟, 胡天跃, 刘韬, 等. 数据增广的编解码卷积网络地震层间多次波压制方法[J]. 石油地球物理勘探, 2022, 57(4): 757-767. LIU Xiaozhou, HU Tianyue, LIU Tao, et al. Seismic internal multiple suppression method with encoder-decoder convolutional network based on data augmentation[J]. Oil Geophysical Prospecting, 2022, 57(4): 757-767. |
| [18] |
GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial networks[J]. Communications of the ACM, 2020, 63(11): 139-144. DOI:10.1145/3422622 |
| [19] |
ISOLA P, ZHU J Y, ZHOU T H, et al. Image-to-image translation with conditional adversarial networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, 5967-5976.
|
| [20] |
QUAN T, HILDEBRAND D G C, JEONG W K. FusionNet: a deep fully residual convolutional neural network for image segmentation in connectomics[J]. Frontiers in Computer Science, 2016, 3: 613981. |
| [21] |
HU J, SHEN L, ALBANIE S, et al. Squeeze-and-excitation networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 2011-2023. |
| [22] |
WANG T C, LIU M Y, ZHU J Y, et al. High-resolution image synthesis and semantic manipulation with conditional GANs[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, 8798-8807.
|
| [23] |
TAO L, JIANG J, REN H, et al. The separation of seismic surface-related multiples based on CAE-SAGAN[C]. SEG Technical Program Expanded Abstracts, 2021, 40: 2914-2918.
|



 彭博, 四川省成都市新都区新都大道8号西南石油大学(成都校区),610500。Email:
彭博, 四川省成都市新都区新都大道8号西南石油大学(成都校区),610500。Email: