2. 崂山实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266237
2. Laboratory for Marine Mineral Resources, Laoshan Laboratory, Qingdao, Shandong 266237, China
传统地震储层预测技术是通过反演从地震资料中获取纵波速度、横波速度、波阻抗及弹性模量、泊松比等参数,然后根据测井数据回归分析,建立物性参数与弹性参数的岩石物理模型或经验公式,从而实现储层物性参数的定量评价。
随着油气勘探程度的不断提高,基于线性假设和经验公式的传统地震储层预测方法已无法满足储层精细定量评价的要求[1],主要问题有:①大多数情况下,储层孔隙结构复杂,非均质性较强,难以满足储层为各向同性孔隙充填的假设条件,这导致预测结果的可靠性降低[2];②物性参数与弹性参数之间存在复杂的非线性关系,难以建立精准的经验公式,并且参数的选择受主观因素的影响较大[3],降低了定量评价的精度;③每一种经验公式都有其适用范围,增加了岩石物理分析工作量。
充分挖掘地震弹性参数与储层物性参数之间的非线性关系对提高储层定量评价精度至关重要。深度学习技术具有强大的特征提取和高维数据处理能力,可以在大量的数据中有效挖掘更深层的特征[4];对复杂非线性关系的学习能力强,可以更准确地逼近地震数据与目标之间复杂的非线性关系[5]。与传统的神经网络算法相比,深度学习网络(Deep Neural Network,DNN)在反演精度、分辨率和抗噪能力等方面具有更显著的优势[6],因此它在地震反演和储层预测方面均有着巨大的应用潜力[7-8]。为此,本文深入讨论深度学习技术在地震储层预测领域的研究进展,分析它在实际应用中面临的挑战,并提出未来的发展方向。
1 深度学习技术及其特点 1.1 方法原理深度学习网络由输入层、隐藏层和输出层组成。与传统机器学习方法相比,深度学习技术最大的特点是网络结构深度的增加,通常包含3个以上的隐藏层,经过隐藏层的逐层特征提取和转换,可将样本特征从原空间变换为新的高维空间,从而建立由输入到输出高维的映射关系。因此,深度学习具有强大的特征提取能力,能够解决复杂的非线性问题。
深度学习技术和传统机器学习相同,均具有三种学习方式:监督学习(Supervised Learning)、无监督学习(Unsupervised Learning)和半监督学习(Semi-Supervised Learning)。
深度学习技术的应用包括了分类和回归,二者都属于监督学习,不同点在于:①输出不同。分类的输出是离散型变量,为定性输出;而回归的输出是连续型变量,为定量输出。②目的不同。分类的目的是寻找决策面,对集中的数据进行分类;而回归的目的是寻找最优拟合,通过回归算法得到一个最优拟合线,可以最好地接近数据集中的各个点。③评价结果的标准不同。分类的结果只有对与错之分,回归的结果则以是否更接近真实值作为标准,而不是简单的判断对与错。④使用场景不同。在地球物理领域,分类通常用于识别、分类地下储层类型、岩性、地质体等,从而提高资料解释的工作效率;而回归通常用于预测连续性的地下属性,如速度、密度等物性参数,可以根据已知的属性数据,通过深度学习训练,构建地球物理数据与属性之间的映射模型,从而预测未知位置的属性值。因此,回归是预测地下物性的重要工具。
1.2 技术特点区别于传统的模型驱动方法,深度学习技术是一种数据驱动的方法,即通过大量数据的训练,有效融合地球物理数据与地质信息,求解数据与目标之间复杂的非线性映射模型。在完成地震储层预测任务中,深度学习具有3个方面优势:①数据驱动,无需明确测井数据与地震数据之间的物理关系;②非线性,克服了传统地震反演中不合理的线性假设,可以更精准地建立地震数据与物性参数之间的联系;③在测井数据充足的情况下,可以通过测井数据和地震数据的训练,建立物性参数与地震数据之间的联系,从而直接由地震数据反演物性参数,并且可以同时反演多种物性参数;④数据驱动的方法虽然在训练阶段需要花费较多的时间,但在实际预测阶段所需的时间非常少,因此,模型一旦建立好,就可以大大减少地震储层预测的计算时间,提高工作效率。
2 深度学习技术在地震储层预测中的应用在地震储层预测中,深度学习技术的应用主要包括3个方面:烃类定性检测、非线性地震反演和储层参数预测。其中,烃类定性检测属于分类,非线性地震反演和储层参数预测属于回归。
2.1 烃类定性检测基于叠后地震资料的“亮点”技术和基于叠前地震资料的AVO属性分析技术等都是烃类检测常用的手段。但部分非烃类岩性表现出与油气相似的振幅特征,部分含烃地层未表现为明显的强振幅异常,而是弱振幅响应。如致密砂岩气藏具有低孔、低渗、非均质的特点,导致气藏与围岩的地震响应差异较小[9-11]。因此,利用地震资料精准识别油气储层仍然面临巨大的挑战。
深度学习在烃类检测中取得了良好的应用效果[9, 12-15]。林年添等[12]提出了一种在小样本条件下基于卷积神经网络(Convolution Neural Network,CNN)的储层预测方法,有效识别了超致密气藏,并与测井数据具有较高的吻合度。Gao等[14]针对标签数据不足的问题,提出了一种基于CNN和迁移学习的气藏识别方法。Júnior等[15]提出了一种基于卷积长短期记忆模型和粒子群优化算法的天然气富集区检测方法,在最佳条件下准确率达99.42%。Xue等[9]针对致密砂岩气藏弱地震响应的特点,提出了基于量子神经网络(Quantum Gate Set Neural Network,QGSNN)的地震多属性油气检测方法。由图 1可见,气藏(圆圈处)表现为弱地震响应特征(图 1a),利用QGSNN算法的预测结果(图 1d)与反向传播神经网络(Back Propagation Neural Network,BPNN)算法(图 1c)相比准确性更高,能够更精准定位常规方法(图 1b)无法识别的弱地震响应气藏。

|
图 1 四川盆地致密砂岩气藏过井地震剖面及不同方法烃类检测[13] (a)远、近偏移距叠加剖面差值;(b)聚类属性分析;(c) BPNN算法;(d) QGSNN算法 |
叠前AVO分析需要大量的预处理工作,如角度数据生成、噪声衰减、AVO属性提取和分析等,非常耗时,而利用深度学习技术可以有效提高效率。Lim等[16]开发了一套基于CNN架构的自动AVO分析算法,可以直接应用于CMP道集数据,无需角道集数据转换,准确识别了Ⅲ类AVO异常。
纵波地震数据的检测结果存在多解性。对于多分量地震数据,可以利用纵波与横波的差异进行烃类检测以减少多解性[11]。Zhang等[10]提出了一种基于深度学习的多分量地震致密砂岩气藏识别方法,相比于仅使用纵波数据,其预测结果与钻井吻合度更高。
监督式深度学习技术依赖于标签数据的数量和质量,当缺乏标签数据时,难以获得精准的烃类检测结果。无监督聚类技术可以从高维地震属性空间自动识别具有相似特征的聚类,为烃类检测提供模式,从而提高烃类检测的准确性和可靠性[11]。例如,Zhang等[11]提出了一种基于无监督学习自组织映射(Self Organizing Maps,SOM)算法的多分量地震数据气藏识别方法,并成功用于致密砂岩气藏弱地震信号的识别。地震相分析是地震储层定性预测的重要方法之一,无监督学习在地震相分析中得到了广泛的应用。张䶮等[17]提出了一种基于SOM和粒子群优化(Particle Swarm Optimization,PSO) 的K均值聚类地震相分析方法,既减小了计算量,又具有全局寻优能力,有效避免了陷入局部极小值,取得了较好的效果。Wang等[18]引入谱聚类技术实现了无监督的地震相分析,将地震数据视为空间中的点与边所构成的图,通过对图进行最优化切割,以实现地震数据聚类。结果表明该方法无需任何假设,就可适应多种形态的地震数据分析,同时计算结果的准确性和运算效率都能够满足应用需求。因此,无监督学习可以从未标记的数据中发现隐藏的模式和特征,在复杂地质条件下提高了效率和模型的预测能力。
2.2 非线性地震反演地震反演是一个非线性问题。基于模型的传统地震反演方法是把非线性问题近似为线性问题,通过多次迭代求取最优解,这容易陷入局部最优解。深度学习可以实现非线性反演。
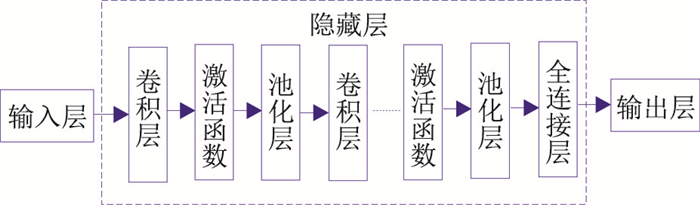
2.2.1 基于监督式学习的地震反演在基于监督式学习的地震反演中,CNN应用最为广泛。CNN是一种前馈网络(图 2),卷积层提取地震数据的有效特征,非线性激活函数用于支撑CNN的复杂性和非线性,在叠后波阻抗反演[7, 19-20]和叠前弹性参数反演[21]等方面均取得了良好的效果。但是,在实际应用中,传统的CNN可能存在难以收敛、训练速度慢的问题,因此出现了一些基于CNN的变体网络结构, 比如残差卷积神经网络(Residual Convolution Neural Network,ResCNN)。与CNN相比,ResCNN增加了跳跃式连接,可以更好地解决深层次网络训练时出现的梯度消失问题,提高了模型的稳定性和泛化能力。
|
图 2 卷积神经网络架构 |
除CNN之外,循环神经网络(Recurrent Neural Network,RNN)也是反演中常用的网络结构,RNN模型包括长短时记忆(Long Short‑Term Memory,LSTM)[22]和门控循环单元(Gate Recurrent Unit,GRU)[23]等。RNN与CNN的区别在于其网络不但与输入、输出存在联系,而且信息可以在回路中循环,是一种可以处理时间序列数据的深度学习模型。因此,与基于CNN的地震反演方法相比,基于RNN的地震反演方法具有以下优势:①可以处理时序数据。传统地震反演方法通常将地震数据作为静态的多维向量,但实际上地震数据是一种动态的时序数据。针对时序信息,RNN可以更好地进行建模和预测。②具有长期记忆功能。RNN存在记忆状态,能够较好地处理长时间跨度的时序信息,并且能够利用这些信息获得更准确的反演结果。而CNN通常只考虑局部信息,无法处理全局的时序关系。③训练效果更稳定。CNN中存在参数共享和梯度消失等,训练过程可能会出现收敛速度慢、容易陷入局部最优解等问题。而RNN具有门控机制,用于解决梯度消失问题,训练效果更加稳定。④更容易扩展到多种输入数据,有效融合地震多属性信息,反演结果的精度和稳定性更高。
监督式深度学习需要大量标签数据集以保证网络的泛化能力,这在实际应用中难以满足。训练样本的不足会导致模型过拟合,是制约深度学习应用的瓶颈。因此,学者们开展了三个方面的研究:①正演模拟。以岩石物理和地质统计为基础,以已有的测井和地质资料为约束,构建多样化的地质模型,合成相应的地震记录,从而扩展标签数据[7]。②迁移学习。虽然合成记录可以扩充训练数据,弥补标签数据不足的缺陷,但训练获得的预测模型不能直接应用于实际地震数据,而使用迁移学习策略,利用少量的测井和地震数据对模型进行更新和优化,可以提高模型的鲁棒性[19]。③数据增强技术。以现有标签数据为约束,采用合理的算法进行数据扩展,生成符合原始样本空间的训练数据,为模型训练提供充足的训练样本。常用的数据增强技术包括灰度系统理论[24]、基于特征提取的方法[25]和虚拟样本生成技术[1]等。其中,虚拟样本生成技术是按照一定的规律挖掘现有数据中的隐藏信息,在数据空间添加新的虚拟样本,从而扩展样本数据,提高预测模型的准确性,在地震反演中取得了较好的效果[1]。
2.2.2 基于无监督或半监督学习的地震反演为了弥补标签数据不足带来的过拟合缺陷,学者们提出了基于无监督或半监督学习的地震反演方法,利用未标记的数据或分别利用标记数据与未标记数据同时训练,从而在标签数据有限的情况下提高反演精度和鲁棒性。常用的算法包括自编码器(Autoencoder,AE)、生成对抗网络(Generative Adversarial Network,GAN)等。
AE网络架构由编码器和解码器组成,编码器可以自适应地对输入数据降维,并提取输入数据中的重要特征;解码器用于将编码器生成的特征向量重构为原始数据的表达形式,通过最小化输入数据与重构数据之间的误差进行学习和训练。因此,AE网络无需特定的输出层,可处理未标记的数据集,并且数据降维可有效地减少模型参数的数量,减少训练所需的数据量,从而提高模型的训练速度和泛化能力。
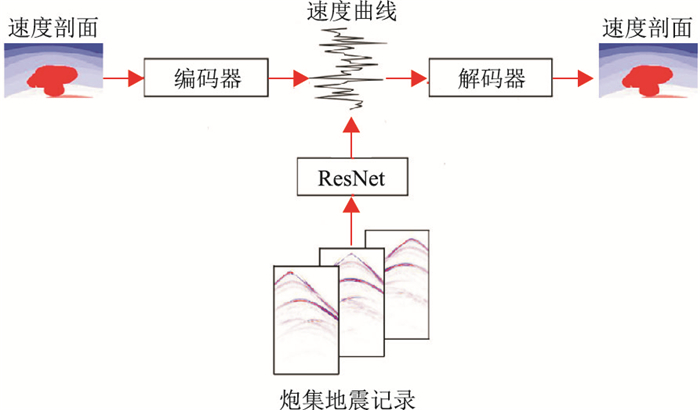
除单一网络架构外,结合CNN与AE的各自优势,可有效提高无监督或半监督地震反演的精度。Yang等[8]利用在CNN中引入自编码器的方法,建立了全卷积神经网络引导的速度建模(Fully Convolutional Neural Network Velocity Model Building,FCNVMB)方法,进行特征提取和降维,提高了速度反演的精度。Liu等[26]结合残差网络与卷积自编码器(Residual Neural Network Convolutional Autoencoder,ResNet-CAE)实现了叠前地震无监督速度反演。该方法首先使用卷积自编码器对地震数据进行特征提取,并将其转换为低维特征空间,然后使用残差网络对特征空间进行处理,从而实现地震速度反演(图 3)。与FCNVMB方法相比,该方法具有更高的反演精度(图 4)。
|
图 3 ResNet-CAE反演算法架构(据文献[26]修改) |

|
图 4 不同地质体速度模型(左)与FCNVMB(中)、ResNet-CAE(右)算法反演结果对比[26] 从上至下模型依次为盐体、地层、断层、盐丘;剖面颜色由深蓝到红,速度逐渐从2000 m/s增加至4500 m/s。 |
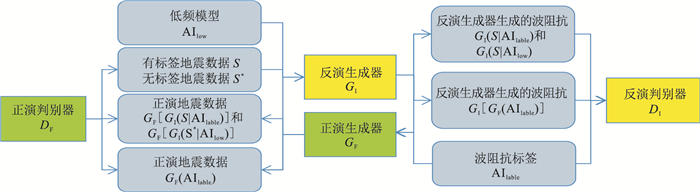
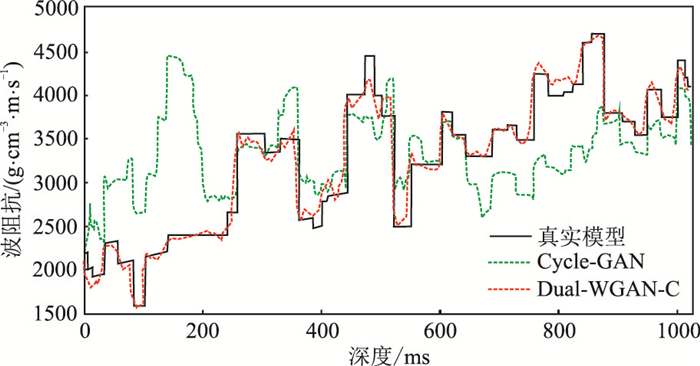
GAN由生成器和判别器组成。其中,生成器用于生成与真实数据相似的合成数据;判别器用于区分真实数据与合成数据。在训练过程中只需使用未标记的真实数据作为训练数据,比较真实数据与合成数据之间的差异进行网络优化,就可以有效避免标签不足而导致的样本不均衡问题。Araya-Polo等[27]将GAN应用于地球物理反演,建立了基于GAN的地球物理反演技术流程。后来,基于GAN算法的一些变体也用于地震反演,如循环生成对抗网络(CycleGAN)[28]、基于Wasserstein距离的Wcycle-GAN (Wasserstein CycleGAN)[29]以及双重Wcycle-GAN(Dual-Wcycle-GAN)[30]等。其中,Dual-Wcycle-GAN网络包含了2个生成网络和2个判别网络(图 5),分别进行地震正演和反演,从而形成由地震数据到目标参数的闭环,并且在网络中引入条件输入模块(Dual-WGAN-C),使少量的有标签数据与大量无标签数据共同训练,通过生成网络与判别网络的相互博弈,构建地震反演预测模型。测试结果(图 6)表明,Dual-Wcycle-GAN网络能够准确地预测地下介质的纵波阻抗信息,同时对于含噪地震数据的反演具有较高的鲁棒性。另一方面,由于GAN具有生成特性,也是一种有效的数据增强技术[31],可以用于合成地震记录[32],从而扩展现有数据集,提高模型的泛化能力。
|
图 5 Dual-Wcycle-GAN网络架构(据文献[30]修改) |
|
图 6 不同方法波阻抗反演结果对比[30] |
大多数基于深度学习的地震反演方法完全由数据驱动。深度学习网络中没有加入地球物理约束,其本质相当于一个黑匣子,无法了解和干预其学习过程,也不确定映射关系是否符合地球物理学的理论基础,导致预测结果不可控,缺乏物理可解释性[23,33]。Raissi等[34]提出了基于物理信息的神经网络结构(Physics-Informed Neural Networks,PINN),结合训练数据和物理方程约束,解决涉及非线性偏微分方程的正、反问题。随后,地球物理学家们在PINN的框架下提出了物理引导与数据驱动相结合的地震反演模型。Vashisth等[35]提出了一种基于PINN的弱监督模型架构,直接由地震道集数据估计孔隙度。在深度学习网络中加入岩石物理模型约束网络训练,不仅可以提高反演结果的可解释性,还可以实现无监督或半监督学习,克服标签数据不足带来的过拟合。因此,基于物理引导的深度学习地震反演方法成为了近年来的热点。
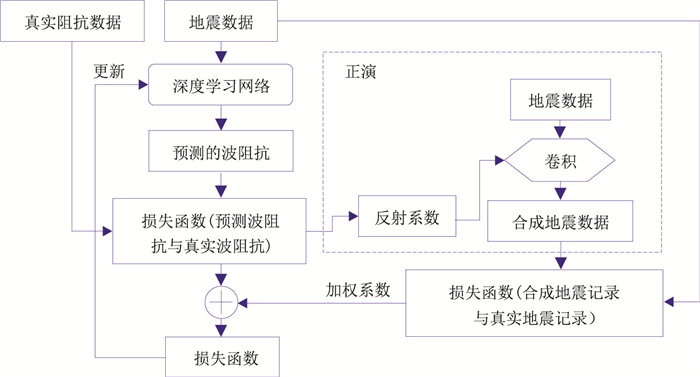
构建基于物理引导的地震反演深度学习网络包含两个方面[23]:①建立包含地球物理理论约束的网络架构, 如图 7所示。②建立具有地球物理约束的损失函数。其中,网络架构类似AE和GAN的思路,它们的区别在于AE中的编码器和GAN中的生成网络都是神经网络模型,需要通过训练去构建;而物理引导网络中是由基于地球物理理论的地震正演取代编码器或生成器[36],将预测结果进行正演以获得合成地震记录,并在损失函数中将合成地震数据与输入的真实地震数据进行比较,然后通过最小化二者之间的差值以实现网络的更新和优化,从而获得更准确的预测结果。
|
图 7 物理引导地震反演深度学习网络架构(据文献[23]修改) |
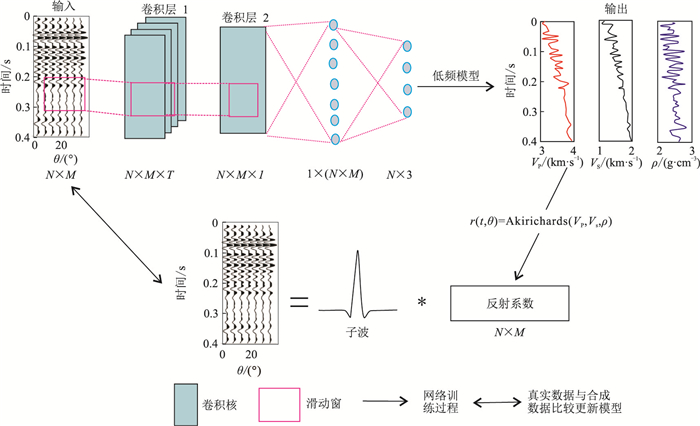
Biswas等[33]利用物理引导的思路实现了地震资料叠后(图 8)和叠前(图 9)无监督反演。网络架构分为两个部分:第一部分由CNN组成,实现由输入的地震数据预测弹性参数,并在模型中加入低频模型作为约束;第二部分为基于褶积模型的地震正演,首先由CNN网络的输出计算反射系数,然后将反射系数与地震子波卷积计算得到合成地震记录,用于与实际地震数据比较,从而更新CNN的模型参数。网络的输入是地震数据、低频模型和地震子波,可以在没有标签数据的情况下实现地震反演。同时,在物理引导网络的输入中加入少量的标签数据,实现半监督学习,可进一步提高预测精度[23]。Zhang等[23]结合物理引导与Cycle-GAN构建了一个用于波阻抗反演的半监督深度学习网络架构(SeisInv-GycleGan)。Cycle-GAN由2个生成器和2个判别器组成,利用褶积模型地震正演代替GAN中用于由波阻抗数据生成地震数据的生成网络,并将损失函数与地球物理理论相结合以约束网络训练。采用5种不同的反演方法对Marmousi模型进行试验和定量评价,结果表明,SeisInv-GycleGan的预测结果在精度方面和符合地球物理规律的程度上都优于其他方法。

|
图 8 基于物理引导的叠后反演CNN网络架构[33] N为地震道采样个数,T为卷积层输出通道个数,r为反射系数,AI为波阻抗,ΔAI为相邻层波阻抗的差值, |
|
图 9 基于物理引导的叠前反演CNN网络架构[33] θ为入射角,M为入射角个数,Vp为纵波速度;Vs为横波速度;ρ为密度,Akirichards为Aki-Rirchards近似式。 |
目前,深度学习技术已用于储层物性参数的预测,并取得了良好的效果[37]。Feng等[38]基于CNN实现了储层孔隙度反演。Zhong等[39]构建了一个基于Cycle-GAN的时移地震反演工作流程,并应用于碳封存CO2迁移的动态监测。李明轩等[40]提出了一种基于数据分布域变换和贝叶斯神经网络的渗透率预测方法,利用贝叶斯神经网络的数据分布特性,在渗透率预测的同时进行了不确定性估计。利用深度学习技术可以有效融合地震多属性数据,充分挖掘地震属性中包含的隐藏信息。Hampson等[41]通过属性优选和多属性变换,优选与反演目标相关性最佳的地震属性组合,建立地震多属性数据与目标数据之间的非线性关系,实现了储层参数的有效预测,提高了预测精度。
上述方法都是基于单任务深度学习完成一种目标预测。如果需要预测的目标类型较多,就会导致多种任务的重复训练,并且忽略了目标之间丰富的关联信息。此时,需要引入多任务学习算法同步反演多个储层参数[42-44]。Song等[6]提出一种基于多任务学习的半监督反演算法,在深度学习网络架构中引入岩石物理正演,利用反演结果生成合成地震数据,通过对比合成地震数据与真实地震数据之间的差异实现网络更新,应用该反演方法利用叠前地震数据同步反演孔隙度、泥质含量和流体饱和度等物性参数,无需进行弹性参数反演以及物性参数换算,避免了经验公式不准确带来的预测误差。在深度学习网络中引入岩石物理模型作为约束,一方面可以减少对标签数据的依赖,避免标签数据不足导致的过拟合问题;另一方面可以为深度学习网络赋予物理意义,提高可解释性。
2.4 不确定性分析深度学习的不确定性分析对于确保模型预测结果的可靠性至关重要。然而,基本的深度学习训练过程通常仅能估计一组模型参数,这意味着对于给定的每个输入观测数据只有一个固定的预测值,而量化输出的不确定性需要得到预测值的方差。为了量化深度学习预测结果的不确定性,国内外学者做了大量的研究[45-48],其基本思想是:在模型训练中加入概率分布,使训练得到的模型参数不是确定的值,而是服从概率分布;通常基于贝叶斯近似的方法,通过学习参数后验概率分布,量化预测参数的不确定性。目前最受欢迎的贝叶斯近似方法主要包括:拉普拉斯近似、变分推断法[45]、蒙特卡洛dropout算法[46]等。
在储层预测领域,应用最多的是蒙特卡洛dropout算法,其利用dropout的正则化技术逼近贝叶斯推理,分析模型参数的后验不确定性。比如,Aleardi等[21]将蒙特卡洛算法引入CNN地震反演模型,获得从叠前地震数据中预测岩石物理参数的不确定性近似值,验证了蒙特卡洛算法用于量化深度学习地震反演模型不确定性的可行性。但通过实验对比认为,蒙特卡洛dropout算法无法获得岩石物理性质小尺度的变化,明显低估了对岩石物理预测的不确定性,预测精度较低[37]。生成对抗网络也可以用于不确定性分析。Feng等[47]通过改变潜在的输入向量,利用生成对抗网络获得预测数据集的分布,从而进行不确定性分析。与蒙特卡洛算法相比,生成对抗网络可以纳入岩石物理模型约束,将马尔可夫链―蒙特卡洛算法引入生成对抗网络进行不确定性分析,进一步提高了确定性分析的精度[28]。Zou等[48]提出了一种基于随机森林的多地震属性预测孔隙度分布的不确定性量化方法,同时利用量化的不确定性优化和校正预测模型, 提高了孔隙度预测的精度。
3 实际应用中面临的挑战尽管深度学习技术在定性和定量储层预测中都取得了较好的效果,但仍面临诸多挑战,主要体现在数据可用性和深度学习技术的局限性两个方面。
3.1 数据可用性在实际应用中,深度学习的模型非常依赖数据,面临主要问题为:
(1) 缺乏足够的标签数据。虽然地震数据量很大,但可用的标签数据却非常有限。一方面,目前标签数据的获取仍然以手工为主,非常耗时且成本昂贵,而且能够公开访问的带有标签的地震数据集非常少;另一方面,对于储层定量预测而言,训练标签为测井数据,成本高昂。尤其海上工区,通常仅有几口井或者没有钻井资料,因此测井数据无法满足深度学习模型训练对数据量的需求。
(2) 样本数据不均衡。针对储层定性预测,非储层的样本数量可能远大于储层的样本数量,这导致模型在预测中偏向占多数的类别,而对于少数类别的预测性能较差。
(3) 数据质量的影响。地震数据在采集和处理过程中可能受到各种因素的影响,如噪声、干扰、缺失和不完整性等,导致深度学习获得不准确或误导性的模型。因此,在使用深度学习技术进行地震储层预测时,需要对数据进行严格的质量控制,包括噪声压制、异常值检测、数据插值和校正等,以确保数据的准确性和可靠性。
(4) 数据的不确定性。主要体现在地震数据解释结果的不确定性。解释结果通常是主观的,可能存在误差或错误。利用错误的地震解释结果进行模型训练,不可避免地导致模型的不确定性。另外,地震数据是时间域数据,测井数据为深度域数据,时深关系的不准确会导致数据的拉伸或压缩,影响数据的准确性[49]。
针对数据的可用性问题,许多学者提出了解决方案,主要包括合成地震记录、数据增强技术和深度学习算法优化等。迁移学习[16]、半监督算法[2]以及引入物理约束的深度学习方法[33]等都在一定程度上缓解了数据压力,提高了模型的泛化能力。为了解决时深关系不准确会带来的数据不确定性问题,Song等[49]提出了一种基于动态时间规整的闭环CNN算法,有效提高了反演精度和空间连续性。虽然在解决数据可用性方面已取得了一定的进展或成效,但该问题仍然是目前深度学习技术全面应用于地震储层预测领域所面临的最大挑战。
3.2 深度学习技术的局限性(1) 高计算成本。与浅层机器学习算法相比,深度学习需要更大量的计算资源和更长的计算时间,尤其针对三维地震数据,还需要更多存储资源。如果计算机配置有限,在训练过程中经常会出现系统崩溃的情况。
为了降低计算量,通常采用一阶优化算法,但一阶优化算法的训练效率较低,容易陷入局部极小值而无法寻找全局最优解。而且,当深度学习网络反向传播时,信号经过多层传播后可能会产生梯度消失或梯度爆炸的问题,从而导致训练不稳定。采用更先进的算法可以在一定程度上提高优化能力,但同时也会带来更大的计算量。在实际应用中,需要综合考虑目标的复杂性、数据规模和计算资源,以平衡优化算法和计算量。
(2) 地震数据的复杂性和高维性。地震多属性数据的复杂性和高维性给深度学习模型训练带来了挑战。虽然深度学习强大的特征学习能力使其在处理高维数据中具有明显的优势,但高维数据往往是稀疏的。对于地震数据而言,每个维度对应不同的地震属性或特征,由于地质结构的复杂性,很多特征可能缺失或冗余,影响模型的训练和预测能力。
针对地震数据的复杂性和高维性,通常采取属性优选与融合、稀疏表征[18]等技术以减少特征的维度并提高模型的泛化能力。常用的属性优选方法包括逐步回归法[41]、遗传算法、主成分分析等。另一方面,选择适当的网络架构、损失函数和优化算法,可以提取地震数据中的有用特征,减少冗余和噪声的影响。
(3) 缺乏物理可解释性。深度学习模型通常以“黑匣子”的形式呈现,在训练过程中无法进行人工干预,缺乏对结果的物理解释[33]。地质学家无法了解结果是如何预测的,也无法得知预测结果是否符合地球物理规律、能否与地质解释相结合等,这会造成地质学家对深度学习结果的不信任。
(4) 不确定性评价。一是在定性预测模型的评价标准方面,目前没有明确的标准评估预测模型的准确性和通用性;二是在不确定性的量化方面,需要更为精细的量化算法以提高不确定性分析的精度。
4 结论与展望与传统方法相比,深度学习技术应用于地震储层预测的优势在于:可以通过大数据的训练,无限逼近地震数据与储层物性参数之间的非线性关系,从而提高预测精度,且模型训练成功后,可大幅提高工作效率。但在实际应用中,仍面临数据可用性不高、计算成本高、物理可解释性差等挑战。未来的研究应致力于解决当前深度学习技术在地震储层预测中面临的挑战,以发挥更重要的作用。
(1) 数据增强技术。综合考虑数据多样性和一致性的平衡、生成数据的质量以及计算成本和工作效率等方面,改进数据生成算法,推动数据增强技术的发展和应用。在数据增强技术中引入物理引导,使数据更符合地球物理特征。
(2) 多源数据融合和跨尺度建模。将地震数据与其他地质数据(如测井数据、地质等)进行融合,利用多源数据的互补提高储层预测的精度。同时,应考虑多尺度建模,从局部到全局,跨尺度进行储层预测。
(3) 深度学习和知识图谱相结合。构建地球物理知识图谱,融合、共享地质、地球物理和测井等多源数据、知识,将深度学习模型和知识图谱相结合,扩充训练数据,增强原始数据的语义信息以及模型的可解释性。
(4) 数据驱动与物理驱动的融合。将数据驱动的深度学习方法与传统物理驱动的方法相结合,充分利用各自的优势,缓解数据压力,提高模型的泛化能力,增强预测结果的物理解释性。
(5) 深度学习的可视化。在基于深度学习的地震储层预测中实现可视化,有助于地质学家有效掌握模型的结构和计算过程,更好地指导储层预测结果的可解释性和不确定性评价,提高决策制定的准确性和效率。
(6) 模型优化和自适应学习。改进深度学习模型的架构和训练算法,探索更有效的模型优化算法、自适应学习策略和损失函数的设计,提高模型的泛化能力和鲁棒性,节省计算成本。
(7) 深度学习与其他机器学习技术相结合。将深度学习与其他机器学习相结合,比如支持向量机、随机森林、主动学习和反馈强化学习等,充分利用不同机器学习技术的优势,取长补短,提高模型的性能、鲁棒性和泛化能力。
综上所述,在地震储层预测领域,深度学习技术的应用得到迅速发展,未来可通过更多的跨学科合作,通过不断地研究和创新,为油气资源勘探与开发提供更准确、可靠的技术支持。
| [1] |
SANG K H, YIN X Y, ZHANG F C. Machine learning seismic reservoir prediction method based on virtual sample generation[J]. Petroleum Science, 2021, 18(6): 1662-1674. DOI:10.1016/j.petsci.2021.09.034 |
| [2] |
LIU X, SHAO G, YUAN C, et al. Mixture of relevance vector regression experts for reservoir properties prediction[J]. Journal of Petroleum Science and Engineering, 2022, 214: 110498. DOI:10.1016/j.petrol.2022.110498 |
| [3] |
SONG L, YIN X, ZONG Z, et al. Semi-supervised learning seismic inversion based on Spatio-temporal sequence residual modeling neural network[J]. Journal of Petroleum Science and Engineering, 2022, 208, Part D: 109549.
|
| [4] |
YU S, MA J. Deep learning for geophysics: current and future trends[J]. Reviews of Geophysics, 2021, 59(3): e2021RG000742. DOI:10.1029/2021RG000742 |
| [5] |
刘力辉, 陆蓉, 杨文魁. 基于深度学习的地震岩相反演方法[J]. 石油物探, 2019, 58(1): 123-129. LIU Lihui, LU Rong, YANG Wenkui. Seismic lithofacies inversion based on deep learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 123-129. DOI:10.3969/j.issn.1000-1441.2019.01.014 |
| [6] |
SONG L, YIN X, ZONG Z, et al. Two-stage semi-supervised learning inversion for reservoir physical parameters[J]. Journal of Petroleum Science and Engineering, 2022, 216: 110794. DOI:10.1016/j.petrol.2022.110794 |
| [7] |
DAS V, POLLACK A, WOLLNER U, et al. Convolutional neural network for seismic impedance inversion[J]. Geophysics, 2019, 84(6): R869-R880. DOI:10.1190/geo2018-0838.1 |
| [8] |
YANG F, MA J. Deep-learning inversion: a next-generation seismic velocity model building method[J]. Geophysics, 2019, 84(4): R583-R599. DOI:10.1190/geo2018-0249.1 |
| [9] |
XUE Y J, WANG X J, CAO J X, et al. Hydrocarbon detections using multi‑attributes based quantum neural networks in a tight sandstone gas reservoir in the Sichuan Basin, China[J]. Artificial Intelligence in Geosciences, 2021, 2: 107-114. DOI:10.1016/j.aiig.2022.02.004 |
| [10] |
ZHANG K, LIN N T, YANG J Q, et al. Predicting gas-bearing distribution using DNN based on multi-component seismic data: quality evaluation using structural and fracture factors[J]. Petroleum Science, 2022, 19(4): 1566-1581. DOI:10.1016/j.petsci.2022.02.008 |
| [11] |
ZHANG K, LIN N, TIAN G, et al. Unsupervised-learning based self‑organizing neural network using multi‑component seismic data: Application to Xujiahe tight-sand gas reservoir in China[J]. Journal of Petroleum Science and Engineering, 2022, 209: 109964. DOI:10.1016/j.petrol.2021.109964 |
| [12] |
林年添, 张栋, 张凯, 等. 地震油气储层的小样本卷积神经网络学习与预测[J]. 地球物理学报, 2018, 61(10): 4110-4125. LIN Niantian, ZHANG Dong, ZHANG Kai, et al. Predicting distribution of hydrocarbon reservoirs with seismic data based on learning of the small-sample convolution neural network[J]. Chinese Journal of Geophysics, 2018, 61(10): 4110-4125. DOI:10.6038/cjg2018J0775 |
| [13] |
王迪, 张益明, 张繁昌, 等. 利用先验信息约束的深度学习方法定量预测致密砂岩"甜点"[J]. 石油地球物理勘探, 2023, 58(1): 65-74. WANG Di, ZHANG Yiming, ZHANG Fanchang, et al. Quantitative prediction of tight sandstone sweet spots based on deep learning method with prior information constraints[J]. Oil Geophysical Prospecting, 2023, 58(1): 65-74. |
| [14] |
GAO J, SONG Z, GUI J, et al. Gas-bearing prediction using transfer learning and CNNs: an application to a deep tight dolomite reservoir[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [15] |
JÚNIOR D A D, BATISTA DA CRUZ L, OTÁVIO BANDEIRA DINIZ J, et al. Detection of potential gas accumulations in 2D seismic images using spatio-temporal, PSO, and convolutional LSTM approaches[J]. Expert Systems With Applications, 2023, 215: 119337. DOI:10.1016/j.eswa.2022.119337 |
| [16] |
LIM B, YU H, YOON D, et al. Machine learning derived AVO analysis on marine 3D seismic data over gas reservoirs near South Korea[J]. Journal of Petroleum Science and Engineering, 2021, 197: 108105. DOI:10.1016/j.petrol.2020.108105 |
| [17] |
张䶮, 郑晓东, 李劲松, 等. 基于SOM和PSO的非监督地震相分析技术[J]. 地球物理学报, 2015, 58(9): 3412-3423. ZHANG Yan, ZHENG Xiaodong, LI Jinsong, et al. Unsupervised seismic facies analysis technology based on SOM and PSO[J]. Chinese Journal of Geophysics, 2015, 58(9): 3412-3423. |
| [18] |
WANG Y J, WANG L J, LI K H, et al. Unsupervised seismic facies analysis using sparse representation spectral clustering[J]. Applied Geophysics, 2020, 17(4): 533-543. DOI:10.1007/s11770-020-0839-1 |
| [19] |
LIU S, NI W, FANG W, et al. Absolute acoustic impedance inversion using convolutional neural networks with transfer learning[J]. Geophysics, 2023, 88(2): R163-R174. DOI:10.1190/geo2022-0045.1 |
| [20] |
王泽峰, 李勇根, 许辉群, 等. 基于深度学习的三种地震波阻抗反演方法比较[J]. 石油地球物理勘探, 2022, 57(6): 1296-1303. WANG Zefeng, LI Yonggen, XU Huiqun, et al. Comparative analysis of three seismic impedance inversion methods based on deep learning[J]. Oil Geophysical Prospecting, 2022, 57(6): 1296-1303. |
| [21] |
ALEARDI M, SALUSTI A. Elastic pre-stack inversion through discrete cosine transform reparamete-rization and convolutional neural networks[J]. Geophysics, 2020, 86(1): R129-R146. |
| [22] |
WEI C, GUO X B, TIAN F, et al. Seismic velocity inversion based on CNN-LSTM fusion deep neural network[J]. Applied Geophysics, 2021, 18(4): 499-514. DOI:10.1007/s11770-021-0913-3 |
| [23] |
ZHANG H, ZHANG G, GAO J, et al. Seismic impedance inversion based on geophysical-guided cycle-consistent generative adversarial networks[J]. Journal of Petroleum Science and Engineering, 2022, 218: 111003. DOI:10.1016/j.petrol.2022.111003 |
| [24] |
HONGFA K, YONGGUANG C, YI L. Data processing of small samples based on grey distance information approach[J]. Journal of Systems Engineering and Electronics, 2007, 18(2): 281-289. DOI:10.1016/S1004-4132(07)60088-7 |
| [25] |
ZHANG X, YU L, YIN H, et al. Integrating data augmentation and hybrid feature selection for small sample credit risk assessment with high dimensionality[J]. Computers & Operations Research, 2022, 146: 105937. |
| [26] |
LIU G, ZHANG L, WANG Q, et al. Data-driven seismic prestack velocity inversion via combining residual network with convolutional autoencoder[J]. Journal of Applied Geophysics, 2022, 207: 104846. DOI:10.1016/j.jappgeo.2022.104846 |
| [27] |
ARAYA-POLO M, FARRIS S, FLOREZ M. Deep learning‑driven velocity model building workflow[J]. The Leading Edge, 2019, 38(11): 872a1-872a9. DOI:10.1190/tle38110872a1.1 |
| [28] |
WANG Y Q, WANG Q, LU W K, et al. Seismic impedance inversion based on cycle-consistent generative adversarial network[J]. Petroleum Science, 2022, 19(1): 147-161. DOI:10.1016/j.petsci.2021.09.038 |
| [29] |
XIE P, HOU J, YIN Y, et al. Seismic inverse modeling method based on generative adversarial networks[J]. Journal of Petroleum Science and Engineering, 2022, 215, Part B: 110652.
|
| [30] |
WANG Z, WANG S, ZHOU C, et al. Dual wasserstein generative adversarial network condition: a generative adversarial network‑based acoustic impedance inversion method[J]. Geophysics, 2022, 87(6): R401-R411. DOI:10.1190/geo2021-0600.1 |
| [31] |
WANG P, SI F, FAN W, et al. Data enhancement for data‑driven modeling in power plants based on a conditional variational‑adversarial generative network[J]. Industrial & Engineering Chemistry Research, 2021, 60(24): 8829-8843. |
| [32] |
冯永基, 陈学华. 融合部分卷积和注意力机制对抗网络模型的地震数据重建[J]. 石油地球物理勘探, 2023, 58(1): 21-30. FENG Yongji, CHEN Xuehua. Seismic data reconstruction based on partial convolution and attentional mechanism adversarial network model[J]. Oil Geophysical Prospecting, 2023, 58(1): 21-30. |
| [33] |
BISWAS R, SEN M K, DAS V, et al. Prestack and poststack inversion using a physics‑guided convolutional neural network[J]. Interpretation, 2019, 7(3): SE161-SE174. DOI:10.1190/INT-2018-0236.1 |
| [34] |
RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707. DOI:10.1016/j.jcp.2018.10.045 |
| [35] |
VASHISTH D, MUKERJI T. Direct estimation of porosity from seismic data using rock‑and wave‑phy-sics‑informed neural networks[J]. The Leading Edge, 2022, 41(12): 840-846. DOI:10.1190/tle41120840.1 |
| [36] |
段友祥, 崔乐乐, 孙歧峰, 等. 波动方程正演引导的深度学习地震波形反演[J]. 石油地球物理勘探, 2023, 58(3): 485-494. DUAN Youxiang, CUI Lele, SUN Qifeng, et al. Deep learning seismic waveform inversion based on the forward modeling guidance of wave equation[J]. Oil Geophysical Prospecting, 2023, 58(3): 485-494. |
| [37] |
DAS V, MUKERJI T. Petrophysical properties prediction from prestack seismic data using convolutional neural networks[J]. Geophysics, 2020, 85(5): N41‑N55.
|
| [38] |
FENG R. Estimation of reservoir porosity based on seismic inversion results using deep learning methods[J]. Journal of Natural Gas Science and Engineering, 2020, 77: 103270. DOI:10.1016/j.jngse.2020.103270 |
| [39] |
ZHONG Z, SUN A Y, WU X. Inversion of time‐lapse seismic reservoir monitoring data using cyclegan: a deep learning‐based approach for estimating dynamic reservoir property changes[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(3): e2019JB018408. DOI:10.1029/2019JB018408 |
| [40] |
李明轩, 韩宏伟, 刘浩杰, 等. 基于数据分布域变换与贝叶斯神经网络的渗透率预测及不确定性估计[J]. 地球物理学报, 2023, 66(4): 1664-1680. LI Mingxuan, HAN Hongwei, LIU Haojie, et al. Permeability prediction and uncertainty quantification base on Bayesian neural network and data distribution domain transformation[J]. Chinese Journal of Geophysics, 2023, 66(4): 1664-1680. |
| [41] |
HAMPSON D P, SCHUELKE J S, QUIREIN J A. Use of multiattribute transforms to predict log properties from seismic data[J]. Geophysics, 2001, 66(1): 220-236. DOI:10.1190/1.1444899 |
| [42] |
孙永壮, 黄鋆. 多任务深度学习技术在储层横波速度预测中的应用[J]. 地球物理学进展, 2021, 36(2): 799-809. SUN Yongzhuang, HUANG Yun. Application of multi-task deep learning in reservoir shear wave prediction[J]. Progress in Geophysics, 2021, 36(2): 799-809. |
| [43] |
李铎, 杨森林, 任玉晓, 等. 基于多任务学习的地震弹性波数据多参数反演[C]∥2020年中国地球科学联合学术年会论文集, 重庆, 2020, 80-83. LI Duo, YANG Senlin, REN Yuxiao, et al. Multi parameter inversion of seismic elastic wave data based on multi task learning[C]∥Proceedings of the 2020 China Earth Science Joint Academic Annual Conference, Chongqing, 2020, 80-83. |
| [44] |
LI D, PENG S, GUO Y, et al. Progressive multitask learning for high-resolution prediction of reservoir elastic parameters[J]. Geophysics, 2023, 88(2): M71‑M86.
|
| [45] |
FENG R, GRANA D, BALLING N. Uncertainty quantification in fault detection using convolutional neural networks[J]. Geophysics, 2021, 86(3): M41‑M48.
|
| [46] |
GAL Y, GHAHRAMANI Z. Dropout as a Bayesian approximation: representing model uncertainty in deep learning[C]∥Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 2016, 1050-1059.
|
| [47] |
FENG R. Physics‑informed deep learning for rock physical inversion and its uncertainty analysis[J]. Geoenergy Science and Engineering, 2023, 230: 212229. DOI:10.1016/j.geoen.2023.212229 |
| [48] |
ZOU C, ZHAO L, XU M, et al. Porosity prediction with uncertainty quantification from multiple seismic attributes using Random Forest[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(7): e2021JB021826. |
| [49] |
SONG C, LU M, WANG Y, et al. New networks findings from Tsinghua University outlined(a dynamic time warping loss-based closed-loop CNN for seismic impedance inversion)[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5925313. |



 山东省青岛市即墨区观山路596号青岛海洋地质研究所,266237。Email:
山东省青岛市即墨区观山路596号青岛海洋地质研究所,266237。Email: