2. 中国冶金地质总局青岛地质勘查院, 山东青岛 266109;
3. 广州海洋地质调查局, 广东广州 511458
2. Qingdao Geological Exploration Institute of Metallurgical Geology of China, Qingdao, Shandong 266109, China;
3. Guangzhou Marine Geological Survey, Guangzhou, Guangdong 511458, China
重力勘探已广泛应用于区域地质调查、矿产和油气勘探[1-2]。重力梯度是一种高精度的勘探数据,与重力异常相比,包含更多高频信息[3],能够更好地表征场源体的细节。通过重力梯度数据反演可以获得地下空间的密度分布,为找矿提供依据。Pilkington[4-5]发现,在不同重力梯度分量的单独反演中,垂直重力梯度数据反演能够提供最佳结果。但是,随着勘探深度增加,由于异常信号衰减、多解性等原因,基于单一数据的反演结果的空间分辨率有待提升。联合多个观测面的重力场可充分利用不同尺度数据包含的信息,有望解决这一问题。
目前,许多学者利用航空—地面—井中(空—地—井)数据开展了联合反演研究。Li等[6]联合地表磁测数据和钻孔三分量数据实现了磁化率成像,其结果优于仅通过地表数据的反演结果。张大莲等[7]联合地面和井中磁测资料进行反演,证实了井—地联合反演具有可行性,为解决危机矿山深部找矿问题提供了技术手段。Geng等[8]在基于重力梯度数据的协克里金法反演中加入井中重力数据,其结果更优。王泰涵等[9]定性、定量地评价了不同飞行高度的航空数据和不同位置的钻孔数据对反演效果的影响。高秀鹤等[10]通过联合不同高度的重力测量数据以及井中密度数据进行反演,提高了反演分辨率。Peng等[11]针对地下异常体与其围岩存在尖锐边界的情况,使用零阶最小熵正则化方法并引入地表和钻孔重力数据改善了反演结果。
加入物性约束可以进一步降低联合反演的多解性。模糊C均值(Fuzzy C-Means, FCM)聚类算法可以将物性约束引入反演,并通过计算聚类中心和隶属度迭代更新密度模型。杨培杰等[12]提出了一种地震属性的聚类方法,并应用到油田地震数据解译,实现了多属性聚类分析。Sun等[13]将FCM聚类算法与经典的Tikhonov正则化反演方法相结合,开发了一种多域聚类的地表和钻孔重力数据联合反演方法。Maag等[14]提出了基于地表和钻孔重力数据的引导FCM聚类技术的离散反演方法,与光滑反演相比,能够获得更准确的密度模型。徐凯军等[15]针对磁异常三维反演计算量大、多解性等问题,开展了基于FCM聚类约束的井—地磁异常联合反演,试验表明引入FCM聚类约束后的结果更接近真实值。易柯等[16]在最小结构模型正则化约束的基础上,在电阻率和介电常数联合反演中引入FCM聚类约束,取得了良好的反演效果。
为此,本文开展基于FCM聚类的联合反演方法研究,在正则化反演中引入FCM聚类约束,开展空—地—井垂直重力梯度数据联合反演,以获得更高分辨率的密度模型。
1 空—地—井垂直重力梯度数据反演方法航空、地面和井中观测的重力数据包含了不同的信息,与地面数据相比,航空数据包含更多的低频信息,而井中观测数据既包括密度异常,还包括地下空间的其他物性信息。因此,空—地—井数据联合反演充分利用了不同数据中包含的信息,能够提升地下密度成像的分辨率。
1.1 正演问题在笛卡尔坐标系中,设地表z=0,将研究区域中的地下空间划分为一系列均匀的小长方体。设观测异常是由这些长方体引起的,则垂直重力梯度Vzz的正演公式为
| $ {V}_{zz}=\gamma \rho \sum\limits_{i=1}^{2}\sum\limits_{j=1}^{2}\sum\limits_{k=1}^{2}{\mu }_{ijk}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{{x}_{i}{y}_{j}}{{z}_{k}{r}_{ijk}} $ | (1) |
| $ \left\{\begin{array}{l}{x}_{i}=x-{\xi }_{i}\\ {y}_{j}=y-{\eta }_{j}\\ {z}_{k}=z-{\zeta }_{k}\end{array}\right. $ | (2) |
| $ {r}_{ijk}=\sqrt{{x}_{i}^{2}+{y}_{j}^{2}+{z}_{k}^{2}} $ | (3) |
| $ {\mu }_{ijk}={(-1)}^{i+j+k} $ | (4) |
式中:(x, y, z)表示测点坐标;(ξi, ηj, ζk)表示长方体的对顶点坐标(即长方体对角线上的一组坐标,可表示长方体分布范围);ρ表示剩余密度;γ表示万有引力常数。
1.2 反演问题 1.2.1 FCM聚类FCM聚类算法是一种机器学习算法,通过计算聚类中心和每个样本对所有聚类中心的隶属度,达到分类的目的。根据Sun等[17]的研究,改进后的FCM聚类算法的目标函数为
| $ \begin{array}{l}{\varPhi }_{\mathrm{F}\mathrm{C}\mathrm{M}}=\sum\limits_{j=1}^{N}\sum\limits_{k=1}^{C}{u}_{jk}^{q}\Vert {m}_{j}-{v}_{k}{\Vert }_{2}^{2}+\\ {\sum\limits_{k=1}^{C}{\eta }_{k}\Vert {v}_{k}-{t}_{k}\Vert }_{2}^{2}\end{array} $ | (5) |
其中
| $ \left\{\begin{array}{l}{u}_{jk}=\frac{\Vert {m}_{j}-{v}_{i}{\Vert }_{2}^{-\frac{2}{q-1}}}{\sum\limits_{i=1}^{C}\Vert {m}_{j}-{v}_{i}{\Vert }^{}{}_{2}^{-\frac{2}{q-1}}}\\ \sum\limits_{k=1}^{C}{u}_{jk}=10\le {u}_{jk}\le 1\end{array}\right. $ | (6) |
| $ {v}_{k}=\frac{\sum\limits_{j=1}^{N}{u}_{jk}^{q}{m}_{j}+{\eta }_{k}{t}_{k}}{\sum\limits_{j=1}^{N}{u}_{j}^{q}+{\eta }_{k}} $ | (7) |
式中:N表示模型参数的总个数;C表示聚类中心数,本文使用光滑反演提供初始模型,结合地质先验信息或其他方法确定地下空间中剩余密度数值的种类数,即聚类中心数C;mj表示第j个待聚类的样本,即剩余密度;vk表示第k个聚类中心值;tk表示先验聚类中心,表示vk的先验值;ujk表示mj对vk的隶属度;q表示模糊因子,本文中q取值范围为[2, 3];ηk用于评价tk的准确度。
在使用FCM聚类方法时,需初始化聚类中心vk和隶属度ujk,它们的初始值会影响反演的速度和效果。此外,光滑反演结果的边界不清晰,但中心位置是准确的。鉴于此特点,本文使用基于预条件共轭梯度法的光滑反演[18]初始化vk和ujk,即:使用光滑反演求解初始密度模型的同时,随机给定ujk或vk的初始值(本文随机给定vk),再基于初始模型、利用式(6)和式(7)计算vk和ujk,作为反演的初始聚类中心和隶属度。
1.2.2 基于FCM聚类的空—地—井数据联合反演目前,大多数三维反演是基于Tikhonov正则化理论[19]开展的。其中,重加权聚焦反演是一种常用的、能获得锐利目标体边界的方法,其目标函数Φ(m)定义为
| $ \begin{array}{l}\varPhi \left(\boldsymbol{m}\right)={\varPhi }_{\mathrm{d}}+\lambda {\varPhi }_{m}\\ =\left|\right|\boldsymbol{G}\boldsymbol{m}-\boldsymbol{d}|{|}_{2}^{2}+\lambda |\left|\boldsymbol{W}\right(\boldsymbol{m}-{\boldsymbol{m}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\left)\right|{|}_{2}^{2}\end{array} $ | (8) |
| $ \boldsymbol{W}={\left(\sum\limits_{i=1}^{N}{{{G}^{2}}_{i}}_{j}\right)}^{-\frac{1}{2}} $ | (9) |
式中:λ表示正则化因子;Φd表示数据不拟合函数;
| $ \left[\begin{array}{c}\boldsymbol{G}\widehat{\boldsymbol{W}}\left(\boldsymbol{m}\right)\\ \sqrt{\lambda }\boldsymbol{I}\end{array}\right]{\boldsymbol{m}}_{w}=\left[\begin{array}{c}\boldsymbol{d}\\ 0\end{array}\right] $ | (10) |
| $ {\widehat{W}}^{2}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\boldsymbol{m}}^{2}+{\beta }^{2}\boldsymbol{I}\right){\boldsymbol{W}}_{m}^{-2} $ | (11) |
式中:I表示单位矩阵;β是一个很小的正数,用于避免产生奇异值;Wm表示加权矩阵,迭代中采用重加权的方式进行计算。令
| $ \left\{\begin{array}{l}{\boldsymbol{m}}_{w}={\boldsymbol{W}}^{-1}\left(\boldsymbol{m}\right)\boldsymbol{m}\\ {\boldsymbol{G}}_{w}=\boldsymbol{G}\widehat{\boldsymbol{W}}\left(\boldsymbol{m}\right)\end{array}\right. $ | (12) |
同时,令第r次迭代中的正则化因子λr为
| $ {\lambda }_{r}=\left\{\begin{array}{c}0\begin{array}{ccc}& & \end{array}r=1\\ {\varPhi }_{d}/{\varPhi }_{m}r=2\\ {\lambda }_{r-1}/2\begin{array}{cc}& \end{array}r > 2\end{array}\right. $ | (13) |
在聚焦反演的迭代过程中,利用聚类算法将地下空间中长方体的密度值划分为不同的类。通过聚类引入物性的先验信息,使密度值归于若干个聚类中心,从而得到更高分辨率的密度模型。因此,使用下式引入约束并对mj进行更新
| $ {m}_{j}={v}_{k}{u}_{jk} $ | (14) |
由于空—地—井数据的联合,式(10)转换为
| $ \left[\begin{array}{c}\boldsymbol{G}\widehat{\boldsymbol{W}}{\left(\boldsymbol{m}\right)}_{\mathrm{空}}\\ \boldsymbol{G}\widehat{\boldsymbol{W}}{\left(\boldsymbol{m}\right)}_{\mathrm{地}}\\ \boldsymbol{G}\widehat{\boldsymbol{W}}{\left(\boldsymbol{m}\right)}_{\mathrm{井}}\\ \sqrt{\lambda }\boldsymbol{I}\end{array}\right]{\boldsymbol{m}}_{w}=\left[\begin{array}{c}{\boldsymbol{d}}_{\mathrm{空}}\\ {\boldsymbol{d}}_{\mathrm{地}}\\ {\boldsymbol{d}}_{\mathrm{井}}\\ 0\end{array}\right] $ | (15) |
式中下标空、地、井分别表示航空、地面和井中观测方式。
基于FCM聚类的空—地—井数据联合反演具体流程如下:
(1) 利用光滑反演建立初始模型;
(2) 根据式(6)和式(7)计算ujk和vk,设定q、C和tk,初始化λ;
(3) 利用聚焦反演计算剩余密度mj;
(4) 更新聚类中心vk和隶属度ujk;
(5) 根据式(14)更新mj;
(6) 判断是否停止迭代:如果观测数据与预测数据的均方根误差RMSE小于预设的阈值ε,停止迭代并退出;否则,返回步骤(2),直到满足迭代停止条件。
1.3 基于GPU的并行反演算法三维反演时,对地下空间剖分得越精细,灵敏度矩阵的规模越大,导致反演计算量增加,运算速度降低。根据本文方法,由式(15)可知,数据联合会进一步增加矩阵规模。因此,为了在网格规模增加的同时保障计算效率,需要对反演进行并行化加速。基于GPU的并行计算技术适用于数据并行模型与算法,广泛应用于位场数据反演的并行化。陈召曦等[21]提出了基于GPU的重力、重力梯度三维快速正演计算方法。Hou等[22]针对大规模数据的反演计算问题,提出一种基于GPU的非线性重力全张量梯度数据并行反演方法。这些研究均取得了良好的加速效果。在基于GPU的并行计算方法中,MATLAB中的Parallel Computing Toolbox提供了一种简洁方法,具有更改代码少、易于维护等优点。本文采用该方法实现反演加速,其运行时间主要消耗在计算矩阵G及与之相关的计算上。因此,可将矩阵运算转换为向量运算,以便能在GPU上进行并行化;为了提高速度,使用Single函数将数据转为单精度,再通过gpuArray函数将数据传到GPU进行计算并计时。
2 数据试验设计两组理论模型,并选择美国文顿盐丘地区实测数据开展试验,以检验本文方法的有效性和可行性。
2.1 理论模型数据试验在笛卡尔坐标系中建立理论模型,垂直向下为z轴正方向。研究区域沿x和y方向范围均为-1000~1000 m,最大深度为1000 m。将地下空间均匀剖分为20×20×20个体积为100 m×100 m×50 m的长方体。航空重力场的观测面为z=-50 m,地面重力场的观测面为地面,即z=0。共观测20×20个测点,测点均匀分布于观测面,点距和线距均为100 m。井中重力场观测沿井孔进行,点距为50 m,共20个测点。为了验证方法的抗噪性,在航空、地面和井中重力数据中均加入5%的高斯噪声。
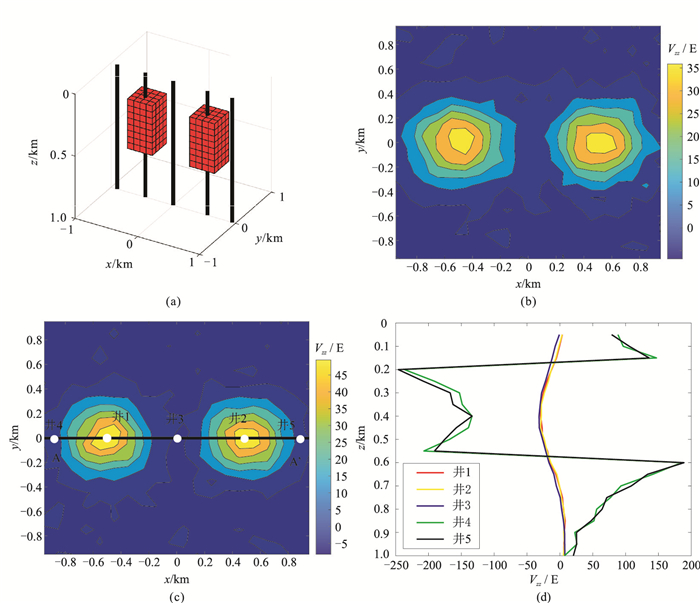
2.1.1 双长方体模型试验首先,设地下空间存在两个完全相同的长方体,体积均为400 m×400 m×400 m,剩余密度为0.5 g/cm3,两个长方体在x方向的分布范围分别为[-700 m,-300 m]和[300 m, 700 m],y方向上的分布范围均为[-200 m,200 m],z方向上的分布范围均为[200 m,600 m]。长方体与井的位置见图 1a,该模型的航空、地面和井中垂直重力梯度观测数据见图 1b~图 1d。
|
图 1 双长方体模型示意图及垂直重力梯度观测数据 (a)模型及井位置;(b)航空观测数据;(c)地面观测数据;(d)井中观测数据。图a中的黑色竖线表示井的位置;图c中AA’表示剖面位置,白色圆点表示井在地面的位置。图 4同。 |
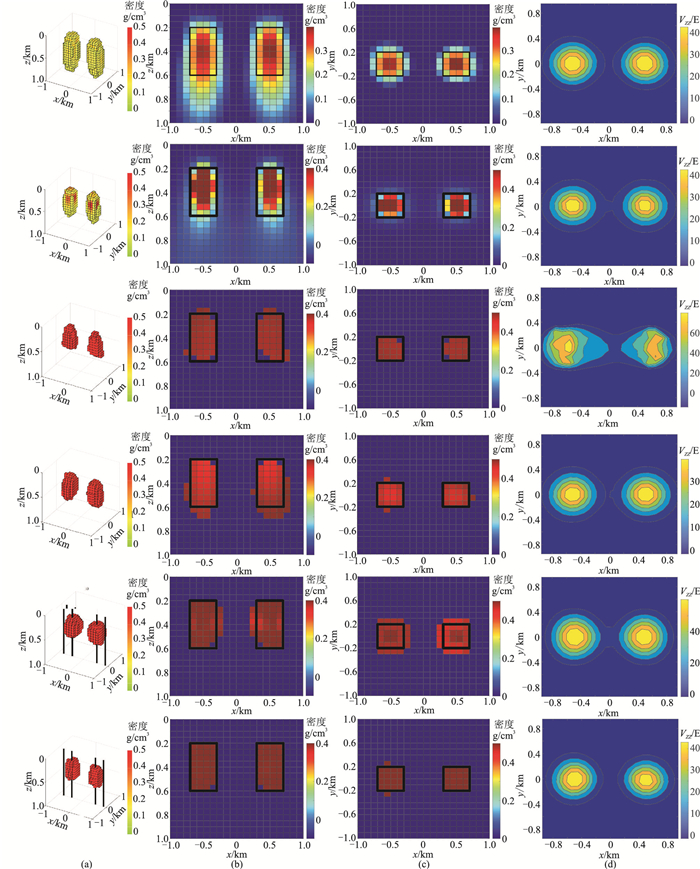
为了检验本文方法的应用效果以及空—地—井数据联合反演的有效性,对基于地面数据的聚焦反演和光滑反演结果、单独使用航空、地面、井中数据及基于FCM聚类的空—地—井数据联合反演结果进行对比。以观测数据与预测数据的RMSE作为迭代停止的判断条件。对于联合反演,设置β =0.0001,C = 2,q = 2,η=15000。对反演结果以三维视图(仅绘制剩余密度大于0.1 g/cm3的长方体)的方式进行展示(图 2a),并绘制y =0(图 2b)和z=375 m(图 2c)剖面,反演模型的重力垂直梯度场见图 2d。该双长方体模型的理论RMSE应为2.68,即设ε=2.68。根据计算结果,图 2中地面数据光滑反演结果、聚焦反演结果及航空数据、地面数据、井数据单独反演结果及基于FCM聚类的空—地—井数据联合反演结果的均方根误差分别为2.67、2.54、5.51、3.52、4.32、3.06。对比图 2可见:本文方法具有更高的成像分辨率,反演得到的模型轮廓更清晰,更接近于实际位置;本文方法反演结果的模型精度更高,即数值范围与模型基本一致;基于本文方法,对于双长方体模型,即便单独使用航空、地面或井中数据进行反演,仍可获得较好的结果。同时,试验结果还验证了该方法具有一定的抗噪性。
|
图 2 双长方体模型不同方法反演结果对比 (a)反演结果三维显示;(b)y =0剖面;(c)z=375 m剖面;(d)图a模型正演垂直重力梯度数据。从上到下第1行、第2行分别为地面数据光滑反演结果和聚焦反演结果,第3行~第6行分别为航空数据、地面数据、井数据单独反演结果及基于FCM聚类的空—地—井数据联合反演结果。图a中的黑色竖线表示井;图b和图c中的黑色线框表示密度异常体。图 3、图 5同。 |
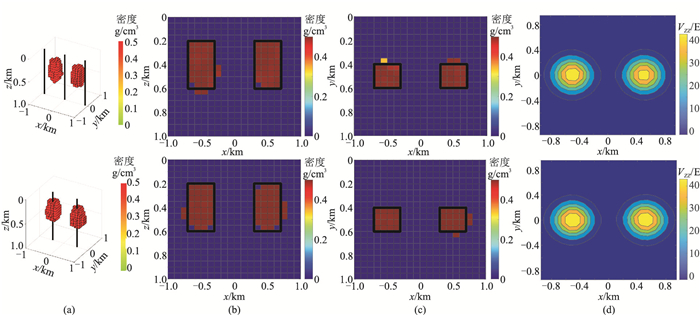
针对使用不同位置井中数据的反演进行对比试验,具体包括异常旁井和穿异常井两种情况(图 3a)。分析反演结果(图 3b~图 3d),发现测井与异常体的相对位置会对反演结果产生一定的影响。该模型的理论RMSE为2.68,异常旁井和穿异常井两种情况下的迭代结果分别收敛至2.85和3.03,可见使用异常旁井数据进行反演的分辨率略低,这与其他学者的研究结论一致[9]。为了进一步讨论井位置对反演结果的影响,对比图 2中同时使用异常旁井与穿异常井数据的反演结果,可见反演结果沿x方向的水平分辨率有所提高;同理,反演时若增加y方向的井数据,也可提高该方向上的水平分辨率。因此,同时使用异常旁井数据和穿异常井数据有助于改善反演效果。
|
图 3 基于异常旁井(上)和穿异常井(下)数据的反演结果 (a) 三维视图;(b) y =0剖面;(c) z =375 m剖面;(d) 预测数据 |
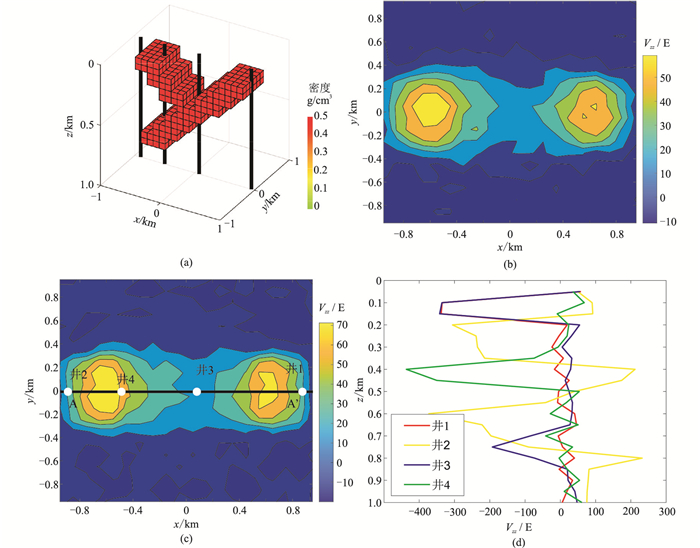
为进一步验证方法的有效性,建立较复杂的Y字型模型(图 4a)进行试验,并对地面重力数据的聚焦反演结果与单独使用航空、地面、井中数据及基于FCM聚类的空—地—井重力数据联合反演结果进行对比。异常体的剩余密度为0.5 g/cm3,x方向的分布范围为[-900 m, 900 m],y方向的分布范围为[-300 m, 300 m],z方向的分布范围为[100 m, 800 m]。该模型产生的航空、地面、井中观测数据分别见图 4b~图 4d。
|
图 4 Y字型模型及其垂直重力梯度观测数据 (a)模型及井的位置;(b)航空观测数据;(c)地面观测数据;(d)井中观测数据 |
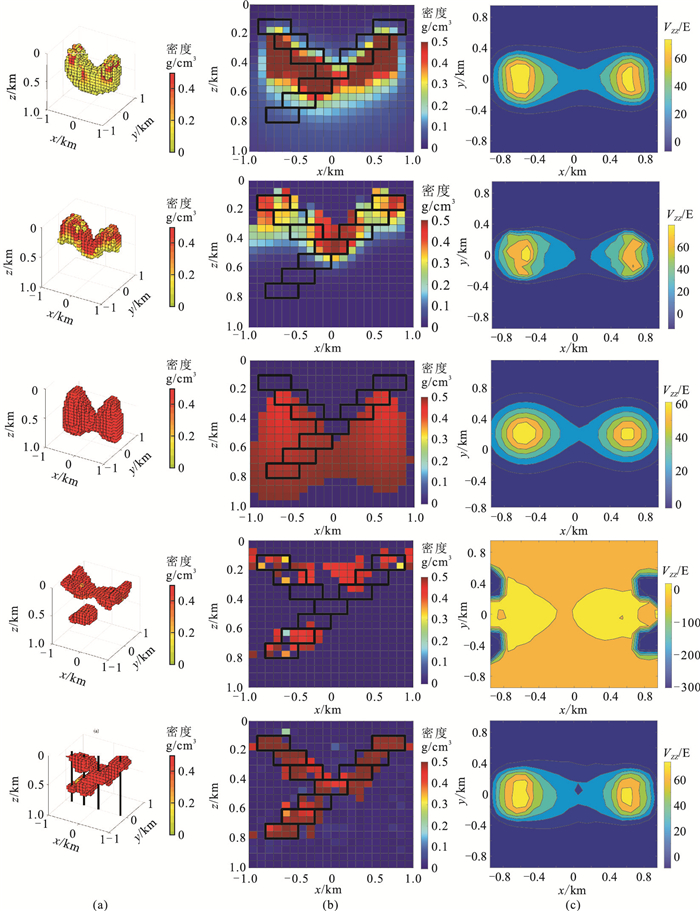
对于本文方法,设β=1,C=2,q=2.85,η=5000,用三维视图(仅绘制剩余密度大于0.1 g/cm3的长方体)及y=0剖面展示反演结果(图 5)。航空、地面和井中数据的RMSE分别为3.25、3.95、17.16,反演后对应的RMSE分别为4.09、3.95、8.24、51.06、3.68。由图 5b可知:聚焦反演的密度分布向模型中心聚焦,无法客观地展现异常体埋深较大的部分;单独利用航空重力数据的反演结果仅能体现异常体的上半部分;单独利用地面数据的反演结果则更多地集中在异常体的中间部分;单独利用井中数据主要反演得到模型的深部信息。本文方法较准确地反演出模型轮廓及形状,反演得到的异常体位置及剩余密度值的范围与模型非常接近,证明了该方法具有反演复杂模型的能力,对于复杂地质条件下的密度反演具有可行性。
|
图 5 Y字型模型不同方法反演结果对比 (a)反演结果三维视图;(b)y=0剖面;(c)预测数据。从上到下第1行是地面数据聚焦反演结果,第2~第5行分别为航空数据、地面数据、井数据及基于FCM聚类的空—地—井数据联合反演结果。 |
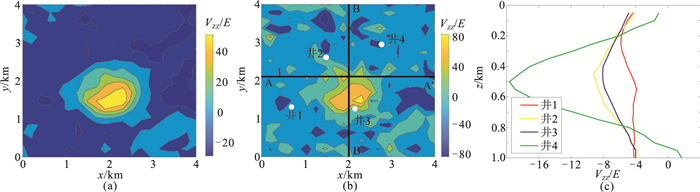
文顿盐丘位于美国路易斯安那州南部与德克萨斯州交界处,盐丘地区有丰富的油气储量,且石油和天然气的聚集及存储与盐丘密切相关,具有重要研究价值。该盐丘包括一个巨大的盐岩和盐盖,盐盖主要由石膏与硬石膏组成[23]。该地区的观测数据是由地下盖岩产生的[24],剩余密度约为0.5 g/cm3。根据相关研究[3],盖岩深度约为200~600 m。本文使用的实测航空重力梯度数据点共20×20个,观测点平均高度为85 m。由于缺少地面和井中的实际测量数据,通过换算可得到这两种数据。根据文献[9-10]对航空数据进行延拓,得到地面数据。对于井中数据,可通过模型正演获得,见图 6。
|
图 6 文顿盐丘地区垂直重力梯度数据 (a)航空观测数据;(b)地面观测数据;(c)井中观测数据 |
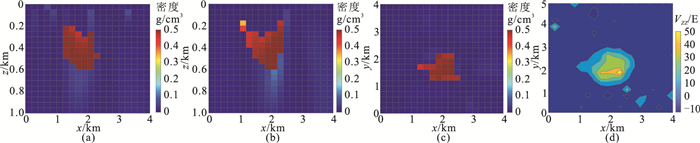
反演区域在x轴和y轴方向上分布范围均为0~4 km,设反演深度为1000 m。将地下反演空间剖分为20×20×20个100 m×100 m×50 m的长方体。设反演参数β=0.8,C=2,q=2.5,η=15,RMSE为9.30。选取x =1.84 km、y =1.64 km和z=325 m三个剖面展示反演结果(图 7)。由图可见:盖岩顶部呈现东南高、西北低的形态,盖岩在东西和南北方向的分布范围分别为1.08~2.18 km和1.19~1.90 km,异常体顶部深度约为200 m,底部最大深度约为600 m。上述结论与其他学者的研究结论[3, 24]基本一致,证明了本文方法的准确性和可行性。
|
图 7 文顿盐丘地区数据反演结果 (a)x=1.84 km剖面;(b)y=1.64 km剖面;(c)z=325 m剖面;(d)预测数据 |
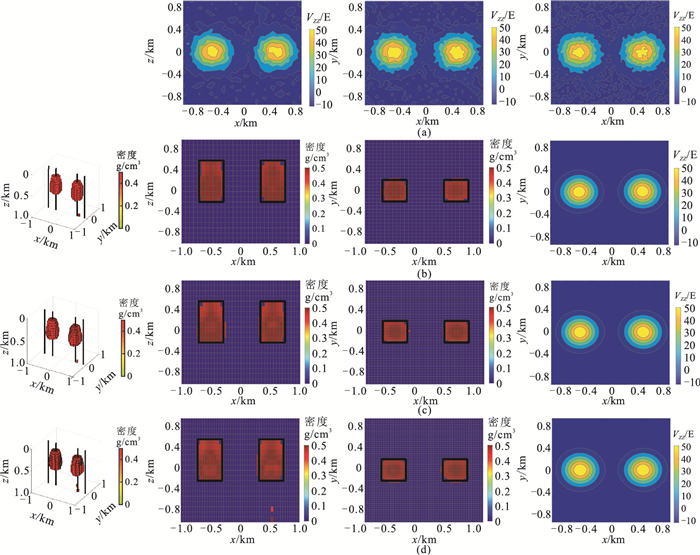
为了检验本文并行反演算法的效率,使用双长方体模型进行试验。对地下空间进一步剖分为30×30×20、40×40×20、50×50×20个网格,对比20×20×20网格剖分情况下的算法性能。不同网格条件下其他的反演参数均相同,反演迭代次数均为100。不同网格剖分情况下的垂直重力梯度观测数据见图 8a,反演结果见图 8b~图 8d。对不同规模网格的反演统计其多次串行和并行时间,记录效率最高的值,并计算加速比(串行时间与并行时间的比值),见表 1。
|
图 8 不同网格剖分的观测数据、反演结果及预测数据 (a)剖分网格数为30×30×20(左)、40×40×20(中)、50×50×20(右)下的垂直重力梯度观测数据;(b)~(d)分别为剖分网格数为30×30×20、40×40×20、50×50×20对应的结果,从左至右分别为反演结果三维视图、y=0剖面、z=375 m剖面、预测数据。 |
|
|
表 1 双长方体模型串行和并行反演程序运行时间统计 |
从统计结果(表 1)可见,随着网格规模的增大,加速比呈增大趋势,但当网格数量增至50×50×20时,加速比开始下降。其原因是:①反演过程中存在串行计算,并非所有运算都被并行化;②数据从CPU传输到GPU需要一定的时间,网格数量的增加导致传输时间增加,影响了加速效率。不同网格剖分条件下数据从CPU传输到GPU的时间统计见表 2。由表可见,随着网格数量增大,数据传输所需时间逐渐增加。这说明当网格数量增加到某一量级时,并行算法仍可加快反演过程,但不会达到预期的加速比。
|
|
表 2 CPU-GPU间数据传输时间统计 |
本文提出一种基于FCM聚类的空—地—井重力梯度数据联合反演方法,并通过理论模型数据和文顿盐丘地区数据检验了反演效果。与其他反演方法相比,本文方法反演结果能够较准确地反映异常体的位置与形态,密度范围与理论值基本一致;反演得到的盖岩模型与其他学者的研究结果基本一致,证明了方法的可行性与抗噪性。分析数据试验结果可以看出,FCM聚类约束可以降低反演的多解性,联合航空、地面和井中重力数据可以进一步提高反演结果在水平方向和深度方向的分辨能力;使用异常旁井和穿异常井数据可以进一步提高反演结果的分辨率。与反演的串行算法相比,基于GPU的并行反演算法能够显著提高计算效率。综上,本文联合反演方法计算效率高,得到的密度模型较可靠,能够为地质找矿等工作提供技术支撑。
感谢Bell Geospace Inc提供的实测重力梯度数据。
| [1] |
张恒磊, 耿美霞, 胡祥云. 基于曲波压缩的重磁异常三维反演及其应用[J]. 石油地球物理勘探, 2023, 58(4): 993-1001. ZHANG Henglei, GENG Meixia, HU Xiangyun. Three-dimensional inversion of gravity/magnetic anomalies based on curvelet compression and its applications[J]. Oil Geophysical Prospecting, 2023, 58(4): 993-1001. |
| [2] |
相鹏, 谭绍泉, 陈学国, 等. 利用高斯径向基函数的拟神经网络重力反演方法[J]. 石油地球物理勘探, 2021, 56(6): 1409-1418. XIANG Peng, TAN Shaoquan, CHEN Xueguo, et al. Gravity inversion method based on quasi-neural network featuring Gaussian radial basis function[J]. Oil Geophysical Prospecting, 2021, 56(6): 1409-1418. |
| [3] |
秦朋波, 黄大年. 重力和重力梯度数据联合聚焦反演方法[J]. 地球物理学报, 2016, 59(6): 2203-2224. QIN Pengbo, HUANG Danian. Integrated gravity and gravity gradient data focusing inversion[J]. Chinese Journal of Geophysics, 2016, 59(6): 2203-2224. |
| [4] |
PILKINGTON M. Analysis of gravity gradiometer inverse problems using optimal design measures[J]. Geophysics, 2012, 77(2): G25-G31. DOI:10.1190/geo2011-0317.1 |
| [5] |
PILKINGTON M. Evaluating the utility of gravity gradient tensor components[J]. Geophysics, 2014, 79(1): G1-G14. DOI:10.1190/geo2013-0130.1 |
| [6] |
LI Y, OLDENBURG D W. Joint inversion of surface and three-component borehole magnetic data[J]. Geophysics, 2000, 65(2): 540-552. DOI:10.1190/1.1444749 |
| [7] |
张大莲, 刘天佑, 陈石羡, 等. 粒子群算法在磁测资料井地联合反演中的应用[J]. 物探与化探, 2009, 33(5): 571-575, 591. ZHANG Dalian, LIU Tianyou, CHEN Shixian, et al. The application of PSO to joint inversion of surface and borehole magnetic data[J]. Geophysical and Geochemical Exploration, 2009, 33(5): 571-575, 591. |
| [8] |
GENG M, YANG Q, HUANG D. 3D joint inversion of gravity-gradient and borehole gravity data[J]. Exploration Geophysics, 2017, 48(2): 151-165. DOI:10.1071/EG15023 |
| [9] |
王泰涵, 马国庆, 熊盛青, 等. 空—地—井重力异常正则化协同密度反演方法[J]. 地球物理学报, 2020, 63(7): 2737-2750. WANG Taihan, MA Guoqing, XIONG Shengqing, et al. Joint regularized density inversion method of airborne, surface and borehole gravity anomaly data[J]. Chinese Journal of Geophysics, 2020, 63(7): 2737-2750. |
| [10] |
高秀鹤, 熊盛青, 于长春, 等. 不同高度重力数据和井中重力数据融合反演研究[J]. 物探与化探, 2020, 44(6): 1361-1367. GAO Xiuhe, XIONG Shengqing, YU Changchun, et al. A study of joint inversion of gravity data from multi-planes and boreholes[J]. Geophysical and Geochemical Exploration, 2020, 44(6): 1361-1367. |
| [11] |
PENG G M, SUN Z Y, LIU Z. 3D joint inversion of surface and borehole gravity data using zeroth-order minimum entropy regularization[J]. Applied Geophysics, 2021, 18(2): 131-144. DOI:10.1007/s11770-020-0849-z |
| [12] |
杨培杰, 印兴耀, 张广智. 模糊C均值地震属性聚类分析[J]. 石油地球物理勘探, 2007, 42(3): 322-324. YANG Peijie, YIN Xingyao, ZHANG Guangzhi. Cluster analysis of seismic attributes by fuzzy C-mean algorithm[J]. Oil Geophysical Prospecting, 2007, 42(3): 322-324. |
| [13] |
SUN J, LI Y. Geophysical inversion using petrophysical constraints with application to lithology differentiation[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 2644-2648.
|
| [14] |
MAAG E, LI Y. Discrete-valued gravity inversion using the guided fuzzy c-means clustering technique[J]. Geophysics, 2018, 83(4): G59-G77. DOI:10.1190/geo2017-0594.1 |
| [15] |
徐凯军, 李猛, 季春晖, 等. 基于模糊C均值聚类约束的井—地磁法联合数据空间反演[J]. 中国石油大学学报(自然科学版), 2021, 45(3): 55-64. XU Kaijun, LI Meng, JI Chunhui, et al. Data space joint inversion of ground and borehole magnetic data with fuzzy C-means clustering constraints[J]. Journal of China University of Petroleum (Edition of Natural Science), 2021, 45(3): 55-64. |
| [16] |
易柯, 张志勇, 李曼, 等. 基于FCM聚类算法的二维RMT电阻率与介电常数联合反演[J]. 地球物理学报, 2022, 65(6): 2340-2350. YI Ke, ZHANG Zhiyong, LI Man, et al. Joint inversion of resistivity and permittivity for two dimensional RMT data based on FCM clustering[J]. Chinese Journal of Geophysics, 2022, 65(6): 2340-2350. |
| [17] |
SUN J, LI Y. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy C-means clustering[J]. Geophysics, 2015, 80(4): ID1-ID18. DOI:10.1190/geo2014-0049.1 |
| [18] |
LI Y, OLDENBURG D W. 3-D inversion of magnetic data[J]. Geophysics, 1996, 61(2): 394-408. DOI:10.1190/1.1443968 |
| [19] |
TIKHONOV A N, ARSENINV Y. Solutions of Ill-posed Problems[M]. New York: Halsted Press, 1977.
|
| [20] |
PORTNIAGUINE O, ZHDANOV M S. 3-D magnetic inversion with data compression and image focusing[J]. Geophysics, 2000, 67(5): 1532-1541. |
| [21] |
陈召曦, 孟小红, 郭良辉, 等. 基于GPU并行的重力、重力梯度三维正演快速计算及反演策略[J]. 地球物理学报, 2012, 55(12): 4069-4077. CHEN Zhaoxi, MENG Xiaohong, GUO Lianghui, et al. Three-dimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU[J]. Chinese Journal of Geophysics, 2012, 55(12): 4069-4077. |
| [22] |
HOU Z, SUN B, QIN P B, et al. Joint nonlinear inversion of full tensor gravity gradiometry data and its parallel algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-12. |
| [23] |
COKER M O, BHATTACHARYA J P, MARFURT K J. Fracture patterns within mudstones on the flanks of a salt dome: syneresis or slumping?[J]. Gulf Coast Association of Geological Societies, 2007, 57: 125-137. |
| [24] |
OLIVEIRA V C, BARBOSA V C F. 3-D radial gravity gradient inversion[J]. Geophysical Journal International, 2013, 195(2): 883-902. DOI:10.1093/gji/ggt307 |



 辽宁省沈阳市和平区文化路11号东北大学,110819。Email:
辽宁省沈阳市和平区文化路11号东北大学,110819。Email: 