2. 电子科技大学资源与环境学院, 四川成都 611731;
3. 电子科技大学长三角研究院(湖州), 浙江湖州 313099;
4. 油气勘探计算机软件国家工程研究中心, 北京 100088
2. School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China;
3. Yangtze Delta Region Institute of University of Electronic Science and Technology of China(Huzhou), Huzhou, Zhejiang 313099, China;
4. National Engineering Research Center for Oil and Gas Exploration Computer Software, Beijing 100088, China
流体(含气性)预测对于裂缝性油气藏的勘探与开发具有重要意义。在成岩作用和后期构造应力作用下,储层常常存在一组或多组定向排列的裂缝[1]。当地震波穿过裂缝时,一方面定向排列的裂缝会造成地震波速度的各向异性[2];另一方面,地震波对裂缝的挤压作用会引起流体流动,该过程伴随着地震波的频散和衰减[3]。因此,裂缝流体的预测在考虑地震波形的振幅、各向异性等信息的同时,应考虑地震波的频散特征。
在裂缝型储层表征方面,振幅与角度和方位角(AVAZ)反演被广泛用于纵波地震数据的各向异性反演[4-5]。具有垂直对称轴的横向各向同性(Transverse Isotropic with a Vertical Symmetry Axis, VTI)背景介质中嵌入一组平行排列的垂直裂缝可等效为正交各向异性介质[6]。为提取正交各向异性介质中的各向异性特征,Bachrach根据Pšenčik等[7]提出的公式和符号研究了基于正交各向异性OA(Orthorhombic Anisotropy, OA) 介质的线性AVAZ反演[8]。潘新朋等[9]研究了贝叶斯框架下基于OA介质的AVAZ反演方法。
裂缝流体预测通常依赖于与流体相关的异常特征的反演,这些异常特征被称为流体因子[10-11]。流体识别的效率主要取决于两个方面:流体因子的敏感性和地震反演的可靠性[12]。对于与频率无关的流体因子,应用最广的是以Zoeppritz方程为基础推导的弹性参数和AVO属性的组合[13-16]。这种传统的流体识别因子在实际应用中取得了较好的效果,但未考虑到地震频散和衰减的影响,导致其分辨率和准确性较低。随着时频分析技术的进步,发展了与频率相关的流体因子[17]。Taner等[18]最先注意到含气层下方的“低频阴影”现象,并推测其由地震波衰减引起。但后续的研究表明,造成“低频阴影”的因素不一定与衰减有关[19]。
在地震波频散和衰减的机制方面,Chapman等[20]、张金伟等[21]、Shuai等[22]提出动态等效介质理论,从地震波诱导流体流动的角度解释了地震波的频散和衰减,即反射系数不仅与入射角和方位角有关,而且还随频率变化。该理论为FDAVO(Frequency-Dependent Amplitude Versus Offset)反演提供了理论基础。
在频散属性反演方面,对于各向同性介质,Wilson等[23]基于Chapman等[20]提出的岩石物理理论,结合时频分析方法和AVO技术初步开发了依赖频率的AVO反演框架,计算反映地震波频散程度的属性并将其作为流体因子。吴小羊[24]将改进的Wigner-Ville分布(SPWVD)方法用于FDAVO反演。程冰洁等[25]基于Smith-Gidlow近似式推导了截距、梯度和拟泊松比等频变AVO属性。罗鑫等[26]根据f-μ-ρ反射系数公式[16]进行了FDAVO反演。不过,实际储层中的孔隙空间具有多样性和复杂性,通过研究各向异性参数随频率的变化可进一步识别有效裂缝(流体饱和)。对于各向异性介质,Zhang等[27]通过计算不同方位反射系数的差值以消除反射系数公式中的各向同性项,推导了表征各向异性参数频散程度的频散项。Ajaz等[28]基于Rüger方程,推导出频变AVAZ反演的频域解析表达式,并在碳酸盐岩应用中进行了验证。上述研究表明,考虑地震波频散有利于裂缝性储层中流体信息的获取。
由于正交各向异性介质中地震响应的复杂性,准确刻画其中的流体分布特征仍然具有一定的挑战性。为此,本文提出了基于OA介质频率相关AVAZ(OA-FDAVAZ)反演的含气性预测方法。首先通过Chapman多组裂缝模型分析弹性参数的频变特性以及孔隙度、裂缝密度等参数对频散特征的影响;其次将OA介质纵波反射系数近似式拓展到频率域,构建OA-FDAVAZ反演的目标方程,给出频散组合因子的计算公式,并提出相应的反演流程;最后利用最小二乘法求解正交各向异性频散属性。模型数据和实际数据的计算结果均验证了方法的有效性和稳定性。
1 Chapman动态等效介质理论考虑到实际储层通常发育多组裂缝,Chapman[29]将单裂缝模型扩展到包含两组不同方向、大小和连通性的裂缝集。双裂缝模型证明了由两个特征频率(速度随频率变化最大时对应的频率)控制了频率相关各向异性。这两个特征频率可由流体流动性和裂缝的尺度定义。包含两组裂缝的频变刚度张量为
| $ \mathit{\boldsymbol{C}}={\mathit{\boldsymbol{C}}}_{0}-{\phi }_{\mathrm{p}}{\mathit{\boldsymbol{C}}}_{{\mathrm{p}}}-{\varepsilon }_{1}{\mathit{\boldsymbol{C}}}_{1}-{\varepsilon }_{2}{\mathit{\boldsymbol{C}}}_{2} $ | (1) |
式中:
在Chapman模型中,最重要的两个参数分别是两种尺度下的弛豫时间。微观尺度下的弛豫时间(
| $ {\tau }_{\mathrm{f}}=\frac{r}{\varsigma }{\tau }_{\mathrm{m}} $ | (2) |
式中:
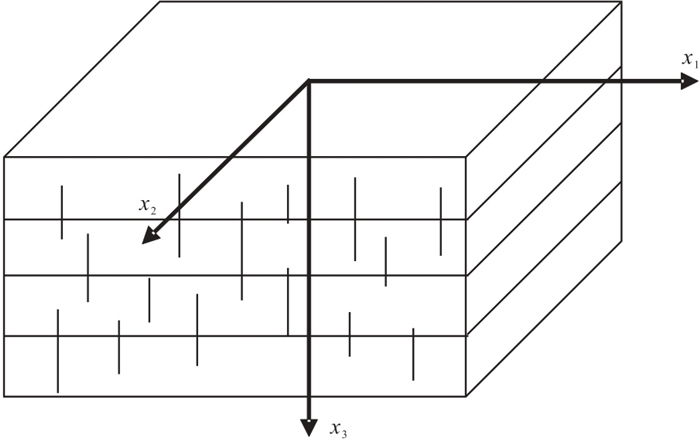
在长波长假设条件下,周期性薄互层中发育一组垂直裂缝可等效为OA介质(图 1)。为了解OA介质中弹性参数的频变特性和流体敏感性,通过Chapman模型进行数值模拟。如图 2所示,设置各向同性背景介质中的拉梅系数
|
图 1 正交各向异性介质示意图
|
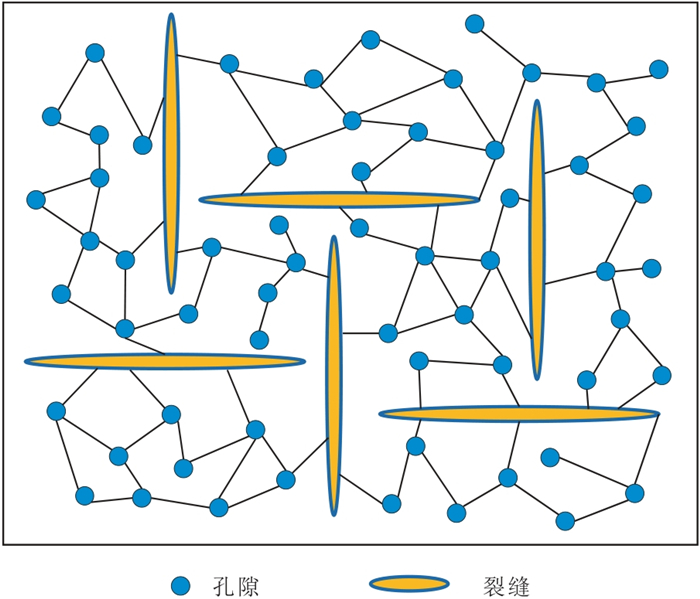
|
图 2 含两组正交裂缝的模型示意图 空白表示各向同性背景介质;黑线表示流体可以在连接的两个孔隙(或裂缝)之间进行流动。 |
通过计算式(1)得到矩阵张量
| $ {V}_{\mathrm{P}}\left(f\right)={\left[\mathrm{R}\mathrm{e}\left(\frac{1}{V\left(f\right)}\right)\right]}^{-1} $ | (3) |
| $ {Q}_{\mathrm{P}}^{-1}\left(f\right)=\frac{\mathrm{I}\mathrm{m}\left[V{\left(f\right)}^{2}\right]}{\mathrm{R}\mathrm{e}\left[V{\left(f\right)}^{2}\right]} $ | (4) |
式中:Im表示取复数的虚部;Re表示取复数的实部;f为频率。
各向异性参数
| $ {\delta }_{x}=\frac{{\left({c}_{13}+{c}_{55}\right)}^{2}-{\left({c}_{33}-{c}_{55}\right)}^{2}}{2{c}_{33}\left({c}_{33}-{c}_{55}\right)} $ | (5) |
| $ {\delta }_{y}=\frac{{\left({c}_{23}+{c}_{44}\right)}^{2}-{\left({c}_{33}-{c}_{44}\right)}^{2}}{2{c}_{33}\left({c}_{33}-{c}_{44}\right)} $ | (6) |
式中:
计算不同含气饱和度
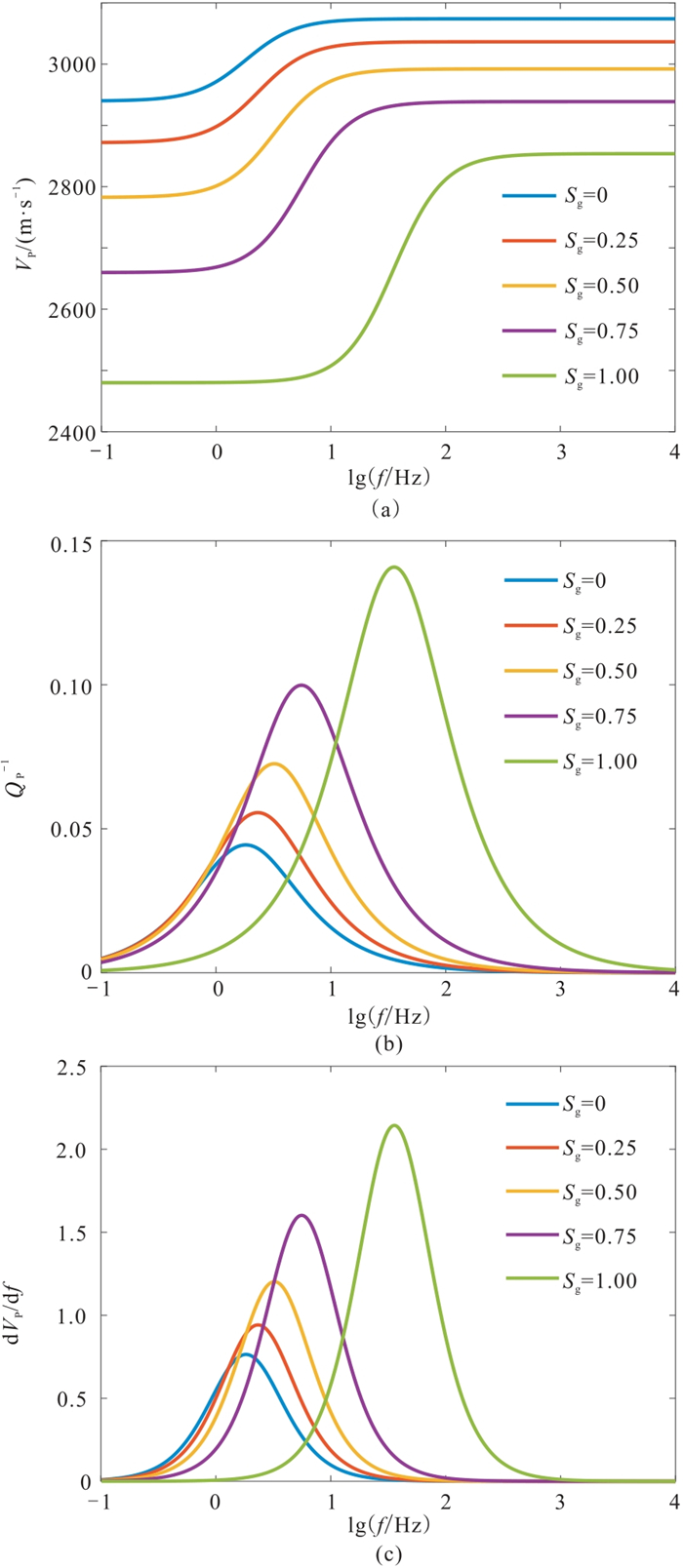
|
图 3 不同含气饱和度的弹性参数随频率的变化 (a)纵波速度;(b)逆品质因子;(c)纵波速度对频率的导数 |
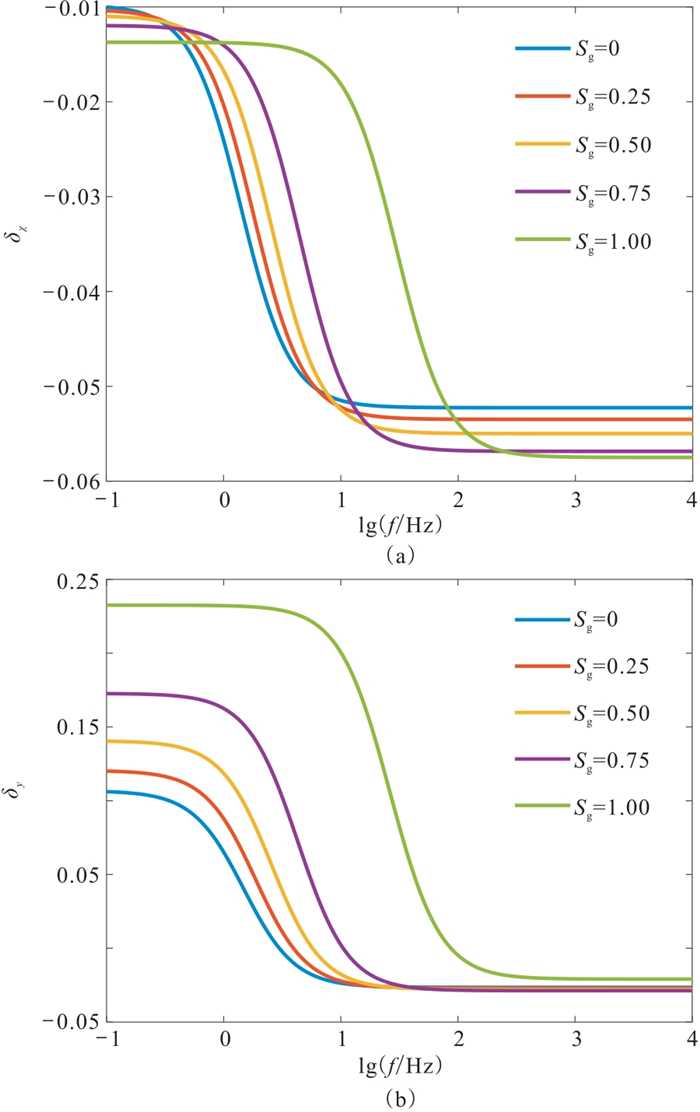
此外,两个各向异性参数分量
|
图 4 不同含气饱和度的各向异性参数随频率的变化 (a) |
|
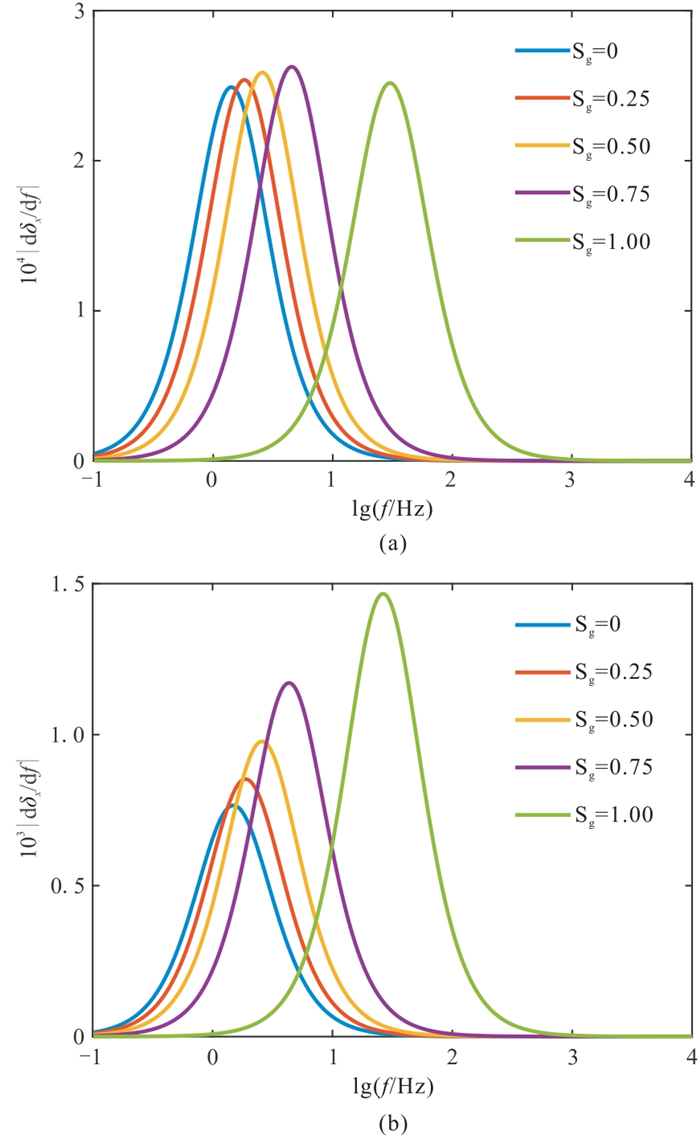
图 5 不同含气饱和度的各向异性参数关于频率的导数的绝对值随频率变化关系 (a) |
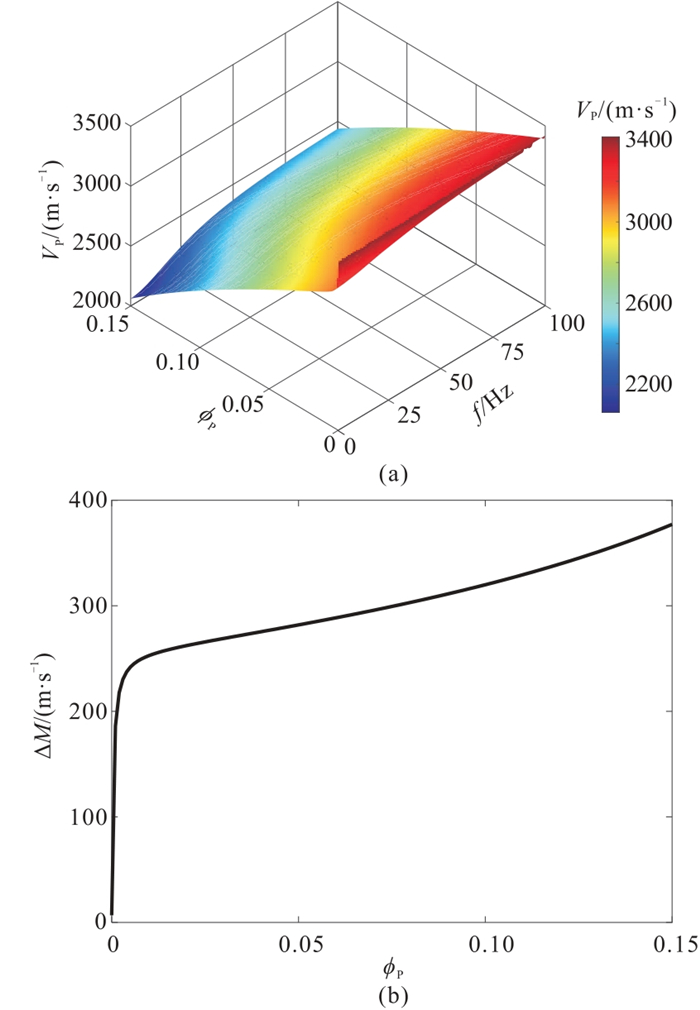
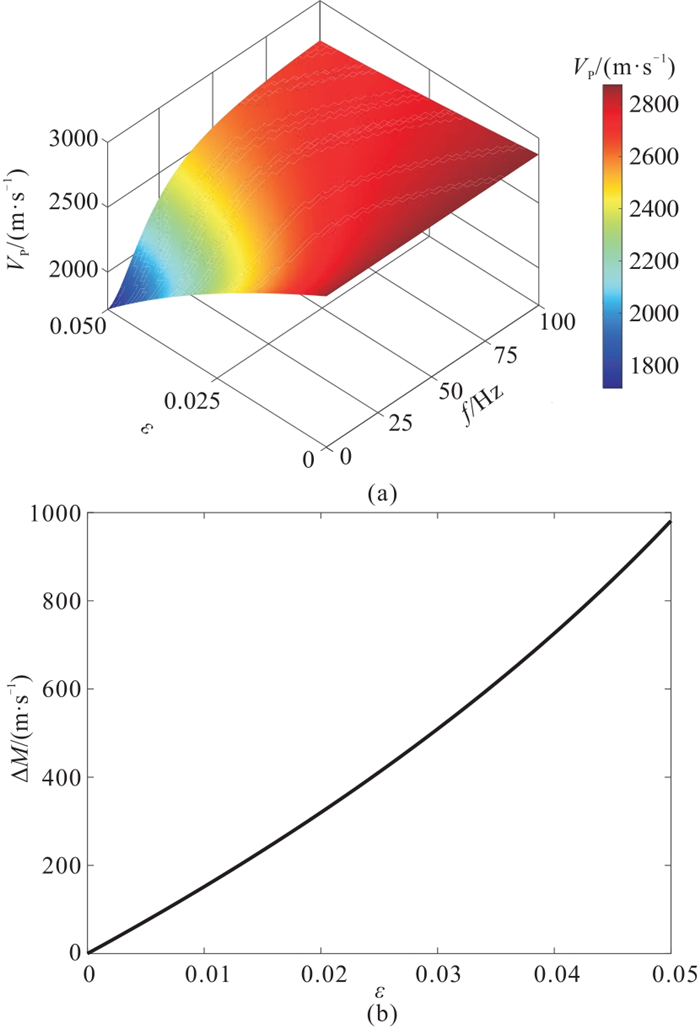
为进一步探究孔隙和裂缝发育程度对地震波频散的影响,在其他参数保持一致的情况下,选择频散现象较明显的饱和气模型,计算地震频带内纵波速度随频率、孔隙度
由图 6a可知,纵波速度随孔隙度和频率而变化,且频散程度随孔隙度的增加先急剧增大、随后增速放缓(图 6b),这表明孔隙度对地震波频散有一定影响,但这种影响难以反映孔隙度的变化。相比之下,纵波速度在低频时随裂缝密度变化更明显(图 7a),频散程度与裂缝密度近似呈线性正相关(图 7b),因此可以利用频散程度表征裂缝发育情况。
|
图 6 纵波速度随频率和孔隙度的变化(a)及纵波速度频散程度随孔隙度的变化(b) |
|
图 7 纵波速度随频率和裂缝密度的变化(a)及纵波速度频散程度随裂缝密度的变化(b) |
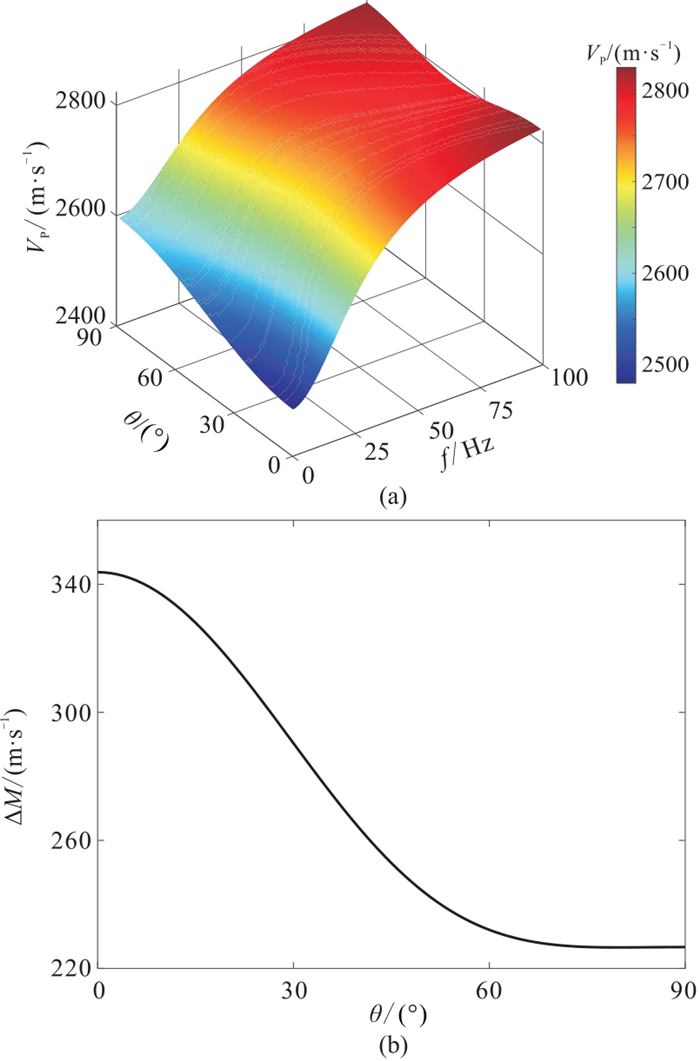
反演各向异性参数时,需要用到OVT域叠前地震数据,其中包含地震波入射角(
|
图 8 纵波速度随频率和入射角的变化(方位角=30°)(a)及纵波速度频散程度随入射角的变化(b) |
|
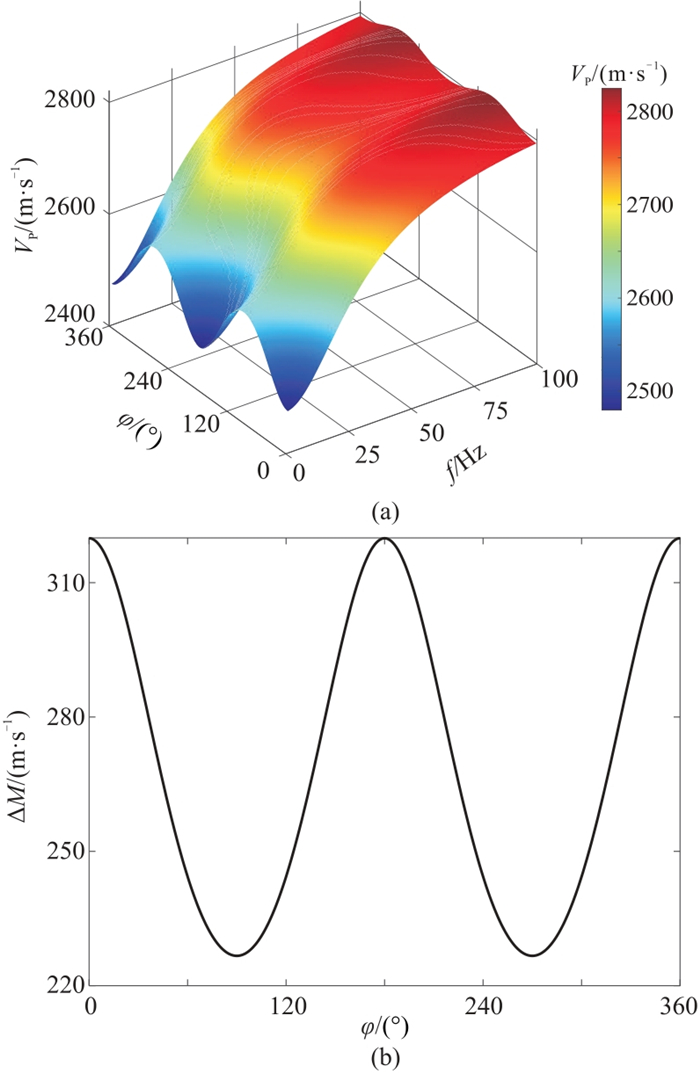
图 9 纵波速度随频率和方位角的变化(入射角=30°)(a)及纵波速度频散程度随方位角的变化(b) |
纵波速度同时随频率和方位角而变化(图 9a),纵波速度随方位角呈现周期性变化,且在低频时这种变化更剧烈。纵波频散程度分别在方位角为
2001年,Pšenčik等[7]推导的任意各向异性和对称轴背景下的正交各向异性介质纵波反射系数近似方程为
| $ R\left(\theta , \varphi \right)={R}^{\mathrm{i}\mathrm{s}\mathrm{o}}\left(\theta \right)+{R}^{\mathrm{a}\mathrm{n}\mathrm{i}}\left(\theta , \varphi -{\varphi }_{\mathrm{s}}\right) $ | (7) |
| $ {R}^{\mathrm{i}\mathrm{s}\mathrm{o}}\left(\theta \right)=P+G\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (8) |
| $ \begin{array}{l}{R}^{\mathrm{a}\mathrm{n}\mathrm{i}}\left(\theta , \varphi \right)=\left[{{\mathit{\Gamma}} }_{x}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)+\right.\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.{{\mathit{\Gamma}} }_{y}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\right]\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \end{array} $ | (9) |
上述式中:
| $ \left\{\begin{array}{l}{{\mathit{\Gamma}} }_{x}=0.5\left(\mathrm{\Delta }{\delta }_{x}-8{\overline{{V}_{\mathrm{S}}}}^{2}\mathrm{\Delta }{\gamma }_{x}/{\overline{{V}_{\mathrm{P}}}}^{2}\right)\\ {{\mathit{\Gamma}} }_{y}=0.5\left(\mathrm{\Delta }{\delta }_{y}-8{\overline{{V}_{\mathrm{S}}}}^{2}\mathrm{\Delta }{\gamma }_{y}/{\overline{{V}_{\mathrm{P}}}}^{2}\right)\\ {\delta }_{x}=\left({A}_{13}+2{A}_{55}-{V}_{\mathrm{P}}^{2}\right)/{V}_{\mathrm{P}}^{2}\\ {\delta }_{y}=\left({A}_{23}+2{A}_{44}-{V}_{\mathrm{P}}^{2}\right)/{V}_{\mathrm{P}}^{2}\\ {\gamma }_{x}=\left({A}_{55}-{V}_{\mathrm{S}}^{2}\right)/\left(2{V}_{\mathrm{S}}^{2}\right.)\\ {\gamma }_{y}=\left({A}_{44}-{V}_{\mathrm{S}}^{2}\right)/\left(2{V}_{\mathrm{S}}^{2}\right.)\end{array}\right. $ | (10) |
式中
Chapman[31]认为纵波速度、横波速度及各向异性参数均与频率有关,当界面两侧频散性质存在差异时,反射系数会随频率而变化,即反射系数可视为入射角、方位角和频率的函数。因此,假设式(7)~式(9)中的
| $ \begin{array}{l}R\left(\theta , \varphi , f\right)=P\left(f\right)+G\left(f\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\Gamma}} }_{x}\left(f\right)\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\Gamma}} }_{y}\left(f\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \end{array} $ | (11) |
将式(11)关于某一参考频率
| $ \begin{array}{l}R\left(\theta , \varphi , f\right)\approx R\left(\theta , \varphi , {f}_{0}\right)+\left(f-{f}_{0}\right)\left[{I}_{\mathrm{a}}+\right.\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {I}_{\mathrm{b}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +{I}_{\mathrm{c}}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.{I}_{\mathrm{d}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right]\end{array} $ | (12) |
式中:
| $ \begin{array}{l}R\left(\theta , \varphi , {f}_{0}\right)\approx P\left({f}_{0}\right)+G\left({f}_{0}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\Gamma}} }_{x}\left({f}_{0}\right)\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\Gamma}} }_{y}\left({f}_{0}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \end{array} $ | (13) |
| $ \left\{\begin{array}{l}{I}_{\mathrm{a}}=\frac{\mathrm{d}}{\mathrm{d}f}\left[P\left(f\right)\right]\\ {I}_{\mathrm{b}}=\frac{\mathrm{d}}{\mathrm{d}f}\left[G\left(f\right)\right]\\ {I}_{\mathrm{c}}=\frac{\mathrm{d}}{\mathrm{d}f}\left[{{\mathit{\Gamma}} }_{x}\left(f\right)\right]\\ {I}_{\mathrm{d}}=\frac{\mathrm{d}}{\mathrm{d}f}\left[{{\mathit{\Gamma}} }_{y}\left(f\right)\right]\end{array}\right. $ | (14) |
式(13)可进一步简化为
| $ \begin{array}{l}\mathrm{\Delta }R\left(\theta , \varphi , f\right)={I}_{\mathrm{a}}\left(f-{f}_{0}\right)+{I}_{\mathrm{b}}\left(f-{f}_{0}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {I}_{\mathrm{c}}\left(f-{f}_{0}\right)\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {I}_{\mathrm{d}}\left(f-{f}_{0}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\left(\varphi -{\varphi }_{\mathrm{s}}\right)\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \end{array} $ | (15) |
式中
OA-FDAVAZ反演技术流程(图 10)如下。
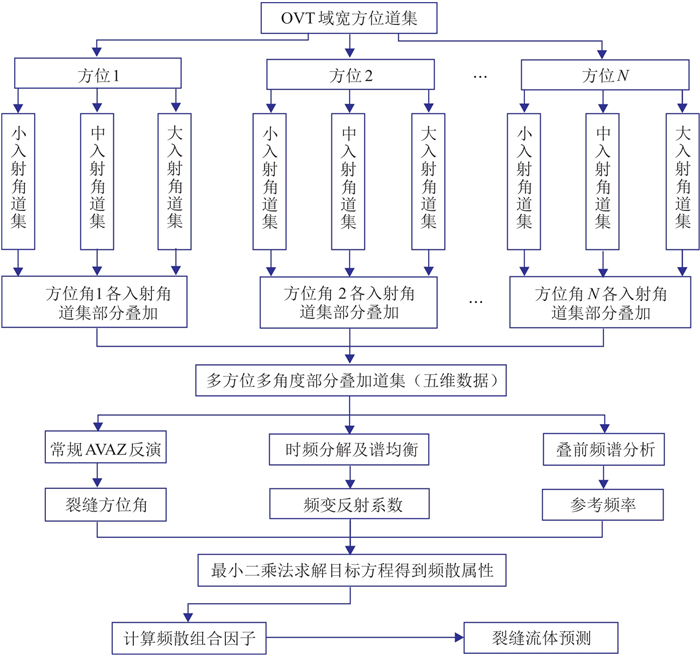
|
图 10 OA-FDAVAZ反演技术流程 |
(1) 获取OVT域宽方位道集,将OVT道集划分为N个方位角扇区的角度道集,并抽取各方位的部分叠加角道集
(2) 通过常规AVAZ反演得到裂缝方位角
(3) 对叠前地震记录进行频谱分析,获取地震记录的主频作为参考频率
(4) 采用平滑伪Wigner-Ville分布(SPWVD)将
| $ \mathit{\boldsymbol{S}}\left(t, \theta , \varphi \right)\to \mathit{\boldsymbol{S}}\left(t, \theta , \varphi , f\right) $ | (16) |
(5) 由于地震子波的影响,不同频率之间的能量分布并不均衡,此现象称为“子波叠印”。为了消除“子波叠印”,设计一种权重函数消除子波的叠加,以平衡不同频率分量的振幅谱,也就是谱均衡,即
| $ \mathit{\boldsymbol{r}}\left(t, \theta , \varphi , f\right)=\mathit{\boldsymbol{S}}\left(t, \theta , \varphi , f\right)\mathit{\boldsymbol{W}}\left(\theta , \varphi , f\right) $ | (17) |
式中:
| $ \mathit{\boldsymbol{W}}\left(\theta , \varphi , f\right)=\frac{\mathrm{m}\mathrm{a}\mathrm{x}\left[\mathit{\boldsymbol{S}}\left(\theta , \varphi , {f}_{0}\right)\right]}{\mathrm{m}\mathrm{a}\mathrm{x}\left[\mathit{\boldsymbol{S}}\left(\theta , \varphi , f\right)\right]} $ | (18) |
式中:
(6) 计算不同频率反射系数振幅谱的差值
(7) 计算频散组合因子。为进一步降低反演的多解性,降低背景干扰,借鉴Russell流体识别因子的思路[16],频散属性的二次及二次以上的幂量纲组合形式有助于突出由孔隙流体导致的储层频散异常。因此,本文定义
| $ {I}_{\mathrm{a}\mathrm{n}\mathrm{i}}^{}={I}_{\mathrm{c}}^{2}+{I}_{\mathrm{d}}^{2} $ | (19) |
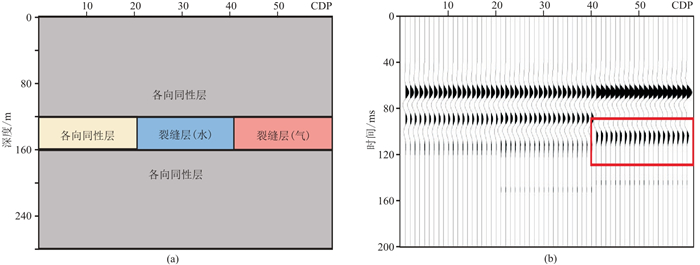
设计三层理论模型(图 11a)测试本文方法的可靠性。第一层为各向同性介质。第二层分为三部分,由左往右依次为各向同性层、饱和水裂缝层和饱和气裂缝层,其中裂缝层的参数设置见图 2模型。第三层的性质与第一层相同。具体参数如表 1所示。
|
图 11 裂缝模型(a)及其合成地震AVAZ响应(方位角=15°,入射角= |
|
|
表 1 裂缝性储层理论模型参数 |
基于Chapman模型和反射率法计算一系列不同频率、方位角和入射角的反射系数后,与Ricker子波褶积合成叠前方位地震数据(方位角为
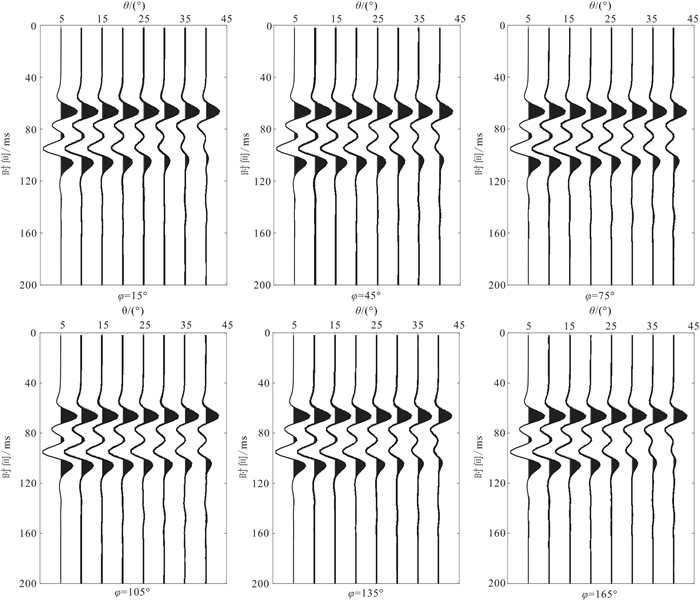
|
图 12 含气模型合成方位角道集 |
对上述数据进行OA-FDAVAZ反演,其中分解频率分别为10、20、30、40、50 Hz。由于所选Ricker子波的主频为35 Hz,故选35 Hz作为反演的参考频率,得到模型的正交各向异性频散属性
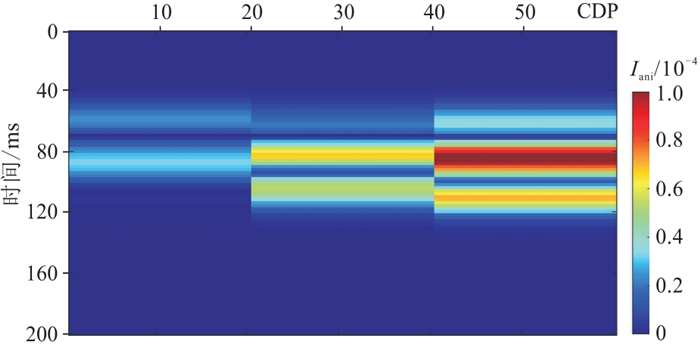
|
图 13 模型的正交各向异性频散属性 |
选择四川盆地东部五百梯气田实际资料测试本文方法效果。研究区目标储层为志留系龙马溪组(
采用研究区A井旁的OVT域叠前地震数据进行测试。通过分析各方位覆盖次数和炮检距范围,将处理好的OVT道集划分为6个方位角扇形区(

|
图 14 过A井方位地震叠加道集(a)及不同入射角、方位角为 |
应用本文方法得到各向异性频散属性,并与对应的测井曲线进行对比(图 15)。由图可见,储层(红色阴影部分)自然伽马为高值异常,而密度和纵波速度均为低值异常,与页岩储层特征一致;同时,正交各向异性频散属性
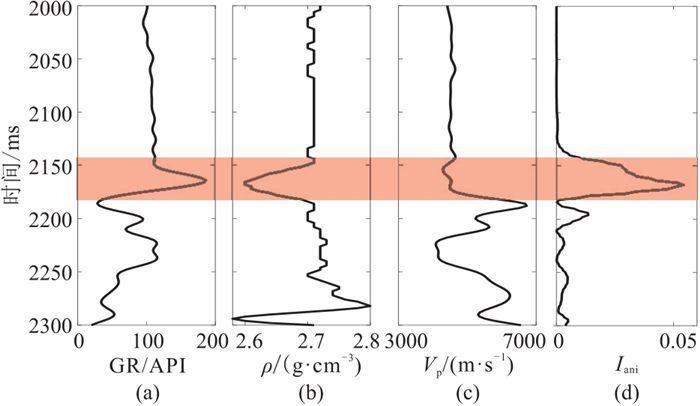
|
图 15 测井曲线及频散属性曲线 (a)自然伽马;(b)密度;(c)纵波速度;(d) |
研究区实际地震数据信噪比较高,横向连续性强,垂向分辨率较高且具有足够的方位覆盖率。图 16为不同方位的大、中、小入射角部分叠加剖面,剖面反演的道集范围、反演参数与单道测试一致。
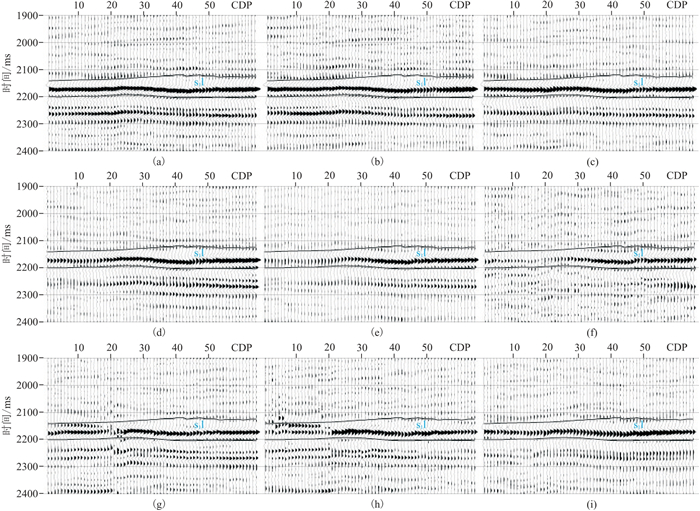
|
图 16 不同观测方位、不同入射角地震剖面 (a)方位角为 |
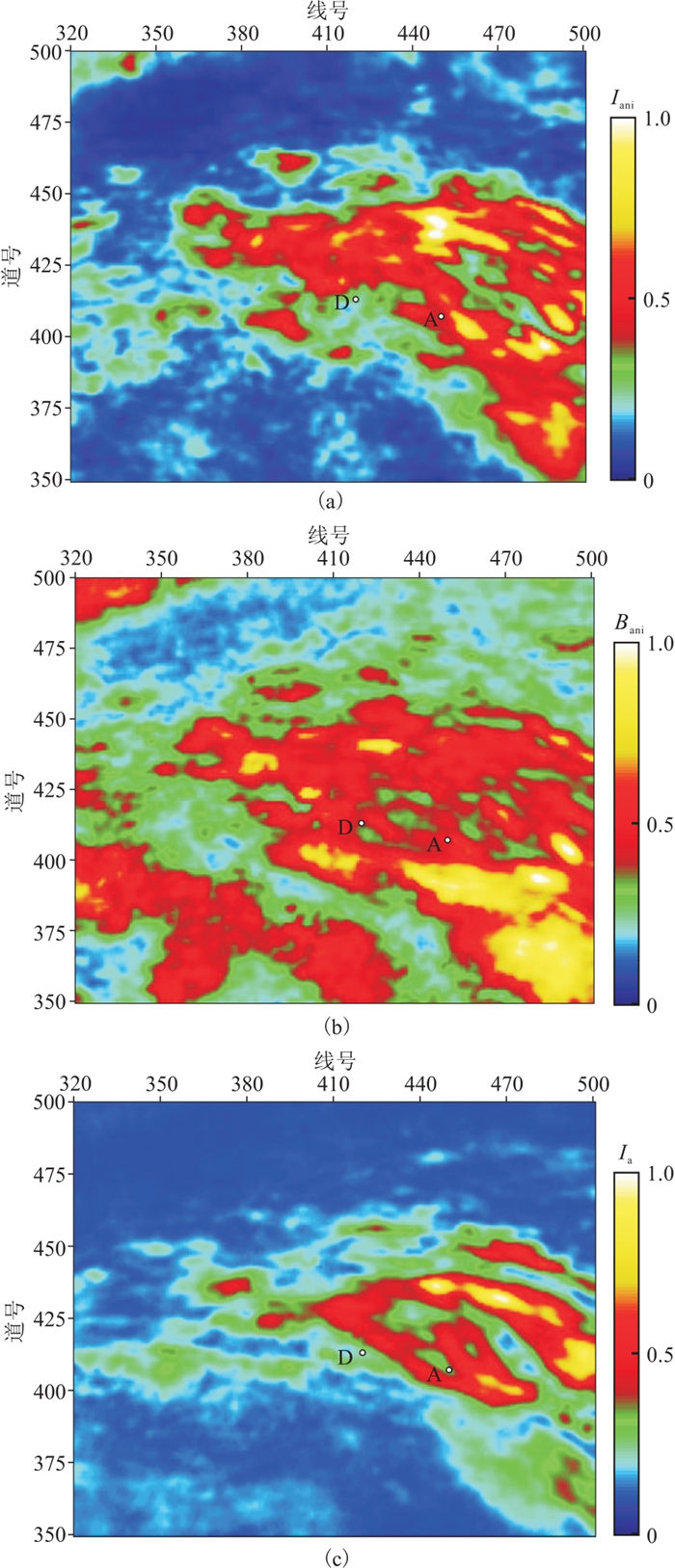
研究区内A井是一口高产井,日产气量为
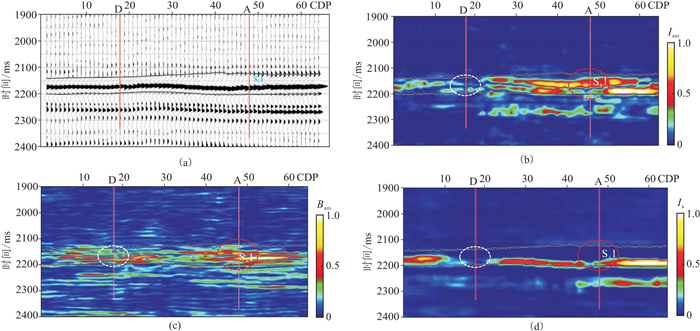
|
图 17 过A井、D井的叠后地震剖面和不同方法反演结果对比 (a)叠后剖面;(b)本文方法反演的正交各向异性梯度频散属性 |
由图 17可见,A井处目标储层的正交各向异性频散幅值
各向异性梯度
FDAVO反演是一种广泛用于流体识别的方法,可根据不同的Zoeppritz方程近似式估算多种频散属性。本文采用基于Shuey近似式[32]推导的纵波速度频散属性
从反演结果平面图(图 18)看,
|
图 18 研究区不同方法储层反演结果 (a)本文方法,正交各向异性梯度频散属性 |
综上所述,
本文基于Chapman双裂缝模型,分析了不同饱和度情况下流体的频率、入射角和方位角等参数与弹性参数的关系,提出了正交各向异性介质频变AVAZ反演方法,并将其应用于四川盆地五百梯页岩储层的裂缝含气性预测,得出以下结论。
(1) 当其他参数保持一致时,含水储层弹性参数的频散程度远小于含气储层,说明利用各向异性频散属性可识别流体类型。此外,弹性参数的频散程度随地震波入射角的增加而减小,随方位角的增加呈现周期性变化,当地震波传播方向与垂直裂缝的法向平行时,频散程度出现最大值。
(2) 本文OA-FDAVAZ反演方法考虑了地震数据的方位和频率信息,通过高分辨率谱分解技术和最小二乘法,得到了正交各向异性频散属性,并提出频散组合因子的计算方法。
(3) 理论模型测试表明含水和含气裂缝层均表现出高值异常,但含气层的频散值要明显高于含水层,可见正交各向异性频散属性不仅对流体敏感,而且易于区分不同类型的流体。
(4) 相比于常规AVAZ反演和FDAVO反演,本文方法在实际资料应用中更能准确地刻画含气储层的分布。
| [1] |
MARTINS J L. Elastic impedance in weakly anisotropic media[J]. Geophysics, 2006, 71(3): D73-D83. DOI:10.1190/1.2195448 |
| [2] |
刘敬寿, 丁文龙, 肖子亢, 等. 储层裂缝综合表征与预测研究进展[J]. 地球物理学进展, 2019, 34(6): 2283-2300. LlU Jingshou, DING Wenlong, XIAO Zikang, et al. Advances in comprehensive characterization and prediction of reservoir fractures[J]. Progress in Geophysics, 2019, 34(6): 2283-2300. |
| [3] |
GUO Z Q, ZHAO D Y, LIU C. A new seismic inversion scheme using fluid dispersion attribute for direct gas identification in tight sandstone reservoirs[J]. Remote Sensing, 2022, 14(21): 5326. DOI:10.3390/rs14215326 |
| [4] |
ZONG Z Y, JI L X. Model parameterization and amplitude variation with angle and azimuthal inversion in orthotropic media[J]. Geophysics, 2021, 86(1): R1-R14. |
| [5] |
刘晓晶, 陈祖庆, 陈超, 等. 方位弹性阻抗傅里叶级数裂缝预测方法[J]. 石油地球物理勘探, 2022, 57(2): 423-433. LIU Xiaojing, CHEN Zuqing, CHEN Chao, et al. Fracture prediction method based on Fourier series of azimuthal elastic impedance[J]. Oil Geophysical Prospecting, 2022, 57(2): 423-433. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.019 |
| [6] |
BAKULIN A, GRECHKA V, TSVANKIN I. Estimation of fracture parameters from reflection seismic data—Part Ⅱ: Fractured models with orthorhombic symmetry[J]. Geophysics, 2000, 65(6): 1803-1817. DOI:10.1190/1.1444864 |
| [7] |
PŠENČIK I, MARTINS J L. Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media[J]. Studia Geophysica et Geodaetica, 2001, 45(2): 176-199. DOI:10.1023/A:1021868328668 |
| [8] |
BACHRACH R. Uncertainty and nonuniqueness in linearized AVAZ for orthorhombic media[J]. The Leading Edge, 2015, 34(9): 1048-1056. DOI:10.1190/tle34091048.1 |
| [9] |
潘新朋, 张广智, 印兴耀. 岩石物理驱动的正交各向异性方位叠前地震反演方法[J]. 中国科学(地球科学), 2018, 48(3): 299-314. PAN Xinpeng, ZHANG Guangzhi, YIN Xingyao. Azimuthally pre-stack seismic inversion for orthorhombic anisotropy driven by rock physics[J]. Scientia Sinica (Terrae), 2018, 48(3): 299-314. |
| [10] |
SMITH G C, GIDLOW P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophysical Prospecting, 1987, 35(9): 993-1014. DOI:10.1111/j.1365-2478.1987.tb00856.x |
| [11] |
印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34, 46. YIN Xingyao, CAO Danping, WANG Baoli, et al. Research progress of fluid discrimination with pre‑stack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34, 46. |
| [12] |
谢春辉, 雍学善, 杨午阳, 等. 裂缝型储层流体识别方法[J]. 地球物理学报, 2015, 58(5): 1776-1784. XIE Chunhui, YONG Xueshan, YANG Wuyang, et al. The method for identification of fluid in fractured reservoirs[J]. Chinese Journal of Geophysics, 2015, 58(5): 1776-1784. |
| [13] |
FATTI J L, SMITH G C, VAIL P J, et al. Detection of gas in sandstone reservoirs using AVO analysis: A 3‑D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [14] |
GOODWAY B, CHEN T, DOWNTON J. Improved AVO fluid detection and lithology discrimination using lamé petrophysical parameters; "λρ", "μρ", &"λ/μ fluid stack", from P and S inversions[C]. SEG Technical Program Expanded Abstracts, 1997, 16: 183-186.
|
| [15] |
GRAY D. Elastic inversion for Lamé parameters[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 197-200.
|
| [16] |
RUSSELL B H, HEDLIN K, HILTERMAN F J. Fluid‑property discrimination with AVO: A Biot‑ Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [17] |
CASTAGNA J P, SUN S J, SIEGFRIED R W. Instantaneous spectral analysis: detection of low‑ frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127. DOI:10.1190/1.1559038 |
| [18] |
TANER M T, KOEHLER F, SHERIFF R E. Complex seismic trace analysis[J]. Geophysics, 1979, 44(6): 1041-1063. DOI:10.1190/1.1440994 |
| [19] |
EBROM D. The low-frequency gas shadow on seismic sections[J]. The Leading Edge, 2004, 23(8): 772. DOI:10.1190/1.1786898 |
| [20] |
CHAPMAN M, MAULTZSCH S, LIU E R, et al. The effect of fluid saturation in an anisotropic multi‑scale equant porosity model[J]. Journal of Applied Geophysics, 2003, 54(3/4): 191-202. |
| [21] |
张金伟, 丁仁伟, 林年添, 等. 裂缝性多孔介质纵波频变特性研究[J]. 石油地球物理勘探, 2022, 57(5): 1097-1104. ZHANG Jinwei, DING Renwei, LIN Niantian, et al. Frequency-dependent characteristics of P-wave infractured porous media[J]. Oil Geophysical Prospecting, 2022, 57(5): 1097-1104. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.010 |
| [22] |
SHUAI D, STOVAS A, WEI J X, et al. Frequency-dependent anisotropy due to two orthogonal sets of mesoscale fractures in porous media[J]. Geophysical Journal International, 2019, 221(1): 1450-1467. |
| [23] |
WILSON A, CHAPMAN M, LI X Y. Frequency‑depen‑ dent AVO inversion[J]. SEG Technical Program Expanded Abstracts, 2009, 28: 341-345. |
| [24] |
吴小羊. 基于频谱分析技术的频散AVO反演研究[D]. 北京: 中国地质大学(北京), 2010. WU Xiaoyang. Frequency Dependent AVO Inversion Using Spectral Decomposition Techniques[D]. China University of Geosciences(Beijing), Beijing, 2010. |
| [25] |
程冰洁, 徐天吉, 李曙光. 频变AVO含气性识别技术研究与应用[J]. 地球物理学报, 2012, 55(2): 608-613. CHENG Bingjie, XU Tianji, LI Shuguang. Research and application of frequency dependent AVO analysis for gas recognition[J]. Chinese Journal of Geophysics, 2012, 55(2): 608-613. |
| [26] |
罗鑫, 陈学华, 张杰, 等. 基于依赖频率AVO反演的高含气饱和度储层预测方法[J]. 石油地球物理勘探, 2019, 54(2): 356-364. LUO Xin, CHEN Xuehua, ZHANG Jie, et al. High gas-saturation reservoir prediction based on frequency-dependent AVO inversion[J]. Oil Geophysical Prospecting, 2019, 54(2): 356-364. DOI:10.13810/j.cnki.issn.1000-7210.2019.02.014 |
| [27] |
ZHANG J W, HUANG H D, ZHU B H, et al. Fluid identification based on P-wave anisotropy dispersion gradient inversion for fractured reservoirs[J]. Acta Geophysica, 2017, 65(5): 1081-1093. DOI:10.1007/s11600-017-0088-8 |
| [28] |
AJAZ M, OUYANG F, WANG G H, et al. Fluid identification and effective fracture prediction based on frequency-dependent AVOAZ inversion for fractured reservoirs[J]. Petroleum Science, 2021, 18(4): 1069-1085. DOI:10.1016/j.petsci.2021.07.011 |
| [29] |
CHAPMAN M. Modeling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy[J]. Geophysics, 2009, 74(6): D97-D103. DOI:10.1190/1.3204779 |
| [30] |
TSVANKIN I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media[M]. Pergamon, New York, 2001.
|
| [31] |
CHAPMAN M. Frequency‑dependent anisotropy due to meso-scale fractures in the presence of equant porosity[J]. Geophysical Prospecting, 2003, 51(5): 369-379. DOI:10.1046/j.1365-2478.2003.00384.x |
| [32] |
ZHANG S X, YIN X Y, ZHANG G Z. Dispersion-dependent attribute and application in hydrocarbon detection[J]. Journal of Geophysics and Engineering, 2011, 8(4): 498-507. DOI:10.1088/1742-2132/8/4/002 |



 程冰洁,四川省成都市成华区二仙桥东三路一号成都理工大学地球物理学院,610059。Email:
程冰洁,四川省成都市成华区二仙桥东三路一号成都理工大学地球物理学院,610059。Email: