为了缓解地震数据高、低频信息缺失问题[1],在带限地震数据反演过程中广泛应用约束和正则化策略,包括模型参数的先验假设、地质先验约束等[2-3],以从不适定反问题中获取更合理的解。对基于模型的反演方法而言,合理的初始模型不仅可以补偿缺失的地震低频信息,也能提高地震反演精度和稳定性[4]。因此,获取可靠的初始模型一直是研究热点。然而,在无井或少井区,地球物理反演面临数据匮乏、资料品质不高的问题,难以直接从井数据中得到较丰富的低频信息,因此获取低频模型是无井区地球物理反演和油藏特征描述的关键。
近年来,基于速度场建立无井区低频模型的方法得到广泛发展[5-6],利用高密度速度分析[7]、叠前深度偏移[8]等方法提高了速度场精度,建立了频带更宽、更符合实际地层变化特征的伪井曲线[6, 9-10],在砂体刻画和水合物预测中取得较好效果。此外,基于离散反演理论的有色反演方法[11-12]缓解了地震反演对初始模型和地震子波的依赖性,提高了无井区储层岩性解释的可靠性。
从地震频谱中挖掘更多的低频信息是填补低频分量空白的另一种方法。目前,压缩感知[13]、小波变换[14-15]、匹配追踪[16]等信号处理手段成为地震资料拓频的主流方法,但这些方法难以避免地震子波的影响,且处理后地震数据的波组特征不明确[17]。近年来,根据拉普拉斯变换引起的梯度相关的畸变现象,开始利用复频域反演策略[11, 18-19]挖掘地震频带中低于5 Hz的低频分量,并发展了对初始模型精度不敏感的拉普拉斯域贝叶斯阻抗反演方法[20-22],减少了地震反演的模型依赖问题。随着油气勘探、开发精度要求的提高,高分辨率、宽频带、高信噪比地震数据逐渐成为新区勘探的主流资料,为无井区宽频地震复频域反演方法奠定了坚实的数据基础。
本文针对新区勘探探索了一种基于地质模型的无井区复频域地震反演方法。在现有地质认识和地震资料的基础上建立初始地质模型,并利用宽频地震复频域反演策略挖掘地震数据的低频信息,以补充初始模型的低频能量,得到符合地质认识的复频域初始低频模型。最后,利用模型和实际工区数据测试了新方法的效果。
1 技术方法 1.1 无井区地质建模低频模型能够补充地震数据缺失的低频信息,对反演结果具约束作用。若不加模型约束,则难以控制随机反演结果。如,缺失层位信息约束时,反演的高阻抗层仅为一个数值结果,可能与实际地层形态相去甚远。因此,为提高无井区反演结果的可靠性,必须综合无井区现有地震、地质资料建立符合地质认识的初始低频模型。
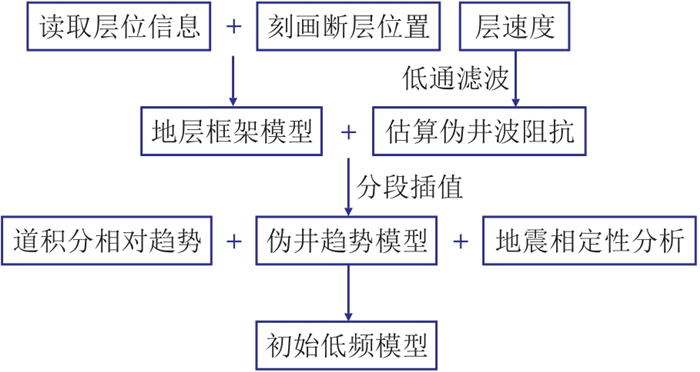
在勘探区无井或者少井的情况下,无法采用井插值方法建立低频模型。在无井区往往将拾取的叠加速度近似作为均方根速度,并利用DIX公式[23]转化为层速度,以此建立初始低频模型,进而补充地震数据的低频成分。在常规层速度建模的基础上,本文在初始模型建立流程中补充地质信息(图 1)。
|
图 1 初始地质模型建模流程 |
建立初始地质模型的步骤如下。
(1)层位解释
利用现有的层位信息搭建层位框架模型。层位时间信息蕴含着地层的构造特征,当地层正常沉积时,同一套地层的时间厚度越大,往往沉积越稳定,且位于沉积盆地的中心位置。因此,建模过程按照层位框架模型插值,以保证初始模型与实际地下构造吻合。
(2)断层解释
在碎屑岩地层中,若地下存在明显的断层,会导致断层两侧相邻地层出现波阻抗突变现象。若在断层发育区不考虑这种突变现象而直接插值,得到的初始模型将与实际地层不吻合。在无井或少井的勘探新区,从地震剖面上寻找明显的地层错动位置,将断层信息补充到层位框架中,以期获得合理的地层结构框架。补充断层信息的地层结构框架将目的层段分为多个部分,考虑了断层两侧地质体的不连续现象,提高了无井区初始模型的可靠性。
(3)建立伪井阻抗曲线
按照地层结构框架在目的层段选定合适的伪井点位,在伪井点处用DIX公式将叠加速度转化为层速度。假设层速度与地层阻抗呈线性相关,按量纲将层速度曲线转化为伪井波阻抗曲线。
(4)定性分析地震相指导模型修正
利用研究区地质资料和地震相分析结果初步圈定储层发育有利区块、定性指示靶区的层序分布,为无井区伪井阻抗曲线提供可靠的参考趋势。将由地震相得到的阻抗趋势与由层速度建立的阻抗曲线按合理权重融合,获得符合工区地质认识的伪井阻抗曲线,大大提高了无井区反演稳定性。
(5)层速度模型建立
在正常沉积环境下,地层波阻抗的横向变化是连续的。为贴合实际地层阻抗横向变化趋势,反演采用多点插值法在层位框架的各个地层分块将伪井曲线内插、外推,以克服线性插值在伪井点的数值突变问题,得到更合理的伪井趋势模型。
(6)融合道积分[24]相对趋势
与层速度建立的初始模型相比,通过道积分方法计算的相对阻抗的横向分辨率更高,可反映地下地层的相对变化细节。因此,考虑将道积分得到的相对波阻抗进行低通滤波,通过加权法将道积分低频趋势加入无井区的低频模型,以改善无井区建模的可靠性。当工区地震资料品质较差时,该步骤可以省略。
以上步骤为无井区初始地质模型的建立流程。和常规无井建模方法相比,上述流程考虑了断层影响,参考地震相定性指导宏观趋势,融合了道积分的低频相对变化,充分运用了无井区的地质、地震数据,为无井区反演提供了可靠的低频信息。
1.2 复频域反演方法地震数据时频特性研究表明:低频缺失导致地震子波旁瓣增大,从而使反射剖面出现虚假同相轴;高频缺失导致子波主瓣变胖进而使反射同相轴变粗,造成地层边界更光滑,降低了对地层边界的刻画精度[11, 18, 25-26]。宽频地震数据具有丰富的低频成分,可以降低子波旁瓣的幅值,从而减小相邻反射同相轴的叠加干扰,反演结果较常规地震数据更准确[19]。
2010年,Shin等[19]发现拉普拉斯变换可增大地震数据的低频能量现象,并引入地球物理数据处理。拉普拉斯变换将时域地震信号转换到复频域(也称拉普拉斯域),是复频域反演的基础理论,可以表示为
| $ \begin{array}{l}Y\left(s\right)={\int }_{0}^{+\mathrm{\infty }}y\left(t\right){\mathrm{e}}^{-st}\mathrm{d}t\\ \begin{array}{cc}& \end{array}={\int }_{0}^{+\mathrm{\infty }}y\left(t\right){\mathrm{e}}^{-\sigma t}{\mathrm{e}}^{-\mathrm{i}\omega t}\mathrm{d}t\end{array} $ | (1) |
式中:
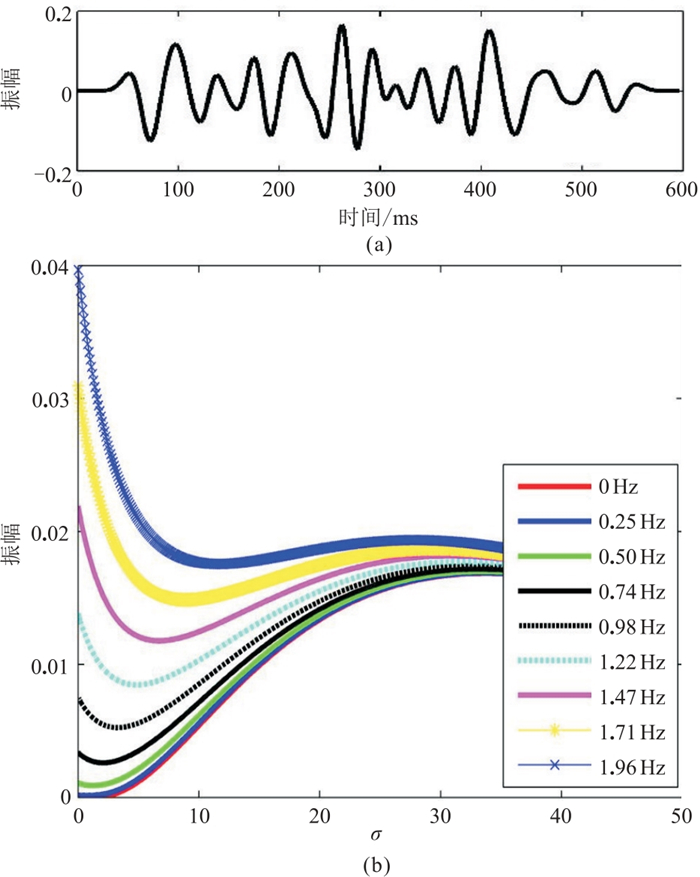
|
图 2 复频域低频能量增大现象示意图 (a)单道地震数据;(b)地震低频响应随着σ的变化曲线 |
褶积模型揭示了地震数据y(t)、子波w(t)和反射系数m(t)之间的关系[23]
| $ y\left(t\right)={\int }_{0}^{+\mathrm{\infty }}w(t-\tau )m\left(\tau \right)\mathrm{d}\tau $ | (2) |
式中τ为时间延迟。根据拉普拉斯变换的时移性质,联立式(1)、式(2)并交换积分顺序,则
| $ Y\left(s\right)=W(\sigma +\mathrm{i}\omega ){\int }_{0}^{+\mathrm{\infty }}m\left(t\right){\mathrm{e}}^{-\sigma t}{\mathrm{e}}^{-\mathrm{i}\omega t}\mathrm{d}t $ | (3) |
式中:
假设有L个频率分量,为方便讨论,令角频率为
| $ {\mathit{\boldsymbol{Y}}}_{{\omega }_{j}}={\mathit{\boldsymbol{W}}}_{{\omega }_{j}}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{E}}}_{{\omega }_{j}}\mathit{\boldsymbol{m}} $ | (4) |
式中:m为待反演模型参数;
| $ \left\{\begin{array}{l}{{\boldsymbol{W}}}_{{\omega }_{j}}=\left(\begin{array}{cccc}W({\sigma }_{1}+{\rm{i}}{\omega }_{j})& 0& \cdots & 0\\ 0& W({\sigma }_{2}+{\rm{i}}{\omega }_{j})& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& 0& \cdots & W({\sigma }_{K}+{\rm{i}}{\omega }_{j})\end{array}\right)\\ {{\boldsymbol{E}}}_{{\omega }_{j}}=\left(\begin{array}{cccc}{\rm{e}}^{-{\rm{i}}{t}_{1}{\omega }_{j}}& 0& \cdots & 0\\ 0& {\rm{e}}^{-{\rm{i}}{t}_{2}{\omega }_{j}}& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& 0& \cdots & {\rm{e}}^{-{\rm{i}}{t}_{n}{\omega }_{j}}\end{array}\right)\\ {\boldsymbol{C}}=\left(\begin{array}{cccc}{\rm{e}}^{-{t}_{1}{\sigma }_{1}}& {\rm{e}}^{-{t}_{2}{\sigma }_{1}}& \cdots & {\rm{e}}^{-{t}_{n}{\sigma }_{1}}\\ {\rm{e}}^{-{t}_{1}{\sigma }_{2}}& {\rm{e}}^{-{t}_{2}{\sigma }_{2}}& \cdots & {\rm{e}}^{-{t}_{n}{\sigma }_{2}}\\ \vdots & \vdots & \ddots & \vdots \\ {\rm{e}}^{-{t}_{1}{\sigma }_{K}}& {\rm{e}}^{-{t}_{2}{\sigma }_{K}}& \cdots & {\rm{e}}^{-{t}_{n}{\sigma }_{K}}\end{array}\right)\end{array}\right. $ | (5) |
式中:
复频域地震正演算子为
| $ \underset{{\boldsymbol{Y}}}{\underbrace{\left(\begin{array}{c}{{\boldsymbol{Y}}}_{{\omega }_{1}}\\ {{\boldsymbol{Y}}}_{{\omega }_{2}}\\ \vdots \\ {{\boldsymbol{Y}}}_{{\omega }_{L}}\end{array}\right)}}=\underset{{\boldsymbol{G}}}{\underbrace{\left(\begin{array}{cccc}{\mathit{\boldsymbol{W}}}_{{\omega }_{1}}\mathit{\boldsymbol{C}}& 0& \cdots & 0\\ 0& {\mathit{\boldsymbol{W}}}_{{\omega }_{2}}\mathit{\boldsymbol{C}}& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& 0& \cdots & {\mathit{\boldsymbol{W}}}_{{\omega }_{L}}\mathit{\boldsymbol{C}}\end{array}\right)}}\underset{{\boldsymbol{E}}}{\underbrace{\left(\begin{array}{c}{\mathit{\boldsymbol{E}}}_{{\omega }_{1}}\\ {\mathit{\boldsymbol{E}}}_{{\omega }_{2}}\\ \vdots \\ {\mathit{\boldsymbol{E}}}_{{\omega }_{L}}\end{array}\right)}}\mathit{\boldsymbol{m}} $ | (6) |
式中:
贝叶斯理论[28-29]组合似然函数和先验概率分布,有助于从不适定反问题中获取更可靠的解。将贝叶斯理论引入复频域地震正演算子建立模型参数映射方程,推导基于贝叶斯理论的复频域反演目标泛函[3, 26]。假设拉普拉斯域地震随机噪声符合Gaussian概率密度分布、模型参数的先验概率分布服从Cauchy分布[27],则后验概率密度分布
| $ p\left({\boldsymbol{m}}\left|{\boldsymbol{Y}}\right.\right)=\\ \ \ \ \frac{1}{({\rm{ \mathsf{ π}}}{\sigma }_{\mathit{\boldsymbol{m}}}{)}^{n}}{\mathrm{e}}^{-\sum\limits_{i=1}^{n}\mathrm{l}\mathrm{n}\left(1+\frac{{m}_{i}^{2}}{{\sigma }_{\mathit{\boldsymbol{m}}}^{2}}\right)}\frac{1}{(2{\rm{ \mathsf{ π}}}{\sigma }_{\mathrm{R}}^{2}{)}^{KL}}{\mathrm{e}}^{-{(\mathit{\boldsymbol{Y}}-{\boldsymbol{GEm}})}^{\mathrm{T}}(\mathit{\boldsymbol{Y}}-{\boldsymbol{GEm}})/\left(2{\sigma }_{\mathrm{R}}^{2}\right)} $ | (7) |
式中:
根据指数函数的单调递增性质,令
| $ \mathit{\boldsymbol{m}}={\left[{\left({\boldsymbol{GE}}\right)}^{\mathrm{T}}\left({\boldsymbol{GE}}\right)+4\frac{{\sigma }_{\mathrm{R}}^{2}}{{\sigma }_{\mathit{\boldsymbol{m}}}^{2}}\mathit{\boldsymbol{Q}}\right]}^{-1}\left[{\left({\boldsymbol{GE}}\right)}^{\mathrm{T}}\mathit{\boldsymbol{Y}}\right] $ | (8) |
式中Q为正则化对角矩阵,对角线元素为
| $ \begin{array}{l}\mathit{\boldsymbol{m}}={\left[{\left({\boldsymbol{GE}}\right)}^{\mathrm{T}}\left({\boldsymbol{GE}}\right)+4\frac{{\sigma }_{\mathrm{R}}^{2}}{{\sigma }_{\mathit{\boldsymbol{m}}}^{2}}\mathit{\boldsymbol{Q}}+{\varepsilon }^{2}{{\boldsymbol{D}}}^{\mathrm{T}}{\boldsymbol{D}}\right]}^{-1}\times \\ \ \ \ \ \ \ \ \begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\left[{\left({\boldsymbol{GE}}\right)}^{\mathrm{T}}{\boldsymbol{Y}}+{\varepsilon }^{2}{{\boldsymbol{D}}}^{\mathrm{T}}\mathit{\boldsymbol{ \boldsymbol{\varsigma} }}\right]\end{array} $ | (9) |
式中:
综上所述,本文提出的复频域无井建模流程(图 3)可以表述为:根据复频域反演挖掘地震数据低频信息,将无井初始模型作为复频域反演的低频模型,结合盲信号理论[30]提取地震盲子波,最终得到补充低频信息的复频域无井低频模型。

|
图 3 复频域无井低频模型建模流程 |
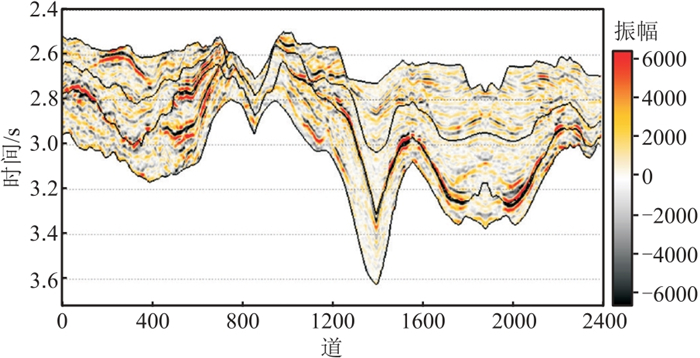
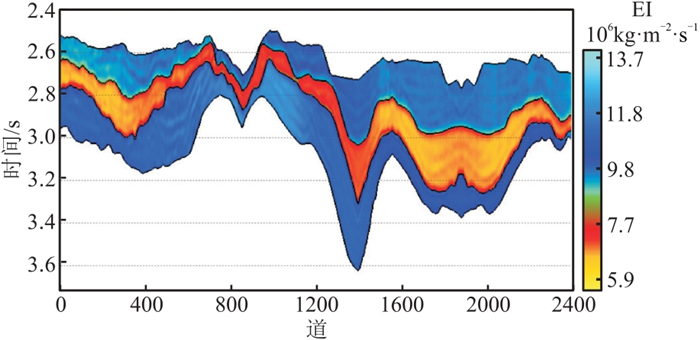
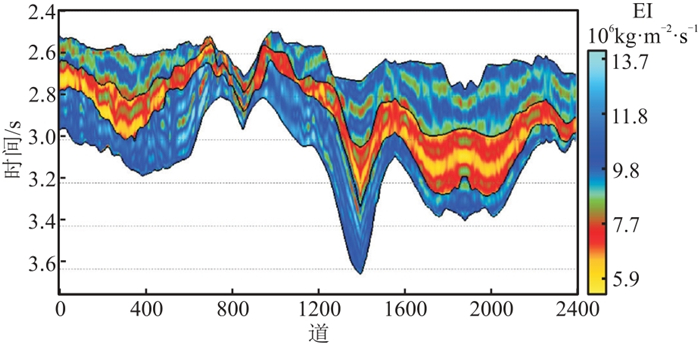
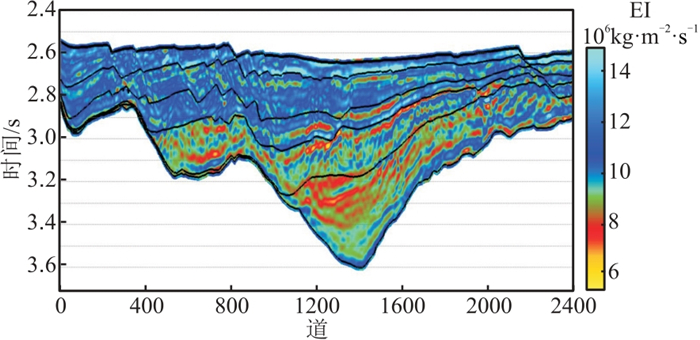
为验证所提方法的适用性,在中国南方L区开展复频域无井反演测试。图 4为L区小角度地震剖面,根据图 4和地质认识,判断沉积盆地目标层段为有利烃源岩发育部位,结合道积分低频趋势得到初始地质模型(图 5)。将图 5作为输入,根据复频域反演策略挖掘地震信号的低频成分, 获得复频域低频模型(图 6),新模型的精度较图 5明显提高。最终得到复频域无井小角度弹性阻抗(EI)反演结果(图 7),可见其低频趋势与图 5相近,表明图 5控制图 7的低频趋势,即初始地质模型的精度对反演结果的影响不可忽视。因此,对于无井区储层预测,综合利用现有的地质与地震信息建立合理、可靠的初始低频模型是成功反演的关键。
|
图 4 L区小角度地震剖面 |
|
图 5 L区初始地质模型 |
|
图 6 L区复频域低频模型 |
|
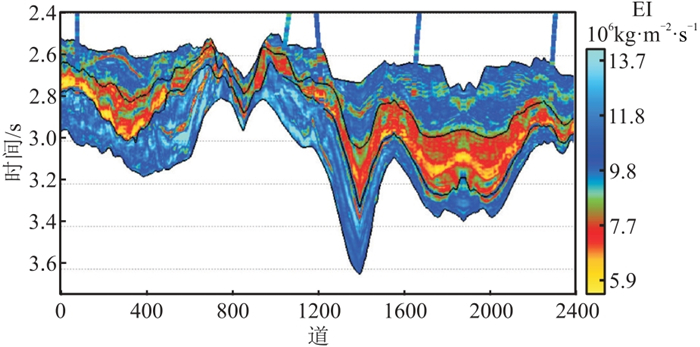
图 7 L区复频域无井小角度EI反演结果 |
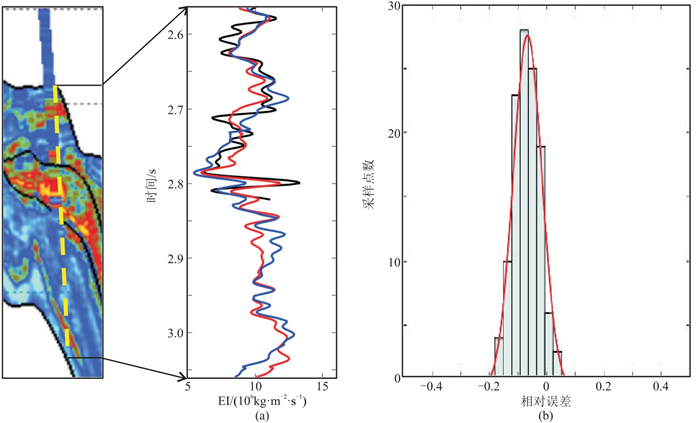
为进一步验证反演效果,对图 7井旁道开展误差分析,结果(图 8)表明,尽管复频域无井反演效果略差于有井参与的稀疏脉冲反演,但反演结果和井段整体匹配良好,相对误差小于20%(图 8b),预测效果较满意。
|
图 8 复频域无井EI反演结果误差分析 (a)3号井井段EI反演曲线;(b)EI反演结果误差分布直方图 图a黑线为井上EI曲线,红线为有井稀疏脉冲反演EI曲线,蓝线为复频域无井反演EI曲线。图b蓝色区域为复频域无井反演结果的相对误差统计分布,红线为根据高斯概率分布估计得到的相对误差后验概率密度分布,图 11同。 |
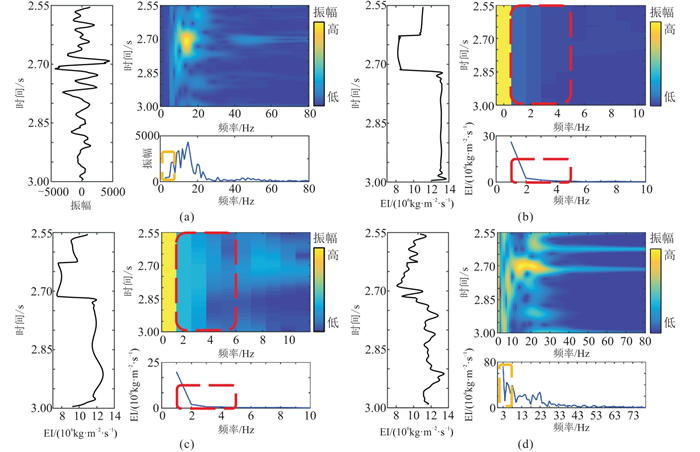
针对无井或少井区资料匮乏的情况,本文所提方法利用拉普拉斯域地震低频能量迅速增大的特点,在反演中提高了低频信息的权重,可以挖掘地震数据低频信息。为研究该方法的拓频效果,针对L区复频域无井反演剖面开展时频分析(图 9)。可见:①L区地震数据频带为5~60 Hz(图 9a左、图 9a右下),初始地质模型的频带为0~3 Hz(图 9b左、图 9b右下),复频域低频模型频带为1~8 Hz(图 9c左、图 9c右下),复频域反演结果频带为0~60 Hz(图 9d左、图 9d右下)。②对比图 9a右下和图 9d右下的低频端能量(橙色方框处)发现,前者缺少5 Hz以下的能量,后者不仅补充了图 9b右下的0~3 Hz的能量,而且提高了3~5 Hz频段的低频能量。③对比初始地质模型(图 9b右上)和复频域低频模型(图 9c右上)的S变换时频图可知,后者在一定程度上拓宽了低频模型的频带范围(红色方框处),为无井区地震反演提供了更丰富的低频信息。
|
图 9 L区复频域无井反演剖面单道数据(左)的S变换时频图(右上)及频谱(右下) (a)小角度地震数据;(b)初始地质模型;(c)复频域低频模型;(d)复频域反演结果 |
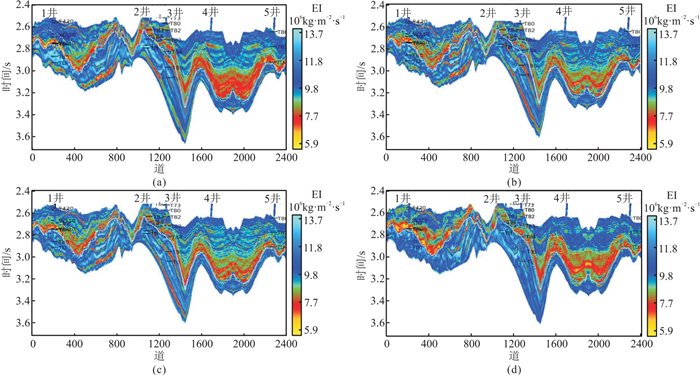
为测试复频域无井反演策略的效果,采用稀疏脉冲反演方法反演L区同一套地震数据。图 10为有井稀疏脉冲反演结果和复频域无井反演结果,图 11为不同井参与反演的误差分析直方图。由图可见:①复频域无井反演结果(图 10d)与稀疏脉冲反演结果(图 10a~图 10c)的总体趋势一致,成功预测了目的层的低阻抗特征,但图 10d的剖面细节与图 10a~图 10c存在一定差别。②稀疏脉冲反演结果(图 11a~图 11c)与井匹配更好,而复频域无井反演结果的相对误差也小于20%(图 11d),可以满足勘探新区地质评价的需要。
|
图 10 有井稀疏脉冲反演结果和复频域无井反演结果 (a)5口井;(b)3口井;(c)单井;(d)复频域无井 |

|
图 11 不同井参与反演的误差分析直方图 (a)5口井;(b)3口井;(c)单井;(d)复频域无井 |
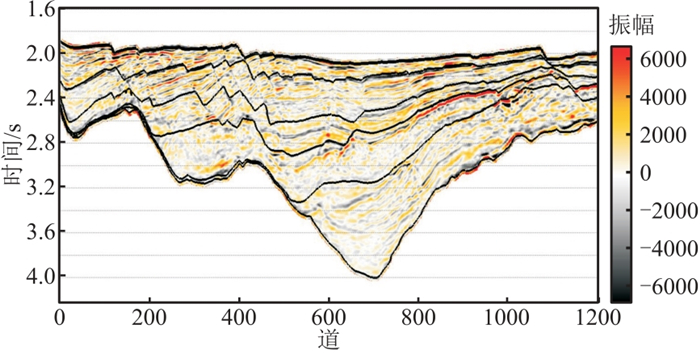
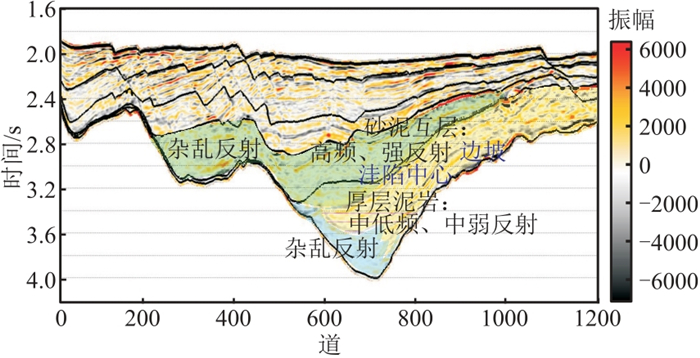
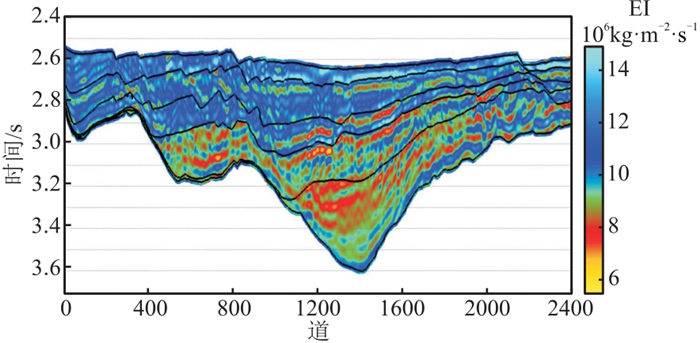
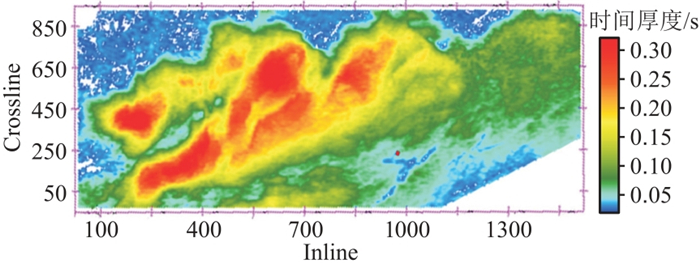
图 12为中国南方H区的小角度地震剖面,该区没有井数据,应用复频域无井反演策略预测泥岩,获得地震相和地质分析图(图 13)。可见:地震剖面下部的滨浅湖相为沉积中心,且地震剖面的顶、底强反射及中间弱反射指示大套泥岩;从洼陷中心到边坡存在大量断点或连续反射,受构造影响明显,推断物源方向为从右向左。根据上述地质认识,构建了复频域低频模型(图 14),并根据复频域无井反演策略,得到复频域无井小角度EI反演结果(图 15)。根据泥质含量(图 16)与叠前弹性阻抗的经验关系预测泥岩厚度(图 17),结果与钻井数据一致。上述结果验证了基于地质模型的无井区复频域反演方法的可行性,为无井或少井区储层预测提供了新思路。
|
图 12 H区小角度地震剖面 |
|
图 13 地震相和地质分析图 |
|
图 14 复频域低频模型 |
|
图 15 复频域无井小角度EI反演结果 |

|
图 16 泥质含量预测结果 |
|
图 17 泥岩厚度刻画结果 |
(1)在无井或少井区,利用层位框架、断层解释、叠加速度和地质认识构建符合工区沉积特征的初始地质模型,可以提高反演精度。
(2)宽频地震数据的低频成分在拉普拉斯域反演过程中,在一定的衰减系数序列下产生低频能量权重增加的现象,有助于提高复频域的低频恢复能力。在无井区,建立准确的初始地质模型并结合宽频地震复频域叠前反演优化算法可以缓解低频缺失问题,从而获得更可靠的低频趋势。
(3)复频域无井反演弹性阻抗与井上弹性阻抗曲线拟合良好,与有井稀疏脉冲反演结果相比,尽管局部精度略低,但复频域无井反演结果的总体趋势及储层展布特征与有井反演结果基本一致,证明了所提方法在无井区的有效性。
| [1] |
KROODE F T, BERGLER S, CORSTEN C, et al. Broadband seismic data-The importance of low frequencies[J]. Geophysics, 2013, 78(2): WA3-WA14. DOI:10.1190/geo2012-0294.1 |
| [2] |
HAMID H, PIDLISECKY A. Multitrace impedance inversion with lateral constraints[J]. Geophysics, 2015, 80(6): M101-M111. DOI:10.1190/geo2014-0546.1 |
| [3] |
TARANTOLA A. Inverse Problem Theory and Me- thods for Model Parameter Estimation[M]. Society for Industrial and Applied Mathematics, Philadelphia, PA, United States, 2005.
|
| [4] |
李坤, 印兴耀, 宗兆云. 利用平滑模型约束的频率域多尺度地震反演[J]. 石油地球物理勘探, 2016, 51(4): 760-768. LI Kun, YIN Xingyao, ZONG Zhaoyun. Seismic multi-scale inversion in the frequency domain based on smooth model constraint[J]. Oil Geophysical Prospec- ting, 2016, 51(4): 760-768. DOI:10.13810/j.cnki.issn.1000-7210.2016.04.018 |
| [5] |
张京思, 王明臣, 李瑞. 叠前无井弹性参数反演技术及其应用[J]. 工程地球物理学报, 2013, 10(1): 66-70. ZHANG Jingsi, WANG Mingchen, LI Rui. The pre-stack without well elastic parameter inversion technique and its application[J]. Chinses Journal of Engineering Geophysics, 2013, 10(1): 66-70. |
| [6] |
唐志远, 郭清正, 刘国昌. 一种无井反演方法在印度河盆地储层预测中的应用[J]. 物探化探计算技术, 2018, 40(3): 324-329. TANG Zhiyuan, GUO Qingzheng, LIU Guochang. A well-absent seismic inversion method and its application on the early exploration of South Asia Indus basin reservoir[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2018, 40(3): 324-329. |
| [7] |
徐云霞, 张宝金, 文鹏飞. 高密度速度分析方法在水合物无井约束波阻抗反演中的应用研究[J]. 物探化探计算技术, 2016, 38(4): 540-545. XU Yunxia, ZHANG Baojin, WEN Pengfei. The application research of high density velocity analysis inhydrate impedance inversion without log constrain[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2016, 38(4): 540-545. |
| [8] |
李元平, 颜承志, 李杰, 等. 宽频地震无井反演技术在神狐海域天然气水合物矿体描述中的应用[J]. 中国海上油气, 2019, 31(1): 51-60. LI Yuanping, YAN Chengzhi, LI Jie, et al. Application of well-free broadband seismic inversion technology on the description of gas hydrate orebody in Shenhu waters, South China Sea[J]. China Offshore Oil and Gas, 2019, 31(1): 51-60. |
| [9] |
杨瑞召, 李松楠, 王媛媛, 等. 无井约束反演在神狐海域水合物预测中的应用[J]. 天然气地球科学, 2012, 23(4): 784-790. YANG Ruizhao, LI Songnan, Wang Yuanyuan, et al. Application of inversion without well constraint to hydrate forecasting in Shenhu area[J]. Natural Gas Geoscience, 2012, 23(4): 784-790. |
| [10] |
支玲, 安勇, 文阳, 等. 虚拟井技术在深水无井区储层预测中的研究及应用[C]. 2014年中国地球科学联合学术年会——专题18: 油藏地球物理论文集, 2014, 1061.
|
| [11] |
曹书红, 陈景波. 频率域全波形反演中关于复频率的研究[J]. 地球物理学报, 2014, 57(7): 2302-2313. CAO Shuhong, CHEN Jingbo. Studies on complex frequencies in frequency domain full waveform inversion[J]. Chinese Journal of Geophysics, 2014, 57(7): 2302-2313. |
| [12] |
李怀懿, 王新, 江建虹, 等. 无井地震梯次反演方法研究[J]. 物探化探计算技术, 2021, 43(2): 147-153. LI Huaiyi, WANG Xin, JIANG Jianhong, et al. Research on the method of well-free cascade inversion[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2021, 43(2): 147-153. |
| [13] |
刘可, 尹成. 地震数据低频补偿方法研究及应用[J]. 中国石油和化工标准与质量, 2019, 39(19): 151-152. |
| [14] |
冯家元, 唐馨. 测井—地震高频信息重建方法地震拓频处理应用效果[J]. 中国石油和化工标准与质量, 2021, 41(24): 92-94. |
| [15] |
刘立彬, 周小平, 魏庆, 等. 面向小尺度地质目标体的地震信号谐波预测拓频技术及应用[J]. 物探化探计算技术, 2020, 42(4): 460-467. LIU Libin, ZHOU Xiaoping, WEI Qing, et al. Techno-logy and application of seismic signal harmonic prediction extension processing for small scale geological target body[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2020, 42(4): 460-467. |
| [16] |
段成祥, 张繁昌, 兰南英. 基于匹配追踪的拓频处理方法[C]. 2020年中国地球科学联合学术年会论文集(十九), 2020, 2869-2871.
|
| [17] |
季焕成, 王江, 刘荷冲, 等. 双向拓频高分辨率地震技术在乌夏断裂带的应用[J]. 地球物理学进展, 2022, 37(1): 201-212. JI Huancheng, WANG Jiang, LIU Hechong, et al. Application of bidirectional extension frequency high-resolution seismic technique in Wuxia fault zone[J]. Progress in Geophysics, 2022, 37(1): 201-212. |
| [18] |
胡英, 张东, 袁建征, 等. Laplace-Fourier域多尺度高效全波形反演方法[J]. 石油勘探与开发, 2015, 42(3): 338-346. HU Ying, ZHANG Dong, YUAN Jianzheng, et al. An efficient multi-scale waveform inversion method in Laplace-Fourier domain[J]. Petroleum Exploration and Development, 2015, 42(3): 338-346. |
| [19] |
SHIN C, KOO N H, CHA Y H, et al. Sequentially ordered single-frequency 2-D acoustic waveform inversion in the Laplace-Fourier domain[J]. Geophysical Journal International, 2010, 181(2): 935-950. |
| [20] |
LI K, YIN X, ZONG Z. Bayesian seismic multi-scale inversion in complex Laplace mixed domains[J]. Petroleum Science, 2017, 14(4): 694-710. DOI:10.1007/s12182-017-0191-0 |
| [21] |
ZONG Z, LI K, YIN X, et al. Broadband seismic amplitude variation with offset inversion[J]. Geophysics, 2017, 82(3): M43-M53. DOI:10.1190/geo2016-0306.1 |
| [22] |
ZONG Z, WANG Y, LI K, et al. Broadband seismic inversion for low-frequency component of the model parameter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(9): 5177-5184. DOI:10.1109/TGRS.2018.2810845 |
| [23] |
陆基孟. 地震勘探原理(上册)[M]. 山东东营: 石油大学出版社, 1996.
|
| [24] |
张军华, 侯静, 辛星, 等. 道积分属性理论诠释及其在薄河道砂体预测中的应用[J]. 地球物理学进展, 2018, 33(1): 326-333. ZHANG Junhua, HOU Jing, XIN Xing, et al. Theory annotation and application of trace integration attribute in the prediction of thin channel sand body[J]. Progress in Geophysics, 2018, 33(1): 326-333. |
| [25] |
公亭, 王兆磊, 顾小弟, 等. 宽频地震资料处理配套技术[J]. 石油地球物理勘探, 2016, 51(3): 457-466. GONG Ting, WANG Zhaolei, GU Xiaodi, et al. Broadband seismic data matching processing[J]. Oil Geophysical Prospecting, 2016, 51(3): 457-466. DOI:10.13810/j.cnki.issn.1000-7210.2016.03.006 |
| [26] |
张宝金, 彭科, 成谷, 等. 倍频视角的宽频地震子波优化[J]. 石油地球物理勘探, 2022, 57(2): 297-302. ZHANG Baojin, PENG Ke, CHENG Gu, et al. Optimization of broadband seismic wavelets from the perspective of octaves[J]. Oil Geophysical Prospecting, 2022, 57(2): 297-302. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.006 |
| [27] |
李坤. 相驱动叠前地震概率化反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2019.
|
| [28] |
赵小龙, 吴国忱, 曹丹平. 多尺度地震资料稀疏贝叶斯联合反演方法[J]. 石油地球物理勘探, 2016, 51(6): 1156-1163. ZHAO Xiaolong, WU Guochen, CAO Danping. A sparse Bayesian joint inversion of multi-scale seismic data[J]. Oil Geophysical Prospecting, 2016, 51(6): 1156-1163. DOI:10.13810/j.cnki.issn.1000-7210.2016.06.015 |
| [29] |
LI K, YIN X, ZONG Z. Resolution enhancement of Robust Bayesian pre-stack inversion in the frequency domain[C]. Extended Abstracts of 78th EAGE Confe-rence & Exhibition, 2016, DOI: https://doi.org/10.3997/2214-4609.201601430.
|
| [30] |
杨培杰. 地震子波盲提取与非线性反演[D]. 山东青岛: 中国石油大学(华东), 2008.
|



 瞿晓阳,重庆市南川区西城街道白果路16号8幢中石化重庆页岩气有限公司,408400。Email:
瞿晓阳,重庆市南川区西城街道白果路16号8幢中石化重庆页岩气有限公司,408400。Email: