0 引言

目前波阻抗反演方法主要有道积分^[1]、稀疏脉冲反演^[2]、基于模型的反演^[3]和相对波阻抗反演^[4]等。道积分技术将地震记录视为低频地层反射系数，通过积分地震记录道可以快捷地得到相对波阻抗剖面；稀疏脉冲反演是基于反褶积的递推反演，假设反射系数是稀疏的，首先通过反褶积得到宽带的反射系数序列，然后给定一个初始波阻抗值，并对该反射系数积分即可得到绝对波阻抗反演结果；基于模型的反演首先建立地层波阻抗模型，然后对比基于模型合成的地震记录与实际地震记录，以迭代方式更新地层模型，使基于模型的合成地震记录在一定的准则下匹配实际地震记录，最终得到反演结果；相对波阻抗反演可以由带限地震数据有效地反演相对波阻抗，反演结果分辨率高并且很好地保持了地震数据的横向连续性，也取得了较好的应用效果。

以上方法属于模型驱动的波阻抗反演，该类方法没有井插值地质模型的参与，反演结果的分辨率往往较低^[5]。主要原因是各种地震数据噪声导致反演解的矩阵条件数太高，也是该类方法的固有问题。因此，在实际勘探中，为了提高反演结果的分辨率，往往需要再融合反演结果与地质模型的频率，以补偿反演缺失的高频信息，进而提高分辨率。但是，对于相变很快的隐蔽型储层，地层模型的高频信息会影响反演结果，导致反演精度降低。因此，在没有高频井信息参与的情况下，有效提高波阻抗反演分辨率是目前地震反演的难点之一。

频率域地震解释主要应用地震振幅谱信息进行地震反演和预测储层^[6]。地层参数的变化引起地震信号相位变化，在子波估计和反褶积时^[7]要考虑子波的相位信息，相位可以作为一种地震属性进行分析和处理，如通过瞬时相位信息识别超剥线^[8]。目前，业界已经实现了相位的分解与重构^[9-10]，通过分相位数据体预测储层。因此，联合应用振幅谱和相位谱信息将是今后频率域地震数据处理和解释的热点。

机器学习是一种数据驱动方法，很早就用于地球物理勘探领域，主要包括浅层神经网络^[11]、支持向量机^[12]等，这些方法需要提取样本特征并进行分析，反演结果的可靠性特别是横向稳定性往往较低，因而实际应用较少。与传统的浅层网络相比，深度网络的层数多、复杂度高，可从海量现有数据中学习隐含知识，进而有效逼近复杂函数，因此应用效果优于传统的机器学习方法。目前，基于深度学习的地震反演发展迅速、应用广泛，首先建立地震波形和波阻抗之间的定量关系^[13-15]，或建立地震振幅谱和待反演参数之间的关系^[16]，并生成大量的标签，然后通过标签训练深度网络，建立地震波形道与波阻抗之间的映射关系，进而实现地震反演。除了地震反演，深度学习在断层识别^[17]、地震相识别^[18]、储层预测^[19]等方面也得到广泛应用。综上所述，人工智能地震反演主要利用地震数据的振幅谱信息，而没有较好地利用相位谱信息。

为了克服模型驱动的波阻抗反演分辨率低的问题，本文从数据驱动的角度出发，结合深度学习和地震数据的振幅谱、相位谱，实现频相智能波阻抗反演，有效提高了反演分辨率和精度。第一，基于高分辨率时频分析提取地震道的频相信息；第二，应用图像处理技术融合频相信息；第三，结合频相信息和地层波阻抗制作数据标签对，用数据标签对训练优选的深度网络；第四，提取待反演三维地震数据的频相信息，输入训练好的深度网络，即可得到高分辨率波阻抗反演结果；最后，在胜利油田工区测试了所提方法的应用效果。与现有的数据驱动深度学习地震反演方法^[13-16]相比，本文方法的主要创新点在于首次在地震反演中同时应用了地震数据的频相信息。

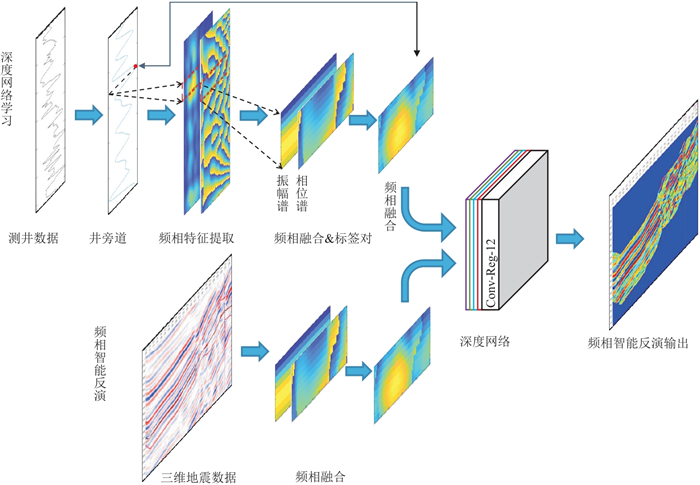
1 频相融合智能高分辨率反演框架 1.1 深度网络学习

基于研究区实际井及其井旁地震道，应用高分辨率时频分析方法提取地震记录的频相信息，通过图像处理有效融合频相信息，并结合井旁道波阻抗制作数据标签对，用这些数据标签对训练优选的深度网络得到训练好的网络模型。

1.2 频相融合智能反演

融合待反演三维地震数据的频相信息，输入训练好的网络模型，即可得到三维波阻抗反演结果。频相融合智能高分辨率反演框架如图 1所示。

2 地震频相信息提取与分析 2.1 地震频相信息提取

通过时频分析提取地震频相信息。目前有很多时频分析方法，其中约束最小二乘时频分析（Improved Constrained Least Squares Time Frequency Analysis, ICLS）^[20-21]的频率分辨率较高且相位谱稳定。因此，本文采用ICLS提取地震数据的频相信息。定义如下正演过程

$ {\boldsymbol{d}}={\boldsymbol{Fm}} $

(1)

式中：$ {\boldsymbol{d}} $为待分析的信号；m为待求的频谱向量；$ {\boldsymbol{F}} $为不同频率的三角函数构成的矩阵。

在式(1)中，已知$ {\boldsymbol{d}} $和$ {\boldsymbol{F}} $求$ {\boldsymbol{m}} $是一个典型的反问题，在实际计算过程中往往没有精确解，通过约束最小二乘法得到ICLS解^[21]

$ {\mathit{\boldsymbol{m}}}_{\mathrm{e}}=({{\boldsymbol{F}}}^{'}{{\boldsymbol{F}}+\mu \mathit{\boldsymbol{ \boldsymbol{\varOmega} }})}^{-1}{{\boldsymbol{F}}}^{'}{\boldsymbol{d}} $

(2)

式中：$ {{\boldsymbol{F}}}^{'} $为$ {\boldsymbol{F}} $的转置；Ω为约束对角矩阵；μ为权重系数，实际求解过程中，通过调节μ值得到不同分辨率的时频分析结果。

在ICLS结果的基础上，求取复数的模即可得到时频振幅谱。

通过

$ B(f, \theta , t)=\frac{\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\left[\mathrm{I}\mathrm{T}\mathrm{F}\mathrm{A}\right(f, t\left)\right]}{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\left[\mathrm{I}\mathrm{T}\mathrm{F}\mathrm{A}\right(f, t\left)\right]}\times 180}{\mathrm{\pi }} $

(3)

得到地震数据在t时刻、频率为f的地震数据相位信息$ B(f, \theta , t) $。式中：$ \mathrm{I}\mathrm{T}\mathrm{F}\mathrm{A}(f, t) $为通过ICLS获得的时频分析结果；$ \mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g} $表示求虚部；$ \mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l} $表示求实部；θ∈[-180°, 180°]为相位角。

2.2 地震频相信息分析

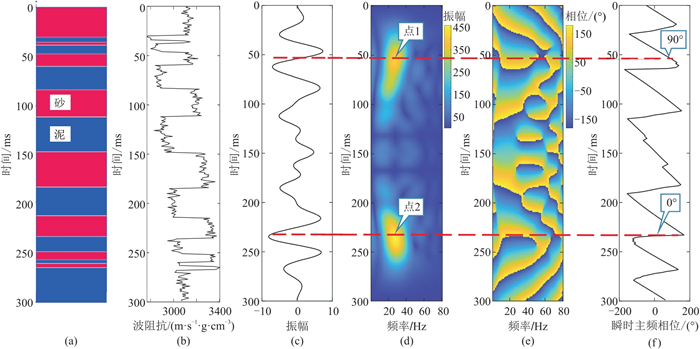
地震数据的振幅和相位信息反映了地层组合的变化^[22]。图 2为反、正旋回组合地质模型及其地震频相特征。由图可见：①在地震有效频带范围内（5~ 40 Hz）相位谱的相位分辨率和稳定性均较高（图 2e）。②薄层对应高频振幅，厚层对应低频振幅，如点1、点2的振幅谱信息相近（图 2d），但是点1的相位角接近90°，点2的相位角接近0°（图 2f）。

文献[23]指出，不同波阻抗的地层组合对应不同相位的地震波形。对图 2中的地层波阻抗、地震振幅、相位进行交会分析和相关分析，相关系数为

$ C({\boldsymbol{x}}, {\boldsymbol{y}})=\frac{H({\boldsymbol{x}}, {\boldsymbol{y}})}{\sqrt{V\left({\boldsymbol{x}}\right)}\sqrt{V\left({\boldsymbol{y}}\right)}} $

(4)

式中：C($ {\boldsymbol{x}} $, $ {\boldsymbol{y}} $)为两个相同长度的向量$ {\boldsymbol{x}} $和$ {\boldsymbol{y}} $的相关系数；H($ {\boldsymbol{x}} $, $ {\boldsymbol{y}} $)为$ {\boldsymbol{x}} $和$ {\boldsymbol{y}} $的协方差；V($ {\boldsymbol{x}} $)和V($ {\boldsymbol{y}} $)分别为$ {\boldsymbol{x}} $和$ {\boldsymbol{y}} $的方差。

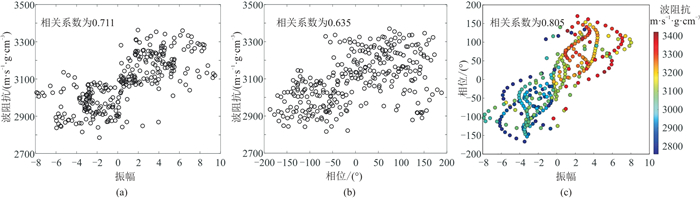
图 3为地层波阻抗、振幅、相位相关分析，其中波阻抗和振幅的相关系数为0.711(图 3a)，波阻抗和相位的相关系数为0.635(图 3b)，相位和振幅的相关系数为0.805(图 3c)，说明结合地震振幅谱和相位谱可以更好地描述波阻抗变化，进一步减小地震反演、属性分析的多解性。

3 频相融合智能高分辨率反演

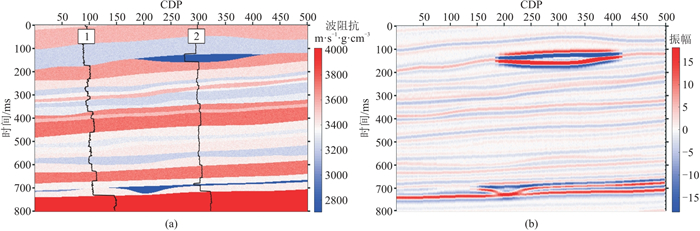
基于频相融合智能高分辨率反演框架，使用局部Marmousi模型（图 4）详细描述方法的细节及效果。

3.1 数据标签对制作

基于频相信息提取和图像处理技术，本文提出并实现了频相融合的数据标签制作。

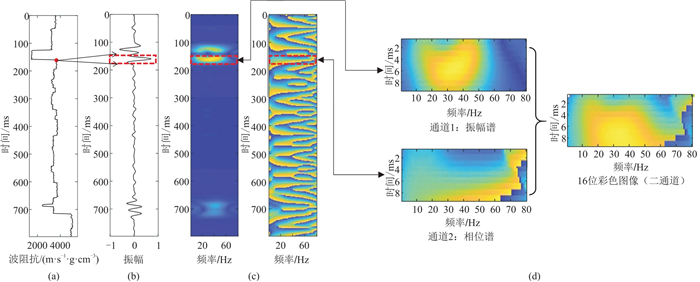
3.1.1 频相信息提取与融合

以2井波阻抗曲线为例（图 5a）。首先，对生成的地震记录（图 5b）进行频相分析；然后，采用点窗模式提取频相信息（图 5c），并设定窗的时间长度和频率范围；最后，将提取的频相图像与地震波形结合，通过RGB融合频相信息（图 5d）。

3.1.2 数据标签对的制作

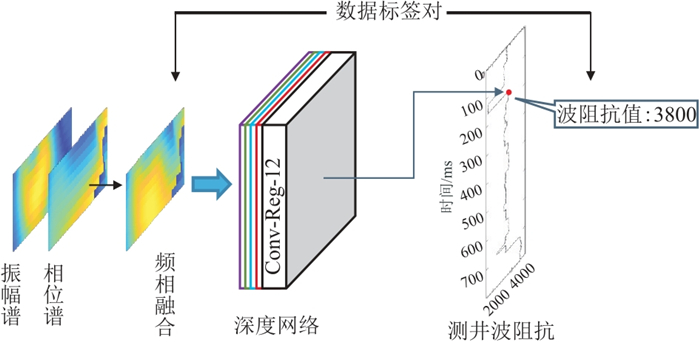
结合生成的16位彩色图像及其对应的地层波阻抗值，即可形成一张数据标签对，其中频相融合图像为“数据”，对应的波阻抗值（3800）为“标签”（图 6）。针对目的层段的地震数据逐点制作数据标签对，一口井可以生成数百个数据标签对，基本可以满足深度学习对数据的要求。

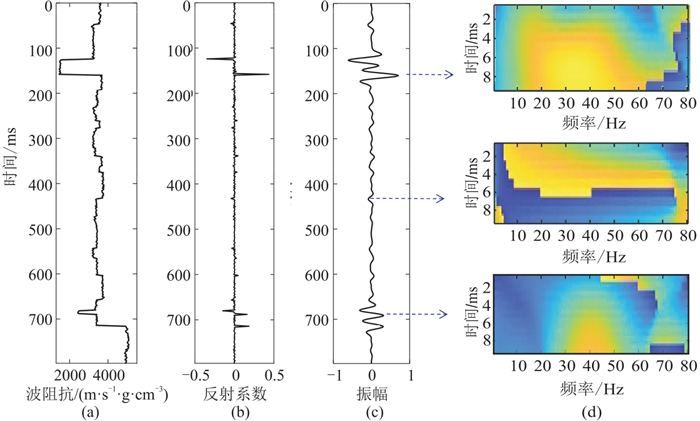
图 7为2井的部分数据标签对。由图可见，不同波阻抗（图 7a）对应不同反射系数（图 7b），导致井旁道的波形（图 7c）、频相信息也不同（图 7d）。因此，通过学习频相信息和波阻抗组成的数据标签对可以反演波阻抗。

3.2 深度网络优选与训练 3.2.1 深度网络优选

地震、地质特征对应关系的复杂性，使浅层网络（BP神经网络、支持向量机等）难以满足实际需求。深度网络^[24]在特征表征方面的结果优于浅层机器学习方法，深度网络相对于传统神经网络增加了多个隐层，提升了神经网络系统的语义描述能力；同时，海量数据标签对的获取使深度学习模型得到充分训练，可更好地提取数据的高层特征表示，因此具有很好的分类和回归效果。

目前常用的深度网络主要有普通深度网络、卷积神经网络、循环神经网络、深度置信神经网络等，这些深度网络往往具有不同的网络结构和应用场景。文中的数据标签对是对图像进行回归分析，因此，有监督的回归型卷积深度神经网络的适用性更好。

一般来说，有监督的深度学习需要考虑网络模型、损失函数和优化方法等关键环节。

（1）网络模型

理论上网络结构越深，提取的图像特征越高级，得到的学习效果更好，但是深层网络会遇到梯度消失、梯度爆炸以及网络退化问题^[25]。为此，本文采用残差网络应对网络退化问题。

深度残差网络因其强大的表征能力得到广泛应用。残差网络通过短路机制加入残差单元，在多个卷积层之间设置一个直接连接，这样的一段网络被称为一个残差块。文中的残差块（图 8）有两层卷积层，输入z在进入第一层卷积层之后先经过归一化，然后通过激活函数，第二层卷积层再经过归一化得到特征F(z)，并与z直接相加。为了保证两个特征图通道数量相同，一般在直接连接时做一个线性变换，即通过1×1大小的卷积核使输出通道数相同。进一步，采用激活函数ReLU克服梯度消失和梯度爆炸等问题，并采用权值衰减、舍弃部分神经元的方法克服深度网络的过拟合问题。

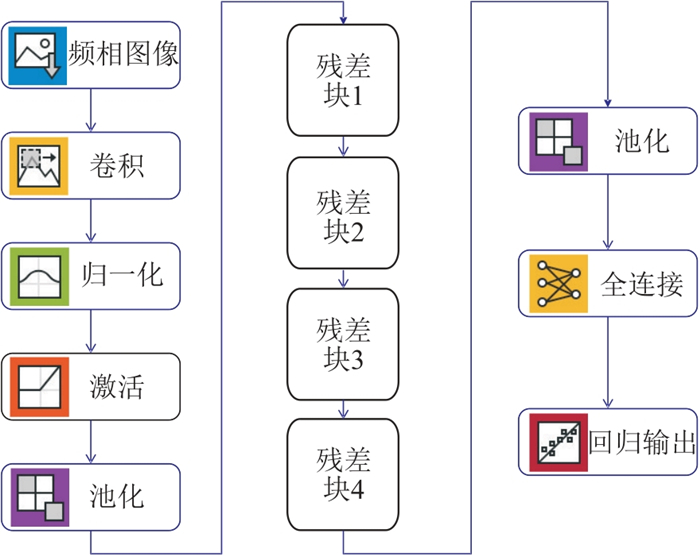
通过反复测试、分析，确定适用于地震频相智能反演的深度网络模型（图 9）。

网络共12层。第1层为频相输入层，输入端的图像尺寸可变，可以根据地震数据频相的频率范围、时窗等参数灵活修改，缺省值为9×80×2的16位彩色图像，即融合后的频相图像、横坐标的频率范围为1~80 Hz，纵坐标的时窗长为9个采样点，图像的深度为2。实际应用中，首先用缺省时窗和频率范围做反演，不断调整参数，直到得到满意的反演效果。第2~5层分别为卷积层、归一化层、激活层、池化层。第6~9层为4个残差块。第10层为池化层。第11层为全连接层。第12层为回归输出层，最终输出一个数值。将该网络简记为Conv-Reg-12网络。

（2）损失函数

结合数据标签对的特征，本文方法归结为图像拟合问题，输入为三通道的彩色图像，输出为一个标量值。因此，采用均方误差（Mean Squared Error, MSE）作为损失函数

$ \mathrm{M}\mathrm{S}\mathrm{E}=\sum\limits_{i=1}^{N}\frac{({t}_{i}-{y}_{i}{)}^{2}}{N} $

(5)

式中：N为数据标签对的数量；t_i为目标输出；y_i为网络预测的输出。

（3）优化方法

确定损失函数后，使损失函数值最小为一个最优化问题，本文采用Adam方法^[26]优化损失函数。Adam是一种基于一阶导数的随机梯度下降优化算法，其优势是简单易用、对于梯度等比缩放不敏感等。

3.2.2 深度网络训练

在确定深度网络结构后，用1井、2井数据制作的数据标签对训练深度网络，将两口井一共生成的3200个数据标签对作为训练数据，分成32个batch，每个batch有100个数据标签对，用CDP200和CDP400的地震道作为验证数据，设置训练500轮，学习率设置可变，初始值为0.001，下降率为0.8。当训练和验证的MSE小于一定的阈值（数据做了归一化处理）且平稳后，终止训练，输出训练模型参数（图 10）。

3.3 频相智能反演效果分析

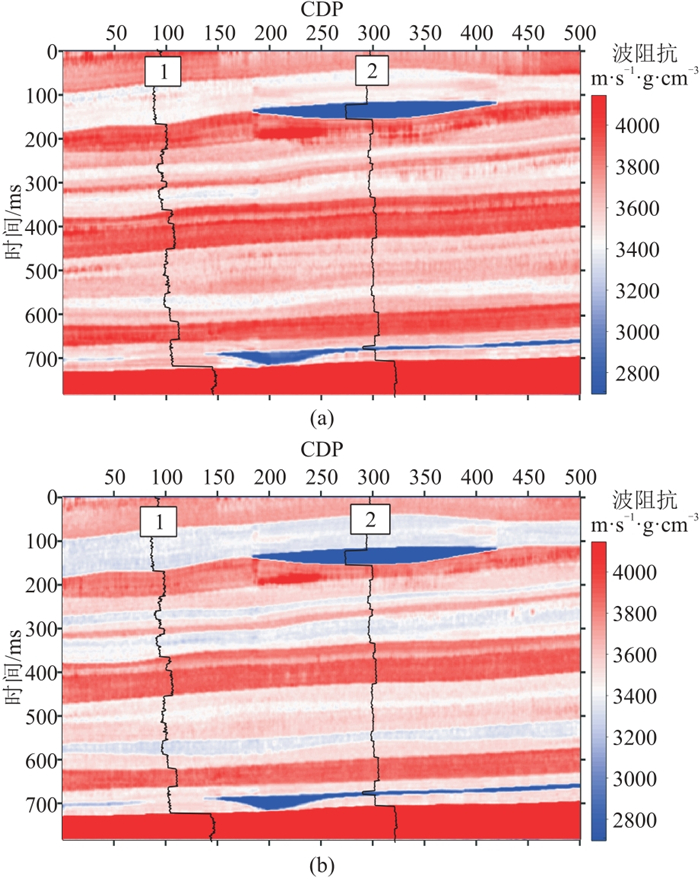
深度网络模型参数训练好后，对地震数据进行频相分析，并输入到深度网络得到频相智能反演结果（图 11）。可见，相对于振幅谱反演结果（图 11a），频相反演结果的横向稳定性和纵向分辨率都得到提高，更好地恢复了原始地质信息（图 4a）的细节（图 11b）。

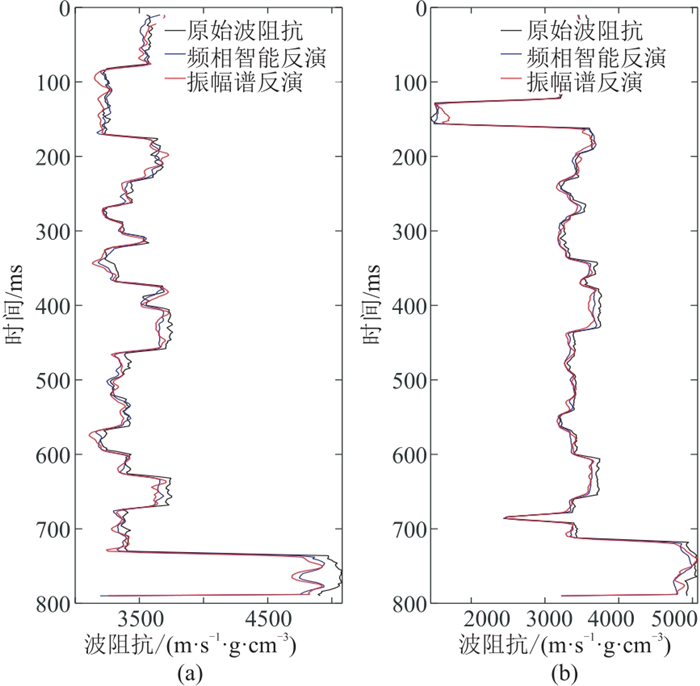
井旁道反演结果（图 12）表明，1井、2井的振幅谱反演结果与原始数据的平均相关系数为0.85，而频相智能反演结果的平均相关系数为0.90，进一步说明了频相智能反演的客观性。

4 实际应用

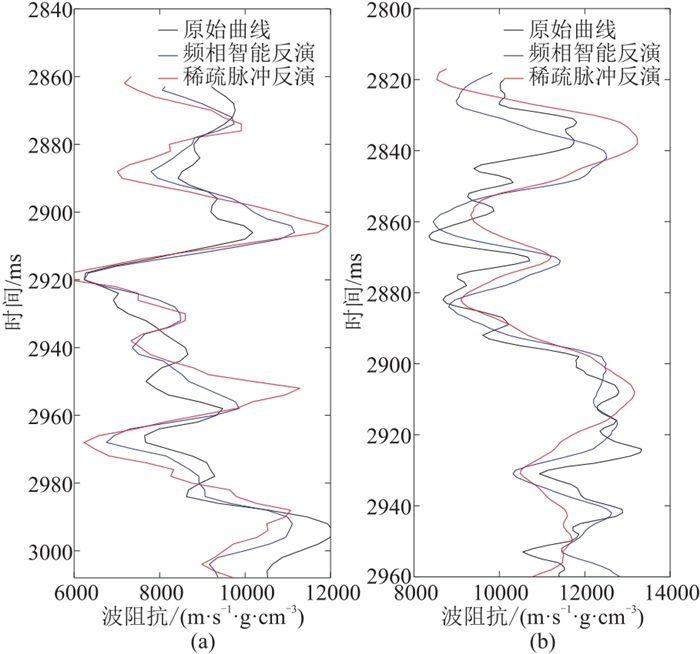
胜利油田DLJ地区古近系渐新统沙河街组三段下亚段资源丰富，是今后重要的储量阵地，其中的4、5、6砂组为由西北陵县凸起方向的物源形成的盘河三角洲沉积。速度分析表明，该区泥岩、油页岩速度为3200~4000 m/s，储层速度大于4200 m/s，储层与盖层的速度差异较大，适合开展波阻抗反演。共有14口井的数据参与反演，其中12口井的数据训练Conv-Reg-12，2口井的数据验证Conv-Reg-12。图 13为参与深度学习的L98井与没有参与深度学习的L985井的井旁道反演结果。由图可见：L98井井旁道的频相智能反演曲线与原始波阻抗曲线的相关系数为0.82，而稀疏脉冲反演曲线与原始波阻抗曲线的相关系数为0.61（图 13a）；L985井井旁道的频相智能反演曲线与原始波阻抗曲线的相关系数为0.75，而稀疏脉冲反演曲线与原始波阻抗曲线的相关系数为0.60，说明频相智能反演精度高于传统的稀疏脉冲反演（图 13b）。

图 14为稀疏脉冲反演与频相智能反演连井剖面。由图可见，稀疏脉冲反演（图 14a）和频相智能反演（图 14b）的横向稳定性均较好，但是图 14b的纵向分辨率高于图 14a，主要是由于反射系数稀疏假设导致图 14a不能较好地反演地震弱信号（箭头处），而频相智能反演可较好地描述地震弱信号。

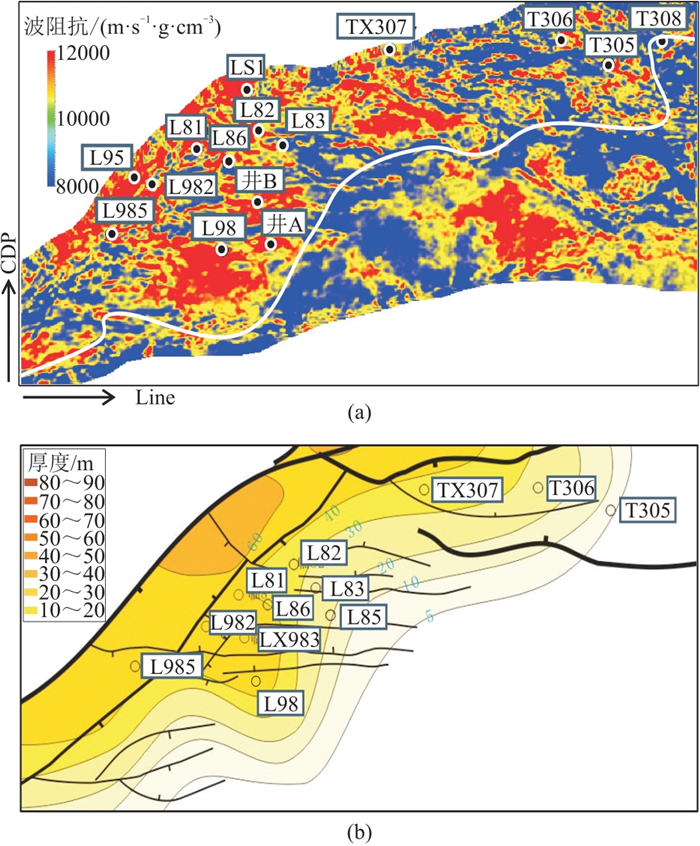
图 15为5砂组频相智能反演波阻抗与厚度图，可见频相智能波阻抗反演结果（图 15a）与砂组厚度（图 15b）分布一致，进一步证实了频相智能反演结果的客观性。

目前，地震频相智能反演已经成功应用于胜利油田的井位论证，根据该区频相智能反演结果，结合构造特征和有效储层分布等因素，部署了井A、井B，取得了显著的应用效果。

5 结束语

针对当前地震反演中存在的问题，本文提出了基于地震频相融合的智能化高分辨率地震反演方法，模型测试和实际应用结果表明：①不同地层组合的地震响应不同，从而导致不同的频相特征，“频”反映了地层厚度变化的快慢和强弱，“相”反映了地层的组合样式；②融合地震频相信息并结合深度学习进行地震反演可以有效降低多解性，从而提高反演精度。