0 引言

声波测井数据在油气勘探中的作用是不可替代的，准确的声波测井数据对地震资料时深转换、合成记录制作、地震反演、油藏建模等具有相当重要的作用。中国学者一直聚焦补偿声波测井的校正方法研究，陈钢花等^[1]通过Faust公式，应用电阻率曲线重构声波曲线，提高了声波曲线的精度；刘浩杰等^[2]分析了声波时差的传播路径，得出了井径坍塌时声波时差校正经验公式；汤小燕等^[3]采用统计方法对研究区主力煤层的声波时差、井径测井响应特征进行了详实剖析, 优选适用性较高的频率法对煤层气储层进行了扩径影响校正；李洪奇等^[4]通过数值模拟计算给出了点声源、无衰减等理想地层条件下，双发双收声系在不同扩径层段新的声速响应规律；隋志强^[5]推导了岩性突变声波时差校正公式，并首次提出了井径坍塌校正门限的方法；郭淑文等^[6]以受钻井泥浆浸泡时间较短的井作为标准井，按均值方差法将发生泥岩蚀变的井校正到标准井的分布范围内，提高了合成记录标定精度；赖生华等^[7]采用时频分析方法对原始声波时差曲线进行分频处理, 完成声波时差长趋势、脱压实校正, 减小储层与围岩的声波时差值重叠区域，提高了对储层的辨识精度。但是，已有研究工作缺乏不同扩径程度、不同扩径位置对补偿声波测井仪器测量声波时差的定量分析。

本文从补偿声波时差仪器的参数入手，基于费马时间最小原理，考虑了不同井径坍塌位置和扩径程度时各个接收器接收声波首波的传播路径，推导了双发双收补偿声波测井仪器基于井径变化的声波时差校正公式，形成针对性的校正方法，并通过实例验证了方法的有效性。

1 方法原理

双发双收补偿声波测井仪器能够较好地补偿井径及泥浆的影响，消除记录点与测量点的深度误差，但在井径扩大位置附近当井径大于某个井径校正门限时，产生的异常无法消除。

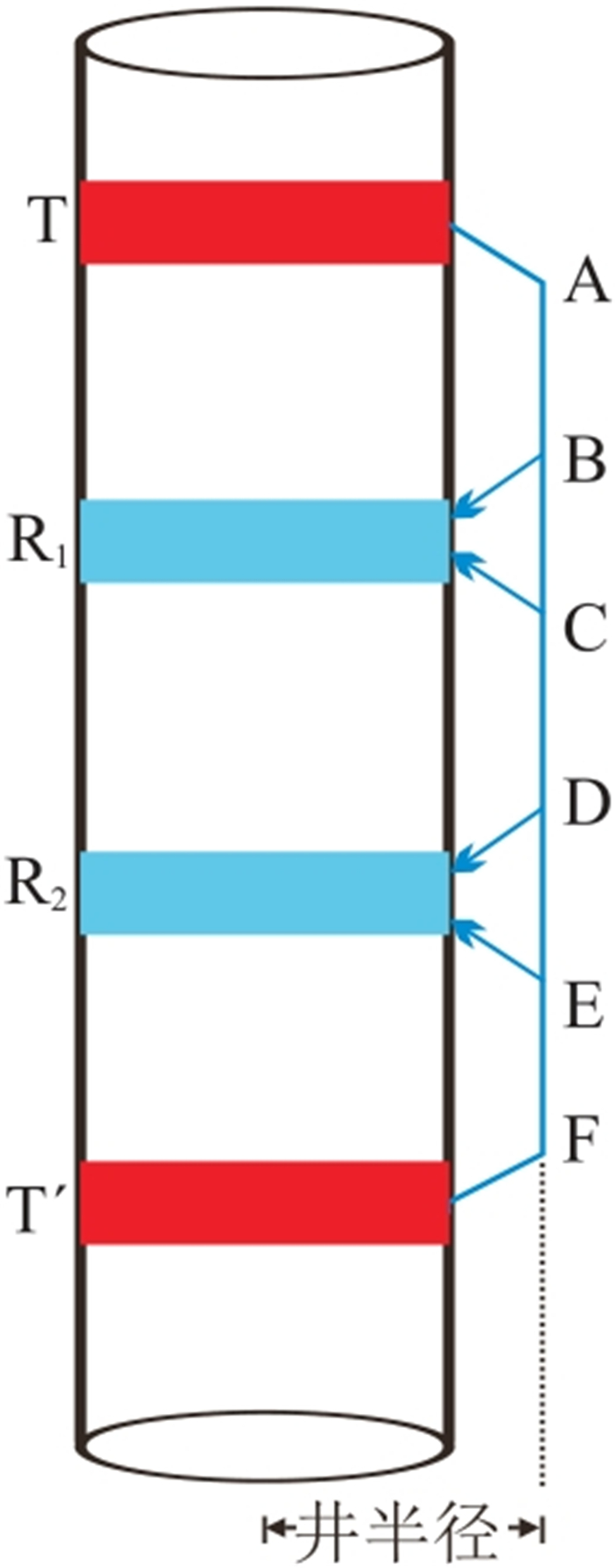
图 1为典型的双发双收补偿声波测井仪器示意图，图中T、T′分别为上、下发射探头；R₁、R₂分别为上、下接收探头。以T′探头发射、R₂和R₁依次接收为例进行分析，当EF段井径坍塌不高于某一数值时，T′探头发射声波信号，R₂探头接收到同时到达的滑行波与直达波，这时的井径被称作第一校正门限(CAL₁)。当声波测井仪器尺寸一定时，给定介质的声波速度，可以计算出声波时差井径第一校正门限

$ \mathrm{C}\mathrm{A}{\mathrm{L}}_{1}=\frac{{l}_{1}\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}{v+{v}_{\mathrm{m}}}+{D}_{0} $

(1)

式中：$ {l}_{1} $为T′到R₂的距离；$ {v}_{\mathrm{m}} $为泥浆速度；$ v $为地层声波速度；$ {D}_{0} $为声波探头直径。

当CD段井径坍塌达到某一数值时，$ {\mathrm{R}}_{1} $接收到的滑行波与直达波同时到达，这时井径被称作第二校正门限。

当井径扩径大于第一校正门限时，滑行波与直达波不是同时到达，R₁接收到的是泥浆直达波，并不包含地层信息，此时补偿声波测井仪器测量声波时差失真，因此必须考虑声波时差校正问题。第二校正门限井径通常超过55 cm，这在实际情况中很少遇到，本文不做研究。

2 不同扩径情况校正方法 2.1 井径坍塌均小于CAL₁

如图 1所示，当AB、EF段的井径均小于CAL₁时，对于T，R₁接收到的声波传播路径为TABR₁，R₂接收到的声波传播路径为TADR₂，记录时间差为

$ \begin{array}{l}\mathrm{\Delta }{t}_{\mathrm{上}}={t}_{\mathrm{T}\mathrm{A}\mathrm{D}{\mathrm{R}}_{2}}-{t}_{\mathrm{T}\mathrm{A}\mathrm{B}{\mathrm{R}}_{1}}\\ =\frac{v({r}_{2}-{r}_{1})}{{v}_{\mathrm{m}}\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}+\frac{{l}_{0}}{v}-\frac{{v}_{\mathrm{m}}({r}_{2}-{r}_{1})}{v\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}\end{array} $

(2)

式中：$ {t}_{\mathrm{T}\mathrm{A}\mathrm{D}{\mathrm{R}}_{2}} $为声波经过传播路径TADR₂所用时间；$ {t}_{\mathrm{T}\mathrm{A}\mathrm{B}{\mathrm{R}}_{1}} $为声波经过传播路径TABR₁所用时间；$ {r}_{1} $、$ {r}_{2} $分别为B、D处的井半径；l₀为R₁、R₂间距。

对于T′，R₂接收到的声波传播路径为T′FER₂，R₁接收到的声波传播路径为T′FCR₁，记录时间差为

$ \begin{array}{l}\mathrm{\Delta }{t}_{\mathrm{下}}={t}_{\mathrm{T}{'}\mathrm{F}\mathrm{C}{\mathrm{R}}_{1}}-{t}_{\mathrm{T}{'}\mathrm{F}\mathrm{E}{\mathrm{R}}_{2}}\\ =\frac{v({r}_{3}-{r}_{4})}{{v}_{\mathrm{m}}\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}+\frac{{l}_{0}}{v}-\frac{{v}_{\mathrm{m}}({r}_{3}-{r}_{4})}{v\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}\end{array} $

(3)

式中：$ {t}_{\mathrm{T}{'}\mathrm{F}\mathrm{C}{\mathrm{R}}_{1}} $为声波经过传播路径T′FCR₁所用时间；$ {t}_{\mathrm{T}{'}\mathrm{F}\mathrm{E}{\mathrm{R}}_{2}} $为声波经过传播路径T′FER₂所用时间；$ {r}_{3} $、$ {r}_{4} $分别为E、C处的井半径。

根据补偿声波仪器测量原理可知，仪器实际测量输出值为

$ \mathrm{\Delta }t=\frac{\mathrm{\Delta }{t}_{\mathrm{上}}+\mathrm{\Delta }{t}_{\mathrm{下}}}{2{l}_{0}} $

(4)

式中$ \mathrm{\Delta }t $为CD段中间点位置实测声波时差。

将式(2)、式(3)代入式(4)，整理得到一元二次方程，有

$ {a}_{0}{v}^{2}-{b}_{0}v+{c}_{0}=0 $

(5)

式中

$ \left\{\begin{array}{l}{a}_{0}={v}_{\mathrm{m}}^{2}\mathrm{\Delta }{t}^{2}-({r}_{2}-{r}_{1}+{r}_{3}-{r}_{4}{)}^{2}\\ {b}_{0}=2\mathrm{\Delta }t{v}_{\mathrm{m}}^{2}\\ {c}_{0}=\left[1+{\left({r}_{2}-{r}_{1}+{r}_{3}-{r}_{4}\right)}^{2}\right]{v}_{\mathrm{m}}^{2}\end{array}\right. $

通过求解式(5)可得地层真实速度。

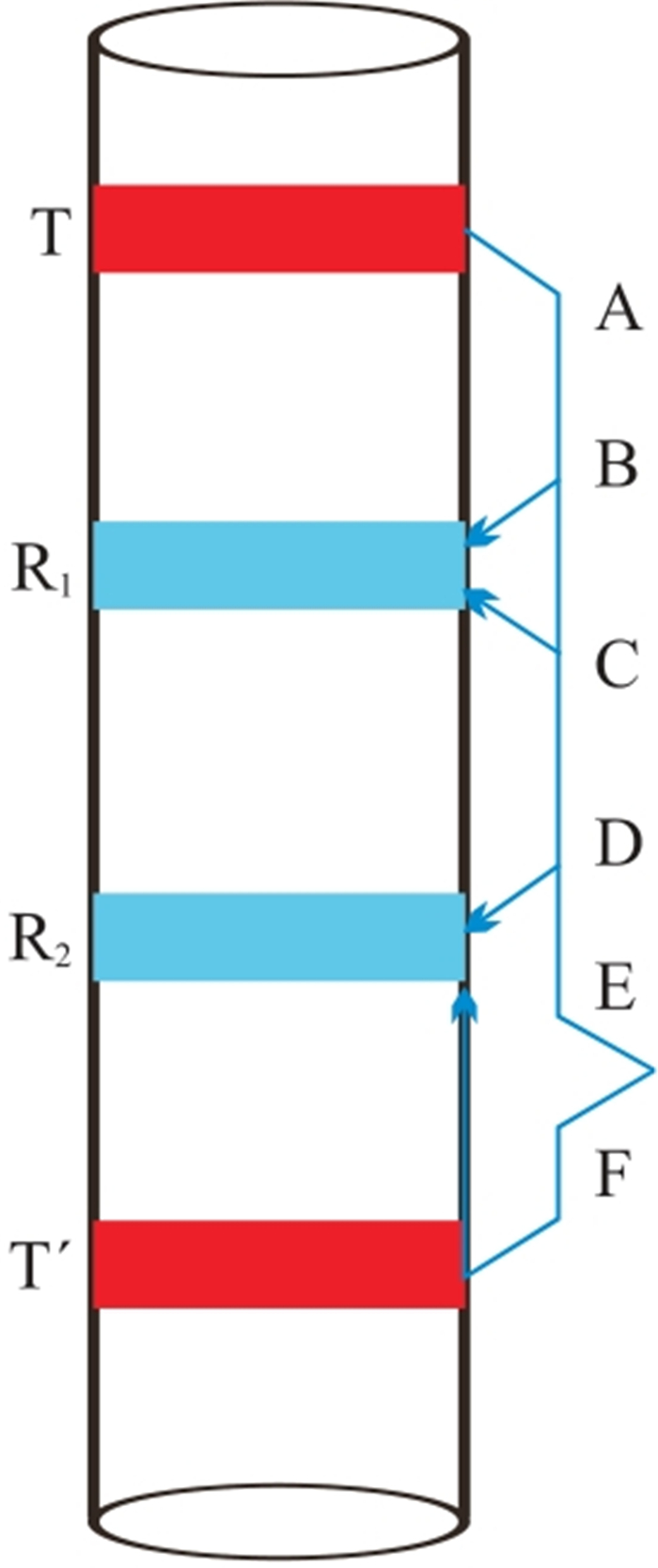
2.2 井径坍塌部分大于CAL₁

如图 2所示，当EF段井径坍塌大于CAL₁，而AB段井径扩径不超过CAL₁时，对于T，R₁接收到的声波传播路径为TABR₁，R₂接收到的声波传播路径为TADR₂，记录时间差同式（2）。

对于T′，由于EF段井径坍塌大于CAL₁，从泥浆传播的直达波时间$ {t}_{\mathrm{T}{'}{\mathrm{R}}_{2}} $小于沿井壁传播滑行波时间$ {t}_{\mathrm{T}{'}\mathrm{F}\mathrm{E}{\mathrm{R}}_{2}} $，因此R₂接收到的声波首波传播路径应为T′R₂，R₁接收到的声波首波不受影响，传播路径为T′FCR₁，此时记录时间差为

$ \begin{array}{l}\mathrm{\Delta }{t}_{\mathrm{下}}={t}_{\mathrm{T}{'}\mathrm{F}\mathrm{C}{\mathrm{R}}_{1}}-{t}_{\mathrm{T}{'}{\mathrm{R}}_{2}}\\ =\frac{v({r}_{3}+{r}_{5})}{{v}_{\mathrm{m}}\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}+\frac{{l}_{2}-\frac{{v}_{\mathrm{m}}({r}_{3}+{r}_{5})}{\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}}{v}-\frac{{l}_{1}}{{v}_{\mathrm{m}}}\end{array} $

(6)

式中：$ {t}_{\mathrm{T}{'}{\mathrm{R}}_{2}} $为声波经过传播路径T′R₂所用时间；$ {r}_{5} $为F处井半径；$ {l}_{2} $为T′R₁的长度。

将式(2)、式(6)代入式(4)，并整理成一元二次方程，有

$ {a}_{1}{v}^{2}-{b}_{1}v+{c}_{1}=0 $

(7)

式中

$ \left\{\begin{array}{l}{a}_{1}={\left(2{l}_{0}\mathrm{\Delta }t+\frac{{l}_{1}}{{v}_{\mathrm{m}}}\right)}^{2}-{\left(\frac{{r}_{3}+{r}_{5}+{r}_{2}-{r}_{1}}{{v}_{\mathrm{m}}}\right)}^{2}\\ {b}_{1}=2({l}_{0}+{l}_{2})\left(2{l}_{0}\mathrm{\Delta }t+\frac{{l}_{1}}{{v}_{\mathrm{m}}}\right)\\ {c}_{1}=({l}_{0}+{l}_{2}{)}^{2}+({r}_{3}+{r}_{5}+{r}_{2}-{r}_{1}{)}^{2}\end{array}\right. $

通过求解式(7)方程可得地层真实速度。

对于AB段井径坍塌大于CAL₁，且EF段井径小于CAL₁的情况，基于仪器的对称性求得的方程与式(7)相似，本文不再赘述。

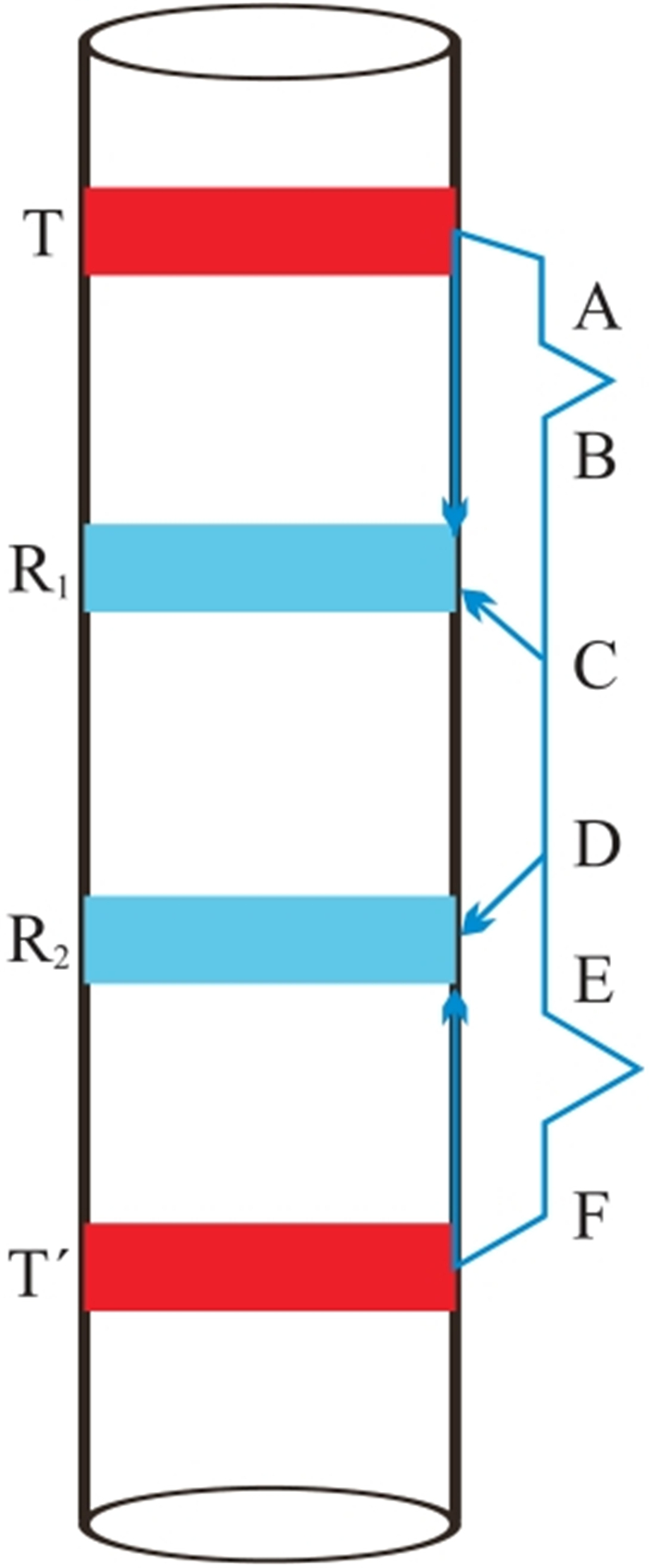
2.3 井径坍塌同时大于CAL₁

如图 3所示，当AB、EF段井径坍塌同时大于CAL₁时，对于T，R₁接收到的首波是经泥浆传播的直达波，传播路径为TR₁，R₂接收到的声波传播路径为TADR₂，此时记录时间差为

$ \begin{array}{l}\mathrm{\Delta }{t}_{\mathrm{上}}={t}_{\mathrm{T}\mathrm{A}\mathrm{D}{\mathrm{R}}_{2}}-{t}_{\mathrm{T}{\mathrm{R}}_{1}}\\ =\frac{v({r}_{2}+{r}_{6})}{{v}_{\mathrm{m}}\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}+\frac{{l}_{2}-\frac{{v}_{\mathrm{m}}({r}_{2}+{r}_{6})}{\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}}{v}-\frac{{l}_{1}}{{v}_{\mathrm{m}}}\end{array} $

(8)

式中：$ {t}_{\mathrm{T}{\mathrm{R}}_{1}} $为声波经过传播路径TR₁所用时间；$ {r}_{6} $为A处井半径。

对于T′，R₂接收到的首波是泥浆传播的直达波，传播路径为T′R₂，R₁接收到的声波传播路径为T′FCR₁，记录时间差为

$ \begin{array}{l}\mathrm{\Delta }{t}_{\mathrm{下}}={t}_{\mathrm{T}{'}\mathrm{F}\mathrm{C}{\mathrm{R}}_{1}}-{t}_{\mathrm{T}{'}{\mathrm{R}}_{2}}\\\ \ \ =\frac{v({r}_{3}+{r}_{5})}{{v}_{\mathrm{m}}\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}+\frac{{l}_{2}-\frac{{v}_{\mathrm{m}}({r}_{3}+{r}_{5})}{\sqrt{{v}^{2}-{v}_{\mathrm{m}}^{2}}}}{v}-\frac{{l}_{1}}{{v}_{\mathrm{m}}}\end{array} $

(9)

将式(8)、式(9)代入式(4)，整理得到一元二次方程，有

$ {a}_{2}{v}^{2}-{b}_{2}v+{c}_{2}=0 $

(10)

式中

$ \left\{\begin{array}{l}{a}_{2}={\left(2{l}_{0}\mathrm{\Delta }t+2\frac{{l}_{1}}{{v}_{\mathrm{m}}}\right)}^{2}-{\left(\frac{{r}_{3}+{r}_{5}+{r}_{2}+{r}_{6}}{{v}_{\mathrm{m}}}\right)}^{2}\\ {b}_{2}=2{l}_{2}\left(2{l}_{0}\mathrm{\Delta }t+2\frac{{l}_{1}}{{v}_{\mathrm{m}}}\right)\\ {c}_{2}=4{{l}_{2}}^{2}+({r}_{3}+{r}_{5}+{r}_{2}+{r}_{6}{)}^{2}\end{array}\right. $

通过求解式(10)即可求得地层真实速度。

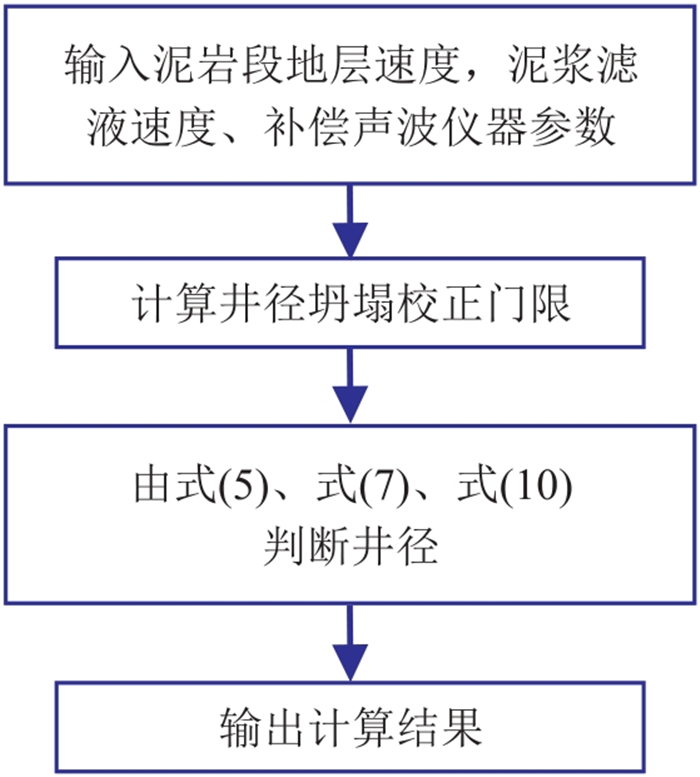
3 应用实例

基于补偿声波测井校正原理和方法开发了声波扩径校正程序，并建立如图 4所示计算流程。选取某实际工区的1^#、2^#井验证补偿声波测井校正方法的有效性。

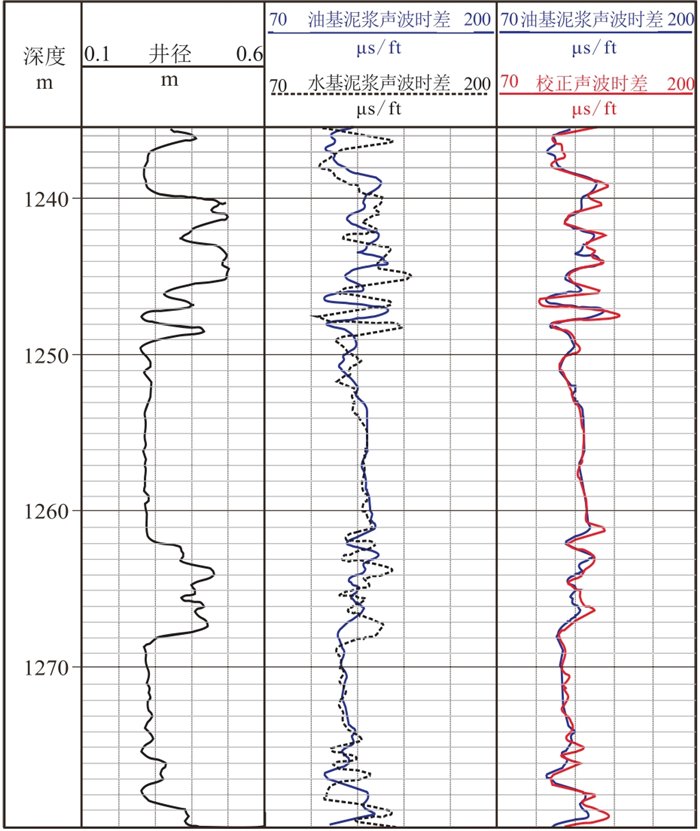
对1^#井同时开展了水基泥浆和油基泥浆两种声波测井。采用水基泥浆时，浅层声波时差测井受井眼垮塌及泥岩蚀变的影响严重；采用油基泥浆时，则能够较精确地获得原状地层的声波时差^[8]，因此，可以采用油基泥浆测井获得的声波时差验证校正效果。图 5展示了1^#井水基泥浆声波时差校正效果，由图可见，井径曲线显示在1240~1250 m和1262~1268 m段坍塌严重（第2列），原始水基泥浆声波时差受井径扩径影响测量失真，与油基泥浆声波时差对比存在显著差异（第3列）。输入探头的声学半径^[9]（0.0255 m）、声波测井仪器参数$ {l}_{1} $（1 m）、$ {l}_{0} $（0.5 m）以及泥浆声波速度（1600 m/s），计算出CAL₁为0.4 m，符合部分井段井径大于CAL₁的情况。采用式（7）计算校正时差，校正后声波时差与油基泥浆测量声波时差吻合度明显提高（第4列），验证了补偿声波测井校正方法的可靠性和合理性。

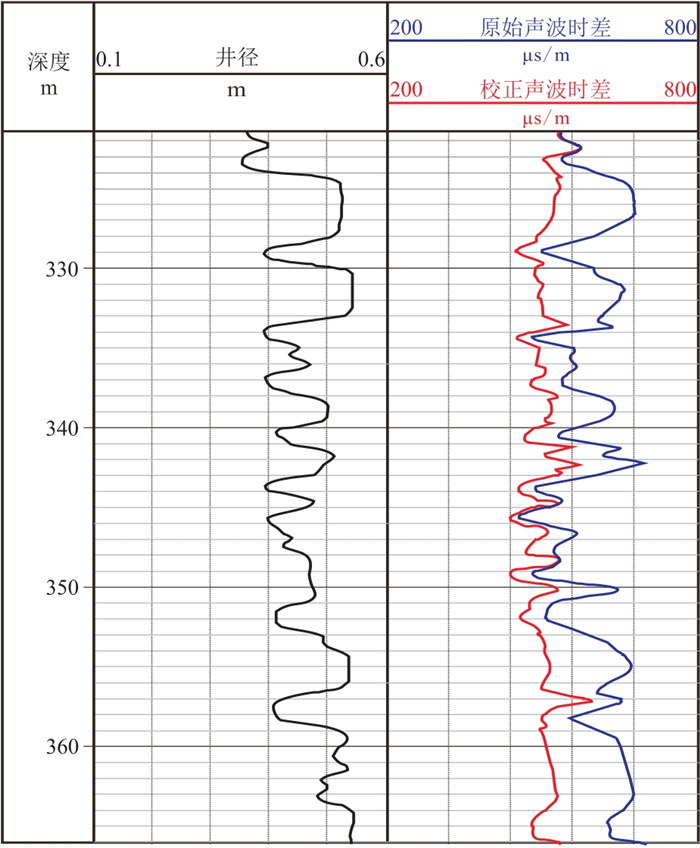
图 6显示2^#井的声波时差数据的校正效果，由图可见，井径曲线显示320~365 m井段坍塌严重，部分超过0.5 m（第2列），并且实测声波时差大于泥浆声波时差（660 μs/m），明显不合常规，此时测量仪器的测量结果完全失真。输入补偿声波测井仪器参数、泥浆声波速度等参数，经计算CAL₁为0.45 m，符合井径扩径大于CAL₁的情况。采用式（10）计算的声波时差校正量达到150 μs/m，有效消除了扩径异常时泥浆的影响，校正后声波时差介于500~550 μs/m之间，更加客观地反映了地层真实速度（第3列）。

4 结束语

本文从双发双收补偿声波测井仪器声波实际传播路径入手，基于井径扩径对应第一校正门限范围和位置等情况，推导了声波时差校正方程，形成针对三种情况的校正方法，进而开发了声波时差校正程序。应用该程序在实际测井中进行声波时差校正处理，处理结果表明：（1）校正声波时差与油基泥浆测量声波时差吻合度较好，验证了该方法的合理性和有效性；（2）在浅层井径垮塌严重处，该方法能够有效消除声波时差测量异常，校正声波时差能更准确地反映地层真实速度。