2. 中国石化石油工程技术研究院, 北京 102200;
3. 中国石油 西南油气田公司工程技术研究院, 四川成都 610050;
4. 西南交通大学信息科学与技术学院, 四川成都 610031
2. SINOPEC Petroleum Engineering Technology Research Institute, Beijing 102200, China;
3. Engineering Technology Research Institute, PetroChina Southwest Oil & Gasfield Company, Chengdu, Sichuan 610050, China;
4. School of Information Science and Technology, Southwest Jiaotong University, Chengdu, Sichuan 610031, China
井筒钻进过程中,井壁状况一直受研究人员高度关注,而通过研究井壁裂缝的形态、角度、填充、破碎等特征,结合地质、钻井液等信息,在一定程度上能反应井筒当前状况。所有的裂缝识别测井资料中,成像测井资料目前最为直观、有效[1],故测井数据分析人员往往需对测井成像图中表征的裂缝状况进行重点关注。
现阶段成像测井技术主要是测量井壁电阻率,通过数据的微小差异反映井壁及井筒状态。由于数据不够直观,分析人员难以充分获取有用信息,后期通过不同窗长的处理,将采集的电阻率等数据制成静态图像和动态图像,降低数据分析难度。但由于常用的电阻率测井仪器测量极板间有一定缝隙,以及测量过程中仪器本身的旋转位移,无法保证测量数据始终紧贴井壁,因此即使在井眼中实现了所谓的全覆盖,也会造成井周测量不完整的现象。最终形成的电阻率测井图像中,会呈现宽度和位置不规则的空白条带,导致图像中的裂缝、孔洞等区域纹理信息缺失、错位。因此目前所得图像中缝洞区域的识别和评价,基本依靠专业人员进行抽象分析判断,显然工作量巨大且分析结果主观性强,难以准确表征和分析图中缝洞等关键构造形态。
对于此问题,测井解释专家进行了长期研究,尝试根据已有测量数据得出客观规律,通过计算机技术实现测井成像图中空白条带的自动填充,进而实现测井图像中各种裂缝的智能识别和精确分割。这类技术的应用可以极大地减少工作量,提升识别的准确率和稳定性。
李潮流等[2]提出了基于样本块的图像填充算法,以边界点周围图像为填充样本,由外向内逐层填充,最后通过滤波平滑,完成图像空白条带的填充。Hurley等[3]提出了基于多点统计的Filtersim算法,并将其应用于电成像记录中的空白条带填充。王俊华[4]提出了基于多点统计的图像填充方法,使用滤波特征匹配方式,将待填充边界位置特征与已有图像特征进行匹配,实现空白条带填充。张翔[5]、李雷刚等[6]在基于多点地质统计方法的基础上加入插值法,利用插值法对空白条带进行初步填充,随后使用多点匹配的方法进一步修复。彭湃[7]提出了改进反距离插值法,加入迭代机制,有效减少了填充图像的台阶现象。Fernández-Ibáñez等[8]提出了一种综合利用成像测井、岩心和地质力学模型的裂缝识别技术,通过该技术获得裂缝定向和频率数据,在一定程度上弥补了空白条带数据缺失的不足。王哲峰等[9]结合深度学习框架, 提出一种基于卷积神经网络(CNN)模型的空白条带充填方法。王磊等[10]使用小波变换对测井图像进行频谱分解,随后使用高阶扩展快速行进算法(FMM)进行局部空白条带的内插重建。Wu等[11]采用对抗性边缘学习的Edge Connect图像复原方法和采用CNN的深度图像先验图像复原方法填充电成像记录中的空白条带。
上述方法虽在一定程度上对空白条带的缺失信息进行了插值填充,但往往实现过程较为复杂,或者采用从像素点微观角度出发进行插值运算的思路,未充分考虑图像与裂缝区域形态分布情况、倾角等关联的纹理宏观信息,而上述信息恰为井壁缝洞区域状况分析的关键要素。就实际应用效果而言,在缝洞区域形态稍显复杂的成像图中,形态信息的缺失会直接导致填充后图像严重失真,错位明显,甚至失去裂缝分析意义。
本文对传统反距离加权插值法进行改进,设计了融合裂缝形态信息的反距离迭代插值法。首先预拟合出裂缝形态拟合线,利用插值点与裂缝形态拟合线的相对位置关系,从图像像素的角度建立了该相对位置与插值权重近似线性的关系,从而动态调整参考点对插值点插值的权重系数,使填充后的裂缝区域纹理连贯平滑,更符合裂缝实际形态和分布的规律,为后续测井图像中裂缝的智能识别和精确分割提供了更好的数据支撑。
1 空白条带反距离加权插值法 1.1 反距离加权插值法反距离加权插值法作为加权插值法的一种,是通过附近已知信息以一种近似的方式进行信息填充[12]。其插值受多点数据影响,而每点的赋值权重与该实测点到正在插值计算点的距离有关,其关系呈现为距离倒数形式,具体表达式为
| $ Yi=\sum\limits_{i=1}^{N}{\lambda }_{i}{X}_{i} $ | (1) |
| $ {\lambda }_{i}=\frac{\frac{1}{{d}_{i}}}{\sum\limits_{i=1}^{N}\frac{1}{{d}_{i}}} $ | (2) |
式中: Yj为待插值点的值;N为影响该插值点的实测点个数;X
| $ \left[\begin{array}{ccccccc}X\left[\mathrm{1, 1}\right]& X\left[\mathrm{1, 2}\right]& X\left[\mathrm{1, 3}\right]& & X\left[\mathrm{1, 9}\right]& X\left[\mathrm{1, 10}\right]& X\left[\mathrm{1, 11}\right]\\ X\left[\mathrm{2, 1}\right]& X\left[\mathrm{2, 2}\right]& X\left[\mathrm{2, 3}\right]& & X\left[\mathrm{2, 9}\right]& X\left[\mathrm{2, 10}\right]& X\left[\mathrm{2, 11}\right]\\ X\left[\mathrm{3, 1}\right]& X\left[\mathrm{3, 2}\right]& X\left[\mathrm{3, 3}\right]& \cdots & X\left[\mathrm{3, 9}\right]& X\left[\mathrm{3, 10}\right]& X\left[\mathrm{3, 11}\right]\\ X\left[\mathrm{4, 1}\right]& X\left[\mathrm{4, 2}\right]& X\left[\mathrm{4, 3}\right]& & X\left[\mathrm{4, 9}\right]& X\left[\mathrm{4, 10}\right]& X\left[\mathrm{4, 11}\right]\\ X\left[\mathrm{5, 1}\right]& X\left[\mathrm{5, 2}\right]& X\left[\mathrm{5, 3}\right]& & X\left[\mathrm{5, 9}\right]& X\left[\mathrm{5, 10}\right]& X\left[\mathrm{5, 11}\right]\end{array}\right] $ |
|
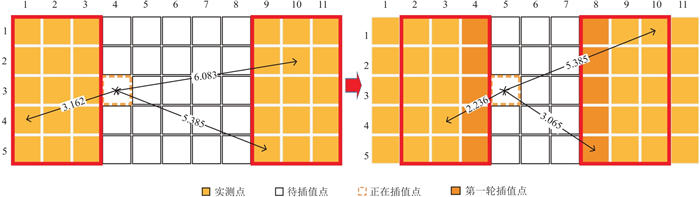
图 1 实测电阻率成像图迭代型插值法示意图 红色框为所有影响点选取窗。 |
反距离加权插值法只利用实测点像素值对测井图像中的空白条带区域进行插值计算,在较窄的空白条带填充时效果尚可,但在空白条带宽度过大时,由于部分实测点与正在进行插值点的距离过远,导致填充后误差较大,会出现台阶现象。因此将该方法改为迭代插值计算的方式。
1.2 迭代型反距离加权插值法及FMM算法迭代型插值法计算方法如图 1右所示[13],第一轮插值采用反距离加权插值法。在完成一轮插值后,移动像素点选取窗,将第一轮已插值计算点划入第二轮插值的影响点,如此依次迭代插值,直至当前窗口内所有待插值点全部完成插值计算。
FMM算法的思想是,先处理待修复区域边缘上的像素点,然后层层向内推进,直到修复完所有的像素点,通过方向因子、几何距离因子、水平集距离因子来确定权重。方向因子保证了越靠近法线方向的像素点对待填充点的贡献越大;几何距离因子保证了离待填充点越近的像素点对该点贡献越大;水平集距离因子保证了离待修复区域的轮廓线越近的像素点对该点的贡献越大。迭代型反距离加权插值法和FMM算法的实际使用效果如图 2。

|
图 2 反距离迭代插值法和FMM算法填充效果 (a)原始测井图像;(b)反距离迭代插值法;(c)FMM算法 |
从图 2可以看出,两种算法基本完成了对空白条带的插值填充,对于纹理较清晰且波动变化连续的区域填充效果较好,填充前、后区域连贯。但对于图中纹理变化规律不明显区域,插值填充后裂缝不连续,裂缝形态破坏严重,且对于高角度裂缝填充效果较差,填充后裂缝区域出现台阶现象,失去裂缝评价的意义。
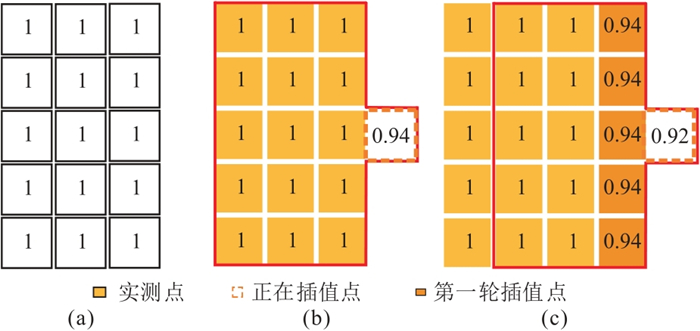
1.3 反距离迭代插值法相关度分析实际应用中,部分成像图中空白条带过宽,信息丢失过多,即使采用插值法填充,也难以有效推算和复现纹理信息。为了保证填充结果的有效性,需要通过相关度模型计算电阻率测井成像图空白条带迭代插值相关度,即
| $ M(x, y)=\frac{\sum\limits_{x=i-2}^{i+2}\sum\limits_{y=j-3}^{j-1}Q(x, y)R(x, y)}{16} $ | (3) |
式中:
|
图 3 迭代插值法相关度计算模型 (a)掩模矩阵Q;(b)第一轮计算结果;(c)第二轮计算结果 |
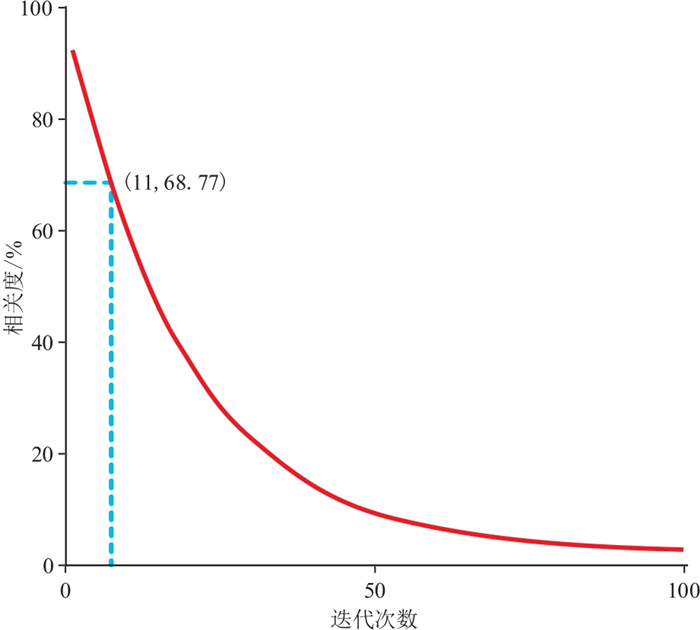
将该相关度模型进行迭代计算,得出如图 4所示关系曲线。从图中不难看出,在迭代计算进行到第11次时,相关度已降至约68.77%。因此对于待填充测井图像,随着空白条带宽度的增加,其相关度逐步下降,填充效果也越来越差,相关度不低于70%时,填充效果相对较好。当空白条带宽度超过20个像素点时,用迭代插值法填充所得结果相关度已低于70%,填充效果较差。本文所收集到的样本, 其空白条带宽度均在20个像素点以下,平均宽度为16个像素点,迭代插值法计算的结果相关度达到80%。
|
图 4 迭代次数与原始数据相关度关系曲线 |
由图 2可知,经过迭代插值和FMM算法填充后的图像存在裂缝不连续的情况,导致裂缝形态破坏严重,失去裂缝评价的意义。因为无论反距离迭代插值法还是FMM算法,仅是从像素点微观角度出发进行数值运算,未充分考虑图像中与裂缝分布情况、倾角等关联的纹理形态信息,而上述信息恰为井壁异常状况分析的关键要素[14]。该类信息的缺失,导致填充结果欠佳,且填充后图像失真较严重,错位明显。
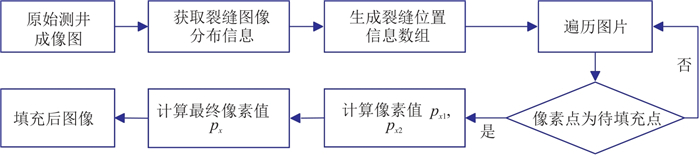
为此本文提出融合纹理形态的反距离迭代插值法。首先获取裂缝总体信息分布,拟合出当前电阻率测井图像中裂缝等纹理形态的大致分布曲线,并生成裂缝位置信息数组,记录表征曲线的所有像素点坐标位置(u,v)。然后遍历图片,计算待填充点的像素值px1,px2。px1是通过本文算法以空白条带左边实际测量像素值来计算的待填充点像素值,px2则是以空白条带右边实际测量像素值来计算的待填充点像素值。根据px1、px2数值以及与空白条带左右两端的距离加权融合,得到待填充点的最终像素值。本文算法流程如图 5所示。
|
图 5 本文填充算法流程图 |
在进行迭代插值前,需要对当前图像进行预处理,拟合出当前电阻率测井图像中裂缝等纹理形态的大致形态分布情况参与计算[15],流程如图 6所示。
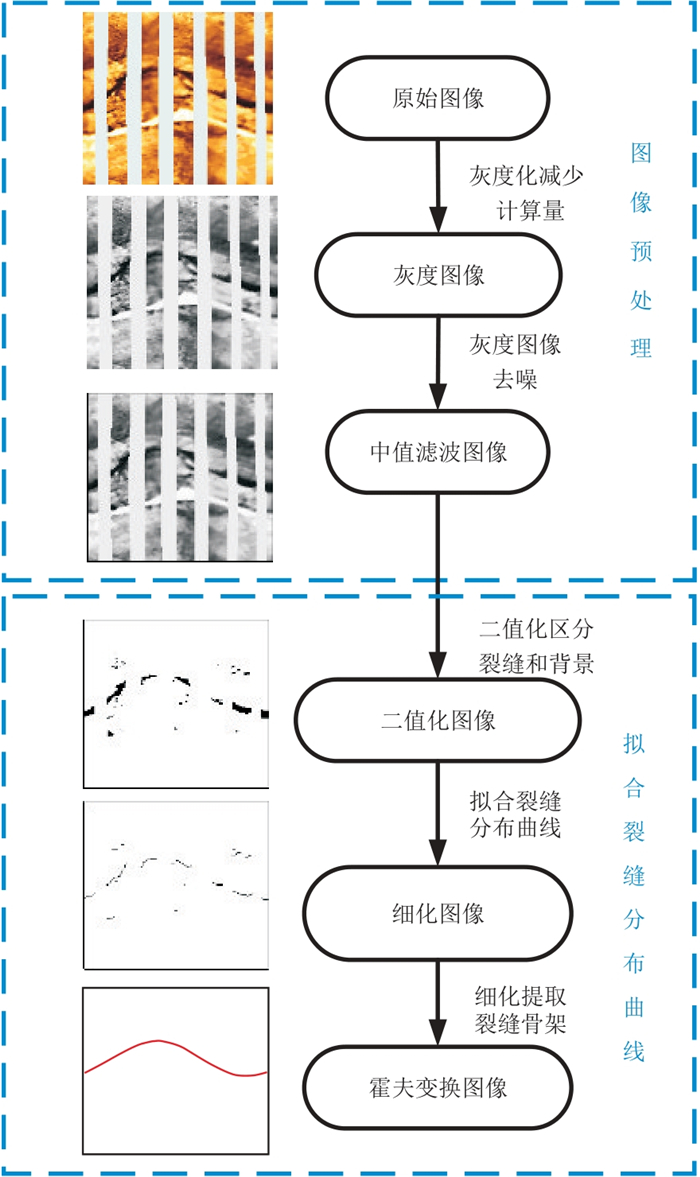
|
图 6 裂缝分布曲线拟合流程 |
获取裂缝纹理总体形态信息分为图像预处理、拟合裂缝分布曲线两步。由于电阻率成像测井图像都是彩色图像,为减少在获取裂缝分布信息过程中的输入量和计算量,故图像预处理首先进行彩色图像灰度化处理。加权平均算法的灰度化效果最为符合人眼主观感受,在保留裂缝特征的情况下,背景区域孔洞信息也有所保留,因此选择该灰度化方法。
由于电阻率测井成像图是根据电阻率测井数据映射形成的图像,因此在裂缝图像区域附近,往往会出现像素值突变的情况,即为部分噪点。对应这部分噪点,使用中值滤波去噪,实现灰度图像平滑处理。裂缝分布曲线拟合首先将预处理后的图像进行二值化处理。二值化处理进一步将灰度图像划分为裂缝图像区域和背景区域。本文选用自动阈值的二值化方法来区分前景(黑色)像素和背景(白色)像素[16]。
然后采用Zhang-Suen算法[17]对二值图像进行细化,即在不破坏图像细节连通性的情况下提取前景图像的骨架信息,在图像细化过程中,图像的骨架信息被突出,冗余信息大量减少。从图 6中可以看出,原始裂缝区域已经细化为几条线段,裂缝分布信息保存良好,未出现失真情况。由于井壁裂缝在电阻率成像测井图中的响应一般为正弦状曲线,因此使用霍夫变换拟合出裂缝分布完整的曲线信息[18],该曲线能表现裂缝纹理形态信息的大致分布情况,如倾角、倾向、裂缝走向等。
此外,根据裂缝分布曲线生成位置信息数组img1,该数组中记录表征曲线的所有像素点坐标位置(u,v)。同时曲线与实际裂缝倾角之间的关系可由如下公式表达
| $ \theta =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{A}{2R} $ | (4) |
式中: A为拟合正弦函数振幅; R为井眼半径。由此可知该曲线能够反映裂缝的倾角情况。通过逐像素点计算该曲线方向导数即可反应该裂缝的倾角参数以及分布情况。
2.2 融合裂缝形态信息的反距离迭代插值法根据图 6的曲线拟合流程得到裂缝形态分布曲线,用于构建融合裂缝形态信息的反距离迭代插值法。为保证插值后图像纹理的平滑过渡,拟合曲线变化的幅度是重要考察因素。
从图像微观角度进行研究,图像是由若干个像素点构成,是一个纵横向像素点矩阵。而由霍夫变换形成的拟合曲线可以看作由多个像素点连接而成的细线,而这些像素点也构成拟合曲线像素点集合。由于拟合曲线贯穿于整幅图像,一般在图像的每一列都至少有一个像素点属于该正弦曲线像素点集合。插值过程中,参考点与对应列拟合曲线像素点距离,以及距离倒数的变化趋势,即可反映拟合曲线的升降趋势以及裂缝的形态信息,故插值过程中利用该距离倒数计算插值,即融合了裂缝形态信息。根据本研究的样本图像尺寸参数,选取插值点左侧5行3列的像素点为参考点计算插值,基本能反映出裂缝形态信息的影响。由于电阻率测井成像图中空白条带宽度、形态一般均不固定,无法使用整体加窗计算的方式,因此可以采用先逐列从左往右,再从右向左插值两轮填充的方式,并将两次结果加权融合。该方法能够有效解决空白条带宽度不固定以及同一空白条带横向位移的问题, 流程如图 7所示。
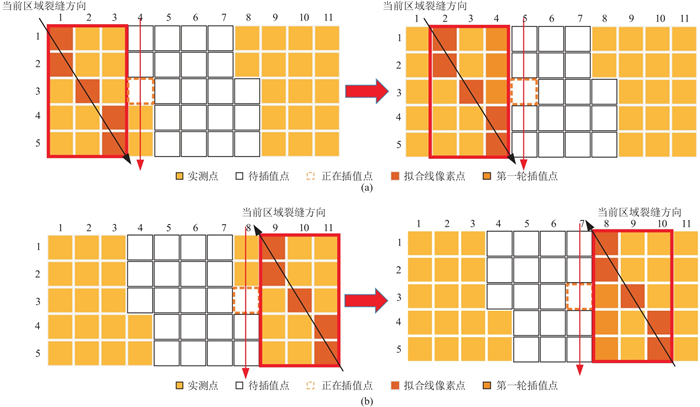
|
图 7 融合裂缝形态信息反距离迭代插值法填充流程 (a)从左向右全图充填;(b)从右向左全图充填 |
图中红色方框内为影响当前插值点的参考点,黑色箭头方向为当前区域裂缝纹理方向,红色箭头方向为填充方向。首先根据待插值点的位置,计算其各参考点相对于裂缝形态的方向权重系数ax, y,即
| $ {a}_{x, y}=\sum\limits_{k=1}^{m}(\frac{1}{{q}_{x, y}}\times \frac{\frac{1}{{q}_{x, y}}}{\sum\limits_{i=1}^{m}\frac{1}{{q}_{x, y}}}) $ | (5) |
式中: qx, y为当前计算参考点(x, y)与裂缝曲线拟合线中同列像素点的距离(即x=u); m表示裂缝条数。若所选参考点恰位于裂缝拟合曲线上,则该点权重为该列其余元素权重之和。若当前区域有多条裂缝,需将多条裂缝的权重加权融合计算。很明显,如果拟合的裂缝线倾角越大,则横向选取参考点距离变化越大,最终各参考点的方向权重值变化就越大。即通过该拟合曲线,充分融入裂缝形态信息。
从像素角度考虑,裂缝曲线由像素点连接而成,假设第一条裂缝纹理图像在所选参考点附近由像素点(2,1)、(4,2)、(5,3)连接而成,第二条裂缝纹理图像由像素点(5,1)、(4,2)、(4,3)连接而成。根据式(5)计算参考点方向权重,得到两个待插值点(3,4)、(4,4)相关联参考点的方向权重矩阵,分别如图 8所示。
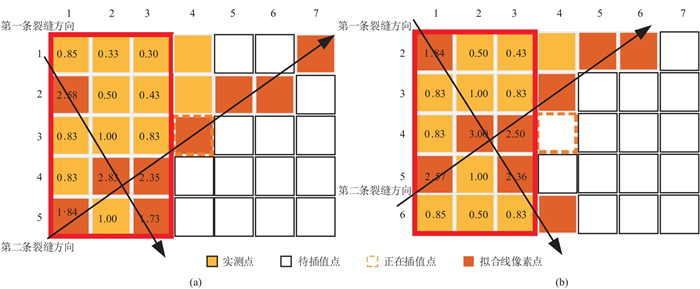
|
图 8 融合多条裂缝形态信息的反距离迭代插值法示意图 (a)待插值点(3,4)方向权重矩阵;(b)待插值点(4,4)方向权重矩阵 |
很明显,图 8中由于两个待插值点的位置不相同,对应选取的参考点集合均不同。即使两次计算过程选取了部分相同的参考点,但由于计算插值点与参考点相对位置的变化,故最终每个参考点的方向权重系数也发生变化。即根据待插值点与裂缝拟合曲线的相对位置,对其参考点的方向权重系数进行了动态调整,体现了裂缝形态对插值数值的影响。同时从图 8中可知,部分插值参考点方向权重系数已低至0.3,如果进一步扩大插值参考点范围,其权重系数值会进一步降低,失去参考意义。故插值过程中将插值计算窗设为5行3列的形式,并将滑动步长设为1是合理的设置。
根据式(5)计算所有参考点方向权重系数得到5行3列方向权重矩阵,对式(2)进行修正,得到最终各参考点权重公式
| $ {\lambda }_{x, y}=\frac{{a}_{x, y}\frac{1}{{d}_{x, y}}}{\sum\limits_{x, y=1}^{n}{a}_{x, y}\frac{1}{{d}_{x, y}}} $ | (6) |
式中dx, y为插值点到参考点(x, y)的距离。矩阵中所有元素除以矩阵元素之和,使各参考点权重之和为1,且最终待插值点像素值不会超出数值范围。
基于式(6),空白条带从左往右、从右往左两个方向迭代插值计算公式分别为
| $ {p}_{x1}=\sum\limits_{x=i-2}^{i+2}\sum\limits_{y=j-3}^{j-1}{\lambda }_{x, y}\mathrm{i}\mathrm{m}\mathrm{g}[x, y] $ | (7) |
| $ {p}_{x2}=\sum\limits_{x=i-2}^{i+2}\sum\limits_{y=j+1}^{j+3}{\lambda }_{x, y}\mathrm{i}\mathrm{m}\mathrm{g}[x, y] $ | (8) |
式中:img[x, y]为参考点实际像素值;
通过式(7)、式(8)从两个方向计算待插值点的像素值,其结果按
| $ {p}_{x}=\frac{{p}_{x1}(D-d)}{D}+\frac{{p}_{x2}d}{D} $ | (9) |
距离加权融合即为该点最终的插值像素值。式中:D为待插值点所在行空白条带宽度; d为待插值点与左边实测点距离。
2.3 填充效果对比本文算法与反距离迭代插值法、FMM算法的对比结果如图 9所示。从图 9不难看出: ①反距离迭代插值算法(图 9c)、FMM算法(图 9b)对低角度裂缝、水平裂缝填充后图像效果较好,但对中、高角度裂缝填充后图像裂缝不连贯,出现断裂、台阶现象,如图中红色区域内。且对于图中纹理变化规律较抽象区域,填充后裂缝不连续,裂缝形态破坏严重,可能失去裂缝评价的意义。②本文算法结果未出现台阶现象的问题,图中空白条带填充有更为良好的填充效果,形成的裂缝区域纹理与实际状况更为吻合,说明该算法能为后续利用电阻率测井成像图进行各种裂缝形态的智能识别和较精确分割,提供了更有利的支撑条件(图 9d)。此外,根据实验测试,填充一张209×190像素大小图片,使用反距离迭代插值法与FMM算法的耗时均为28 ms,使用本文算法的耗时为30 ms。尽管本算法在时间上略有增加,但由于处理时间均在毫秒量级,故在现场应用中,对后续的处理及分析基本无影响。

|
图 9 不同算法空白条带填充效果对比 (a)原始测井图像;(b)FMM算法;(c)反距离迭代插值法;(d)本文设计算法 |
为进一步证明本文填充算法的实际应用效果,选用准噶尔盆地春风油田石炭系火成岩储层的测井成像资料的分析结果进行展示。截取其中10 m左右裂缝发育形态多样且密集的代表性井段,基本能反映全井段经几种算法填充完成后的效果。FMM算法、反距离迭代插值法和本文算法的填充结果对比如图 10所示。从图中可以看出,所收集到的测井成像图有6条空白条带,10 m井段中共有11条裂缝。观察三种算法的实际填充效果, 本文算法效果最好(图 10d),FMM算法(图 10b)填充效果略差于反距离迭代插值法(图 10c)。图 10b和图 10c中红色标记框中存在较多裂缝不连贯,纹理呈现直线状,断裂、甚至出现多次台阶现象,在②号高角度裂缝处尤为严重。而本文算法在填充后裂缝区域纹理连贯,且基本无台阶,符合裂缝的实际形态,在②号高角度裂缝填充后纹理连贯平滑。总体而言,本文算法填充效果明显优于FMM算法和反距离迭代插值法。

|
图 10 不同算法测井成像资料实际填充效果对比 (a)原始图像;(b)FMM算法;(c)反距离迭代插值法;(d)本文算法 |
进一步通过计算裂缝图形分布拟合线(图 11)进行分析。不难看出,使用FMM算法进行填充后,多条裂缝区域出现显著形变,裂缝部分区域存在明显断裂(图 11b)。

|
图 11 不同算法测井成像资料填充效果裂缝细化图 (a)霍夫变换;(b)FMM算法;(c)反距离迭代插值法;(d)本文算法 |
图 11b、图 11c中,标记的红色区域内细化线明显不连续,与电阻率成像测井图中裂缝大致呈现正弦状的规律不符,图 11b中②、⑤号裂缝在FMM算法填充后出现多次台阶现象、失真严重,不能严格认定为裂缝图像;图 11c具有类似问题,但有所改善,即填充后裂缝出现断裂、台阶等现象略为减少,但对于如图 11c中②号高角度裂缝仍出现多次台阶现象、失真严重,不能严格认定为裂缝图像。而本文算法(图 11d)对应标记出的红色区域内细化图像基本呈现正弦趋势,无明显断裂,裂缝纹理信息保存完整,台阶现象大幅减少。
进一步观察这11条裂缝填充后的裂缝细化曲线,统计其出现台阶现象的次数。在这66处裂缝填充区域中,图 11b中出现台阶现象的裂缝共有23处,约占34.8%,其中②、⑤号裂缝处最多。图 11c中出现台阶现象的裂缝共有17处,约占25.8%,②、⑤号裂缝出现台阶现象最多。由于②号裂缝高角度裂缝信息变化大,图 11b和图 11c获取的信息不足,导致出现台阶现象。而图 11d出现台阶现象的裂缝仅有2处,约占3%,数量相比反距离迭代插值法已下降88%。此外,⑤号裂缝处因周围色彩干扰大,纹理轮廓较为模糊,三种算法都出现台阶现象,但图 11d填充后的台阶高度明显低于图 11b和图 11c。
对这66处裂缝区域分布拟合线与经霍夫变换后得到的曲线做相似度对比。首先计算出裂缝细化线最高点与最低点间的距离h,然后逐列计算分布拟合线与霍夫变换曲线在空白条带处的偏差e, 该列的相似度为
| $s=1-\frac{e}{h} $ | (10) |
依次计算空白条带每列相似度,求平均即为该裂缝区域整体相似度。图 11b、图 11c相似度均低于65%,其中图 11b虽在低角度裂缝中相似度为70%左右,但在高角度裂缝中不到50%。图 11c的相似度略有提升,在低角度裂缝达到75%左右,但高角度裂缝也不到60%。图 11d仅在⑤号裂缝出现台阶现象处相似度较低,为65.3%,其余相似度均在86%以上,最高达到96%。
从数据上看本文算法提升明显,说明本文将裂缝区域形态与分布信息作为参量构建插值计算模型,能有效解决传统算法填充后中、高角度裂缝出现台阶现象的问题。
4 结论本文将裂缝纹理形态与分布信息作为参量构建插值计算模型,形成融合裂缝形态分布信息的电阻率测井成像图空白条带填充方法。从图像像素的角度,该模型能根据插值点的位置与拟合线的走向,动态调整参考点对插值点插值的权重系数,填充后裂缝分布拟合线与霍夫变换后曲线相似度明显提升。中、高角度裂缝较FMM算法提升了40%以上,较反距离迭代插值法提升了25%以上,有效解决现有算法填充后中、高角度裂缝不连贯的问题。
相较于反距离迭代插值法,本文算法填充后裂缝区域出现台阶现象的区域数量下降88%以上,性能提升明显,且台阶高度也低于FMM和反距离迭代插值法。充分说明本文算法填充后的裂缝区域纹理连贯平滑,更符合裂缝实际形态和分布的规律,为后续进行测井图像中各种裂缝的智能识别和精确分割提供了更有利的基础。
| [1] |
孟凡顺, 冯庆付, 杨祥瑞. 利用电成像测井资料分析次生孔隙率[J]. 石油地球物理勘探, 2006, 41(2): 221-225. MENG Fanshun, FENG Qingfu, YANG Xiangrui. Using electro‑imaging logging data to analyze secondary porosity[J]. Oil Geophysical Prospecting, 2006, 41(2): 221-225. DOI:10.3321/j.issn:1000-7210.2006.02.021 |
| [2] |
李潮流, 周灿灿, 黄书先. FMI成像测井失真图像的修复及其地质应用[J]. 石油天然气学报, 2007, 29(1): 88-91. LI Chaoliu, ZHOU Cancan, HUANG Shuxian. Inpainting of distorted FMI image and its geologic application[J]. Journal of Oil and Gas Technology, 2007, 29(1): 88-91. DOI:10.3969/j.issn.1000-9752.2007.01.022 |
| [3] |
HURLEY N F, ZHANG T F. Method to generate full-bore images using borehole images and multipoint statistics[J]. SPE Reservoir Evaluation & Engineering, 2011, 14(2): 204-214. |
| [4] |
王俊华. 基于电成像测井图像处理关键技术研究[D]. 湖北荆州: 长江大学, 2015. WANG Junhua. A Key Technology Research Based on Imaging Logging Image Processing[D]. Yangtze University, Jingzhou, Hubei, 2015. |
| [5] |
张翔, 张猛, 肖小玲, 等. 复杂地层情况下全井周电成像图像修复方法[J]. 石油物探, 2018, 57(1): 148-153. ZHANG Xiang, ZHANG Meng, XIAO Xiaoling, et al. Image inpainting for fullbore electrical imaging logging in complex formations[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 148-153. DOI:10.3969/j.issn.1000-1441.2018.01.019 |
| [6] |
李雷刚. 基于Criminisi的图像修复新方法研究[D]. 宁夏银川: 北方民族大学, 2020. LI Leigang. Research on New Methods of Image Inpainting Based on Criminisi[D]. North Minzu University, Yinchuan, Ninxia, 2020. |
| [7] |
彭湃. 基于迭代插值法的全井周电成像图像修复方法[J]. 中国锰业, 2018, 36(6): 182-186. PENG Pai. Image inpainting on iterative interpolation for fullboreelecreic imaging logging[J]. China's Manganese Industry, 2018, 36(6): 182-186. |
| [8] |
FERNÁNDEZ‑IBÁÑEZ F. DEGRAFF J M, IBRAYEV F. Integrating borehole image logs with core: a method to enhance subsurface fracture characterization[J]. AAPG Bulletin, 2018, 102(6): 1067-1090. DOI:10.1306/0726171609317002 |
| [9] |
王哲峰, 高娜, 曾蕊, 等. 基于深度学习模型的测井电成像空白条带充填方法[J]. 测井技术, 2019, 43(6): 578-582. WANG Zhefeng, GAO Na, ZENG Rui, et al. A Gaps filling method for electrical logging images based on a deep learning model[J]. Well Logging Technology, 2019, 43(6): 578-582. |
| [10] |
王磊, 沈金松, 苏朝阳, 等. 基于小波变换与快速行进算法的电成像数据空白带填充和响应畸变修复[J]. 工程地球物理学报, 2020, 17(5): 531-540. WANG Lei, SHEN Jinsong, SU Chaoyang, et al. Blank block interpolation and distorted response restoration of the electric image based on wavelet transforming and fast matching method[J]. Chinese Journal of Engineering Geophysics, 2020, 17(5): 531-540. DOI:10.3969/j.issn.1672-7940.2020.05.001 |
| [11] |
WU Y Y, DENG R, LINGHU S, et al. Method of image restoration of the blank strips of electric imaging logs[J]. Arabian Journal of Geosciences, 2022. DOI:10.1007/s12517-022-10434-6 |
| [12] |
龙敬文, 蒲亦非, 周激流. 基于BPANN噪声检测的反距离加权法滤除椒盐噪声[J]. 计算机应用研究, 2018, 35(4): 1266-1269, 1273. LONG Jingwen, PU Yifei, ZHOU Jiliu. Removal of salt and pepper noise by inverse distance weighted based on BPANN noise detection[J]. Application Research of Computers, 2018, 35(4): 1266-1269, 1273. DOI:10.3969/j.issn.1001-3695.2018.04.066 |
| [13] |
崔维嘉, 鲁航, 巴斌. 基于细化频谱的频率迭代插值估计算法[J]. 电子与信息学报, 2017, 39(9): 2141-2147. CUI Weijia, LU Hang, BA Bin. Iterative frequency estimation algorithm based on interpolated zoom spectrum[J]. Journal of Electronics & Information Technology, 2017, 39(9): 2141-2147. |
| [14] |
QIN Q R, DENG H. Influence of rock fractures on mechanical stability of well wall[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2007, 29(4): 167-170. DOI:10.3863/j.issn.1674-5086.2007.04.044 |
| [15] |
闫建平, 蔡进功, 首祥云, 等. 成像测井图像中的裂缝信息智能拾取方法[J]. 天然气工业, 2009, 29(3): 51-53. YAN Jianping, CAI Jingong, SHOU Xiangyun, et al. Intelligent picking method of the fracture information from imaging logging[J]. Natural Gas Industry, 2009, 29(3): 51-53. DOI:10.3787/j.issn.1000-0976.2009.03.014 |
| [16] |
张晓峰, 潘保芝. 二维小波变换在成像测井识别裂缝中的应用研究[J]. 石油地球物理勘探, 2012, 47(1): 173-176. ZHANG Xiaofeng, PAN Baozhi. Two‑dimensional wavelet transform to identify fractures in imaging logging[J]. Oil Geophysical Prospecting, 2012, 47(1): 173-176. |
| [17] |
CAI H M, YANG Z, CAO X H, et al. A new iterative triclass thresholding technique in image segmentation[J]. IEEE Transactions on Image Processing, 2014, 23(3): 1038-1046. DOI:10.1109/TIP.2014.2298981 |
| [18] |
MUKHOPADHYAY P, CHAUDHURI B B. A survey of Hough Transform[J]. Pattern Recognition, 2015, 48(3): 993-1010. DOI:10.1016/j.patcog.2014.08.027 |



 夏文鹤,四川省成都市新都区新都大道8号西南石油大学电气信息学院,610500。Email:
夏文鹤,四川省成都市新都区新都大道8号西南石油大学电气信息学院,610500。Email: