2. 东华理工大学地球物理与测控技术学院, 江西南昌 330013;
3. 东方地球物理公司物探技术研究中心, 河北涿州 072751;
4. 中海油研究总院有限责任公司勘探开发研究院, 北京 100028;
5. 海洋油气勘探国家工程研究中心, 北京 100028;
6. 中国石油大学(北京)油气资源与工程全国重点实验室, 北京 102249;
7. 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
8. 中国石油大学(北京)地球物理学院, 北京 102249
2. School of Geophysics and Measurement-Control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China;
3. Geophysical Exploration Technology Research Center, BGP Inc, CNPC, Zhuozhou, Hebei 072751, China;
4. Exploration and Development Research Institute of CNOOC Research Institute Co., Ltd, Beijing 100028, China;
5. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China;
6. National Key Laboratory of Petroleum Resources and Engineering, China University of Petroleum (Beijing), Beijing 102249, China;
7. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum (Beijing), Beijing 102249, China;
8. College of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China
全波形反演(Full Waveform Inversion,FWI)利用波动方程模拟得到的合成地震记录与实际地震记录的残差构建目标函数求取地下介质的参数,包括纵横波速度、各向异性参数和密度等。相较于其他简化波动方程的地震反演技术,如基于射线追踪的旅行时层析反演、基于褶积正演模型的地震反演等,FWI运用波动方程能更精确地模拟波场的传播过程,特别是地下构造复杂时,FWI可以获得更高精度和分辨率的反演结果。因此,近些年FWI成为了热点研究领域[1-3]。
为了保证复杂构造模型的正演模拟精度,通常需要使用细小空间网格对低速层采样。然而,对整个介质进行细网格剖分会导致巨大的计算量以及存储需求,同时在模型的高速区也会产生过采样现象。为解决该问题,最优的方法是采用不同的空间网格步长对模型的不同区域进行剖分,在模型的浅层低速区使用细网格剖分,在中深层高速区使用粗网格剖分。基于变网格的波场模拟技术通常通过对粗、细网格过渡带的波场插值技术和基于变差分系数的变网格波场模拟技术实现[4-5]。
粗细网格过渡带的波场插值技术在井间管波数值模拟[6-7]、变网格逆时偏移成像[8]、黏弹介质波场正演模拟[9]等方面都有应用。该方法使用规则的矩形网格对模型中的高、低速体进行剖分,粗、细网格步长比只能是整数倍,在粗、细网格过渡带,需要对细网格波场下采样赋值给粗网格,并且需要对粗网格波场值进行插值以确定细网格各点波场值,通常采用的插值方法有线性插值、三角函数多项式插值等[10-11]。目前,基于插值法的变网格技术依然面临着两大难题:一是地震波传播到粗、细网格分界面处时存在波场虚反射问题,二是波场在传播时间较长时会出现不稳定现象[12-13]。Adriano等[14]分析并总结了在变网格波动方程数值模拟中粗、细网格分界面存在虚反射的问题。Kang等[15-16]提出时间、空间双变网格弹性波波动方程正演模拟方法,通过合成数据测试验证了该方法的可靠性和可行性。在此基础上,许多学者进行了进一步的研究。虽然在抑制虚反射上有一定效果,但是当介质复杂时,依旧会存在虚反射现象[17]。针对粗、细网格过渡带插值不稳定的现象,许多学者改进了插值方法,如采用时空双变插值[15-16]、波数域插值[9]、转置矩阵法[18],或采用Lanczos滤波[19]、Gaussian滤波[20]、时间域滤波[21]等方法,提高了波场模拟的稳定性。但对于介质变化剧烈、长时间模拟,依旧存在不稳定问题。
基于变差分系数的变网格技术不需要对波场进行插值,因此可以有效避免粗、细网格分界面造成的虚反射问题[22]。鉴于变差分系数波场模拟方法的优势,许多学者进行了深入的研究和应用,例如基于变差分系数的起伏地表弹性波波动方程波场模拟[23]、声学孔隙模型波场模拟[24]、倾斜界面声波模拟[25]等。
基于变差分系数的变网格波场模拟技术对网格进行非规则四边形的划分,通过直接求取各网格节点处的差分系数实现变网格波场模拟。目前,计算差分系数的方法主要包括基于Taylor展开式和基于最小二乘法求解两种方法。本文采用基于Taylor展开式的方法求取差分系数并进行变网格波场模拟。在此基础上,本文基于Zhang等[26]提出的变网格方法,提出了一种基于变差分系数的变网格弹性波全波形反演方法。该方法在全波形反演的正演模拟和残差反向延拓过程中,针对不同尺度和速度的目标体,分别采用不同尺寸的网格进行剖分。对近地表低速带或小尺度目标体,使用细网格剖分,以保证波场模拟和反演精度;对中深层大尺度高速目标体,使用粗网格剖分,从而提高计算效率,并有效抑制正演模拟中出现的空间频散现象。
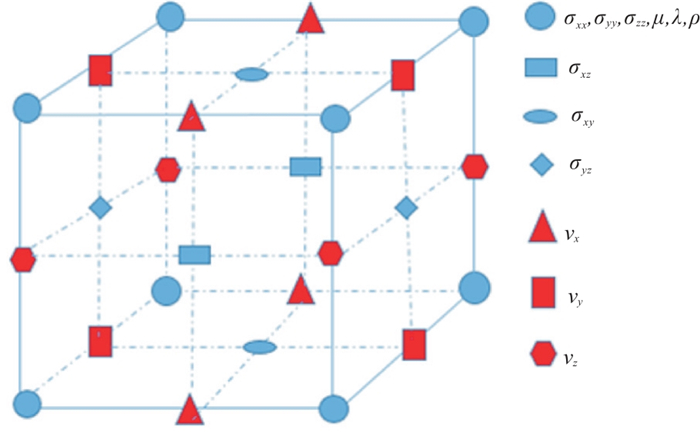
1 方法原理 1.1 弹性波动方程有限差分格式有限差分正演模拟需要对地下整体空间进行网格离散化。规则网格有限差分方法将弹性介质参数、振动速度和应力设置在相同的网格点上进行正演模拟;而交错网格有限差分方法则是将它们分别放置于整网格节点、半网格点以及面元中心点进行正演模拟。交错网格有限差分方法相较于规则网格有限差分方法数值频散更小,模拟精度更高。三维弹性波动方程交错网格有限差分不同量的网格节点离散化分布如图 1所示。
|
图 1 三维弹性波场分量空间网格节点分布示意图 vx、vy、vz为质点振动速度的三个方向分量;σxx、σyy、σzz、σxy、σyz、σxz为应力分量;λ、μ为拉梅系数;ρ为密度。 |
使用交错网格有限差分模拟一阶速度—应力弹性波方程时,速度对时间的偏导可以通过应力在空间各个方向的偏导获得,而应力的时间偏导则可以通过速度的空间偏导求得。计算当前时间节点上的应力(速度)值,只需要前一个时间节点上的应力(速度)值以及两个时间节点之间的速度(应力)值,可以大量减少存储空间。当使用二阶时间精度差分时,一阶速度—应力弹性波方程的第一项可以写成
| $ {v}_{x}\left(t+\frac{\mathrm{\Delta }t}{2}\right)={v}_{x}\left(t-\frac{\mathrm{\Delta }t}{2}\right)+\frac{\mathrm{\Delta }t}{\rho }\left(\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{xy}}{\partial y}+\frac{\partial {\sigma }_{xz}}{\partial z}\right) $ | (1) |
式中:Δt为时间采样间隔。由Taylor级数展开得到应力空间导数的任意2M阶空间精度的差分格式(
| $ \frac{\partial {\sigma }_{xx}}{\partial x}=\sum\limits_{i=1}^{2M}{C}_{i}{\sigma }_{xx}\left[x+{\left(-1\right)}^{i+1}\mathrm{\Delta }x\left(i-\frac{1}{2}\right)\right] $ | (2) |
式中:Δx为空间采样间隔;
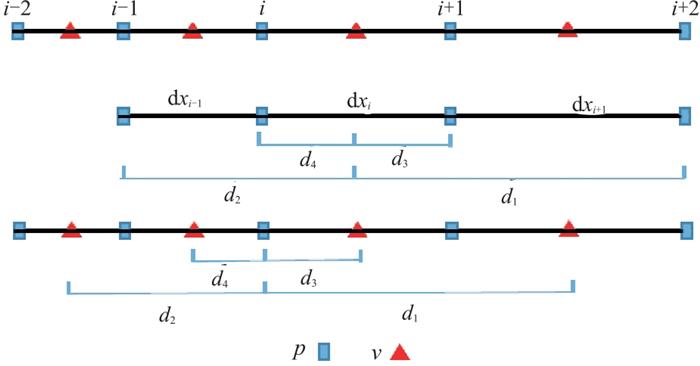
在基于变差分系数的变网格有限差分正演模拟方法中,差分系数的推导方式主要有两种:第一种基于Taylor展开式[27-29],第二种通过最小二乘拟合法求取最优差分系数。本文使用前一种方法。在任意方向的网格剖分如图 2所示,其中,蓝色方框表示整节点的应力值p,红色三角形表示半网格节点的质点振动速度v,i表示网格节点号,
|
图 2 一维波场分量及介质参数的网格节点分布 |
基于Taylor展开的任意波场分量对空间方向的导数为
| $ \frac{\partial f}{\partial x}=\sum\limits_{i=1}^{2M}{C}_{i}f\left[x+{\left(-1\right)}^{i+1}{d}_{i}\right] $ | (3) |
将式(3)变换到波数域,有
| $ ik=\sum\limits_{i=1}^{2M}{C}_{i}\mathrm{e}\mathrm{x}\mathrm{p}\left[{\left(-1\right)}^{i+1}ik{d}_{i}\right] $ | (4) |
式中k表示有效波数。
根据Pitarka[29]的推导,有限差分系数能够展开到2M阶精度,本文基于空间四阶精度推导式(4)。对
| $ \begin{array}{l}\mathrm{e}\mathrm{x}\mathrm{p}\left[{\left(-1\right)}^{i+1}ik{d}_{i}\right]=1+{\left(-1\right)}^{i+1}ik{d}_{i}+\frac{1}{2}{\left[{\left(-1\right)}^{i+1}ik\right]}^{2}{d}_{i}^{2}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \begin{array}{cc}& \end{array}\frac{1}{6}{\left[{\left(-1\right)}^{i+1}ik\right]}^{3}{d}_{i}^{3}+O\left({d}_{i}^{4}\right)\begin{array}{cc}& i=\mathrm{1, 2}, \mathrm{3, 4}\end{array}\end{array} $ | (5) |
将式(5)代入式(4),推导出四阶差分系数满足方程组
| $ \left(\begin{array}{cccc}1& 1& 1& 1\\ {d}_{1}& -{d}_{2}& {d}_{3}& -{d}_{4}\\ {d}_{1}^{2}& {d}_{2}^{2}& {d}_{3}^{2}& {d}_{4}^{2}\\ {d}_{1}^{3}& -{d}_{2}^{3}& {d}_{3}^{3}& -{d}_{4}^{3}\end{array}\right)\left(\begin{array}{c}{C}_{1}\\ {C}_{2}\\ {C}_{3}\\ {C}_{4}\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right) $ | (6) |
对于任意2M阶有限差分系数矩阵可以统一表示为
| $ \boldsymbol{A}\boldsymbol{C}=\boldsymbol{b} $ | (7) |
式中:
| $ {A}_{n, i}={\left[{\left(-1\right)}^{i+1}\right]}^{n-1}{d}_{i}^{n-1} $ | (8) |
图 2所示网格剖分的空间差分步长增量
| $ \left\{\begin{array}{l}{\boldsymbol{d}}^{\mathrm{h}}={\boldsymbol{A}}^{\mathrm{h}}{\boldsymbol{d}}_{x}^{\mathrm{h}}\\ {\boldsymbol{d}}^{\mathrm{f}}={\boldsymbol{A}}^{\mathrm{f}}{\boldsymbol{d}}_{x}^{\mathrm{f}}\end{array}\right. $ | (9) |
式中:
| $ {\boldsymbol{A}}_{4}^{\mathrm{h}}=\left(\begin{array}{ccc}0& \frac{1}{2}& 1\\ 1& \frac{1}{2}& 0\\ 0& \frac{1}{2}& 0\\ 0& \frac{1}{2}& 0\end{array}\right) $ | (10) |
空间高阶精度变换矩阵可以通过空间四阶精度变换矩阵获得
| $ {\boldsymbol{A}}_{2M}^{\mathrm{h}}=\left[{\boldsymbol{\alpha }}_{1}, \left(\begin{array}{c}{\boldsymbol{B}}^{\mathrm{h}}\\ {\boldsymbol{A}}_{2\left(M-1\right)}^{\mathrm{h}}\end{array}\right), {\boldsymbol{\alpha }}_{2}\right] $ | (11) |
| $ \left\{\begin{array}{l}{\boldsymbol{\alpha }}_{1}={\left(\mathrm{0, 1}, 0, \cdots , 0\right)}^{\mathrm{T}}\\ {\boldsymbol{B}}^{\mathrm{h}}=\left(\begin{array}{c}0, \cdots , 0, \frac{1}{2}, 1, \cdots , 1\\ 1, \cdots , 1, \frac{1}{2}, 0, \cdots , 0\end{array}\right)\\ {\boldsymbol{\alpha }}_{2}={\left(\mathrm{1, 0}, \cdots , 0\right)}^{\mathrm{T}}\end{array}\right. $ | (12) |
式中:Bh为矩阵,其维度与空间差分阶数有关,为2×(2M-3);α1和α2均为2M×1的一维向量。空间四阶精度半网格节点上变换系数矩阵可以表示为
| $ {\boldsymbol{A}}_{4}^{\mathrm{f}}=\left(\begin{array}{cccc}0& 0& 1& \frac{1}{2}\\ \frac{1}{2}& 1& 0& 0\\ 0& 0& \frac{1}{2}& 0\\ 0& \frac{1}{2}& 0& 0\end{array}\right) $ | (13) |
任意空间高阶半网格节点变换矩阵,可由空间四阶精度获得
| $ {\boldsymbol{A}}_{2M}^{\mathrm{f}}=\left[{\boldsymbol{\beta }}_{1}, \left(\begin{array}{c}{\boldsymbol{B}}^{\mathrm{f}}\\ {\boldsymbol{A}}_{2\left(M-1\right)}^{\mathrm{f}}\end{array}\right), {\boldsymbol{\beta }}_{2}\right] $ | (14) |
| $ \left\{\begin{array}{l}{\boldsymbol{\beta }}_{1}={\left(0, \frac{1}{2}, 0, \cdots , 0\right)}^{\mathrm{T}}\\ {\boldsymbol{B}}^{\mathrm{f}}=\left(\begin{array}{c}0, \cdots , \mathrm{0, 1}, \cdots , 1\\ 1, \cdots , \mathrm{1, 0}, \cdots , 0\end{array}\right)\\ {\boldsymbol{\beta }}_{2}={\left(\frac{1}{2}, \mathrm{0, 0}, \cdots , 0\right)}^{\mathrm{T}}\end{array}\right. $ | (15) |
式中:Bf的维度为2×(2M-2); β1和β2的维度均为2M×1。在获得变换矩阵和差分空间步长增量后,可通过式(6)求取差分系数。
1.3 基于变差分系数的弹性波全波形反演全波形反演的目标函数可以表示为模拟记录和观测记录残差的L2范数
| $ \chi \left(\boldsymbol{m}\right)=\frac{1}{2}{||{\boldsymbol{D}}^{\mathrm{s}\mathrm{y}\mathrm{n}}-{\boldsymbol{D}}^{\mathrm{o}\mathrm{b}\mathrm{s}}||}_{2}^{2} $ | (16) |
式中:
| $ {\boldsymbol{m}}_{k+1}={\boldsymbol{m}}_{k}+{\gamma }_{k}{\rm{ \mathsf{ δ} }}{\boldsymbol{m}}_{k} $ | (17) |
式中:mk表示第k次迭代的反演结果;
本文首先采用一维变网格波场模拟验证方法的正确性。其中,纵波速度为4000 m/s,震源为30 Hz主频的Ricker子波。当网格变化比r=1.0时,所有网格步长均为4 m;当r=2.0时,表示网格步长在0~400 m深度范围内为2 m,在400~1600 m内为4 m, 在1600~3500 m内为8 m;当r=2.5时,网格步长在0~320 m内为1.6 m, 在320~1520 m内为4 m, 在1520~3500 m内为10 m。图 3为三种网格模拟的200、400 ms时的波形,可以看出,三种网格模拟结果非常一致,说明了变网格模拟方法的正确性。

|
图 3 一维不同网格比正演模拟不同时刻波形对比 (a)200 ms;(b)400 ms |
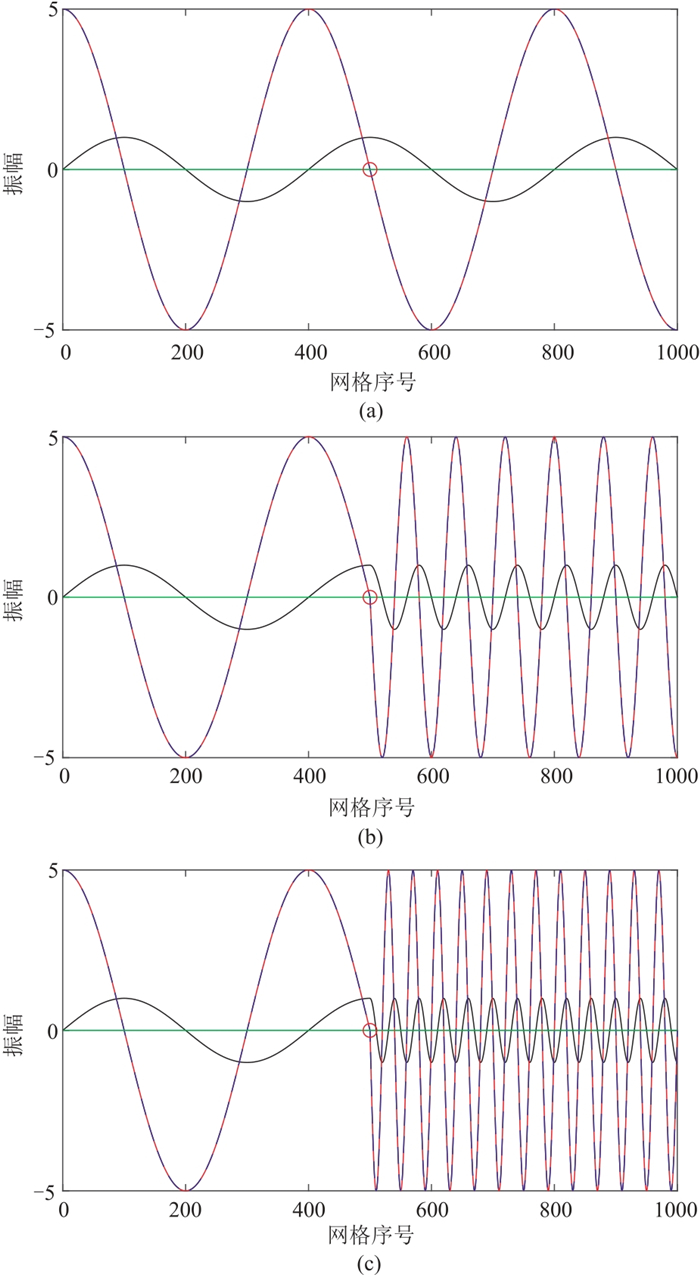
本文对变网格剖分下波场对空间方向求导的精度也进行了测试。当网格步长变化比为1.0和5.0时,正弦函数离散化差分求导与真实导数曲线几乎没有差异(图 4a、图 4b),当网格步长变化比为10.0时,二者的差异也非常小(图 4c)。
|
图 4 正弦函数(黑线)不同网格变化比离散求导值(蓝色虚线)与解析解(红线)的对比及其误差曲线(绿线) (a)r=1.0;(b)r=5.0;(c)r=10.0 |
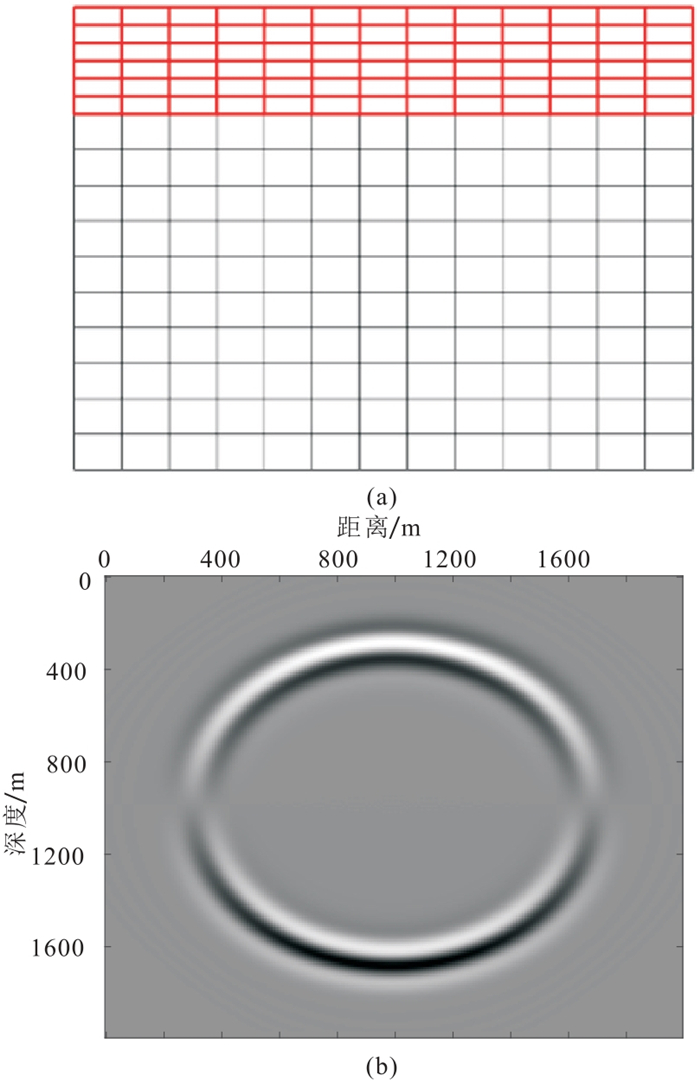
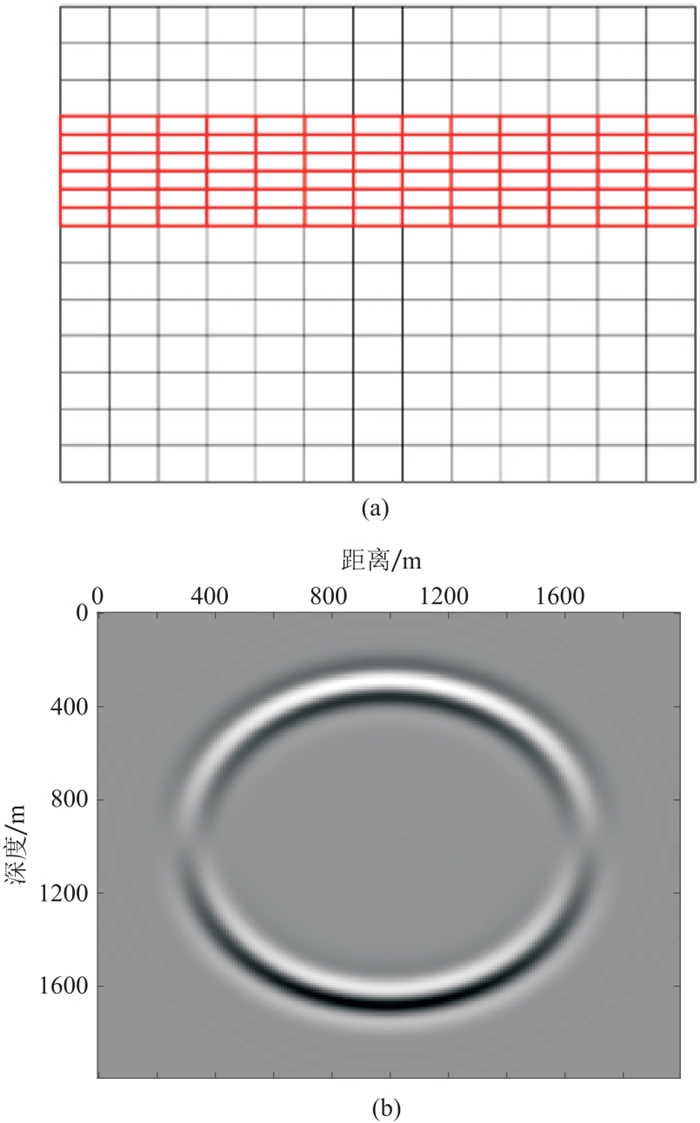
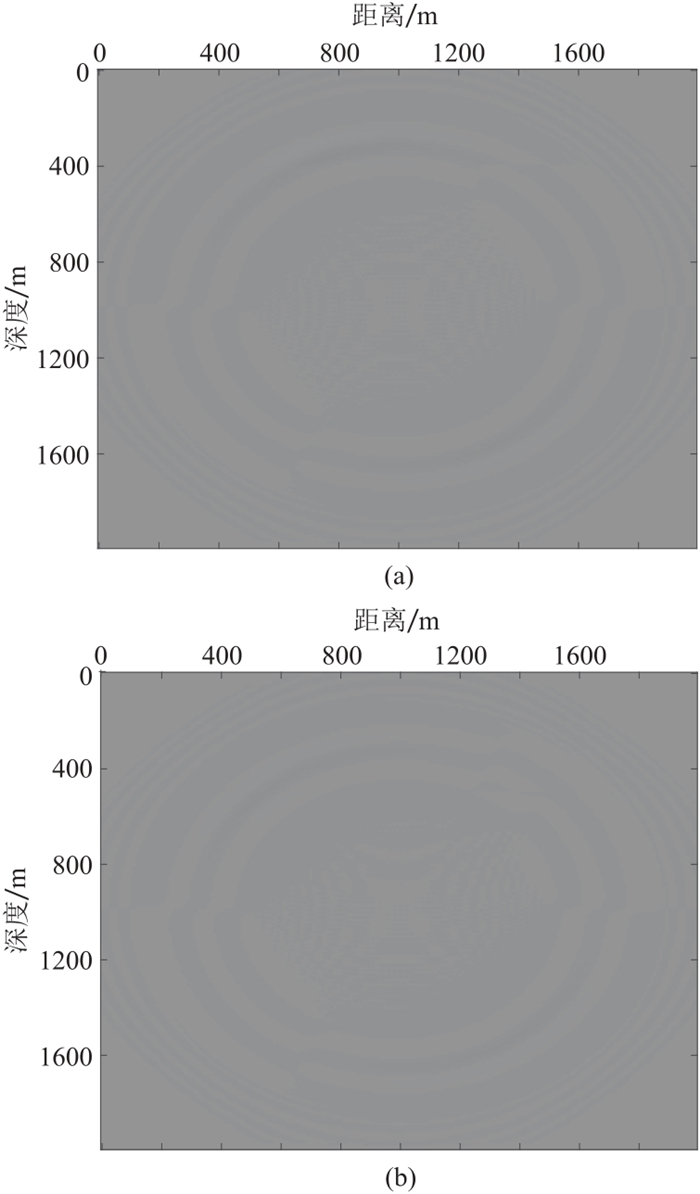
对二维常速度模型(纵波速度为4000 m/s,横波速度为2353 m/s)在浅层进行变网格剖分(图 5a),其中横向网格步长固定为10 m,深度0~400 m内纵向网格步长为5 m,400~2000 m为10 m。变网格模拟的vz分量0.24 s的波场快照如图 5b所示,与细网格(两个方向网格步长均为5 m)模拟结果的差如图 7a所示。常速度模型中层变网格剖分(图 6a,在深度500~900 m纵向网格步长为5 m,其他为10 m),其变网格模拟的vz分量0.24 s的波场快照如图 6b所示,与细网格(两个方向网格步长均为5 m)模拟结果的差如图 7b所示。由图 5~图 7可见,两种变网格剖分模拟结果非常接近,与细网格的残差非常小,进一步验证了方法的正确性和灵活性。三种网格剖分正演的计算耗时和内存占用如表 1所示,可见,变网格正演模拟可以在保证模拟精度的同时,提高计算效率、减小内存的占用。
|
图 5 二维均匀模型浅层变网格剖分(a)及其波场快照(b) |
|
图 6 二维均匀模型中层变网格剖分(a)及其波场快照(b) |
|
图 7 二维均匀模型浅层(a)、中层(b)变网格与细网格模拟结果的残差 |
|
|
表 1 不同网格剖分正演模拟的耗时和内存占用对比 |
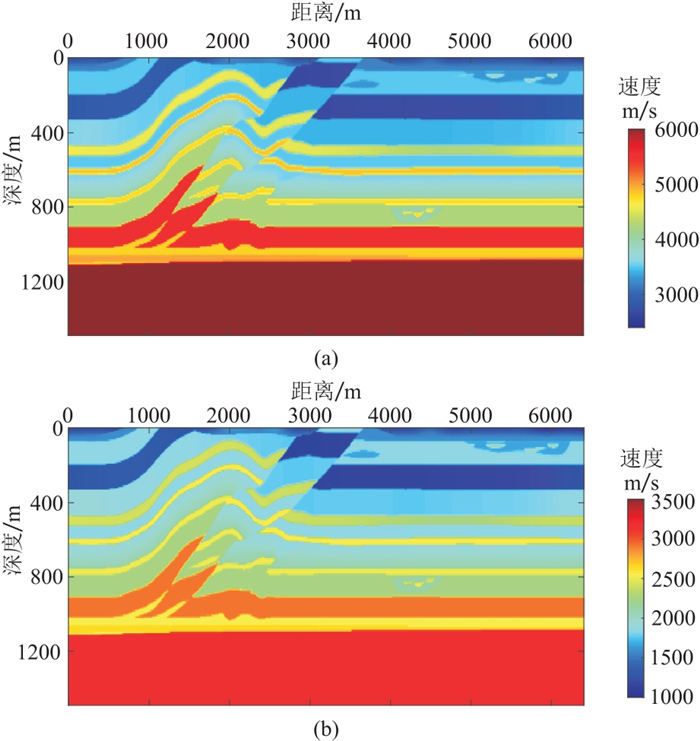
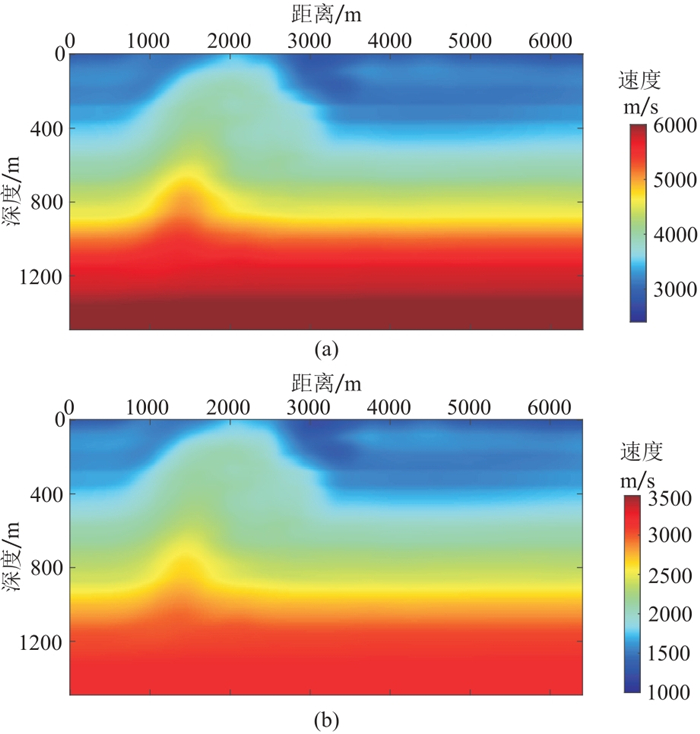
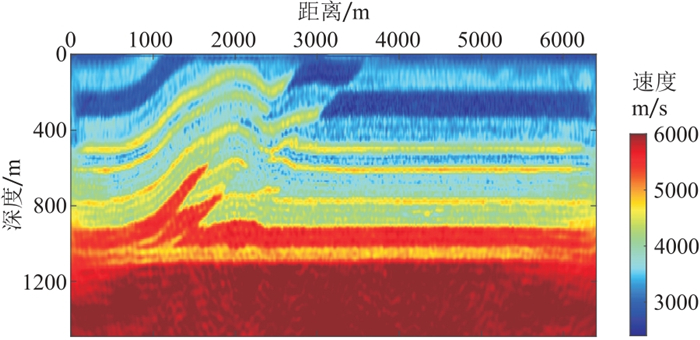
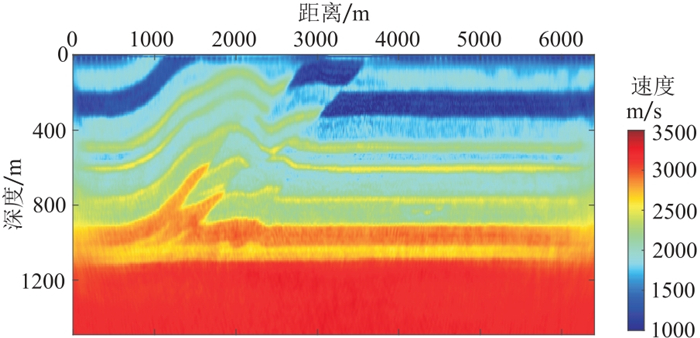
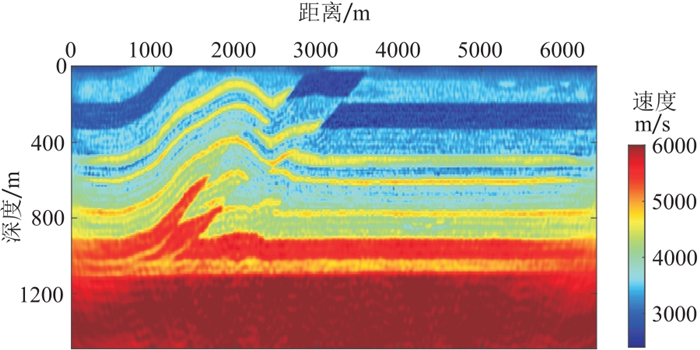
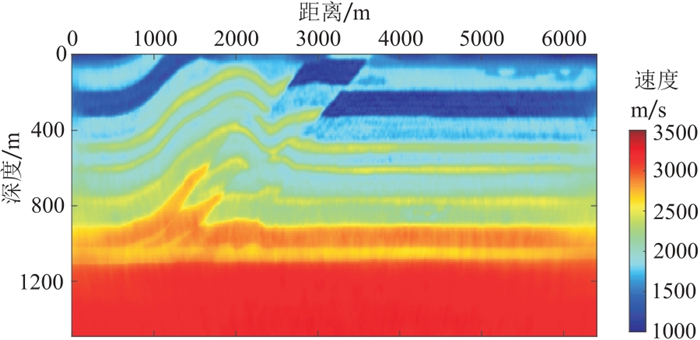
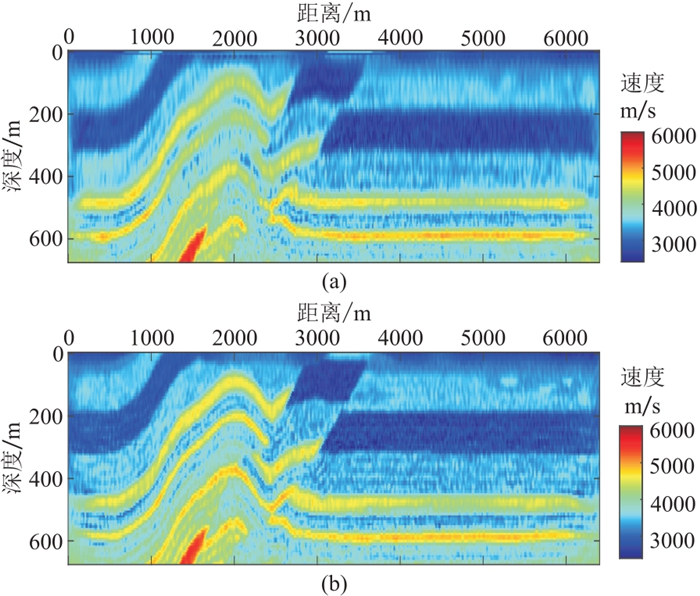
将基于变差分系数正演方法应用于多尺度弹性波全波形反演。图 8为真实的二维推覆体速度模型,用120 m×120 m的平滑半径其平滑结果如图 9所示。首先对初始模型进行8 m×8 m的均匀网格剖分,分别采用主频为2.5、3.5、5.5、9.0、13.0 Hz和20 Hz的雷克子波进行多尺度弹性波全波形反演,从低频到高频逐步更新模型,将低频反演结果作为高频反演的初始模型,主频20 Hz的子波反演结果如图 10~图 11所示。然后采用空间变网格进行剖分(横向网格步长固定为8 m,深度0~320 m范围内纵向网格步长为4 m,其余为8 m),其反演结果如图 12~图 13所示。图 14~图 15为均匀网格反演结果和变网格反演结果的浅层放大对比,可以看出,变网格反演结果中的浅层更准确,并且层界面也比均匀网格反演结果更清晰。
|
图 8 二维推覆体模型 (a)纵波速度;(b)横波速度 |
|
图 9 初始速度模型 (a)纵波;(b)横波 |
|
图 10 均匀网格多尺度全波形纵波速度反演结果 |
|
图 11 均匀网格多尺度全波形横波速度反演结果 |
|
图 12 变网格多尺度全波形纵波速度反演结果 |
|
图 13 变网格多尺度全波形横波速度反演结果 |
|
图 14 均匀网格(a)与变网格(b)反演的纵波速度浅层放大对比 |
|
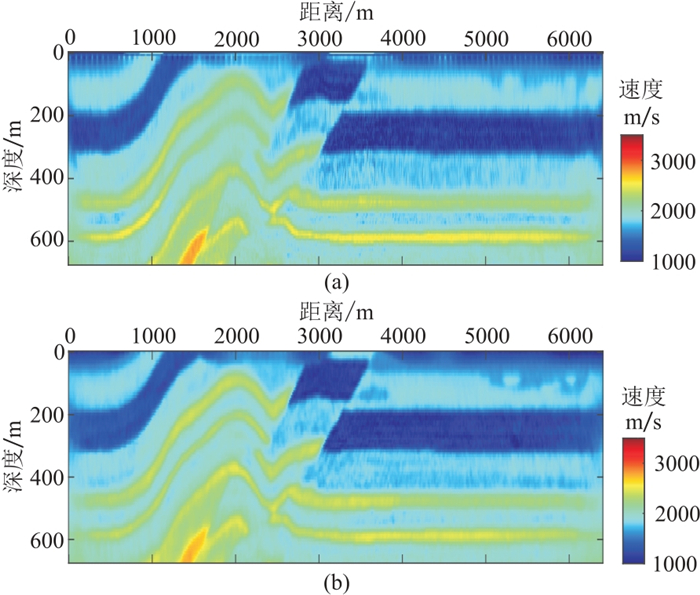
图 15 均匀网格(a)与变网格(b)反演的横波速度浅层放大对比 |
为了测试本文方法的抗噪性,分别对合成炮集数据添加不同信噪比的噪声,纵波速度的反演相对误差曲线如图 16所示。与无噪声的全波形反演结果相比,噪声会降低反演结果精度,但由于炮集数据的多次覆盖,反演结果精度降低有限。

|
图 16 不同信噪比情况下多尺度纵波速度反演相对误差曲线对比 |
为了提高近地表低速异常体的反演精度,本文在多尺度全波形反演方法的基础上进行了基于变差分系数的变网格正演和反演研究。基于变差分系数的变网格正演模拟可以在一定条件下实现任意网格变化比的波场模拟。该方法几乎不存在虚反射问题,并且波场能够稳定传播。变差分系数的变网格正演模拟方法在达到细网格模拟精度的基础上,可以有效减少计算量和内存占用。将基于变差分系数的变网格正演模拟应用于时间域弹性波多尺度全波形反演,针对浅地表低速体进行细网格剖分,可以在保证计算效率的同时提高浅层空间采样率,更精确地刻画近地表的速度变化。
本文采用的变差分系数变网格模拟方法局限性在于无法根据速度模型自适应剖分网格。
| [1] |
秦宁, 梁鸿贤, 郭振波, 等. 基于区域分解的3D弹性波全波形反演并行实现策略[J]. 石油地球物理勘探, 2023, 58(2): 351-357. QIN Ning, LIANG Hongxian, GUO Zhenbo, et al. A parallel implementing strategy for full waveform inversion of 3D elastic waves based on domain decomposition[J]. Oil Geophysical Prospecting, 2023, 58(2): 351-357. DOI:10.13810/j.cnki.issn.1000-7210.2023.02.012 |
| [2] |
杨瑞冬, 黄建平, 杨振杰, 等. 基于双对角通量校正的多尺度全波形反演[J]. 石油地球物理勘探, 2022, 57(5): 1120-1128. YANG Ruidong, HUANG Jianping, YANG Zhenjie, et al. Multi-scale full waveform inversion based on double diagonal flux correction transport[J]. Oil Geophysical Prospecting, 2022, 57(5): 1120-1128. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.013 |
| [3] |
李青阳, 吴国忱, 王玉梅, 等. 基于最优输运原理的陆上单分量资料弹性波全波形反演[J]. 石油地球物理勘探, 2021, 56(5): 1060-1073. LI Qingyang, WU Guochen, WANG Yumei, et al. Elastic full-waveform inversion of land single-component seismic data based on optimal transport theory[J]. Oil Geophysical Prospecting, 2021, 56(5): 1060-1073. DOI:10.13810/j.cnki.issn.1000-7210.2021.05.013 |
| [4] |
陈亮, 黄建平, 王自颖, 等. 应用自适应变网格紧致差分的地震波数值模拟及逆时偏移[J]. 石油地球物理勘探, 2023, 58(3): 641-650, 712. CHEN Liang, HUANG Jianping, WANG Ziying, et al. Seismic numerical simulation and reverse time migration with adaptive variable-grid and compact difference method[J]. Oil Geophysical Prospecting, 2023, 58(3): 641-650, 712. DOI:10.13810/j.cnki.issn.1000-7210.2023.03.017 |
| [5] |
MOCZO P. Finite difference technique for SH waves in 2D media using irregular grid: Application to the seismic response problem[J]. Geophysical Journal International, 1989, 99(2): 321-329. DOI:10.1111/j.1365-246X.1989.tb01691.x |
| [6] |
FALK J, TESSMER E, GAJEWSKI D. Tube wave modeling by the finite-difference method with varying grid spacing[J]. Pure and Applied Geophysics, 1996, 148(1): 77-93. |
| [7] |
FALK J, TESSMER E, GAJEWSKI D. Efficient finite-difference modelling of seismic waves using locally adjustable time steps[J]. Geophysical Prospecting, 1998, 46(6): 603-616. DOI:10.1046/j.1365-2478.1998.00110.x |
| [8] |
MUFTI I R, PITA J A, HUNTLEY R W. Finite-difference depth migration of exploration-scale 3-D seismic data[J]. Geophysics, 1996, 61(3): 776-794. DOI:10.1190/1.1444003 |
| [9] |
WANG Y, XU J, SCHUSTER G T. Viscoelastic wave simulation in basins by a variable-grid finite-difference method[J]. Bulletin of the Seismological Society of America, 2001, 91(6): 1741-1749. DOI:10.1785/0120000236 |
| [10] |
JASTRAM C, BEHLE A. Acoustic modeling on a grid of velocity varying spacing[J]. Geophysical Prospecting, 1992, 40(2): 157-169. DOI:10.1111/j.1365-2478.1992.tb00369.x |
| [11] |
JASTRAM C, TESSMER E. Elastic modelling on a grid with vertically varying spacing[J]. Geophysical Prospecting, 1994, 42(4): 357-370. DOI:10.1111/j.1365-2478.1994.tb00215.x |
| [12] |
孙成禹, 丁玉才. 波动方程有限差分双变网格算法的精度分析[J]. 石油地球物理勘探, 2012, 47(4): 545-551. SUN Chengyu, DING Yucai. Accuracy analysis of wave equation finite difference with dual-variable grid algorithm[J]. Oil Geophysical Prospecting, 2012, 47(4): 545-551. |
| [13] |
TESSMER E. Seismic finite-difference modeling with spatially varying time steps[J]. Geophysics, 2000, 65(4): 1290-1293. DOI:10.1190/1.1444820 |
| [14] |
ADRIANO S, OLIVEIRA M. A fourth-order finite-difference method for the acoustic wave equation on irregular grids[J]. Geophysics, 2003, 68(2): 672-676. DOI:10.1190/1.1567237 |
| [15] |
KANG T S, BAAG C E. An efficient finite-difference method for simulating 3D seismic response of localized basin structures[J]. Bulletin of the Seismological Society of America, 2004, 94(5): 1690-1705. DOI:10.1785/012004016 |
| [16] |
KANG T S, BAAG C E. Finite-difference seismic simulation combining discontinuous grids with locally variable time steps[J]. Bulletin of the Seismological Society of America, 2004, 94(1): 207-219. DOI:10.1785/0120030080 |
| [17] |
孙卫涛, 杨慧珠. 各向异性介质弹性波传播的三维不规则网格有限差分方法[J]. 地球物理学报, 2004, 47(2): 332-337. SUN Weitao, YANG Huizhu. A 3-D finite difference method using irregular grids for elastic wave propagation in anisotropic media[J]. Chinese Journal of Geophysics, 2004, 47(2): 332-337. |
| [18] |
NIE S, WANG Y, OLSEN K, et al. Fourth-order staggered-grid finite-difference seismic wavefield estimation using a discontinuous mesh interface[J]. Bulletin of the Seismological Society of America, 2017, 107(5): 2183-2193. DOI:10.1785/0120170077 |
| [19] |
KRISTEK J, MOCZO P, GALIS M. Stable discontinuous staggered grid in the finite-difference modelling of seismic motion[J]. Geophysical Journal International, 2010, 183(3): 1401-1407. DOI:10.1111/j.1365-246X.2010.04775.x |
| [20] |
ZHANG W, CHEN X. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J]. Geophysical Journal International, 2006, 167(1): 337-353. DOI:10.1111/j.1365-246X.2006.03113.x |
| [21] |
GAO L, BROSSIER R, VIRIEUX J. Using time filtering to control the long-time instability in seismic wave simulation[J]. Geophysical Journal International, 2016, 204(3): 1443-1461. DOI:10.1093/gji/ggv534 |
| [22] |
ZHANG Z, ZHANG W, LI H, et al. Stable discontinuous grid implementation for collocated-grid finite-difference seismic wave modelling[J]. Geophysical Journal International, 2012, 192(3): 1179-1188. |
| [23] |
张剑锋. 弹性波数值模拟的非规则网格差分法[J]. 地球物理学报, 1998, 41(增刊1): 357-366. ZHANG Jianfeng. Non-orthogonal grid finite-difference method for numerical simulation of elastic wave propagation[J]. Chinese Journal of Geophysics, 1998, 41(S1): 357-366. |
| [24] |
WU C, HARRIS J M, NIHEI K T, et al. Two-dimensional finite-difference seismic modeling of an open fluid-filled fracture: comparison of thin-layer and linear-slip models[J]. Geophysics, 2005, 70(4): T57-T62. DOI:10.1190/1.1988187 |
| [25] |
朱生旺, 魏修成. 波动方程非规则网格任意阶精度差分法正演[J]. 石油地球物理勘探, 2005, 40(2): 149-153. ZHU Shengwang, WEI Xiucheng. Differential forward modeling of wave-equation having irregular grid and any-order precision[J]. Oil Geophysical Prospecting, 2005, 40(2): 149-153. |
| [26] |
ZHANG W, ZHANG J. Full waveform tomography with consideration for large topography variations[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 2539-2542.
|
| [27] |
黄超, 董良国. 可变网格与局部时间步长的交错网格高阶差分弹性波模拟[J]. 地球物理学报, 2009, 52(11): 2870-2878. HUANG Chao, DONG Liangguo. Staggered-grid high-order finite-difference method in elastic wave simulation with variable grids and local time-steps[J]. Chinese Journal of Geophysics, 2009, 52(11): 2870-2878. |
| [28] |
张慧, 李振春. 基于时空双变网格算法的碳酸盐岩裂缝型储层正演模拟[J]. 中国石油大学学报, 2011, 35(3): 51-57. ZHANG Hui, LI Zhenchun. Forward modeling of carbonate fracture reservoir based on time-space dual variable grid algorithm[J]. Journal of China University of Petroleum, 2011, 35(3): 51-57. |
| [29] |
PITARKA A. 3D elastic finite-difference modeling of seismic motion using staggered grids with nonuniform spacing[J]. Bulletin of Seismological Society of America, 1999, 89(1): 54-68. |



 周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: