2. 中国石油勘探开发研究院西北分院, 甘肃兰州 730020;
3. 中国石油集团公司油藏描述重点实验室, 甘肃兰州 730020
2. Research Institute of Petroleum Exploration & Development-Northwest, PetroChina, Lanzhou, Gansu 730020, China;
3. CNPC Key Laboratory of Reservoir Description, Lanzhou, Gansu 730020, China
黄土塬区广泛分布于中国鄂尔多斯盆地和塔里木盆地西南部等地区,其中,鄂尔多斯盆地黄土塬区分布面积广阔,占中国总黄土面积的72.4%,发育了世界上最典型的黄土地貌。黄土塬区地下油气资源储量丰富,2018年鄂尔多斯盆地黄土塬区石油产量占长庆油田总产量的92%,天然气产量占41%[1]。由于黄土塬区地表高程变化剧烈,同时表层覆盖干燥疏松的巨厚黄土,地震波衰减严重,地震资料静校正问题突出、干扰波发育、信噪比和分辨率非常低[2]。
黄土塬区地震资料采集和处理面临的主要挑战是如何提高地震资料的信噪比和分辨率。这需要对黄土塬区地震波的传播规律和噪声的产生机理进行深入解析,而目前业界在这方面的研究还不是很充分,如近炮点强能量噪声的产生机制、成分组成、单炮初至的构成以及衰减对深层反射影响的定量分析等。波动方程数值模拟是研究复杂介质波场传播规律的重要工具,常用的数值模拟方法包括有限差分法、有限元法、伪谱法、谱元法等,其中有限差分法以其占用内存小、计算速度快、实现简单等优点成为应用最广泛的一种波动方程数值模拟方法[3-4]。但黄土塬区由于同时存在地形剧烈起伏和低速黄土层横向变化剧烈两种情况,有限差分法在实现过程中面临两个较棘手的问题:一是起伏地形界面的网格化离散只能尽可能逼近真实地形的几何形状,但仍存在一定误差,同时阶梯状边界还会产生人为的虚假绕射波,影响数值模拟精度;二是固体地球与空气的界面可认为是自由边界,数值模拟时要求垂直地表面的应力或应变为零,相对于水平地表,起伏地表自由边界条件的实施困难。近年来,起伏地表条件下的有限差分法数值模拟主要是围绕上述两个难题开展针对性的研究,很多学者提出了不同的处理方法。为消除阶梯状边界产生的虚假绕射波现象,业界提出变网格差分方法,但并不能从根本上解决阶梯状边界的影响[5-6];为从根本上解决这一问题,有学者提出了映射法、贴体网格等方法[7-8],通过映射关系或者坐标变换法将物理空间中的不规则区域变换为计算空间中的规则矩形区域,该方法可以较好地拟合起伏地形,同时在计算空间中可以采用水平地表下常用的真空法、应力镜像法等方法实现自由边界条件[9]。
目前针对黄土塬区波动方程数值模拟和波场传播规律的研究相对较少。王大兴等[10]根据鄂尔多斯盆地南部新安边地区实际测量数据,建立了二维黄土塬区地质—地球物理模型,采用交错网格有限差分法开展了二维弹性波方程数值模拟,并对模拟数据进行静校正和去噪处理;梁岳等[11]对黄土塬斜坡带不同激发位置和激发参数的地震波场进行二维数值模拟,确定了黄土塬区的最佳地震采集参数;王雪秋[12]研究了起伏地表情况下自由边界条件的处理方法,并对凹陷模型、凸起模型等简单模型开展二维数值模拟和波场分析。以上文献均采用二维波动方程数值模拟方法,也没有考虑介质的吸收效应,对黄土塬区地震波场的模拟结果与实际资料仍存在较大差异。
为了准确模拟黄土塬区巨厚黄土层的吸收效应,必须采用三维起伏地表黏滞介质波动方程数值模拟方法。本文为研究鄂尔多斯盆地黄土塬区地震波场的传播规律、分析噪声的产生机理,以庆城北三维工区实际地表高程和速度结构为参考,建立了黄土塬区三维数字模型。三维波动方程数值模拟以基于品质因子显式表达的黏滞声波方程为基础,采用坐标变换法将非规则的物理空间转换到规则的计算空间,并在计算空间中实施自由边界条件。三维黏滞声波方程数值模拟结果与实际资料的吻合度较高。为分析黄土塬区地震资料噪声的产生机理,以庆城北三维数字模型为基础,设计了水平地表无黄土层、水平地表有黄土层、起伏地表无黄土层及起伏地表有黄土层四个三维数字模型,通过从简单模型到复杂模型的三维数值模拟和波场分析,逐步厘清了模拟结果中近炮点强能量噪声和多次反射、多次折射的产生机理。最后分析了庆城北三维数字模型不同位置(塬、梁、坡、沟)及不同炮点深度的数值模拟结果,与对应位置的实际资料对比、分析波场特征,并对野外地震采集提出了针对性建议。
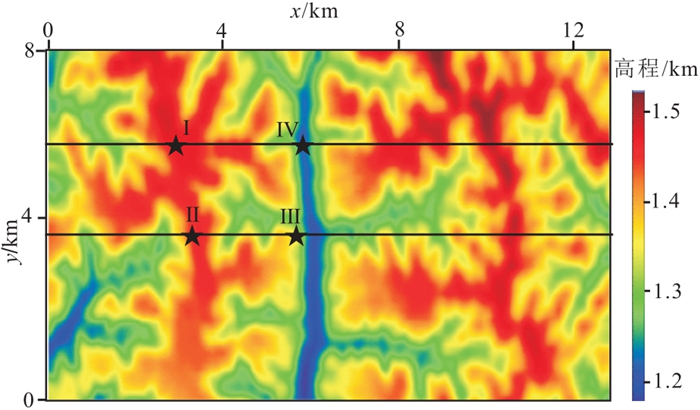
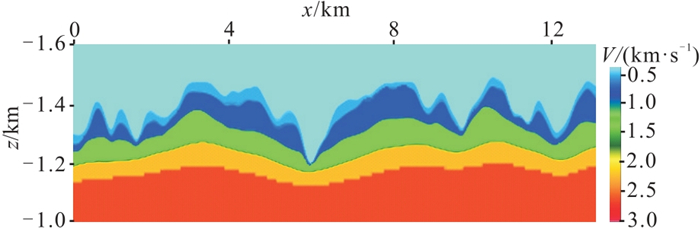
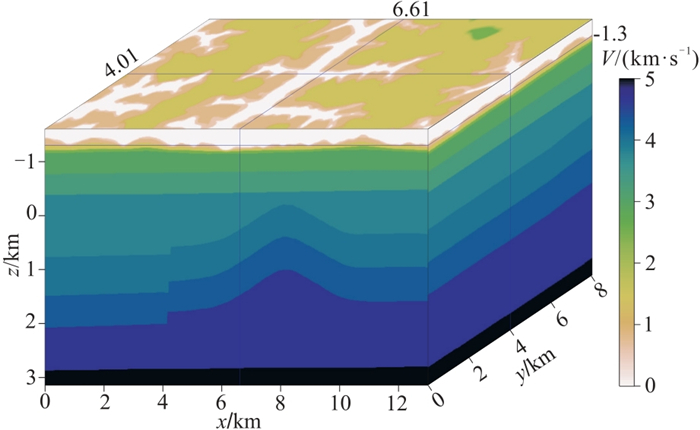
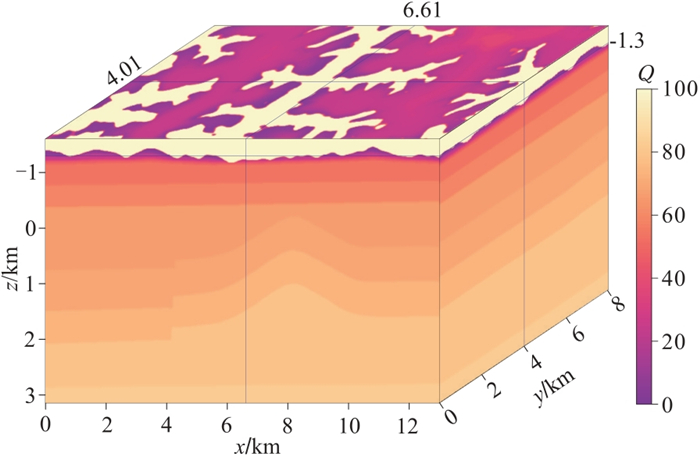
1 黄土塬区三维数字模型建立鄂尔多斯盆地南部分布着典型的黄土塬地貌,地形起伏剧烈,黄土层厚度变化大。本文选择2019年施工的庆城北三维工区作为建立黄土塬区三维数字模型的依据。在工区北部选取东西(x或Inline方向)长13 km、南北(y或Crossline方向)宽8 km的矩形范围作为模拟区域,该区域的地表高程如图 1所示,地表高程范围1180~1525 m,黄土层厚度为10~300 m。根据该区微测井等近地表调查测量数据,可将近地表分为四层结构,自上而下分别为风化层、低速层、降速层和高速层,对应的岩性和纵波速度范围分别为干黄土(300~600 m/s)、湿黄土(600~1300 m/s)、胶泥(1300~1800 m/s)和砂岩(2500 m/s以上)。近地表黄土层速度一般随深度增大呈线性增加,表层干黄土层的品质因子Q最小,吸收效应最强;随着压实作用的增强,Q值从地表向下逐渐增大。为便于建模,近地表四层纵波速度分别取值550、800、1500、2500 m/s,Q值分别为5、12、48、70,建立的近地表速度模型如图 2所示,密度取常数。庆城北工区近地表以下实际地层形态较平缓,为观测复杂近地表对地下构造的影响,在高速层以下设计了7套地层,包括1个背斜构造和1个正断层。最终建立的三维纵波速度模型和Q模型分别如图 3和图 4所示,三维模型网格尺寸为5 m×5 m×5 m。
|
图 1 研究区地表高程图 |
|
图 2 y=5.7 km处近地表速度剖面 |
|
图 3 黄土塬区三维速度模型 |
|
图 4 黄土塬区三维Q模型 |
Q是表征介质吸收强弱的重要参数,目前在地震频带范围内,业界广泛使用广义标准线性体模型和常Q模型描述介质的衰减效应。广义标准线性体模型是一种近似的常Q模型,通过多个标准线性体的组合近似模拟介质的吸收衰减,由此建立的标准线性体黏滞波动方程虽然数值计算方便,但包含较多的表征参数,而这些参数物理意义不明确,需要将Q转换为应力和应变的驰豫时间[13-14]。常Q模型由Kjartansson[15]提出,认为在地震勘探频带内Q不随频率变化。基于常Q模型推导的波动方程含有分数阶时间偏导数,可以更好地描述地震波在黏滞介质中的衰减和频散效应。但计算分数阶时间偏导数需要使用当前时刻以前所有的波场值,导致巨大的内存需求。针对这一问题,近几年学者提出分数阶拉普拉斯算子来近似分数阶时间偏导数[16-17],并采用最小二乘拟合[18]、低秩近似[19]等方法计算分数阶拉普拉斯算子。
本文针对鄂尔多斯盆地黄土塬区的三维数值模拟, 采用Hu等[20]提出的品质因子显式表达的黏滞声波方程。该方程基于在一个频带内Q与频率无关的特性进行非线性优化而得到,Q在方程中显式表达,不需要将其转换为应力和应变的弛豫时间,并且该方程不涉及傅里叶变换或者混合域算子,可以采用时间域有限差分算法求解,数值模拟实现相对简单。
Hu等[20]提出的品质因子显式表达的黏滞介质声波方程为
| $ \left\{\begin{array}{l}\rho \left(\boldsymbol{x}\right)\frac{\partial \boldsymbol{v}(\boldsymbol{x}, t)}{\partial t}=\nabla p(\boldsymbol{x}, t)\\ \frac{\partial p(\boldsymbol{x}, t)}{\partial t}=\rho \left(\boldsymbol{x}\right){V}^{2}\left(\boldsymbol{x}\right)\left[\left(1+\frac{s}{Q\left(\boldsymbol{x}\right)}\right)\nabla \boldsymbol{v}(\boldsymbol{x}, t)-\right.\\ \begin{array}{cc}& \left.\frac{1}{Q\left(\boldsymbol{x}\right)}\sum\limits_{l=1}^{N}{M}^{\left(l\right)}(\boldsymbol{x}, t)\right]\end{array}+f\\ \frac{\partial {M}^{\left(l\right)}(\boldsymbol{x}, t)}{\partial t}=-\frac{1}{{\tau }^{\left(l\right)}}{M}^{\left(l\right)}(\boldsymbol{x}, t)+\frac{{D}^{\left(l\right)}}{{\tau }^{\left(l\right)}}\nabla \boldsymbol{v}(\boldsymbol{x}, t)\end{array}\right. $ | (1) |
式中:
为适应黄土塬区剧烈起伏地形,采用坐标变换法将非规则的物理空间
| $ \left\{\begin{array}{l}\alpha =x\\ \beta =y\\ \gamma ={\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}\frac{z+\zeta (x, y)}{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\zeta (x, y)}\end{array}\right. $ | (2) |
式中:
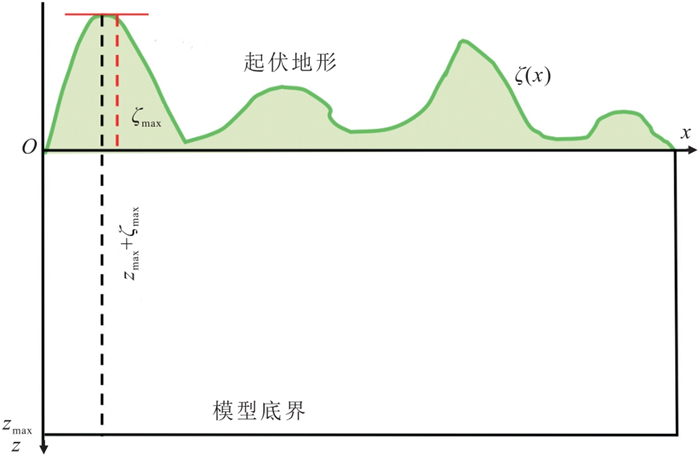
|
图 5 二维起伏地形中的坐标映射关系示意图 |
根据式(2)中的映射关系,物理空间中的偏导数可表示为
| $ \left\{\begin{array}{l}\frac{\partial }{\partial x}=\frac{\partial }{\partial \alpha }+\left[\frac{{\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\gamma }{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\zeta (x, y)}\frac{\partial \zeta (x, y)}{\partial x}\right]\frac{\partial }{\partial \gamma }\\ \frac{\partial }{\partial y}=\frac{\partial }{\partial \beta }+\left[\frac{{\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\gamma }{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\zeta (x, y)}\frac{\partial \zeta (x, y)}{\partial y}\right]\frac{\partial }{\partial \gamma }\\ \frac{\partial }{\partial z}=\left[\frac{{\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\zeta (x, y)}\right]\frac{\partial }{\partial \gamma }\end{array}\right. $ | (3) |
定义
| $ \left\{\begin{array}{l}{c}_{x}=\frac{{\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\gamma }{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\zeta (x, y)}\frac{\partial \zeta (x, y)}{\partial x}\\ {c}_{y}=\frac{{\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\gamma }{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\zeta (x, y)}\frac{\partial \zeta (x, y)}{\partial y}\\ {c}_{z}=\frac{{\gamma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}+\zeta (x, y)}\end{array}\right. $ | (4) |
则新坐标系下的黏滞介质声波方程为
| $ \left\{\begin{array}{l}\rho \left(\boldsymbol{\alpha }\right)\frac{\partial \boldsymbol{v}(\boldsymbol{\alpha }, t)}{\partial t}=\nabla p(\boldsymbol{\alpha }, t)\\ \frac{\partial p(\boldsymbol{\alpha }, t)}{\partial t}=\rho \left(\boldsymbol{\alpha }\right){V}^{2}\left(\boldsymbol{\alpha }\right)\left[\left(1+\frac{s}{Q\left(\boldsymbol{\alpha }\right)}\right)\overline {\nabla }\boldsymbol{v}(\boldsymbol{\alpha }, t)-\right.\\ \begin{array}{cc}& \left.\frac{1}{Q\left(\boldsymbol{\alpha }\right)}\sum\limits_{l=1}^{N}{M}^{\left(l\right)}(\boldsymbol{\alpha }, t)\right]\end{array}+f\\ \frac{\partial {M}^{\left(l\right)}(\boldsymbol{\alpha }, t)}{\partial t}=-\frac{1}{{\tau }^{\left(l\right)}}{M}^{\left(l\right)}(\boldsymbol{\alpha }, t)+\frac{{D}^{\left(l\right)}}{{\tau }^{\left(l\right)}}\overline {\nabla }\boldsymbol{v}(\boldsymbol{\alpha }, t)\end{array}\right. $ | (5) |
式中
| $ \overline {\nabla }=\left[\begin{array}{c}\frac{\partial }{\partial \alpha }+{c}_{x}\frac{\partial }{\partial \gamma }\\ \frac{\partial }{\partial \beta }+{c}_{y}\frac{\partial }{\partial \gamma }\\ {c}_{z}\frac{\partial }{\partial \gamma }\end{array}\right] $ | (6) |
在实施起伏地表黏滞介质声波方程数值模拟时,首先计算地表高程关于x和y的偏导数,然后通过坐标变换法将非规则的物理空间映射到规则的计算空间,最后在规则网格中采用目前常用的时间域交错网格高阶有限差分算法。由于需要计算地表高程关于x和y的偏导数,要求地表高程具有一定光滑性,避免出现负倾角及直立形态,因此在建立庆城北速度模型时,对野外测量的地表高程采用100 m×100 m的网格进行适当平滑,作为模型的地表高程。图 6a、图 6b分别为物理空间和计算空间中y=4 km处的速度剖面,可以看出,在计算空间中起伏地表被映射为水平地表,而模型内部的平缓地层则出现起伏,自由边界条件可以采用水平地表常用的应力镜像法实现。

|
图 6 不同空间中y=4 km处的速度剖面 (a)物理空间;(b)计算空间 |
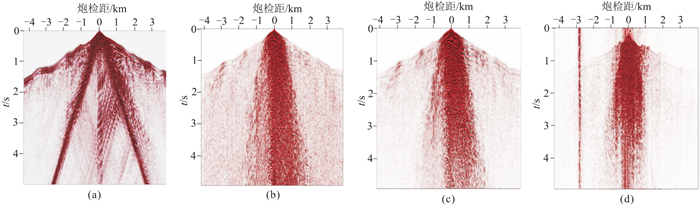
在庆城北黄土塬数字模型上分别开展二维和三维黏滞介质声波方程数值模拟试算,二维测线选择y=4 km处的Inline线,对应的速度剖面如图 6a所示。炮点位于(6.5 km,4.0 km)处,埋深为40 m,检波点位于地表,震源为主频10 Hz的Ricker子波。图 7为二维黏滞介质声波方程、三维声波方程、三维黏滞介质声波方程数值模拟单炮与实际资料的对比。
|
图 7 不同波动方程数值模拟记录与实际资料的对比 (a)二维黏滞声波方程;(b)三维声波方程;(c)三维黏滞声波方程;(d)实际资料 |
从图 7中可以得出以下认识:①二维数值模拟结果可以清晰地看到直达波和地形侧面反射,但与实际数据还存在较大差异;②相对于二维,三维数值模拟结果与实际数据的吻合度明显提高,尤其是黄土塬区实际资料典型的近炮点强能量噪声可以较好地模拟出来;③相比于三维声波方程,三维黏滞声波方程数值模拟结果的远炮检距信号展现了较强的衰减效应,与实际资料吻合度更高。
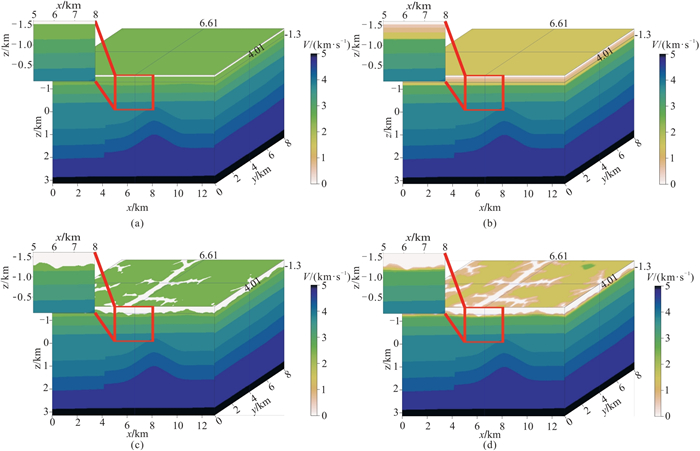
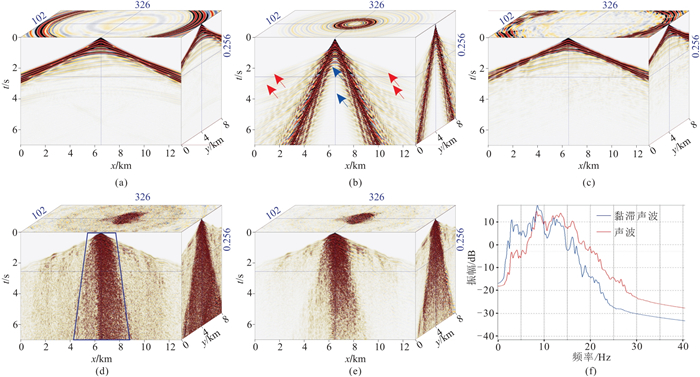
3 黄土塬区地震波场传播规律分析 3.1 黄土塬区地震资料噪声机理分析黄土塬区地震资料噪声严重,尤其是近炮点强能量噪声发育,多次折射、线性干扰也较发育。为厘清黄土塬区地震资料噪声的产生机理,以庆城北三维数字模型为基础,设计了水平地表无黄土层、水平地表有黄土层、起伏地表无黄土层及起伏地表有黄土层四个三维速度模型(图 8)。选取同一个山坡位置(6.5 km,4.0 km)作为激发点,炮点深度为40 m,检波点位于地表,对前三个模型实施三维声波方程数值模拟,对第四个模型实施三维声波和黏滞声波方程数值模拟,模拟记录和t=2.4 s时刻的波场快照分别如图 9和图 10所示。
|
图 8 不同复杂程度的三维速度模型 (a)水平地表无黄土层;(b)水平地表有黄土层;(c)起伏地表无黄土层;(d)起伏地表有黄土层。子图为红色方框内的放大显示。 |
|
图 9 不同复杂程度模型数值模拟记录分析 (a)水平地表无黄土层模型;(b)水平地表有黄土层模型;(c)起伏地表无黄土层模型;(d)起伏地表有黄土层模型声波模拟;(e)起伏地表有黄土层模型黏滞声波模拟;(f)起伏地表有黄土层模型声波与黏滞声波模拟结果频谱对比 |
|
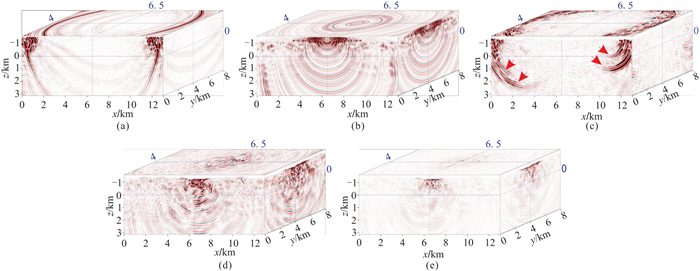
图 10 不同复杂程度模型数值模拟t=2.4 s时刻波场快照 (a)水平地表无黄土层模型;(b)水平地表有黄土层模型;(c)起伏地表无黄土层模型;(d)起伏地表有黄土层模型声波模拟;(e)起伏地表有黄土层模型黏滞声波模拟 |
对比图 9和图 10各个模型的模拟记录和波场快照,可以得到以下几点认识。①水平地表无黄土层时,模拟记录初至光滑、地层反射清晰、噪声较少。②水平地表加入低速黄土层后,高速砂岩顶界与自由地表之间产生多次反射(图 9b蓝色箭头所示);当多次反射入射到高速层顶界的入射角等于临界角时,就会产生多次折射(图 9b红色箭头所示),其传播路径如图 11所示,当多次反射的入射角θ等于临界角时,即产生多次折射,这种现象在东部地表较平缓的地区和西部大沙漠区比较常见。③起伏地表无黄土层时,地形起伏会导致初至和地层反射出现扭曲现象,同时产生一定的地形侧面反射和散射噪声(图 10c红色箭头所示)。④起伏地表加入低速黄土层后,表面多次波和直达波等与地表相关的波场受到剧烈起伏地形的影响会产生多次散射噪声,表现为近炮点强能量散射噪声(图 9d蓝色梯形框所示),多次折射也会产生一定的扭曲现象。⑤对起伏地表有黄土层模型采用黏滞介质声波方程模拟时,中、远炮检距能量衰减严重。⑥声波和黏滞声波两种方程模拟结果在炮检距3500~7000 m范围内的频谱对比(0~6.5 s时窗)如图 9f所示,可以看出,与声波方程相比,采用黏滞介质声波方程模拟时,地层吸收衰减导致信号主频降低4~5 Hz,高频成分明显衰减。

|
图 11 多次折射的传播路径示意图 |
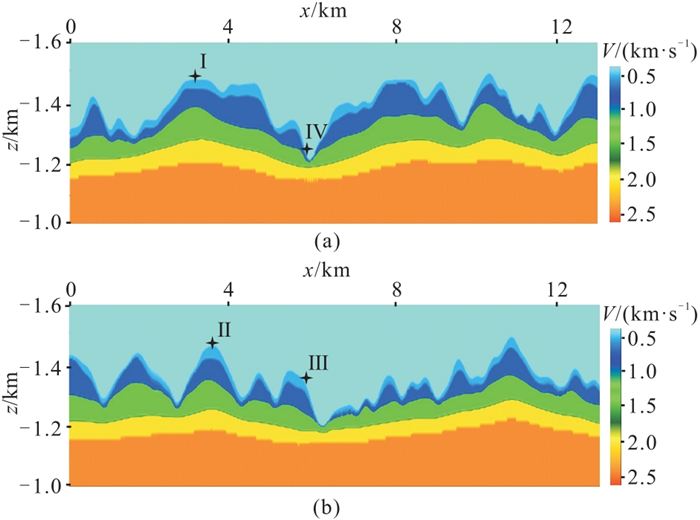
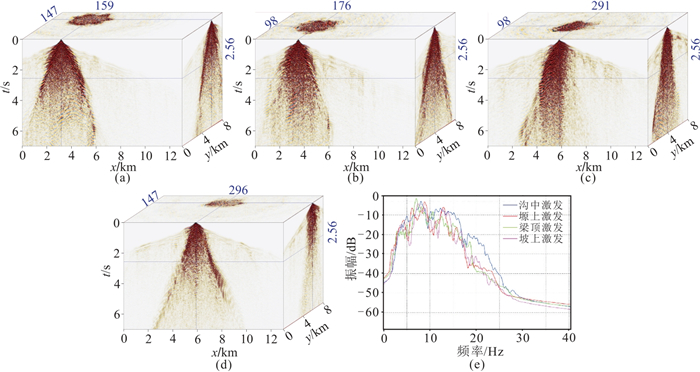
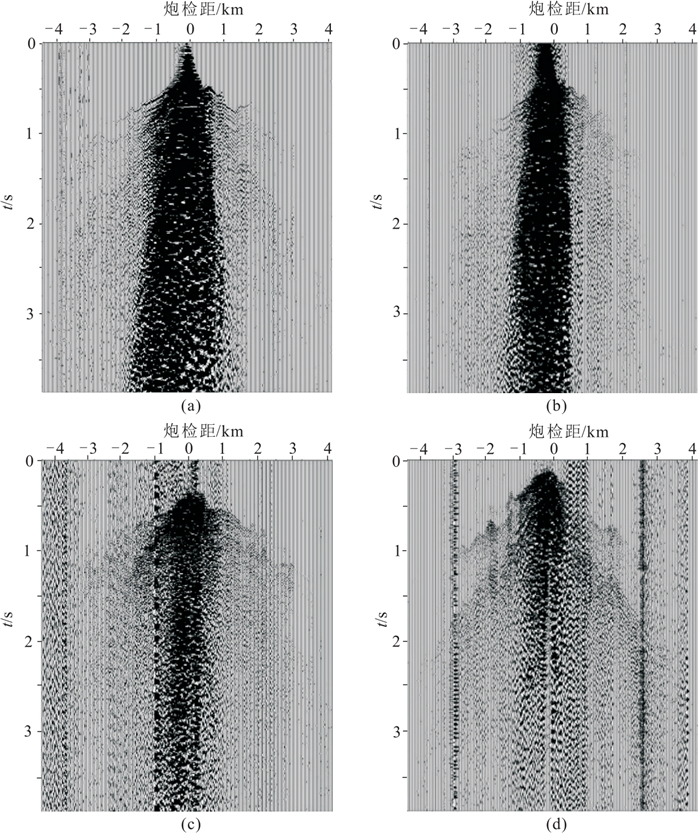
黄土塬区地貌特征多样,发育塬、梁、沟、坡等地貌,不同地貌采集的实际资料特征差异较大。在庆城北工区中选取四个不同的激发位置,分别位于塬上、梁顶、坡上和沟中(图 1中Ⅰ、Ⅱ、Ⅲ、Ⅳ所示),对应的近地表速度剖面如图 12所示。在这四个激发位置上分别开展三维黏滞介质声波方程数值模拟,炮点深度为40 m,检波点位于地表,模拟记录如图 13所示,图 14为对应位置的实际资料。综合分析数值模拟结果和实际资料,可以得到以下认识:①塬上和梁顶激发,巨厚黄土层对地震波场的衰减作用较强,远炮检距能量弱,近炮检距发育强能量噪声;②坡上激发,上坡一侧的强能量噪声明显强于下坡一侧;③沟中激发,近炮点强能量噪声明显减弱,资料品质相对较好;④四个不同位置模拟结果3500~7000 m炮检距的频谱对比(0~6.5 s时窗)如图 13e所示,可以看到,相比其他位置,沟中激发时由于黄土层厚度较薄,信号的高频成分会有一定程度的增强。
|
图 12 y=5.85 km(a)和y=3.88 km(b)近地表速度剖面 |
|
图 13 不同位置激发的模拟记录及频谱对比 (a)塬上;(b)梁顶;(c)坡上;(d)沟中;(e)频谱对比 |
|
图 14 不同位置激发的实际资料 (a)塬上;(b)梁顶;(c)坡上;(d)沟中 |
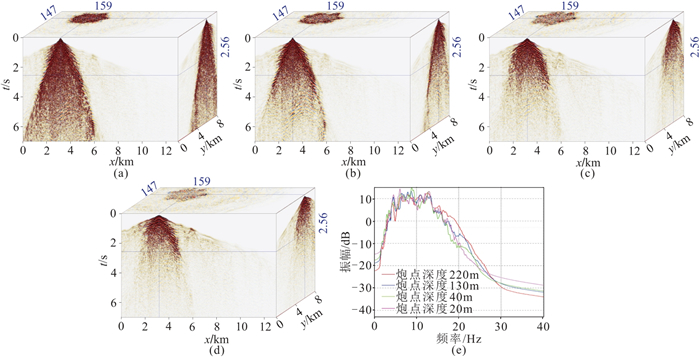
黄土塬近地表结构通常包括干黄土、湿黄土、胶泥和砂岩等四层,在不同地层进行激发波场受地表吸收和起伏地形的影响程度会有明显差异。为分析近地表不同地层激发的波场特征差异,选择图 12中的“Ⅰ”处(塬上)开展三维黏滞介质声波方程数值模拟,炮点分别位于近地表四个层中,炮点深度分别为20、40、130、220 m,检波点位于地表,数值模拟记录如图 15所示。分析模拟记录可以得到以下认识:①当炮点位于干黄土层时,近炮点强能量噪声发育最为严重;②随着炮点深度增强,近炮点噪声能量逐渐降低,当炮点位于胶泥层和砂岩层时,近炮点噪声相对较弱,单炮记录信噪比相对较高;③图 15e为不同炮点深度激发模拟记录全炮检距的频谱对比(0~6.5 s),可以看出,不同炮点深度激发记录的主频基本一致,但随着炮点深度增大,信号的高频端能量会逐步增强。基于以上认识,在黄土塬地区野外地震采集时,应避免在干黄土层中激发,尽可能选择胶泥层或更深地层激发,才能保证黄土塬地区地震资料的质量。
|
图 15 塬上不同炮点深度激发的模拟记录及频谱对比 (a)20 m;(b)40 m;(c)130 m;(d)220 m;(e)频谱对比 |
鄂尔多斯盆地黄土塬区地震波场数值模拟要同时考虑剧烈起伏地形和低速黄土层的吸收问题,本文以基于品质因子显式表达的三维黏滞声波方程为基础,采用坐标变换法处理起伏地表问题,实现了黄土塬区的三维起伏地表黏滞声波方程数值模拟。庆城北三维数字模型的模拟结果与实际资料具有较高的吻合度。
通过不同复杂程度模型的数值模拟和波场分析,厘清了黄土塬区地震资料近炮点强能量噪声和多次反射、多次折射的产生机理:低速黄土层的存在会产生多次反射、多次折射,当低速黄土层和剧烈起伏地表同时存在时,表面多次波和直达波等与地表相关的波场受到剧烈起伏地形的影响产生多次散射噪声,从而出现黄土塬区典型的近炮点强能量散射噪声。
综合分析黄土塬区不同位置(塬、梁、坡、沟)的数值模拟结果和实际资料及不同炮点深度的模拟结果,认为:沟中激发时,近炮点强能量噪声较弱,资料品质相对较好;随着炮点深度增强,信号的高频端能量逐步增强;黄土塬地区野外地震采集时,应避免在干黄土层中激发,尽可能选择胶泥层或更深位置激发。
本文对数值模拟结果和实际资料的波场分析可有效指导黄土塬区地震采集施工中炮点位置及深度的选择,同时对识别实际资料噪声的特征、选择针对性的去噪方法具有一定指导意义。
因黄土塬区的横波速度模型难以准确建立,本文采用黏滞介质声波方程模拟黄土塬区波场传播过程。而实际黄土塬区地下介质用黏弹性波动方程描述更准确。实际资料中也发育较强的面波, 未来的研究重点是采用三维黏弹性波动方程模拟黄土塬区波场传播,理论上可以模拟出近地表散射面波,也是近炮点强能量噪声的成分之一,与实际资料的吻合度会进一步提高。
| [1] |
付锁堂, 王大兴, 姚宗惠. 鄂尔多斯盆地黄土塬三维地震技术突破及勘探开发效果[J]. 中国石油勘探, 2020, 25(1): 67-77. FU Suotang, WANG Daxing, YAO Zonghui. Progress of 3D seismic exploration technologies and oil and gas exploration and development performance in the loess tableland area of the Ordos Basin[J]. China Petroleum Exploration, 2020, 25(1): 67-77. |
| [2] |
赵邦六, 董世泰, 曾忠, 等. 中国石油"十三五"物探技术进展及"十四五"发展方向思考[J]. 中国石油勘探, 2021, 26(1): 108-120. ZHAO Bangliu, DONG Shitai, ZENG Zhong, et al. Geophysical prospecting technology progress of PetroChina in the 13th Five-Year Plan period and development direction consideration in the 14th Five-Year Plan period[J]. China Petroleum Exploration, 2021, 26(1): 108-120. |
| [3] |
CARCIONE J M, HERMAN G C, TEN KROODE A P E. Seismic modeling[J]. Geophysics, 2002, 67(4): 1304-1325. DOI:10.1190/1.1500393 |
| [4] |
ETGEN J T, O'BRIEN M J. Computational methods for large-scale 3D acoustic finite-difference modeling: A tutorial[J]. Geophysics, 2007, 72(5): SM223-SM230. DOI:10.1190/1.2753753 |
| [5] |
OPRSAL I, ZAHRADNIK J. Elastic finite-difference method for irregular grids[J]. Geophysics, 1999, 64(1): 240-250. DOI:10.1190/1.1444520 |
| [6] |
李振春, 张慧, 张华. 一阶弹性波方程的变网格高阶有限差分数值模拟[J]. 石油地球物理勘探, 2008, 43(6): 711-716. LI Zhenchun, ZHANG Hui, ZHANG Hua. Variable-grid high-order finite-difference numeric simulation of first-order elastic wave equation[J]. Oil Geophysical Prospecting, 2008, 43(6): 711-716. |
| [7] |
刘志强, 黄磊, 李钢柱, 等. 基于正交贴体网格的黏弹介质地震波模拟[J]. 石油地球物理勘探, 2023, 58(4): 839-846. LIU Zhiqiang, HUANG Lei, LI Gangzhu, et al. Numerical simulation of seismic waves in viscoelastic media based on orthogonal body-fitted grid[J]. Oil Geophysical Prospecting, 2023, 58(4): 839-846. DOI:10.13810/j.cnki.issn.1000-7210.2023.04.009 |
| [8] |
孙建国, 蒋丽丽. 用于起伏地表条件下地球物理场数值模拟的正交曲网格生成技术[J]. 石油地球物理勘探, 2009, 44(4): 494-500. SUN Jianguo, JIANG Lili. Orthogonal curvilinear grid generation technique used for numeric simulation of geophysical fields in undulating surface condition[J]. Oil Geophysical Prospecting, 2009, 44(4): 494-500. |
| [9] |
ZHANG W, SHEN Y, ZHAO L. Three-dimensional anisotropic seismic wave modelling in spherical coordinates by a collocated-grid finite-difference method[J]. Geophysical Journal International, 2012, 188(3): 1359-1381. DOI:10.1111/j.1365-246X.2011.05331.x |
| [10] |
王大兴, 张盟勃, 杨文敬, 等. 黄土塬区致密储集层模型地震正反演模拟[J]. 石油勘探与开发, 2017, 44(2): 243-251. WANG Daxing, ZHANG Mengbo, YANG Wenjing, et al. Seismic forward and inverse simulation in a tight reservoir model of loess plateau region[J]. Petroleum Exploration and Development, 2017, 44(2): 243-251. |
| [11] |
梁岳, 顾汉明, 李丛, 等. 黄土塬斜坡带地震波激发数值模拟与波场特征[J]. 科学技术与工程, 2019, 19(22): 70-75. LIANG Yue, GU Hanming, LI Cong, et al. Numerical simulation of seismic wave excitation in loess slope zone and wave field characteristics[J]. Science Technology and Engineering, 2019, 19(22): 70-75. |
| [12] |
王雪秋. 复杂近地表地震波响应特征研究——以中国西部地区为例[D]. 吉林长春: 吉林大学, 2009.
|
| [13] |
蔡瑞乾, 孙成禹, 伍敦仕, 等. 黏声波动方程变机制数有限差分正演[J]. 石油地球物理勘探, 2019, 54(3): 529-538. CAI Ruiqian, SUN Chengyu, WU Dunshi, et al. Finite-difference numerical modeling with variable mechanisms for viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2019, 54(3): 529-538. DOI:10.13810/j.cnki.issn.1000-7210.2019.03.005 |
| [14] |
徐世刚, 包乾宗, 任志明. 简化的三维TTI介质黏滞纯声波方程及其数值模拟[J]. 石油地球物理勘探, 2022, 57(2): 331-341. XU Shigang, BAO Qianzong, REN Zhiming. A simplified pure visco-acoustic wave equation for 3D TTI media and its numerical simulation[J]. Oil Geophysical Prospecting, 2022, 57(2): 331-341. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.010 |
| [15] |
KJARTANSSON E. Constant Q-wave propagation and attenuation[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |
| [16] |
CARCIONE J M. Theory and modeling of constant-Q P- and S-waves using fractional time derivatives[J]. Geophysics, 2008, 74(1): T1-T11. |
| [17] |
ZHU T Y, HARRIS J M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians[J]. Geophysics, 2014, 79(3): T105-T116. DOI:10.1190/geo2013-0245.1 |
| [18] |
LI Q Q, ZHOU H, ZHANG Q C, et al. Efficient reverse time migration based on fractional Laplacian viscoacoustic wave equation[J]. Geophysical Journal International, 2016, 204(1): 488-504. DOI:10.1093/gji/ggv456 |
| [19] |
顾汉明, 张奎涛, 刘春成, 等. 基于Low-Rank一步法波场延拓的黏声各向异性介质纯qP波正演模拟[J]. 石油地球物理勘探, 2020, 55(4): 733-746. GU Hanming, ZHANG Kuitao, LIU Chuncheng, et al. Low-rank one-step wave extrapolation for pure qP-wave forward modeling in viscoacoustic anisotropic media[J]. Oil Geophysical Prospecting, 2020, 55(4): 733-746. DOI:10.13810/j.cnki.issn.1000-7210.2020.04.004 |
| [20] |
HU Z D, YANG J D, HAN L H, et al. Modeling seismic wave propagation in the Loess Plateau using a viscoacoustic wave equation with explicitly expressed quality factor[J]. Frontiers in Earth Science, 2023, 10(1): 1-24. |



 狄帮让, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
狄帮让, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: