0 引言

地震波经过地层的吸收衰减、散射、透射等，深层反射信号相对较弱，常常淹没在背景噪声中^[1-2]。目前较为常用的地震弱信号识别方法包括：基于奇异值分解(Singular Value Decomposition，SVD)的方法^[3]、基于非线性动力系统的混沌理论^[4]、基于经验模式分解的Hilbert-Huang变换^[5]和基于独立分量分析的盲源分离技术^[6]等。

2006年Aharon等^[7]提出了K-SVD(K-means Singular Value Decomposition)算法，需多次SVD分解，计算效率较低；Rubinstein等^[8]在K-SVD的基础上提出了AK-SVD算法(Approximate K-SVD)，提高了计算效率，但去噪效果变差；Irofti等^[9]将正则化引入AK-SVD的字典学习，Dumitrescud等^[10]在K-SVD基础上引入了正则化，完善了正则化近似K-SVD(Regularized Approximate K-SVD, RAK-SVD)算法，极大地提高了计算效率。但由于正则化参数取固定值，在SVD迭代分解过程中，样本预测值与真实值之间的误差项缩小，而系数误差项相对扩大，导致最终结果不准确。

正则化参数的选取方式不仅影响着算法的收敛速度，而且影响着能否收敛于真实解。国内外的许多学者提出了不同的正则化参数选取方法，其中L曲线法^[11]通过将解的向量模间接引入稳定性分析，应用很广泛。但解的范数与解的稳定性之间的定量关系有时会失效。此外，L曲线方法有局限性，Xu等^[12]指出L曲线上的曲率极大点可能不止一个，除“全局”角点外，还存在其他曲率极大点所对应的角点。

正则化参数的自动优选本质上是通过求解展平泛函的最小值规划一个最优化的过程。聂笃宪等^[13]在Tikhonov正则化原理的基础上，应用粒子群优化算法代替一般的优化方法处理泛函问题，但存在初始粒子在解空间分布不均匀，导致收敛速度下降甚至无法收敛的情况；余瑞艳^[14]研究了基于混沌粒子群算法的Tikhonov正则化参数选取，但不能同时兼顾粒子群的全局搜索能力和局部搜索能力；徐龙秀等^[15]利用自适应粒子群算法优化最小二乘支持向量机的模型参数，一定程度上提高了模型的预测精度，但惯性因子不能随迭代次数的变化而变化；廖庆陵等^[16]利用改进后的自适应粒子群算法优化支持向量机的关键参数，进行了短期负荷预测，给出了自适应调整惯性因子的计算公式，并应用到支持向量机模型的优化中，但并没有与自适应动态优化正则化参数建立联系。

粒子群算法容易陷入局部最优，无法保障获得最佳参数设定的成功率，从而影响预测结果。本文在吸取了其他算法先进经验的基础上，针对粒子群算法的不足，采用自适应动态粒子群算法自动优化正则化参数，提高了稀疏分解的确定性，形成了基于自适应动态粒子群算法的RAK-SVD去噪方法。该方法在对低信噪比地震弱信号进行去噪处理时，不仅能使强反射信号达到较为理想的去噪效果，而且还能有效保护弱信号。去噪后的地震弱信号基本不发生畸变，在地震弱信号的提取和识别方面具有良好的应用前景。

1 RAK-SVD算法

K-SVD算法是通过训练信号对初始化字典进行逐列更新、寻找一个最佳字典的过程。假定训练信号集为$ {\boldsymbol{Y}}\in {{\boldsymbol{R}}}^{m\times n} $(m为信号的长度，n为样本信号个数)，对于给定的学习字典$ {\boldsymbol{D}}\in {{\boldsymbol{R}}}^{m\times p} $(p为字典原子个数)，模型可以描述为

$ \underset{{\boldsymbol{X}}}{\mathrm{a}\mathrm{r}\mathrm{g}\;\mathrm{m}\mathrm{i}\mathrm{n}}{||{\boldsymbol{Y}}-{\boldsymbol{D}}{\boldsymbol{X}}||}_{\mathrm{F}}^{2}\;\;\mathrm{s}.\mathrm{t}.\;{||{\boldsymbol{X}}||}_{0}\le nT $

(1)

式中：D为学习字典；$ {\boldsymbol{X}}\in {{\boldsymbol{R}}}^{p\times n} $为稀疏分解系数矩阵；$ {||\cdot ||}_{\mathrm{F}} $表示Frobenius范数；T为X的所有列非零元素个数的最大值。

首先固定字典D，用正交匹配追踪(Orthogonal Matchin of Pursuit，OMP)算法对每一个样本进行稀疏表示，获取稀疏分解系数矩阵。然后用K-SVD对字典原子逐列进行更新。

每更新一列都要进行SVD分解，计算效率较低，实际应用价值不大。基于此，Rubinstein等^[8]提出了近似K-SVD(AK-SVD)算法。AK-SVD算法更新后的字典原子和稀疏分解系数分别为

$ {\boldsymbol{d}}_{k}=\frac{{\boldsymbol{E}}_{k}^{}}{{||{\boldsymbol{E}}_{k}^{}||}_{{}_{\text{F}}}^{2}} $

(2)

$ {\boldsymbol{x}}_{k}={\boldsymbol{E}}_{k}^{}{\boldsymbol{d}}_{k} $

(3)

式中：d_k为当前正在更新的第k个字典原子；x_k为与第k个字典原子对应的稀疏分解系数；$ {\boldsymbol{E}}_{k}^{} $表示剩余残差矩阵

$ {\boldsymbol{E}}_{k}^{}={\boldsymbol{Y}}-\sum \limits_{j\ne k}{\boldsymbol{d}}_{j}{\boldsymbol{x}}_{j}^{\mathrm{T}} $

(4)

地震信号的稀疏分解过程通常存在不确定性，而正则化方法是解决此问题的一种有效方法。正则化字典模型问题可转化为求解极小化问题

$ \underset{{\boldsymbol{X}}}{\mathrm{a}\mathrm{r}\mathrm{g}\;\mathrm{m}\mathrm{i}\mathrm{n}}{||{\boldsymbol{Y}}-{\boldsymbol{D}}{\boldsymbol{X}}||}_{\mathrm{F}}^{2}+\mu {||{\boldsymbol{X}}||}_{\mathrm{F}}^{2} $

(5)

式中μ > 0为正则化参数。第一项用来衡量样本的预测值与真实值之间的误差，第二项通过对参数加一个系数来调整其权重值。

对于式(5)的求解极值问题，其目标函数为

$ f\left({\boldsymbol{d}}_{k}, {\boldsymbol{x}}_{k}^{\mathrm{T}}\right)=(1+\mu ){||{\boldsymbol{x}}_{k}^{\mathrm{T}}||}_{\mathrm{F}}^{2}-2{\boldsymbol{x}}_{k}^{\mathrm{T}}{\left({\boldsymbol{E}}_{k}^{}\right)}^{\mathrm{T}}{\boldsymbol{d}}_{k}+{||{\boldsymbol{E}}_{k}^{}||}_{\mathrm{F}}^{2} $

(6)

则RAK-SVD的稀疏系数更新公式为

$ {\boldsymbol{x}}_{k}=\frac{{\boldsymbol{E}}_{k}^{}{\boldsymbol{d}}_{k}}{(1+\mu )} $

(7)

字典原子的更新公式与式(2)相同。

2 基于自适应动态粒子群算法的正则化参数自动优选

正则化参数μ对正则化效果影响较大，迫切需要对正则化参数进行自动优选。本文在粒子群算法的动态自适应性方面进行了改进。

2.1 粒子群算法及其改进

粒子群优化(Particle Swarm Optimization，PSO)算法是一种从生物种群行为特性中得到启发的求解优化问题的算法。相较于其他优化算法，粒子群算法参数较少，寻优思路清晰，编码过程易于实现，因此在多个领域有广泛的应用。粒子群算法首先初始化一群随机粒子，然后迭代找到最优解，在迭代过程中的每一个粒子都由一个适应度函数对其进行评价，并通过一定的操作，调整自身在空间中的位置。

粒子群算法在优化过程中，种群的多样性和算法的收敛速度之间始终存在着矛盾。通过参数的选取或是其他技术与粒子群的融合，对粒子群算法进行改进，期望在加强算法局部搜索能力的同时，保持种群的多样性。

种群初始化对粒子群算法的求解精度和收敛速度有着较大的影响。传统粒子群算法一般采用随机初始化确定初始种群的位置

$ {z}_{ij}={r}_{i}\left({u}_{\mathrm{b}j}-{l}_{\mathrm{b}j}\right)+{l}_{\mathrm{b}j} $

(8)

式中：$ \{{z}_{ij}, i=\mathrm{1, 2}, \cdots , I;j=\mathrm{1, 2}, \cdots , J\} $表示第i个粒子的第j维空间的位置分量，其中I表示生成的粒子数，J表示维数；r为[0, 1]内的随机数；u_b、l_b分别为解空间的上界和下界。这种算法能够生成每次不一样的初始种群，操作方便，但也存在初始粒子在解空间分布不均匀的问题，对优化算法的前期收敛非常不利，可能导致收敛速度下降甚至无法收敛的情况发生。

混沌初始化可以有效地避免上述问题。混沌初始化具有随机性、遍历性和规律性的特点，是在一定范围内按照自身规律不重复地遍历搜索空间，这样生成的初始种群在求解精度和收敛速度方面有着明显改进。

混沌初始化可选用TentMap混沌模型

$ {z}^{(h+1)}=\gamma (1-2|{z}^{\left({h}\right)}-0.5\left|\right) $

(9)

式中：$ \gamma \in \left(\mathrm{0, 4}\right] $，为混沌模型的映射参数，$ \gamma $=1时混沌系统处于完全混沌状态；h为粒子群算法在优化过程中的迭代次数；z⁽⁰⁾为初始值，可在[0, 1] 随机取值。

常用的粒子群算法通常都带有惯性因子ω，能在一定程度上平衡全局搜索能力与局部搜索能力。增大ω可以提高全局探测能力；减小ω则能提高局部搜索能力。带有惯性权重的粒子速度更新公式为

$ {\boldsymbol{v}}_{i}^{(h+1)}=\omega {\boldsymbol{v}}_{i}^{\left(h\right)}+{c}_{1}{r}_{1}({\boldsymbol{p}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}, i}-{\boldsymbol{z}}_{i})+{c}_{2}{r}_{2}({\boldsymbol{g}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}-{\boldsymbol{z}}_{i}) $

(10)

式中：$ {\boldsymbol{z}}_{i}=({z}_{i1}, {z}_{i2}, \cdots , {z}_{iJ}) $，为第i个粒子的位置向量；$ {\boldsymbol{v}}_{i}=({v}_{i1}, {v}_{i2}, \cdots , {v}_{iJ}) $，为第i个粒子的速度向量；c₁和c₂为加速因子，c₁反映了粒子向自身历史最优位置逼近的速度，c₂反映了粒子向群体最优位置逼近的速度；r₁和r₂是值为[0, 1] 的随机数；$ {\boldsymbol{p}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}, i}=({p}_{i1}, {p}_{i2}, \cdots , {p}_{iJ}) $是第i个粒子的历史最优位置，亦称个体极值；$ {\boldsymbol{g}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}=({g}_{1}, {g}_{2}$, $ \cdots , {g}_{J}) $为全部粒子的历史最优位置，称为全局极值。

每个粒子的位置分别对应一组正则化参数μ的取值，当迭代次数为h时，输出全局极值$ {\boldsymbol{g}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $，将该位置对应的μ值作为正则化参数$ {\mu }_{h} $；若达到最大迭代次数h_max，则将全局最优位置$ {\boldsymbol{g}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $对应的μ值作为最终寻优的正则化参数$ {\mu }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $。

常数惯性因子粒子群算法能调节粒子群的全局搜索能力或者局部搜索能力，但是两者不能同时兼顾，于是有学者提出一种随着迭代次数的增加线性降低惯性因子的方法^[13]

$ \omega ={\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\frac{{\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{h}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\times h $

(11)

式中ω_max和ω_min分别为惯性因子的最大和最小值。线性下降惯性因子的粒子群算法在开始时惯性较大，适合大面积的搜索，能快速找到最优解的大致位置；之后随着ω逐渐减小，粒子惯性减弱，能加强局部搜索能力，更精确地搜寻最优解。此方法相较于常数惯性因子粒子群算法较大地提升了搜索效率，但是因为不管适应度是否变得更优，惯性因子都会以同样的速度下降，寻优效果未能达到最佳。

本文吸取前人算法的优点，提出一种动态自适应惯性因子，计算每次迭代更新所有粒子位置后的种群适应度$ {\phi }_{h} $。如果$ {\phi }_{h} $ > $ {\phi }_{h-1} $，则减小ω提高粒子群的局部搜索能力；相反，如果$ {\phi }_{h} $ < $ {\phi }_{h-1} $，则调大ω提高粒子群的全局搜索能力。动态自适应ω的计算公式为

$ {\omega }_{h+1}={\omega }_{h}-\eta \frac{{\phi }_{h}-{\phi }_{h-1}}{|{\phi }_{h}-{\phi }_{h-1}|} $

(12)

式中：$ {\phi }_{h} $为h次迭代时的种群适应度值；ω_h为h次迭代时ω的值，取值范围为[0.4，0.9]，初始值设置为0.75；$ \eta $为增益系数，取值范围是[0.02，0.05]。

2.2 稀疏分解效果对比

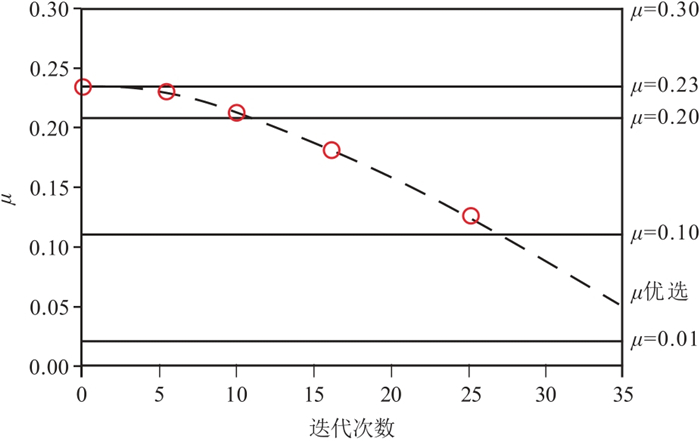
为了对比稀疏分解的效果，设计如图 1a所示的包含多种火成岩相带的复杂地质模型，对地震正演模拟得到的含噪记录进行分析。图 1b是利用正演模拟的炮集记录经叠前深度偏移得到的深度域地震剖面。火山岩通道相表现为倾角较大的强反射，通道内部为空白反射或杂乱反射；火山岩爆发相和喷溢相的横向厚度变化较大，中间厚，向两边逐渐变薄，多个界面的反射叠合在一起形成复波，同相轴呈凸起状，并且淹没了下伏地层弱反射。图 1c是加入峰值信噪比PSNR=3.42的随机噪声后的结果，用于学习字典的训练样本。图 2是经优选得到的每次迭代所对应的正则化参数取值结果，图中5个圆圈代表了每次迭代时由自适应粒子群算法优化得到的正则化参数μ值。不同μ值所对应的训练信号与稀疏分解结果之间的均方根误差RMSE随迭代次数的变化如图 3所示，其中均方根误差定义为

$ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{||{\boldsymbol{Y}}-{\boldsymbol{D}}{\boldsymbol{X}}||}_{\mathrm{F}}^{2}} $

(13)

正则化参数的选择影响RAK-SVD的优化效果，由图 3可看出，当学习字典在25次迭代后RMSE大体趋于稳定，其中RAK-SVD(μ=0)训练误差最大。当使用自适应动态粒子群算法迭代优化时，由于避免了需要选取到准确固定值，每次迭代后，其值自适应调整，训练结束时RMSE=0.93，能够取得最优稀疏分解效果。

3 基于自适应动态粒子群优化算法的RAK-SVD去噪方法

在对地震资料进行去噪处理时，由于数据量较大，首先将其分割成若干个较小且大小相等的地震数据子块，考虑到地震数据的整体稀疏分解问题，在式(5)中加入一个约束项，转变为下面优化问题

$ \begin{array}{c}f({\boldsymbol{D}}, {\boldsymbol{X}}, \boldsymbol{N})=\lambda {||\boldsymbol{N}-{\boldsymbol{Y}}||}_{\mathrm{F}}^{2}+\mu {||{\boldsymbol{X}}||}_{\mathrm{F}}^{2}+\\ {||{\boldsymbol{D}}{\boldsymbol{X}}-\boldsymbol{L}{\boldsymbol{Y}}||}_{\mathrm{F}}^{2} \end{array} $

(14)

式中：λ为拉格朗日参数；Y是输入信号，即含噪的地震数据；D是需要更新的学习字典；N是重构信号；L为对应的每个Y的位置矩阵，这些子块也是RAK-SVD字典的训练样本。本文的算法步骤如下。

(1) 设置初始值N₀=Y。

(2) 设定最大迭代次数h_max。

(3) 稀疏编码阶段，通过OMP算法求取每个子块在当前字典D下的稀疏分解系数X，然后优化问题式（14)转化为

$ f({\boldsymbol{D}}, {\boldsymbol{X}}, \boldsymbol{N})=\mu {||{\boldsymbol{X}}||}_{\mathrm{F}}^{2}+{||{\boldsymbol{D}}{\boldsymbol{X}}-\boldsymbol{L}{\boldsymbol{Y}}||}_{\mathrm{F}}^{2} $

(15)

(4) 当h=1时，由自适应动态粒子群算法得到正则化参数μ₁值，更新该次迭代的学习字典D与稀疏分解系数X。

(5) 当1 < h≤h_max时，按照式(10)更新正则化系数$ {\mu }_{h} $($ {\mu }_{h} $ > 0)，更新学习字典D，并求出稀疏分解系数X。

(6) 去噪后地震数据的重构：在更新学习字典D、获得最优正则化参数$ {\mu }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $的基础上固定正则项，使优化问题式（14)简化为

$ f({\boldsymbol{X}}, \boldsymbol{N})=\lambda {||\boldsymbol{N}-{\boldsymbol{Y}}||}_{\mathrm{F}}^{2}+{||{\boldsymbol{D}}{\boldsymbol{X}}-\boldsymbol{L}{\boldsymbol{Y}}||}_{\mathrm{F}}^{2} $

(16)

在更新后的学习字典D下，应用稀疏算法对每个子块求解相应的稀疏分解系数矩阵X，利用

$ \boldsymbol{N}=(\lambda \boldsymbol{I}+{\boldsymbol{L}}_{}^{\mathrm{T}}{\boldsymbol{L})}^{-1}(\lambda {\boldsymbol{Y}}+{\boldsymbol{L}}_{}^{\mathrm{T}}{\boldsymbol{D}}{\boldsymbol{X}}) $

(17)

进行地震数据重构，得到去噪后的结果N。式中I为单位矩阵。

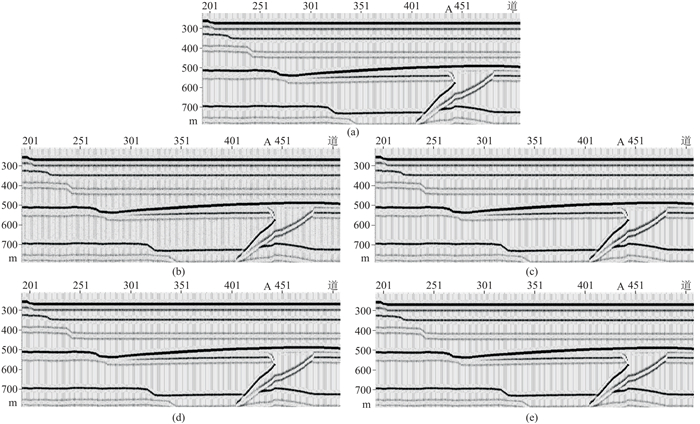
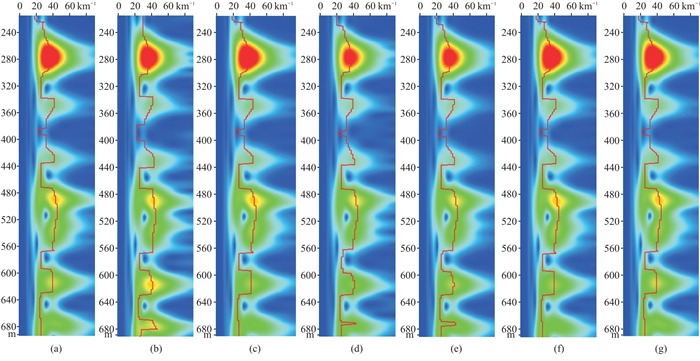
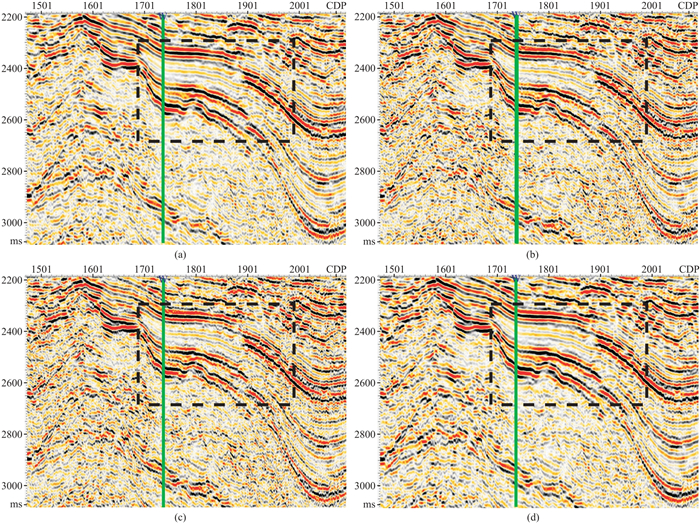
4 弱信号模型测试

图 1c中存在较强的高斯白噪声，虽然强同相轴明显可识别，但弱同相轴淹没在噪声中不易识别。图 4和图 5分别为RAK-SVD不同正则化参数的去噪结果及其残差剖面；图 6是去噪处理前后模型中A点(火山通道中，对第435道地震道进行分析的位置)的深度—波数谱；表 1是正则化参数对去噪效果的影响统计。通过图 4和表 1可以分析得到不同的正则化参数对去噪效果的影响。从图 5虚线方框中所圈出的位置可以看出，采用K-SVD和AK-SVD去噪处理后，强同相轴存在一定程度的残差，而采用μ自适应优选的算法去噪处理后，强同相轴的残差明显减小，从而达到了较高的保真度。同时为了将本方法与K-SVD和AK-SVD进行对比，统计出不同方法的去噪效果和运行时间(表 2)。

从图 4、图 5和表 1中可看到：对于低信噪比弱地震信号，当μ=0时，去噪结果虽能保留弱信号，但去噪效果较差，残余一定的毛刺，同时地震波同相轴有一定程度的损失，PSNR=11.12；当根据正则化参数自适应优化选取时，每次迭代后，参数值自适应调整，此时PSNR=12.87，能够达到最佳去噪效果，说明正则化参数自适应优选的RAK-SVD方法能提高弱信号的去噪效果和识别能力。从图 6的深度—波数谱可以进一步看到，高斯白噪声的影响主要集中在60 km^-1以上的波数范围内，在深度600~700 m之间，由于高斯白噪声的存在，记录能量明显增强。虽然不同正则化参数的去噪处理都能在一定程度上压制噪声，但在深度600~700 m之间，μ=0和μ=0.1的去噪结果对反射信号的能量和波数谱具有一定的影响，反射信号会出现局部失真。当μ=0.23以及μ值自适应优化选取时，在压制噪声的同时，较好地保持了弱反射信号的能量和波数谱特征，从而达到了较高的保真度。

从表 2可以看出：AK-SVD相较K-SVD，计算时间缩减了57.6%，去噪效果有所下降；正则化参数自动优选的RAK-SVD计算时间与AK-SVD差不多，但去噪效果明显提升。

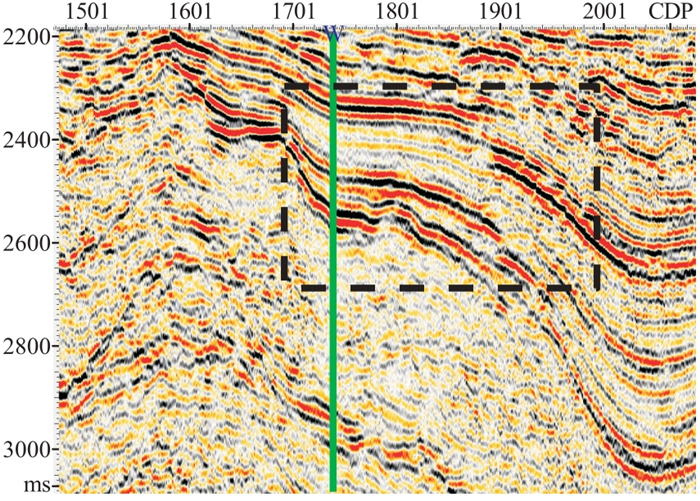
5 实际资料处理

图 7是某工区过W井的实际地震剖面，方框中目标层段强、弱信号之间振幅差异较大。存在一定程度的随机噪声，对强信号影响不大，但对弱信号的影响较大，强轴之间的弱信号同相轴不清晰、不连续或错断。

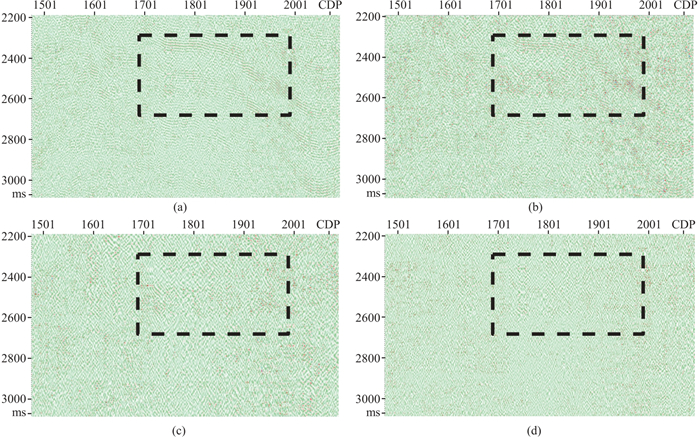
为了消除随机噪声的影响，分别采用不同的正则化系数K-SVD方法进行去噪处理。从图 8、图 9和表 3可以看出，正则化参数的选取影响去噪效果，其中μ=0时去噪效果最差，PSNR=9.67；加入正则项，去噪效果就会有所提升。采用正则化参数自适应优化的RAK-SVD方法，可避免由于μ取固定值不准确对去噪效果的影响，每次迭代自适应选取μ值，迭代结束后PSNR提升到11.56，达到了最佳去噪效果。从表 4可以看出，AK-SVD方法相较K-SVD方法，计算效率得到了明显提升，但去噪效果下降明显，PSNR=9.67；而RAK-SVD方法在提升计算效率的同时，还提升了去噪效果。对比图 7~图 9方框中的强信号和弱信号的去噪结果可以看出，K-SVD方法去噪结果中地震反射信号发生了一定程度的畸变，说明该方法对弱地震信号产生了较大影响，会产生过度去噪问题；AK-SVD方法去噪后的PSNR值比K-SVD方法有所降低，总体去噪效果不如K-SVD方法，但能够保留弱信号特征，这是因为AK-SVD使用了所有奇异值分量；正则化参数自动优选的RAK-SVD去噪方法在达到最佳去噪效果的同时，能够使弱信号的畸变程度降到最低，有利于对弱信号的提取和识别。

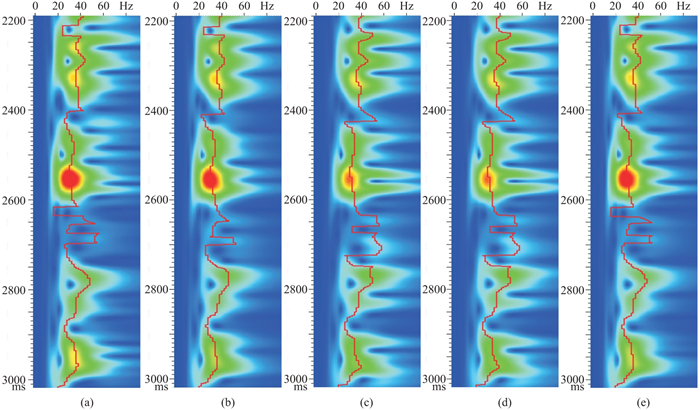
对比去噪处理前、后W井旁道的时频谱(图 10)可以看到：K-SVD方法以及AK-SVD方法(μ=0)对弱反射信号的能量和频谱特征有一定程度的改造，会出现局部信号失真现象；当采用μ值自适应优化选取的K-SVD方法处理后，在压制高频噪声的同时，较好地保持弱反射信号的能量和频谱特征，主频和频带基本不发生改变，保真度较高。

6 结束语

K-SVD方法在对低信噪比地震弱信号进行去噪处理时，有其独特的优势，但对于弱信号容易产生去噪过度问题，且计算效率较低；AK-SVD通过修改更新的字典原子和相关参数，极大提高了计算效率，但去噪效果有所下降；将正则化系数引入AK-SVD后，其去噪效果有明显提升，但正则化参数的选取严重影响去噪效果。基于自适应动态粒子群算法自动优选正则化参数的RAK-SVD方法能显著提高弱地震信号的去噪效果，在对强反射信号进行去噪的同时加强了对弱信号的保护，去噪后地震弱信号基本不发生畸变，提高了信号的保真度，在地震弱信号的提取和识别中具有广阔的应用前景。