2. 天然气水合物勘查开发国家工程研究中心, 广东广州 511458
2. National Engineering Research Center for Gas Hydrate Exploration and Development, Guangzhou, Guangdong 511458, China
地震波速度是影响地震成像和解释结果的重要参数之一[1],可以反映地层岩性和构造特征[2]。速度分析是速度建模的常用手段,速度谱是其最核心的参考依据,通常通过对共中心点叠前道集进行速度扫描得到[3],并且需要综合考虑多种因素多次迭代和验证,以获得准确可靠的结果[4]。
海洋地震数据在速度分析时受崎岖地层、多次波和绕射波等多种因素影响,导致速度谱能量团发散,单一同相轴呈现多能量团的特征,给速度分析增加了难度。优化速度谱能帮助更精准地捕捉地下岩层的速度信息,直接提高速度建模的准确性并降低其多解性,有效提升地震资料的成像品质。
近年来,随着人工智能的迅速发展,不少专家致力于半自动/自动速度拾取的研究工作,没有考虑速度谱本身的精度问题。方法主要有蒙特卡罗法[5]、非线性函数优化法、共轭梯度法、基于加权相似性[6-9]等自动寻优速度拾取算法,以及BP神经网络、卷积神经网络、循环神经网络和混合神经网络等更加智能化的速度拾取算法[10-13]。影响速度谱的精度和分辨率的主要因素包括炮检距分布、覆盖次数、信噪比、切除和地震数据的频带宽度等。刘立彬等[14]、潘宏勋[15-16]、Xu等[17]、谢玉洪等[18]、王小青等[19]、周锦明[20]采用的方法都是从炮检距分布、信噪比、切除等角度改进速度谱品质。
本文提出基于经验模态分解(EMD)的地震数据速度谱优化方法。首先对地震数据进行频移处理,通过Hilbert变换获得地震数据的瞬时振幅,对瞬时振幅进行EMD;然后在分解后的本征模量(IMF)中,选择具有有益表达速度谱信息的本征模态模量,构建新的速度谱数据,最终拓宽共中心点道集的有效频带,加强速度谱超道集的低频成分,从而实现优化速度谱的目的,为后续速度拾取提供高品质数据。
1 频移处理与速度谱优化本文的目的是通过对地震数据频移处理,突出数据低频能量,进而提升速度谱的精度,为后续偏移成像提供精确可靠的速度基础。图 1是本文速度谱优化的技术方案。
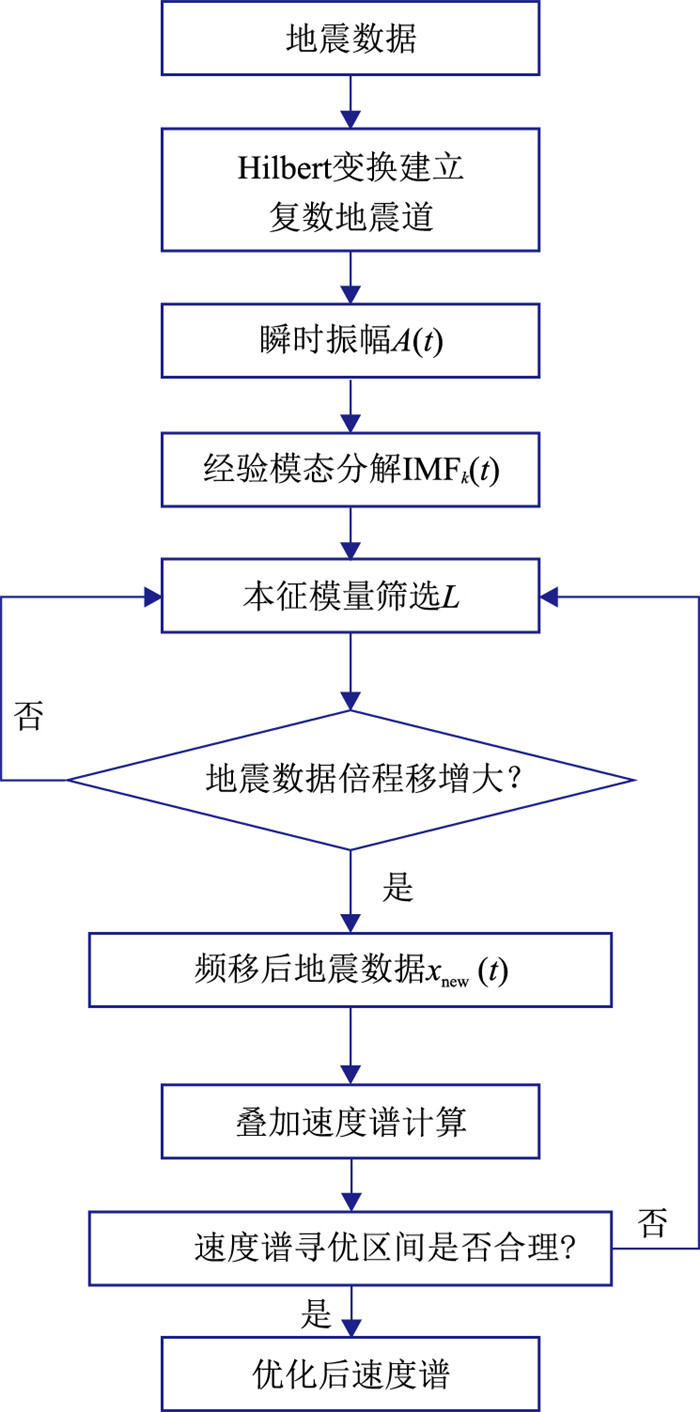
|
图 1 速度谱优化技术方案流程 L为有效本征模量个数;IMFk(t)为第k个本征模量,t为时间。 |
对于一个实值的地震信号
| $ c\left(t\right)=x\left(t\right)+\mathrm{i}H\left(t\right) $ | (1) |
式中:
| $ H\left(t\right)=x\left(t\right)\mathrm{*}\frac{1}{\mathrm{\pi }t}=\frac{1}{\mathrm{\pi }}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{x\left(\tau \right)}{t-\tau }\mathrm{d}\tau $ | (2) |
式中
| $ c\left(t\right)=A\left(t\right){\mathrm{e}}^{\mathrm{i}\phi \left(t\right)} $ | (3) |
式中
| $ A\left(t\right)={\left[{x}^{2}\left(t\right)+{H}^{2}\left(t\right)\right]}^{\frac{1}{2}} $ | (4) |
| $ \phi \left(t\right)=\mathrm{a}\mathrm{r}\mathrm{g}\left[c\right(t\left)\right] $ | (5) |
Hilbert变换是地震信号处理中常用的方法。地震信号是实信号,在复信号分析方法中需计算其对应的复信号。因此,可以将待分析的地震信号作为实部,其Hilbert变换作为虚部,即可构成复信号,该复信号可用于计算信号的瞬时属性。基于Hilbert变换获得地震资料的三瞬属性,即瞬时振幅、瞬时频率和瞬时相位,可用于地震数据的频率研究。这些瞬时属性可以揭示地震信号的时变特性,对地震数据的频域分析提供了有价值的信息。EMD是由Huang等[21]于1998年提出的一种新型自适应信号时频处理方法,特别适用于非线性非平稳信号的分析处理。EMD可将地震信号分解成一系列IMF,每个IMF都代表了信号在不同尺度上的振动模式。EMD有助于更好地理解地震信号的时变特性和频率分布。
EMD可以将非线性非平稳信号分解为几个本征模态分量和一个残差之和,对式(4)求得的瞬时振幅
| $ A\left(t\right)=\sum\limits_{k=1}^{K}\mathrm{I}\mathrm{M}{\mathrm{F}}_{k}\left(t\right)+\mathrm{R}\mathrm{e}\mathrm{s}\left(t\right) $ | (6) |
式中:
本征模态分量必须满足以下两个条件:
(1) 整个时间范围内,局部极值点和过零点的数目必须相等,或最多相差一个;
(2) 任意时刻点,局部最大值的包络(上包络线)和局部最小值的包络(下包络线)平均必须为零。
1.3 筛选本征模态分量根据实际地震数据的频带范围及本征模态分量的频率范围,筛选出有益于提高速度谱品质的本征模态分量
| $ {x}_{\mathrm{n}\mathrm{e}\mathrm{w}}\left(t\right)=\sum\limits_{k=1}^{L}IM{F}_{k}\left(t\right) \quad L\le K $ | (7) |
新的残差
| $ \mathrm{R}\mathrm{e}{\mathrm{s}}_{\mathrm{n}\mathrm{e}\mathrm{w}}\left(t\right)=A\left(t\right)-{x}_{\mathrm{n}\mathrm{e}\mathrm{w}}\left(t\right) $ | (8) |
与原始地震数据
在CMP道集中,使用频移后的地震数据
(1) 在待分析速度点附近取出若干CMP道集。
(2) 对这些CMP道集使用一系列常速度值进行动校正和叠加。每个速度值对应一个叠加剖面,这一系列由不同速度得到的叠加剖面称为CVS剖面。CVS剖面的叠加能量随“一系列速度”变化而增大或减小,叠加能量相对速度的变化就构成了速度谱。
(3) 当速度合适时,经过动校正后,反射波同相轴被拉平,此时叠加效果最好,叠加振幅出现极大值,叠加能量最强。通过在CVS叠加能量图像中寻找叠加能量最大的位置,可以解释出理想的叠加速度,即所求动校正速度。
叠加能量计算公式如下
| $ \overline{A}=\frac{1}{M}\sum\limits_{m=1}^{M}\sum\limits_{n=1}^{N}x_{\text {new }}^{\prime}\left(t_{m, n}\right) $ | (9) |
式中:
速度分析是以人工经验干预为主的过程,修改
以一条实际海洋拖揽地震资料的叠加数据为例进行频移处理,该数据记录长度为7 s,采样率为1 ms,道间距为3.125 m,有效频带范围约为4~120 Hz,该叠加数据总体上纵横向分辨率较好。从图 2中可以看出,瞬时振幅(图 2b)主要反应了原始叠加数据(图 2a)的反射振幅强度。由图 3可见,第一次分解出的本征模态分量
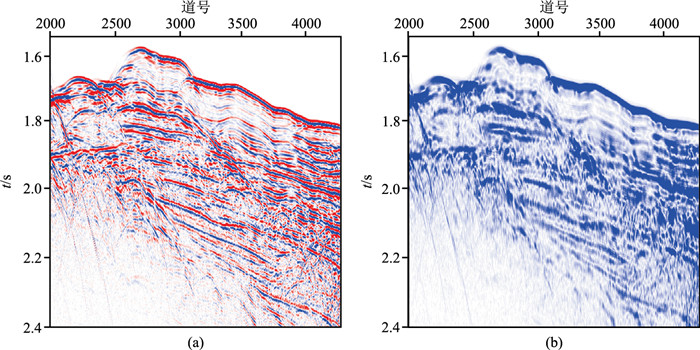
|
图 2 原始叠加数据(a)及瞬时振幅(b) |
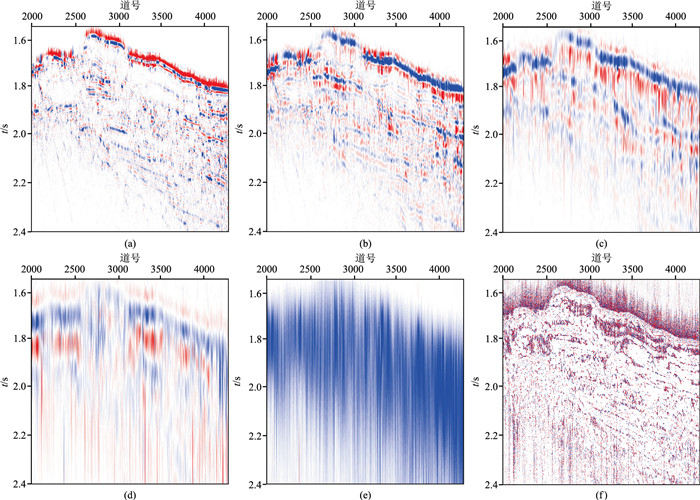
|
图 3 叠加数据瞬时振幅EMD图
(a) |
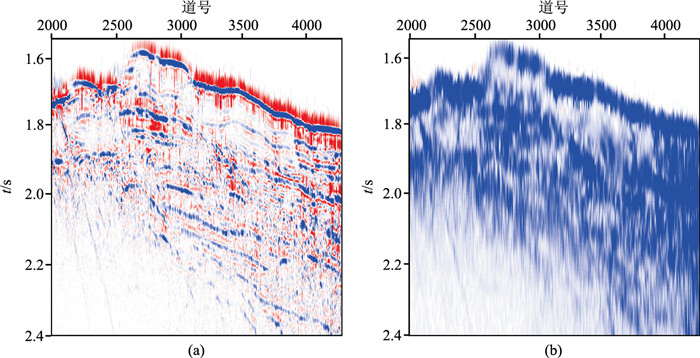
|
图 4 频移处理后叠加数据及残差 (a)本征模量 |
|
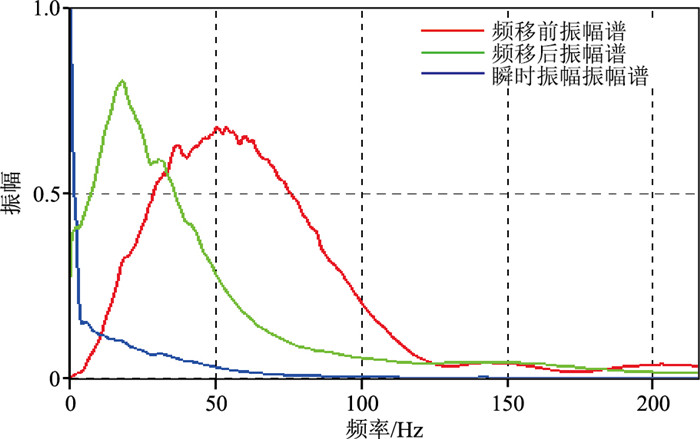
图 5 图 2频移处理前(图 2)、后(图 4)叠加数据频谱对比 |
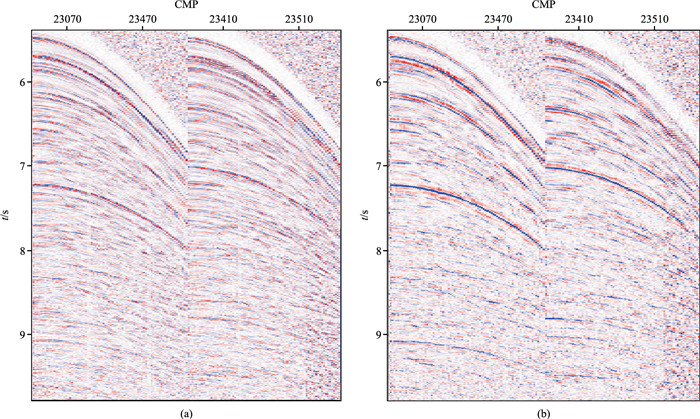
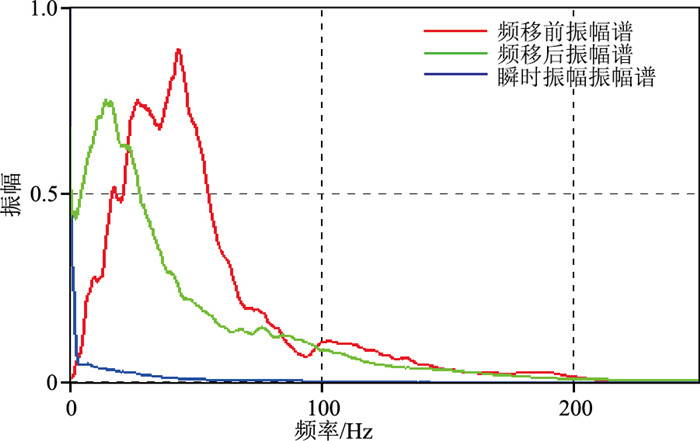
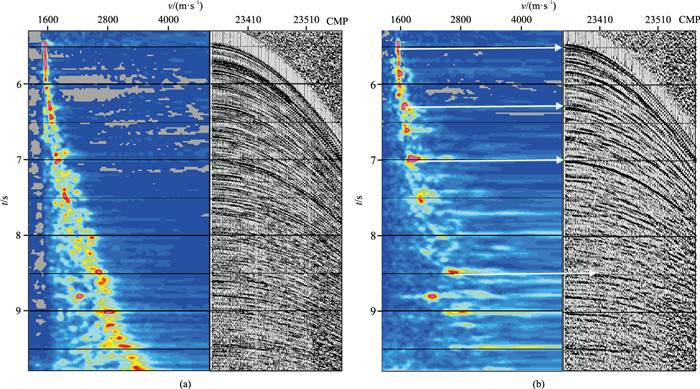
以一条发育崎岖地层的海洋拖缆数据为例,覆盖次数为80,记录长度为12 s,采样率为2 ms,道间距为12.5 m,有效频带相对较窄(约为4~90 Hz)。由图 6可见:处理前,有效反射层较多但缺乏波组特征,呈窄带信号特征;处理后,振幅强弱对比明显,波组关系清晰明确。由图 7可见,频移处理后,有效频带向低频端移动,增加了道集的低频信息。此外,由图 8也可看到,优化前,受崎岖地层的影响,速度谱能量团发散,道集上单一同相轴在速度谱上对应多个能量团,造成速度拾取多解性,进而增加速度误差。优化后,能量团空间上更加聚焦,且与CMP道集主要反射同相轴能一一对应,有效降低了速度分析难度,为精细速度建模提供良好数据基础。该实例证明本文研究方法在崎岖地层发育的拖缆数据中具有显著应用效果。
|
图 6 二维拖缆地震数据频移处理前(a)、后(b)CMP道集对比 |
|
图 7 二维拖缆地震数据频移处理前、后共中心点道集频谱对比图 |
|
图 8 二维拖缆地震数据频移处理前(a)、后(b)速度频谱(左)及共中心点道集(右)对比图 |
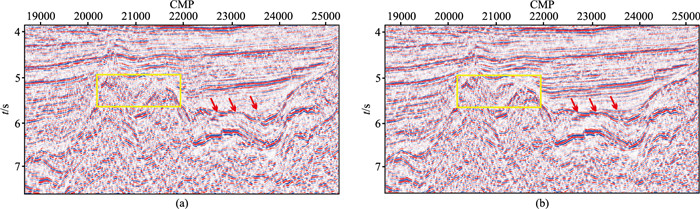
由图 9可见,速度整体趋势一致,基于优化前的速度谱建立的速度场较平滑(图 9a),能确定速度的宏观趋势,而经速度谱优化处理后拾取的速度更加精细(图 9b),能够更清晰地显示局部速度特征。图 10展示了采用图 9的速度场进行偏移的局部结果。整体成像品质略有提升,并在复杂凹陷内幕构造和高倾角基底成像方面有所改善。虽然速度场更加精细,但由于时间偏移对速度信息不够敏感,无法在偏移剖面上呈现显著的效果。

|
图 9 二维拖缆地震数据速度谱优化前(a)、后(b)的速度剖面 |
|
图 10 二维拖缆地震数据速度谱优化前(a)、后(b)的偏移剖面 |
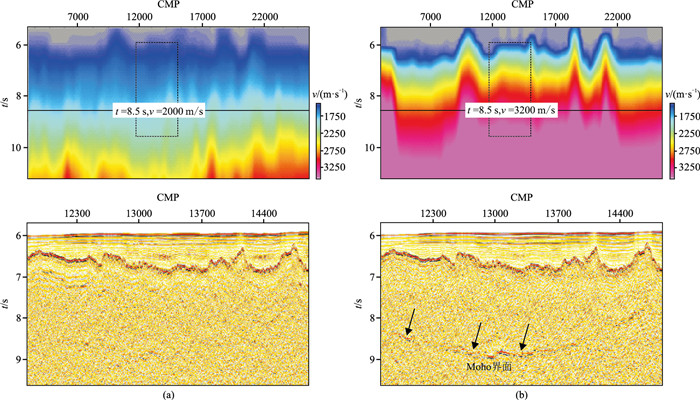
低频信息相对于高频信息具有衰减慢、穿透能力强的特点[22]。受波前扩散和地层吸收衰减作用的影响,地震波在传播至深部时信号变得非常微弱。因此,深部地壳结构和莫霍面的成像主要依赖于低频有效反射能量。深层目标反射通常在双程旅行时间为6~10 s之间,且在基底以下的地层通常具有低信噪比特征,在速度谱上表现为能量团成片的特点[23]。图 11展示了南海一条深反射地震测线在应用本文速度谱优化技术前(图 11a)、后(图 11b)的速度模型(图 11上)和偏移剖面(图 11下)。由图可见,低频能量突出之后,优化后拾取的叠加速度在目的层(双程旅行时8.5 s附近)与优化前相比提高了1000 m/s以上,更符合壳幔地层的真实速度规律。同时,深部的Moho界面反射也得以凸显,连续性显著提升,这为深部成像特征和南海构造演化研究提供了更可靠的数据基础。
|
图 11 二维深反射地震数据速度谱优化前(a)、后(b)的速度(上)及偏移剖面(下) |
本文研究的速度谱优化方法在处理深部低信噪比的壳幔结构成像地震数据速度谱时效果显著,利用频移处理技术将地震数据的有效带宽向低频端拓展,增大了倍频程,提高了速度谱的分辨率。偏移剖面只是从一个角度验证了其效果,沉积层发育较厚的地质条件下无法体现本文速度场的精度优势。另外,地震数据速度谱优化只是频移处理技术应用的一个领域,如果将频移处理应用于地震成果数据,也能有效提高成果数据的解释能力。
| [1] |
R E谢里夫, 吉尔达特. 勘探地震学[下册][M]. 北京: 石油工业出版社, 1999. SHERIF R E, GELDART L P. Exploration Seismology (Volume 2) [M]. Petroleum Industry Press, Beijing, 1999. |
| [2] |
谢俊法, 孙成禹, 王兴谋, 等. 地震资料的多准则速度分析方法[J]. 物探与化探, 2017, 41(3): 513-520. XIE Junfa, SUN Chengyu, WANG Xingmou, et al. The multi⁃criteria velocity analysis of seismic data[J]. Geophysical and Ceochemical Exploration, 2017, 41(3): 513-520. |
| [3] |
王辉, 丁志峰. 浅层地震勘探资料处理中的速度分析参数选取[J]. 地震地质, 2006, 28(4): 597-603. WANG Hui, DING Zhifeng. Parameters selection for velocity analysis in shallow seismic data processing[J]. Seismology and Geology, 2006, 28(4): 597-603. DOI:10.3969/j.issn.0253-4967.2006.04.007 |
| [4] |
郭树祥, 韩永治, 李建明, 等. 高分辨率地震资料处理中的优化速度分析方法[J]. 石油物探, 2004, 43(1): 80-82. GUO Shuxiang, HAN Yongzhi, LI Jianming, et al. Optimal velocity analysis in high resolution seismic data processing[J]. Geophysical Prospecting for Petroleum, 2004, 43(1): 80-82. |
| [5] |
DAVID E L. Monte Carlo automatic velocity picks[J]. Stanford Exploration Project, 1997, SEP⁃75: 1-25. |
| [6] |
ZHANG L. Velocity analysis without picking[J]. Geophysics, 1989, 54(2): 191-199. DOI:10.1190/1.1442643 |
| [7] |
LIN Z, ALGORITHM K. Automatic picking and its applications[J]. Standford Exploration Project, 1991, SEP⁃70: 275-292. |
| [8] |
AHMED M A, FERAN Y A. Automatic seismic velocity picking[J]. 82nd Annual Internat SEG Mtg Expanded Abstracts, 2012, 31: 1-5. |
| [9] |
ABBAD B, URSIN B, RAPPIN D. Automatic nonhyperbolic velocity analysis[J]. Geophysics, 2009, 74(2): U1-U12. DOI:10.1190/1.3075144 |
| [10] |
SCHMIDT J, HADSELL F A. Neural network stacking velocity picking[J]. 62nd Annual Internat SEG Mtg Expanded Abstracts, 1992, 11: 18-21. |
| [11] |
FISH B C, KUSUMA T. A neural network approach to automate velocity picking[J]. 64th Annual Internat SEG Mtg Expanded Abstracts, 1994, 13: 185-188. |
| [12] |
查朝阳. 利用神经网络拾取叠加速度[J]. 石油地球物理勘探, 1996, 31(6): 892-899. ZHA Chaoyang. Picking stack velocity using artificial neural network[J]. Oil Geophysical Prospecting, 1996, 31(6): 892-899. |
| [13] |
张昊, 朱培民, 顾元, 等. 基于深度学习的地震速度谱自动拾取方法[J]. 石油物探, 2019, 58(5): 724-733. ZHANG Hao, ZHU Peimin, GU Yuan, et al. Velo⁃ city auto⁃picking from seismic velocity spectra based on deep learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 724-733. |
| [14] |
刘立彬, 汪浩, 高侠, 等. 一种速度谱三维滤波优化速度分析方法: CN201410316146.7[P]. 2018⁃02⁃02. LIU Libin, WANG Hao, GAO Xia, et al. A velocity analysis method optimized by three⁃dimensional velocity spectrum filtering: CN201410316146.7[P]. 2018⁃ 02⁃02. |
| [15] |
潘宏勋. 一种多道相似相干速度谱计算方法: CN201510657080.2[P]. 2018⁃08⁃07. PAN Hongxun. A multichannel similar coherent velocity spectrum calculation method: CN201510657080.2[P]. 2018⁃08⁃07. |
| [16] |
潘宏勋. 一种优选道加权速度谱计算方法: CN201510657079. X[P]. 2019⁃02⁃01. PAN Hongxun. An optimal track weighted velocity spectrum calculation method is presented: CN20151065⁃7079. X[P]. 2019⁃02⁃01. |
| [17] |
XU X, SU Q, XIE J, et al. Method for obtaining high⁃resolution velocity spectrum based on weighted similarity[J]. Applied Geophysics, 2020, 17(2): 221-232. |
| [18] |
谢玉洪, 赫建伟, 黎孝璋, 等. 一种基于匹配追踪的超低信噪比高精度速度谱生成方法: CN202010068543.2[P]. 2021⁃06⁃25. XIE Yuhong, HAO Jianwei, LI Xiaozhang, et al. An ultra⁃low signal⁃to⁃noise ratio and high precision velo⁃ city spectrum generation method based on matching tracking: CN201810798724.3[P]. 2021⁃06⁃29. |
| [19] |
王小青, 陈金焕, 杨文广, 等. 提高速度谱精度的处理方法及系统: CN201810798724.3[P]. 2021⁃06⁃29. WANG Xiaoqing, CHEN Jinhuan, YANG Wenguang, et al. A processing method and system for improving the accuracy of velocity spectrum: CN201810⁃ 798724.3[P]. 2021⁃06⁃29. |
| [20] |
周锦明. 自适应走向速度谱求取方法和系统: CN201910049867.9[P]. 2021⁃10⁃15. ZHOU Jinming. Method and system for obtaining adaptive strike velocity spectrum: CN201910049867.9[P]. 2021⁃10⁃15. |
| [21] |
HUANG N, SHEN Z, LONG S, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non⁃stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995. |
| [22] |
PANEA I, PRISACARI S, MOCANU V, et al. The use of seismic modeling for the geologic interpretation of deep seismic reflection data with low signal⁃to⁃noise ratios[J]. Interpretation, 2017, 5(1): T23-T31. |
| [23] |
PICHOT T, DELESCLUSE M, CHAMOT⁃ROOKE N, et al. Deep crustal structure of the conjugate margins of the SW South China Sea from wide⁃angle refraction seismic data[J]. Marine and Petroleum Geo⁃logy, 2014, 58: 627-643. |



 张衡, 广东省广州市南沙区海滨路1133号广州海洋地质调查局,511458。Email:
张衡, 广东省广州市南沙区海滨路1133号广州海洋地质调查局,511458。Email: