0 引言

全球海域油气资源潜力巨大，海洋油气储量占全球油气总资源量的1/3，待发现石油资源量占47%，近10年新油气发现有74%分布在海域，所以，海洋石油是世界油气产量增长的重要引擎。中国海域蕴藏着丰富的石油和天然气，是未来中国油气资源的重要接替区，海洋油气资源勘探与开发尤为迫切。然而，海域油气勘探开发正面临从浅层向深层、由构造油气藏向复杂岩性油气藏转移的新形势，勘探难度不断增大，对地震资料品质提出了更高的要求。如何提高海洋地震资料成像精度，降低勘探风险，对油气资源的可持续发展具有重要战略意义。

由于两个强波阻抗界面(海面和海底)的存在，海洋地震数据普遍发育强能量多次反射波。经过常规的方法处理后，多次波在地震剖面上表现为与真实构造难以有效区分的构造假象，可能导致对地下实际情况的误判，尤其是微幅度构造下的储层更易受多次波假象干扰。所以长期以来多次波一直被视为噪声并尽可能地从地震数据中消除，以免在地震解释中造成误解。

目前多次波的消除方法可以分为三类。第一类是基于一次波和多次波在空间上的特性差异的去噪方法。早在1986年Hampson^[1]就提出了在Radon域基于一次波与多次波的时差来衰减多次反射波；Herrmann等^[2]采用了一种高分辨率的抛物线Radon变换区分一次波和多次波；顾建平^[3]改进了Radon滤波压制多次波技术，通过拾取产生多次波的一次波强反射层来有效压制多次波；石颖等^[4]基于波动方程预测和双曲Radon变换联合压制表面多次波；王维红等^[5]为了克服空间截断效应对Radon变换的影响，提出了一种$ \lambda \mathrm{⁃}f $域抛物Radon变换方法，大幅度提高计算效率；范景文等^[6]通过在双曲Radon变换积分路径中引入各向异性参数，描述了VTI介质和海洋大炮间距地震数据的时距曲线关系，实现了各向异性条件下的高分辨率Radon变换多次波压制；薛亚茹等^[7]将迭代加权最小二乘法嵌入迭代软阈值(ISTA)，形成了加权ISTA的高分辨率Radon变换方法；马继涛等^[8]针对数据中振幅随炮检距变化的特点，引入正交多项式变换，进而形成了三维高精度保幅Radon变换多次波压制方法。该类方法的应用有两个假设条件：动校后的CMP道集能够用双曲线或抛物线描述以及一次波与多次波在Radon域可分离。当地层横向变化剧烈或一次波与多次波速度差异较小时，利用该类方法难以有效压制多次波。

第二类是基于多次波的周期性和可预测性的去噪方法。在20世纪50年代，Robinson^[9]通过滤波器来衰减这种重复性的地震信号，并对预测反褶积技术开展了深入的研究，这种方法尤其对于压制浅水多次波非常有效^[10-11]。预测反褶积技术依赖于多次波严格的周期性，这种情况只有在水平层状介质条件下才满足，对于大炮检距地震道，会产生较大误差。Lokshtanov^[12-13]研究了扩展的预测反褶积方法在Radon域的应用，并进一步分析了线性Radon域反褶积和基于波动方程多次波压制之间的关系，证明了在水底形态变化不大的情况下，基于波动方法压制多次波的一些元素可以在线性Radon域中进行调节。赵昌垒等^[14]利用线性Radon域的预测反褶积较好地压制了海洋多次反射波。多年来业界应用最为普遍的是自由表面多次波压制方法(SRME)，这是利用叠前地震数据中的反射波信息构建地表相关多次反射波的数据驱动型方法，因其不需地下信息被广泛应用^[15]。Weglein等^[16]基于多次波传播的“低—高—低”关系，提出了逆散射级数(ISS)多次波压制方法，已经在生产处理中初步应用。Jakubowicz^[17]在SRME基础上进行了拓展应用，利用与产生多次波界面有关一次反射的逆时数据和地震数据预测出与该层相关的层间多次波。SRME技术的假设条件是观测系统规则分布，但是实际情况往往难以满足，尤其是三维地震的情况。Dragoset^[18]提出了三维广义地表多次波预测技术(3D⁃GSMP)，基于采集的真实坐标并能够准确地预测复杂多次波。Groenestijn等^[19]提出了最速下降法(梯度法)的最优化反演方法估计一次反射波(EPSI)，该方法具有广阔的研究前景和应用价值。

第三类是智能化的多次波衰减技术。近年来，得益于计算机软硬件的发展，基于深度学习的智能化技术被应用到了各个领域，推动着产业的快速革新^[20]。人工智能的本质就是利用机器模拟人的思维并做出判断^[21]，而深度学习就是让机器变“聪明”的过程^[22]，对海量数据的学习甚至会让人工智能超越“人工”。由于随机噪声标签容易获取，所以随机噪声衰减是深度学习在地震去噪领域首先应用的场景^[23]。王钰清等^[24]进行数据增广并利用CNN网络结构进一步提高随机噪声的压制效果。李海山等^[25]和Yu等^[26]利用CNN网络深度学习的方法探索研究了随机噪声、线性噪声和多次波的压制。于四伟等^[27]使用迁移学习方法压制地震散射面波，能够利用较少的训练样本实现与大量训练样本类似的效果。宋欢等^[28]采用的深层神经网络是一种改进的具有卷积编码器和卷积解码器的U⁃Net网络，提出了一种基于深层神经网络的多次波压制方法。刘小舟等^[29针对层间多次波压制研究了数据增广的编/解码卷积网络地震层间多次波压制方法^]。张猛^[30]将自注意力机制(SA)引入到了多次波压制策略中，避免了实际计算中的超参数选取。

在前人研究的基础上，针对海洋多次波压制问题，本文提出了一种基于自注意力机制对抗网络(SA⁃GAN)的海洋多次波压制方法。该方法首先选取特征数据利用多域分步组合法压制多次波获得标签数据集，然后在U⁃Net生成器网络$ \boldsymbol{G}({\boldsymbol{x}}_{g};{\boldsymbol{\theta }}_{g}) $中引入SA，$ {\boldsymbol{x}}_{g}\mathrm{、}{\boldsymbol{\theta }}_{g} $分别为生成器输入数据和网络参数集，构建基于SA⁃GAN网络的多次压制深度学习模型，并进行网络训练，最后利用训练完备的SA⁃GAN网络对整体数据进行多次波压制处理。SA⁃GAN收敛速度快且计算稳定，并且在地震样本数据集上具有更好的数据泛化能力。该方法克服了传统多次波压制采用的多步骤组合的繁琐过程，复杂模型和NH地区实际资料试处理验证了方法的有效性，也为海洋实际地震数据的多次波压制提供了一种高效手段。

1 方法原理

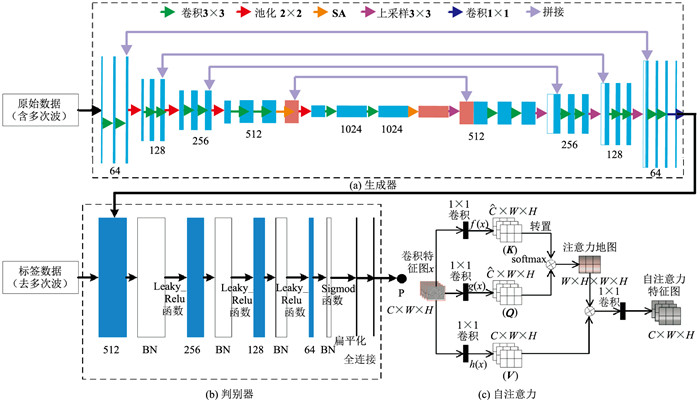
基于深度学习的智能化多次波衰减方法关键因素在两个方面：标签制作和合理的网络结构。由于实际资料多次波类型多样，难以用正演模拟的方法获取，所以本文标签制作方式是对少量特征炮在多域分布处理，关键点在于网络结构的优化。将SA引入对抗网络(GAN)中，注意力机制模仿了生物观察行为的内部过程，将内部经验和外部感觉对齐从而增加部分区域的观察精细度的机制。SA是注意力机制的改进，其减少了对外部信息的依赖，更擅长捕捉数据或特征的内部相关性，能够提升深度学习网络的性能。多次波压制在生成器U⁃Net网络中引入SA，构建基于SA⁃GAN网络的多次压制深度学习模型，利用原始数据和标签数据对网络模型进行学习训练，整个网络结构如图 1所示，其中包含了三个部分：生成器(图 1a)、判别器$ \boldsymbol{D}({\boldsymbol{x}}_{d};{\boldsymbol{\theta }}_{d})( $$ {\boldsymbol{x}}_{d}\mathrm{、}{\boldsymbol{\theta }}_{d} $分别为判别器输入数据和网络模型参数$ ) $(图 1b)和SA(图 1c)。

1.1 自注意力机制

在深度学习过程中，神经网络的输入往往来自于不同的向量，而这些输入向量之间可能存在着一定的联系。网络模型实际训练的时候，不同层级间的局部学习可能会丢失不同输入向量之间的这种关联信息。针对神经网络深度学习时多个相关输入无法建立相关性的问题，通过注意力机制来解决。注意力机制的作用就是在深度学习时，考虑到全局不同输入部分之间的相关性信息，SA是注意力机制的变体，它减少了对外部信息的依赖，更多地关注数据内部的相关性。自注意力函数可以描述为查询(Q)和键—值对(K, V)映射到输出(O)，Q、K、V和O均为向量。分配给每个值的权重由查询及相应键的函数计算，输出计算则是值的加权求和，SA表达式为

$ \boldsymbol{A}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{softmax}\left(\frac{\boldsymbol{Q K}^{\mathrm{T}}}{\sqrt{d_k}}\right) V $

(1)

式中：$ {d}_{\mathit{k}} $为缩放因子{$ {d}_{\mathit{k}} $}的元素，{$ {\boldsymbol{d}}_{\mathit{k}} $}与K向量同维度，k为缩放因子的序号标识；softmax为归一化处理函数。设输入特征图向量$ \boldsymbol{x}\in {\boldsymbol{R}}^{C\times W\times H} $，C为通道数，W和H分别为单通道向量的宽和高；定义$ \boldsymbol{f}\left(\boldsymbol{x}\right) $、g$ \left(\boldsymbol{x}\right) $和h$ \left(\boldsymbol{x}\right) $均为特征图x通过1$ \times $1核大小的卷积映射，分别对应式(1)中Q、K、V三个向量。$ \boldsymbol{f}\left(x\right)={\boldsymbol{W}}_{\boldsymbol{f}}\boldsymbol{x} $，$ \boldsymbol{g}\left(\boldsymbol{x}\right)={\boldsymbol{W}}_{\boldsymbol{g}}\boldsymbol{x} $，$ \boldsymbol{h}\left(\boldsymbol{x}\right)={\boldsymbol{W}}_{\boldsymbol{h}}\boldsymbol{x} $。$ {\boldsymbol{W}}_{\boldsymbol{f}},{\boldsymbol{W}}_{\boldsymbol{g}},{\boldsymbol{W}}_{\boldsymbol{h}}\in {R}^{C\times C} $，$ \hat{C}=C/8 $。

1.2 网络结构

GAN的核心包括生成器和判别器两部分，分别对应两个子网络模型。生成器网络的目的是模仿真实数据的分布规律，而判别器网络则是尽量分辨输入数据的真伪，双方在相互博弈竞争中不断优化和提升各自网络的能力，最终实现两者之间的均衡。

本文提出的海洋多次波压制深度学习网络结构中的生成器网络采用了自编码和解码的U⁃Net网络，该网络为四层跳层连接(图 1a)。下采样在原始输入后，通道数从64逐次翻倍至1024。下采样编码过程中，每组功能运算包括两次卷积和一次最大池化。卷积核采用3$ \times $3矩阵，最大池化后特征图的长度和宽度均减为一半，而在上采样解码过程中，每组功能运算包括两次卷积和一次反卷积。上采样卷积核也采用3$ \times $3矩阵，通过跳层连接和卷积运算，特征图的长度和宽度均翻倍扩展，直到特征图的大小恢复至原始数据。在U⁃Net网络下采样的最后一组跳层连接层引入SA，对特征图进行自注意力值的计算，将更多的特征图关联细节反馈到网络模型的深度学习和训练中。

判别器网络采用卷积神经网络模型(图 1b)，该网络由四组卷积和批规范化层(BN)完成数据特征的逐级提取，上一组批规范化层的输出经过激活函数Leaky_Relu的非线性映射后成为下一组卷积层的输入。第一组特征图通道数为512，第二组为256，逐组特征提取的通道数减半。网络模型各卷积层的卷积核均设置为4$ \times $4的矩阵。第四组特征图数据批规范化后，进行扁平化处理，并通过Sigmod激活函数，映射到全连接层。模型最后输出对训练样本数据辨别的真伪概率，判别器网络的输入样本来自生成器网络的输出数据或标签数据。当判别器网络输入多次波去噪后的标签数据时，模型进行网络学习训练输出的数据真实概率导向于1。当判别器网络输入为生成器网络输出的多次波衰减的结果时，模型学习训练的输出真实性概率则导向于0。通过网络的对抗深度学习和训练，生成器网络和判别器网络的能力将处于近似平衡的状态。在这种网络模型状态下，生成器网络产生的样本去噪数据趋近于标签数据，而判别器网络对生成器网络产生数据的辨识真伪概率和对标签数据的辨识概率也趋于相近。

1.3 训练策略

网络模型训练包括生成器网络和判别器网络训练两部分。为了保证网络模型深度学习过程的稳定，使网络快速收敛，样本数据和标签数据在训练前均进行了去中心规范化处理

$ \hat{x}_i=\frac{x_i-\frac{1}{N} \sum\limits_{i=1}^N x_i}{\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(x_i-\frac{1}{N} \sum\limits_{i=1}^N x_i\right)^2}} $

(2)

式中：$ {x}_{i} $为数据元素，i=1，2，…，N，$ N $为数据量；$ \widehat{{x}_{i}} $为$ {x}_{i} $处理后对应的数据。判别器网络的激活函数采用修正的Leaky_Relu函数，$ \mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\_\mathrm{R}\mathrm{e}\mathrm{l}\mathrm{u}\left(x\right)=\left\{\begin{array}{c}x,f\left(x\right)\ge 0\\ \alpha x,f\left(x\right) < 0\end{array}\right. $，本文取$ \alpha =0.02\mathrm{。} $判别器网络定义$ {L}_{2} $最小化损失函数

$ \begin{aligned} L\left(\boldsymbol\theta_d\right)= & \min \left\{\left\|1-D\left(\boldsymbol{y}_{\text {label }} ; \boldsymbol\theta_d\right)\right\|_2^2+\right. \\ & \left.\left\|D\left[G\left(x_{\text {inpuu }} ; \boldsymbol\theta_g\right)\right]\right\|_2^2\right\} \end{aligned} $

(3)

式中：$ {‖\bullet ‖}_{2} $表示用于度量误差的2范数；$ {\boldsymbol{y}}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}} $为标签数据；$ {\boldsymbol{x}}_{\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}} $为样本数据。

生成器为引入SA而组成的四层跳层对称连接的U⁃Net网络，在生成器网络定义的最小化损失函数$ {L}_{1} $中，引入了生成器网络输出数据对标签数据依赖的约束项，该约束项对损失函数贡献的权重由超参数$ \lambda $设定。生成器网络训练损失函数$ {L}_{1} $定义为

$ \begin{gathered} L\left(\boldsymbol\theta_g\right)=\min \left\{\left|1-D\left[G\left(\boldsymbol{x}_{\text {input }}\right) ; \boldsymbol\theta_d\right]\right|+\right. \\ \left.\lambda\left|\boldsymbol{y}_{\text {label }}-G\left(\boldsymbol{x}_{\text {inpuu }} ; \boldsymbol\theta_g\right)\right|\right\} \end{gathered} $

(4)

在网络模型训练过程中，深度学习率设置为0.001，梯度优化器采用Adam。

1.4 网络性能测试

在装有GPU的工作站上对该深度学习网络性能进行了测试，GPU卡硬件配置为Quadro RTX 5000，显存128 G。样本数据和标签数据均为326个二维地震剖面，随机抽样60%参与网络模型训练测试，20%用于模型校验，20%的样本用做预测。模型深度学习训练的更新次数Epoch设置为100。在网络模型测试中，文中将引入了自注意力的U⁃Net称为SAU⁃Net。在生成器网络的模型训练中，测试了SAU⁃Net跳层对称连接数为2层(L2网络)、3层(L3网络)和4层(L4网络)结构的性能效果(表 1)。由于模型层数不同，涉及的参数量级差别较大，L3网络的参数量是L2网络参数量的近3倍，而在L4网络中，参数总量达到了L3网络的4倍。从模型训练的残差和验证方差对比上看，L3网络模型训练的效果已经接近了L4网络模型，因此，权衡计算效率和效果方面，生成器可以用L3网络模型。

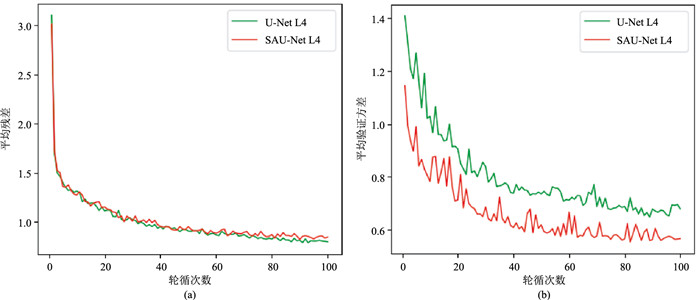
本文生成器采用了L3级SAU⁃Net网络模型，U⁃Net网络参数量为8.02 M左右，引入SA机制的SAU⁃Net生成器网络参数量增长到了9.24 M。为了对比对两种模型的效果，在同样的软硬件环境和样本数据集下进行了网络训练和测试，两种网络结构的平均残差和验证方差如图 2所示。从SAU⁃Net与U⁃Net两种不同生成器网络的对抗模型训练测试结果可以看出，两者的平均残差曲线均快速收敛，平均残差相近。对比整体网络模型的平均校验方差曲线，生成器网络中引入SA的对抗网络模型平均校验方差明显优于未引入SA的对抗网络模型。说明在生成器网络中引入SA构建的海洋多次波压制对抗网络模型对样本训练及验证数据集具有更好的数据拟合能力。

2 数值模型测试

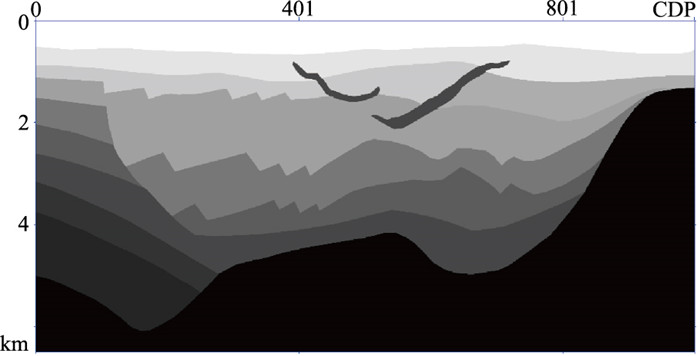
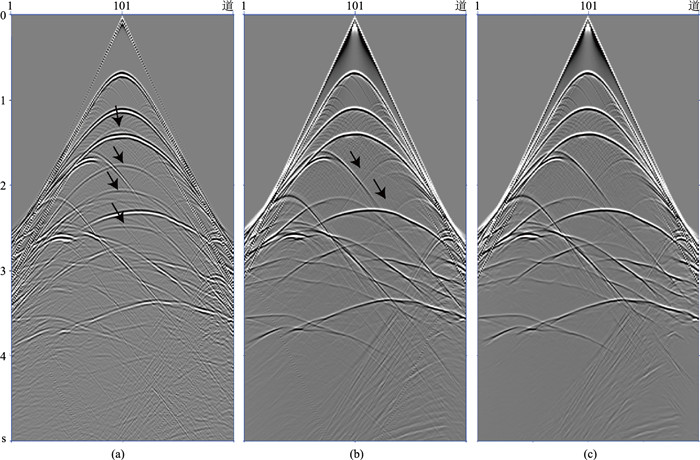
为了测试本方法的效果，首先用北部湾探区火成岩发育区典型模型进行测试。该模型速度场如图 3所示。该模型深度6500 m，CDP间距20 m，浅层包含两套平层，在模型中部有局部火成岩侵入体，速度达到4500 m/s，浅、中和深部普遍发育小断裂。图 4a是利用高阶有限差分正演模拟得到的单炮记录，子波主频30 Hz，共201道接收，道距40 m，最大炮检距4000 m，中间放炮两边接收的采集方式，记录时间5 s。复杂的地下构造导致地震波场关系复杂，顶部采用吸收边界条件，如图 4a中箭头所示是表面相关多次反射波场，在1.3 s附近的多次反射波在中远炮检距和地层一次反射波重叠，但是在近炮检距对有效反射波的影响显著。图 4b是顶边界采用吸收边界条件计算得到的反射波场，理论上该波场是不含表面相关多次反射波，但是，如图 4b箭头所示，仍有微弱的多次反射波残留。

正演模拟200炮地震数据，根据相邻炮间多次波具有相似性的特点，每隔5炮选取1炮作为标签数据(标签数据40炮，占数据总量的20%)，通过基于SA⁃GAN进行训练。为了实现网络模型更好的去噪效果，对抗网络中的生成器损失函数使用了联合平均绝对值误差，该误差对离群数据点不敏感，且梯度稳定，有利于地震数据的去噪。判别器网络对数据误差范围要求较高，所以采用联合最小均方差损失函数进行约束。深度学习的梯度优化器采用Adam算法。对抗网络模型深度学习训练的Epoch设置为100，从模型的训练过程看，在前期的迭代阶段，计算已经能够快速收敛。当Epoch到达60附近时，生成器网络的误差和判别器网络的误差基本进入相对较小的波动区间，模型训练收敛趋于相对稳定的状态。

预测结果如图 4c所示，在计算高效的同时，图 4b中部分残余多次也得到了较好地压制(图 4中箭头所指)。从图 5的局部放大中能够更清楚地看到，利用本文方法，图 5b标签数据中箭头所指的残留多次波也被较好地压制。该复杂模型测试结果表明，基于自注意力机制对抗网络的多次波压制技术，能够实现多次波高效压制。

3 实际资料试处理

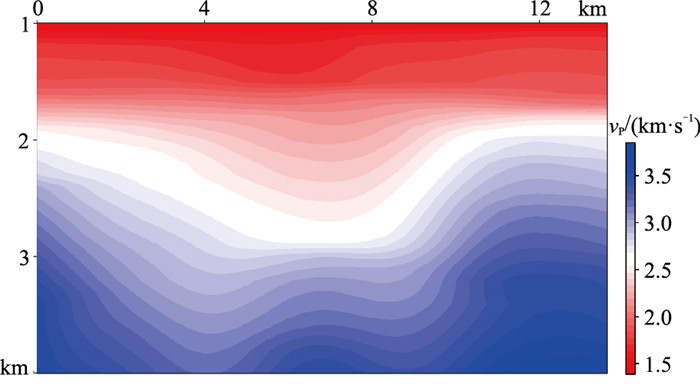
模型测试结果证明了本方法的正确性，为了进一步验证实际资料的适用性，对NH深水探区实际资料进行了试处理。该探区属于中国深海水域，盆地内含油气构造发育，地层和构造条件具有良好的油气运聚和成藏体系，是中国深海油气勘探开发的重要目标区域。图 6是该地区实际资料的深度域速度(v_P)场，海底深度在1 km以上，海水速度1500 m/s，具有稳定的海底反射面，工区内发育强深水海底反射的长周期自由表面相关多次波和部分非规律层间多次波，海底鸣震十分明显，高速层间会产生较多的层间多次波，多次波压制处理对于提高该地区资料品质起着至关重要的作用。图 7所示的记录共200炮，每炮301道，道距是12.5 m，最小炮检距为125 m，最大炮检距约为3600 m，记录时间为6 s，采样间隔为4 ms。

图 7a是含多次波单炮记录，其中箭头所指2.8和4.4 s附近强能量同相轴就是高频多次反射波。每个单炮二维图像横纵向尺度是300×1000，由于相邻炮间多次波具有类似的特征，每隔10炮选1炮制作标签数据，利用常规处理手段得到多次波压制后的标签数据如图 7b所示，大部分多次波能够被较好的压制，但由于拖揽漂移等问题，仍有一些残留。在训练过程中，需要4.14 GB内存，设置800个Epoch，每个Epoch的计算时间为64.7 s，总训练时间约为14 h，准确率高达99%。图 7c为应用常规CNN卷积神经网络衰减多次波后的单炮记录，与图 7b所示的标签结果相比，效果相当。图 7d是应用本文基于自注意力机制的对抗网络衰减多次波后的单炮记录，与常规卷积神经网络结果相比(图 7c)，能够更加有效的压制多次反射波。图 8是图 7矩形框处的局部放大，可清楚看出，应用本文方法，多次波得到了更好地压制。

4 结论

多次波压制是陆地和海洋地震资料处理长期面临的难题，尤其是海洋地震资料处理，由于海水面和海底两个强波阻抗界面的影响，整个地震资料噪声衰减过程是围绕着多次波压制而开展。多次波类型复杂多样，尤其是小尺度火成岩发育区的多次波存在识别难和压制难的“两难”问题，工业处理中往往需要在不同域(炮域、CMP域和共炮检距域等)逐步压制，多域的转换和压制造成了误差累计，而且高密度采集的数据量多达几十个T，耗费大量的机时。利用人工智能深度学习的方法可以提高计算效率和精度，改善多次波压制处理的过程。模型和实际资料测试表明，本文提出的基于自注意力机制对抗网络的多次波压制方法能够提高多次波压制的效果和效率，为多次波压制处理提供了新的技术手段，得到以下结论。

(1) 标签获取仍然是基于深度学习算法的关键，也是制约智能技术在勘探地球物理领域应用的关键因素。利用工业化的处理手段，通过对少量具有代表性特征的数据处理获得多次波压制标签的方法是现有比较实用化的策略，其核心就是让深度学习的网络系统学习处理员的丰富经验。

(2) 网络结构对于多次波噪声压制是至关重要的。基础的网络结构一般实用的是DnCNN的残差网络结构，计算机领域提出了越来越多的网络类型，但是，并不是最新的网络结构就是最好的，需要根据实际资料的特点和应用的场景，测试出最适合的网络结构。

(3) 受制于标签制作、泛化性等影响，现有智能化的噪声压制方法还不能够完全替代传统工业化的多次波压制技术，需要在深度学习策略等方面持续开展研究，逐步提高智能化的多次波压制方法的高效性和泛化性。