2. 东方地球物理公司, 河北涿州 072750;
3. 中油奥博(成都)科技有限公司, 四川成都 610051
2. BGP Inc., CNPC, Zhuozhou, Heibei 072750, China;
3. Optical Science and Technology (Chengdu) Ltd., Chengdu, Sichuan 610051, China
地震波在地下介质中传播,能量会被地层吸收,造成地震波的振幅衰减、相位畸变,导致地震资料分辨率降低。研究[1-2]表明:与深部地层介质的吸收衰减效应相比,近地表介质对地震波高频成分的吸收约占地层吸收总量的80%[3],由于表层岩性、速度、厚度的横向变化,吸收衰减程度会有所不同,还会造成地震波道间能量、频率和相位的不一致,影响同相叠加结果的横向分辨率。因此,研究地下介质对地震波的吸收特性,对于改善地震资料分辨率、油气地球物理属性反演和储层描述等有着重要的意义[4-5]。
地层品质因子Q值可定量刻画地震波在黏弹性介质中的能量吸收和速度频散[6],准确求取近地表Q值再进行反Q滤波补偿可有效消除表层地震波吸收衰减的影响,实现波形保真保幅并提高分辨率的效果。其中的关键是如何获得准确的近地表Q值和Q模型。
对于表层Q值求取及建模方法,很多学者进行了研究。于承业等[7]利用双井微测井资料,通过建立和求解地面和井下检波器的峰值频率方程组,求得近地表Q值的解析解;裴江云等[8]利用地震数据中不同类型的波场进行近地表Q反演;李国发等[9]采用井—地联合观测方式就近地表吸收结构进行了实验分析,提出了不受激发因素影响的吸收参数层析反演方法;肖永新等[10]提出了利用双井微测井高速层中多个炮点的数据,通过拟合方法得到精确的近地表Q值;李伟娜等[11]基于微测井资料发展了双线性回归稳定Q估计方法,取得了较好的效果;李拥军等[12]提出了一种复数域快速匹配追踪分解并结合对数谱比法估算微测井数据近地表Q值的方法;许李囡等[13]提出了一种基于S变换和变分法提取品质因子的方法,克服了Q值计算对地震子波类型及窗函数长度的依赖。以上均是基于Q值求取进行的研究。宋吉杰等[14]提出基于信息融合的近地表介质Q估计方法,利用多井微测井和地面联合的观测系统,通过统计反演估算全区Q值[15];苏勤等[16]引入表层相对衰减系数的概念,在共炮检域迭代计算相对衰减系数,进而求取表层Q模型;马凯等[17]采用双井微测井获取的绝对Q值和频移法计算的相对Q值,建立了准确的Q场并进行Q补偿,获得了良好的效果。以上方法都利用了微测井和地面地震数据,但都是先得到相对Q值,通过标定和插值得到最终表层Q模型,该表层Q模型具有横向空间变化,但缺少纵向时间变化。
为提高近地表Q建模精度,本文针对四川盆地近地表厚度较薄的特点,提出了一种结合单、双微测井及地面地震数据信息进行近地表Q建模的方法。首先,对于单井微测井数据,本文提出了一种改进的谱比法进行Q值计算,通过构造统计子波谱,消除子波效应,提高了计算结果的稳定性;然后拟合Q与速度v的关系,将层析反演得到的近地表速度场转换成Q场,从而得到一个时空变的Q场。由于层析反演的近地表速度场深度采样间隔为10 m,难以反映近地表几米厚的表层变化。为此结合双井微测井的多炮拟合算法,计算表层绝对Q值,再结合表层速度模型和地面地震振幅及走时信息计算相对Q场,用绝对Q值对其标定,得到表层等效的平面Q场。将该表层平面Q场镶嵌在用Q⁃V拟合关系转成的近地表Q场的浅层,得到该工区最终的近地表Q场。最后对工区内的地震数据进行表层Q补偿,消除了近地表对地震资料的影响,提高了地震资料的分辨率。
1 近地表Q场计算方法及实现步骤 1.1 改进的谱比法求Q值首先处理单井微测井于井下的12级检波器采集的数据。对该数据进行初至拾取,通过波场分离得到下行波,选取子波时窗范围内的数据,对每道数据进行傅里叶变换,求取每道频谱对数谱的截距和斜率,根据截距和斜率将每道的对数谱拉平,将下行波对数谱叠加求取未衰减的拟下行子波谱,利用各道对数谱减去拟下行子波谱,得到初步消除子波影响的各道对数谱。在此基础上求取每道对数谱的斜率,对其进行平滑拟合,保证斜率值随深度的增加而增大,再利用平滑后的斜率和初至求取等效Q,再根据等效Q与层Q的关系,求取层Q值。通过以上步骤求取的Q可用于后续的反Q滤波,以获得高分辨率的剖面成果。
依据该方法,首先进行模型试算。设计一个5层的水平层状模型(表 1),激发子波为Ricker子波,主频为50 Hz,检波器的深度范围为120~1660 m,检波点间隔为20 m,井源距为0,垂直入射,正演含Q值衰减的下行波记录。从正演的下行波记录(图 1)可以看出,随着深度的增加,振幅能量发生衰减,相位改变,子波波形变胖,从记录的频谱上也可以看出,振幅能量减弱,主频降低,频带变窄。
|
|
表 1 地层模型 |

|
图 1 含Q衰减的下行波正演模拟记录(左)及其频谱(右) |
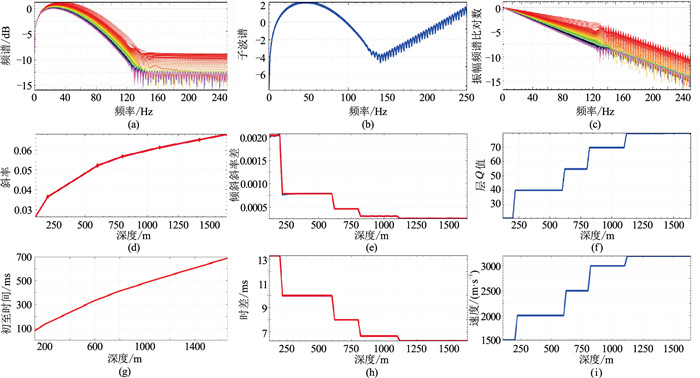
图 2展示了改进谱比法Q值求取的过程。图 2a是图 1中下行子波记录的振幅谱对数谱,选择两个频率点,一般选择主频和高频点的位置,将每道振幅谱对数按照该斜率拉平,然后多道数据进行叠加平均,得到拟下行子波的频谱(图 2b)。然后将每道的振幅谱与拟下行子波频谱进行谱比,得到谱比曲线(图 2c)。在单调递减的频率段上,计算每道数据的斜率,绘出斜率随深度变化的关系(图 2d),斜率值应该随深度的增加而增加。其中斜率
|
图 2 Q值求取过程 (a)每道记录的频谱;(b)拟下行子波谱;(c)每道的谱比曲线;(d)斜率值;(e)相邻道的斜率差;(f)层Q值;(g)初至时间;(h)相邻道间的时差;(i)层速度 |
| $ \frac{{t}_{n}-{t}_{n-1}}{{Q}_{\mathrm{i}\mathrm{n}\mathrm{t}}}=\frac{{t}_{n}}{{Q}_{\mathrm{e}\mathrm{f}\mathrm{f},n}}-\frac{{t}_{n-1}}{{Q}_{\mathrm{e}\mathrm{f}\mathrm{f},n-1}} $ | (1) |
由(1)式可以推出
| $ {Q}_{\mathrm{i}\mathrm{n}\mathrm{t}}=\frac{{t}_{n}-{t}_{n-1}}{\frac{{G}_{n}}{\mathrm{\pi }}-\frac{{G}_{n-1}}{\mathrm{\pi }}} $ | (2) |
即层Q值等于相邻道间的时差除以相邻道间的斜率差,初至时间和斜率必须是随深度递增的,才能保证计算的Q值没有负值。图 2e是模型数据相邻道间的斜率差,可以看出,同一地层的斜率差相等,图 2f是根据式(2)计算的层Q值。
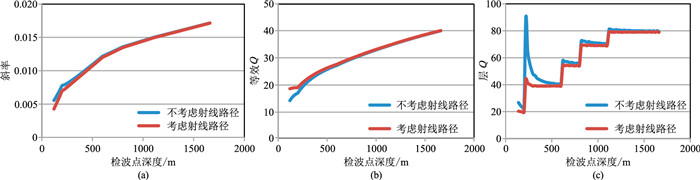
模型试算的数据考虑的是垂直入射的情况,当炮检距为非零时,需要考虑对射线路径进行校正,将初至时间和斜率校正到垂直入射的情况,才能得到正确的解。如图 3所示,可以看出不考虑射线路径校正时,特别是在分界面位置存在较明显的抖动,浅层计算结果与真实值差距较大,但对深层结果影响较小。当考虑射线路径进行校正后,可以得到正确Q值解。
|
图 3 考虑射线路径和不考虑射线路径计算的斜率、等效Q和层Q值的对比图 |
对实际单井微测井数据进行试算。此次单井微测井数据,选用12级检波器同时接收的记录,保证了激发子波的一致性,同时12级检波器已覆盖表层,计算结果能够反应表层的Q值。具体做法如下:
(1) 井中检波器接收,地面利用爆炸震源或重锤在近井口激发,多级检波器同时采集数据,保证了激发子波的一致性。
(2) 对接收数据进行预处理,剔除坏道,经过拾取纵波初至和上下行波分离处理,得到预处理后下行纵波数据和纵波初至时间。
(3) 利用步骤(2)中所得到的数据,截取出下行子波数据,对每道数据进行FFT变换,得到每道数据的对数频谱,即对FFT变换后的振幅谱取对数。
(4) 取频谱中的峰值频率和高截频,计算每道对数频谱的斜率和截距。
(5) 对每道的对数频谱按照步骤(4)中的斜率和截距进行拉平处理,并进行叠加,得到初始下行子波的对数频谱。
(6) 每道下行波对数频谱减去步骤(5)的下行子波对数谱,得到去除下行子波影响的下行子波对数频谱。
(7) 在峰值频率和高截频范围内,做线性拟合,拟合的斜率可以计算该道数据对应的等效Q值,
(8) 利用式(2)求第n层的层Q参数,即可得到每个深度点的层Q值。
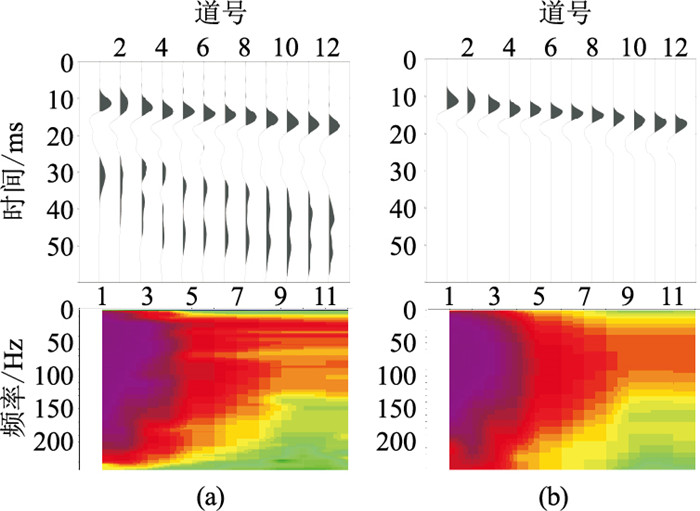
下面进行实际单井微测井数据的Q值估算。图 4a是实际单井微测井数据及其振幅谱,图 4b是截取的微测井的初至子波及其频谱,由图可见,随着检波点深度的增加,频带逐渐变窄。利用截取的子波数据来进行Q值的估算。
|
图 4 微测井数据(上)及其振幅谱(下) (a)原始微测井数据及其振幅谱;(b)下行子波数据及其振幅谱 |
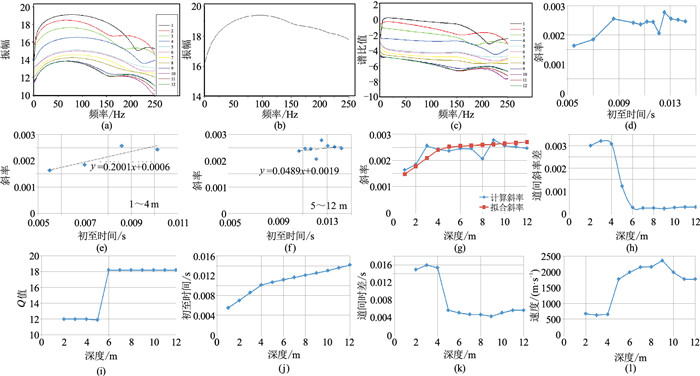
图 5是实际的单井微测井数据估算Q值的过程图。图 5a是每道下行子波的经傅里叶变换的振幅谱取对数的曲线;图 5b是统计平均得到的拟下行子波的振幅对数谱;图 5c是每道数据的振幅谱与统计子波谱的谱比曲线,选择频段范围,每一道的谱比曲线可以求得一个斜率;图 5d是每道数据的初至和斜率交会图。由于计算的斜率与初至的关系不一定是单调递增的,可以按照微测井解释成果的层位,进行拟合平滑,保证层位内的斜率是单调递增,从而保证结果的稳定性。图 5e是按照微测井分层的第一层, 得到的斜率与时间的拟合关系;图 5f是按照微测井分层第二层,得到的的斜率与时间的拟合关系;图 5g是拟合后的斜率与计算的斜率的对比图,拟合后的斜率与图 5j每道数据的初至时间存在对应关系;图 5h相邻道间斜率差和图 5k相邻道间时差也存在对应关系。由斜率差可得出图 5i层Q值;由初至时差可得出图 5l层速度。因此可见,层Q值与层速度间存在着一定的对应关系。
|
图 5 实际微测井资料Q值估算 (a)每道下行子波的振幅对数谱曲线;(b)拟下行子波的振幅对数谱;(c)每道数据的谱比曲线;(d)每道数据的初至和斜率交会图;(e)第一层的斜率与时间的拟合关系;(f)第二层的斜率与时间的拟合关系;(g)拟合后的斜率与计算的斜率;(h)相邻道间斜率差;(i)层Q值;(j)每道数据的初至时间;(k)相邻道间时差;(l)层速度 |
采用肖永新等[10]提出的多炮拟合算法,利用双井微测井资料计算表层Q值。双井微测井调查方法以两口浅井开展,一口为激发井,一口为接收井。具体做法是:将地层看成表层和高速层两层模型,选取高速层中某一炮的地面道和井底道数据,利用谱比法求取表层的等效Q值(
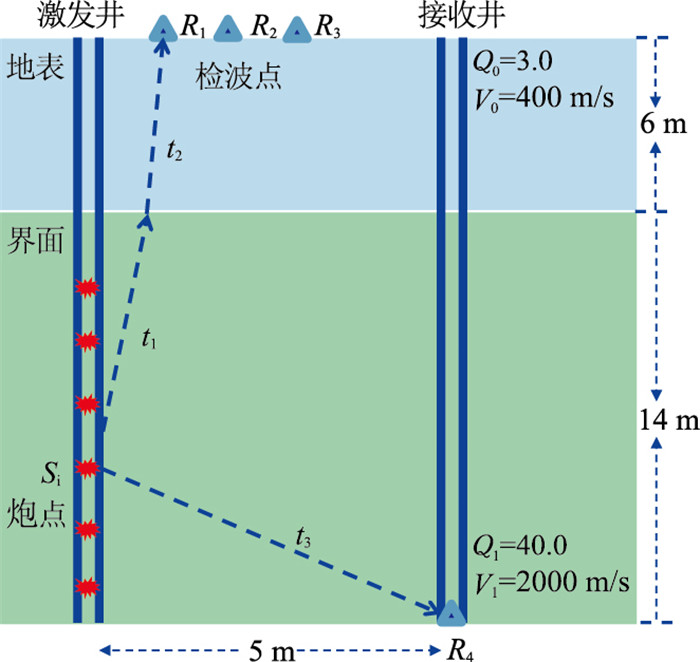
图 6为两层速度模型的双井微测井射线传播示意图。假设表层Q值为
|
图 6 两层模型双井微测井观测系统示意图 |
| $ \mathrm{l}\mathrm{n}\frac{{B}_{1}(f,{t}_{1}+{t}_{2})}{{B}_{4}(f,{t}_{3})}=C-\frac{\mathrm{\pi }f({t}_{1}-{t}_{3})}{{Q}_{1}}-\frac{\mathrm{\pi }f{t}_{2}}{{Q}_{0}} $ | (3) |
如果
| $ \mathrm{l}\mathrm{n}\frac{{B}_{1}(f,{t}_{1}+{t}_{2})}{{B}_{4}(f,{t}_{3})}=C-\frac{\mathrm{\pi }{t}_{2}}{{Q}_{0}}f $ | (4) |
式中:
实际野外施工过程中,很难提前知道满足t1-t3=0的激发点位置,所以不可能在该深度设置激发点,因此选取高速顶以下多个炮点进行表层Q值计算,然后再对多个不同深度炮点计算的表层Q值进行拟合,找到t1-t3=0位置时的Q值,即为该点的表层等效Q值,即为
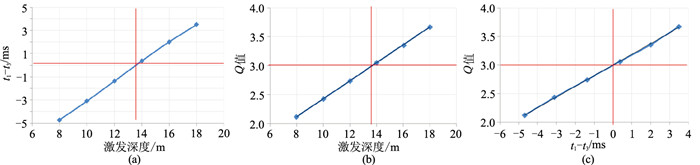
由图 7可知,随着激发点深度的增加,Q值逐渐增大,这里的Q值指的是该激发点深度位置以上地层的等效Q值(
|
图 7 激发深度-(t1-t3)-Q值曲线 (a)激发深度与(t1-t3);(b)激发深度与Q值;(c)(t1-t3)与Q值 |
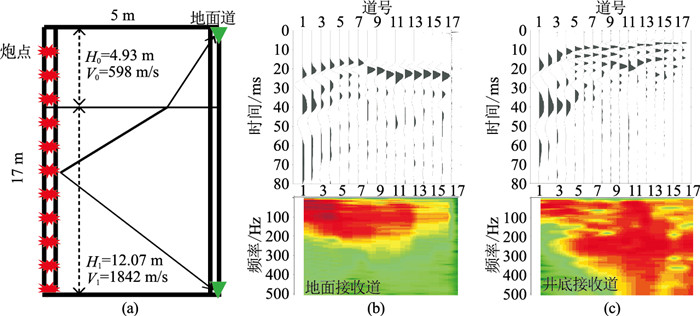
图 8a为四川盆地蓬莱气区内的一口双井微测井观测系统示意图及近地表结构图,图中红色点为炮点,绿色点为接收点。该双井微测井点井深17 m两口井之间的距离5 m;图 8右为该口双井微测井数据的地面接收道记录和井底接收道记录及其频谱。
|
图 8 双井微测井观测系统(a)及其地面接收道(b)和井底接收道(c)的记录(上)及频谱(下) |
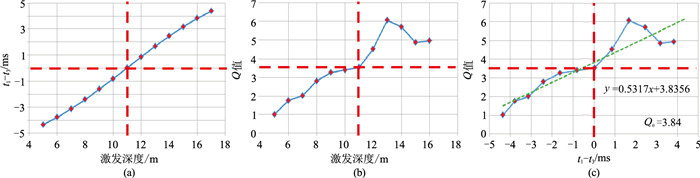
首先拾取地震数据的初至时间,通过常规的微测井解释方法获得近地表速度模型。然后根据近地表速度模型信息,选择高速层中的炮点,本例中,选择激发深度5~16 m的炮点(激发深度17 m处的地面接收点记录存在异常,已剔除)。选择高速顶之下的每一炮的一个地面接收道和井底接收道,每一炮的地面道和井底道采用常规谱比法计算该炮点深度位置以上的等效Q值。根据图 8所示近地表速度模型进行射线追踪,得到每炮地面道和井底道的射线路径,及每一段射线的传播时间。计算每一炮的地面道和井底道在高速层中的传播时间差,即t1-t3。Q值与t1-t3的关系如图 9右所示,多项式拟合t1-t3和Q值,当t1-t3=0时的Q值即为所求
|
图 9 实际双井微测井数据激发深度-(t1-t3)-Q值关系 (a)激发深度与(t1-t3);(b)激发深度与Q值;(c)(t1-t3)与Q值 |
采用地面地震的地表一致性振幅补偿相对系数和表层旅行时,通过谱比法求取表层相对Q场。此时求得的相对Q场也是将表层看作一个等效地层。再用双井微测井的计算出的Q值进行标定,得到最终的表层平面Q场。将双井微测井求得的Q值称为绝对Q值,将地面地震振幅信息求得的Q场称为相对Q场,然后用绝对Q值对相对Q场进行约束,采用反距离加权内插法[18]对相对Q场进行标定。基于谱比法求相对Q值
| $ R\times \mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}=\frac{A\left(f\right)}{{A}_{0}\left(f\right)}={\mathrm{e}}^{-\frac{\mathrm{\pi }ft}{Q}} $ | (5) |
对上式两边取对数,可转换成相对Q值的表达式
| $ Q=-\frac{\mathrm{\pi }ft}{\mathrm{l}\mathrm{n}\mathrm{ }(R\times \mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e})} $ | (6) |
式中:
计算步骤:①由地表一致性振幅补偿模块做振幅相对系数的计算,沿初至开小窗;②导出文本,利用相对Q值的表达式,求解相对Q场;③再用双井微测井计算的Q值进行标定,可以求出平面Q场。平面Q场的建立流程如图 10。
|
图 10 平面Q场建立流程 |
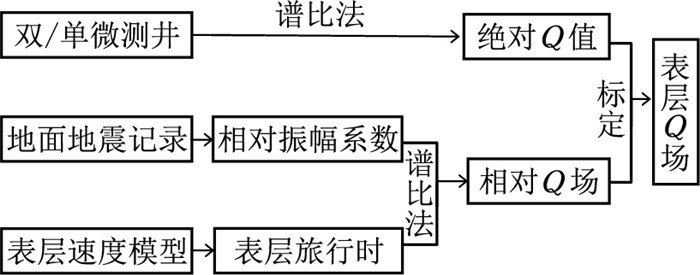
图 11展示了工区实际表层平面Q场的建立过程。由图 11a的表层旅行时和图 11b的相对振幅系数,利用相对Q值的式(6),求解相对Q场(图 11c);再用单、双井微测井计算的表层Q值插值成平面的Q场(图 11d),对计算的相对Q场采用反距离加权内插方法进行约束,可以求出等效的平面Q场(图 11e)。
|
图 11 实际工区平面等效Q场的求取过程 (a)表层旅行时;(b)相对振幅系数;(c)计算的相对Q场;(d)Q控制点插值;(e)控制点标定 |
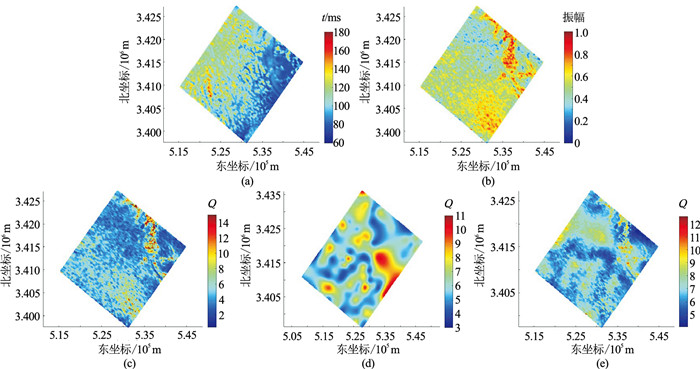
根据实际的单井微测井资料得到速度和Q值的拟合关系,利用该拟合关系,将层析反演得到的近地表速度场转换成Q场(图 12)。由于层析反演的近地表速度场的深度采样间隔为10 m,而该工区的微测井解释成果中,表层厚度较小,一般为2~8 m,表层反演的速度较微测井实测速度要大,所以速度场转换的Q场不能反应表层真正的Q值,所以将双井微测井结合地面地震信息求取的表层平面Q场镶嵌在由Q⁃V关系转换后的近地表Q场的表层,得到最终的近地表Q场(图 13)。
|
图 12 立体Q场建模 (a)近地表速度模型;(b)Q⁃V拟合关系;(c)近地表Q场 |

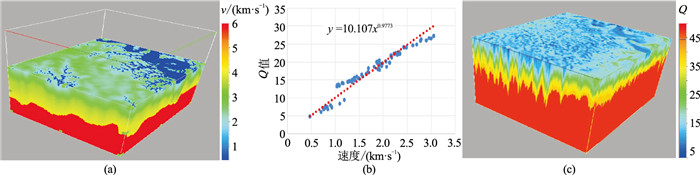
|
图 13 平面等效Q场与三维立体Q场融合 (a)平面等效Q场;(b)根据Q⁃V关系转换的近地表Q场;(c)融合后的近地表Q场 |
为了能恢复工区复杂地表情况所导致的振幅能量衰减和相位畸变等情况,将工区近地表综合调查微测井资料和地面地震资料综合运用,进行近地表Q补偿,具体步骤如下:
(1) 利用工区近地表微测井资料求取表层的绝对Q值,双井微测井资料利用多炮拟合法可求取表层薄层的Q值,单井微测井资料利用改进的谱比法求Q值,进而可得到表层速度和Q值的关系;
(2) 根据地震资料计算各个检波点响应的相对振幅系数和近地表层析反演的表层旅行时,通过谱比法计算出相对Q值;
(3) 用求取的绝对Q值来标定相对Q值,进而获得优化后的表层平面Q场;
(4) 对于表层以下到高速顶处的降速带部分,采用步骤(1)得到的Q⁃V拟合关系,将近地表速度场转换成Q场;
(5) 将优化后的表层平面Q场镶嵌在Q⁃V关系转换后的Q体的表层;
(6) 利用求取的优化Q场,使用稳定因子的Q补偿算法对工区实际地震数据体进行Q补偿处理,具体补偿效果详见后面内容。
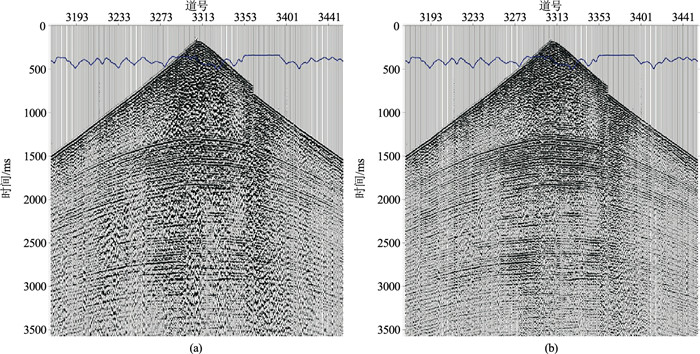
通过使用上文所提及的方法对工区进行Q补偿处理,对比分析Q补偿前、后的地震数据的一致性、分辨率和频谱特征。图 14为近地表Q补偿前、后的单炮记录对比图,可见Q补偿后的单炮记录同相轴更细,横向连续性得以改善,子波一致性更好。
|
图 14 近地表Q补偿前(a)、后(b)的单炮记录对比 |
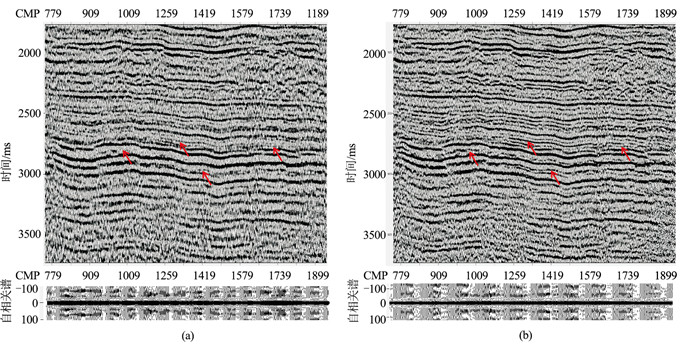
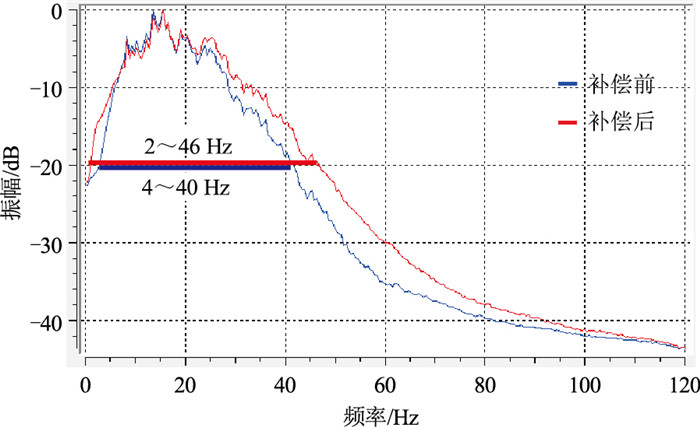
由于本文涉及的工区低降速带厚度较小,表层起伏,使得不同位置处的子波波形存在差异。如图 15所示,经过近地表Q补偿后,地震剖面的分辨率得到了提高,部分小细轴得到了恢复,从自相关记录上可以看出,子波的横向一致性得到了改善,从频谱图上可以看出,应用近地表Q补偿后,频带拓宽6 Hz左右(图 16)。
|
图 15 近地表Q补偿前(a)、后(b)的剖面(上)及自相关谱(下) |
|
图 16 近地表Q补偿前、后的频谱 |
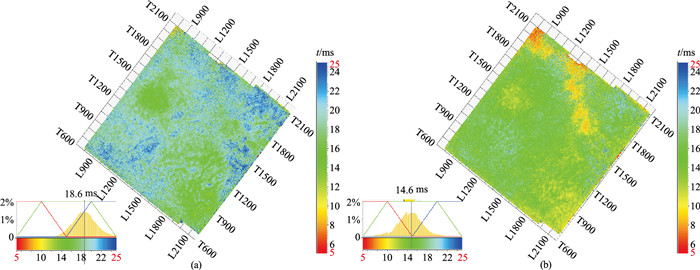
对近地表Q补偿前、后的地震剖面的第一零交叉时平面属性进行质控,如图 17所示,可以看出,应用近地表Q补偿后,第一零交叉时的值变小,说明子波得到了压缩,而且从整个工区的平面图上可以看出,应用近地表Q补偿后,第一零交叉时的变化趋于一致,说明子波一致性变好。
|
图 17 近地表Q补偿前(a)、后(b)的第一零交叉时平面属性图 |
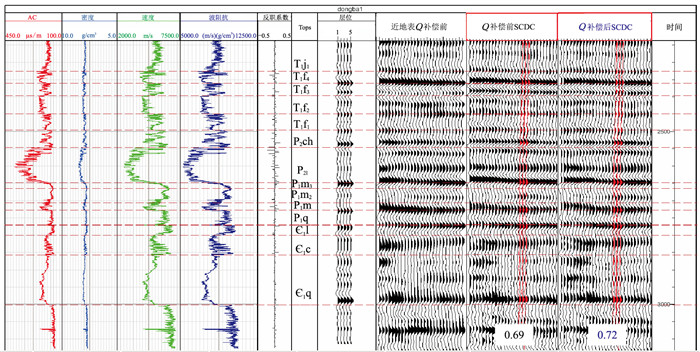
将近地表Q补偿前、后的地震记录与合成记录进行井震标定,可以看出,应用近地表Q补偿后的地震记录与合成记录的相关系数是0.72,高于没有应用近地表Q补偿的地震记录与合成记录的相关系数,(图 18)。
|
图 18 地表Q补偿前、后地表一致性反褶积标定分析 |
利用单井微测井资料,采用改进的谱比法,计算Q值,然后拟合Q⁃V关系,可以很好地将层析反演出的降速带的速度场转换成Q场。利用双井微测井资料,采用多炮拟合的算法,计算井点位置处的绝对Q值,再结合地面地震的振幅和走时信息计算相对Q场,再利用绝对Q值对相对Q场进行标定,可以得到表层低速带的等效平面Q场。由于该工区表层厚度较薄,一般为2~8 m,而层析反演的速度场的采样间隔是10 m,很难将小于10 m的低速带反应出来。所以,将标定后的表层平面Q场镶嵌在由Q⁃V关系转换的近地表Q场的浅表层,得到最终的近地表Q场。然后应用此Q场,对地面地震资料进行近地表Q补偿,可以有效消除近地表对地震资料的吸收衰减影响,改善子波的一致性,有效拓宽地震资料的频带,提高资料的分辨率。
| [1] |
王建民, 陈树民, 苏茂鑫, 等. 近地表高频补偿技术在三维地震勘探中的应用研究[J]. 地球物理学报, 2007, 50(6): 1837-1843. WANG Jianmin, CHEN Shumin, SU Maoxin, et al. A study of the near surface high⁃frequency compensation technology in 3⁃D seismic exploration[J]. Chinese Journal of Geophysics, 2007, 50(6): 1837-1843. |
| [2] |
石战结, 田钢. 西部大沙漠区近地表地震波衰减及高频补偿技术研究[J]. 石油地球物理勘探, 2007, 42(4): 392-395. SHI Zhanjie, TIAN Gang. Technique of attenuation of near⁃surface seismic wave and high⁃frequency compensation in western large desert area[J]. Oil Geophysical Prospecting, 2007, 42(4): 392-395. |
| [3] |
赵秋芳, 云美厚, 朱丽波, 等. 近地表Q值测试方法研究进展与展望[J]. 石油地球物理勘探, 2019, 54(6): 1397-1418. ZHAO Qiufang, YUN Meihou, ZHU Libo, et al. Progress and outlook of near⁃surface quality factor Q measurement and inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1397-1418. DOI:10.13810/j.cnki.issn.1000-7210.2019.06.026 |
| [4] |
马昭军, 刘洋. 地震波衰减反演研究综述[J]. 地球物理学进展, 2005, 20(4): 1074-1082. MA Zhaojun, LIU Yang. A summary of research on seismic attenuation[J]. Progress in Geophysics, 2005, 20(4): 1074-1082. DOI:10.3969/j.issn.1004-2903.2005.04.031 |
| [5] |
刘洋, 李向阳, 杨东方. 基于线性分解的解析信号法估算品质因子Q[J]. 石油地球物理勘探, 2018, 53(4): 784-790. LIU Yang, LI Xiangyang, YANG Dongfang. Quality factor Q estimation with complex trace analysis based on linear decomposition[J]. Oil Geophysical Prospec⁃ting, 2018, 53(4): 784-790. DOI:10.13810/j.cnki.issn.1000-7210.2018.04.016 |
| [6] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [7] |
于承业, 周志才. 利用双井微测井资料估算近地表Q值[J]. 石油地球物理勘探, 2011, 46(1): 89-92. YU Chengye, ZHOU Zhicai. Estimation of near surface Q value based on the datasets of the uphole survey in double hole[J]. Oil Geophysical Prospecting, 2011, 46(1): 89-92. |
| [8] |
裴江云, 陈树民, 刘振宽, 等. 近地表Q值求取及振幅补偿[J]. 地球物理学进展, 2001, 16(4): 18-22. PEI Jiangyun, CHEN Shumin, LIU Zhenkuan, et al. Near surface Q value extraction and amplitude compensation[J]. Progress in Geophysics, 2001, 16(4): 18-22. |
| [9] |
LI G F, ZHENG H, ZHU W, et al. Tomographic inversion of near⁃surface Q factor by combining and cross⁃hole seismic surveys[J]. Applied Geophysics, 13: 93-102. |
| [10] |
肖永新, 徐丽军, 吴蔚, 等. 一种多炮拟合近地表Q值计算方法[C]. 2021油气田勘探与开发国际会议(IFEDC2021)论文集, 青岛, 2021, 1⁃9. XIAO Yongxin, XU Lijun, WU Wei, et al. A calculation method of near surface Q value by multi shots fitting[C]. 2021 International Conference on Oil and Gas Field Exploration and Development (IFEDC2021) Proceedings, Qingdao, 2021, 1⁃9. |
| [11] |
李伟娜, 云美厚, 党鹏飞, 等. 基于微测井资料的双线性回归稳定Q估计[J]. 石油物探, 2017, 56(4): 483-490. LI Weina, YUN Meihou, DANG Pengfei, et al. Stability Q estimation by dual linear regression based on uphole survey data[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 483-490. |
| [12] |
李拥军, 宋炜, 唐传章, 等. 复数域匹配追踪近地表Q值估计及深度学习建模[J]. 石油物探, 2021, 60(1): 123-135. LI Yongjun, SONG Wei, TANG Chuanzhang, et al. Complex domain⁃matching pursuit for near⁃surface Q⁃estimate and deep learning modeling[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 123-135. |
| [13] |
许李囡, 高静怀, 杨阳, 等. 基于S变换和变分法的品质因子Q估计方法[J]. 石油地球物理勘探, 2022, 57(1): 82-90. XU Li'nan, GAO Jinghuai, YANG Yang, et al. Qua⁃lity factor Q estimation based on S transform andvariationalmethod[J]. Oil Geophysical Prospecting, 2022, 57(1): 82-90. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.009 |
| [14] |
宋吉杰, 禹金营, 王成, 等. 近地表介质Q估计及其在塔河北部油田的应用[J]. 石油物探, 2018, 57(3): 436-442. SONG Jijie, YU Jinying, WANG Cheng, et al. Q estimation for near⁃surface media and its application in the Northern Tahe Oilfield, China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 436-442. |
| [15] |
赵忠华. 面向粘滞声学介质叠前吸收补偿偏移的等效Q值模型建立——以松辽盆地北部为例[J]. 石油物探, 2022, 61(5): 801-811. ZHAO Zhonghua. Establishment of equivalent Q⁃model for pre⁃stack absorption compensation migration in viscous acoustic media—A case study in Northern Songliao Basin[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 801-811. |
| [16] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near⁃surface Q value estimation and quantitative amplitude compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. DOI:10.13810/j.cnki.issn.1000-7210.2019.05.006 |
| [17] |
马凯, 彭玉林, 张欣吉, 等. 近地表Q补偿技术在准噶尔盆地南缘山前带的应用[J]. 石油地球物理勘探, 2022, 57(增刊1): 1-5. MA Kai, PENG Yulin, ZHANG Xinji, et al. Application of near⁃surface Q compensation technology in piedmont zone of southern margin of Junggar Basin[J]. Oil Geophysical Prospecting, 2022, 57(S1): 1-5. DOI:10.13810/j.cnki.issn.1000-7210.2022.S1.001 |
| [18] |
何立恒, 鲍其胜, 王庆. 基于反距离夹角加权算法的地理信息空间插值内插[J]. 测绘通报, 2014(1): 33-36. HE Liheng, BAO Qisheng, WANG Qing. Geographic information spatial interpolation methods based on the weighted algorithm of inverse distance and Angle[J]. Bulletin of Surveying and Mapping, 2014(1): 33-36. |



 王静, 河北省涿州市甲秀路东安小区新兴物探开发处,072750。Email:
王静, 河北省涿州市甲秀路东安小区新兴物探开发处,072750。Email: