2. 四川大学数学学院, 四川成都 610064;
3. 西北大学地质学系大陆动力学国家重点实验室, 陕西西安 710069
2. School of Mathematics, Sichuan University, Chengdu, Sichuan 610064, China;
3. State Key Laboratory of Continental Dynamics, Department of Geology, Northwest University, Xi'an, Shaanxi 710069, China
地震信号的时—频表示(TFR)在地震数据处理和解释中得到广泛应用,如时—频域去噪[1-2]、油气储层识别与储层描述[3-4]等,因此,TFR方法研发一直受到业界的重视[5-8]。基于傅里叶变换(FT)导出了一系列时频分析方法,如短时傅里叶变换(STFT)、连续小波变换(CWT)、S变换(ST)以及各种广义S变换(GST)[9-15]。ST的时间窗是频率的函数,其时—频谱的时间分辨率依赖于频率[11]。GST能够优化频率依赖性,但没有通用的优化标准分析窗函数,需要根据具体应用调节窗函数[4, 15]。在上述TFR方法中,ST在有效性与计算效率之间具有好的平衡,已被广泛用于储层描述,但存在以下不足:①时—频谱的能量分布中心不在地震波主频处,而向高频方向偏移;②时—频谱的高频时间分辨率较高、低频时间分辨率较低;③在数值计算时奇异频率引起不稳定现象。上述不足导致ST时—频谱不能表示地震属性随深度的变化,而且较低的低频时间分辨率也不适合储层识别,因为低频振幅异常往往是油气储层的标志[16-19]。由于地震波通过储层时高频能量被吸收[20],因此地震记录低频阴影区的能量分布可指示储层分布。
W变换(WT)[21]是近年来提出的一种新时—频分析技术,它克服了ST的不足,其时—频谱的能量集中在地震波主频附近,而且提高了低频时间分辨率,适合于储层描述。Li等[3]注意到WT的时—频谱在主频处出现振幅分裂现象,这是由WT的标准偏差函数在主频处的奇异性(不可微)所致;为此,设计了一种新的变频高斯标准偏差函数,具有主频的双参数多元复合指数形式,通过引入趋势因子p,获得了更光滑、更灵活的窗函数,得到广义WT(GWT)。由于新的标准偏差函数在主频处是可微的,消除了WT的时—频谱在主频处的振幅分裂现象,时—频谱的能量集中在主频附近,GWT提供了更好的TFR性能。随后,Chen等[4]又在GWT中增加了一个标量因子,提出三参数WT(TPWT),可更灵活地调节时—频分辨率。TPWT是分析非平稳信号的有效工具,已成功用于油气储层识别。然而,前人没有详细论述TPWT的可逆性。为此,本文研究了TPWT的可逆性,首先从理论上证明TPWT不是严格可逆的,而是一种近似可逆的变换工具。合成地震数据与实际地震记录的数值计算展示了TPWT逆变换的重建精度,所做工作为TPWT的合理应用提供了参考。
1 TPWT数学理论 1.1 WT地震记录
| $ W(\tau ,f)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x\left(t\right){g}_{\sigma }\left(t-\tau ,f;\tau \right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{i}2\mathrm{\pi }ft\right)\mathrm{d}t $ | (1) |
式中:
| $ {g}_{\sigma }(t,f;\tau )=\frac{1}{\sqrt[]{2\mathrm{\pi }}\sigma (\tau ,f;k)}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{t}^{2}}{2{\sigma }^{2}(\tau ,f;k)}\right] $ | (2) |
式中
| $ \sigma (\tau ,f;k)=\frac{k}{{f}_{0}\left(\tau \right)+\left|{f}_{0}\left(\tau \right)-f\right|} $ | (3) |
式中:k为标量因子;
| $ \sigma (\tau ,f;k)=\left\{\begin{array}{c}\begin{array}{cc}\frac{k}{f}& f > {f}_{0}\end{array}\\ \begin{array}{cc}\frac{k}{2{f}_{0}-f}& \begin{array}{c}\end{array}f\le {f}_{0}\end{array}\end{array}\right. $ | (4) |
| $ \frac{\partial \sigma(\tau, f ; k)}{\partial f}=\left\{\begin{array}{cl} -\frac{\sigma^2(\tau, f ; k)}{k} & f>f_0 \\ \text { 不存在 } & f=f_0 \\ \frac{\sigma^2(\tau, f ; k)}{k} & f<f_0 \end{array}\right. $ | (5) |
可见
把
| $ g_\sigma(t, f ; \tau)=\frac{1}{\sqrt{2 \pi} \sigma(\tau, f ; \boldsymbol{\varPhi})} \exp \left[-\frac{t^2}{2 \sigma^2(\tau, f ; \boldsymbol{\varPhi})}\right] $ | (6) |
则标准偏差函数定义为
| $ \sigma(\tau, f ; \boldsymbol{\varPhi})=\frac{1}{\sqrt[p]{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p}} $ | (7) |
式中
结合式(6)和式(7),得到TPWT[4]
| $ \begin{array}{l}\mathrm{T}\mathrm{P}\mathrm{W}\mathrm{T}(\tau ,f)\mathrm{ }=\frac{\sqrt[p]{{\left[\frac{{f}_{0}\left(\tau \right)}{{k}_{1}}\right]}^{p}+{\left[\frac{\left|{f}_{0}\left(\tau \right)\mathrm{ }-f\right|}{{k}_{2}}\right]}^{p}}}{\sqrt[]{2\mathrm{\pi }}}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x\left(t\right)\times \\ \\ \mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{(t-\tau )}^{2}}{2}{\left\{\sqrt[p]{{\left[\frac{{f}_{0}\left(\tau \right)}{{k}_{1}}\right]}^{p}+{\left[\frac{\left|{f}_{0}\left(\tau \right)\mathrm{ }-f\right|}{{k}_{2}}\right]}^{p}}\right\}}^{2}\right)\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{i}2\mathrm{\pi }f\right)\mathrm{d}t\end{array} $ | (8) |
不同参数的TPWT的表现形式不同:
(1)当
(2)当
(3)当
(4)当
式(7)可改写为
| $ \sigma(\tau, f ; \boldsymbol{\varPhi})= \begin{cases}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f-f_0(\tau)}{k_2}\right]^p\right\}^{-\frac{1}{p}} & f>f_0 \\ f_0(\tau) & f=f_0 \\ \left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f_0(\tau)-f}{k_2}\right]^p\right\}^{-\frac{1}{p}} & f<f_0\end{cases} $ | (9) |
| $ \begin{array}{l}\frac{\partial \sigma (\tau ,f;k)}{\partial f}=\\ \begin{cases}-\frac{\left[f-f_0(\tau)\right]^{p-1}}{k_2^p\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f-f_0(\tau)}{k_2}\right]^p\right\}^{\frac{1+p}{p}}} & f>f_0 \\ 0 & f=f_0 \\ \frac{\left[f_0(\tau)-f\right]^{p-1}}{k_2^p\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f_0(\tau)-f}{k_2}\right]^p\right\}^{\frac{1+p}{p}}} & f<f_0 \\ \end{cases}\end{array} $ | (10) |
可见
TPWT引入趋势因子
在理论上,TPWT的逆变换具有如下形式
| $ x\left(t\right)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\mathrm{T}\mathrm{P}\mathrm{W}\mathrm{T}(\tau ,f)\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{i}2\mathrm{\pi }ft\right)\mathrm{d}\tau \mathrm{d}f $ | (11) |
可分解为
| $ X\left(f\right)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\mathrm{T}\mathrm{P}\mathrm{W}\mathrm{T}(\tau ,f)\mathrm{d}\tau $ | (12) |
| $ x\left(t\right)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}X\left(f\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{i}2\mathrm{\pi }ft\right)\mathrm{d}f $ | (13) |
式(12)为无损可逆条件[13, 21],式(13)为傅里叶逆变换(IFT)。当且仅当式(12)和式(13)同时成立时,才能保证式(11)成立。由式(8)可知
| $ \begin{array}{l}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\mathrm{T}\mathrm{P}\mathrm{W}\mathrm{T}\left(\tau ,f\right)\mathrm{d}\tau ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\sqrt[p]{{\left[\frac{{f}_{0}\left(\tau \right)}{{k}_{1}}\right]}^{p}+{\left[\frac{\left|{f}_{0}\left(\tau \right)\mathrm{ }-f\right|}{{k}_{2}}\right]}^{p}}}{\sqrt[]{2\mathrm{\pi }}}\times \\ {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{(t-\tau )}^{2}}{2}{\left\{\sqrt[p]{{\left[\frac{{f}_{0}\left(\tau \right)}{{k}_{1}}\right]}^{p}+{\left[\frac{\left|{f}_{0}\left(\tau \right)\mathrm{ }-f\right|}{{k}_{2}}\right]}^{p}}\right\}}^{2}\right)\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{i}2\mathrm{\pi }ft\right)\mathrm{d}t\mathrm{d}\tau \\ ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\left\{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{1}{\sqrt[]{2\mathrm{\pi }}}{\left\{{\left[\frac{{f}_{0}\left(\tau \right)}{{k}_{1}}\right]}^{p}+{\left[\frac{\left|{f}_{0}\left(\tau \right)\mathrm{ }-f\right|}{{k}_{2}}\right]}^{p}\right\}}^{\frac{1}{p}}\right.\times \\ \left.\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{(\tau -t)}^{2}}{2}{\left\{{\left[\frac{{f}_{0}\left(\tau \right)}{{k}_{1}}\right]}^{p}+{\left[\frac{\left|{f}_{0}\left(\tau \right)-f\right|}{{k}_{2}}\right]}^{p}\right\}}^{\frac{2}{p}}\right)\mathrm{d}\tau \right\}\times \\ x\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{i}2\mathrm{\pi }ft\right)\mathrm{d}t\end{array} $ | (14) |
对比式(14)与式(12)可知
| $ \begin{aligned} & \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2 \pi}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{1}{p}} \times \\ & \exp \left(-\frac{(\tau-t)^2}{2}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{2}{p}} \mathrm{~d} \tau=1\right. \end{aligned} $ | (15) |
令
| $ \begin{aligned} & \mathrm{d} u=\frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{1}{p}} \mathrm{~d} \tau+ \\ & (\tau-t) \mathrm{d}\left(\frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{1}{p}}\right) \\ & =\left\{\begin{array}{l} \frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{1}{p}} \mathrm{~d} \tau+ \\ (\tau-t) \frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{1}{p}} \times \\ \left\{\frac{\left[f_0(\tau)\right]^{p-1}}{k_1^p}+\frac{\left[f_0(\tau)-f\right]^{p-1}}{k_2^p}\right\} f_0^{\prime}(\tau) \mathrm{d} \tau \quad f<f_0 \\ \frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f-f_0(\tau)}{k_2}\right]^p\right\}^{\frac{1}{p}} \mathrm{~d} \tau+ \\ (\tau-t) \frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f-f_0(\tau)}{k_2}\right]^p\right\}^{\frac{1}{p}} \times \\ \left\{\left[\frac{\left[f_0(\tau)\right]^{p-1}}{k_1^p}+\frac{\left[f-f_0(\tau)\right]^{p-1}}{k_2^p}\right\} f_0^{\prime}(\tau) \mathrm{d} \tau \quad f>f_0\right. \end{array}\right. \end{aligned}$ | (16) |
只有当
| $ \mathrm{d}u\approx \frac{1}{\sqrt[]{2}}{\left\{{\left[\frac{{f}_{0}\left(\tau \right)}{{k}_{1}}\right]}^{p}+{\left[\frac{\left|{f}_{0}\left(\tau \right)-f\right|}{{k}_{2}}\right]}^{p}\right\}}^{\frac{1}{p}}\mathrm{d}\tau $ | (17) |
时,才能得到
| $ \begin{aligned} & \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2 \pi}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{1}{\rho}} \times \\ & \exp \left(-\frac{(\tau-t)^2}{2}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{\left|f_0(\tau)-f\right|}{k_2}\right]^p\right\}^{\frac{2}{p}} \mathrm{~d} \tau\right. \\ & \approx \frac{1}{\sqrt{\pi}} \int_{-\infty}^{+\infty} \exp \left(-u^2\right) \mathrm{d} u=1 \end{aligned} $ | (18) |
此时,由式(14)可得
| $ \begin{aligned} & \int_{-\infty}^{+\infty} \operatorname{TPWT}(\tau, f) \mathrm{d} \tau \approx \int_{-\infty}^{+\infty} x(t) \exp (-\mathrm{i} 2 \pi f t) \mathrm{d} t \\ & \quad=X(f) \end{aligned} $ | (19) |
因此
| $ {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\mathrm{T}\mathrm{P}\mathrm{W}\mathrm{T}(\tau ,f)\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{i}2\mathrm{\pi }ft\right)\mathrm{d}\tau \mathrm{d}f\approx x\left(t\right) $ | (20) |
式(20)在理论上证明了TPWT并不是严格可逆的,而是一种近似可逆的变换工具,这是由于在定义高斯窗函数时使用了非平稳的频率权重所致。
比较式(16)和式(17)可知,在推导近似逆变换公式(式(20))的过程中引入了近似表达式(式(17)),而忽略了
| $ \begin{gathered} (\tau-t) \frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f_0(\tau)-f}{k_2}\right]^p\right\}^{\frac{1}{p}} \times \\ \left\{\frac{\left[f_0(\tau)\right]^{p-1}}{k_1^p}+\frac{\left[f_0(\tau)-f\right]^{p-1}}{k_2^p}\right\} f_0^{\prime}(\tau) \mathrm{d} \tau \quad f<f_0 \end{gathered} $ | (21) |
或
| $ \begin{gathered} (\tau-t) \frac{1}{\sqrt{2}}\left\{\left[\frac{f_0(\tau)}{k_1}\right]^p+\left[\frac{f-f_0(\tau)}{k_2}\right]^\rho\right\}^{\frac{1}{p}} \times \\ \left\{\frac{\left[f_0(\tau)\right]^{p-1}}{k_1^\rho}+\frac{\left[f-f_0(\tau)\right]^{p-1}}{k_2^\rho}\right\} f_0^{\prime}(\tau) \mathrm{d} \tau \quad f>f_0 \end{gathered} $ | (22) |
式(21)和式(22)均与
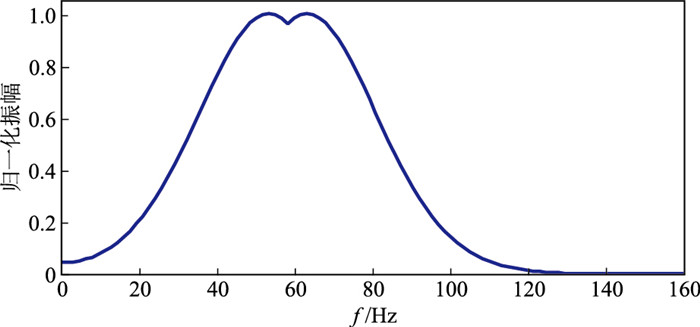
图 1为不同方法计算的主频为60 Hz的Morlet小波
|
图 1 不同方法计算的主频为60 Hz的Morlet小波 |
|
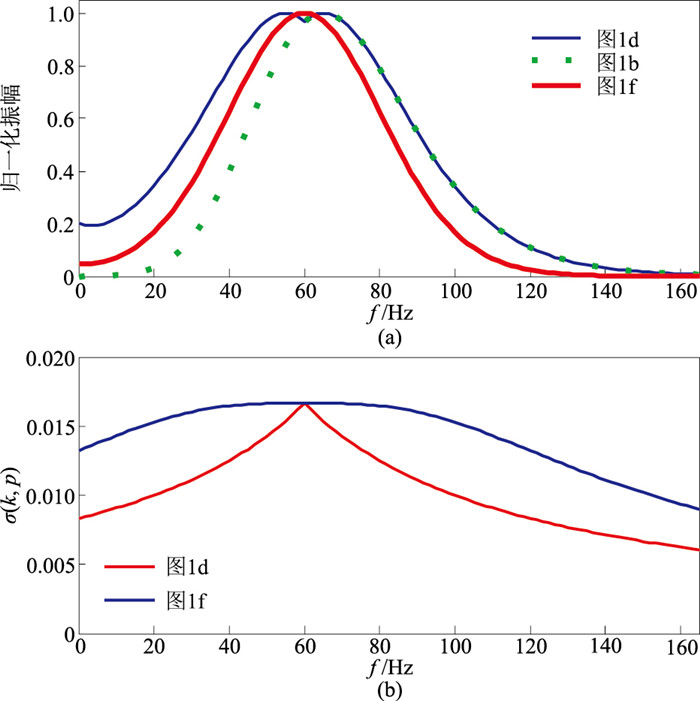
图 2 图 1e在0.4 s处的归一化振幅 |
|
图 3 图 1b、图 1d、图 1f在0.4 s处的归一化振幅(a)与图 1d、图 1f的标准偏差函数σ随频率的变化(b) |
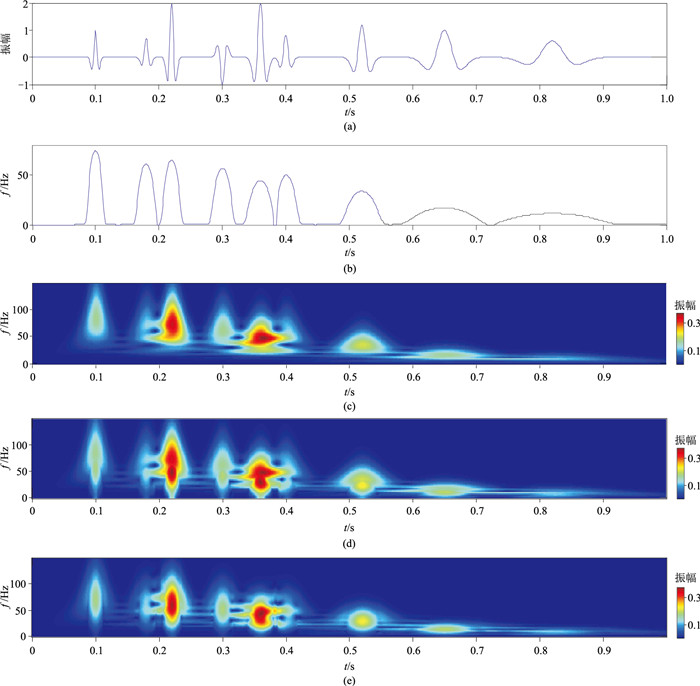
为了检验TPWT逆变换的近似程度,分别采用合成地震记录和实际地震数据进行分解与重构计算。首先,合成了一个地震记录
|
图 4 合成地震记录及其时—频谱 (a)合成地震记录;(b)图a的主频;(c)ST的时—频谱;(d)WT的时—频谱;(e)TPWT的时—频谱 |
|
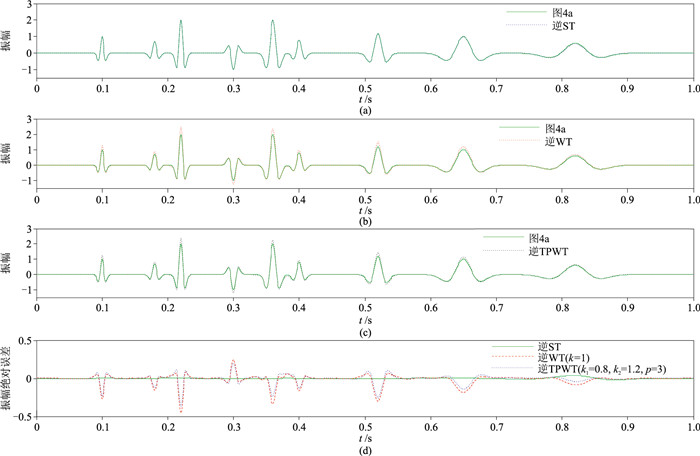
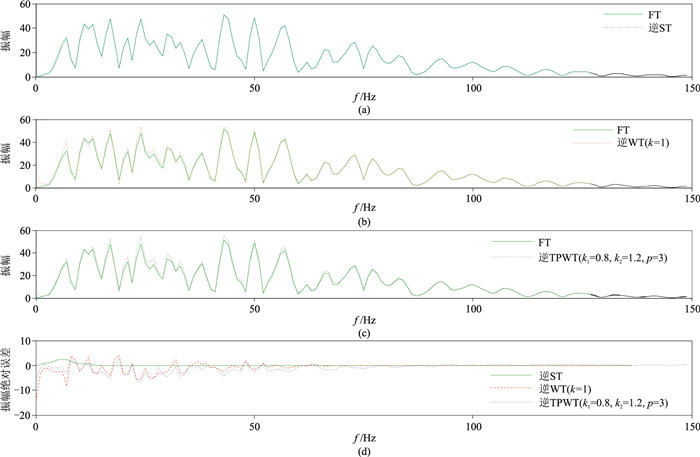
图 5 不同逆变换重建的振幅谱与标准傅里叶谱|X(f)|的对比 (a)逆ST;(b)逆WT;(c)逆TPWT;(d)图a、图b和图c与|X(f)|之差 |
|
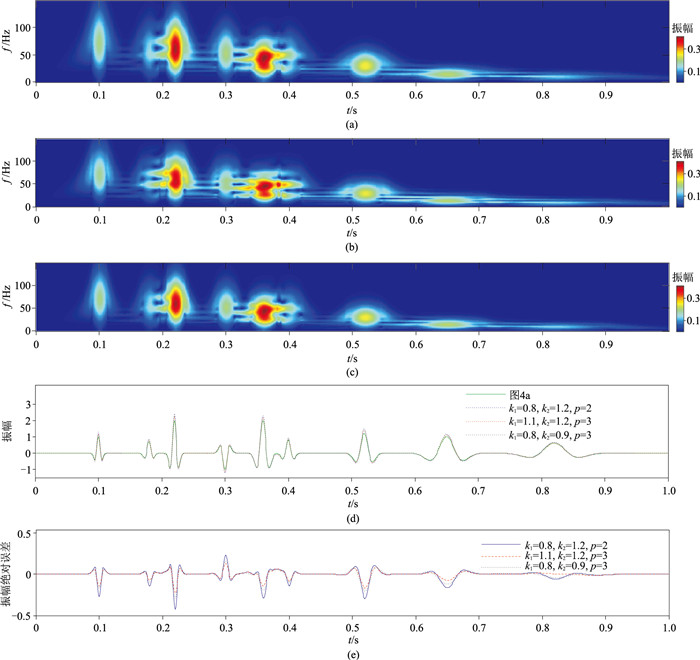
图 7 TPWT的时—频谱及其不同 |
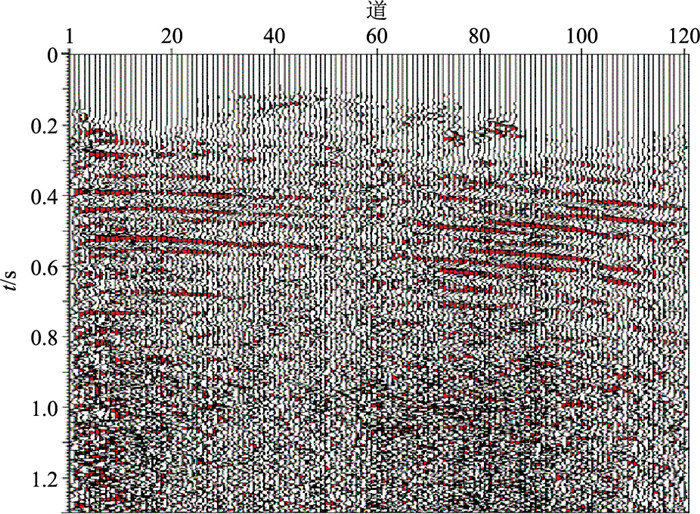
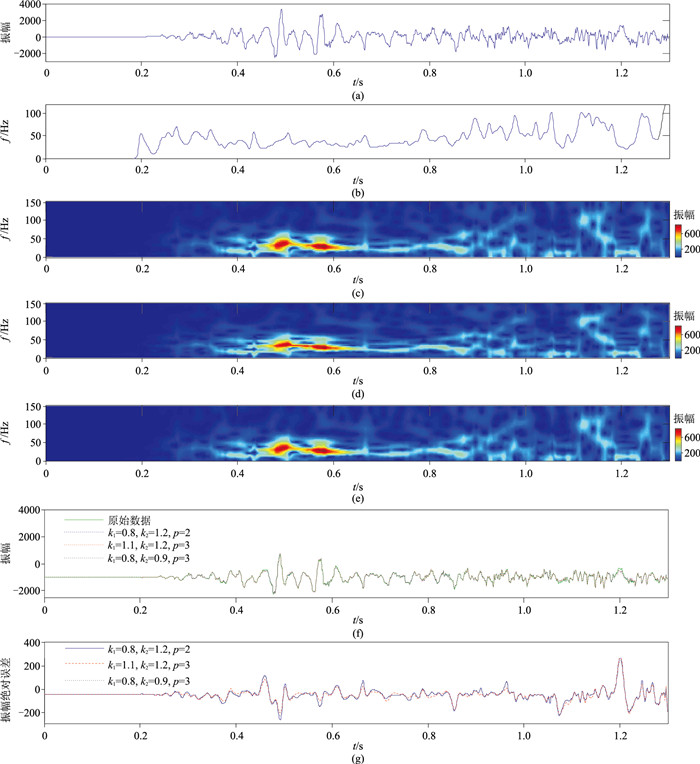
图 8为实际资料叠加剖面,随机抽取第95道(图 9a),利用复数道分析方法计算瞬时频率,再用一个低通滤波器通过加权平均消除数值噪声[21],从而获得主频(图 9b),最终得到不同变换参数的TPWT时—频谱(图 9c~图 9e)。可见,重建数据的最大振幅误差的绝对值分别为401.45、426.92、381.55,即相对误差分别为12.07%、12.83%、11.47%(图 9f、图 9g)。在上述数值计算中,相对误差最小值为11.47%,最大值为21.35%,即误差是明显的。因此,TPWT的不可逆导致其应用受到局限,在去噪、高分辨率处理等需要重建数据的处理领域不宜使用。
|
图 8 实际资料叠加剖面 |
|
图 9 图 8的第95道地震记录的时—频谱及重建地震记录 (a)图 8的第95道地震记录;(b)图a的主频;(c)TPWT的时—频谱(k1=0.8,k2=1.2,p=2);(d)TPWT的时—频谱(k1=1.1,k2=1.2,p=3);(e)TPWT的时—频谱(k1=0.8,k2=0.9,p=3);(f)逆TPWT重建的地震道;(g)图f与图a之差 |
(1)TPWT既解决了ST的低频时间分辨率低与时—频谱能量分布中心向高频偏移的问题,也克服了WT时—频谱在主频处的振幅分裂现象,能更准确地描述油气储层,更有利于地震解释。
(2)在理论上TPWT不是严格可逆的,而是一种近似可逆的变换工具,这与FT、ST不同。
(3)合成地震数据与实际地震记录的数值计算结果显示,与原始地震数据相比,利用逆TPWT重建地震道的相对误差为11.47%~21.35%,即理论上的不可逆导致较大的重建误差,严重影响TPWT的应用范围,在去噪、高分辨率处理等需要重建数据的处理领域不宜使用。
| [1] |
LIU B, LIU Q, KANG X. Application of improved time⁃frequency representation to local noise removal[J]. Journal of Petroleum Exploration and Production Technology, 2021, 11(5): 2091-2096. DOI:10.1007/s13202-021-01171-9 |
| [2] |
国胧予, 刘财, 刘洋. 滤波类方法衰减地震数据噪声[J]. 地球物理学进展, 2018, 33(5): 1890-1896. GUO Longyu, LIU Cai, LIU Yang. Filtering methods attenuate seismic data noise[J]. Progress in Geophy⁃sics, 2018, 33(5): 1890-1896. |
| [3] |
LI R, ZHU X, ZHOU Y, et al. Generalized W transform and its application in gas⁃bearing reservoir characterization[J]. IEEE Geoscience and Remote Sensing Letters, 2022. DOI:10.1109/LGRS.2021.3108836 |
| [4] |
CHEN H, PENG L, CHEN X, et al. A three⁃para⁃meter W transform and its application to gas reservoir identification[J]. Geophysics, 2022, 87(5): V521-V532. DOI:10.1190/geo2021-0803.1 |
| [5] |
李思源, 徐天吉. 基于Wigner⁃Ville分布与Chrip⁃Z变换的高分辨时频分析方法[J]. 石油地球物理勘探, 2022, 57(1): 168-175, 211. LI Siyuan, XU Tianji. A new high⁃resolution time⁃frequency analysis method based on Wigner⁃Ville distribution and Chirp⁃Z transform[J]. Oil Geophysical Prospecting, 2022, 57(1): 168-175, 211. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.018 |
| [6] |
郝亚炬, 张华, 张生, 等. 应用组稀疏正则化反演的高分辨率自适应Gabor时频分析方法[J]. 石油地球物理勘探, 2023, 58(2): 412-421. HAO Yaju, ZHANG Hua, ZHANG Sheng, et al. High⁃resolution self⁃adaptive Gabor time⁃frequency analysis method based on group⁃sparse regularized inversion[J]. Oil Geophysical Prospecting, 2023, 58(2): 412-421. DOI:10.13810/j.cnki.issn.1000-7210.2023.02.018 |
| [7] |
陆文凯, 张学工, 李衍达, 等. 时频域零炮检距地震道拟合[J]. 石油地球物理勘探, 2001, 36(1): 56-59, 71. LU Wenkai, ZHANG Xuegong, LI Yanda, et al. Fitting a zero⁃offset seismic trace in time⁃frequency domain[J]. Oil Geophysical Prospecting, 2001, 36(1): 56-59, 71. |
| [8] |
高建虎, 雍学善, 刘洪. 频率域储层预测技术研究[J]. 天然气地球科学, 2007, 18(6): 808-812. GAO Jianhu, YONG Xueshan, LIU Hong. Study of reservoir prediction technology in frequency donain[J]. Natural Gas Geoscience, 2007, 18(6): 808-812. |
| [9] |
DAUBECHIES I. Ten Lectures on Wavelets[M]. PA, United States: Society for Industrial and Applied Mathematics, 1992.
|
| [10] |
张建军, 魏修成, 刘洋. 地震资料小波时频分析中小波母函数的选取[C]. 中国地球物理学会第十九届年会论文集, 2003, 37.
|
| [11] |
STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [12] |
MCFADDEN P D, COOK J G, FORSTER L M. Decomposition of gear vibration signals by the generalized S transform[J]. Mechanical Systems and Signal Processing, 1999, 13(5): 691-707. DOI:10.1006/mssp.1999.1233 |
| [13] |
PINNEGAR C R, EATON D W. Application of the S transform to prestack noise attenuation filtering[J]. Journal of Geophysical Research, 2003, 108(B9): ESE9.1-ESE9.10. |
| [14] |
PINNEGAR C R, MANSINHA L. The S⁃transform with windows of arbitrary and varying shape[J]. Geophysics, 2003, 68(1): 381-385. DOI:10.1190/1.1543223 |
| [15] |
LI D, CASTAGNA J, GOLOSHUBIN G. Investigation of generalized S⁃transform analysis windows for time⁃frequency analysis of seismic reflection data[J]. Geophysics, 2016, 81(3): V235-V247. DOI:10.1190/geo2015-0551.1 |
| [16] |
EBROM D. The low⁃frequency gas shadow on seismic sections[J]. The Leading Edge, 2004, 23(8): 772-772. DOI:10.1190/1.1786898 |
| [17] |
Ten KROODE F, BERGLER S, CORSTEN C, et al. Broadband seismic data⁃The importance of low frequencies[J]. Geophysics, 2013, 78(2): WA3-WA14. DOI:10.1190/geo2012-0294.1 |
| [18] |
刘兰锋, 刘全新, 雍学善, 等. 基于广义S变换的低频瞬时能量谱油气检测技术[J]. 天然气地球科学, 2005, 16(2): 238-241. LIU Lanfeng, LIU Quanxin, YONG Xueshan, et al. Hydrocarbon detection using instantaneous energy spectrum of low frequency based on general S transform[J]. Natural Gas Geoscience, 2005, 16(2): 238-241. |
| [19] |
刘俊杰, 陈学华, 吴昊杰, 等. 稀疏广义S变换及其在储层地震低频异常检测中的应用[J]. 石油地球物理勘探, 2023, 58(3): 690-699. LIU Junjie, CHEN Xuehua, WU Haojie, et al. Sparse generalized S⁃transform and its application to detection of low⁃frequency seismic anomalies in reservoirs[J]. Oil Geophysical Prospecting, 2023, 58(3): 690-699. DOI:10.13810/j.cnki.issn.1000-7210.2023.03.010 |
| [20] |
李庆忠. 走向精确勘探的道路——高分辨率地震勘探系统工程剖析[M]. 北京: 石油工业出版社, 1994.
|
| [21] |
WANG Y. The W transform[J]. Geophysics, 2021, 86(1): V31-V39. DOI:10.1190/geo2020-0316.1 |
| [22] |
LIU B T. Numerical S transform: Error analysis and application[C]. Proceedings of 2015 International Conference on Computer Science and Environmental Engineering, 2015, 1336⁃1342.
|
| [23] |
SIMON C, VENTOSA S, SCHIMMEL M, et al. The S⁃transform and its inverses: side effects of discretizing and filtering[J]. IEEE Transactions on Signal Processing, 2007, 55(10): 4928-4937. DOI:10.1109/TSP.2007.897893 |
| [24] |
地震信号瞬时频率的估算[J]. 地球物理学报, 2009, 52(1): 206-214. CHEN Lin, SONG Haibin. The estimation of instantaneous frequency of seismic signal[J]. Chinese Journal of Geophysics, 2009, 52(1): 206-214. |
| [25] |
基于经验模态分解和小波变换的地震瞬时频率提取方法及应用[J]. 石油地球物理勘探, 2016, 51(3): 565-571. ZHANG Meng, WANG Huazhong, SUI Zhiqiang, et al. Seismic instantaneous frequency extraction based on empirical mode decomposition and wavelet transform[J]. Oil Geophysical Prospecting, 2016, 51(3): 565-571. DOI:10.13810/j.cnki.issn.1000-7210.2016.03.019 |



 刘保童, 甘肃省天水市秦州区藉河南路天水师范学院电子信息与电气工程学院,741001。Email:
刘保童, 甘肃省天水市秦州区藉河南路天水师范学院电子信息与电气工程学院,741001。Email: