2. 中国石化弹性波理论与探测技术重点实验室, 北京 102206;
3. 中国石化石油勘探开发研究院, 北京 102206
2. SINOPEC Key Laboratory of Seismic Elastic Wave Technology, Beijing 102206, China;
3. SINOPEC Petroleum Exploration and Production Research Institute, Beijing 102206, China
自由表面多次波预测(Surface-related Multiple Prediction,SRMP)是自由表面多次波成像[1]以及自由表面多次波压制[2-7]的一个关键步骤。Vercshuur等[8-10]发展的自由表面多次波消除(SRME)方法基于波动理论、采用数据驱动模式,不需要地下构造信息,可以预测出地震记录中所有自由表面多次波,是目前多次波压制的重要方法之一[11-15]。
然而SRME方法要求全波场数据,即炮点与检波点空间采样足够密而且一致,而实际野外采集的地震数据通常炮点、检波点分布稀疏,不能满足SRME的理论需求。因此在SRME之前,需要对原始地震数据做数据规则化。数据规则化将直接决定预测得到的自由表面多次波模型数据的质量以及自由表面多次波衰减的效果。因此SRME在实际应用中受到一定限制,尤其是将SRME应用于实际三维地震数据时,数据规则化会带来计算成本和数据存储成本的增加。
为避免在SRME之前数据规则化,van Demem等[16-17]、Dragoset等[18-19]提出了广义自由表面多次波预测方法。这一方法不需要提前为SRME算法预备一个密集采样的规则数据体,而是从记录的地震数据中通过实时插值得到需要的数据。同时这一方法能适应各种观测系统以及各种地质条件,对于常见的近炮检距道缺失、三维横测线方向采样不足以及海洋勘探的羽状漂移等情况,均能给出较好的多次波预测结果。
然而广义自由表面多次波预测方法计算量巨大,三维情况下,任何一道地震数据在相应的孔径内,可能包含上万个向下反射点(DRP)[2]。而孔径内的每一个DRP都需要通过两次数据搜索来找到与炮点及检波点相关的地震数据。由此可见对一个常规的三维数据体而言,涉及到大量的数据搜索工作。如何高效地从三维数据体中查找到最合适的近似地震道以及通过高效率的校正方法得到参与褶积运算的目标地震道是一个关键点。本文首先简要回顾了SRMP的基本理论,介绍了数据搜索误差函数,然后分析了SRMP数据搜索的时间成本,着重讨论了如何利用地震数据的中心点坐标、炮检距以及方位角信息建立索引数据树,详细阐述了基于树形数据结构的非线性K近邻(K-nearest Neighbor,KNN)算法实现实时搜索的原理以及利用部分动校正消除旅行时误差的策略,最后通过理论模型数据以及实际地震数据证明了本文SRMP方法的有效性。
1 方法原理 1.1 自由表面多次波预测理论Vershuur等[8-10]提出的SRME方法包含自由表面多次波预测和最小二乘自适应相减两部分。其中基于反馈迭代模型的SRMP将包含自由表面多次波的单一频率地震记录表示为[8, 10-12]
| $ P\left({z}_{0}\right)={D}^{-}\left({z}_{0}\right){X}_{0}({z}_{0}, {z}_{0})\left[{S}^{+}\left({z}_{0}\right)+\\\;\;\;\;{R}^{-}\left({z}_{0}\right){P}^{-}\left({z}_{0}\right)\right] $ | (1) |
式中:P(z0)为包含多次波和一次波的地震记录;P-(z0)表示上行波记录;D-(z0)代表仪器接收因素;z0为记录面;X(z0,z0)为大地滤波器响应;S+(z0)为下行震源子波;
| $ {P}_{0}\left({z}_{0}\right)={D}^{-}\left({z}_{0}\right){X}_{0}({z}_{0}, {z}_{0}){S}^{+}\left({z}_{0}\right) $ | (2) |
自由表面多次波记录可表示为
| $ M\left({z}_{0}\right)={D}^{-}\left({z}_{0}\right){X}_{0}({z}_{0}, {z}_{0}){R}^{-}\left({z}_{0}\right){P}^{-}\left({z}_{0}\right) $ | (3) |
总地震波记录为一次反射波与多次波成分之和。
由于记录波场与上行波存在如下关系
| $ P\left({z}_{0}\right)={D}^{-}\left({z}_{0}\right){P}^{-}\left({z}_{0}\right) $ | (4) |
再结合一次反射波、多次波的表达式,可以得到
| $ P\left({z}_{0}\right)={P}_{0}\left({z}_{0}\right)+{P}_{0}\left({z}_{0}\right)A\left({z}_{0}\right)P\left({z}_{0}\right) $ | (5) |
式中
| $ M\left({z}_{0}\right)={P}_{0}\left({z}_{0}\right)P\left({z}_{0}\right) $ | (6) |
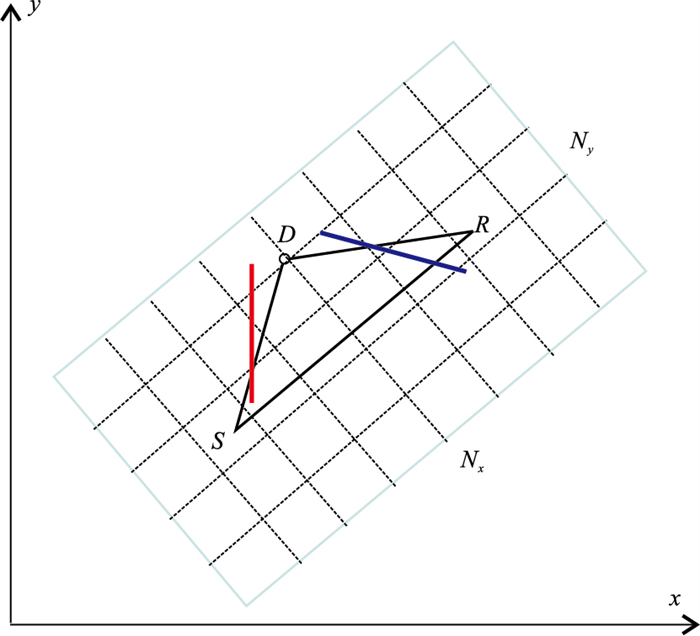
图 1展示了三维SRMP数据搜索的空间几何关系。对于每一道地震数据SR预测其中的自由表面多次波,确定一个与该道方位一致的矩形区域[2, 16-17]作为这一道的孔径范围。孔径内沿SR方向和垂直SR方向按照一定的间隔采样,图中虚线代表网格线,虚线的交点代表孔径内分布的向下反射点。例如,D点作为其中一个向下反射点,与其相关的SRMP过程可表示为
| $ {M}_{\mathrm{S}\mathrm{R}}^{D}=\mathrm{S}\mathrm{D}\mathrm{\Theta }\mathrm{D}\mathrm{R} $ | (7) |
|
图 1 三维自由表面多次波预测数据搜索示意图 |
式中:
| $ {M}_{\mathrm{S}\mathrm{R}}=\sum\limits_{D}{M}_{\mathrm{S}\mathrm{R}}^{D} $ | (8) |
然而由于不规则的地震采集,实际地震数据中并不总是恰好存在SD和DR这两道地震数据,因此需要从实际地震数据中找出与SD和DR最相似的两道地震数据。按下式误差函数
| $ \begin{array}{l}{E}^{2}={\left[{\omega }_{h}({h}_{\mathrm{d}}-{h}_{\mathrm{i}})\right]}^{2}+{\left[{\omega }_{\alpha }({\alpha }_{\mathrm{d}}{h}_{\mathrm{d}}-{\alpha }_{\mathrm{i}}{h}_{\mathrm{i}})\right]}^{2}+\\ {\left[{\omega }_{x}({x}_{\mathrm{d}}-{x}_{\mathrm{i}})\right]}^{2}+{\left[{\omega }_{y}({y}_{\mathrm{d}}-{y}_{\mathrm{i}})\right]}^{2}\end{array} $ | (9) |
寻找与SD和DR最接近的地震数据,即为最优的近似数据。式中:h表示炮检距;α表示方位角;(x,y)为中心点坐标;ωh、ωα、ωx、ωy为对应项的权系数;下标d代表实际采集的地震数据;下标i表示单道孔径内规则采样向下反射点D对应的地震数据SD或DR。式(9)考虑了炮检距、方位角与炮检距的乘积、中心点两个坐标四个维度,通过调节权系数强调各个维度的重要性。图 1中红线和蓝色线分别代表按式(9)误差求得的与SD和DR最近的实际地震数据。
假设实际三维地震数据包含NTR道,每一道地震数据SR在孔径范围内,如图 1所示沿道方向和垂直道方向分别包含Nx、Ny个向下反射点,则每一道总的向下反射点个数为Nx×Ny个。三维叠前地震数据SRMP数据搜索的耗时TSM可大致估计为
| $ {T}_{\mathrm{S}\mathrm{M}}={N}_{\mathrm{T}\mathrm{R}}\times \left({N}_{x}\times {N}_{y}\right)\times {T}_{\mathrm{S}\mathrm{D}/\mathrm{D}\mathrm{R}} $ | (10) |
式中:TSD/DR为获得SD和DR对应的近似数据的耗时。NTR基本不可减少;孔径大小尽管可以优化,但是必须保证足够大的范围,否则影响预测精度,因此确定合理的孔径后Nx×Ny也是一个确定的值。所以TSD/DR是降低三维叠前地震数据SRMP数据搜索耗时的关键。
为每一个向下反射点从实际数据体中搜索最接近SD和DR的近似数据,如果仅依据式(9)选择一个最接近的近似数据,采用线性KNN算法则需2NTR次搜索,每次搜索包含式(9)所示的误差计算及判断是否最接近。对应单道的所有向下反射点则需要执行2Nx×Ny×NTR次搜索,而整个数据体需要执行2NTR×Nx×Ny×NTR次搜索。
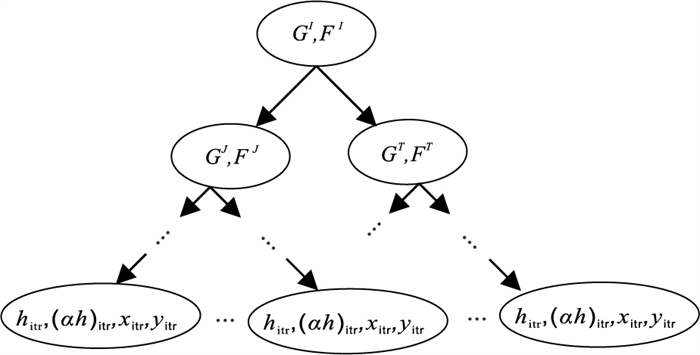
为了减少TSD/DR,采用非线性KNN算法。该算法采用高维索引树形数据结构,可将单个向下反射点D对应的SD或DR地震道的搜索时间复杂度从O(NTR)降低至O(logNTR)[20-21]。具体做法是采用基于炮检距h、方位角与炮检距的乘积αh、中心点坐标x和y四个维度的索引数据树管理实际采集的地震数据。图 2为四维索引数据树示意图,椭圆代表一个节点,最上面的为根节点,中间的椭圆为中间节点,最下面的椭圆为叶节点。
|
图 2 四维树形数据结构示意图 下标itr代表地震道的索引号 |
第一步根据四个维度对应的数值对整个三维叠前数据体分别计算各个维度对应的方差,选择方差最大的维度G分割数据,找到这一维度所有数值的中值F作为分割点。第二步建立最上面的根节点,存放(GI,FI),其中GI代表此时找到的分割维度,FI代表对应的分割点数值,上标I表示根节点的编号,不同节点对应不同的节点编号。假设由Q表示地震数据的四维坐标点,依据分割维度取Q(GI),当Q(GI) ≤FI则对应的Q点属于左边,Q(GI) > FI时则对应的Q点属于右边,直到将整个三维叠前数据体分为左、右两个部分,称为左子树和右子树。第三步继续分别在左子树和右子树上重复上述过程,寻找各自的分割维度和分割点数值。如图 2所示,左、右子树各自的分割维度和分割点数值分别为(GJ,FJ)和(GT,FT), 上标J、T分别表示左、右子树节点的编号;依据新的分割维度和分割点数值分别在左、右子树上继续分割,各自获得下一个层级的左、右子树;不断重复上述过程,直到左子树和右子树无法继续分割为止,此时建立的节点为叶节点,并在其中保存完整四个维度的数值(h,αh,x,y)。
以地震道SD为例,用QSD表示这一道对应的四维坐标点,基于四维索引数据树搜索时,首先根据根节点(G,F),比较QSD(G)和F的大小,QSD(G)≤F则选择左子树;QSD(G) > F则选择右子树。从根节点一直往下经过各个中间层节点,重复QSD点与各节点保存的分割点数值的比较,选择左、右子树,直至叶节点。将该叶节点,假设由Q表示,作为QSD的一个近似结果,然后依据式(9)计算QSD和Q的误差,假设由
| $ \left|Q\left(G\right)-F\right| < {d}_{\mathrm{S}\mathrm{D}}^{Q} $ | (11) |
从上述过程可以看出非线性KNN搜索在寻找叶节点的过程中始终通过比较分割维度数值完成,而避免了反复按式(9)计算误差函数,同时在首次与根节点进行比较后将缩小一半的搜索范围,在后续每一次与中间节点比较的过程中近似按1/2等比例缩小搜索范围,因此能快速达到初步搜索的叶节点。尽管进一步优化的回溯过程需要计算误差函数,但是涉及的数据分支被限定在一个相对小的范围,如式(11)所示,因此基于四维索引数据树的非线性KNN算法能快速搜索到最优近似地震道。
当根据上述过程寻找到最近似SD和DR的地震数据后,炮检距往往存在差异,可利用下式
| $ {t}_{\mathrm{i}}^{2}={t}_{\mathrm{d}}^{2}-\frac{{h}_{\mathrm{d}}^{2}}{{v}_{\mathrm{r}\mathrm{m}\mathrm{s}}^{2}}+\frac{{h}_{\mathrm{i}}^{2}}{{v}_{\mathrm{r}\mathrm{m}\mathrm{s}}^{2}} $ | (12) |
校正由于炮检距差异引起的旅行时误差[19]。式中:ti表示理想地震道双程旅行时;td表示搜索到的实际地震数据双程旅行时;vrms为均方根速度。
本文的自由表面多次波预测的步骤如下:
(1) 输入三维叠前数据体;
(2) 读入单道地震数据SR并确定孔径大小,按照一定网格大小确定向下反射点D;
(3) 对单个向下反射点D采用非线性搜索得到SD、DR的近似地震数据;
(4) 对两道近似地震数据进行旅行时校正;
(5) 由校正后的两道近似地震数据褶积,获得对应该向下反射点的自由表面多次波模型道;
(6) 是否完成孔径内最后一个向下反射点?如否返回步骤(3),如是对单道孔径内所有向下反射点对应的自由表面多次波模型道叠加,获得单道自由表面多次波模型;
(7) 是否完成最后一道地震数据?如否返回步骤(2),如是输出整个叠前三维数据体的自由表面多次波模型。
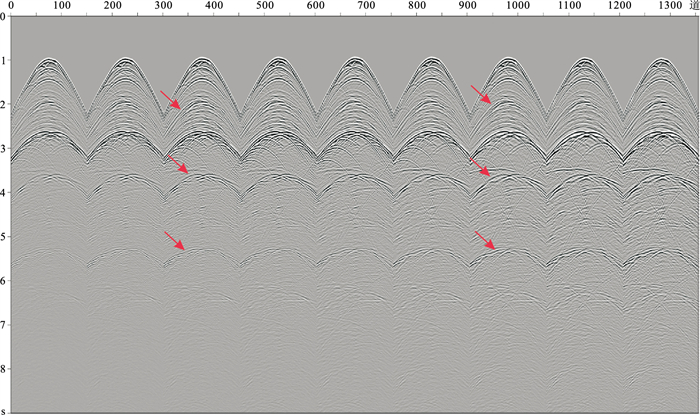
2 理论模型测试Pluto模型是用来检验二维多次波消除的经典模型,本文将Pluto模型直接扩展到三维形成一个2.5维模型,其中x方向6960个网格点,y方向211个网格点,两个方向的网格点间距均为7.62 m。三维模拟的观测系统如图 3所示,模拟得到的单炮记录如图 4所示,可见其中自由表面多次波发育,如红色箭头指示了海底界面相关的自由表面多次波和盐丘顶界面相关的自由表面多次波。

|
图 3 2.5D Pluto模型观测系统 四个角点黑色圆点表示观测范围,括号内为对应的坐标和网格索引号;红色虚线表示炮线,炮线距为400 m,炮点距为320 m,每条炮线3炮,一共80条炮线;蓝色实线表示检波线,检波线距为80 m,检波点距为40 m,每炮9条检波线接收,每条检波线151个接收点,炮点位于接收线的中间位置。 |
|
图 4 2.5维Pluto模型模拟的单炮记录 |
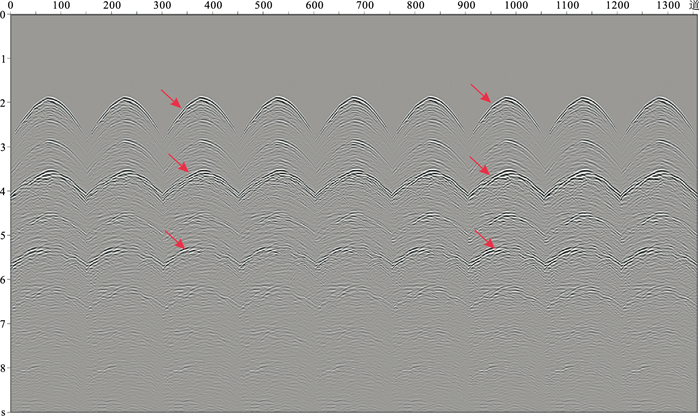
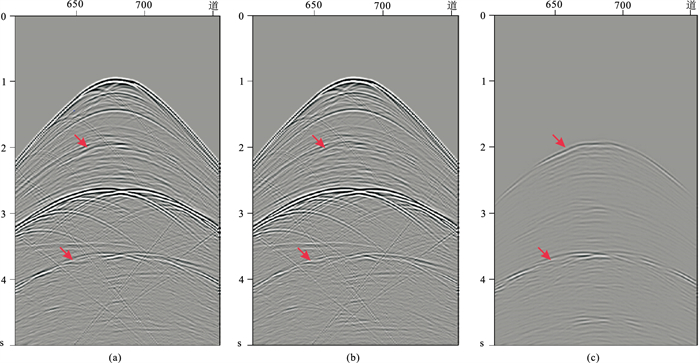
根据模拟观测系统,在进行自由表面多次波预测时,采用20 m×20 m的小网格,这样会导致每道地震数据的孔径范围内很多向下反射点的数据必须通过数据搜索和炮检距校正获得。本文方法预测的单炮自由表面多次波模型如图 5所示,红色箭头指示了部分强能量的自由表面多次波,即与海底界面相关的自由表面多次波及与盐丘顶界面相关的自由表面多次波。图 6为去自由表面多次波前、后的单炮单排列对比,红色箭头指示的自由表面多次波得到有效压制。
|
图 5 2.5维Pluto模型预测的自由表面多次波单炮数据 |
|
图 6 去自由表面多次波前(a)、后(b)单炮数据及去掉的多次波(c)对比 |
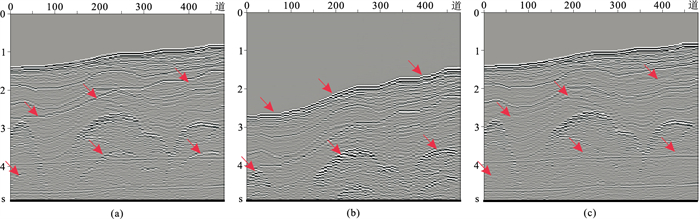
共炮检距剖面能更清楚地显示多次波预测结果和压制效果。图 7a是炮检距为681 m的原始数据共炮检距剖面,图 7b为对应的预测多次波模型共炮检距剖面,红色箭头分别指示出了海底以及盐丘顶部的自由表面多次波在原始数据以及预测结果中的位置。图 7c为自适应相减的结果,与图 7a对比可见,红色箭头所指的与海底以及盐丘顶界面相关的自由表面多次波得到了有效衰减。
|
图 7 2.5维Pluto模型原始数据(a)、预测的多次波(b)及多次波相减后(c)的共炮检距剖面对比 |
采用中国西北部M探区采集的一条二维宽线地震数据测试表面多次波预测效果。一共两条接收线,检波线间距50 m,每条线720道接收,道间距20 m,炮线位于两条接收线中间。该区侏罗系煤层发育,煤层速度低,与围岩(速度3800~4800 m/s)形成强反射,且与地面产生很强的全程多次波。煤层产生的多次波掩盖了深层二叠系的反射波组,使得该地区的勘探工作推进艰难[22]。将二维宽线当作三维资料处理,在自由表面多次波预测时采用10.0 m×12.5 m的网格定义向下反射点,因此大量的向下反射点需要通过搜索和部分炮检距校正获得适用于自由表面多次波预测的地震数据。
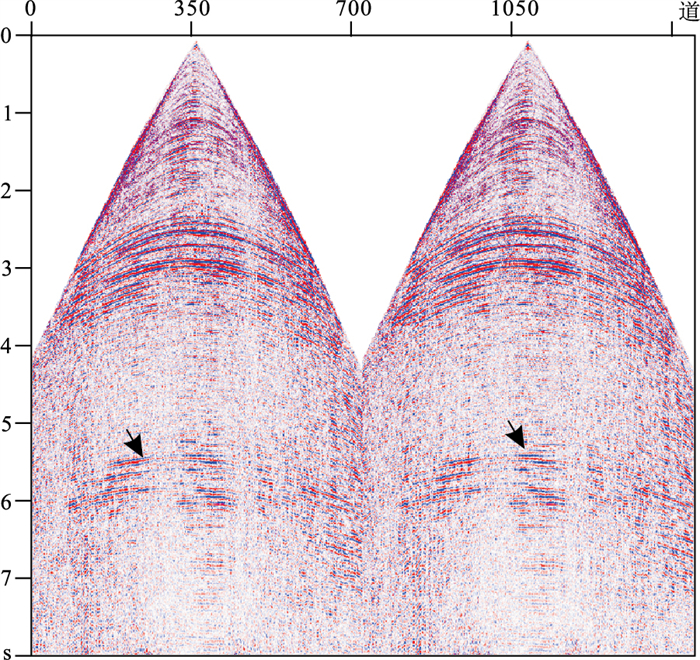
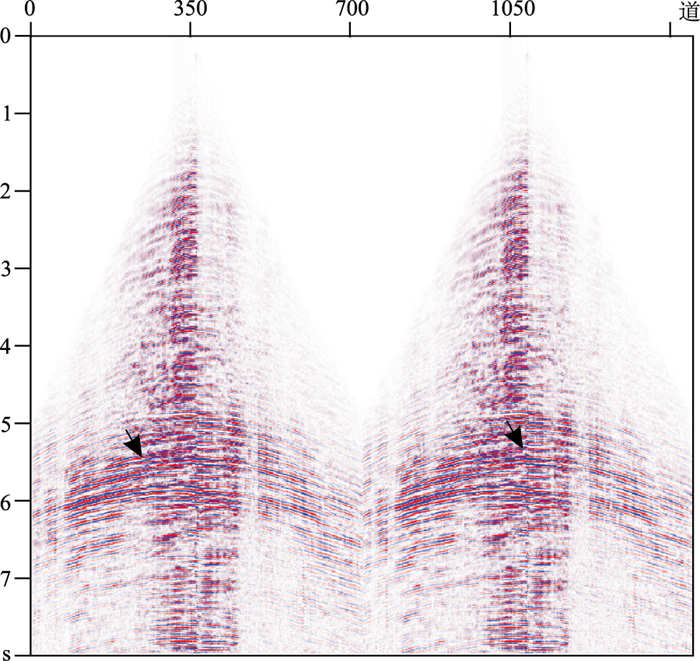
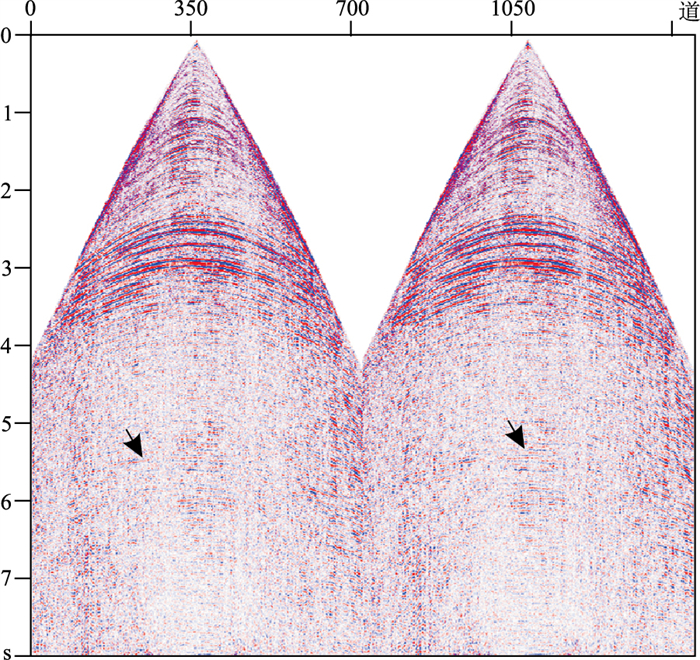
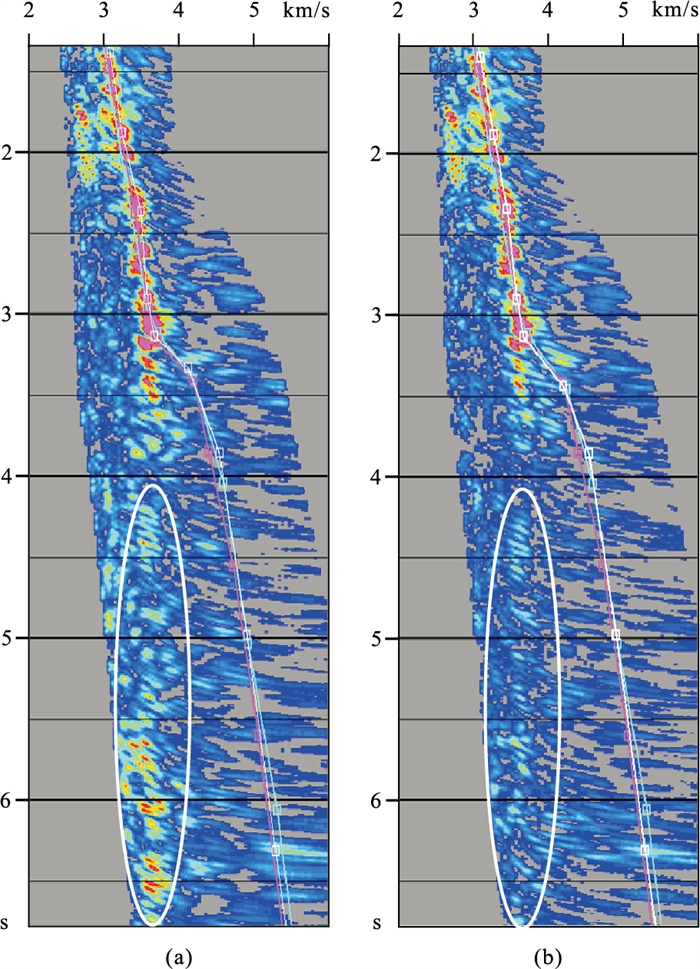
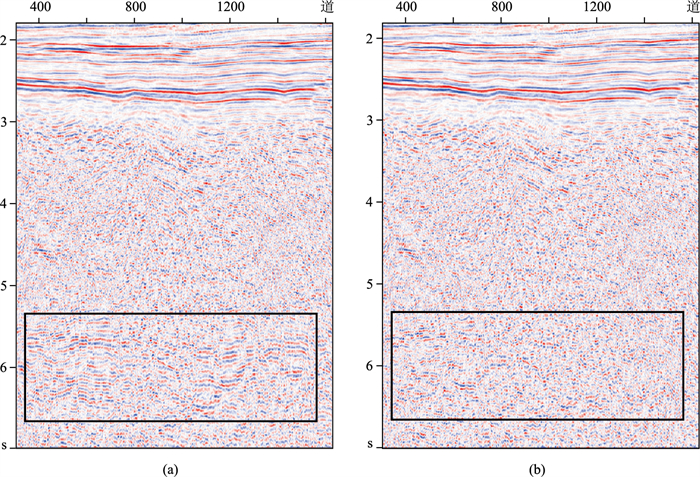
宽线采集的实际单炮数据如图 8所示,5.5 s附近的黑色箭头处存在大量的自由表面多次波,该时间段的多次波形态与3 s附近的煤层强反射同相轴相似。图 9为预测得到的自由表面多次波模型单炮数据,5.5 s附近的黑色箭头处较强能量为预测的自由表面多次波模型数据。图 10为衰减自由表面多次波之后的单炮数据,5.5 s附近黑色箭头处的自由表面多次波得到了有效衰减。图 11为自由表面多次波衰减前、后的速度谱对比,衰减前白色椭圆内低速能量团表明自由表面多次波发育,同时可看出5.5 s附近的低速能量团与3 s附近的煤层相关的能量团有相似的速度值,结合该区地质认识可以确定5.5 s附近发育与煤层相关的自由表面多次波;衰减后的速度谱在白色椭圆内低速能量团能量明显变弱,表明与煤层相关的自由表面多次波得到了有效压制。图 12为压制自由表面多次波前、后叠加剖面对比,黑色矩形框内与煤层相关的自由表面多次波干扰得到有效压制。
|
图 8 宽线采集的单炮 |
|
图 9 预测的单炮自由表面多次波 |
|
图 10 自由表面多次波衰减后的单炮数据 |
|
图 11 去自由表面多次波前(a)、后(b)速度谱对比 |
|
图 12 去自由表面多次波前(a)、后(b)叠加剖面对比 |
针对三维叠前地震数据体炮点、检波点分布稀疏,不满足自由表面多次波预测理论假设的问题,本文提出一种实时搜索地震数据的自由表面多次波预测实现策略,避免了在SRMP之前数据规则化及其带来的计算量和存储成本的增加,对叠前三维实际地震数据处理具有重要意义。综合利用地震道中心点坐标、炮检距以及方位角信息建立四维索引数据树,数据树上的每个叶节点均对应三维叠前地震数据中的地震道。利用树型数据结构,通过比较目标地震道的分割维度的坐标值与中间节点存储的分割值的大小,避免了反复的误差计算,可快速搜索到一个叶节点。在该叶节点附近较小的范围内,进一步搜索得到最优的近似地震数据,实现了非线性KNN实时地震数据搜索,理论上将数据搜索时间复杂度从O(NTR)降低至O(logNTR)。结合部分炮检距动校正消除近似地震道与目标地震道的旅行时误差,获得适用于SRMP的地震数据,最终运用SRMP原理预测自由表面多次波。应用2.5维Pluto模型合成地震数据和实际二维宽线地震数据验证了本方法的正确性和有效性。
将本文方法扩展用于三维叠前层间多次波预测是今后的研究重点。
| [1] |
LIU Y K, CHANG X, JIN D G, et al. Reverse time migration of multiples for subsalt imaging[J]. Geophysics, 2011, 76(5): WB209-WB216. DOI:10.1190/geo2010-0312.1 |
| [2] |
DRAGOSET B, VERSCHUUR E, MOORE I, et al. A perspective on 3D surface-related multiple elimination[J]. Geophysics, 2010, 75(5): 75A245-75A261. DOI:10.1190/1.3475413 |
| [3] |
井洪亮, 张少华, 方云峰, 等. λ-f域三维抛物Radon变换多次波压制方法[J]. 石油地球物理勘探, 2022, 57(5): 1066-1075, 1087. JING Hongliang, ZHANG Shaohua, FANG Yunfeng, et al. Multiple attenuation method based on 3D parabolic Radon transform in the λ-f domain[J]. Oil Geophysical Prospecting, 2022, 57(5): 1066-1075, 1087. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.007 |
| [4] |
王维红, 催宝文, 刘洪. 表面多次波衰减的研究现状与进展[J]. 地球物理学进展, 2007, 22(1): 156-164. WANG Weihong, CUI Baowen, LIU Hong. Research progress in surface-related multiple attenuation[J]. Progress in Geophysics, 2007, 22(1): 156-164. DOI:10.3969/j.issn.1004-2903.2007.01.022 |
| [5] |
李鹏, 刘伊克, 常旭, 等. 均衡拟多道匹配滤波法在波动方程压制多次波中的应用[J]. 地球物理学报, 2007, 50(6): 1844-1853. LI Peng, LIU Yike, CHANG Xu, et al. Application of the equipoise pseudomultichannel matching filter in multiple elimination using wave-equation method[J]. Chinese Journal of Geophysics, 2007, 50(6): 1844-1853. DOI:10.3321/j.issn:0001-5733.2007.06.027 |
| [6] |
金德刚, 常旭, 刘伊克. 逆子波域消除多次波方法研究[J]. 地球物理学报, 2008, 51(1): 250-259. JIN Degang, CHANG Xu, LIU Yike. Research of multiple elimination method in inverse wavelet domain[J]. Chinese Journal of Geophysics, 2008, 51(1): 250-259. DOI:10.3321/j.issn:0001-5733.2008.01.031 |
| [7] |
马继涛, 刘仕友, 廖震. 三维高精度保幅Radon变换多次波压制方法[J]. 石油地球物理勘探, 2022, 57(3): 582-592. MA Jitao, LIU Shiyou, LIAO Zhen. Research on multiple attenuation using 3D high-precision amplitude-preserving Radon transform[J]. Oil Geophysical Prospecting, 2022, 57(3): 582-592. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.009 |
| [8] |
VERSCHUUR D J, BERKHOUT A J. Adaptive surface-related multiple elimination[J]. Geophysics, 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [9] |
BERKHOUT A J, VERSCHUUR D J. Estimation of multiple scattering by iterative inversion, part Ⅰ: Theoretical considerations[J]. Geophysics, 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [10] |
VERSCHUUR D J, BERKHOUT A J. Estimation of multiple scattering by iterative inversion, part Ⅱ: Practical aspects and examples[J]. Geophysics, 1997, 62(5): 1596-1611. DOI:10.1190/1.1444262 |
| [11] |
黎孝章, 邓勇, 赫建伟, 等. 复杂海底自由表面多次波预测方法[J]. 石油地球物理勘探, 2020, 55(1): 64-70. LI Xiaozhang, DENG Yong, HE Jianwei, et al. Free-surface-related multiple prediction for complex seafloor[J]. Oil Geophysical Prospecting, 2020, 55(1): 64-70. DOI:10.13810/j.cnki.issn.1000-7210.2020.01.008 |
| [12] |
石颖, 刘洪. 基于GPU的表面多次波预测技术[J]. 石油地球物理勘探, 2010, 45(4): 540-544. SHI Ying, LIU Hong. GPU-based surface multiple prediction technique[J]. Oil Geophysical Prospecting, 2010, 45(4): 540-544. |
| [13] |
田继强, 胡天跃. 反馈迭代法在自由表面多次波压制中的应用[J]. 石油物探, 2008, 47(5): 449-454. TIAN Jiqiang, HU Tianyue. Application of feedback iteration method in free surface multiple attenuation[J]. Geophysical Prospecting for Petroleum, 2008, 47(5): 449-454. DOI:10.3969/j.issn.1000-1441.2008.05.004 |
| [14] |
孙维蔷, 王华忠. 基于平面波编码的水体相关多次波压制方法研究[J]. 石油物探, 2016, 55(4): 516-523. SUN Weiqiang, WANG Huazhong. Water-layer related multiple suppression based on plane-wave coding[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 516-523. DOI:10.3969/j.issn.1000-1441.2016.04.006 |
| [15] |
马继涛. 基于三维抛物线Radon变换的多次波压制算法对比分析[J]. 石油物探, 2022, 61(3): 444-453, 511. MA Jitao. Comparison and analysis of multiple attenuation algorithms based on three-dimensional parabolic Radon transform[J]. Geophysical Prospecting for Petroleum, 2022, 61(3): 444-453, 511. DOI:10.3969/j.issn.1000-1441.2022.03.006 |
| [16] |
VAN DEDEM E J, VERSCHUUR D J. 3D surface-related multiple elimination and interpolation[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 1321-1324.
|
| [17] |
VAN DEDEM E J, VERSCHUUR D J. 3D surface multiple prediction using sparse inversion[C]. SEG Technical Program Expanded Abstracts, 2001, 20: 1285-1288.
|
| [18] |
DRAGOSET B, MOORE I, YU M, et al. 3D general surface multiple prediction: An algorithm for all surveys[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2426-2430.
|
| [19] |
MOORE I, DRAGOSET B. General surface multiple prediction: a flexible 3D SRME algorithm[J]. First Break, 2008, 26(9): 89-100. |
| [20] |
MUJA M, LOWE D G. Scalable nearest neighbor algorithms for high dimensional data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(11): 2227-2240. DOI:10.1109/TPAMI.2014.2321376 |
| [21] |
FRIEDMAN J H, BENTLEY J L, FINKEL R A. An algorithm for finding best matches in logarithmic expected time[J]. ACM Transactions on Mathematical Software, 1977, 3(3): 209-226. DOI:10.1145/355744.355745 |
| [22] |
林娟, 蒋立, 潘龙, 等. 复杂近地表多次波分析及压制方法探讨——准噶尔盆地腹部地震资料处理实例[J]. 石油地球物理勘探, 2021, 56(6): 1229-1235. LIN Juan, JIANG Li, PAN Long, et al. Analysis of complex near-surface multiple waves and discussion on suppression methods: a case of seismic data in the hinterland of the Junggar Basin[J]. Oil Geophysical Prospecting, 2021, 56(6): 1229-1235. DOI:10.13810/j.cnki.issn.1000-7210.2021.06.004 |



 谢飞,北京市昌平区沙河镇百沙路197号中国石化科学技术研究中心,102206。Email:
谢飞,北京市昌平区沙河镇百沙路197号中国石化科学技术研究中心,102206。Email: