2. 广东省地球物理高精度成像 技术重点实验室(南方科技大学), 广东深圳 518055;
3. 上海佘山地球物理国家野外科学观测研究站, 上海 200062
2. Guangdong Provincial Key Laboratory, Geophysical High-Resolution Imaging Technology, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China;
3. Shanghai Sheshan National Geophysical Observatory, Shanghai 200062, China
近年来,水力压裂技术被广泛用于页岩气、煤层气等非常规油气资源开发[1-5]。在水力压裂过程中,通过检测岩石破裂产生的微地震信号,可以反演震源位置、震源机制解、震级等参数,从而监测裂缝的发育过程并评估压裂效果[6-11]。地面监测和井中监测是两种常用的监测方式。与地面监测相比,井中监测的检波器记录具有较高的信噪比,可通过拾取P波和S波到时进行微地震定位[12]。野外记录通常为连续的波形,对微地震信号的识别直接决定了微地震定位的准确度和可靠性。
目前,微地震事件自动检测主要应用于天然地震领域,方法包括基于振幅的长短时窗比法(Short Term Average/Long Term Average,STA/LTA)[13-16]、基于Akaike信息准则(Akaike Information Criteria,AIC)的方法[17-18]以及基于波形相似性的波形互相关法[19-22]等。目前,应用较为广泛的为STA/LTA算法,其基本原理是通过计算短、长时间窗内波形的平均能量值比值来评估信号的能量变化。该方法原理简单、计算效率高,地震学家对该方法做了一系列的改进。例如,Withers等[13]实现了一种自适应窗口的STA/LTA算法,结合地震图频谱特性满足事件检测与定位的要求。宋维琪等[14]在STA/LTA算法的基础上,讨论了基于特征值分析且抗噪能力较强的识别方法。邱磊等[15]通过建立阈值和背景噪声之间的关系,提出了两种基于参考阈值拾取地震波初至的方法,拾取结果的正确率比传统STA/LTA方法有所提高。刘晗等[16]对STA/LTA算法和改进的加权系数法、多窗口算法和修正能量比法进行了对比,了解了时窗长度、触发阈值和特征函数对算法性能的影响特征及其选取规律。STA/LTA法具有较好的通用性且高效,但其拾取结果受阈值影响较大,依赖人工经验,同时该方法对中强度背景噪声十分敏感,容易出现漏检事件。
近年来,随着计算机领域人工智能的发展,深度学习相关技术在计算机视觉、自然语言处理、语音识别、医学图像处理等多个领域取得了巨大的成功[23-24]。机器学习算法也被广泛地应用在地震勘探领域,尤其是地震信号的检测和拾取,发展了一系列的智能算法[25-35]。例如,Mousavi等[36]采用卷积神经网络以及循环神经网络搭建模型,形成了CRED模型,用于噪声与地震事件分类,该模型对于背景噪声、非地震脉冲有着极高鲁棒性,能够高效地处理海量地震数据。赵明等[37]使用汶川地震余震事件构建训练数据集,利用卷积神经网络方法进行训练,并用未参与模型训练的汶川余震事件作为检测数据集,其训练和检测准确率均达到95%以上。Zhao等[38]采用卷积神经网络对连续数据进行时窗分割并分类,其输入为一维的地震数据,验证集精度达到93%。Zhang等[39]构建了基于卷积神经网络的微地震检测网络,通过比较分析多种微地震检测分类方法,论证了深度学习算法在微地震事件检测中具有较高的准确度,展示了在微地震实时监测领域中良好的应用前景。王维波等[40]利用卷积神经网络算法构建微地震检测二分类模型,通过水力压裂实际监测的微地震信号构建训练样本集,训练得到的网络模型具有较好的抗噪性。随后,王维波等[41]又提出利用残差网络对微地震监测数据的地震发射层析成像数据进行处理, 实现微地震事件自动识别。
深度学习算法可以直接从训练数据中挖掘地震事件特征。预测新的数据时,只需要将微震事件分割成相互独立的窗口,然后输入到训练好的模型中即可迅速进行事件检测,节省大量的计算时间。现有的基于深度学习的微地震事件检测方法通常把事件检测看作图像二分类问题,需要对连续监测的波形数据按照一定时窗长度进行分割。通常,相邻时窗会有部分重叠以尽量减少漏检。这种处理方法不仅增加了计算时间,降低了运算效率,同时如何选取重叠时窗大小也决定了分类结果的准确度。因此,本文提出一种基于深度学习的微震事件五分类检测方法。首先,把野外采集的连续记录波形等分,人工标定为噪声、完整的P波和S波、只含有P波、只含有S波和多个微震事件五类;其次,通过研究数据增广方法,利用较少的原始标定样本获得多样性的训练集数据进行模型训练;最后,将训练得到的五分类模型应用于实际微震数据检测,通过对检测得到的微震事件进行到时拾取和震源定位评估检测精度,并与二分类算法结果进行对比验证。
1 数据处理本文使用了东方地球物理公司(BGP)提供的一套单井监测的水力压裂数据,共有12个三分量检波器分布在深度为2800~3020 m的监测井中,间隔为20 m,检波器位于压裂井段的上方。图 1为本文使用的P波和S波速度模型,参数经测井数据提取并利用射孔事件校正。数据的时间采样率为0.5 ms。

|
图 1 P波速度(vP)与S波速度(vS)模型 |
本文把微地震事件检测视为五分类问题:图 2a为噪声,被归为第一类,简称C1;图 2b为一个完整的微震事件,包含完整的P波和S波信息,被归为第二类,简称C2;图 2c只含有完整的P波信息,被归为第三类,简称C3;图 2d只含有完整的S波信息,被归为第四类,简称C4;第五类较为复杂,定义为在一个样本窗口中包含多个微震事件(图 2e)。此外,样本中同时包含一个微震事件和另一个事件的P波或者S波也被归为第五类,简称C5。

|
图 2 微震五分类样本 (a)噪声(C1);(b)微震事件(C2);(c)只含P波(C3);(d)只含S波(C4);(e)多个微震事件(C5) |
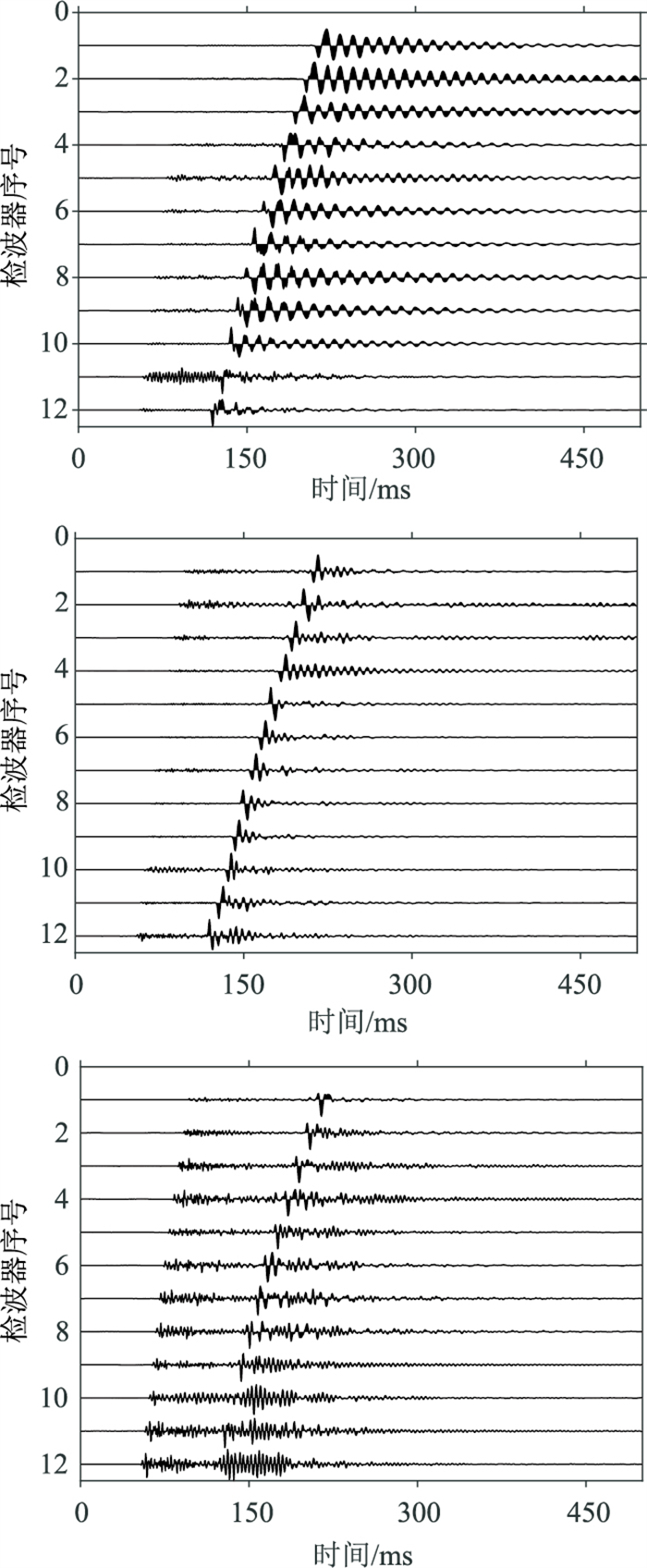
数据增广可以提高模型的泛化能力和鲁棒性,有助于减少过拟合问题。在训练神经网络模型时,通常需要大量的训练数据,但是大多数地球物理的数据集比较有限。通过数据增广,能够扩展数据集,增加训练样本的多样性。常见的数据增广方法包括旋转、翻转、裁剪、平移、缩放、添加噪声等[23, 37]。针对井下微震事件检测,本文参考Zhang等[42]提出的方法进行数据增广。其中,针对C2样本的增广方法共有5种。图 3为原始样本的三分量数据波形记录, 图 4为对图 3数据增广后的结果。
|
图 3 原始样本的三分量数据波形记录 |
图 4a为颠倒检波器顺序:微震事件可能发生在检波器阵列的上方或下方,颠倒检波器顺序可以模拟发生在不同位置的微震事件。
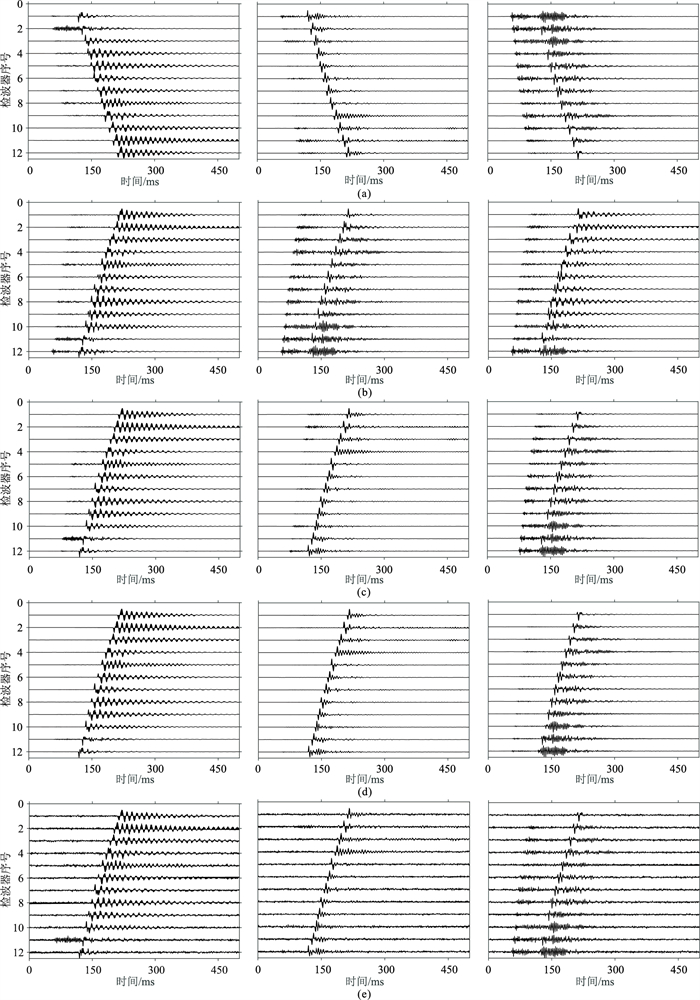
|
图 4 图 3数据用不同方法增广处理结果 (a)颠倒检波器顺序;(b)旋转分量;(c)移动P波、S波相位;(d)调整P波振幅;(e)添加噪声 |
图 4b为旋转分量:微震事件可能发生在不同的方位角和不同的震源机制作用下。不同的方位角导致波形数据中的粒子运动变化。旋转分量可以模拟具有不同偏振角产生的复杂波形的微地震事件[42]。
图 4c为移动P波或S波相位:P波与S波的到时差与检波器的几何分布、地下速度模型以及事件发生的位置等因素有关。通过随机移动P波和S波波形来模拟由各种物理因素引起的到时差。本文从-15 ms到15 ms之间随机选择一个值进行移动P波到时或者S波到时。此外,为了防止移动后S波的到时早于P波到时,选择最小P、S波到时差为25 ms。
图 4d为调整P波振幅:调整P波振幅有助于提高模型的泛化能力。我们选择对S波之前的P波波形随机乘以值为0.2~1.2的因子。当因子较小时,样本主要显示S波波形,可模拟单震相事件。
图 4e为添加噪声:信噪比是影响微地震事件检测精度的一个重要因素。噪声类型的多样性有利于提高网络模型的检测准确度。本文选择了4种不同类型的噪声改变事件的信噪比。第一种为实际数据噪声。首先从原始的监测数据中截取了50个噪声窗口,随机选择一个噪声窗口叠加到微震事件波形中。通过随机设置信噪比模拟被不同程度噪声污染的事件。第二种为高斯白噪声。本文选择的高斯白噪声约为信号最大值的5
C3与C4样本的数据增广方法通过截取C2样本实现。以C2样本中所有检波器中最后的P波到时与最初的S波到时的平均值为基点,随机选择-25 ms~25 ms的扰动,拆分窗口。分别得到一个C3样本以及一个C4样本。然而,拆分的样本不满足时窗长度要求,需要对P、S波前后的噪声进行插值或截断,得到满足时窗长度要求数据集。
针对C5的数据增广方法一共两种:
(1) 两个C2样本叠加。从C2样本中随机选取两个事件进行叠加。如果两个选取的C2样本距离较近,则叠加后的样本难以区分是C2或是C5,因此本文规定两个叠加事件的P波到时差需要超过100 ms。此外,通过乘以值为0.5~1.0的一个因子改变振幅,更加贴合实际情况。
(2) 一个C2样本与一个C3或者C4样本叠加。具体做法是将一个位于时窗前部S波与一个任意位置的C2样本叠加,或者是一个位于时窗后部的P波与一个任意位置的C2样本叠加。
本文从野外原始记录的波形数据中分别截取5种数据样本,并通过以上数据增广方法进行数据增广,数据集增广前、后个数如表 1所示。数据集个数从91增加到22431,5种数据样本的比例分别为19.83%,20.28%,19.97%,20.01%以及19.98%。最后将数据集按8:2的比例划分为训练集以及验证集,训练集与验证集个数分别为17944、4487。
|
|
表 1 五分类数据集 |
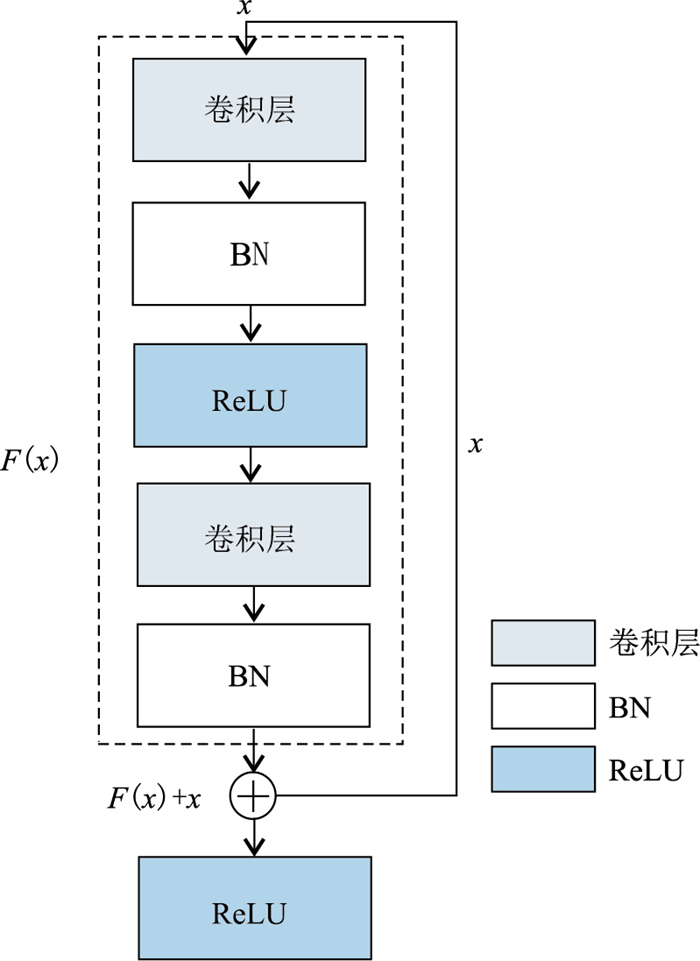
传统卷积神经网络层数增加时,易出现梯度消失的问题。He等[24]在传统卷积神经网络的基础上,增加跨层数据通路(图 5黑色折线),加强了层与层之间的沟通,该神经网络被称为残差网络(Residual Network,简称ResNet)。该网络主要由残差块堆叠而成。图 5是本文所使用的残差块结构,输入x依次进入卷积层、批量规范化层(Batch Normalization Layer, 简称BN层)、ReLU激活层、卷积层、BN层以及ReLU层,同时在最后一个ReLU层之前,加入了跨层连接,得到映射函数F(x)+x。需要注意的是,残差块的输入x与最终输出的数据形状是相同的。
|
图 5 残差块结构 |
图 6为本文残差模型的架构。模型的输入大小为n
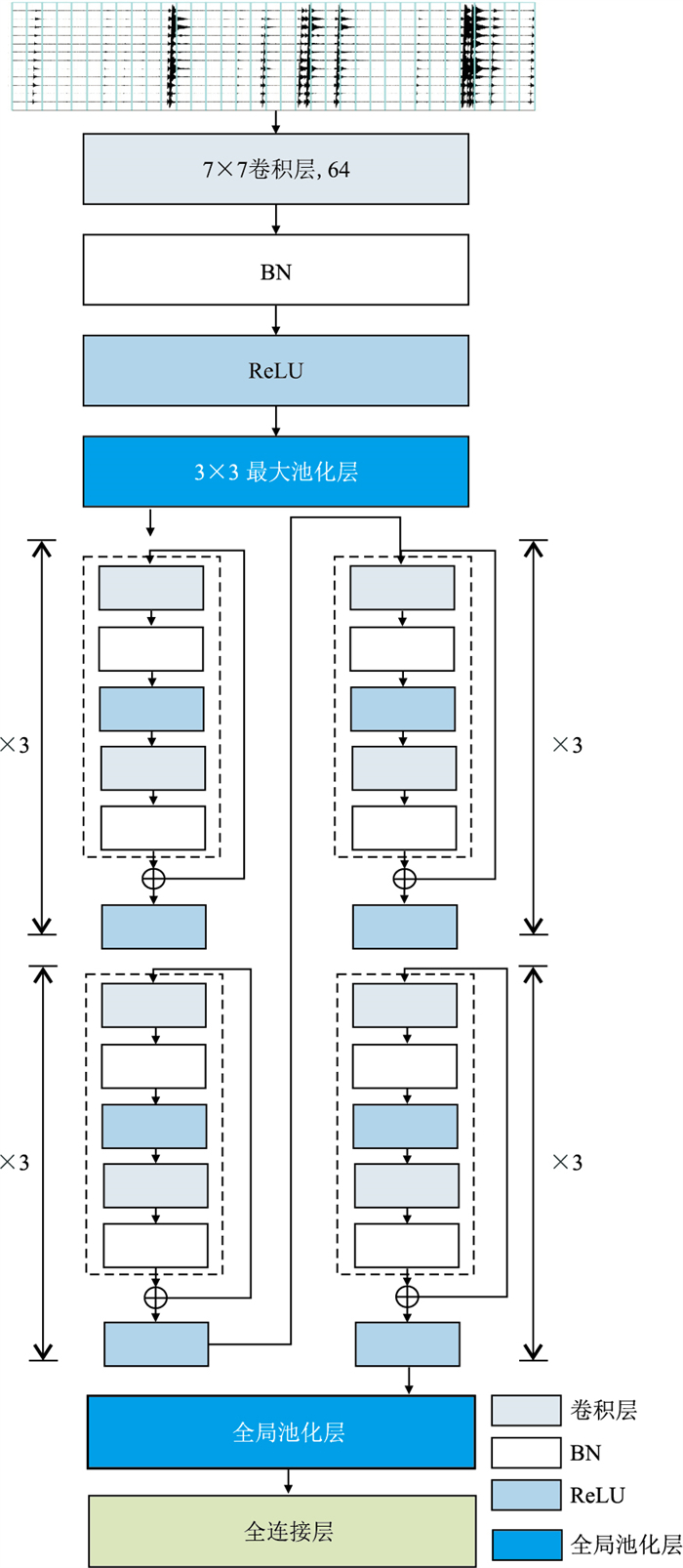
|
图 6 残差网络模型架构 |
深度学习的损失函数与地球物理反演中的目标函数十分相似,用于估计模型的预测值与真实值的差别程度。在分类问题中,多使用交叉熵损失函数衡量输入的真实概率分布
| $ H\left(p, q\right)=-\frac{1}{N}\left\{p\left({x}_{i}\right)\mathrm{l}\mathrm{g}\left[q\left({x}_{i}\right)\right]+\right.\\\;\;\;\;\;\;\;\;\;\;\;\; \left.\left[1-p\left({x}_{i}\right)\right]\mathrm{l}\mathrm{g}\left[1-q\left({x}_{i}\right)\right]\right\} $ | (1) |
式中:
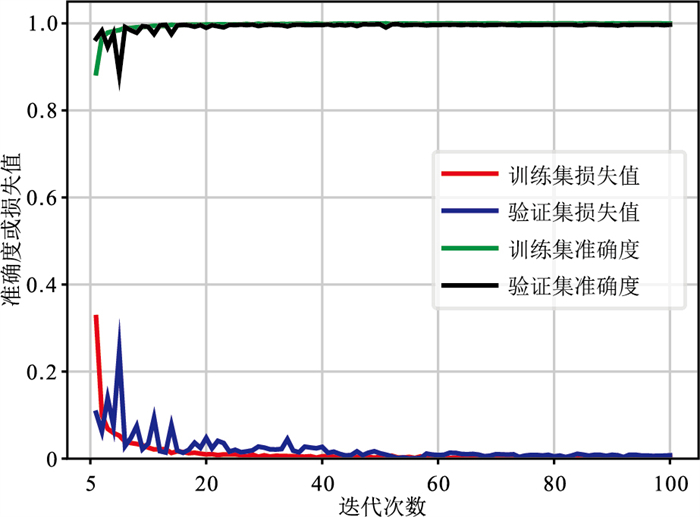
模型在RTX3060图像处理器上进行训练,训练时长约为145 min。经过100次迭代后,训练集和验证集的准确度损失曲线均得到收敛(图 7)。其中,训练集准确度达到99.96%,训练集损失值约为0.0017;验证集准确度达到99.82%,验证集损失值约为0.0082。
|
图 7 五分类模型的准确度与损失曲线 |
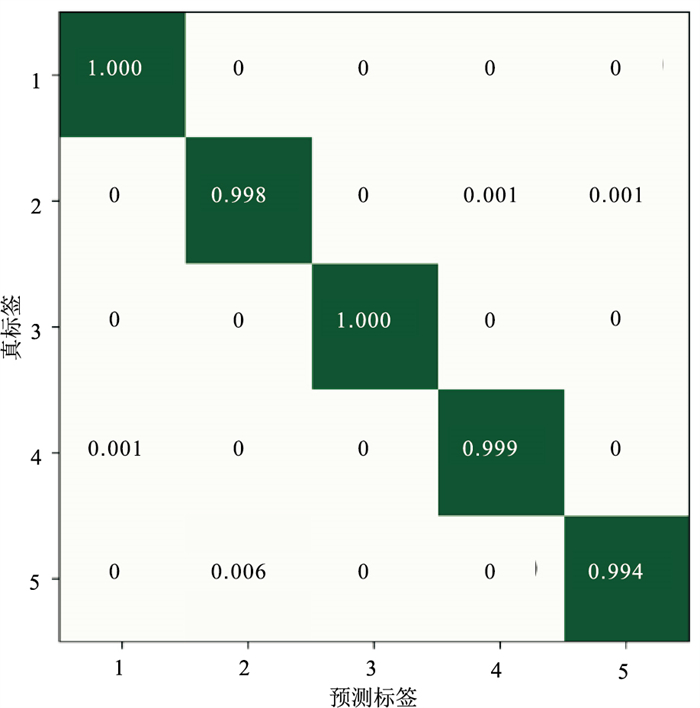
本文使用归一化的混淆矩阵(Confusion Matrix)进一步分析了模型性能。混淆矩阵展示了一个分类器对样本进行分类时产生的错误,即真实类别被分为其他类别的错误。图 8为五分类模型验证集的归一化混淆矩阵, 矩阵主对角线为预测标签与真标签吻合的概率值。在验证集中C1与C3样本全部预测正确,个数分别为890与896,所以对应的主对角线的值为1;C2个数为个910个,其中被正确预测的个数为908,占比为99.8%; 898个C4样本中有897个预测正确,占比99.9%;893个C5样本中有887个预测正确,占比99.4%,其中有6个C5样本被错误预测为C2样本。
|
图 8 五分类模型在验证集的归一化混淆矩阵 |
降维可视化是将高维数据转换为二维或三维的可视化展示,有助于更好地理解和分析数据,从而找到数据中的模式和规律。
神经网络可以把高维度复杂的数据输出为线性可分的语义特征,最后只需要一层线性分类器即可把数据进行分类,这说明倒数第二层的语义特征在高维度中线性可分。本文使用T-SNE(t-Distributed Stochastic Neighbor Embedding)降维方法。T-SNE是一种用于高维数据降维可视化的算法,其主要思想是将高维数据映射到低维空间中,使数据点之间的相对距离在低维空间中保持不变或最大化。
本文将验证集在倒数第二层(全局池化层)输出的语义特征进行降维(图 9)。虽然个别事件被错误分类,但五分类数据集确实线性可分。

|
图 9 T-SNE降维可视化 |
本文提出的五分类算法将输入样本预测为噪声、完整的微震事件、只含P波、只含S波、多个微震事件五类。但在实际应用中,最终需要获得同时包含P波和S波的微地震事件,而五分类算法中的C3与C4样本并不是完整的微震事件。因此,需要通过移动时窗再次处理C3与C4样本,从而得到完整的微震事件用于震源定位。
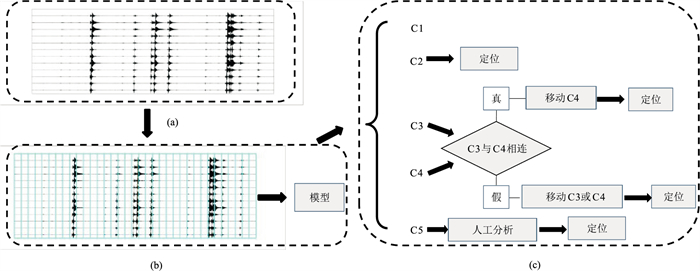
首先,把野外采集的连续波形记录(图 10a)按照长度为1001的时窗(约为500 ms)进行切分(图 10b),不同于二分类模型,五分类样本的时窗没有重叠。得到规定长度时窗后,进行归一化处理,输入到训练好的模型中进行分类;然后利用训练好的ResNet模型把时窗预测为C1、C2、C3、C4和C5五类(图 10c)。C2类型可直接用于微地震定位。通过分析可知,若相邻两个样本预测结果为C3和C4,则大概率是一个微地震事件被截断成两部分,将C3样本向后时移或者C4样本向前时移即可。本文选取200 ms进行时窗移动能够获得完整的微震事件。如果C3或C4类型单独出现,同样向后或者向前移动200 ms,然后用于微地震定位。此外,C5样本情况较为复杂,可以对样本进行人工处理后再用于定位。
|
图 10 基于残差网络的微地震事件检测定位流程图 (a)连续波形记录;(b)样本截取和微地震事件检测;(c)预测结果后续处理 |
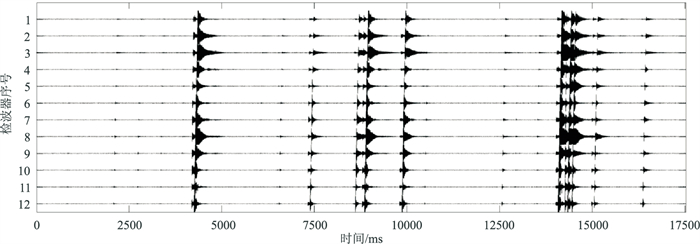
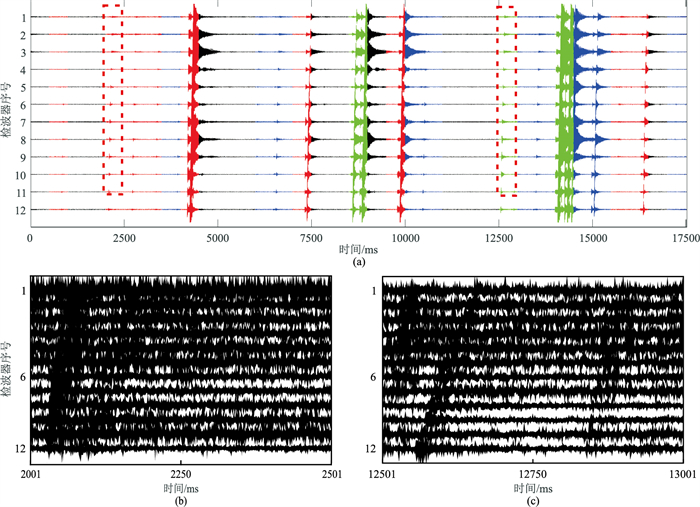
随机选取未用于模型训练的原始波形记录作为测试数据进行模型测试, 数据长度为17517 ms(图 11)。该段数据的水力压裂事件较为密集,信噪比范围较广,可充分测试五分类模型性能。首先,把该测试数据按1001数据点的时窗大小截取,可以得到35个样本。所有样本经过归一化处理后,输入到ResNet模型中进行预测。通过人工检查,测试数据中一共包括23个微地震事件。
|
图 11 测试数据的波形记录 |
把预测结果按照顺序并把不同类别标签的时窗用不同颜色标注出来(图 12a)。据统计,五分类模型预测结果为:9个C2、5个C3、5个C4以及3个C5。其中,相邻两个样本预测结果为C3和C4的情况有3次,为了防止反复拾取,此时只移动C4,故从C3和C4中一共得到7个微地震事件。经过人工检查,3个C5事件一共包含7个微地震事件,故成功拾取的微地震事件个数为23。
|
图 12 测试数据标注图 (a)五分类预测结果。黑色为预测的C1,红色为C2,蓝色为C3或C4,绿色为C5;(b)成功预测为C2的低信噪比事件(放大显示);(c)成功预测为C5的低信噪比事件(放大显示) |
图 12b与图 12c是图 12a中的两个红色虚线框位置的放大图,分别是预测结果为C2与C5的低信噪比事件。该结果表明,ResNet模型有很强的抗噪能力。
然后,将训练好的五分类模型应用到该套水力压裂数据的第14个压裂段的微地震事件检测中。第14个压裂段的压裂时长约为135 min,把该数据按1001数据点(约为500 ms)的时窗大小截取,得到16204个样本。经过统计,该压裂段样本的预测结果为:10889个C1、2830个C2、955个C3、824个C4以及706个C5。预测时间为82 s。本文还利用不重叠时窗的二分类模型对该16204个样本进行预测,预测结果为:12440个C1、3764个C2。
为了评估微地震检测的准确度,利用Zhang等[42]提出的微地震到时拾取泛化模型对检测出的事件进行P、S波到时拾取。该泛化模型的输入为12道三分量波形数据,输出为12道的P波、S波和噪声的概率分布。对于输入时窗的任意一道,可以将两个最大概率值所在横坐标作为拾取的P或S波到时。Zhang等[42]规定这两个拾取点之间的距离需要大于高斯分布半径(20 ms),且拾取点的概率值大于0.7。由于很多检测的事件信噪比较低,拾取模型[42]的泛化能力不足够完全正确拾取P波和S波到时。为了保证定位的准确性,需要剔除拾取结果较差的事件。剔除标准为:①拾取网络只拾取到单震相;②拾取的P波或S波走时个数少于3个;③时窗内包含多个事件。
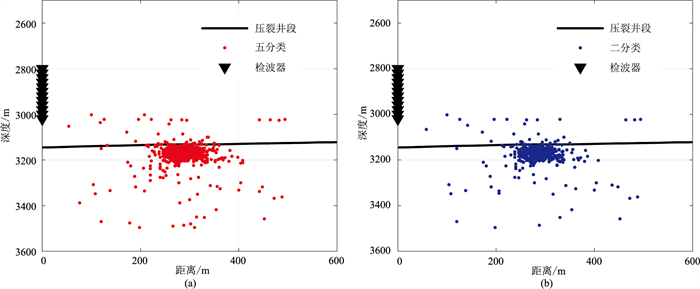
经过剔除拾取结果较差的事件后,最终定位得到的五分类和二分类微震事件数分别为2844个和1789个。文中利用网格搜索的方法进行微地震定位。震源搜索深度为2900~3500 m,水平方向为0~500 m,搜索间隔为2 m。定位结果如图 13所示。定位结果分布在压裂井的附近,较为合理,表明两种模型的检测结果均具有较高的准确度。但五分类检测方法检测出了更多数量的微震事件,进而可更好地监测压裂过程和评估压裂效果。
|
图 13 微地震定位结果 (a)五分类模型检测后定位;(b)二分类模型检测后定位 |
本文提出了一种基于残差网络的微地震事件五分类检测方法。通过有针对性的数据增广方法,用较少的标注数据获得了较高精度的训练模型,模型训练集精度达到99.96%,验证集精度达到99.82%。分别采用五分类与二分类算法对野外监测的连续数据进行检测,并对检测结果进行到时拾取,用于微地震定位。测试结果表明,五分类检测方法检测出了更多数量的微震事件。
值得注意的是,针对信噪比较差的实际数据,如果人工难以给出标签,可以先通过绕射叠加算法(不需要拾取P波和S波到时)进行部分震源定位[43],然后将能定位出事件的时窗作为训练样本,并通过数据增广方法扩充数据集,从而用于模型的训练和后续压裂数据的处理。此外,本文提出的五分类检测算法的泛化性有待进一步测试,未来可针对不同压裂监测数据特征进行重新训练或者使用迁移学习算法以提高网络模型的泛化能力。处理新的工区数据时,只需获得较少的微地震事件,通过文中采用的数据增广方法,便可进行模型训练。
| [1] |
张山, 刘清林, 赵群, 等. 微地震监测技术在油田开发中的应用[J]. 石油物探, 2002, 41(2): 226-231. ZHANG Shan, LIU Qinglin, ZHAO Qun, et al. Application of microseismic monitoring technology in development of oil field[J]. Geophysical Prospecting for Petroleum, 2002, 41(2): 226-231. DOI:10.3969/j.issn.1000-1441.2002.02.021 |
| [2] |
WARPINSKI N. Microseismic monitoring: inside and out[J]. Journal of Petroleum Technology, 2009, 61(11): 80-85. DOI:10.2118/118537-JPT |
| [3] |
MAXWELL S. Microseismic: growth born from success[J]. The Leading Edge, 2010, 29(3): 338-343. DOI:10.1190/1.3353732 |
| [4] |
刘振武, 撒利明, 杨晓, 等. 页岩气勘探开发对地球物理技术的需求[J]. 石油地球物理勘探, 2011, 46(5): 810-818. LIU Zhenwu, SA Liming, YANG Xiao, et al. Needs for geophysical technologies for shale gas exploration[J]. Oil Geophysical Prospecting, 2011, 46(5): 810-818. |
| [5] |
张少华, 邓小江, 冯许魁, 等. 川南地区深层页岩气地球物理勘探技术新进展与攻关方向[J]. 石油地球物理勘探, 2023, 58(1): 238-248. ZHANG Shaohua, DENG Xiaojiang, FENG Xukui, et al. New progress and research direction of geophysical prospecting techniques for deep shale gas in southern Sichuan Basin[J]. Oil Geophysical Prospecting, 2023, 58(1): 238-248. DOI:10.13810/j.cnki.issn.1000-7210.2023.01.025 |
| [6] |
常旭, 李政, 王鹏, 等. 基于频率衰减补偿的微地震定位方法[J]. 地球物理学报, 2018, 61(1): 250-257. CHANG Xu, LI Zheng, WANG Peng, et al. Micro-seismic location based on frequency attenuation compensation[J]. Chinese Journal of Geophysics, 2018, 61(1): 250-257. |
| [7] |
李宏, 杨心超, 朱海波, 等. 水力压裂微地震震源定位与震源机制联合反演研究[J]. 石油物探, 2018, 57(2): 312-320. LI Hong, YANG Xinchao, ZHU Haibo, et al. Joint inversion of source location and microseismic focal mechanism[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 312-320. DOI:10.3969/j.issn.1000-1441.2018.02.017 |
| [8] |
李晗, 姚振兴. 基于"剪切+张裂"一般位错模型频率域求解微震震源机制[J]. 地球物理学报, 2018, 61(3): 905-916. LI Han, YAO Zhenxing. Microseismic focal mechanism inversion in frequency domain based on general dislocation point model[J]. Chinese Journal of Geophysics, 2018, 61(3): 905-916. |
| [9] |
谭玉阳, 胡隽, 张海江, 等. 利用全波形匹配方法确定水力压裂诱发地震震源机制[J]. 地球物理学报, 2019, 62(11): 4417-4436. TAN Yuyang, HU Juan, ZHANG Haijiang, et al. Source mechanism determination for hydraulic fracturing induced seismicity using full-waveform matching[J]. Chinese Journal of Geophysics, 2019, 62(11): 4417-4436. DOI:10.6038/cjg2019M0516 |
| [10] |
LIANG C T, YU Y Y, YANG Y H, et al. Joint inversion of source location and focal mechanism of microseismicity[J]. Geophysics, 2016, 81(2): KS41-KS49. DOI:10.1190/geo2015-0272.1 |
| [11] |
LI L, TAN J Q, SCHWARZ B, et al. Recent advances and challenges of waveform-based seismic location methods at multiple scales[J]. Reviews of Geophysics, 2020, 58(1): e2019RG000667. DOI:10.1029/2019RG000667 |
| [12] |
尹陈, 刘鸿, 李亚林, 等. 微地震监测定位精度分析[J]. 地球物理学进展, 2013, 28(2): 800-807. YIN Chen, LIU Hong, LI Yalin, et al. The precision analysis of the microseismic location[J]. Progress in Geophysics, 2013, 28(2): 800-807. |
| [13] |
WITHERS M, ASTER R, YOUNG C, et al. A comparison of select trigger algorithms for automated global seismic phase and event detection[J]. Bulletin of the Seismological Society of America, 1998, 88(1): 95-106. DOI:10.1785/BSSA0880010095 |
| [14] |
宋维琪, 冯超. 微地震有效事件自动识别与定位方法[J]. 石油地球物理勘探, 2013, 48(2): 283-288. SONG Weiqi, FENG Chao. Automatic identification and location of microseismic effective events[J]. Oil Geophysical Prospecting, 2013, 48(2): 283-288. |
| [15] |
邱磊, 李彩华. STA/LTA方法拾取天然地震波初至及其改进分析[J]. 地球物理学进展, 2023, 38(4): 1497-1506. QIU Lei, LI Caihua. STA/LTA method for picking up the first arrival of natural seismic waves and its improvement analysis[J]. Progress in Geophysics, 2023, 38(4): 1497-1506. |
| [16] |
刘晗, 张建中. 微震信号自动检测的STA/LTA算法及其改进分析[J]. 地球物理学进展, 2014, 29(4): 1708-1714. LIU Han, ZHANG Jianzhong. STA/LTA algorithm analysis and improvement of microseismic signal automatic detection[J]. Progress in Geophysics, 2014, 29(4): 1708-1714. |
| [17] |
AKAIKE H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723. DOI:10.1109/TAC.1974.1100705 |
| [18] |
张唤兰, 朱光明, 王云宏. 基于时窗能量比和AIC的两步法微震初至自动拾取[J]. 物探与化探, 2013, 37(2): 269-273. ZHANG Huanlan, ZHU Guangming, WANG Yanhong. Automatic microseismic event detection and picking method[J]. Geophysical and Geochemical Exploration, 2013, 37(2): 269-273. |
| [19] |
TAN Y Y, HE C. Improved methods for detection and arrival picking of microseismic events with low signal-to-noise ratios[J]. Geophysics, 2016, 81(2): KS93-KS111. DOI:10.1190/geo2015-0213.1 |
| [20] |
HUANG Y H, BEROZA G C. Temporal variation in the magnitude-frequency distribution during the Guy-Greenbrier earthquake sequence[J]. Geophysical Research Letter, 2015, 42(16): 6639-6646. DOI:10.1002/2015GL065170 |
| [21] |
YOON C E, HUANG Y H, ELLSWORTH W L, et al. Seismicity during the initial stages of the Guy-Greenbrier, Arkansas, earthquake sequence[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(11): 9253-9274. DOI:10.1002/2017JB014946 |
| [22] |
刘玉海, 尹成, 潘树林, 等. 基于互相关函数法的地面微地震信号检测研究[J]. 石油物探, 2012, 51(6): 633-637. LIU Yuhai, YIN Cheng, PAN Shulin, et al. Ground microseismic signal detection based on cross correlation function[J]. Geophysical Prospecting for Petroleum, 2012, 51(6): 633-637. DOI:10.3969/j.issn.1000-1441.2012.06.013 |
| [23] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [24] |
HE K M, ZAHNG X Y, REN S Q, et al. Deep residual learning for image recognition[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, 2016: 770-778.
|
| [25] |
ZHU W Q, BEROZA G C. PhaseNet: a deep-neural-network-based seismic arrival-time picking method[J]. Geophysical Journal International, 2019, 216(1): 261-273. |
| [26] |
于子叶, 储日升, 盛敏汉. 深度神经网络拾取地震P和S波到时[J]. 地球物理学报, 2018, 61(12): 4873-4886. YU Ziye, CHU Risheng, SHENG Minhan. Pick onset time of P and S phase by deep neural network[J]. Chinese Journal of Geophysics, 2018, 61(12): 4873-4886. DOI:10.6038/cjg2018L0725 |
| [27] |
MOUSAVI S M, ELLSWORTH W L, ZHU W Q, et al. Earthquake transformer-an attentive deep-learning model for simultaneous earthquake detection and phase picking[J]. Nature Communications, 2020, 11(1): 3952. DOI:10.1038/s41467-020-17591-w |
| [28] |
张逸伦, 喻志超, 胡天跃, 等. 基于U-Net的井中多道联合微地震震相识别和初至拾取方法[J]. 地球物理学报, 2021, 64(6): 2073-2085. ZHANG Yilun, YU Zhichao, HU Tianyue, et al. Multi-trace joint downhole microseismic phase detection and arrival picking method based on U-Net[J]. Chinese Journal of Geophysics, 2021, 64(6): 2073-20852085. |
| [29] |
CHEN Y K. Automatic microseismic event picking via unsupervised machine learning[J]. Geophysical Journal International, 2020, 222(1): 1750-1764. |
| [30] |
陈国艺, 杨文, 谭玉阳, 等. 基于机器学习和台阵相关性的水力压裂微地震事件自动识别及到时拾取[J]. 地球物理学报, 2023, 66(4): 1558-1574. CHEN Guoyi, YANG Wen, TAN Yuyang, et al. Automatic phase detection and arrival picking for microseismic events in hydraulic fracturing based on machine learning and array correlation[J]. Chinese Journal of Geophysics, 2023, 66(4): 1558-1574. |
| [31] |
邓飞, 蒋沛凡, 蒋先艺, 等. 应用图像语义分割网络的微地震事件识别和初至拾取方法[J]. 石油地球物理勘探, 2022, 57(5): 1011-1019. DENG Fei, JIANG Peifan, JIANG Xianyi, et al. Microseismic event recognition and first break picking method based on image semantic segmentation network[J]. Oil Geophysical Prospecting, 2022, 57(5): 1011-1019. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.004 |
| [32] |
李建平, 张硕伟, 丁仁伟, 等. 面向地震波初至智能拾取的超分辨率深度残差方法研究[J]. 石油地球物理勘探, 2023, 58(2): 251-262. LI Jianping, ZHANG Shuowei, DING Renwei, et al. Research on depth residual method of super-resolution for intelligent seismic wave first arrival pickup[J]. Oil Geophysical Prospecting, 2023, 58(2): 251-262. DOI:10.13810/j.cnki.issn.1000-7210.2023.02.002 |
| [33] |
COVA D, 刘洋, 丁成震, 等. 人工智能和视速度约束的地震波初至拾取方法[J]. 石油地球物理勘探, 2021, 56(3): 419-435. COVA D, LIU Yang, DING Chengzhen, et al. First break picking method based on artificial intelligence and apparent velocity constraint[J]. Oil Geophysical Prospecting, 2021, 56(3): 419-435. DOI:10.13810/j.cnki.issn.1000-7210.2021.03.001 |
| [34] |
ZHENG J, SHEN S S, JIANG T Q, et al. Deep neural networks design and analysis for automatic phase pickers from three-component microseismic recordings[J]. Geophysical Journal International, 2020, 220(1): 323-334. DOI:10.1093/gji/ggz441 |
| [35] |
ZHU L J, PENG Z G, MCCLELLAN J, et al. Deep learning for seismic phase detection and picking in the aftershock zone of 2008 MW7.9 Wenchuan earthquake[J]. Physics of the Earth and Planetary Interiors, 2019, 293: 106261. DOI:10.1016/j.pepi.2019.05.004 |
| [36] |
MOUSAVI S M, ZHU W Q, SHENG Y X, et al. CRED: a deep residual network of convolutional and recurrent units for earthquake signal detection[J]. Scientific Reports, 2019, 9(1): 10267. DOI:10.1038/s41598-019-45748-1 |
| [37] |
赵明, 陈石, YUEN D. 基于深度学习卷积神经网络的地震波形自动分类与识别[J]. 地球物理学报, 2019, 62(1): 374-382. ZHAO Ming, CHEN Shi, YUEN D. 2019. Waveform classification and seismic recognition by convolution neural network[J]. Chinese Journal of Geophysics, 2019, 62(1): 374-382. |
| [38] |
ZHAO Z, GROSS L, ZHOU Y, et al. Automatic microseismic event detection using deep learning: a classification is detection method[C]. Extended Abstracts of 81st EAGE Conference and Exhibition, 2019, 1-5.
|
| [39] |
ZHANG H, MA C C, PAZZI V, et al. Deep convolutional neural network for microseismic signal detection and classification[J]. Pure and Applied Geophysics, 2020, 177(12): 5781-5797. DOI:10.1007/s00024-020-02617-7 |
| [40] |
王维波, 徐西龙, 盛立, 等. 卷积神经网络微地震事件检测[J]. 石油地球物理勘探, 2020, 55(5): 939-949. WANG Weibo, XU Xilong, SHENG Li, et al. Detection of microseismic events based on convolutional neural network[J]. Oil Geophysical Prospecting, 2020, 55(5): 939-949. DOI:10.13810/j.cnki.issn.1000-7210.2020.05.001 |
| [41] |
王维波, 官强, 高明, 等. 利用残差网络和地震发射层析成像的微地震事件检测[J]. 石油地球物理勘探, 2022, 57(2): 251-260. WANG Weibo, GUAN Qiang, GAO Ming, et al. Detection of microseismic events based on residual neural network and seismic emission tomography[J]. Oil Geophysical Prospecting, 2022, 57(2): 251-260. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.001 |
| [42] |
ZHANG X, CHEN H H, ZHANG W, et al. Generalized neural network trained with a small amount of base samples: application to event detection and phase picking in downhole microseismic monitoring phase picking neural network[J]. Geophysics, 2021, 86(5): KS95-KS108. DOI:10.1190/geo2020-0955.1 |
| [43] |
田宵, 张雄, 张华, 等. 全干涉成像的微地震定位方法研究[J]. 地球物理学报, 2020, 63(8): 3105-3115. TIAN Xiao, ZHANG Xiong, ZHANG Hua, et al. Full-interferometry imaging method for microseismic location[J]. Chinese Journal of Geophysics, 2020, 63(8): 3105-3115. |



 田宵,江西省南昌市经开区广兰大道418号东华理工大学江西省防震减灾与工程地质灾害探测工程研究中心,330013。Email:
田宵,江西省南昌市经开区广兰大道418号东华理工大学江西省防震减灾与工程地质灾害探测工程研究中心,330013。Email: