2. 北京雁栖湖应用数学研究院, 北京 101408;
3. 中国石油天然气股份 有限公司勘探开发研究院, 北京 100083;
4. 中国石油天然气股份有限公司地球物理重点实验室, 北京 100083
2. Yanqi Lake Beijing Institute of Mathematical Sciences and Applications, Beijing 101408, China;
3. China National Petroleum Corporation Exploration and Development Research Institute, Beijing 100083, China;
4. China National Petroleum Corporation Key Laboratory of Geophysics, Beijing 100083, China
纵波速度、横波速度与岩石密度在地震资料的AVA及AVO分析、叠前地震反演[1-2]、储层物性预测及流体识别[3-5]等方面具有重要作用,尤其对于以测井资料为基础的地震反演,迫切需要横波速度数据。由于横波速度解释难度大、获取成本高,在生产中横波速度数据较缺乏[6],而预测横波速度可有效解决这些问题,具有重要意义。
前人系统研究了横波速度预测,提出了一系列预测方法。这些方法大致分为经验公式法和岩石物理模型法。经验公式法主要以纵波测井数据为基础,通过建立纵波速度、横波速度、孔隙度、岩石矿物组分、泥质含量和密度等参数的关系计算横波速度。Pickett[7]通过分析大量数据给出了灰岩的纵、横波速度经验公式;Castagna等[8]基于测井资料得到了饱水状态下白云岩、砂岩、灰岩与页岩之间的纵、横波速度经验回归公式;Han等[9]研究了孔隙度和黏土含量对波速的影响,得到了75块砂岩样品在不同压力的纵、横波速度线性回归方程。但经验公式法适用于岩石矿物组分相对单一的储层,且受区域限制等因素的影响,不具有普适性,预测精度较低。岩石物理模型法主要根据实际地质条件构建各种岩石物理模型,通过计算岩石的等效弹性参数,进而计算纵波、横波速度。Xu等[10]结合微分等效介质理论、Kuster-Toksöz模型[11]和Gassmann方程[12],提出了砂泥岩地层的横波速度预测模型。随后,人们在岩石物理分析的基础上,发展了各种适用于不同地质条件的横波速度预测模型[13-15]。但在岩石物理建模过程中,需要考虑岩石骨架矿物组分与结构、岩石孔隙结构与连通性、岩石孔隙流体等各种影响因素,并根据不同的实际情况选择合适的岩石物理模型,才能达到预期的目的。
随着机器学习(如深度神经网络,DNN)的快速发展和计算技术的提高,基于机器学习的智能化方法在油气勘探领域引起广泛关注[16-17]。机器学习技术已用于由测井数据预测横波速度[18-21],如支持向量回归(SVR)、门控循环单元(GRU)、长短期记忆网络(LSTM)和梯度增强(GB)。大多数机器学习横波速度预测方法基于纯数据驱动,数据集的质量和数量将直接决定横波预测模型精度。此外,基于纯数据驱动的机器学习方法缺乏充分的物理内涵[17]。
为此,本文基于DNN的方法,假设研究区储层波传播方程的数学形式已知,而弹性参数未知,需通过测井数据训练DNN得到,以确立目的层的波传播方程。利用平面波分析法得到相应的纵波、横波速度,实现神经网络与理论模型的结合。此外,针对传统Xu-White模型的不足,考虑随深度变化的孔隙纵横比,提出了改进横波速度预测岩石物理模型。利用研究区较丰富的测井数据,分别采用构建的神经网络模型和改进横波速度预测岩石物理模型预测横波速度,并与传统的Xu-White模型预测结果进行对比、分析。
1 研究区基本特征及数据 1.1 研究区基本特征鄂尔多斯盆地位于中国中西部地区,是稳定的大型多旋回克拉通盆地,构造形态为一平缓的西倾单斜。鄂尔多斯盆地分为6大构造单元,以天环坳陷和陕北斜坡为主(图 1)——主要的油气分布区,其中面积最大的陕北斜坡是古生界天然气、中生界油的主要赋存单元[22-23]。延长组自上而下分为10个油层组(长1段~长10段),目的层为庆城地区的长7段。长7段主要发育3类页岩油:第1类为多期叠置砂岩发育型,储层主要为中厚层细砂岩,石英、长石含量一般为55%~78%,砂地比大于15%,单砂体厚度大于4 m;第2类为页岩夹薄层砂岩型,储层主要为由泥页岩所夹的薄层细砂岩、粉砂岩,石英、长石含量一般大于50%,砂地比为5%~15%,单砂体厚度为2~5 m;第3类为纯页岩型,储层主要为富有机质暗色泥岩和黑色页岩,石英、长石含量可达50%,加上碳酸盐、黄铁矿等,脆性组分含量可大于70%,砂地比小于5%,单砂体厚度小于2 m[24]。
|
图 1 鄂尔多斯盆地构造单元划分及研究区位置 |
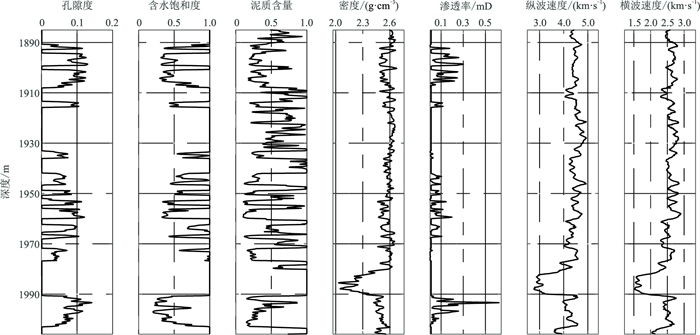
选取研究区19口井的测井数据,经过预处理得到23630个有效数据点,用于训练神经网络和测试。每口井的数据量是不同的,本文选择其中数据点较丰富的3口井(井1~井3)的数据作为测试集,其余的14830个数据点组成训练集,图 2为某井的测井数据。
|
图 2 某井测井数据 |
当储层含有黏弹性流体时,液体的振动速度梯度会产生剪切应变,从而在液体中产生剪应力和附加法向应力。根据牛顿内摩擦定律,并考虑黏性摩擦引起的应力偏量,卢明辉等[25]基于Biot理论[26]推导了含黏滞性流体的多孔介质弹性波传播方程
| $ \left\{\begin{array}{l} A \nabla^2 \boldsymbol{u}+(A+N) \nabla e+Q \nabla \zeta=\rho_{11} \ddot{\boldsymbol{u}}+\rho_{12} \ddot{U}+b(\dot{\boldsymbol{u}}-\dot{U}) \\ Q \nabla e+R \nabla \zeta+\eta \nabla \dot{\zeta}+\eta \nabla^2 \dot{U}=\rho_{12} \ddot{\boldsymbol{u}}+\rho_{22} \ddot{U}-b(\dot{\boldsymbol{u}}-\dot{\boldsymbol{U}}) \end{array}\right.$ | (1) |
其中
| $ \left\{\begin{array}{l}N={\mu }_{\mathrm{b}}\\ A=\frac{(1-\phi )(1-\phi -{K}_{\mathrm{b}}/{K}_{\mathrm{s}}){K}_{\mathrm{s}}+\phi {K}_{\mathrm{b}}{K}_{\mathrm{s}}/{K}_{\mathrm{f}}}{1-\phi -{K}_{\mathrm{b}}/{K}_{\mathrm{s}}+\phi {K}_{\mathrm{s}}/{K}_{\mathrm{f}}}-\frac{2}{3}N\\ Q=\frac{(1-\phi )(1-\phi -{K}_{\mathrm{b}}/{K}_{\mathrm{s}})\phi {K}_{\mathrm{s}}}{1-\phi -{K}_{\mathrm{b}}/{K}_{\mathrm{s}}+\phi {K}_{\mathrm{s}}/{K}_{\mathrm{f}}}\\ R=\frac{{\phi }^{2}{K}_{\mathrm{s}}}{1-\phi -{K}_{\mathrm{b}}/{K}_{\mathrm{s}}+\phi {K}_{\mathrm{s}}/{K}_{\mathrm{f}}}\end{array}\right. $ | (2) |
式中:ρ11、ρ22和ρ12分别为固相、液相和流—固耦合相的密度参数;A、N、Q和R为Biot弹性参数,A和N与拉梅常数
利用平面波分析法得到纵波速度VP、横波速度VS[25]
| $ \left\{\begin{array}{l}{V}_{\mathrm{P}}=\frac{\omega }{\mathrm{R}\mathrm{e}\left({k}_{\mathrm{P}}\right)}\\ {V}_{\mathrm{S}}=\frac{\omega }{\mathrm{R}\mathrm{e}\left({k}_{\mathrm{S}}\right)}\end{array}\right. $ | (3) |
式中:ω为角频率;kP、kS分别为纵波、横波的复波数。
2.2 基于DNN预测VS式(2)中,A、N、Q和R依赖于
| $ \left\{\begin{array}{l}A\left(\tilde{\boldsymbol{X}}\right)\approx \widehat{A}(\tilde{\boldsymbol{X}};{{\vartheta }}_{1})=\varTheta (\tilde{\boldsymbol{X}};{{\vartheta }}_{1})\\ N\left(\tilde{\boldsymbol{X}}\right)\approx \widehat{N}(\tilde{\boldsymbol{X}};{{\vartheta }}_{2})=\varTheta (\tilde{\boldsymbol{X}};{{\vartheta }}_{2})\\ Q\left(\tilde{\boldsymbol{X}}\right)\approx \widehat{Q}(\tilde{\boldsymbol{X}};{{\vartheta }}_{3})=\varTheta (\tilde{\boldsymbol{X}};{{\vartheta }}_{3})\\ R\left(\tilde{\boldsymbol{X}}\right)\approx \widehat{R}(\tilde{\boldsymbol{X}};{{\vartheta }}_{4})=\varTheta (\tilde{\boldsymbol{X}};{{\vartheta }}_{4})\end{array}\right. $ | (4) |
式中:
| $ \left\{\begin{array}{l}{V}_{\mathrm{P}}\approx {\widehat{V}}_{\mathrm{P}}(\boldsymbol{X};\boldsymbol{\vartheta } )\\ {V}_{\mathrm{S}}\approx {\widehat{V}}_{\mathrm{S}}(\boldsymbol{X};\boldsymbol{\vartheta } )\end{array}\right. $ | (5) |
式中
| $ L=\sum\limits_{i=1}^{n}\left({\left|{V}_{\mathrm{P}, i}-{\widehat{V}}_{\mathrm{P}, i}(\boldsymbol{X};\boldsymbol{\vartheta } )\right|}^{2}+{\left|{V}_{\mathrm{S}, i}-{\widehat{V}}_{\mathrm{S}, i}(\boldsymbol{X};\boldsymbol{\vartheta } )\right|}^{2}\right) $ | (6) |
式中:
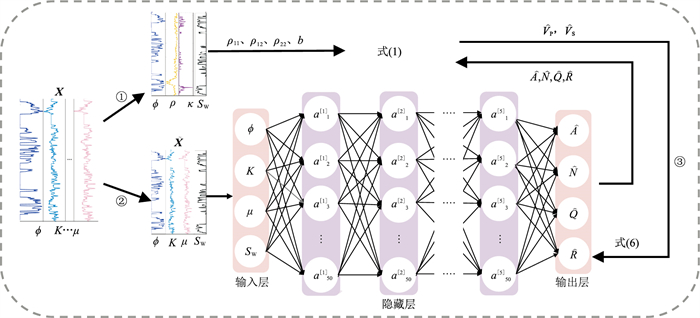
在本文研究过程中假设研究区储层波传播方程的形式与式(1)一致,但其中4个Biot弹性参数是未知的,需通过测井数据训练DNN得到。图 3为基于DNN的VS预测流程。由图可见:①利用X中的
|
图 3 基于DNN的VS预测流程 使用全连接神经网络,共有5个隐藏层,每层有50个单元,如a |
本文采用均方根误差(Root Mean Square Error,RMSE)和决定系数(R2)表达预测值与实际值之间的偏差,以此评价模型的预测效果
| $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{M}\sum\limits_{I=1}^{M}({y}_{I}-{\widehat{y}}_{I}{)}^{2}} $ | (7) |
| $ \left\{\begin{array}{l}{R}^{2}=1-\frac{\sum\limits_{I=1}^{M}({y}_{I}-{\widehat{y}}_{I}{)}^{2}}{\sum\limits_{I=1}^{M}({y}_{I}{-\stackrel{-}{y})}^{2}}\\ \stackrel{-}{y}=\frac{\sum\limits_{I=1}^{M}{y}_{I}}{M}\end{array}\right. $ | (8) |
式中:yI为实际速度值;
在岩石物理建模过程中,计算岩石干骨架弹性模量是重要的一步。Kuster等[11]利用孔隙纵横比(孔隙最短轴与最长轴之比)表征复杂孔隙结构,并基于长波一阶散射理论,建立了弹性模量与孔隙度及孔隙形状间的关系,即K-T模型。随后,Xu等[10]利用K-T模型计算岩石干骨架弹性模量,并由此建立了预测VS的岩石物理模型(Xu-White模型)。K-T模型表达式为
| $ \left\{\begin{array}{l}{K}_{\mathrm{b}}-{K}_{\mathrm{m}}=\mathrm{ }({K}^{\mathrm{*}}-{K}_{\mathrm{m}})\frac{3{K}_{\mathrm{b}}+4{\mu }_{\mathrm{m}}}{9{K}_{\mathrm{m}}+12{\mu }_{\mathrm{m}}}\sum\limits_{l=\mathrm{s}, \mathrm{c}}{\nu }_{l}{T}_{1122}\left({\alpha }_{l}\right)\\ {\mu }_{\mathrm{b}}-{\mu }_{\mathrm{m}}=({\mu }^{\mathrm{*}}-{\mu }_{\mathrm{m}})\frac{6{\mu }_{\mathrm{b}}({K}_{\mathrm{m}}+2{\mu }_{\mathrm{m}})\mathrm{ }+{\mu }_{\mathrm{m}}(9{K}_{\mathrm{m}}+8{\mu }_{\mathrm{m}})}{25{\mu }_{\mathrm{m}}(3{K}_{\mathrm{m}}+4{\mu }_{\mathrm{m}})}\\ \sum\limits_{l=\mathrm{s}, \mathrm{c}}{\nu }_{l}\left[{T}_{1212}\left({\alpha }_{l}\right)\mathrm{ }-\frac{{T}_{1122}\left({\alpha }_{l}\right)}{3}\right]\end{array}\right.\times $ | (9) |
式中:
采用K-T模型计算岩石干骨架弹性模量时,体积模量与剪切模量是相互耦合的。为了简化计算过程,Keys等[28]假设岩石干骨架的泊松比不随
| $ \left\{\begin{array}{l}{K}_{\mathrm{b}}\left(\phi \right)={K}_{\mathrm{m}}{(1-\phi )}^{p}\\ {\mu }_{\mathrm{b}}\left(\phi \right)={\mu }_{\mathrm{m}}{(1-\phi )}^{q}\end{array}\right. $ | (10) |
假设岩石骨架的泊松比为常数时,p和q为一组只与
在Xu-White模型中,设置αs和αc分别为0.1和0.035。然而,
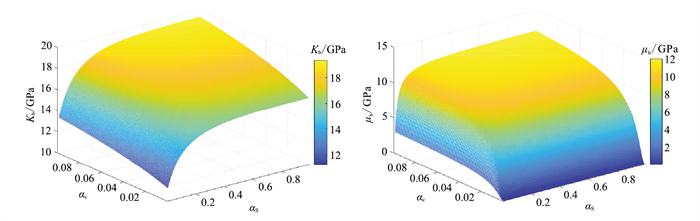
图 4为αs和αc对Kb、μb的影响。由图可见,αs和αc的不同组合会引起岩石干骨架弹性模量的较大变化,例如,当αc=0.06、αs∈[0.2, 0.6]时,Kb增加约10 GPa。因此,对于孔隙结构复杂的储层,不宜忽略αs对岩石干骨架弹性模量的影响。
|
图 4 αs和αc对Kb、μb的影响 |
本文在Xu-White模型的基础上,给出了一种VS预测模型——改进岩石物理模型,该模型与传统Xu-White模型最大的区别在于建模过程中考虑了随深度变化的
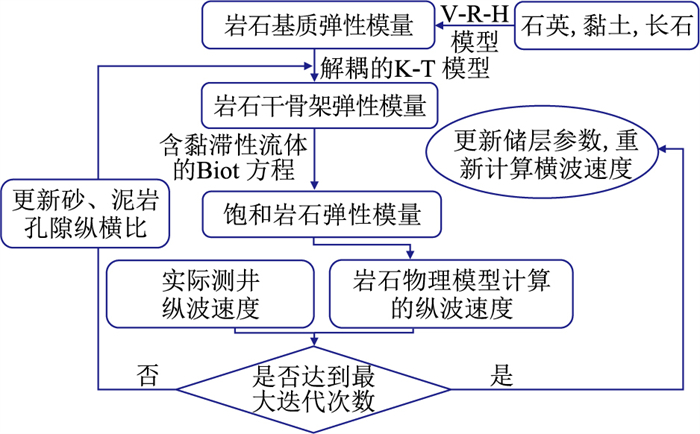
|
图 5 岩石物理建模流程 |
(1)通过Voigt-Reuss-Hill(V-R-H)模型计算岩石基质弹性模量
| $ \left\{\begin{array}{l}{K}_{\mathrm{m}}=\sum\limits_{J=1}^{D}\frac{{K}_{J}({{f}_{J}}^{2}+1)}{2{f}_{J}}\\ {\mu }_{\mathrm{m}}=\sum\limits_{J=1}^{D}\frac{{\mu }_{J}({{f}_{J}}^{2}+1)}{2{f}_{J}}\end{array}\right. $ | (11) |
式中:KJ、
|
|
表 1 矿物和流体的弹性参数[29] |
(2)采用式(10)计算岩石干骨架的弹性模量,由式(3)得到饱和流体岩石的VP、VS。
(3)在VS预测过程中考虑了αl随深度的变化特征,旨在描述复杂的孔隙结构。通过将αs和αc作为未知参数(αs和αc的取值范围分别为0.1~0.4和0.001~0.100),基于误差最小原则,以测井纵波速度VP-log作为观测数据,通过优化算法估算αs和αc,目标函数为
| $ ({\widehat{\alpha }}_{\mathrm{s}}, {\widehat{\alpha }}_{\mathrm{c}})=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}{‖{\boldsymbol{V}}_{\mathrm{P}\mathrm{‑}\mathrm{p}\mathrm{r}\mathrm{e}}({\alpha }_{\mathrm{s}}, {\alpha }_{\mathrm{c}})-{\boldsymbol{V}}_{\mathrm{P}\mathrm{‑}\mathrm{l}\mathrm{o}\mathrm{g}}‖}^{2} $ | (12) |
式中VP-pre为由岩石物理模型计算的纵波速度。
Nur等[30]认为αs与
| $ {\alpha }_{\mathrm{s}}=0.1762{\mathrm{e}}^{-2.22\phi } $ | (13) |
(4)更新储层参数,重新计算VS。
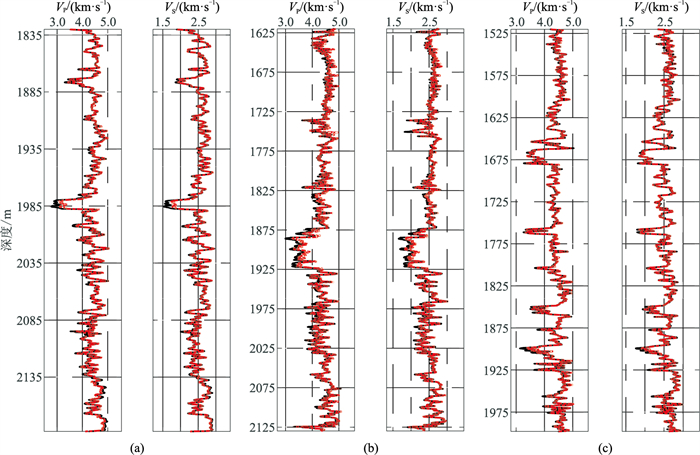
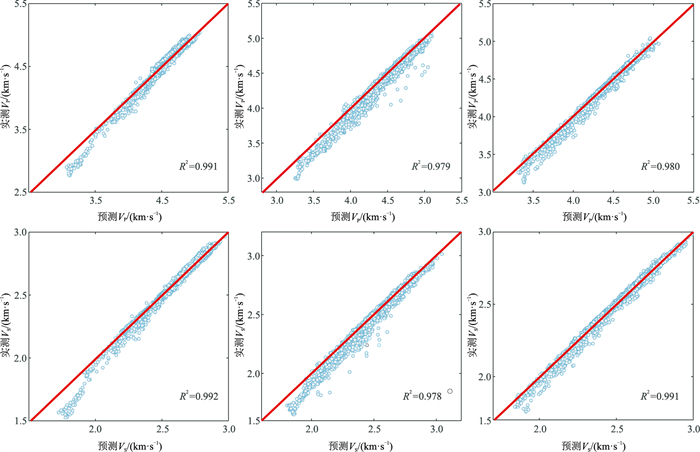
3 预测结果 3.1 深度神经网络预测结果为了分析本文构建的基于DNN的VS预测模型的精度,选用研究区16口井的测井数据(共计14830个数据点)构成训练集,分别将井1、井2和井3的数据点作为测试集测试模型的预测性能。图 6为DNN模型VP、VS预测结果。由图可见,通过DNN模型得到的VP、VS与实际数据吻合度较高。表 2为井1~井3的DNN模型VP、VS预测精度分析。由表可见,基于DNN模型预测的VP、VS的相对均方根误差(R-RMSE)为0.77%~1.41%,R2为0.978~0.992,精度较高。图 7为基于DNN模型预测VP、VS与实际数据交会分析。由图可知,预测结果与实际数据呈明显的正相关,散点基本上落在标准线附近。
|
图 6 DNN模型VP、VS预测结果 (a)井1;(b)井2;(c)井3 黑线为实际测井数据,红线为DNN模型预测结果,图 8同。 |
|
|
表 2 井1~井3的DNN模型VP、VS预测精度分析 |
|
图 7 基于DNN模型预测VP、VS与实际数据交会分析 |
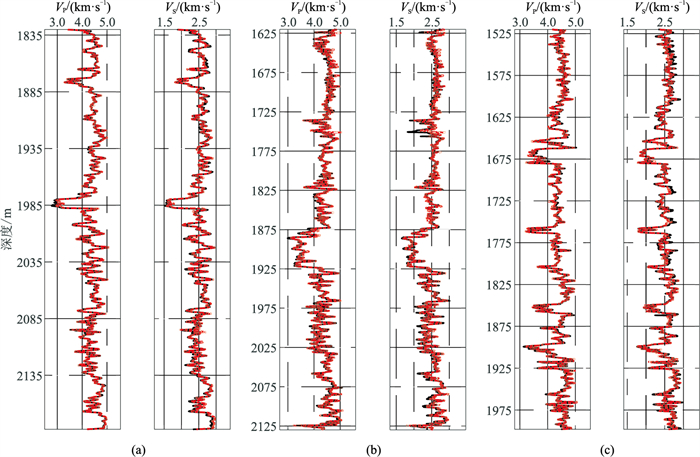
考虑到实际测井资料可能缺失VS数据的情况,无法根据VP、VS和ρ获得饱和流体岩石的弹性模量K和μ。此时直接通过VP和ρ构建与弹性模量间的联系,即令
|
图 8 缺失VS数据时DNN模型VP、VS预测结果 (a)井1;(b)井2;(c)井3 |
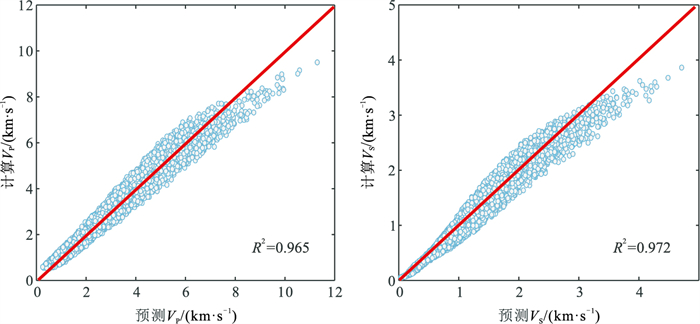
为了验证本文的基于DNN的VS预测方法的普适性,利用蒙特卡罗方法随机生成20000个数据构建合成数据集。在数据生成过程中,假设基本参数是随机独立的,且各参数在一定范围内均匀分布。在空间上随机采样,得到这些基本参数的可能组合,然后根据式(3)计算VP、VS。表 3为7个基本参数的取样范围,取其中12000个数据点作为训练集,其余8000个数据点作为测试集。图 9为基于合成数据由式(3)与DNN模型预测的VP、VS交会图。由图可知,DNN模型与式(3)预测结果呈明显的正相关,总体精度较高,R2分别为0.965和0.972。
|
|
表 3 参数的取样范围[29] |
|
图 9 基于合成数据由式(3)与DNN模型预测的VP、VS交会图 |
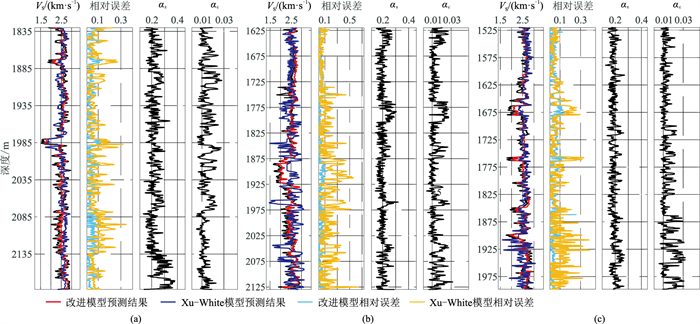
为了验证改进岩石物理模型的有效性,针对井1~井3数据,分别采用改进岩石物理模型与传统的Xu-White模型预测VS,并计算相对误差作为评价指标(图 10)。可见:①改进岩石物理模型的3口井的VS平均相对误差分别为2.20%(图 10a)、3.75%(图 10b)和2.35%(图 10c),相对误差集中在5%以内,而Xu-White模型相对误差较大,对应的平均相对误差分别为8.01%(图 10a)、13.1%(图 10b)和5.25%(图 10c),即改进岩石物理模型的VS预测精度高于Xu-White模型;②αs和αc在纵向变化较大。由于文中考虑了测井数据的建模、预测问题,需要考虑纵向非均质性因素,所以主要引入随深度变化的αs和αc,而横向非均质性不是本文的研究对象。因此,改进岩石物理模型在一定程度上提高了VS预测精度,且αs和αc较好地表征了研究区的复杂孔隙结构特征。
|
图 10 改进岩石物理模型与Xu-White模型VS预测结果、相对误差及αs和αc曲线 (a)井1;(b)井2;(c)井3 |
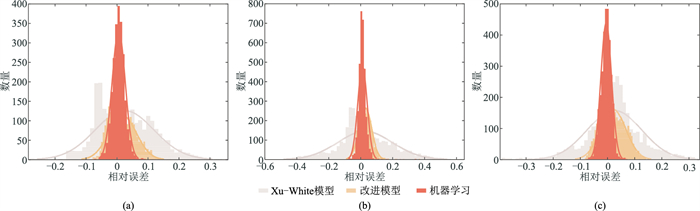
图 11为DNN模型、改进岩石物理模型和Xu-White模型VS预测相对误差直方图。由图可见,DNN模型和改进岩石物理模型均能提高VS预测精度(前者的相对误差主要集中在原点附近,误差较小,后者的相对误差主要集中在10%以内),且改进岩石物理模型预测结果的R2(0.787、0.782和0.721)小于DNN模型,而传统Xu-White模型预测误差较大(最大相对误差达60%)。因此,在数据较丰富时,DNN模型的VS预测精度高于Xu-White模型,但传统岩石物理建模理论不依赖于数据量,在数据较缺乏的条件下,所提改进岩石物理模型的预测结果仅具有参考价值。
|
图 11 DNN模型、改进岩石物理模型和Xu-White模型VS预测相对误差直方图 (a)井1;(b)井2;(c)井3 |
本文针对鄂尔多斯盆地研究区的长7段页岩油层系致密储层,基于DNN和岩石物理模型预测横波速度。在假设已知描述储层波传播方程数学形式的基础上,通过训练机器学习模型得到弹性参数,以此确定储层波传播方程,进而通过平面波分析法得到横波速度。针对传统Xu-White模型,考虑随深度变化的孔隙纵横比,得到改进横波速度预测岩石物理模型。基于DNN模型的方法较依赖数据量,在实际资料充足时的横波速度预测结果较精确,而在实际资料缺乏时,改进岩石物理模型能更好地表征复杂储层的孔隙结构,进而更精确地预测横波速度。因此,由DNN模型和改进岩石物理模型均获得较高精度的横波速度预测结果,且前者的预测效果更好。必须指出,本文采用了全连接神经网络模型,在未来的研究中,可尝试不同的网络模型。
| [1] |
巴晶, 方志坚, 符力耘, 等. 基于可变临界孔隙度模型的致密砂岩储层参数地震反演方法[J]. 地球物理学报, 2023, 66(6): 2576-2591. BA Jing, FANG Zhijian, FU Liyun, et al. Seismic inversion method for tight sandstone reservoir properties based on a variable critical porosity model[J]. Chinese Journal of Geophysics, 2023, 66(6): 2576-2591. |
| [2] |
郭强, 雒聪, 刘红达, 等. 自适应优化参数模拟退火的叠前地震联合反演方法[J]. 石油地球物理勘探, 2023, 58(3): 670-679. GUO Qiang, LUO Cong, LIU Hongda, et al. Prestack seismic hybrid inversion based on simulated annealing algorithm with adaptive optimization parameters[J]. Oil Geophysical Prospecting, 2023, 58(3): 670-679. DOI:10.13810/j.cnki.issn.1000-7210.2023.03.020 |
| [3] |
曲志鹏, 温瑨, 韩宏伟, 等. 基于BISQ模型的储层物性参数贝叶斯反演方法[J]. 石油地球物理勘探, 2023, 58(4): 942-948. QU Zhipeng, WEN Jin, HAN Hongwei, et al. Baye-sian inversion based on BISQ model for reservoir physical properties[J]. Oil Geophysical Prospecting, 2023, 58(4): 942-948. DOI:10.13810/j.cnki.issn.1000-7210.2023.04.019 |
| [4] |
刘诗琼, 刘向君, 孙杨沙, 等. 考虑孔隙结构的砾岩储层物性分类评价方法[J]. 石油地球物理勘探, 2022, 57(4): 926-936. LIU Shiqiong, LIU Xiangjun, SUN Yangsha, et al. Physical property classification and evaluation method based on the pore structure for conglomerate reservoirs[J]. Oil Geophysical Prospecting, 2022, 57(4): 926-936. DOI:10.13810/j.cnki.issn.1000-7210.2022.04.019 |
| [5] |
刘仕友, 段治川, 周凡, 等. 基于布谷鸟算法的储层物性参数同步反演[J]. 石油地球物理勘探, 2022, 57(3): 638-646. LIU Shiyou, DUAN Zhichuan, ZHOU Fan, et al. Simultaneous inversion of petrophysical parameters of reservoir based on cuckoo search algorithm[J]. Oil Geophysical Prospecting, 2022, 57(3): 638-646. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.014 |
| [6] |
武陈月, 印兴耀, 印林杰, 等. 考虑压力的深部页岩储层地震岩石物理建模方法及应用[J]. 石油地球物理勘探, 2023, 58(4): 893-901. WU Chenyue, YIN Xingyao, YIN Linjie, et al. Rock physical modelling for deep shale reservoirs involving the influence of pressure[J]. Oil Geophysical Prospec-ting, 2023, 58(4): 893-901. DOI:10.13810/j.cnki.issn.1000-7210.2023.04.014 |
| [7] |
PICKETT G R. Acoustic character logs and their applications in formation evaluation[J]. Journal of Petroleum Technology, 1963, 15(6): 659-667. DOI:10.2118/452-PA |
| [8] |
CASTAGNA J P, BATZLE M L, EASTWOOD R L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophysics, 1985, 50(4): 571-581. DOI:10.1190/1.1441933 |
| [9] |
HAN D, NUR A, MORGAN D. Effect of porosity and clay content on wave velocity in sandstones[J]. Geophysics, 1986, 51(11): 2093-2107. DOI:10.1190/1.1442062 |
| [10] |
XU S, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [11] |
KUSTER G T, TOKSÖZ M N. Velocity and attenuation of seismic waves in two-phase media: Part Ⅰ. Theoretical formulations[J]. Geophysics, 1974, 39(5): 587-606. DOI:10.1190/1.1440450 |
| [12] |
GASSMANN F. Uber die elastizitatporoser medien[J]. Vier. DerNatur. Gesellschaft in Zurich, 1951, 96(1): 1-23. |
| [13] |
刘致水, 王康宁, 包乾宗, 等. 致密砂岩储层岩石物理横波速度预测方法——以鄂尔多斯盆地延长组为例[J]. 石油学报, 2022, 43(9): 1284-1294. LIU Zhishui, WANG Kangning, BAO Qianzong, et al. Prediction method of rock physics S-wave velocity in tight sandstone reservoir: a case study of Yanchang Formation in Ordos Basin[J]. Acta Petrolei Sinica, 2022, 43(9): 1284-1294. |
| [14] |
FANG Z, BA J, CARCIONE J M, et al. Estimation of the shear-wave velocity of shale-oil reservoirs: a case study of the Chang 7 member in the Ordos Basin[J]. Journal of Seismic Exploration, 2022, 31(1): 81-104. |
| [15] |
杨文强, 宗兆云, 姜曼, 等. 基于等效介质理论的天然气水合物岩石物理建模方法[J]. 石油地球物理勘探, 2021, 56(3): 528-535. YANG Wenqiang, ZONG Zhaoyun, JIANG Man, et al. Rock physics modeling method of natural gas hydrate based on equivalent medium theory[J]. Oil Geophysical Prospecting, 2021, 56(3): 528-535. DOI:10.13810/j.cnki.issn.1000-7210.2021.03.011 |
| [16] |
张少龙, 闫建平, 郭伟, 等. 基于岩石物理相的深层页岩气地质—工程甜点参数测井评价方法——以四川盆地LZ区块五峰组—龙马溪组为例[J]. 石油地球物理勘探, 2023, 58(1): 214-227. ZHANG Shaolong, YAN Jianping, GUO Wei, et al. Logging evaluation method of geological-engineering sweet spot parameters for deep shale gas based on petrophysical facies: A case study of the Wufeng-Longmaxi Formation in LZ block of Sichuan Basin[J]. Oil Geophysical Prospecting, 2023, 58(1): 214-227. DOI:10.13810/j.cnki.issn.1000-7210.2023.01.023 |
| [17] |
XIONG F, BA J, GEI D, et al. Data-driven design of wave-propagation models for shale-oil reservoirs based on machine learning[J]. Journal of Geophysical Research: Solid Earth, 2021. DOI:10.1029/2021JB022665 |
| [18] |
ZHANG Y, WANG D, LI H, et al. S-wave velocity prediction using physical model-driven Gaussian process regression: A case study of tight sandstone reservoir[J]. Geophysics, 2023, 88(2): D85-D93. DOI:10.1190/geo2021-0708.1 |
| [19] |
马乔雨, 张欣, 张春雷, 等. 基于一维卷积神经网络的横波速度预测[J]. 岩性油气藏, 2021, 33(4): 111-120. MA Qiaoyu, ZHANG Xin, ZHANG Chunlei, et al. Shear wave prediction based on one-dimensional convolutional neural network[J]. Lithologic Reservoirs, 2021, 33(4): 111-120. |
| [20] |
王俊, 曹俊兴, 赵爽, 等. 基于深度混合神经网络的横波速度反演预测方法[J]. 中国科学: 地球科学, 2022, 65(4): 724-741. WANG Jun, CAO Junxing, ZHAO Shuang, et al. S-wave velocity inversion and prediction using a deep hybrid neural network[J]. Science China Earth Sciences, 2022, 65(4): 724-741. |
| [21] |
杨庭威, 曹丹平, 杜南樵, 等. 基于深度学习的接收函数横波速度预测[J]. 地球物理学报, 2022, 65(1): 214-226. YANG Tingwei, CAO Danping, DU Nanqiao, et al. Prediction of shear-wave velocity using receiver functions based on the deep learning method[J]. Chinese Journal of Geophysics, 2022, 65(1): 214-226. |
| [22] |
王文枫, 岳大力, 赵继勇, 等. 利用地震正演模拟方法研究地层结构——以鄂尔多斯盆地合水地区延长组三段为例[J]. 石油地球物理勘探, 2020, 55(2): 411-418. WANG Wenfeng, YUE Dali, ZHAO Jiyong, et al. Research on stratigraphic structure based on seismic forward modeling: A case study of the third member of the Yanchang Formation in Heshuiarea, Ordos Basin[J]. Oil Geophysical Prospecting, 2020, 55(2): 411-418. DOI:10.13810/j.cnki.issn.1000-7210.2020.02.020 |
| [23] |
赵玉华, 陈娟, 段毅, 等. 长庆油田GFZ三维可控震源资料关键处理技术[J]. 石油地球物理勘探, 2017, 52(增刊2): 50-55. ZHAO Yuhua, CHEN Juan, DUAN Yi, et al. Key processing techniques for 3D vibroseis data in the GFZ area, Changqing Oilfield[J]. Oil Geophysical Prospecting, 2017, 52(S2): 50-55. DOI:10.13810/j.cnki.issn.1000-7210.2017.S2.009 |
| [24] |
付锁堂, 付金华, 牛小兵, 等. 庆城油田成藏条件及勘探开发关键技术[J]. 石油学报, 2020, 41(7): 777-795. FU Suotang, FU Jinhua, NIU Xiaobing, et al. Accumulation conditions and key exploration and development technologies in Qingcheng oilfield[J]. Acta Petrolei Sinica, 2020, 41(7): 777-795. |
| [25] |
卢明辉, 巴晶, 杨慧珠. 含粘滞流体孔隙介质中的弹性波[J]. 工程力学, 2009, 26(5): 36-40. LU Minghui, BA Jing, YANG Huizhu. Propagation of elastic waves in a viscous fluid-saturated porous solid[J]. Engineering Mechanics, 2009, 26(5): 36-40. |
| [26] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [27] |
ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1957, 241(1226): 376-396. |
| [28] |
KEYS R G, XU S. An approximation for the Xu-White velocity model[J]. Geophysics, 2002, 67(5): 1406-1414. |
| [29] |
MAVKO G, MUKERJI T, DVORKIN J. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media[M](2nd ed). Cambridge University Press, 2009.
|
| [30] |
NUR A, SIMMONS G. Stress-induced velocity anisotropy in rock: An experimental study[J]. Journal of Geophysical Research, 1969, 74(27): 6667-6674. |



 巴晶,江苏省南京市江宁区佛城西路8号河海大学地球科学与工程学院,211100。Email:
巴晶,江苏省南京市江宁区佛城西路8号河海大学地球科学与工程学院,211100。Email: