量子计算(Quantum Computation,QC)是一种遵循量子力学规律,调控量子单元进行计算的新型技术,在算法、软件、硬件等领域[1-5]都有所应用。由于量子力学中叠加态的存在,量子计算天然地具有并行处理信息的能力,为一些复杂问题的求解提供了新思路,受到了工业界和学术界的重视。量子计算的思想起源于20世纪80年代,Feynman[1]首先提出“量子模拟”的构想,即采用基于量子力学理论构建的装置模拟量子体系的演化,Deutsch[2]提出“量子图灵机”的概念并定义了“量子电路模型”,为量子计算的发展奠定了基础。
量子计算是一个广阔的研究领域,作为以量子力学原理为基础而形成的计算体系,可分为构造量子计算机和发展多类型量子计算算法两个方面。
量子计算机是一类遵循量子力学规律、进行逻辑运算并储存、处理量子信息的物理装置。量子计算机的出现和发展推动了量子计算从理论走向实践。近年来,量子计算机的物理实现取得了长足的发展,目前正处于含噪中尺度量子(Noisy Intermediate Scale Quantum, NISQ)计算机阶段,量子比特数目一般在50~100,计算能力超过经典电子计算机,但量子位状态易受干扰,只能在相干时间内处理特定问题,难以完成大规模科学计算[3-4]。通用量子计算机可用于求解任何可解的问题,是量子计算机研制的终极目标。其实现过程需采用基于量子纠错码的有效容错构架并精准调控百万数量级的量子比特,但由于目前对量子态操控技术尚不成熟,实现通用量子计算机仍需要经历一个很长的研究和发展历程[5-7]。
随着量子计算机的研发,学者们也对量子计算算法展开了深入研究。早期的Deutsch-Jozsa算法[8]、Simon算法[9]的提出展示了量子计算相对于经典计算方法的优势。随后,Shor算法[10]、Grover算法[11]分别展示出量子计算在求解代数问题与优化搜索问题方面的强大计算能力。它们相比于已知最优经典算法拥有指数倍加速性能,从而引起了学术界对量子计算算法的广泛关注。如今,可应用于线性系统求解的HHL算法[12]、多种量子智能优化算法[13-15]等的研究明确了量子计算在人工智能领域的应用前景。随着量子计算算法不断成熟,该交叉领域的研究成果将为多学科或领域提供强有力的大数据处理工具。
地球物理学是探测地球内部构造与资源的重要方法,首先通过先进的地球物理仪器测量地下地球物理场[16],进而对所获得的信息进行分析和计算,最后通过地下介质的物理性质的差异得到其结构、构造及资源分布特征[17-18]。近年来,量子效应逐步应用于地球物理领域,量子地球物理探测设备不断向更高精度发展[19],量子计算算法也逐步应用于地球物理模拟、反演等需大量计算的领域。地球物理学作为一门需要高性能计算的学科,需不断发展更适合求解地球物理问题的算法。目前,多种量子智能优化算法已在求解地球物理反问题中取得了很好的效果,有效提高了计算效率和精度[20-21]。这些算法通过引入量子计算概念及数学机制,有效利用了量子计算中的并行性与叠加性的特点,在很大程度上提高了算法性能。此外,量子计算机作为可以高效并行计算、处理信息的硬件装置,可以显著提高计算效率。使用量子计算机求解地球物理问题的实例也初步证明了量子计算硬件方面在本领域的可实现性[22]。由此可见,量子算法因其天然并行性及叠加性显著提高了运算效率,提供了问题求解的新思路;同时,量子计算机也具有高效求解地球物理问题的能力。目前,量子计算从算法和硬件两个方面为地球物理领域带来了求解问题的新思路与里程碑式的进步,具有很强的发展潜力。
本文首先系统介绍了量子计算原理、量子计算机发展概况和常用量子计算算法及其在地球物理学中的应用;然后通过建立理论模型并进行地球物理反问题求解,有效验证了量子算法的可行性与优越性;最后分析了量子计算在地球物理领域存在的问题与挑战,并展望了其发展方向。
1 量子计算原理 1.1 量子比特在经典计算体系中,比特是组成信息的最小单元,有0或1两种状态。而在量子计算体系中,量子比特是处理信息的最基本单元。量子比特除0、1两种基本态外,还可以表示这两种状态的叠加态。即一个量子位为一个定义在一个二维Hilbert空间中的双量子系统,使用Dirac符号表示量子态,记为
| $ \left|\varphi 〉\right.=\alpha \left|0〉\right.+\beta \left|1〉\right. $ | (1) |
式中:
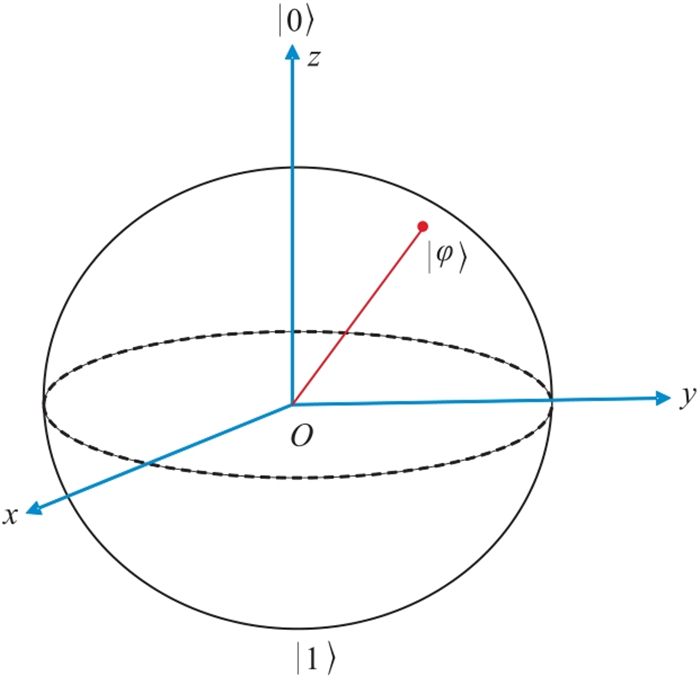
此外,也可以通过Bloch球直观表示量子比特的状态。如图 1所示,Bloch球是量子比特状态作为单位球表面上的点的几何表示。
|
图 1 Bloch球示意图 |
对于n个量子比特系统的状态,可以表示为
| $ \left|\varphi 〉\right.=\sum \limits_{k=1}^{n}{C}_{k}\left|{d}_{1}{d}_{2}\cdots {d}_{n}〉\right. $ | (2) |
式中:
目前,量子计算机通常由两级量子比特系统构成,但实际上也存在着其他信息存储单元,如量子三元(可表示状态0、1、2及它们的叠加态)、量子多元(状态空间可为任意有限维)。因组建量子多元系统难度较大,当前量子计算机还是普遍基于量子比特进行构建,但无论选择哪种系统,它们执行的算法相同,可以互相模拟。
1.2 量子逻辑门1985年,Deutsch[2]描述了量子理论与通用量子计算机的关系,证明量子计算机原则上可以模拟任何物理过程并提出了量子逻辑门的概念。不同于多数传统逻辑门,量子逻辑门必须是可逆的。作为量子计算过程中操作量子位状态的算子,它对应于量子态的演化,可通过Hilbert空间中的酉变换来描述。量子门常用酉矩阵U形式表示,满足
依据所作用的量子比特数的不同,量子门可分为单量子比特门和多量子比特门。表 1列举了常用的量子逻辑门及矩阵表达式。单量子比特门可以通过2
|
|
表 1 常用量子逻辑门 |
在经典物理学中,测量可直接输出处理结果,且不改变系统的属性。当继续测量该系统其他属性时,已完成测量的属性依旧保持观察值。然而,在量子系统中,测量行为对系统状态有很大影响。量子比特通过量子门的操作来转换量子态,但量子态中的信息不可以直接读取,需要测量完成[23]。量子测量通过测量算子
| $ p\left(m\right)=〈\varphi \left|{\boldsymbol{M}}_{m}^{†}{\boldsymbol{M}}_{m}\right|\varphi 〉 $ | (3) |
式中
量子系统在进行测量的过程中引入了测量设备,导致原孤立系统不再封闭,且测量后原量子态塌陷,与测量前的量子态无相干性,故量子测量是不可逆的,也不必满足酉变换。需要注意的是,量子测量只测量某一可观测量的性质,因此对于一个量子系统来说,量子测量只能得到局部关于原量子态的性质。若想要获取量子系统的全部信息,需要进行量子层析,即对系统中的多个可观测量进行量子态测量[24]。
1.4 量子计算特点量子计算遵循量子力学原理,通过量子态的演化实现信息储存与数据计算,利用叠加性、相干性、纠缠性等量子特征,提高了计算速度与储存能力。量子计算具有以下特点。
(1) 并行性。经典计算中,通常是将一个计算任务分配给多个处理器同时执行以达到并行性,而量子计算具独特的叠加性和酉变换本质,可对处于叠加态的所有分量同时变换[1],因此量子计算机处理信息的能力相较于经典计算机有显著提升。
(2) 量子信息存储量大。经典计算中,通过电平的高、低状态分别表示二进制数据0和1,而量子计算中量子比特可以表示叠加态,n个量子比特存储的信息量等同于
(3) 低能耗性。经典计算机不可逆过程导致的热耗散、产生的热耗效应和元件的尺寸效应制约着运算速度。量子计算中的酉变换为可逆变换,可以显著降低能耗。
1.5 量子计算物理实现量子计算机的研究分为量子算法和物理实现两部分。近年来,随着微观控制技术的发展,学者们积极探索了可能实现量子比特的物理系统,如超导量子系统[25]、离子阱系统[26]、光子体系[27-28]、碳化硅系统[29]、冷原子系统[30]等,且已实现从理论基础研究到实用器件研发的突破。其中,超导量子计算和离子阱体系是目前量子计算机物理实现的两个主流方向。
超导量子计算是固态器件路线的一个重要研究领域。超导量子计算的核心元件是约瑟夫森结(Josephson Junction),该元件是一种“超导体—绝缘体—超导体”的三层电子元件,可控制超导宏观波函数的自由度[31-32]。当温度低于临界温度时,电子会以库珀对(Cooper Pair)的形式穿透绝缘体,形成超导电流。超导量子电路的能级结构可通过外加电磁场进行调控,通过选取满足要求的量子态作为基态组成量子比特。基于目前的集成电路工艺,量子电路具有很强的扩展性,因此超导路线在加工制造及与经典计算兼容等方面都具有明显的优势。但是,环境噪声或磁通量噪声所引起的退相干现象(量子态失去相干性,破坏波函数的相位关系,进而变为经典态的现象)以及超导体系运行所需的超低温物理环境仍制约着此技术的发展[25]。目前国内、外诸多团队采用超导路线研制量子计算机,谷歌(Google)公司在2019年发布了53量子比特的超导量子计算机“Sycamore”, 首次实现了量子优越性[12];IBM公司(International Business Machines Corporation)提出了基于量子比特数目、测量误差、软件编译效率等因素综合衡量量子计算机性能的新标准“量子体积”,并于2020年宣布实现了64量子体积的超导量子计算机[33]。潘建伟团队的Wu等[34]、Gong等[35]于2021年发布了62比特可编程超导量子计算机“祖冲之号”及66比特的“祖冲之二号”,实现了量子计算优越性,其中“祖冲之二号”可以实现对量子随机线路取样的快速求解,计算复杂度远高于“Sycamore”。2021年11月,IBM公司发布了含127个量子位的处理器设备“Eagle”,可以探索复杂度更高的问题[36]。2021年12月,浙江大学发布了超导量子芯片“天目1号”[37],实现了高保真度通用量子门。2022年11月,芬兰阿尔托大学(Aalto University)与IQM(IQM Quantum Computers)公司共同研究出一种新的超导量子比特“独角兽”,提高了量子计算的准确性[38]。
离子阱体系通过电荷与电磁场间的相互作用力控制带电粒子的行为,常见系统包括使用射频电场和静电场束缚离子的Paul阱、利用静磁场和电场囚禁电子的Penning阱[39]等。Cirac等[40]将离子阱应用于量子计算中,认定单个离子的内部能级为一个量子比特,通过激光照射影响其量子态。离子阱体系具有较长的相干时间,对量子比特门的保真度较高,可更高效地制备和读出量子态。但该体系的扩展性较差,也难以与经典计算兼容而多应用于科学研究中。2020年,Honeywell团队[41]发布了64量子体积的离子阱量子计算机;同年,IonQ公司Chaoman[42]宣布实现了基于离子阱体系搭载32量子比特并突破400万量子体积的量子计算机。
此外,2020年潘建伟团队的Zhong等[43]基于光量子路线实现了76个光子的量子计算原型机“九章”;2021年成功研制了113个光子的“九章二号”[44]。量子计算机的物理实现方式多种多样,但每种技术路线在实现过程中均存在一定弊端。目前,已研制了用于解决某些问题的专用量子计算机,而通用量子计算机的实现依旧存在技术难题。主要技术难点在于:①量子比特具有不确定性,易导致信息丢失,降低输出结果的准确性,纠错技术对量子比特的保真度要求较高,现有水平难以达到;②构造大规模通用量子计算机需要上千有效量子比特,目前控制量子态及其演化的技术水平有限,无法做到精准调控。
2 量子算法为了确定量子计算能力是否能够超越经典计算方法,学者们开展了大量研究,提出并发展了Shor大数分解算法[10]、Grover量子搜索[11]、量子傅里叶变换(Quantum Fourier Transform,QFT)[45]等新型算法,并结合人工智能技术提出了多种量子机器学习算法,因而对量子计算的计算能力有了进一步的理解。
2.1 量子傅里叶变换傅里叶变换(Fourier Transform,FT)是一种线性积分变换,能够将满足一定条件下的某个函数表示为三角函数或它们的积分线性组合,在多个学科或领域均有着广泛应用[45]。作为数字信号处理领域的重要算法,傅里叶变换可将时域信号转变为频域信号,通常有离散傅里叶变换(Discrete Fourier Transform,DFT)和快速傅里叶变换(Fast Fourier Transform,FFT)。
以时域信号转换为频域信号为例,离散傅里叶变换是傅里叶变换在时域和频域都呈离散的形式,输入为一个N维复向量
| $ \boldsymbol{X}=\left({x}_{0}, \dots , {x}_{N-1}\right)\to \boldsymbol{Y}=({y}_{0}, \dots , {y}_{N-1}) $ | (4) |
| $ {y}_{k}=\frac{1}{\sqrt{N}}\sum \limits_{j=0}^{N-1}{x}_{j}{\mathrm{e}}^{\mathrm{i}2{\rm{ \mathsf{ π}}}jk/N} $ | (5) |
式中k=0, 1, …, N-1。快速傅里叶变换是利用计算机计算离散傅里叶变换的高效、快速计算方法,该算法可大幅度减少变换时所需要的乘法次数。
在量子领域中,存在与离散傅里叶变换相同的映射,即量子傅里叶变换。量子傅里叶变换是处理量子信息的重要手段,也是很多量子算法的基础。可以理解为一个定义在N维Hilbert空间上的离散傅里叶变换,由于量子态的叠加性,将其分配到N维空间中,仅需要
| $ \left|j〉=\right.\frac{1}{N}\sum \limits_{k=0}^{N-1}{\mathrm{e}}^{\frac{\mathrm{i}2\pi jk}{N}}\left|k〉\right. $ | (6) |
对任意状态可描述为
| $ \left|\boldsymbol{x}〉=\right.\sum \limits_{j=0}^{N-1}{x}_{j}\left|j〉\to \left|\boldsymbol{y}〉=\right.\right.\sum \limits_{k=0}^{N-1}{y}_{k}\left|k〉\right. $ | (7) |
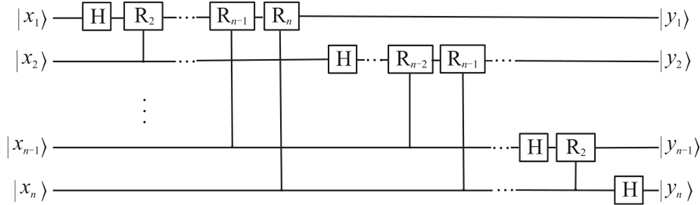
在由n个量子位构成的
|
图 2 量子傅里叶变换线路图 |
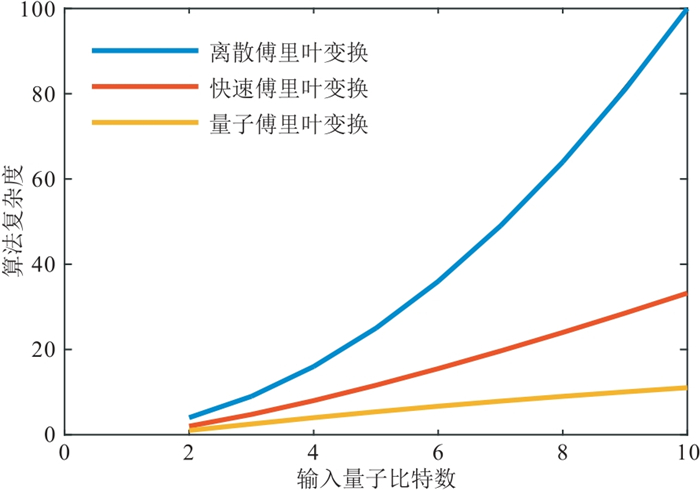
当对于
|
图 3 不同傅里叶变换复杂度对比 |
Shor[10]提出了针对大数质因子分解问题的Shor算法,将大数的质因子分解问题转化为求解函数的周期问题,利用量子计算并行搜索的特点,使用量子手段求解周期,将大数分解问题的时间从指数级缩减到多项式规模。Shor算法的实现对经典公钥密码体制(Public Key Cryptosystem)产生了巨大威胁,使量子计算机受到广泛重视,是量子计算领域里程碑式的事件。
大数分解问题可描述为:设
(1) 随机选取一个大于1的正整数
(2) 设函数
(3) 若
(4) 如果
其中,通过量子傅里叶变换求取函数的周期是Shor算法的核心。首先,对两组存有h个量子比特的寄存器进行酉变换得到纠缠态
关于Shor算法的优化、改进也颇受瞩目,Grifiths等[46]提出使用1量子比特完成量子傅里叶变换的半经典量子傅里叶方法,降低了Shor算法中寄存器的量子比特数;Long等[47-48]提出了利用经典并行加速量子计算算法的思想并在对偶量子计算机上实现了Shor算法;Duan等[49]使用量子点单光子源编译了Shor算法。
2.3 Grover量子搜索算法Grover[11]提出的量子搜索算法,利用量子计算的叠加性与并行性,大大提高了在无序数据库中搜索目标元素的速度。经典计算机完成搜索问题的时间复杂度为
(1) 制备初始叠加态。假设搜索任务有
| $ \left|{s}_{t}\right.〉={H}^{\otimes n}{\left|0\right.〉}^{\otimes n}=\frac{1}{\sqrt{N}}\sum \limits_{x=0}^{N-1}\left|x\right.〉 $ | (8) |
式中n为N项对应的量子比特数。
(2) Oracle操作。Oracle是一个可以识别目标解的酉算子,通过构造一个映射
(3) 通过构造一个酉矩阵,将目标态振幅相对于平均振幅做翻转,从而达到放大目标态概率幅的目的。
(4) 重复迭代并测量。将上述步骤(2)与步骤(3)共称为Grover迭代。随着迭代次数的增加,搜索到目标项的概率也随之改变。
Grover算法实现了对无序数据库搜索的平方量级加速,因其不考虑搜索问题的内部结构,将重心放在对目标元素的搜索上,具有很强的通用性,极大地推动了量子计算技术的发展。一般情况下,Grover算法需要确切知道数据库中待搜索项的数目才能确定最佳迭代次数,Tulsi等[51]和Mizel[52]分别提出了在搜索空间目标数量未知的情况下,搜索成功率随着迭代次数增加而增加的改进算法,这在一定程度上降低了算法的运算速度。Yoder等[53]提出了在保留平方加速条件下迭代一直趋向搜索目标的改进算法。
2.4 量子机器学习算法量子机器学习是结合量子力学与机器学习的交叉领域,一方面借助量子计算的并行性提高传统机器学习算法的效率;另一方面结合量子力学性质,创新更智能的机器学习算法。目前已有的量子机器学习算法主要分为三类:①第一类算法是利用量子计算方法实现机器学习中复杂度较高部分的计算。此类算法沿用经典机器学习算法的框架,但将其中的复杂运算转换为量子版本运行在量子计算机上,从而提高计算效率。代表性成果为量子支持向量机算法[54]。②第二类算法是通过寻找传统机器学习处理流程与量子系统动力学特性的相似点,将物理过程应用于经典算法中,以此提出新的量子机器学习算法。常见有量子退火算法[14]、量子遗传算法[55]、基于量子力学的聚类算法[56]。③第三类算法主要应用于量子物理领域,物理学家们借助传统机器学习方法的数据分析能力来分析量子效应,以对量子物理微观效应有更深层次的了解。其代表为基于压缩感知的量子断层分析[57]等算法。
目前,第二类量子机器学习算法常应用于地球物理问题的优化求解,故下文主要介绍该类量子机器学习算法。在进行优化问题求解时,许多优化算法缺乏完备的理论体系,部分基于自然模型的智能优化算法往往缺乏具体描述算法原理的数学框架。量子力学揭示了微观粒子的运动规律[1],具备完善的理论体系和数学框架。因此,采用量子力学原理描述优化算法的物理模型是可行的。
常见的量子视角下的智能优化算法包括量子退火算法(Quantum Annealing, QA)、量子遗传算法(Quantum Genetic Algorithm,QGA)、量子粒子群算法等[20, 55]。其中,量子退火算法从模型角度引入量子隧穿机制(当粒子总能量小于势垒高度时,该粒子仍能穿透势垒的量子现象),将模拟过程量子化,运用量子力学的框架对问题进行求解。量子退火算法通过薛定谔方程建模,有效提高了寻找最优解的效率[58-59]。类似地,量子粒子群算法通过引入量子理论对传统粒子群算法进行改进。在这一算法中,量子空间中的所有粒子都遵循量子动力学理论,即使用量子力学中的波函数描述粒子位置,并由薛定谔方程决定粒子的状态变化。在此基础上,通过建立量子引力势场束缚粒子运动,将搜索域扩大为全局搜索,有效减小了陷入早熟收敛的概率。而量子遗传算法则通过引入量子计算中的概念和机制提升算法性能[56]。该算法使用量子位编码染色体,通过量子旋转门更新种群,从收敛速度、寻优效率等角度提高了算法的性能。
2.4.1 量子退火算法Metropolis等[58]最早提出了模拟退火算法(Simulated Annealing,SA),它基于固体退火原理,进行随机寻优,即在给定初始温度的条件下,缓慢降低系统温度参数,从而使算法在搜索空间内进行搜索。然而,模拟退火算法的性能在很大程度上取决于温度参数的选取,温度下降过快或过慢都会影响寻优效果。同时,算法所需时间较长且需要反复迭代,搜索易陷入局部最小值。为了解决这些问题,Apolloni等[59]将量子隧穿机制引入模拟退火算法,生成了更大概率寻找全局最优解的量子退火算法。不同于模拟退火算法,量子退火算法将优化问题从模型上视为量子问题,使用量子力学框架对优化问题进行求解。在此思想基础上,该算法通过量子隧穿机制进行全局寻优,降低了求解全局最优解的难度,有效改正了传统算法中降温时间久的缺点并减少了计算量。同时,量子退火算法也证明了优化问题的量子可描述性,并体现出量子理论与优化算法之间的紧密联系。
该算法模型由势能项和动能项两部分组成。势能项为优化目标函数映射在量子系统的势场,动能项为控制量子波动的可控穿透场。算法具体过程为:在经典物理场中引入外界磁场即穿透场,穿透场的初始能量较大,以保障粒子可在整个能量场空间中波动,进而按一定规律减小穿透场能量,直至为零。在穿透场能量减小的过程中,量子系统会逐渐趋于稳定,系统最终达到的稳定态即为寻找的能量基态。
在势能场和动能场的共同作用下,可以用薛定谔方程描述量子系统的演化过程
| $ \left\{\begin{array}{c}\mathrm{i}\mathrm{\hslash }\frac{\partial }{\partial t}\left|\varphi \left(t\right)〉\right.=H\left(t\right)\left|\varphi \left(t\right)〉\right.\\ H\left(t\right)={H}_{\mathrm{c}\mathrm{l}}\left(t\right)+{H}_{\mathrm{k}\mathrm{i}\mathrm{n}}\left(t\right)\end{array}\right. $ | (9) |
式中:
量子退火算法将待求解的目标函数视为量子系统中的势能项,由量子系统的演化过程描述优化算法中的迭代过程。量子退火算法克服了传统退火算法陷入局部最小值的不足,具有更高的收敛效率,可以更高效地求解出全局最优解,在密码学[60-61]、地球物理反演[62]、交通路径[63-65]等领域都有着广泛的应用。
2.4.2 量子遗传算法遗传算法(Genetic Algorithm,GA)是通过模拟达尔文进化论的自然选择和遗传学中生物进化过程的计算模型,对染色体进行编码,并进行交叉、变异等操作繁衍、进化,直到收敛至最适合环境的个体即为算法所求最优解[66]。量子遗传算法是量子理论与遗传算法相结合的优化算法,利用量子位编码代替传统的二进制编码,利用量子旋转门更新种群,加快了算法的搜索速度并具有更强的全局寻优能力[67]。
在量子遗传算法中,具有p个基因的染色体可以表示为
| $ \left|\begin{array}{c}{\alpha }_{1}\\ {\beta }_{1}\end{array}\right|\left|\begin{array}{c}{\alpha }_{2}\\ {\beta }_{2}\end{array}\right|\cdots \left|\begin{array}{c}{\alpha }_{p}\\ {\beta }_{p}\end{array}\right| $ | (10) |
式中
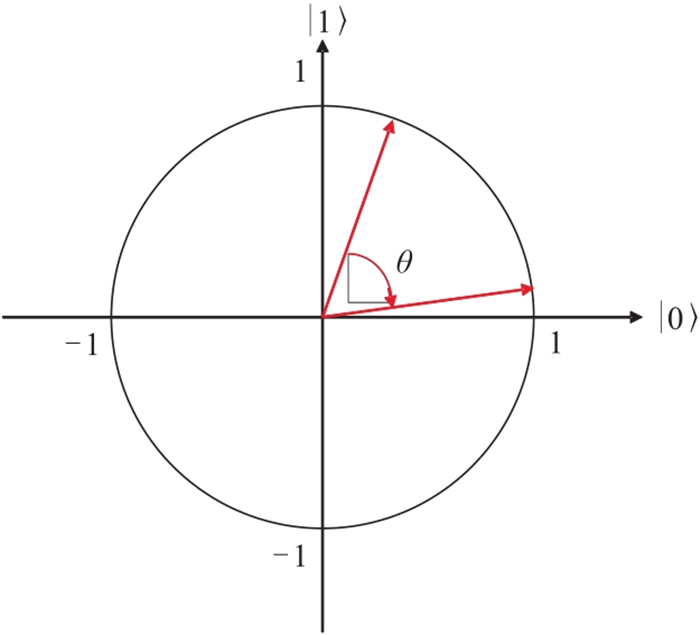
| $ \boldsymbol{G}=\left[\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}\theta & -\mathrm{s}\mathrm{i}\mathrm{n}\theta \\ \mathrm{s}\mathrm{i}\mathrm{n}\theta & -\mathrm{c}\mathrm{o}\mathrm{s}\theta \end{array}\right] $ | (11) |
|
图 4 量子旋转门更新示意图 |
|
|
表 2 旋转角调整策略 |
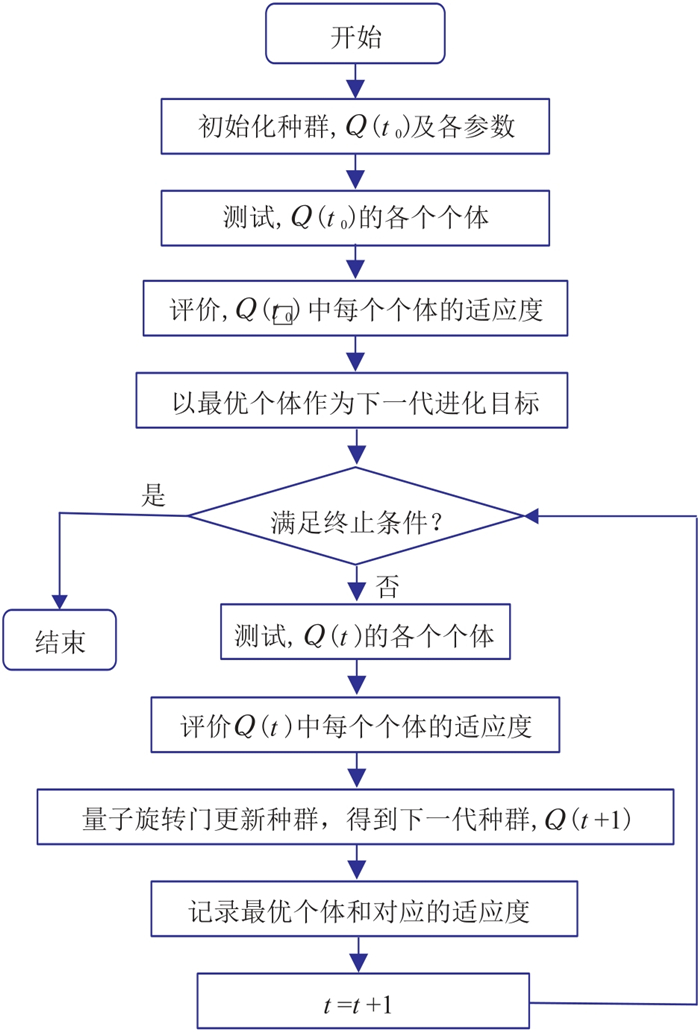
图 5为量子遗传算法的流程图。量子遗传算法结合了传统遗传算法寻求最优解能力突出的特性与量子计算的高效性,许多学者对现有量子遗传算法进行了多方向的改良与优化。杨俊安等[68]提出多宇宙并行量子衍生遗传算法,利用移民和量子交叉两种信息交互方式,有效克服了过早成熟现象;Yin等[69]提出量子免疫克隆算法;李盼池等[70]采用量子比特编码个体,通过Bloch球面绕轴旋转更新个体,提出了量子衍生布谷鸟算法。
|
图 5 量子遗传算法流程图 |
量子地球物理探测技术是使用量子传感器对磁场、重力场等目标场进行有效探测,对深部资源探测及地球精细结构划分有着颠覆性影响。量子传感器是基于量子纠缠、量子干扰、量子态挤压等量子力学特性研制的超高灵敏度的传感器,在工业生产与科学研究中都占据着重要地位[16]。
量子磁场传感器通过磁场对量子自身特性的影响实现高精度测量,主要装备包括铯光泵磁力仪、超导全张量磁探测系统、SERF原子磁力仪等。铯光泵磁力仪以铯原子能级结构为基础,具有较快的响应速度,广泛应用于地面和航空磁探测领域。代表性产品有加拿大Scintrex公司研发的CS-3型和美国Geometrics公司研制的G-824A型[19]。超导全张量磁梯度测量仪将超导磁力仪设计成梯度装置,可测量地磁场矢量三个分量的空间变化率[71]。2021年,中国自然资源航空物探遥感中心与吉林大学合作研发出了适用于高温超导全张量磁梯度测量仪样机,成功获取了试验区全张量磁梯度分布图[72]。
重力梯度是重力位的二阶微分,可以更精准地体现重力位在空间上的变化。高精度重力梯度测量常用于地质调查、地球重力场探测等领域。量子重力梯度仪利用超低温原子团代替惯性质量感应重力作用,不易受到测量区域环境的影响[73-74]。意大利佛罗伦萨大学研制的量子重力梯度仪MAGIA采用单磁光阱多次抛射原子团的方法,对共模噪声抑制效果较好[75]。法国巴黎天文台研发的量子重力梯度仪采用镜面磁光阱技术[76-77]。2022年,英国国家量子技术中心研制出可应用于实验室条件外的量子重力梯度仪,在实地条件下可找到位于地面下方1m处的隧道[78]。目前,国内研制量子重力梯度仪的主要单位有浙江工业大学、中国科学院精密测量科学与技术创新研究院、华中科技大学等[79-80]。
3.2 量子计算在地球物理反问题中的应用地球物理反问题是研究如何将地球物理学中的观测数据映射到相应的地球物理模型的科学问题。典型的地球物理反问题有震源定位[81]、地震层析成像[82]、全波形反演[83-87]、大地电磁测深反演[88-89]、重力异常反演[90]等。求解反问题的核心在于使用可行的反演算法,面对计算数据量越来越大、待求参数更多、结果精度要求更高、地下构造更复杂的地球物理反演现状,如何优化反演算法仍然是重要研究内容。
按照观测数据与地球物理模型参数之间的关系,地球物理反演方法可分为线性反演和非线性反演两类。目前,线性反演方法已形成完整的理论系统并广泛应用,但其对初始模型依赖性较强,处理多极值问题时存在一定限制[17-18, 91]。非线性反演方法将反演问题转化为求解一个泛函极值问题,通过各类优化算法求解[92-93]。寻找收敛速度快、不易陷入局部极小值、计算效率高的反演算法一直以来都是地球物理反演问题的研究重点。近年来,一些学者将量子算法与优化算法相结合形成量子优化算法,并应用于地球物理反演中,取得了较好的效果。
魏超等[20]利用量子退火算法进行大地电磁反演和波阻抗反演,该算法将待反演的模型参数视为量子体系中的粒子,将目标函数做为Hamilton量的势能部分。量子退火反演算法在收敛速度与反演结果精度方面都具有优势,但未能证明该算法不陷入局部最小值的条件且粒子跃迁条件仍需完善。Alulaiw等[94]将量子退火反演算法应用于Cana油田的地震叠前反演;张广智等[95]将量子退火算法引入传统Metropolis‑Hastings方法,通过一个逐渐变小的正变量调整状态接受的概率,提高了反演方法的稳定性和收敛性。王保丽等[96]利用非常快速量子退火算法优化目标函数得出反演结果,该算法采用依赖于温度的似Cauchy分布产生新的扰动模型,加快了收敛速度。Souza等[22]使用D-Wave量子退火计算机求解地下小规模地震反演问题,证明量子计算机适用于地球科学领域。
罗红明等[97]使用量子遗传算法对大地电磁数据进行反演,提高了寻优质量和反演效果。尽管量子遗传算法具有更强的搜索能力,但在一定程度上存在着早期收敛的缺点。对此,师学明等[21]引入自适应量子遗传算法;范建柯等[98]基于搜索步长改进了量子遗传算法。这些改进有效压制了常规遗传算法的早熟收敛性,在实际资料处理中也取得了较好的效果。范建柯等[99]将自适应量子遗传算法引入地震定位中,理论测试证明该方法具有更强大的全局搜索能力、更强的抗噪能力,对台站数量的依赖性较低。Cheng等[100]将混合量子遗传算法应用于非线性AVO反演,该算法结合自适应理论、量子位交叉变异及群体灾变思想,在反演过程中体现了强大的全局搜索能力和较高的计算效率。
聂茹等[101]将量子粒子群算法应用于地震波阻抗反演中,通过概率密度函数以及随机参数进行迭代反演,在收敛速度及反演结果精度方面具有优越性,但该算法的并行性及全局优化能力还有待进一步提升。Jamasb等[102]基于量子行为粒子群算法对重力数据进行非线性反演;Liu等[103]将量子粒子群优化算法引入基于反射率法的地震反演中;Liu等[104]提出了结合量子粒子群优化算法与光滑约束最小二乘算法的瞬变电磁反演算法,在不设置初始模型的情况下仍具有较高的优化效率。
量子算法因其优越性逐渐在地球物理领域有所应用,然而使用量子算法求解地球物理反问题时还存在以下问题需要解决:①由于通用量子计算机尚未实现,目前绝大多数量子优化算法的编程实现都是在基于经典计算机的量子模拟器上进行,并非在量子环境下运行,无法展示真正的量子并行能力,这在一定程度上影响了量子算法的运算效果;②量子优化算法的发展还处于初级阶段,尽管上述算法分别在不同反演领域取得了较好的结果,算法的改进以及更高效率的新算法的提出依旧是值得发展的方向;③优化算法具有广泛的应用领域,其中部分优化算法模型来源于对自然现象的模拟,将其运用至地球物理反问题的求解时,如何就算法体系建立完备的理论模型仍需思考。
3.3 量子计算在地震波场模拟中的应用可能性地震波场数值模拟是认识地震波在地下介质中的传播规律、建立地震响应与储层参数关系的重要手段,在油气勘探与检测、地震灾害预测、地球内部构造研究等领域都有着广泛的应用。尽管模拟算法不断改进优化、计算设备不断更新,模拟复杂介质中的波场依旧是地球物理学中具有挑战性的目标。有限差分法是目前最广泛应用于求解波动方程的算法[105-108]。在频率域,有限差分方法将波动方程的解简化为线性方程组。量子计算的发展为求解线性方程组提供了强有力的计算手段,Harrow等 [12] 提出了HHL(Harrow-Hassidim-Lloyd)算法,相对于经典算法可实现求解速度指数级加速,具体如下。
设A为N×N维的Hermitian矩阵,b和xl均为长度为N的列向量,则求解线性方程组Axl=b可转换为寻找合理的xl=A-1 b的过程。当A为稀疏矩阵且每行或每列最多具有c个非零元时,使用共轭梯度法所需要的时间为
首先对A进行本征值分解,得到
| $ \boldsymbol{A}=\sum \limits_{j}{\lambda }_{j}\left|{u}_{j}〉\right.\left.〈{u}_{j}\right| $ | (12) |
式中:
| $ \left|\boldsymbol{b}〉\right.=\sum \limits_{j}{\beta }_{j}\left|{u}_{j}〉\right. $ | (13) |
此时,待求量子态可表示为
| $ \left|{\boldsymbol{x}}_{\mathrm{l}}〉\right.={\boldsymbol{A}}^{-1}\left|\boldsymbol{b}〉\right.=\sum \limits_{j}{\lambda }_{j}^{-1}{\beta }_{j}\left|{u}_{j}〉\right. $ | (14) |
根据式(12)~式(14),该算法可将求解线性方程问题转化成为求解A的本征值信息。HHL算法并没有将方程组的解直接呈现出来,而是将其编码在量子态中,需要经过后续算法设计提取最终解。
在实际的科学研究与工程计算中,许多问题都与解线性方程组有关,并且绝大多数待求的是高维线性方程组。HHL算法表明,当使用量子计算机求解高维线性方程组时,最高加速比将达到指数级。Ambainis[109]对HHL算法进行改进,降低了算法复杂度对矩阵条件数的依赖。Somma等[110]加强了量子算法对线性问题的求解能力。
多学科(或领域)研究中涉及到线性方程组的求解,地球物理学也不例外。2018年,Moradi等[111]提出了将HHL算法应用于波动方程求解的新思路,并于2019年进行了初步探索。该研究通过分析量子算法模拟地震波场时的计算复杂度以讨论HHL算法的应用前景。研究结果表明,在进行波场模拟时,使用量子算法虽未实现理想的指数倍加速,但计算速度仍优于经典算法[112]。由此可见,量子计算与波场模拟领域的结合是具有研究价值的。若能实现数值模拟方法的量子形式,则会显著减少离散网格数量、提高模拟速度、减少存储空间[113]。目前,使用HHL算法求解线性方程组的研究多是基于量子云平台进行的,因平台提供的量子比特较少,多数研究规模都比较小,基本集中在求解2×2矩阵和4×4矩阵中。由此可见,使用量子算法求解线性方程组仍需探索[114-115]。在未来的研究中,地球物理学家们可以尝试使用并改进HHL算法及其他量子算法求解波动方程,开发可用于求解此问题的量子计算机,提高求解问题的计算效率,更高效地研究复杂介质地震波传播及成像问题。
4 算例分析本文通过设计双层、三层、四层大地电磁理论模型(具体参数设置见表 3),对量子遗传算法与遗传算法的反演效果进行比较,并针对量子遗传算法进行抗噪性分析。其中,遗传算法采用染色体进行编码,种群大小为100,交叉概率为0.9,变异概率为0.1,迭代次数为500。量子遗传算法采用量子位编码,通过量子门旋转更新种群,旋转角策略如表 2所示,种群大小为100,迭代次数为500。
|
|
表 3 理论模型参数 |
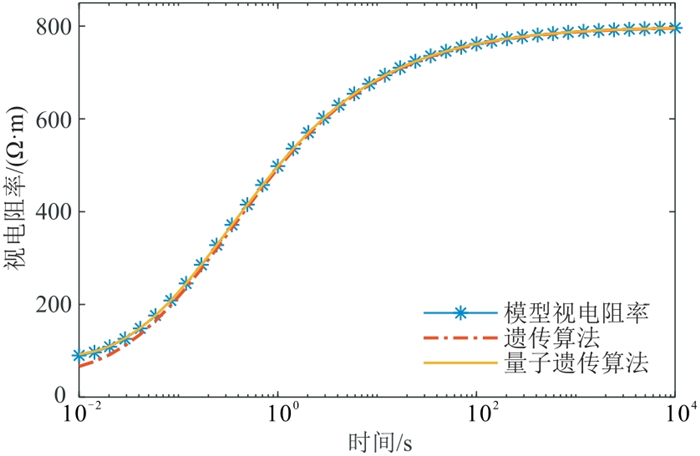
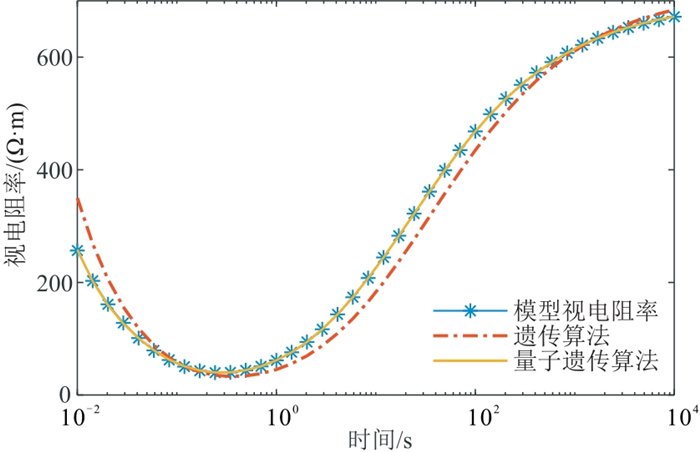
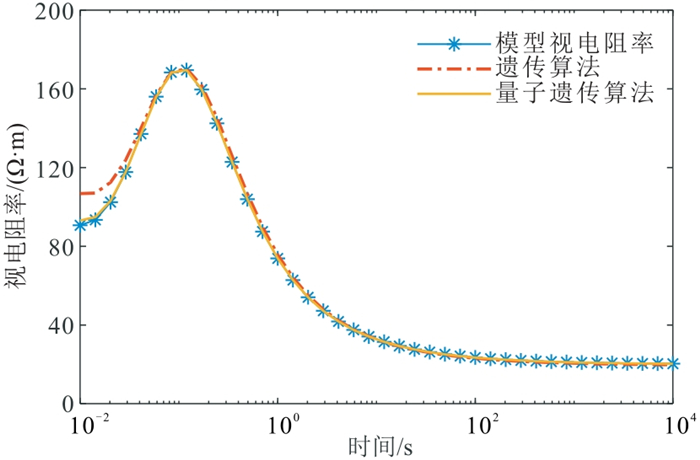
图 6~图 8分别为双层、三层、四层理论模型条件下使用量子遗传算法与遗传算法反演视电阻率曲线效果对比。由图可见,无论是简单模型还是复杂模型,量子遗传算法的反演结果始终相较于遗传算法更接近于理论模型的视电阻率值,这体现了量子遗传算法不依赖于初始模型的优点。同时,传统遗传算法在三个理论模型条件下都存在早熟收敛现象,而量子遗传算法有效地避免了此现象。
|
图 6 双层理论模型视电阻率与不同方法反演结果对比 |
|
图 7 三层理论模型视电阻率与不同方法反演结果对比 |
|
图 8 四层理论模型视电阻率与不同方法反演结果对比 |
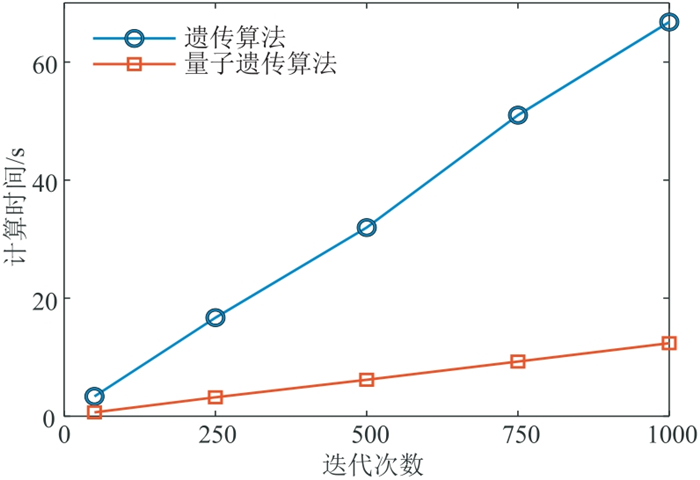
此外,由于量子算法所具有的天然并行性,量子遗传算法的计算时间相对于遗传算法计算时间有了大幅度的降低。比较了两种算法分别在迭代250、500、750、1000次时所需的时间(图 9),可见量子算法所需时间明显缩短,计算效率显著提高。
|
图 9 四层理论模型遗传算法与量子遗传算法不同迭代次数计算时间对比 |
上述对比结果可知:量子遗传算法可以高效搜索全局空间,在提高搜索速度的同时,有效避免了陷入局部极小值,寻优能力较强,且避免了早熟收敛,可以很好地应用于地球物理领域。
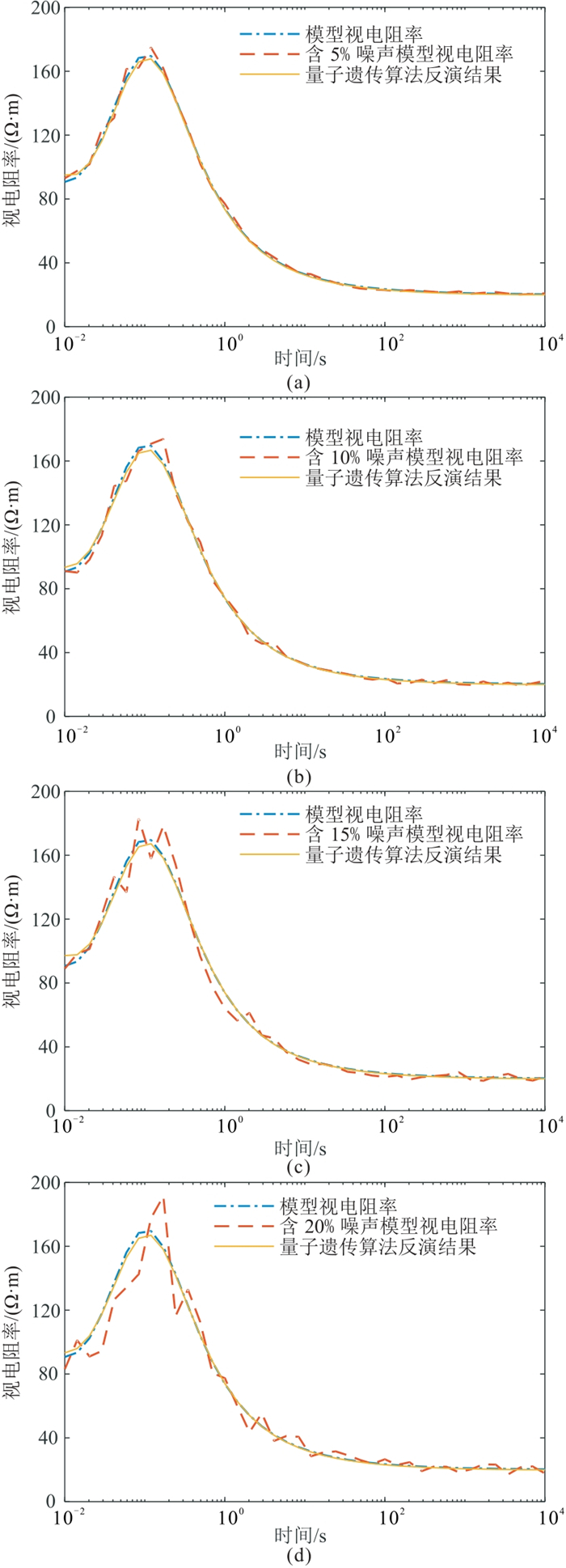
然而,在地球物理实际数据的处理过程中,噪声干扰难以避免,因此将上述四层模型的理论视电阻率数据分别加入不同程度的噪声,用以检验量子遗传算法的抗噪性。由图 10可见,在较复杂模型中加入不同程度噪声时,该算法依旧有很好的反演效果,反演结果与模型理论值十分接近。这也证明了量子遗传算法抗干扰能力强,稳定性高,在含噪数据的处理中将会有很大优势。
|
图 10 不同含噪数据量子遗传算法反演效果 (a)5%噪声;(b)10%噪声;(c)15%噪声;(d)20%噪声 |
从上述两类测试结果可以看出,量子优化算法因其天然并行性在很大程度上提高了计算效率;同时,算法的抗干扰能力相较普通优化算法有显著的提高。这些优势表明量子优化算法在地球物理领域有很大的应用空间。
5 结论与展望由于量子计算在海量信息存储和并行运算能力方面具有特殊优势,近年来已成为受人瞩目的研究领域。目前,其涉及内容包含多个学科(领域),从数学、物理等学科的前沿理论研究到与诸多工程学科的交叉融合,再到应用技术的开发,都为多学科求解复杂计算问题提供了新思路。而在需要高性能计算工具的地球物理领域,量子计算的应用还并未深入,量子计算在地球物理领域具有良好的应用前景。目前,面对着资源勘探走向深部、地下介质模型越来越复杂、反演精度要求越来越高的现状,量子方法这一革新技术具有很大优势,未来可以考虑从以下几方面进行研究。
(1) 量子计算机是基于叠加性、纠缠性等微观体系的量子力学性质,对信息进行逻辑计算、存储、传输的计算装置,通过运行量子算法,量子计算机解决复杂计算问题的速度与效率相较传统计算机有大幅度的提高。但目前对量子状态及其演化的操控能力及“纠错—容错”技术尚不成熟,实现通用量子计算机仍需要一个艰难的历程。而这也导致了许多量子算法无法达到最佳运算效果,对新量子算法的提出也有一定制约。
在地球物理领域,目前已有学者通过专用量子计算机对小尺度地震问题进行求解,初步验证了量子计算机在地球物理领域的可行性。量子计算机的并行处理能力使其能够高效处理海量地球物理数据,在进行复杂介质数值模拟与反演计算等领域有很大的应用潜力。随着量子计算机的不断发展,地球物理学家也可与量子计算机研发专家展开合作,探索如何设计、开发更高效地解决复杂地球物理问题的量子计算机,从而进一步推动地球物理学的发展。
(2) 基于量子力学理论框架的多种量子智能优化算法在地球物理问题的求解中取得了很好的应用效果。但已取得的研究成果仅为交叉领域的一个开端,量子优化算法的应用仍待从以下几方面进行深化探索。首先,需要明确量子优化算法在哪种算法形式及目标函数的作用下可以发挥最大优势;其次,需要探索算法执行过程中的参数选择;最后,目前应用于地球物理反演中的算法多为量子退火算法、量子遗传算法、量子粒子群算法等,如何增强现有方法的实用性,拓宽它们的应用范围,是进一步需要实现的关键问题。同时,如何针对地球物理问题的需要创建高效的量子算法也是未来研究的重要目标。
量子计算无论是理论体系还是物理实现技术路线都与现有信息技术存在极大的差异。自其提出至今的四十多年里,量子计算领域蓬勃发展,为复杂问题的求解提供了新角度、新思路。目前,地球物理勘探对更高效的计算方法有迫切的需求。尽管现在量子计算在地球物理领域的应用尚处于起步阶段,但随着量子计算机的开发与量子算法的改进、创新,相信在未来量子计算必会在地球物理领域有所突破。
| [1] |
FEYNMAN R P. Simulating Physics with Computers[M]// Hey A G C. Feynman and Computation: Exploring the Limits of Computers. Perseus Books, Cambridge, 1999, 133-153.
|
| [2] |
DEUTSCH D. Quantum theory, the Church-Turing principle and the universal quantum computer[J]. Proceedings of the Royal Society A. Mathematical, Physical and Engineering Sciences, 1985, 400(1818): 97-117. |
| [3] |
PRESKILL J. Quantum computing in the NISQ era and beyond[J]. Quantum, 2018, 2: 79. DOI:10.22331/q-2018-08-06-79 |
| [4] |
LAU J W Z, LIM K H, SHROTRIYA H, et al. NISQ computing: where are we and where do we go?[J]. AAPPS Bulletin, 2022, 32(1): 1-30. DOI:10.1007/s43673-021-00031-2 |
| [5] |
GIBNEY E. Physics: Quantum computer quest[J]. Nature, 2014, 516(7529): 24-26. DOI:10.1038/516024a |
| [6] |
BRAINARD J. What's coming up in 2018[J]. Science, 2018, 359(6371): 10-12. DOI:10.1126/science.359.6371.10 |
| [7] |
DYAKONOV M. When will useful quantum computers be constructed? Not in the foreseeable future, this physicist argues. Here's why: The case against[J]. IEEE Spectrum, 2019, 56(3): 24-29. DOI:10.1109/MSPEC.2019.8651931 |
| [8] |
DEUTSCH D, JOZSA R. Rapid solution of problems by quantum computation[J]. Proceedings of the Royal Society A: Mathematical and Physical Sciences, 1992, 439(1907): 553-558. |
| [9] |
SIMON D R. On the power of quantum computation[J]. SIAM Journal on Computing, 1997, 26(5): 1474-1483. DOI:10.1137/S0097539796298637 |
| [10] |
SHOR P W. Algorithms for quantum computation: discrete logarithms and factoring[C]. Proceedings 35th Annual Symposium on Foundations of Computer Science, IEEE, Santa Fe, New Mexico, 1994, 124-134.
|
| [11] |
GROVER L K. Fixed-point quantum search[J]. Physical Review Letters, 2005, 95(15): 150501. DOI:10.1103/PhysRevLett.95.150501 |
| [12] |
HARROW A W, HASSIDIM A, LLOYD S. Quantum algorithm for linear systems of equations[J]. Physical Review Letters, 2009, 103(15): 150502. DOI:10.1103/PhysRevLett.103.150502 |
| [13] |
REBENTROST P, MOHSENI M, LLOYD S. Quantum support vector machine for big data classification[J]. Physical Review Letters, 2014, 113(13): 130503. DOI:10.1103/PhysRevLett.113.130503 |
| [14] |
FINNILA A B, GOMEZ M A, SEBENIK C, et al. Quantum annealing: A new method for minimizing multidimensional functions[J]. Chemical Physics Letters, 1994, 219(5/6): 343-348. |
| [15] |
HAN K H, KIM J H. Genetic quantum algorithm and its application to combinatorial optimization problem[C]. Proceedings of the 2000 Congress on Evolutionary Computation, IEEE, a Jolla, California, 2000, 1354-1360.
|
| [16] |
KNEE G C, BRIGGS G, BENJAMIN S C, et al. Quantum sensors based on weak-value amplification cannot overcome decoherence[J]. Physical Review A, 2013, 87(1): 012115. DOI:10.1103/PhysRevA.87.012115 |
| [17] |
BACKUS G E, GILBERT J F. Numerical applications of a formalism for geophysical inverse problems[J]. Geophysical Journal International, 1967, 13(1/2/3): 247-276. |
| [18] |
BACKUS G, GILBERT F. The resolving power of gross earth data[J]. Geophysical Journal International, 1968, 16(2): 169-205. DOI:10.1111/j.1365-246X.1968.tb00216.x |
| [19] |
KIM B, LEE S, PARK G, et al. Development of an unmanned airship for magnetic exploration[J]. Exploration Geophysics, 2021, 52(4): 462-467. DOI:10.1080/08123985.2020.1827949 |
| [20] |
魏超, 李小凡, 张美根. 量子退火最优化与地球物理反演方法[J]. 地球物理学进展, 2007, 22(3): 785-789. WEI Chao, LI Xiaofan, ZHANG Meigen. Quantum annealing optimization and geophysical inverse method[J]. Progress in Geophysics, 2007, 22(3): 785-789. |
| [21] |
师学明, 范建柯, 罗红明, 等. 层状介质大地电磁的自适应量子遗传反演法[J]. 地球科学(中国地质大学学报), 2009, 34(4): 691-698. SHI Xueming, FAN Jianke, LUO Hongming, et al. Adaptive quantum genetic inversion algorithm for one-dimensional magnetotelluric inverse problem[J]. Editorial Committee of Earth Science-Journal of China University of Geosciences, 2009, 34(4): 691-698. |
| [22] |
SOUZA A M, MARTINS E O, RODITI I, et al. An application of quantum annealing computing to seismic inversion[J]. Frontiers in Physics, 2022, 9: 748285. DOI:10.3389/fphy.2021.748285 |
| [23] |
GIOVANNETTI V, LLOYD S, MACCONE L. Quantum-enhanced measurements: beating the standard quantum limit[J]. Science, 2004, 306(5700): 1330-1336. DOI:10.1126/science.1104149 |
| [24] |
SMITH III J F. Quantum entangled radar theory and a correction method for the effects of the atmosphere on entanglement[C]. Quantum Information and Computation Ⅶ. SPIE, Orlando, Florida, 2009, 73420A.
|
| [25] |
ARUTE F, ARYA K, BABBUSH R, et al. Quantum supremacy using a programmable superconducting processor[J]. Nature, 2019, 574(7779): 505-510. DOI:10.1038/s41586-019-1666-5 |
| [26] |
DEHMELT H G. Radio frequency spectroscopy of stored ions Ⅰ: Storage[J]. Advances in Atomic and Molecular Physics, 1968, 3(c): 53-72. |
| [27] |
KNILL E, LAFLAMME R, MILBURN G J. A scheme for efficient quantum computation with linear optics[J]. Nature, 2001, 409(6816): 46-52. DOI:10.1038/35051009 |
| [28] |
PELUCCHI E, FAGAS G, AHARONOVICH I, et al. The potential and global outlook of integrated photonics for quantum technologies[J]. Nature Reviews Physics, 2022, 4(3): 194-208. |
| [29] |
ZWANENBURG F A, DZURAK A S, MORELLO A, et al. Silicon quantum electronics[J]. Reviews of Modern Physics, 2013, 85(3): 961. DOI:10.1103/RevModPhys.85.961 |
| [30] |
YANG B, SUN H, HUANG C J, et al. Cooling and entangling ultracold atoms in optical lattices[J]. Science, 2020, 369(6503): 550-553. DOI:10.1126/science.aaz6801 |
| [31] |
KWON S, TOMONAGA A, LAKSHMI BHAI G, et al. Gate-based superconducting quantum computing[J]. Journal of Applied Physics, 2021, 129(4): 041102. DOI:10.1063/5.0029735 |
| [32] |
YAN F, KRANTZ P, SUNG Y K, et al. Tunable coupling scheme for implementing high-fidelity two-qubit gates[J]. Physical Review Applied, 2018, 10(5): 054062. DOI:10.1103/PhysRevApplied.10.054062 |
| [33] |
JURCEVIC P, JAVADI-ABHARI A, BISHOP L S, et al. Demonstration of quantum volume 64 on a superconducting quantum computing system[J]. Quantum Science and Technology, 2021, 6(2): 025020. DOI:10.1088/2058-9565/abe519 |
| [34] |
WU Y L, BAO W S, CAO S R, et al. Strong quantum computational advantage using a superconducting quantum processor[J]. Physical Review Letters, 2021, 127(18): 180501. DOI:10.1103/PhysRevLett.127.180501 |
| [35] |
GONG M, WANG S Y, ZHA C, et al. Quantum walks on a programmable two-dimensional 62-qubit superconducting processor[J]. Science, 2021, 372(6545): 948-952. DOI:10.1126/science.abg7812 |
| [36] |
DI PAOLO EMILIO M. IBM advances quantum roadmap with 127-qubit eagle processor [EB/OL]. (2021-11-19)[2023-04-27]. https://www.eetimes.com/ibm-advances-quantum-roadmap-with-127-qubit-eagle-processor/.
|
| [37] |
ZHANG X, JIANG W J, DENG J F, et al. Digital quantum simulation of Floquet symmetry-protected topological phases[J]. Nature, 2022, 607(7919): 468-473. DOI:10.1038/s41586-022-04854-3 |
| [38] |
HYYPPÄ E, KUNDU S M, CHAN C F, et al. Unimon qubit[J]. Nature Communications, 2022, 13(1): 6895. DOI:10.1038/s41467-022-34614-w |
| [39] |
PAUL W, STEINWEDEL H. Notizen: ein neues massenspektrometer ohne magnetfeld[J]. Zeitschrift für Naturforschung a, 1953, 8(7): 448-450. DOI:10.1515/zna-1953-0710 |
| [40] |
CIRAC J I, ZOLLER P. Quantum computations with cold trapped ions[J]. Physical Review Letters, 1995, 74(20): 4091-4094. DOI:10.1103/PhysRevLett.74.4091 |
| [41] |
HONEYWELL TEAM. The world's highest performing quantum computer is here [EB/OL]. (2020-09-15) [2023-04-27]. https://www.honeywell.com/enus/newsroom/news/2020/06/the-worlds-highest-performing-quantum-computer-is-here.
|
| [42] |
CHAOMAN P. Introducing the world's most powerful quantum computer [EB/OL]. (2020-10-01)[2023-04-27]. https://ionq.com/posts/october-01-2020-introducing-most-powerful-quantum-computer.
|
| [43] |
ZHONG H S, WANG H, DENG Y H, et al. Quantum computational advantage using photons[J]. Science, 2020, 370(6523): 1460-1463. DOI:10.1126/science.abe8770 |
| [44] |
ZHONG H S, DENG Y H, QIN J, et al. Phase-programmable gaussian boson sampling using stimulated squeezed light[J]. Physical Review Letters, 2021, 127(18): 180502. DOI:10.1103/PhysRevLett.127.180502 |
| [45] |
FOURIER J B J. The Analytical Theory of Heat[M]. Cambridge: Cambridge University Press, 1878.
|
| [46] |
GRIFFITHS R B, NIU C S. Semiclassical Fourier transform for quantum computation[J]. Physical Review Letters, 1996, 76(17): 3228. DOI:10.1103/PhysRevLett.76.3228 |
| [47] |
LONG G L, XIAO L. Parallel quantum computing in a single ensemble quantum computer[J]. Physical Review A, 2004, 69(5): 052303. DOI:10.1103/PhysRevA.69.052303 |
| [48] |
LONG G L. General quantum interference principle and duality computer[J]. Communications in Theoretical Physics, 2006, 45(5): 825-844. DOI:10.1088/0253-6102/45/5/013 |
| [49] |
DUAN Z C, LI J P, QIN J, et al. Proof-of-principle demonstration of compiled Shor's algorithm using a quantum dot single-photon source[J]. Optics Express, 2020, 28(13): 18917-18930. DOI:10.1364/OE.390209 |
| [50] |
BRASSARD G. Searching a quantum phone book[J]. Science, 1997, 275(5300): 627-628. DOI:10.1126/science.275.5300.627 |
| [51] |
TULSI T, GROVER L K, PATEL A. A new algorithm for fixed point quantum search[J]. Quantum Information & Computation, 2006, 6(6): 483-494. |
| [52] |
MIZEL A. Critically damped quantum search[J]. Physical Review Letters, 2009, 102(15): 150501. DOI:10.1103/PhysRevLett.102.150501 |
| [53] |
YODER T J, LOW G H, CHUANG I L. Fixed-point quantum search with an optimal number of queries[J]. Physical Review Letters, 2014, 113(21): 210501. DOI:10.1103/PhysRevLett.113.210501 |
| [54] |
ANGUITA D, RIDELLA S, RIVIECCIO F, et al. Quantum optimization for training support vector machines[J]. Neural Networks, 2003, 16(5/6): 763-770. |
| [55] |
NARAYANAN A, MOORE M. Quantum-inspired genetic algorithms[C]. Proceedings of IEEE International Conference on Evolutionary Computation, IEEE, Nagoya, 1996, 61-66.
|
| [56] |
HORN D, GOTTLIEB A. Algorithm for data clustering in pattern recognition problems based on quantum mechanics[J]. Physical Review Letters, 2002, 88(1): 018702. |
| [57] |
GROSS D, LIU Y K, FLAMMIA S T, et al. Quantum state tomography via compressed sensing[J]. Physical Review Letters, 2010, 105(15): 150401. DOI:10.1103/PhysRevLett.105.150401 |
| [58] |
METROPOLIS N, ROSENBLUTH A W, ROSENBLUTH M N, et al. Equation of state calculations by fast computing machines[J]. The Journal of Chemical Physics, 1953, 21(6): 1087-1092. DOI:10.1063/1.1699114 |
| [59] |
APOLLONI B, CARVALHO C, DE FALCO D. Quantum stochastic optimization[J]. Stochastic Processes and their Applications, 1989, 33(2): 233-244. DOI:10.1016/0304-4149(89)90040-9 |
| [60] |
王宝楠, 姚皓南, 胡风, 等. 具有稳定性Ising模型局部场系数h和耦合项系数J的量子退火分布式整数分解研究[J]. 中国科学(物理学力学天文学), 2020, 50(3): 127-137. WANG Baonan, YAO Haonan, HU Feng, et al. Quantum annealing distributed integer decomposition study of local field coefficient h and coupling coefficient J with stability Ising model[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2020, 50(3): 127-137. |
| [61] |
HU F, LAMATA L, SANZ M, et al. Quantum computing cryptography: Finding cryptographic Boolean functions with quantum annealing by a 2000 qubit D-wave quantum computer[J]. Physics Letters A, 2020, 384(10): 126214. DOI:10.1016/j.physleta.2019.126214 |
| [62] |
魏超, 朱培民, 王家映. 量子退火反演的原理和实现[J]. 地球物理学报, 2016, 49(2): 577-583. WEI Chao, ZHU Peiming, WANG Jiaying. Quantum annealing inversion and its implementation[J]. Chinese Journal of Geophysics, 2016, 49(2): 577-583. |
| [63] |
CRISPIN A, SYRICHAS A. Quantum annealing algorithm for vehicle scheduling[C]. 2013 IEEE International Conference on Systems, Manchester, 2013, 3523-3528.
|
| [64] |
STOLLENWERK T, O 'GORMAN B, VENTURELLI D, et al. Quantum annealing applied to de-conflicting optimal trajectories for air traffic management[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(1): 285-297. DOI:10.1109/TITS.2019.2891235 |
| [65] |
HUSSAIN H, JAVAID M B, KHAN F S, et al. Optimal control of traffic signals using quantum annealing[J]. Quantum Information Processing, 2020, 19(9): 312. DOI:10.1007/s11128-020-02815-1 |
| [66] |
HOLLAND J H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence[M]. Cambridge: MIT Press, 1992.
|
| [67] |
MALOSSINI A, BLANZIERI E, CALARCO T. Quantum genetic optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(2): 231-241. DOI:10.1109/TEVC.2007.905006 |
| [68] |
杨俊安, 庄镇泉. 多宇宙并行量子衍生遗传算法研究[J]. 计算机工程与应用, 2004, 40(20): 23-26, 61. YANG Jun'an, ZHUANG Zhengquan. Research of multi-universe parallel quantum-inspired genetic algorithm[J]. Computer Engineering and Applications, 2004, 40(20): 23-26, 61. |
| [69] |
YIN Q Y, LI W L, CAO J C. Continuous quantum immune clonal optimization and its application to calculation and analysis of electromagnetic in induction motor[C]. 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems, Xiamen, China, 2010, 364-368.
|
| [70] |
李盼池, 杨淑云, 刘显德, 等. 量子衍生布谷鸟搜索算法[J]. 计算机系统应用, 2017, 26(9): 122-127. LI Panchi, YANG Shuyun, LIU Xiande, et al. Quantum-inspired Cuckoo search algorithm[J]. Computer Systems & Applications, 2017, 26(9): 122-127. |
| [71] |
WU P L, ZHANG Q Y, CHEN L Z, et al. Aeromagnetic compensation algorithm based on principal component analysis[J]. Journal of Sensors, 2018, 2018: 5798287. |
| [72] |
郭华, 王明, 岳良广, 等. 吊舱式高温超导全张量磁梯度测量系统研发与应用研究[J]. 地球物理学报, 2022, 65(1): 360-370. GUO Hua, WANG Ming, YUE Liangguang, et al. Development and application of a full-tensor magnetic gradient measurement system for the cabin HTS[J]. Chinese Journal of Geophysics, 2022, 65(1): 360-370. |
| [73] |
PREVEDELLI M, CACCIAPUOTI L, ROSI G, et al. Measuring the Newtonian constant of gravitation G with an atomic interferometer[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical, and Engineering Sciences, 2014, 372(2026): 20140030. DOI:10.1098/rsta.2014.0030 |
| [74] |
PERRIN I, BIDEL Y, ZAHZAM N, et al. Proof-of-principle demonstration of vertical-gravity-gradient measurement using a single-proof-mass double-loop atom interferometer[J]. Physical Review A, 2019, 99(1): 013601. DOI:10.1103/PhysRevA.99.013601 |
| [75] |
SORRENTINO F, BODART Q, CACCIAPUOTIL, et al. Sensitivity limits of a Raman atom interferometer as a gravity gradiometer[J]. Physical Review A, 2013, 89(2): 023607. |
| [76] |
PEREIRA DOS SANTOS F. Differential phase extraction in an atom gradiometer[J]. Physical Review A, 2015, 91(6): 063615. DOI:10.1103/PhysRevA.91.063615 |
| [77] |
LANGLOIS M, CALDANI R, TRIMECHE A, et al. Differential phase extraction in dual interferometers exploiting the correlation between classical and quantum sensors[J]. Physical Review A, 2017, 96(5): 053624. DOI:10.1103/PhysRevA.96.053624 |
| [78] |
STRAY B, LAMB A, KAUSHIK A, et al. Quantum sensing for gravity cartography[J]. Nature, 2022, 602(7898): 590-594. DOI:10.1038/s41586-021-04315-3 |
| [79] |
吴彬, 周寅, 程冰, 等. 基于原子重力仪的车载静态绝对重力测量[J]. 物理学报, 2020, 69(6): 35-42. WU Bin, ZHOU Yin, CHENG Bing, et al. Static measurement of absolute gravity in truck based on atomic gravimeter[J]. Acta Physica Sinica, 2020, 69(6): 35-42. |
| [80] |
DUAN X C, ZHOU M K, MAO D K, et al. Operating an atom-interferometry-based gravity gradiometer by the dual-fringe-locking method[J]. Physical Review A, 2014, 90(2): 023617. DOI:10.1103/PhysRevA.90.023617 |
| [81] |
WALDHAUSER F, ELLSWORTH W L. A double-difference earthquake location algorithm: Method and application to the northern Hayward fault, California[J]. Bulletin of The Seismological Society of America, 2000, 90(6): 1353-1368. DOI:10.1785/0120000006 |
| [82] |
WOODHOUSE J H, DZIEWONSKI A M. Mapping the upper mantle: Three-dimensional modeling of Earth structure by inversion of seismic waveforms[J]. Journal of Geophysical Research Solid Earth, 1984, 89(B7): 5953-5986. DOI:10.1029/JB089iB07p05953 |
| [83] |
GAUTHIER O, VIRIEUX J, TARANTOLA A. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results[J]. Geophysics, 1986, 51(7): 1387-1403. DOI:10.1190/1.1442188 |
| [84] |
HU W Y, JIN Y C, WU X Q, et al. Progressive transfer learning for low-frequency data prediction in full-waveform inversion[J]. Geophysics, 2021, 86(4): R369-R382. DOI:10.1190/geo2020-0598.1 |
| [85] |
OVCHARENKO O, KAZEI V, ALKHALIFAH T A, et al. Multi-task learning for low-frequency extrapolation and elastic model building from seismic data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-17. |
| [86] |
LIU Y S, TENG J W, XU T, et al. Robust time-domain full waveform inversion with normalized zero-lag cross-correlation objective function[J]. Geophysical Journal International, 2017, 209(1): 106-122. |
| [87] |
刘宇航, 黄建平, 杨继东, 等. 弹性波全波形反演中的四种优化方法对比[J]. 石油地球物理勘探, 2022, 57(1): 118-128. LIU Yuhang, HUANG Jianping, YANG Jidong, et al. Comparison of four optimization methods in elastic full-waveform inversion[J]. Oil Geophysical Prospecting, 2022, 57(1): 118-128. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.013 |
| [88] |
TIKHONOV A N. On determining electric characteristics of the deep layers of the Earth's crust[J]. Doklady Akademii Nauk Sssr, 1950, 73(2): 295-297. |
| [89] |
CAGNIARD L. Basic theory of the magneto-telluric method of geophysical prospecting[J]. Geophysics, 1953, 18(3): 605-635. DOI:10.1190/1.1437915 |
| [90] |
LI Y G, OLDENBURG D W. 3-D inversion of gravity data[J]. Geophysics, 1998, 63(1): 109-119. DOI:10.1190/1.1444302 |
| [91] |
BACKUS G, GILBERT F. Uniqueness in the inversion of inaccurate gross earth data[J]. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1970, 266(1173): 123-192. DOI:10.1098/rsta.1970.0005 |
| [92] |
王一鸣, 宋先海, 张学强. 瑞雷面波频散曲线的粒子群蚁群混合优化反演[J]. 石油地球物理勘探, 2022, 57(2): 303-310, 356. WANG Yiming, SONG Xianhai, ZHANG Xueqiang. Seismic impedance inversion method based on temporal convolutional neural network[J]. Oil Geophysical Prospecting, 2022, 57(2): 303-310, 356. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.007 |
| [93] |
王泽峰, 许辉群, 杨梦琼, 等. 应用时域卷积神经网络的地震波阻抗反演方法[J]. 石油地球物理勘探, 2022, 57(2): 279-286, 296. WANG Zefeng, XU Huiqun, YANG Mengqiong, et al. Seismic impedance inversion method based on temporal convolutional neural network[J]. Oil Geophysical Prospecting, 2022, 57(2): 279-286, 296. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.004 |
| [94] |
ALULAIW B, SEN M K. Prestack Seismic inversion by quantum annealing: Application to Cana field[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 3507-3511.
|
| [95] |
张广智, 赵晨, 涂奇催, 等. 基于量子退火Metropolis-Hastings算法的叠前随机反演[J]. 石油地球物理勘探, 2018, 53(1): 153-160. ZHANG Guangzhi, ZHAO Chen, TU Qicui, et al. Prestack stochastic inversion based on the quantum annealing Metropolis-Hastings algorithm[J]. Oil Geophysical Prospecting, 2018, 53(1): 153-160. DOI:10.13810/j.cnki.issn.1000-7210.2018.01.019 |
| [96] |
王保丽, 蔺营, 张广智, 等. 非均匀介质特征参数地震随机反演方法[J]. 石油地球物理勘探, 2021, 56(6): 1301-1310. WANG Baoli, LIN Ying, ZHANG Guangzhi, et al. Study on seismic stochastic inversion method based on characteristic parameters of inhomogeneous media[J]. Oil Geophysical Prospecting, 2021, 56(6): 1301-1310. DOI:10.13810/j.cnki.issn.1000-7210.2021.06.012 |
| [97] |
罗红明, 王家映, 朱培民, 等. 量子遗传算法在大地电磁反演中的应用[J]. 地球物理学报, 2009, 52(1): 260-267. LUO Hongming, WANG Jiaying, ZHU Peiming, et al. Quantum genetic algorithm and its application in magnetotelluric data inversion[J]. Chinese Journal of Geophysics, 2009, 52(1): 260-267. |
| [98] |
范建柯, 师学明, 吴时国, 等. 基于子空间的二维大地电磁量子遗传反演法研究[J]. 地球物理学报, 2011, 54(10): 2682-2689. FAN Jianke, SHI Xueming, WU Shiguo, et al. A study of 2-D magnetotelluric quantum genetic inversion algorithm based on subspace[J]. Chinese Journal of Geophysics, 2011, 54(10): 2682-2689. |
| [99] |
范建柯, 丁志峰, 徐小明, 等. 基于自适应量子遗传算法的地震重定位及其在山东地区的应用[J]. 地球物理学报, 2016, 59(11): 4075-4088. FAN Jianke, DING Zhifeng, XU Xiaoming, et al. Seismic relocation based on Adaptive Quantum Genetic Algorithm and its application to the Shandong area[J]. Chinese Journal of Geophysics, 2016, 59(11): 4075-4088. |
| [100] |
CHENG J W, ZHANG F, LI X Y. Nonlinear amplitude inversion using a hybrid quantum genetic algorithm and the exact zoeppritz equation[J]. Petroleum Science, 2022, 19(3): 1048-1064. DOI:10.1016/j.petsci.2021.12.014 |
| [101] |
聂茹, 岳建华. 量子微粒群在波阻抗反演中的应用[J]. 计算机工程与应用, 2009, 45(5): 23-25, 28. NIE Ru, YUE Jianhua. Quantum Particle Swarm Optimization impedance inversion and its implementation[J]. Computer Engineering and Applications, 2009, 45(5): 23-25, 28. |
| [102] |
JAMASB A, MOTAVALLI-ANBARAN S H, ZEYEN H. Non‐linear stochastic inversion of gravity data via quantum‐behaved particle swarm optimization: Application to Eurasia-Arabia collision zone (Zagros, Iran)[J]. Geophysical Prospecting, 2017, 65(S1): 274-294. DOI:10.1111/1365-2478.12558 |
| [103] |
LIU X Y, CHEN X H, CHEN L, et al. Nonlinear prestack inversion using the reflectivity method and quantum particle swarm optimization[J]. Journal of Seismic Exploration, 2020, 29(4): 305-326. |
| [104] |
LIU X, PAN C W, ZHENG F K, et al. Transient electromagnetic 1-dimensional inversion based on the quantum particle swarms optimization-smooth constrained least squares joint algorithm and its application in karst exploration[J]. Advances in Civil Engineering, 2022, 2022: 1555877. |
| [105] |
ALTERMAN Z, Jr KARAL F C. Propagation of elastic waves in layered media by finite difference methods[J]. Bulletin of the Seismological Society of America, 1968, 58(1): 367-398. |
| [106] |
ALFORD R M, KELLY K R, BOORE D M. Accuracy of finite‐difference modeling of the acoustic wave equation[J]. Geophysics, 1974, 39(6): 834-842. DOI:10.1190/1.1440470 |
| [107] |
KELLY K R, WARD R W, TREITEL S, et al. Synthetic seismograms; a finite-difference approach[J]. Geophysics, 1976, 41(1): 2-27. DOI:10.1190/1.1440605 |
| [108] |
杨庆节, 刘财, 郭智奇, 等. 基于BISQ模型双相各向同性介质弹性波传播的频率—空间域有限差分模拟[J]. 地球物理学进展, 2015, 30(1): 249-260. YANG Qingjie, LIU Cai, GUO Zhiqi, et al. Wave propagation in two-phase isotropic medium based on BISQ model in frequency-space domain[J]. Progress in Geophysics, 2015, 30(1): 249-260. |
| [109] |
AMBAINIS A. Variable time amplitude amplification and quantum algorithms for linear algebra problems[C]. 29th Symposium on Theoretical Aspects of Computer Science (STACS 12), Dagstuhl, 2012, 636-647.
|
| [110] |
SOMMA R, CHILDS A, KOTHARI R. Quantum linear systems algorithm with exponentially improved dependence on precision[C]. APS March Meeting Abstracts, Baltimore, 2016, H44-001.
|
| [111] |
MORADI S, TRAD D, INNANEN K A. Quantum computing in geophysics: Algorithms, computational costs, and future applications[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 5520.
|
| [112] |
MORADI S, TRAD D, INNANEN K A. When quantum computers arrive on seismology's doorstep[J]. Canadian Journal of Exploration Geophysics, 2019, 44(1): 1-20. |
| [113] |
BIAMONTE J, WITTEK P, PANCOTTI N, et al. Quantum machine learning[J]. Nature, 2017, 549(7671): 195-202. DOI:10.1038/nature23474 |
| [114] |
CAI X D, WEEDBROOK C, SU Z E, et al. Experimental quantum computing to solve systems of linear equations[J]. Physical Review Letters, 2013, 110(23): 230501. DOI:10.1103/PhysRevLett.110.230501 |
| [115] |
CAO Y D, DASKIN A, FRANKEL S, et al. Quantum circuit design for solving linear systems of equations[J]. Molecular Physics, 2012, 10(15-16): 1675-1680. |



 刘财, 吉林省长春市朝阳区西民主大街938号吉林大学朝阳校区地球探测科学与技术学院,130061。Email:
刘财, 吉林省长春市朝阳区西民主大街938号吉林大学朝阳校区地球探测科学与技术学院,130061。Email: