2. 长江大学油气资源与勘探技术教育部重点实验室, 湖北武汉 430100
2. Key Laboratory of Petroleum Resources and Exploration Technology of Ministry of Education, Yangtze University, Wuhan, Hubei 430100, China
瞬变电磁勘探方法是地球物理勘探方法中电磁法的一个重要分支,具有探测精度高、深度大、施工效率高及对低阻异常体反应敏感等优势[1-3]。美国科学家于1933年首先提出瞬变电磁法的概念,并应用于地球物理勘探领域。在20世纪中期开始开展瞬变电磁野外实验,但是当时人们并没有意识到瞬变电磁方法的发展前景[4]。1973年Wait等[5]针对瞬变电磁法寻找金属矿藏提出了一套完整的开发步骤,但该方法仍然未得到推广应用。这种情况一直持续到20世纪70年代,之后瞬变电磁一维层状水平介质的理论推导才逐步完善,瞬变电磁法开始应用于实际勘探。西方国家对瞬变电磁反演的研究较早,1991年,Nabighian等[6]提出,电流环产生的磁场可以等效为地下产生的感应涡流场,并据此总结了地层沿深度方向的电阻率变化规律;Leppin[7]通过有限差分算法实现了回线源瞬变电磁场的数值模拟。Miernik等[8]等对长偏移距瞬变电磁法和中心回线瞬变电磁法进行联合反演的方法,并将该方法应用到了火山泥电阻测量当中,取得了较好的效果。在中国,殷长春等[9]早在20世纪70年代就把脉冲式航电仪应用于矿藏探测和地质填图,开启了瞬变电磁研究的先河。为了解决频时转换导致的瞬变电磁晚期响应计算精度偏低的问题,王华军[10]首先将余弦变换算法引入中国,实现了瞬变电磁法时间域到频率域的转换。李建慧等[11-12]从垂直磁偶源激发的电场出发,推导了矩形发射回线激发的频率域电场响应公式,采用逆拉普拉斯变换算法实现了瞬变电磁场的正演模拟。
目前,瞬变电磁数据反演方法主要分为两大类:一类是“烟圈”反演,另一类是最优化反演[13]。“烟圈”反演由纳比吉安提出,主要基于实测瞬变电磁数据研究电阻率与深度的关系,进而开展反演[14]。虽然该方法精度不高,但是不依赖初始模型且计算速度快,通常情况下其反演结果可用于定性解释。最优化反演法将初始模型代入正演算法,通过不断修改模型实现正演结果与实测数据的最佳拟合[15]。差分进化(Diffe-rential Evolution,DE)算法是一种基于群体差异的启发式随机搜索算法,优点是原理简单、受控参数少、鲁棒性强,适于求解不连续、不可微、或者没有函数解析式的全局优化问题,在地球物理领域的资料处理领域获得了广泛应用[16-17]。熊杰等[18]将差分进化算法应用于大地电磁一维反演,对加噪理论模型数据进行了一系列反演试算,反演结果表明该方法反演效果不依赖于初始模型,具有良好的抗噪能力与全局优化能力。董莉等[19]基于Dias复电阻率模型的MT正演数据提出了基于自适应差分进化算法的MT信号激电信息提取方法。王天意等[20]提出了改进差分进化(TDE)算法,将其应用于MT反演,实现了MT的一维及二维完全非线性反演。
然而,现阶段将差分进化算法应用于电磁勘探领域还处于探索阶段,未能广泛应用于实际生产。因此,如何将该方法与实际生产相结合是急需探讨的问题。反向学习(Opposition-based Learning,OBL)[21]是一种基于对立学习的优化策略。本文将差分进化算法应用于时间域瞬变电磁一维反演,并在常规差分进化算法中引入基于反向学习策略的种群初始化及控制参数自适应调节,可明显提高计算效率与精度。相较于常规反演方法,本文算法的收敛效果不依赖于初始模型与目标模型的拟合程度,降低了反演陷入局部极值的可能性。
1 方法原理 1.1 基于Cole-Cole模型的有限长时域电磁一维正演理论由于时域瞬变电磁响应包含激发极化(IP)效应,将频率域的激电模型引入电偶源频率域正演,计算含IP效应的频率域电磁场响应,再通过时频转换得到包含IP效应的时间域电磁场。本文基于Cole-Cole模型[22]研究考虑激电效应的有限长电性源瞬变电磁法的一维正反演研究。
1.1.1 频率域Cole-Cole模型频率域Cole-Cole模型的数学表达式为
| $ \rho \left(\omega \right)={\rho }_{0}\left\{m\left[1-\frac{1}{1+{\left(\mathrm{j}\omega \tau \right)}^{c}}\right]\right\} $ | (1) |
式中:ω=2πf表示圆频率,其中f表示频率;ρ(ω)与
在实际勘探中,发射源一般为有限长导线源。为了准确模拟有限长导线源产生的电磁响应,本文采用高斯勒让德积分法对有限长源的电磁响应进行求解[23],这样可以利用有限次数的迭代得到理想的结果,减少计算时间。
如图 1所示,设有限长源沿x轴布设,有限长源AB的中点位于坐标原点O,长度为2l,MN为接收电极对,平行于发射源AB。假设高斯积分节点的电磁场响应为F(i),有限长源频率域响应Y(ω)和时间域响应Y(t)的计算公式分别为
| $ \left\{\begin{array}{c}Y\left(\omega \right)=l\sum \limits_{i=1}^{n}\left[a\left(i\right)F\left(i\right)\right]\\ Y\left(t\right)=\sum \limits_{i=1}^{250}\left[Y\left(\omega \right)b\left(i\right)\right]\end{array}\right. $ | (2) |

|
图 1 基于高斯勒让德积分法的有限长导线源示意图 |
式中:a(i)表示第i个高斯积分节点权系数;b(i)表示正余弦变换系数;n为整数,表示高斯积分节点数。
1.2 自适应差分进化算法自适应差分进化算法是基于传统DE算法[24]衍生而来,在DE算法的基础上增加了对控制参数的调节,以此解决传统DE算法对控制参数敏感的问题。目前常见的DE算法主要有两种:一是Brest等[25]提出的JDE(Jitter Differential Evolution)算法,该算法主要采用固定概率、在一定范围内对控制参数进行自适应调节;另一种是Zhang等[26]提出的JADE(Jittered Adaptive Differential Evolution)算法,根据进化过程中成功进化个体的信息、利用柯西分布以及高斯分布对控制参数进行自适应调节。本文选取JADE算法对时域电磁信号进行电性参数的提取。
1.2.1 标准DE算法标准DE算法[24]主要包括以下步骤:
(1)初始化。在规定的定义域内随机生成含有
(2)变异操作。从当前种群中随机选取2个不同的个体
| $ {\boldsymbol{v}}_{i}^{\left(t+1\right)}={\boldsymbol{x}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}+\alpha \left[{\boldsymbol{x}}_{\mathrm{r}1}^{\left(t\right)}-{\boldsymbol{x}}_{\mathrm{r}2}^{\left(t\right)}\right] $ | (3) |
式中:
(3) 交叉操作。交叉操作是为了增加群体的多样性,对每个个体的每一维进行操作,具体形式为
| $ {\boldsymbol{u}}_{i}^{\left(t+1\right)}\left(j\right)=\left\{\begin{array}{l}{\boldsymbol{v}}_{i}^{\left(t+1\right)}\left(j\right)\begin{array}{cc}& \end{array}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\le \mathrm{C}\mathrm{R}\mathrm{或}j=z\\ {\boldsymbol{x}}_{i}^{\left(t\right)}\left(j\right)\begin{array}{cc}& \end{array}\;\;\;\;\;\;\;\;\;\;\;\mathrm{其}\mathrm{他}\end{array}\right. $ | (4) |
式中:CR∈[0, 1]表示交叉概率因子;rand∈[0, 1]表示第j维分量对应的一个随机数;z为第i个个体对应的系数,从[1, N]中随机选取,其中N为模型参数个数,一般为模型地层层数乘以每一层的参数的个数减1,z的作用是确保至少有一维分量来自于变异个体
(4)选择操作。DE法采用“优胜劣汰”的思想贪婪选择优异个体,保证算法逐步向全局最优解靠近。该操作是对种群中的个体进行的,具体操作为
| $ {\boldsymbol{x}}_{i}^{\left(t+1\right)}=\left\{\begin{array}{l}{\boldsymbol{u}}_{i}^{\left(t+1\right)}\begin{array}{cc}& \end{array}D\left[{\boldsymbol{u}}_{i}^{\left(t+1\right)}\right] < D\left[{\boldsymbol{x}}_{i}^{\left(t\right)}\right]\\ \boldsymbol{x}{}_{i}{}^{\left(t\right)}\begin{array}{cc}& \end{array}\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{其}\mathrm{他}\end{array}\right. $ | (5) |
式中D(·)表示目标函数。
对于最小优化问题,重复执行步骤(2)~步骤(4),直到迭代次数达到最大值Q。
1.2.2 控制参数自适应调节对于维持种群多样性的杂交因子CR,则从范围较大的高斯分布中选取适合的CRi,以此保证搜索过程中种群的多样性,避免陷入局部最优解。具体表达式为
| $ \left\{\begin{array}{l}\mathrm{C}{\mathrm{R}}_{i}=\mathrm{G}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{s}\mathrm{i}\mathrm{a}\mathrm{n}({\mu }_{\mathrm{C}\mathrm{R}}, \delta )\\ {\mu }_{\mathrm{C}\mathrm{R}}=(1-C){\mu }_{\mathrm{C}\mathrm{R}}+C\mathrm{m}\mathrm{e}\mathrm{a}{\mathrm{n}}_{}\left\{\mathrm{C}{\mathrm{R}}_{\mathrm{s}}\right\}\end{array}\right. $ | (6) |
式中:Gaussian(·)表示正态分布随机数产生器;
对于容易引起算法早熟的缩放因子α,每次都需从柯西分布中选取较大的缩放因子αi,避免搜索过程中算法早熟。具体公式为
| $ \left\{\begin{array}{l}{\alpha }_{i}=\mathrm{C}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{y}({\mu }_{\alpha }, \epsilon )\\ {\mu }_{\alpha }=(1-C){\mu }_{\alpha }+C\mathrm{m}\mathrm{e}\mathrm{a}{\mathrm{n}}_{\mathrm{L}}\left({\alpha }_{\mathrm{S}}\right)\end{array}\right. $ | (7) |
式中:Cauchy(·)表示柯西分布随机数产生器;
| $ \mathrm{m}\mathrm{e}\mathrm{a}{\mathrm{n}}_{\mathrm{L}}=\frac{\sum \limits_{I=1}^{{{N}_{\alpha }}_{\mathrm{S}}}\stackrel{2}{{\alpha }_{I}}}{\sum \limits_{I=1}^{{{N}_{\alpha }}_{\mathrm{S}}}{\alpha }_{I}} $ | (8) |
式中NαS表示集合
如果生成的变异个体优于其父代,则将此次迭代的α与CR分别放入集合
变异策略的选择是差分进化算法中最重要的一步,其中DE/rand/1是最常用的策略,广泛应用于实际工作,同时也是工程应用中最常用的变异策略。不同的变异策略具有不同的搜索与开发能力,其收敛性能也不同。表 1为以二项交叉(bin)为例的7种差分策略[27],其中,x表示变异基向量,
|
|
表 1 差分策略[27] |
本文选取的差分策略是Zhang等[26]基于DE/current-to-best/bin策略改进的一种可归档的DE/current-to-pbest/1,其表达式为
| $ {\boldsymbol{v}}_{i, j}={\boldsymbol{x}}_{i, \mathrm{g}}+{\alpha }_{i}\left({\boldsymbol{x}}_{\mathrm{b}, \mathrm{g}}^{p}-{\boldsymbol{x}}_{i, \mathrm{g}}\right)+{\alpha }_{i}\left({\boldsymbol{x}}_{r1, \mathrm{g}}-{\tilde{\boldsymbol{x}}}_{r2, \mathrm{g}}\right) $ | (9) |
式中:
从概率学的角度来看,随机产生的个体靠近最优解的概率也是随机的,相应的算法迭代至最优解的速率也是不可控的。因此,本文利用反向学习策略产生初始种群,一定程度上可加快算法收敛速度。
首先,以随机方式产生原始种群
| $ {\boldsymbol{x}}_{i, j}={\boldsymbol{s}}_{j}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}({\boldsymbol{k}}_{j}-{\boldsymbol{s}}_{j}) $ | (10) |
式中:
然后,对
| $ {{\boldsymbol{x}}^{\text{'}}}_{i, j}={\boldsymbol{s}}_{j}+{\boldsymbol{k}}_{j}-{\boldsymbol{x}}_{i, j} $ | (11) |
式中
最后,将反向个体
对于含极化介质的一维层状模型,水平电场分量
| $ {D}_{\boldsymbol{d}}\left(\boldsymbol{m}\right)={\left(\boldsymbol{d}-{\boldsymbol{d}}_{0}\right)}^{\mathrm{T}}\left(\boldsymbol{d}-{\boldsymbol{d}}_{0}\right) $ | (12) |
式中:m为模型向量参数;d为一维观测数据向量,其大小为频点数或时间点的个数;
地球物理反演问题具有多解性,为了降低反演结果的多解性,通常可采用约束函数对反演进行约束。本文通过在目标函数中引入约束条件,进行最小构造反演。因此,可将式(9)改写为新的目标函数
| $ D\left(\boldsymbol{m}\right)={D}_{\boldsymbol{d}}\left(\boldsymbol{m}\right)+\lambda {D}_{\boldsymbol{m}}\left(\boldsymbol{m}\right) $ | (13) |
式中:λ表示正则化因子;
| $ {D}_{\boldsymbol{m}}\left(\boldsymbol{m}\right)={\left(\boldsymbol{R}\boldsymbol{m}\right)}^{\mathrm{T}}\left(\boldsymbol{R}\boldsymbol{m}\right) $ | (14) |
式中R为粗糙度矩阵。上式可改写为
| $ {D}_{\boldsymbol{m}}\left(\boldsymbol{m}\right)={\sum \limits_{t=2}^{T}\left({\boldsymbol{m}}_{t}-{\boldsymbol{m}}_{t-1}\right)}^{2} $ | (15) |
式中T表示地层数。λ可以用陈小斌等[28]提出的自适应正则化思想求取
| $ {\lambda }^{\left(t\right)}=\frac{{D}_{\boldsymbol{d}}^{(t-1)}\left(\boldsymbol{m}\right)}{{D}_{\boldsymbol{d}}^{(t-1)}\left(\boldsymbol{m}\right)+{D}_{\boldsymbol{m}}^{(t-1)}\left(\boldsymbol{m}\right)} $ | (16) |
在自适应差分进化反演算法中,选择操作是对个体的
以三层H型地电模型(表 2)为例,研究极化层位于不同位置时反演效果,验证本文方法的正确性。自适应差分进化的基本参数设置为:种群规模NP=36,参数α和CR采用自适应方式获取,初始正则化参数λ=0.5,
|
|
表 2 三层H型模型参数 |
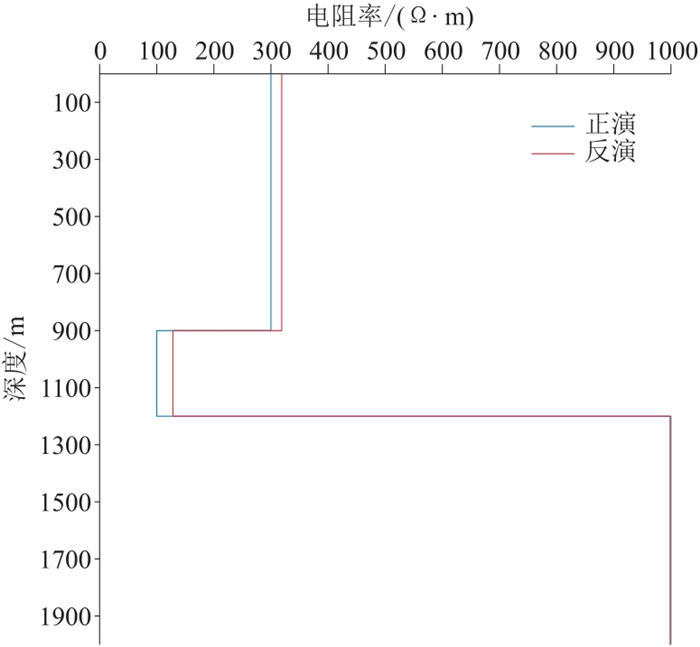
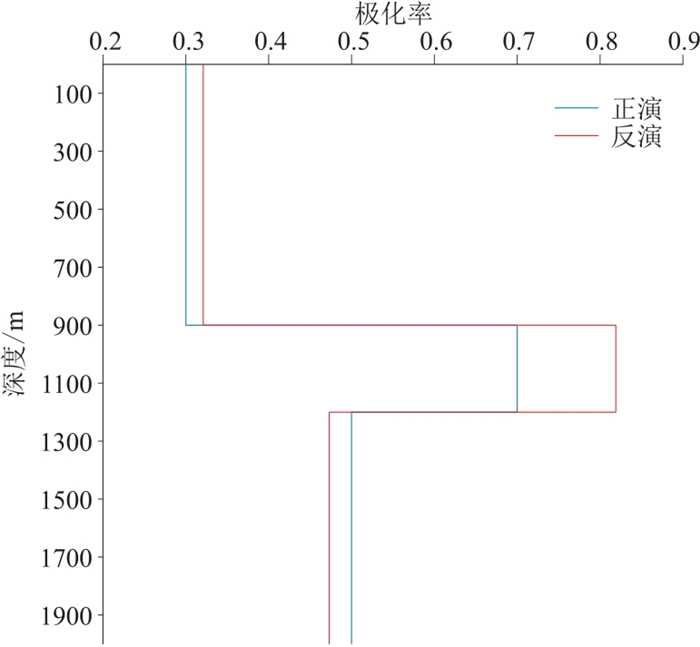
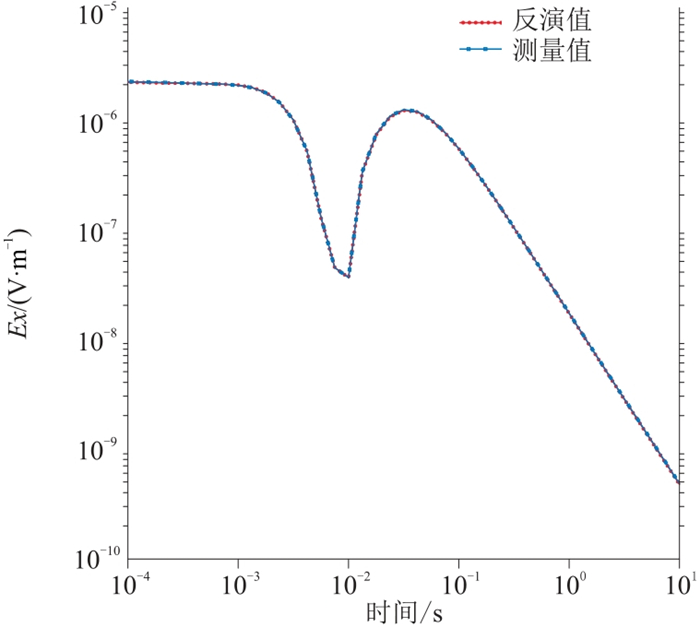
图 2和图 3分别为采用本文方法反演的电阻率和极化率,可见提取的电阻率和极化率与模型基本一致,误差在5%以内,符合预期范围。图 4是反演模型的电场分量Ex拟合曲线,可见拟合效果较好。图 5是函数拟合误差,可见随迭代次数增加,反演拟合误差稳步减少。对比图 2与图 3,极化率反演效果不及电阻率反演效果,但整体来说,利用本文算法反演的极化率与模型极化率变化趋势基本一致。
|
图 2 H型模型电阻率反演结果 |
|
图 3 H型模型极化率反演结果 |
|
图 4 H型模型Ex拟合曲线 |

|
图 5 H型模型反演拟合误差曲线 |
建立表 3所示包含十层地层的地电模型。自适应差分进化的基本参数设置为:种群规模NP=120,参数α和CR采用自适应方式获取,初始正则化参数λ=0.5,
|
|
表 3 十层地电模型参数 |
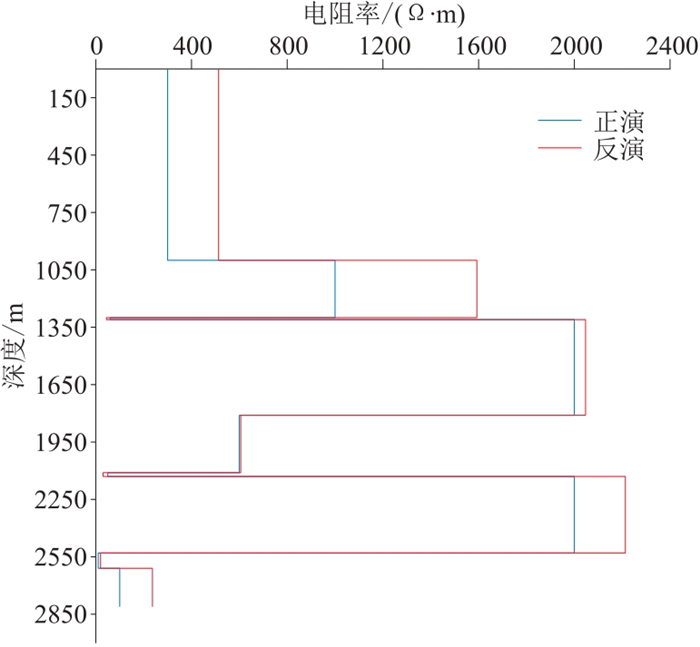
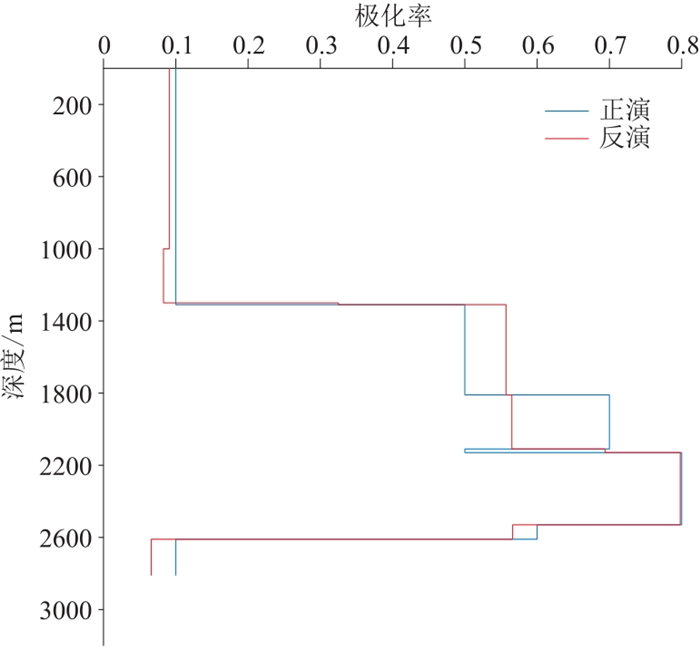
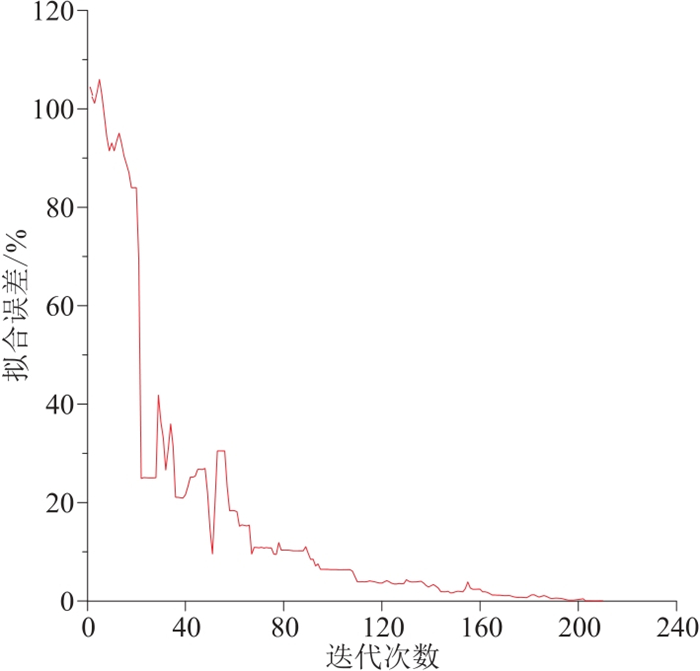
图 6和图 7分别是十层模型的电阻率和极化率反演结果。可以看出利用本文算法开展多层地电模型电阻率和极化率反演,电阻率的变化趋势和数值拟合都取得了很好的效果,极化率拟合效果较好,能够清楚反映十层理论模型的极化构造;图 8和图 9是电场分量Ex的拟合曲线及拟合误差,可以看出,本文方法对于复杂模型的反演也有着较好的效果。电场分量Ex拟合误差稳步下降;模拟的电阻率值与理论模型基本符合;反演极化率曲线可准确反映理论模型中高极化层。综上,利用本文方法对十层地电模型的反演效果较好,证明该方法适用于复杂地电模型的反演。
|
图 6 十层地电模型电阻率反演结果 |
|
图 7 十层地电模型极化率反演结果 |

|
图 8 10层地电模型Ex拟合曲线 |
|
图 9 10层地电模型反演拟合误差曲线 |
为了测试本文算法的准确性和适用性,对野外实测资料进行一维反演。
3.1 反演结果对比为了分析本文算法的效果,将电阻率反演结果与一维OCCAM反演结果进行对比。选取位于同一条测线上的两个测点(点号2275、1275)数据进行反演。初始化参数为:正则化参数初始值λ=0.5,种群规模NP=400,
(1)不考虑极化率(极化率为0)的条件下,反演电阻率以及地层厚度。由于缺乏可参考的地层厚度信息,将浅部10层地层的和厚度范围设定为10~100 m,深部9层地层的厚度范围设定为50~200 m。电阻率的反演范围均设定为10~2000 Ω·m。
(2)以步骤(1)得到的地层电阻率和厚度作为已知信息,进行极化率约束反演。
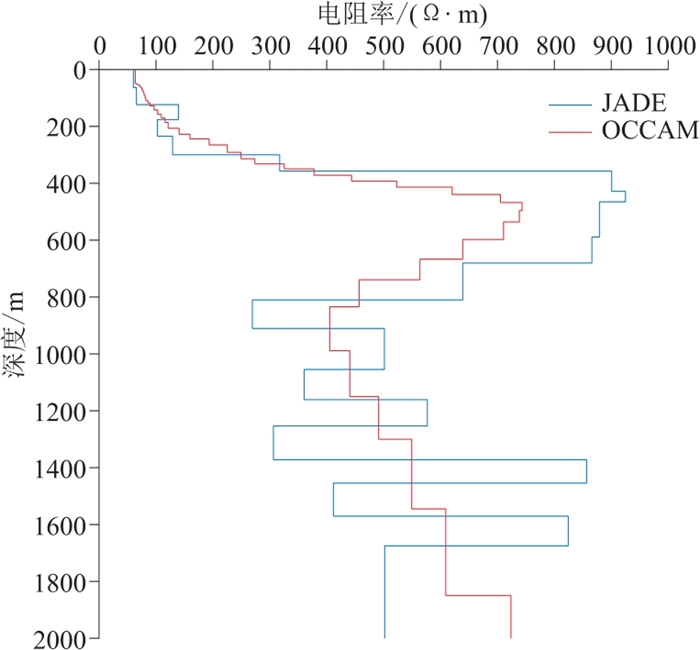
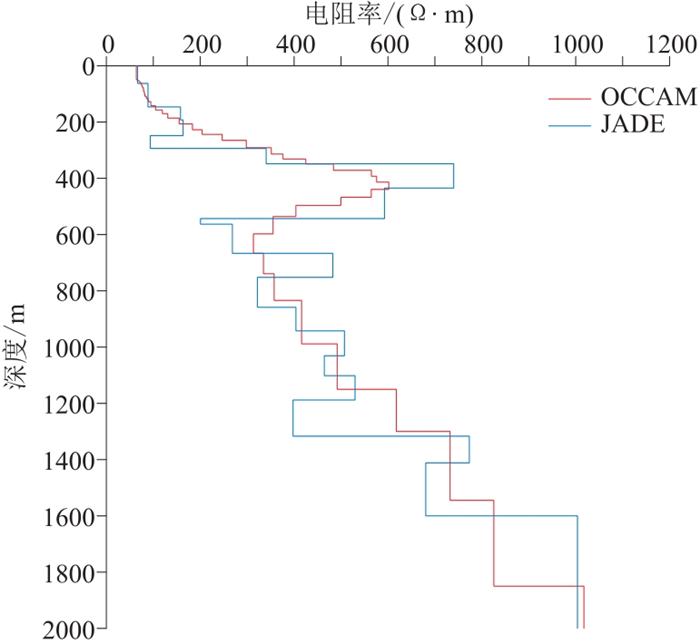
对比两个测点的电阻率反演结果(图 10和图 11),可见本文算法反演结果与OCCAM反演结果基本一致,基本可反映地层电阻率随深度的变化趋势。对比这两个测点的极化率反演结果(图 12、图 13),可见本文反演结果对于浅层的低阻—低极化信息基本反映准确。对比这两个测点的反演模型的正演Ex响应与实测数据(图 14和图 15)及其拟合曲线(图 16和图 17),可见拟合效果较好,随迭代次数的增加,拟合误差稳步降低。
|
图 10 测点2275电阻率反演结果对比 |
|
图 11 测点1275电阻率反演结果对比 |
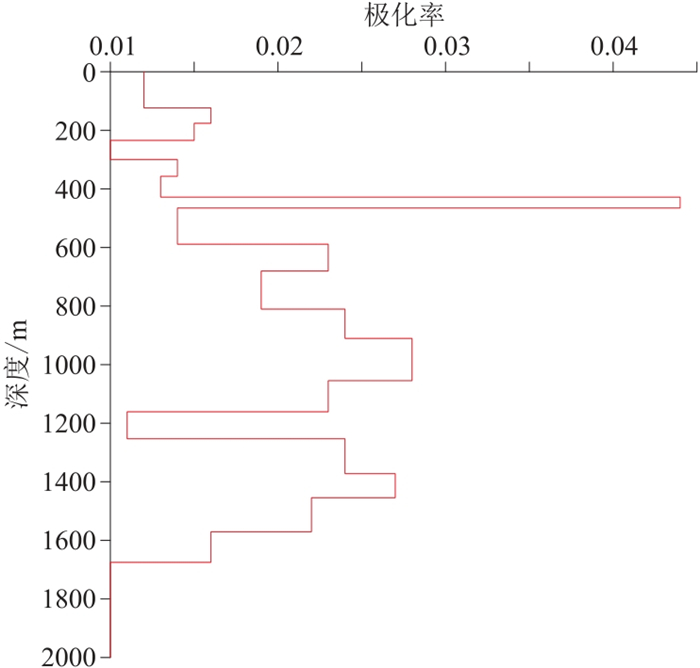
|
图 12 测点2275极化率反演结果 |
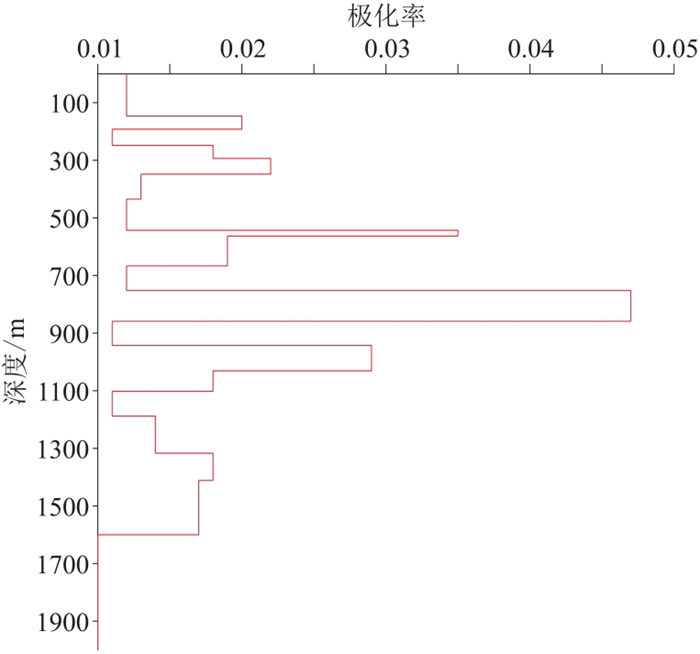
|
图 13 测点1275极化率反演结果 |
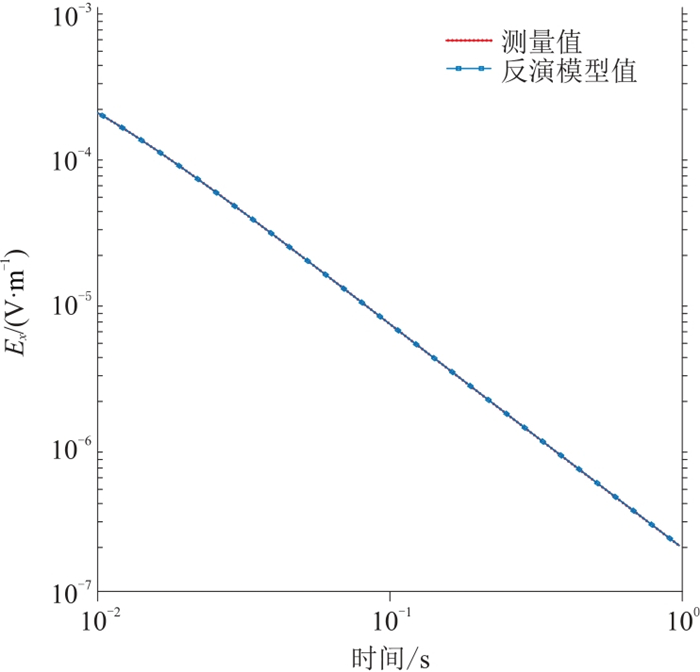
|
图 14 测点2275时间域Ex拟合曲线 |
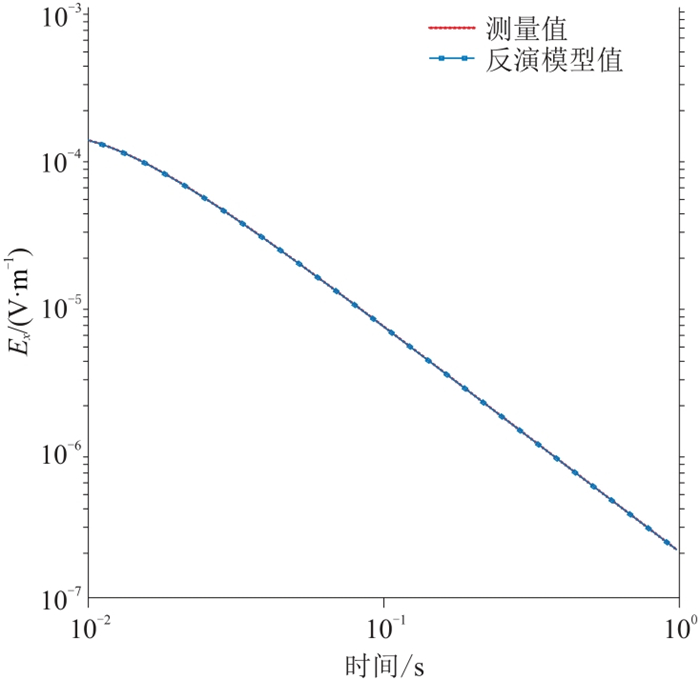
|
图 15 测点1275时间域Ex拟合曲线 |
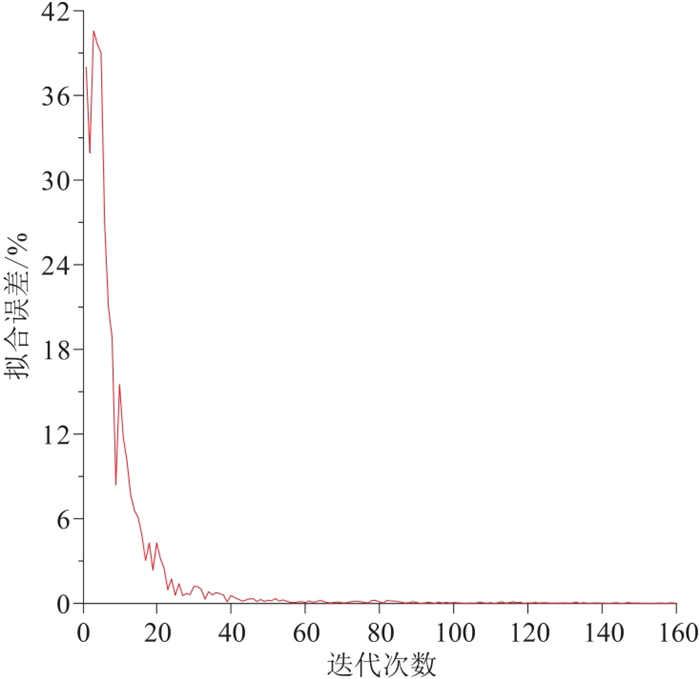
|
图 16 测点1275拟合误差曲线 |

|
图 17 测点2275拟合误差曲线 |
针对实际采集的瞬变电磁数据包含电磁感应和激发极化效应这一问题,本文提出一种基于差分进化算法的电性源瞬变电磁一维反演方法,可准确提取电阻率和极化率信息。该算法首先基于Cole-Cole复电阻率模型实现有限长电性源瞬变电磁法一维正演;然后,在传统差分进化算法的基础上引入反向学习策略及控制参数自适应调节,加快反演的收敛速度,同时在目标函数中引入约束条件,构成最小构造反演,降低反演的多解性。对典型的三层地电模型和复杂多层模型进行理论测试,利用本文方法进行反演,可有效恢复模型的电阻率和极化率。利用实测资料进行反演,反演得到的电阻率与OCCAM反演电阻率基本一致。基于反演电阻率进行极化率约束反演,反演结果准确地提取了实测数据中的电阻率信息,得到了地下介质的极化率分布,证明了算法的准确性和适用性。
将反向学习策略引入算法,可提高反演速度,但对于层数很多的模型,反演效率有限,以后的研究方向是进一步开发并行反演算法。
| [1] |
王新宇, 严良俊, 毛玉蓉. 电性源瞬变电磁法油气藏动态监测模拟分析[J]. 石油地球物理勘探, 2022, 57(2): 459-466. WANG Xinyu, YAN Liangjun, MAO Yurong. Simulation and analysis of dynamic monitoring of oil and gas reservoir based on grounded electric source TEM[J]. Oil Geophysical Prospecting, 2022, 57(2): 459-466. |
| [2] |
DANIELSEN J E, AUKEN E, JØRGENSEN F, et al. The application of the transient electromagnetic method in hydrogeophysical surveys[J]. Journal of Applied Geophysics, 2003, 53(4): 181-198. DOI:10.1016/j.jappgeo.2003.08.004 |
| [3] |
杨云见, 王绪本, 刘雪军, 等. 横向约束瞬变电磁拟三维反演[J]. 石油地球物理勘探, 2021, 56(1): 201-208. YANG Yunjian, WANG Xuben, LIU Xuejun, et al. A quasi-3D TEM inversion based on lateral constraints[J]. Oil Geophysical Prospecting, 2021, 56(1): 201-208. |
| [4] |
金杨. 长导线源瞬变电磁约束反演[D]. 四川成都: 电子科技大学, 2019. JIN Yang. Long Wire Source Transient Electromagnetic Constrained Inversion[D]. University of Electronic Science and Technology of China, Chengdu, Sichuan, 2019. |
| [5] |
WAIT J R, FULLER J A. Transmission line theory for an insulated linear antenna in a fluid- or air-filled borehole[J]. Applied Physics, 1973, 1(6): 311-316. DOI:10.1007/BF00884400 |
| [6] |
NABIGHIAN M N. Macnae J C. Time domain electromagnetic prospecting methods[J]. Electromagnetic Methods in Applied Geophysics, 1991, 2: 991. |
| [7] |
LEPPIN M. Electromagnetic modeling of 3-D sources over 2-D in homogeneities in the time domain[J]. Geophysics, 1992, 57(8): 994-1003. DOI:10.1190/1.1443325 |
| [8] |
MIERNIK K, BOGACZ A, KOZUBAL A, et al. Pareto joint inversion of 2D magnetotelluric and gravity data: Towards practical applications[J]. Acta Geophysica, 2016, 64: 1655-1672. DOI:10.1515/acgeo-2016-0035 |
| [9] |
殷长春, 朴化荣. 电磁测深法视电阻率定义问题的研究[J]. 物探与化探, 1991(4): 290-299. YIN Changchun, PIAO Huarong. A study of the definition of apparent resistivity in electromagnetic sounding[J]. Geophysical and Geochemical Exploration, 1991(4): 290-299. |
| [10] |
王华军. 正余弦变换的数值滤波算法[J]. 工程地球物理学报, 2004, 1(4): 329-335. WANG Huajun. Digital filter algorithm of the sine and cosine transform[J]. Chinese Journal of Engineering Geophysics, 2004, 1(4): 329-335. |
| [11] |
李建慧, 刘树才, 朱自强, 等. 矩形回线激发的电磁场与磁场的对称关系研究[J]. 中南大学学报(自然科学版), 2010, 41(2): 638-642. LI Jianhui, LIU Shucai, ZHU Ziqiang, et al. Relationship between electromagnetic field and magnetic field's symmetric excited by rectangular loop[J]. Journal of Central South University (Science and Technology), 2010, 41(2): 638-642. |
| [12] |
李建慧, 朱自强, 刘树才, 等. 基于Gaver-Stehfest算法的矩形发射回线激发的瞬变电磁场[J]. 石油地球物理勘探, 2011, 46(3): 489-492. LI Jianhui, ZHU Ziqiang, LIU Shucai, et al. Rectangular loop transient electromagnetic field expressed by Gaver-Stehfest algorithm[J]. Oil Geophysical Prospec-ting, 2011, 46(3): 489-492. |
| [13] |
翁爱华, 刘云鹤, 陈玉玲, 等. 矩形大定源层状模型瞬变电磁响应计算[J]. 地球物理学报, 2010, 53(3): 646-650. WENG Aihua, LIU Yunhe, CHEN Yuling, et al. Computation of transient electromagnetic field from a rec-tangular loop over stratified earths[J]. Chinese Journal of Geophysics, 2010, 53(3): 646-650. |
| [14] |
NABIGHIAN M N. Quasi-static transient response of a conducting half-space: an approximate representation[J]. Geophysics, 1979, 44(10): 1637-1769. DOI:10.1190/1.1440927 |
| [15] |
王家映. 地球物理反演理论[M]. 湖北武汉: 中国地质大学出版社, 1998.
|
| [16] |
潘克家, 王文娟, 谭永基, 等. 基于混合差分进化算法的地球物理线性反演[J]. 地球物理学报, 2009, 52(12): 3083-3090. PAN Kejia, WANG Wenjuan, TAN Yongji, et al. Geophysical linear inversion based on hybrid differential evolution algorithm[J]. Chinese Journal of Geophysics, 2009, 52(12): 3083-3090. |
| [17] |
宋维琪, 高艳珂, 朱海伟. 微地震资料贝叶斯理论差分进化反演方法[J]. 地球物理学报, 2013, 56(4): 1331-1339. SONG Weiqi, GAO Yanke, ZHU Haiwei. The diffe-rential evolution inversion method based on Bayesian theory for micro-seismic data[J]. Chinese Journal of Geophysics, 2013, 56(4): 1331-1339. |
| [18] |
熊杰, 孟小红, 刘彩云, 等. 基于差分进化的大地电磁反演[J]. 物探与化探, 2012, 36(3): 448-451. XIONG Jie, MENG Xiaohong, LIU Caiyun, et al. Magnetotelluric inversion based on differential evolution[J]. Geophysical and Geochemical Exploration, 2012, 36(3): 448-451. |
| [19] |
董莉, 江沸菠, 李帝铨. 基于自适应差分进化算法的MT信号激电信息提取[J]. 石油地球物理勘探, 2016, 51(3): 613-624. DONG Li, JIANG Feibo, LI Diquan. IP extraction from magnetotelluric sounding data based on adaptive differential evolution inversion[J]. Oil Geophysical Prospecting, 2016, 51(3): 613-624. DOI:10.13810/j.cnki.issn.1000-7210.2016.03.025 |
| [20] |
王天意, 侯征, 何元勋, 等. 基于改进差分进化算法的大地电磁反演[J]. 地球物理学进展, 2022, 37(4): 1605-1612. WANG Tianyi, HOU Zheng, HE Yuanxun, et al. Magnetotelluric inversion based on the improved diffe-rential evolution algorithm[J]. Progress in Geophysics, 2022, 37(4): 1605-1612. |
| [21] |
RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition-based differential evolution[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 64-79. DOI:10.1109/TEVC.2007.894200 |
| [22] |
PELTON W H. Interpretation of Induced Polarization and Resistivity Data[D]. The University of Utah, Salt Lake City, USA, 1977.
|
| [23] |
程见中. 时频电磁法全参数反演方法研究与应用[D]. 湖北荆州: 长江大学, 2018. CHENG Jianzhong. Study and Application of Full-Para-meter Inversion Method in Time-Frequency Electromagnetic Method[D]. Yangtze University, Jingzhou, Hubei, 2018. |
| [24] |
STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [25] |
BREST J, GREINER S, BOSKOVIC B, et al. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-657. DOI:10.1109/TEVC.2006.872133 |
| [26] |
ZHANG J Q, SANDERSON A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. DOI:10.1109/TEVC.2009.2014613 |
| [27] |
杨启文, 蔡亮, 薛云灿. 差分进化算法综述[J]. 模式识别与人工智能, 2008, 21(4): 506-513. YANG Qiwen, CAI Liang, XUE Yuncan. A survey of differential evolution algorithms[J]. Pattern Recognition and Artificial Intelligence, 2008, 21(4): 506-513. |
| [28] |
陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946. CHEN Xiaobin, ZHAO Guoze, TANG Ji, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946. |



 周磊, 湖北省武汉市蔡甸区长江大学(武汉校区)地球物理与石油资源学院,430100。Email:
周磊, 湖北省武汉市蔡甸区长江大学(武汉校区)地球物理与石油资源学院,430100。Email: