2. 海军工程大学电气工程学院, 湖北武汉 430033;
3. 上海联影智能医疗科技有限公司, 上海 200100;
4. 中国地质大学(武汉)数理学院, 湖北武汉 430074
2. College of Electrical Engineering, Naval University of Engineering, Wuhan, Hubei 430033 China;
3. United Imaging Surgical Technology Co., Ltd, Shanghai 200100, China;
4. School of Mathematics and Physics, China University of Geosciences, Wuhan, Hubei 430074, China
重力梯度测量是一种相对较新的地球物理技术,具有信息量大、测量精度高、抗干扰性强等优点,在地球物理勘探领域得到广泛应用[1]。重力梯度场即重力场的二阶导数,每个梯度分量反映不同的地质体信息,重力梯度不同分量联合反演能够更好地反映地下密度异常体的形态和分布[2]。
重力梯度数据广泛应用于传统反演方法。Zhdanov等 [3]将重力曲率的概念引入重力场和重力梯度的联合反演;Wu等[4]使用一种自适应加权函数进行重力场及重力梯度的联合反演;Capriotti等[5]通过建立一种自适应加权函数推导出重力数据和重力梯度联合反演的一般公式;秦朋波等[6]利用非线性共轭梯度算法对重力梯度各分量进行联合反演,进行重力场与梯度分量联合反演,通过实例验证了联合反演的优越性;侯振隆等[7]使用欧拉反褶积方法进行重力场及梯度的联合反演,有效降低了反演的不稳定性。
近年来,深度学习逐渐应用于地球物理领域。张岩等[8]利用深度学习方法进行地震数据的去噪;马国庆等[9]基于注意力机制开展重磁数据网络化及滤波;唐杰等[10]运用U-Net网络的多分辨性开展断层检测。相比传统方法,深度学习具有自学习和自适应的优点,即网络只需要通过训练大量的样本就可以实现输入数据到输出数据间的映射,因此神经网络广泛应用于地球物理研究。Yang等[11]利用3D-Unet实现了简单的多尺度重力反演,训练后的网络可以直接输出三维密度分布矢量;张志厚等[12]基于U-Net网络框架提出了GraInNet,该网络实现了重力梯度全张量数据联合反演,为重力梯度张量数据联合反演提供了新思路。
Chaurasia等[13]提出了LinkNet网络结构,该结构结合U-Net网络与残差网络的特点,对U-Net网络下采样中由卷积层—归一化层—激活层组成的模块用残差结构代替。该网络的主要贡献是在原始U-Net网络中引入残差连接,同时将编码器和解码器进行连接,提高网络准确率。
本文基于LinkNet网络和残差块结构构建网络,实现重力异常反演。在LinkNet网络基础上加入残差结构,利用反卷积实现上采样。为了方便表达,本文将新构建的网络记为U-Rnet。将该网络用于重力梯度张量的联合反演问题,并将图像分割领域中的Tversky损失函数引入该反演问题[14]。模拟实验表明,利用该网络能够获得物性参数分布集中和场源边界清晰的反演结果。为了进一步验证该网络在实际应用中的可靠性,将其应用于美国文顿(Vinton)盐丘的全张量重力梯度(Full Tensor Gra-diometry, FTG)数据反演,获得了符合真实地质特征的反演结果。
1 重力梯度张量正演 1.1 重力梯度张量梯度张量正演是解决反演问题的基础。在笛卡尔坐标系中,设重力场为
| $ \left[\begin{array}{l}\partial x\\ \partial y\\ \partial z\end{array}\right]\left[{V}_{x}{V}_{y}{V}_{z}\right]=\left[\begin{array}{ccc}{V}_{xx}& {V}_{xy}& {V}_{xz}\\ {V}_{yx}& {V}_{yy}& {V}_{yz}\\ {V}_{zx}& {V}_{zy}& {V}_{zz}\end{array}\right] $ | (1) |
式中Vij代表重力场
| $ {V}_{xx}+{V}_{yy}+{V}_{zz}=0 $ | (2) |
在三维正演中,将地下空间进行离散化处理,划分为M个大小相同、密度均匀的立方体单元。假设地面上的观测面完全覆盖场源区域,观测面上有N个等间隔的采样点,记地下空间中第j个单元对观测面上第i个观测点产生的重力场的梯度为
| $ {\boldsymbol{d}}_{ij}^{\alpha \beta }={\boldsymbol{G}}_{ij}^{\alpha \beta }{m}_{j} $ | (3) |
式中:α,β=x, y, z,本文仅研究
| $ {\boldsymbol{d}}^{\alpha \beta }={\boldsymbol{G}}^{\alpha \beta }\boldsymbol{m}={\left[{d}_{i}^{\alpha \beta }\right]}_{N\times 1} $ | (4) |
令
| $ \boldsymbol{D}=\boldsymbol{G}\boldsymbol{m} $ | (5) |
式中
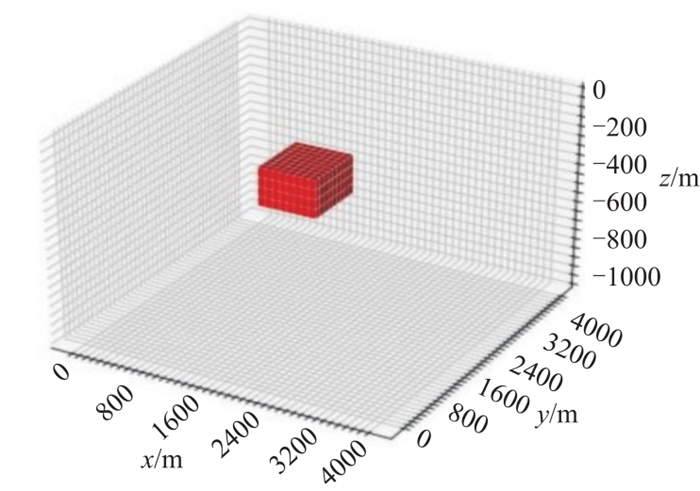
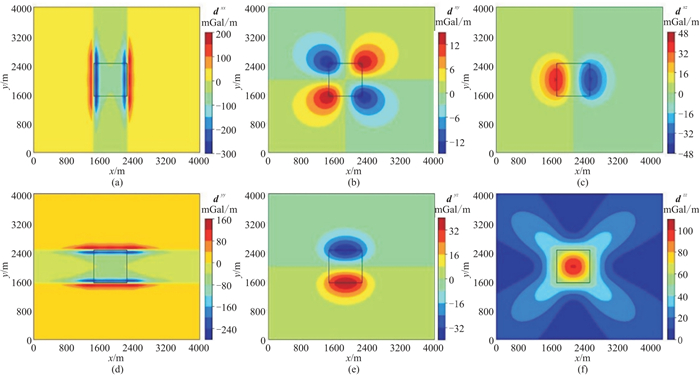
建立图 1所示的长方体密度模型。密度异常体埋深为250~450 m,模型大小为400 m×450 m×200 m,与背景的密度差为1.0 g·cm-3。通过正演可计算该模型产生的重力梯度的六个分量(图 2)。可以看出:
|
图 1 长方体密度模型 |
|
图 2 长方体密度模型重力梯度分量平面图 (a) |
重力的反演问题主要是利用正演得到的重力场
| $ \tilde{\boldsymbol{m}}=\mathrm{N}\mathrm{e}\mathrm{t}(\boldsymbol{D}, \theta ) $ | (6) |
式中:
卷积神经网络自提出以来就广泛用于图像处理等计算机识别领域。随着网络的不断发展,产生了很多基于CNN结构的变体,如残差神经网络(Residual Neural Networks, Resnet)[18]、生成对抗神经网络(Generate Adversarial Networks, GAN) [19]、循环神经网络(Recurrent Neural Networks, RNN) [20]等。其中,Resnet可在一定程度上解决网络加深引起的梯度消失和梯度爆炸问题。
因此,本文提出一种基于残差结构和U-Net结构搭建的网络U-Rnet(图 3)实现重力全梯度张量反演。U-Rnet结构分为编码和解码两部分(图 4),每一个编码块和解码块都引入了残差结构,目的更好地进行特征提取。网络中每个卷积层后都添加了归一化函数[21]和PReLU激活函数[22],其中输出层使用Sigmoid激活函数,将输出限制在0~1[23]。
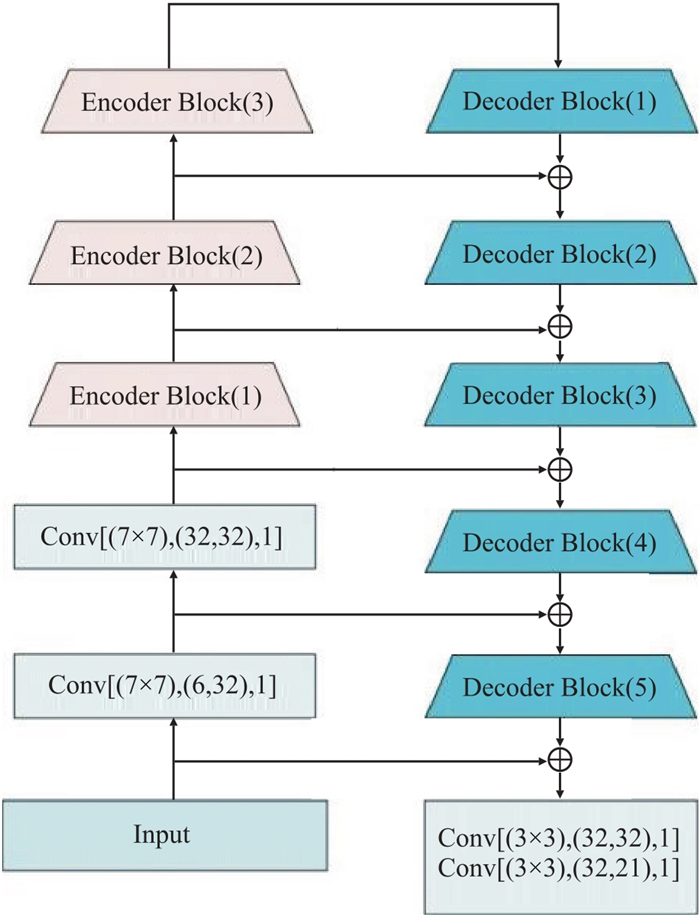
|
图 3 U-Rnet网络结构 Conv代表卷积,Deconv代表反卷积,Encoder表示编码,Decoder表示解码。 |

|
图 4 编码器块结构(a)和解码器块结构(b)
编码块中,卷积核大小均为 |
网络的编码器和解码器见图 3。网络首先通过两个
同理,解码器也是由一系列的解码块Decoder Block
神经网络通过误差反向传播算法更新网络参数,因此损失函数在网络的学习中起主导作用,对整个网络的训练至关重要。在神经网络中,常用的损失函数为L2范数,但L2范数是基于误差平方和最小化的一类回归损失函数,在反演问题中通常会造成较平滑的反演结果,无法确定尖锐的地质界面[24]。因此,从图像分割的角度出发,本文提出使用Tversky损失函数聚焦反演
| $ \begin{array}{l}\mathrm{T}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{k}\mathrm{y}\mathrm{ }\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}=\\ 1-\frac{{\boldsymbol{m}}_{\mathrm{\rho }}{\tilde{\boldsymbol{m}}}_{\mathrm{\rho }}}{{\boldsymbol{m}}_{\mathrm{\rho }}{\tilde{\boldsymbol{m}}}_{\mathrm{\rho }}+\omega (1-{\boldsymbol{m}}_{\mathrm{\rho }}){\tilde{\boldsymbol{m}}}_{\mathrm{\rho }}+(1-\omega )(1-{\tilde{\boldsymbol{m}}}_{\mathrm{\rho }}){\boldsymbol{m}}_{\mathrm{\rho }}}\end{array} $ | (7) |
式中:ω表示权重系数;
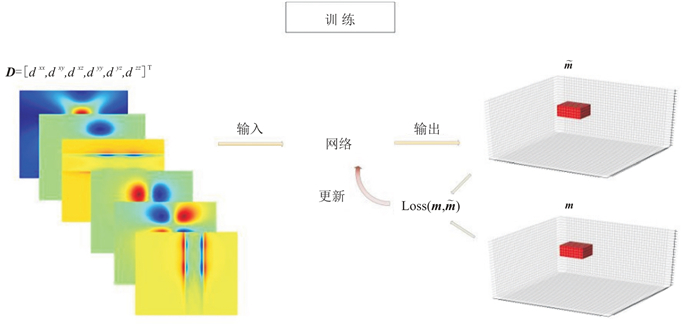
采用U-Rnet解决重力梯度张量三维反演问题可以分为训练和测试两个阶段。训练过程如图 5所示,网络将重力梯度张量
网络完成训练后,在测试集中测试网络效果,测试过程如图 6所示。此时网络不需要更新参数,通过输入数据可以直接得到
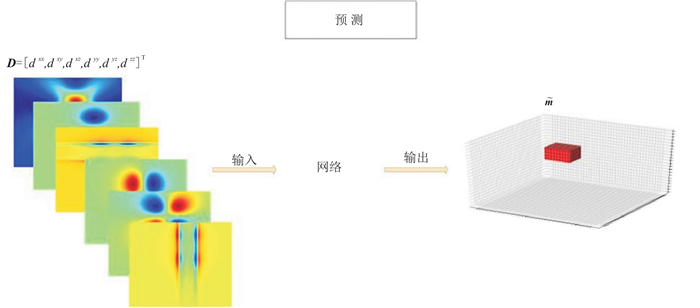
|
图 6 神经网络测试过程示意图 |
神经网络的训练过程依赖于大量的数据集,网络性能在很大程度上也取决于数据集的多样性及可靠性。本文构造了训练集、验证集和测试集,使用训练集来训练网络,训练过程中同时使用验证集验证网络的训练效果,避免网络出现过拟合或者欠拟合,最后使用测试集测试网络。训练集、验证集和测试集的样本数分别为10000、1000、1000。构造数据集时,地下空间大小设置为4.10 km×4.10 km×1.05 km,被离散为35301个100 m×100 m×50 m的单元块,单元块密度设置为0或者1.0 g·cm-3。训练集中的样本采用图 7所示的随机模型,其中图 7a模型是通过一个密度为1.0 g·cm-3的单元块在随机步长内随机游走得到的随机模型,图 7b模型是通过两个密度为1.0 g·cm-3的单元块在随机步长内随机游走得到的随机模型。验证集和测试集采用的样本为图 8所示的六类常用规则模型,模型的位置和大小随机变化。
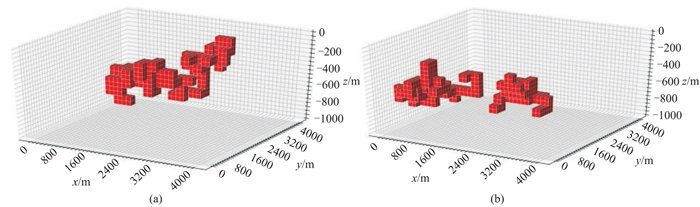
|
图 7 训练集随机模型一(a)和随机模型二(b) 红色单元块的密度为1 g·cm-3,其余区域密度为0。图 8同。 |

|
图 8 六类(a~f)测试集和验证集模型 |
本文开展了三组对比实验:第一组实验对比L2和Tversky两种损失函数的反演结果,网络选取本文提出的U-Rnet,网络的输入数据为六种梯度张量组合数据,最后对反演结果进行对比和分析,讨论不同损失函数的优势;第二组实验对比不同梯度张量组合的反演结果;最后一组实验对比不同噪声水平下的反演结果,分析网络的鲁棒性。实验使用Adam优化器,学习率为5×10-4,迭代次数为100。
3.2.1 损失函数的对比本节对L2和Tversky两种损失函数的反演结果进行对比。首先对反演模型
|
|
表 1 不同损失函数的反演结果与理论值的差值比 |
图 9分别为采用L2损失函数和Tversky损失函数对应的反演模型和反演结果。可以看出,L2损失函数反演结果能够识别地质体的形状以及位置,中心位置的密度接近于真实密度,边缘处的密度值较小,整体上模型较为发散。Tversky损失函数的反演结果与真实模型较吻合,反演密度趋于真实密度。与L2损失函数相比,采用Tversky损失函数的反演结果能较清晰地反演出模型的边界位置。
表 1中,Tversky函数对应的差值比
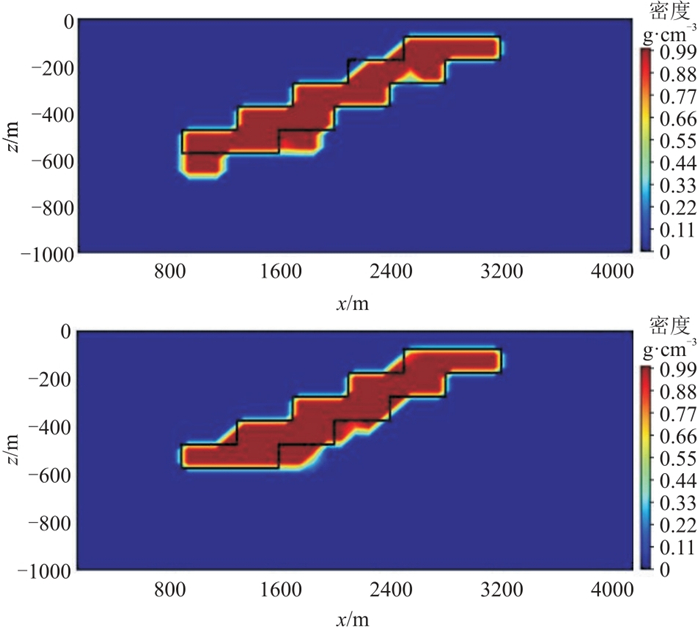
如上节所述,不同张量反映地质体的不同特征,因此本节对比不同梯度张量数据组合的反演结果。台阶模型(图 8d)可以很好地描述模型在x、y、z方向上的形状及走势,因此选取台阶模型讨论不同梯度组合的反演结果。将梯度张量分为四个组合实验,其对应的梯度组合及输入数据、输出数据的大小见表 2[25]。
|
|
表 2 台阶模型不同梯度张量组合实验参数 |
实验中,输入梯度张量组合,输出反演密度
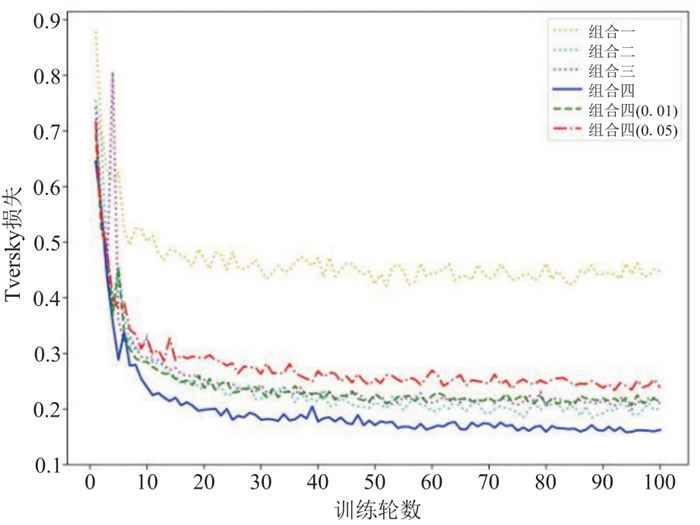
|
图 10 四组实验测试集误差曲线 |

|
图 11 组合一(a)、组合二(b)、组合三(c)、组合四(d)实验密度反演剖面 |
表 3为不同张量组合的反演结果,可见四组实验在三个方向上具有不同的反演精度。
|
|
表 3 不同实验组的反演结果与理论值的差值比 |
组合一实验的反演结果(图 11a)可以粗略地体现地质体在x、y方向的走势,但是整体反演效果较差。该组实验的输入数据是
组合二实验的反演结果(图 11b)清晰地展示了地质体的位置及形状。与组合一相比,该组合主要关注
组合三实验的反演结果(图 11c)也较好地展示出地质体的形状及走势,尤其是对于靠近地表的地质体边界指示得非常清晰。与组合二相比,该组合实验增加了z方向的信息,因此在
组合四实验结合了六种梯度张量数据,即综合了所有的梯度分量信息,因此在三个方向上的反演精度都有所提升,反演模型与理论模型无论是位置信息还是形状信息都较吻合(图 11d),梯度差值比亦较小。
3.2.3 数据加噪实验网络的鲁棒性通常表现为抗噪能力。本文通过在数据中加入不同水平的高斯噪声测试网络的鲁棒性。噪声添加方式如下
| $ {\boldsymbol{d}}_{{}^{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}}^{\alpha \beta }={\boldsymbol{d}}^{\alpha \beta }+\lambda {\left[\mathrm{v}\mathrm{a}\mathrm{r}\left({\boldsymbol{d}}^{\alpha \beta }\right)\right]}^{2}\times \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\left[\mathrm{0, 1};\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}\left({\boldsymbol{d}}^{\alpha \beta }\right)\right] $ |
式中:
|
图 12 台阶模型添加权重系数 |
|
|
表 4 台阶模型不同噪声下的反演结果与理论值的差值比 |
对比表 3和表 4,可见随着噪声水平的提升,反演模型与理论模型的差值比逐渐增加。
4 应用实例将本文提出的网络应用于美国得克萨斯州的文顿(Vinton)盐丘反演。Vinton盐丘位于路易斯安那州西南部,该盐丘是一个典型的油气聚集区,是重要的油气产区[26]。根据Coker等[26]的研究,Vinton盐丘是一个延伸到盐岩之上巨大的盖层,盖层由石膏和硬石膏组成,嵌在砂岩和页岩夹层的沉积物中。2008年贝尔公司采集了Vinton盐丘机载全张量重力梯度(Full Tensor Gradiometry,FTG)数据,并对其开展了常规的飞机残余运动和自梯度处理和修正[27]。
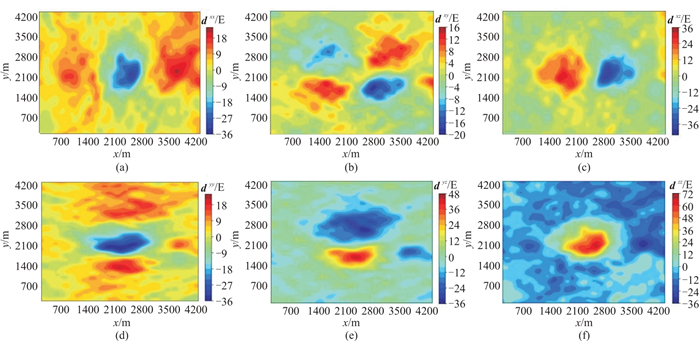
研究表明,Vinton盐丘及周围沉积物(页岩和砂岩)的密度范围为1.75~3.25 g·cm-3 [28]。对FTG数据进行处理后,可识别密度为2.75 g·cm-3的高密度盖层。基于Coker等[26]和Oliveira等[28]的研究成果,选择2.20 g·cm-3作为背景密度开展地形校正,因而盖层与岩丘的密度差为0.55 g·cm-3。地面研究区域的大小为4.1 km×4.1 km,点间距为100 m;地下研究深度为z≤1.05 km。地下研究空间划分为41×41×21个100 m×100 m×50 m的单元。经本文方法处理后的重力梯度张量各分量如图 13所示。
|
图 13 Vinton盐丘重力梯度图 (a) |
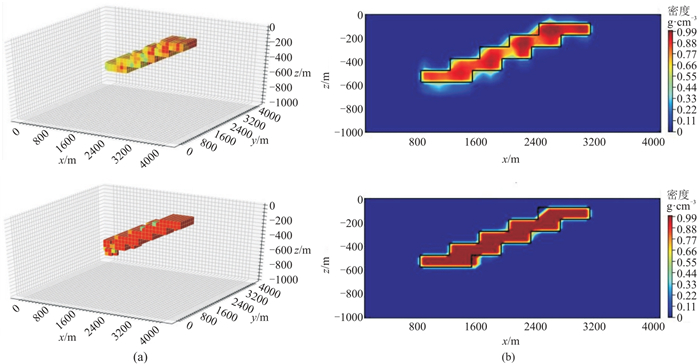
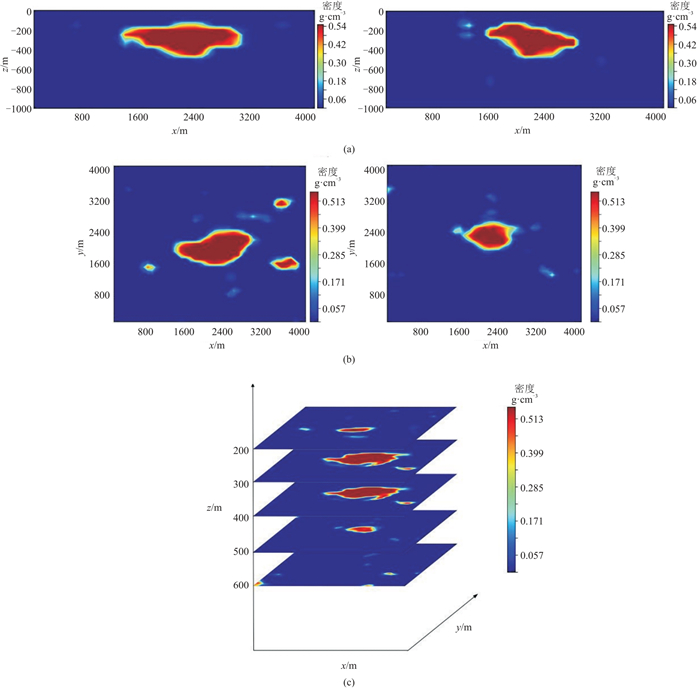
图 14展示了密度反演结果在不同深度的切片。可以看出,盖层横向延拓约1600 m,高度约200~600 m.表 5是不同研究人员关于文顿盐丘的反演结果[28-30]。可以看出,本文反演的岩丘埋深和厚度与地质资料建模资料相近,与前人的研究结果较吻合,验证了本文方法的正确性与有效性。
|
图 14 Vinton盐丘密度反演结果在不同位置的切片 (a)y=2.25 km处的xOz切片(左)和x=2.45 km处的yOz切片(右);(b)z=250 m(左)和450 m(右)处的xOy切片;(c)z=200、300、400、500、600 m处的xOy切片 |
|
|
表 5 不同文献关于文顿盐丘埋深的反演结果 |
本文通过搭建U-Rnet网络实现重力梯度张量到密度模型的直接映射。在网络构造中引入了残差和Unet网络结构,实现了深层次的特征提取。通过Tversky损失函数训练网络,得到了密度较为集中的反演结果,能较准确地反映地下密度体的位置。网络在训练过程中使用不规则模型,在测试过程中使用规则模型,测试结果表明该网络具有一定的泛化能力。另外,加噪实验结果也表明网络具有较好的鲁棒性。最后,将网络应用于Vinton盐丘的FTG数据的反演,得到了与真实地质信息较吻合的反演结果,证实了网络的有效性。下一步工作是讨论基于U-Rnet的重力梯度多值反演问题。
| [1] |
孟嘉春, 蔡喜楣. 卫星重力梯度测量及其应用前景探讨[J]. 地球物理学报, 1991, 34(3): 369-376. MENG Jiachun, CAI Ximei. Approach on satellite gravity gradiometry and its vistas of applications[J]. Acta Geophysics Sinica, 1991, 34(3): 369-376. |
| [2] |
周文月, 马国庆, 侯振隆, 等. 重力全张量数据联合欧拉反褶积法研究及应用[J]. 地球物理学报, 2017, 60(12): 4855-4865. ZHOU Wenyue, MA Guoqing, HOU Zhenlong, et al. The study on the joint Euler deconvolution method of full tensor gravity data[J]. Chinese Journal of Geophy-sics, 2017, 60(12): 4855-4865. |
| [3] |
ZHDANOV M S, ELLIS R, MUKHERJEE S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data[J]. Geophysics, 2004, 69(4): 925-937. DOI:10.1190/1.1778236 |
| [4] |
WU L, KE X P, HSU H, et al. Joint gravity and gra-vity gradient inversion for subsurface object detection[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 865-869. DOI:10.1109/LGRS.2012.2226427 |
| [5] |
CAPRIOTTI J, LI Y G. Gravity and gravity gradient data: Understanding their information content through joint inversions[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 1329-1333.
|
| [6] |
秦朋波, 黄大年. 重力和重力梯度数据联合聚焦反演方法[J]. 地球物理学报, 2016, 59(6): 2203-2224. QIN Pengbo, HUANG Danian. Integrated gravity and gravity gradient data focusing inversion[J]. Chinese Journal of Geophysics, 2016, 59(6): 2203-2224. |
| [7] |
侯振隆, 王恩德, 周文纳, 等. 重力梯度欧拉反褶积及其在文顿盐丘的应用[J]. 石油地球物理勘探, 2019, 54(2): 472-479. HOU Zhenlong, WANG Ende, ZHOU Wenna, et al. Euler deconvolution of gravity gradiometry data and the application in Vinton Dome[J]. Oil Geophysical Prospecting, 2019, 54(2): 472-479. DOI:10.13810/j.cnki.issn.1000-7210.2019.02.027 |
| [8] |
张岩, 李新月, 王斌, 等. 基于深度学习的鲁棒地震数据去噪[J]. 石油地球物理勘探, 2022, 57(1): 12-25. ZHANG Yan, LI Xinyue, WANG Bin, et al. Robust seismic data denoising based on deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 12-25. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.002 |
| [9] |
马国庆, 王泽坤, 李丽丽. 基于自注意力机制深度学习的重磁数据网格化和滤波方法[J]. 石油地球物理勘探, 2022, 57(1): 34-42. MA Guoqing, WANG Zekun, LI Lili. Gridding and filtering method of gravity and magnetic data based on self-attention deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 34-42. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.004 |
| [10] |
唐杰, 孟涛, 韩盛元, 等. 基于多分辨率U-Net网络的地震数据断层检测方法[J]. 石油地球物理勘探, 2021, 56(3): 436-445. TANG Jie, MENG Tao, HAN Shengyuan, et al. A fault detection method of seismic data based on MultiResU-Net[J]. Oil Geophysical Prospecting, 2021, 56(3): 436-445. DOI:10.13810/j.cnki.issn.1000-7210.2021.03.002 |
| [11] |
YANG Q G, HU X Y, LIU S, et al. 3-D gravity inversion based on deep convolution neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [12] |
张志厚, 廖晓龙, 曹云勇, 等. 基于深度学习的重力异常与重力梯度异常联合反演[J]. 地球物理学报, 2021, 64(4): 1435-1452. ZHANG Zhihou, LIAO Xiaolong, CAO Yunyong, et al. Joint gravity and gravity gradient inversion based on deep learning[J]. Chinese Journal of Geophysics, 2021, 64(4): 1435-1452. |
| [13] |
CHAURASIA A, CULURCIELLO E. LinkNet: exploiting encoder representations for efficient semantic segmentation[C]. 2017 IEEE Visual Communications and Image Processing (VCIP), 2017, 1-4.
|
| [14] |
ALTINI N, PRENCIPE B, BRUNETTI A. A tversky loss-based convolutional neural network for liver vessels segmentation[C]. International Conference on Intelligent Computing, 2020, 342-354.
|
| [15] |
LI X, CHOUTEAU M. Three-dimensional gravity modeling in all space[J]. Surveys in Geophysics, 1998, 19(4): 339-368. DOI:10.1023/A:1006554408567 |
| [16] |
马国庆, 杜晓娟, 李丽丽. 解释位场全张量数据的张量局部波数法及其与常规局部波数法的比较[J]. 地球物理学报, 2012, 55(7): 2450-2461. MA Guoqing, DU Xiaojuan, LI Lili. Comparison of the tensor local wavenumber method with the conventional local wavenumber method for interpretation of total tensor data of potential fields[J]. Chinese Journal of Geophysics, 2012, 55(7): 2450-2461. |
| [17] |
高秀鹤, 黄大年. 基于共轭梯度算法的重力梯度数据三维聚焦反演研究[J]. 地球物理学报, 2017, 60(4): 1571-1583. GAO Xiuhe, HUANG Danian. Research on 3D focu-sing inversion of gravity gradient tensor data based on a conjugate gradient algorithm[J]. Chinese Journal of Geophysics, 2017, 60(4): 1571-1583. |
| [18] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 770-778.
|
| [19] |
RADFORD A, METZ L, CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[EB/OL]. (2015-11-19)[2024-01-26]. https://www.science-open.com/document?vid=d0480825-f6f6-4176-9f25-28d199b6f86a.
|
| [20] |
POLLACK J B. Recursive distributed representations[J]. Artificial Intelligence, 1990, 46(1-2): 77-105. DOI:10.1016/0004-3702(90)90005-K |
| [21] |
ZHOU Y X, YANG G Z. Normalization in training U-Net for 2-D biomedical semantic segmentation[J]. IEEE Robotics and Automation Letters, 2019, 4(2): 1792-1799. DOI:10.1109/LRA.2019.2896518 |
| [22] |
HE K M, ZHANG X Y, REN S Q, et al. Delving deep into rectifiers: surpassing Human-Level performance on ImageNet classification[C]. 2015 IEEE International Conference on Computer Vision (ICCV), 2015, 1026-1034.
|
| [23] |
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]. Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010, 249-256.
|
| [24] |
FARQUHARSON C G. Constructing piecewise-constant models in multidimensional minimum-structure inversions[J]. Geophysics, 2008, 73(1): K1-K9. DOI:10.1190/1.2816650 |
| [25] |
GENG M X, HUANG D N, YANG Q J, et al. 3D inversion of airborne gravity-gradiometry data using Cokriging[J]. Geophysics, 2014, 79(4): G37-G47. DOI:10.1190/geo2013-0393.1 |
| [26] |
COKER M O, BHATTACHARYA J P, MARFURT K J. Fracture patterns within mudstones on the flanks of a salt dome: syneresis or slumping?[J]. Gulf Coast Association of Geological Societies Transactions, 2007, 57: 125-137. |
| [27] |
DAVIS K, LI Y G. 3D joint inversion of gradient and total-field magnetic data[C]. SEG Technical Program Expanded Abstracts, 2010, 19: 1784-1788.
|
| [28] |
OLIVEIRA V C, BARBOSA V C F. 3-D radial gra-vity gradient inversion[J]. Geophysical Journal International, 2013, 195(2): 883-902. DOI:10.1093/gji/ggt307 |
| [29] |
ENNEN C. Mapping Gas-charged Fault Blocks Around the Vinton Salt Dome, Louisiana Using Gravity Gradiometry Data[D]. University of Houston, Houston, USA, 2012.
|
| [30] |
QIN P B, HUANG D N, YUAN Y, et al. Integrated gravity and gravity gradient 3D inversion using the non-linear conjugate gradient[J]. Journal of Applied Geophysics, 2016, 126: 52-73. DOI:10.1016/j.jappgeo.2016.01.013 |



 李厚朴, 湖北省武汉市硚口区解放大道717号海军工程大学电气工程学院,430033。Email:
李厚朴, 湖北省武汉市硚口区解放大道717号海军工程大学电气工程学院,430033。Email: