0 引言

准噶尔盆地二叠系为一套深湖相暗色泥岩与云质岩混杂沉积，其中暗色泥岩为主力烃源岩层，云质岩是致密油主要富集层^[1]。目前，已在准东地区吉木萨尔凹陷二叠系芦草沟组探明地质储量1.279×10⁹ t，并且多口井获得了新的油气发现，展示了准东地区良好的油气勘探前景^[2]。针对准东地区致密油储层的勘探与开发，脆性是一种重要指标，用于评价可压裂性。高脆性储层压裂更容易，形成的次生裂缝更丰富，因此储层脆性的准确预测对油气压裂增产至关重要。

脆性反映的是物体受力变形时发生破裂的性质，与延性、弹性、塑性等都属于岩石的力学特性。脆性大小一般通过脆性指数来衡量，其计算方法主要包括岩石矿物组分法、测井参数统计和弹性参数反演等。

矿物组分法考虑的是脆性矿物的占比。储层类型不同，脆性矿物不同，计算公式也有所不同。Jarvie等^[3]用石英的矿物比重计算脆性指数(BI)；Wang等^[4]将石英和白云石作为脆性矿物用于BI计算；陈吉等^[5]则将方解石、长石等加入到脆性指数计算；Jin等^[6]将硅酸盐矿物(石英、长石和云母)和脆性碳酸盐矿物(方解石和白云石)一起纳入计算BI。

测井参数统计法是通过分析岩石物理实验结果和矿物组分与测井参数之间的关系，或通过测井资料估计岩石的组分以间接计算脆性指数^[7-8]。矿物组分法和测井参数统计法仅限于井点，无法用于整个研究区。本文研究区勘探程度低、钻井少，适合利用叠前地震反演得到的弹性参数进行储层脆性预测。

弹性参数反映岩石受力后的应力、应变，也能够体现脆性的含义。Rickman等^[9]将归一化后的杨氏模量(E)和泊松比(σ)二者的平均值作为脆性指数，这是目前业界比较经典的脆性计算方法。Goodway等^[10]用拉梅常数$ (\lambda +2\mu )/\lambda $表达脆性指数；Guo等^[11]用E、σ的比值表征脆性大小。另外，还有很多学者围绕E、σ和拉梅常数等进行方法的改进与推广应用。如张丰麒等^[12]将Zoeppritz方程推广为BI-Zoeppritz方程，直接反演脆性指数；Zhang等^[13]基于多孔介质理论和AVO理论，推导出E与密度($ \rho $)的乘积的脆性反演方程；张瑞等^[14]通过幂指数经验公式替换Aki近似方程中的密度项，推导得到了以E和σ两项参数表达的近似方程，建立了一套直接反演岩石脆性参数的方法。

此外，学者们还研究了影响压裂的因素，熊健等^[15]通过建立的地层参数预测模型，明确了影响压裂效果的主要因素排序，其中脆性指数排序靠前，并利用层次分析法建立的压裂评价模型为储层压裂、优化提供参考；马霄一等^[16]通过对页岩岩石物理性质的超声测试，发现了弹性模量在不同方向上具有不同的变化规律，可以为页岩脆性评价提供依据。

在前人研究基础上，本文依据录井、测井信息与岩石物理实验成果，以W1井三维工区为例，开展了基于叠前角度域数据体的反演方法研究，提取了AVO属性P（截距）与G（梯度），并计算了P+G与P×G组合属性；进行了基于E和σ以及拉梅系数的弹性参数反演，通过不同反演方法的效果对比，筛选出适合该区的反演方法；根据不同的脆性表征公式计算、对比了云质岩目标层的脆性预测效果，对研究区“甜点”有利分布区进行了预测。该研究成果可为准东地区二叠系致密油的勘探与开发提供指导。

1 云质岩储层地球物理特征 1.1 地震反射特征

以W1井为例，由图 1可见，深度308.0~345.5 m二叠系云质岩层主要发育灰质白云岩、泥质白云岩、白云质灰岩、泥质灰岩、灰岩和灰质泥岩。321.6 m处为泥质白云岩的底面，同时也是一速度分界面。根据电阻率(RT)、声波时差(DT)特征，可以将云质岩层分为上“甜点”段(312.0~321.6 m)和下“甜点”段(334.0~341.5 m)两部分。

从图 2a可见，W1井云质岩层顶面为强反射界面、底面为一波谷反射，符合云质岩高速度、高密度特征(顶面正反射系数、底面负反射系数)。但总体来说，云质岩层表现为复合波。从图 2b可见，云质岩具有比较清晰的分段特征，可见上、下两个“甜点”。

1.2 岩石物理特征

利用钻井岩心开展岩石物理实验，获取纵波速度(V_P)、横波速度(V_S)、$ \rho $、E、σ等参数，以便准确描述储层岩性、电性、物性和脆性等。

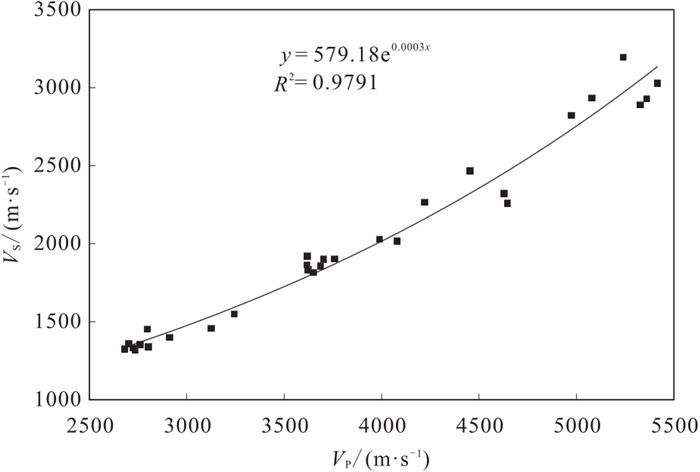
根据准东地区5口井29块岩样的岩石物理实验结果(图 3)，统计横波速度与纵波速度的关系，即

$ {V}_{\mathrm{S}}=579.18{\mathrm{e}}^{0.0003{V}_{\mathrm{P}}} $

(1)

由图 3可见横波速度与纵波速度二者之间具有较好的相关性。由于目前没有横波测井资料，而叠前反演必须利用横波速度信息，为此可根据式(1)通过声波测井资料换算得到横波速度。

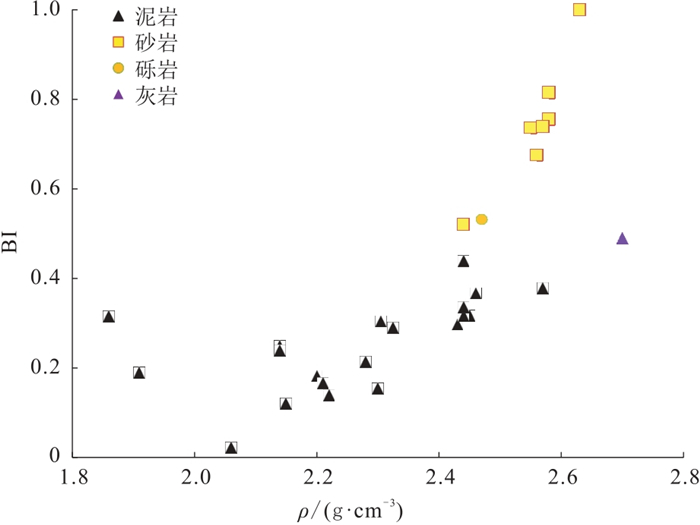
图 4给出了准东地区云质岩层静态E、静态σ与岩性的统计结果。由图可见，云质岩等非泥岩储层具有高E、低σ特征，而泥岩段规律正好相反，即具低E、高σ特征，而且泥岩样本的分布更集中。这为开展储层精细描述和脆性计算提供了很好的岩石物理数据基础。

图 5是准东地区云质岩层$ \rho $、BI与岩性的统计结果。由图可见，$ \rho $与BI相关性较好，即脆性强，密度大；密度大，脆性也强。因此，在BI计算中引入密度，可以在一定程度上提高储层岩性的区分度。

1.3 模型AVO正演及脆性特征

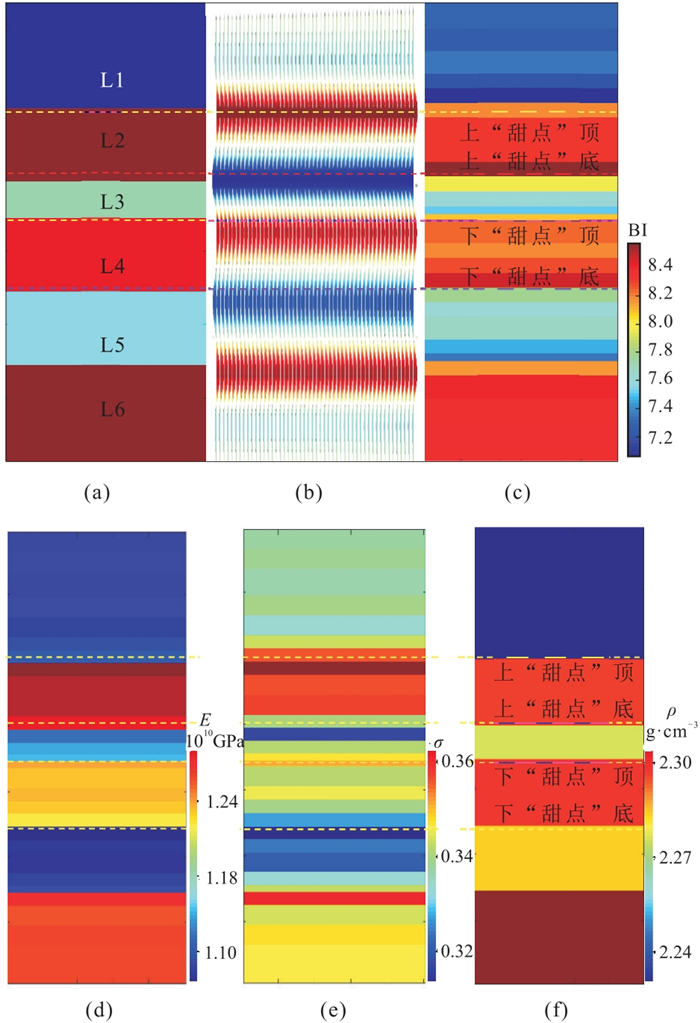
建立如图 6a所示地质模型进行模型测试，研究云质岩储层地震响应及脆性特征。该模型为6层，其中云质岩层顶面到底面4个层(第L2~第L5小层)之间的时间厚度分别为20、10、20、20 ms，具体参数见表 1。子波采用与实际资料主频比较接近的30 Hz雷克子波，采样间隔取2 ms。

利用Aki-Richards近似式^[17]，得到角度域纵波速度、横波速度、密度表征的反射系数

$ \begin{array}{l}R\left(\theta \right)=\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{2}\frac{ {\Delta }{V}_{\mathrm{P}}}{{V}_{\mathrm{P}}}-4\frac{{V}_{\mathrm{S}}^{2}}{{V}_{\mathrm{P}}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{ {\Delta }{V}_{\mathrm{S}}}{{V}_{\mathrm{S}}}+\\ \;\;\;\;\;\;(\frac{1}{2}-2\frac{{V}_{\mathrm{S}}^{2}}{{V}_{\mathrm{P}}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta )\frac{ {\Delta }\rho }{\rho }\end{array} $

(2)

式中：$ \theta $为纵波入射角；$ {\Delta } $表示某个参数的界面两侧相对差值。利用该反射系数公式进行AVO正演模拟。从8°入射角的正演模拟剖面(图 6b)可以看到，储层上“甜点”顶面为强波峰反射，下“甜点”底面为强波谷反射，云质岩层反射特征与实际资料(图 2a)一致。

利用稀疏正则化反演方法^[18]对图 6b中正演模拟数据进行反演，得到E、σ和$ \rho $等弹性参数(图 6d~图 6f)。与层状模型对比，E和$ \rho $分层明显，结果较为稳定；而σ数值范围跨度大，稳定性不如E和$ \rho $。从脆性反演结果(图 6c)可以看出，储层上、下“甜点”段反演的脆性数值较大，与实际模型储层段相吻合。

2 叠前弹性参数反演 2.1 叠前AVO属性提取及分析

根据Shuey近似式^[19]，角度域纵波反射系数可以由

$ \begin{array}{l} R\left(\theta \right)={R}_{0}+\left[{A}_{0}{R}_{0}+\frac{ {\Delta }\sigma }{{(1-\sigma )}^{2}}\right]\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\\ \;\;\;\;\;\;\frac{1}{2}\frac{ {\Delta }{V}_{\mathrm{P}}}{{V}_{\mathrm{P}}}(\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta -\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta ) \end{array} $

(3)

计算。式中：$ {A}_{0}=\frac{1}{2{R}_{0}}\frac{ {\Delta }{V}_{\mathrm{P}}}{{V}_{\mathrm{P}}}-\left(2+\frac{1}{2{R}_{0}}\frac{ {\Delta }{V}_{\mathrm{P}}}{{V}_{\mathrm{P}}}\right)\times \frac{1-2\sigma }{1-\sigma } $; $ {R}_{0}=\frac{1}{2}\left(\frac{ {\Delta }\rho }{\rho }+\frac{ {\Delta }{V}_{\mathrm{P}}}{{V}_{\mathrm{P}}}\right) $。在小角度($ \theta < 30° $)情况下，等式右边第三项可以省略，则反射系数R和$ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $近似成线性关系，进一步简化可得^[20]

$ R\left(\theta \right)=P+G\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $

(4)

组合属性P+G与σ的变化有关，可以称为拟泊松比^[21]。P×G乘积属性加大了数据的绝对幅度差异，可以拓宽数据变化范围，提高识别精度^[22]。

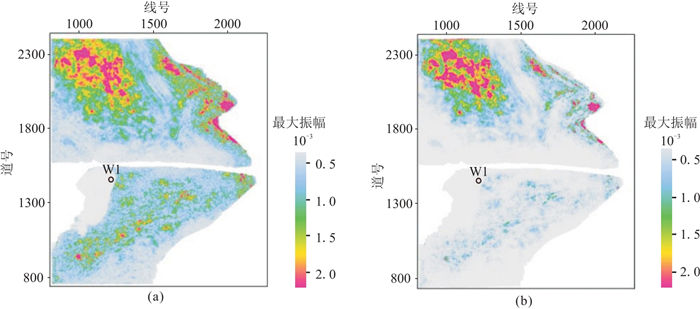
根据研究区特点和试验结果，选取4°、8°、12°三个道集数据体进行AVO属性分析。图 7为研究区下“甜点”AVO属性沿层切片。由图可见，由P+G和P×G属性预测的云质岩发育有利区位于工区西北部，该区域位于古沉积中心附近，云质岩普遍发育。

2.2 基于弹性参数变化率的反演方法

依据式(2)，在小角度条件下，纵波反射系数可以用纵波速度、横波速度、密度变化率来计算。反之，弹性参数也可通过3个角度的角道集反演得到。通过推导，可得E、σ、$ \rho $的变化率反演公式(YPD法)^[23]，即

$ \begin{array}{l}R\left(\theta \right)=(\frac{1}{4}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -2k\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta )\frac{ {\Delta }E}{E}+\left[\frac{1}{4}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta \frac{(2k-3){(2k-1)}^{2}}{k(4k-3)}+\right.\\ \;\;\;\;\;\;\;\;\; \left.2k\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{1-2k}{3-4k}\right]\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta +\frac{ {\Delta }\sigma }{\sigma }+(\frac{1}{2}-\frac{1}{4}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta )\frac{ {\Delta }\rho }{\rho }\end{array} $

(5)

式中$ k=({V}_{\mathrm{S}}/{V}_{\mathrm{P}}{)}^{2} $。也可用拉梅系数表征的弹性参数(LMR法，弹性参数为$ \lambda $、$ \mu $、$ \rho $)^[24]，即

$ \begin{array}{l}R\left(\theta \right)=(\frac{1}{4}-\frac{1}{2}k)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta \frac{ {\Delta }\lambda }{\lambda }+\\ \;\;\;\;\;\;\;\;\;\; (\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -2\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta )k\times \frac{ {\Delta }\mu }{\mu }-\\ \;\;\;\;\;\;\;\;\;\; \frac{1}{4}(1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta )\frac{ {\Delta }\rho }{\rho }\end{array} $

(6)

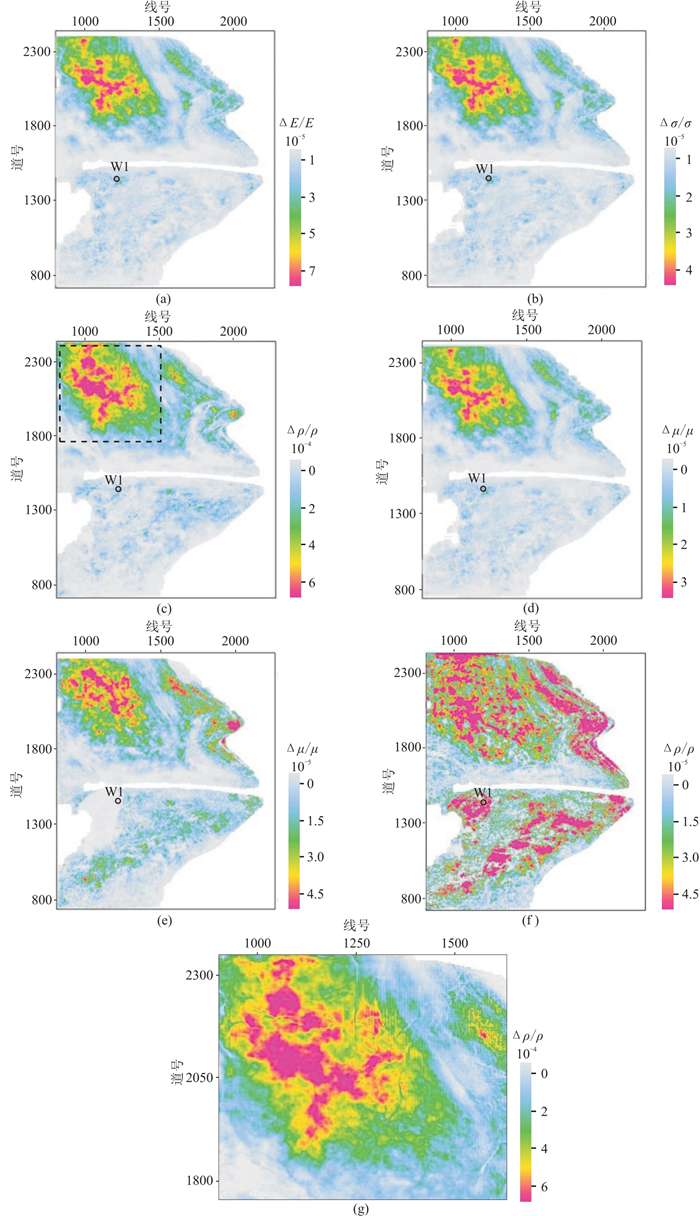
图 8展示了W1井工区下“甜点”弹性参数反演沿层切片。由图可见：①YPD方法$ {\Delta }E $/$ E $、$ {\Delta }\sigma $/$ \sigma $、$ {\Delta }\rho $/$ \rho $ 3个参数与LMR方法的$ {\Delta }\lambda $/$ \lambda $特征相似；②LMR方法$ {\Delta }\mu $/$ \mu $(图 8e)与以上属性有一定差别，但它与AVO属性，特别是P+G属性有较好的相似性；③ LMR方法的$ {\Delta }\rho $/$ \rho $无明显规律，反演效果较差。从局部放大图(图 8g)可以清晰地看到扇三角洲及分支河道特征。根据研究区沉积特征，可以认为YPD方法$ {\Delta }\rho $/$ \rho $参数为最佳反演弹性参数。

2.3 井约束叠前阻抗及弹性参数反演

由于没有井约束，上述弹性参数反演只能得到其变化率，均没有量纲，缺乏具体的地质含义。

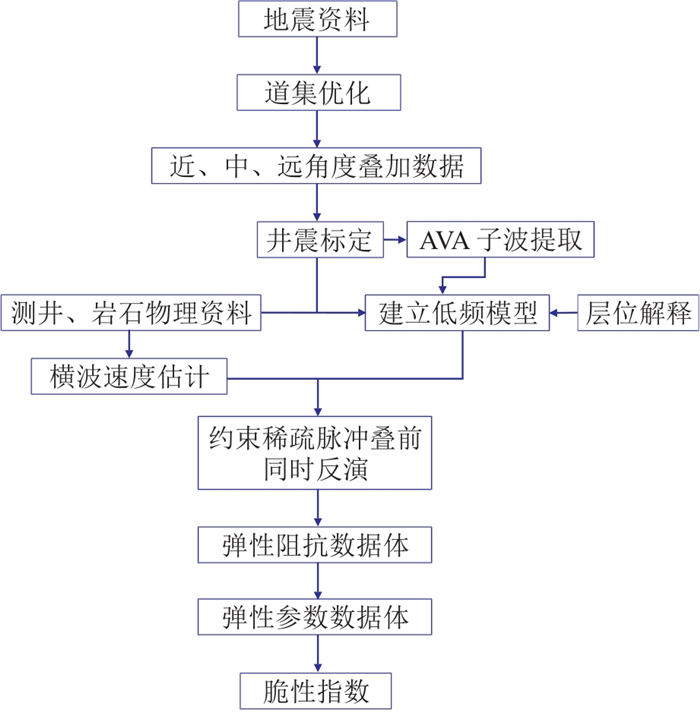
根据式(1)得到横波速度信息，在测井约束下，融入低频模型，可以反演得到绝对弹性阻抗等多种弹性参数^[25]，反演流程如图 9所示。

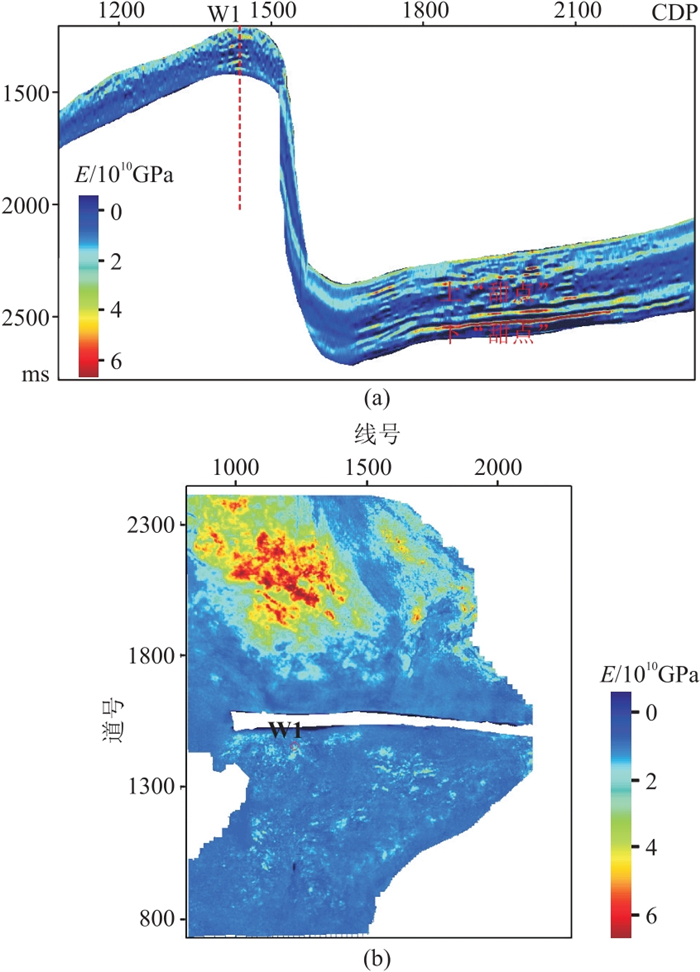
杨氏模量变化率（图 8）与井约束叠前反演的E（图 10）特征类似，但前者是相对值，范围为0~7.5×10^-5；后者是真实值，范围为0~45 GPa，这与岩石物理实验结果基本一致。与密度变化率（图 8c）比较，其分辨率略有降低，扇三角洲特征并不明显。

3 准东云质岩储层脆性预测

脆性是致密油气储层评价的一种重要指标。脆性的评价主要有矿物组分法、测井参数统计法和弹性参数法。其中，利用不同弹性参数计算脆性评价指数公式及其特点如表 2所示。

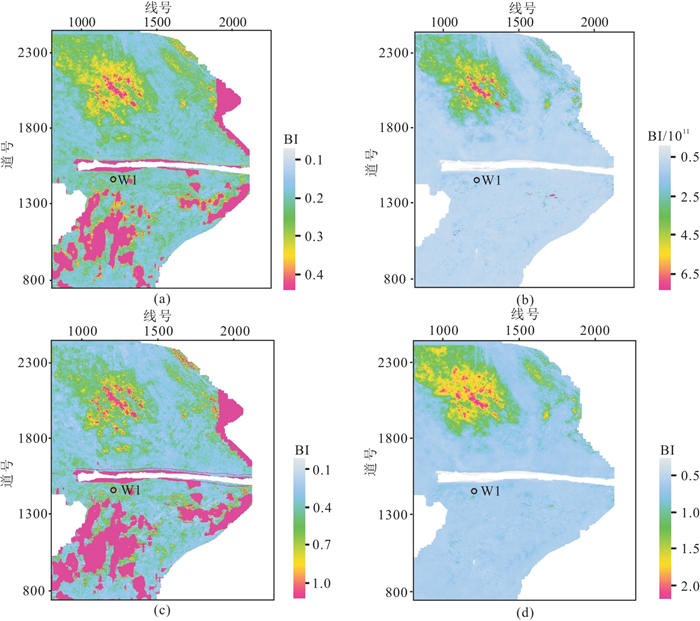
图 11为4种方法计算的下“甜点”脆性沿层切片，均指示出了条带状甜点特征。其中，图 11a、图 11c可见目标区南部脆性数值较大，这与实际地质认识不一致，白云岩多分布于北部区域，南部古沉积高部位不发育；而图 11b、图 11d脆性预测结果与实际地质特征更吻合。总体来看，杨氏模量/泊松比法具有类似“甜点”属性的优势(杨氏模量数量级大，泊松比数量级小)，预测的脆性平面特征更可靠。

4 结束语

准东地区二叠系中下部云质岩储层发育双“甜点”。通过岩石物理实验，获取了纵波速度与横波速度之间的关系，指示了杨氏模量、密度与脆性呈正相关，泊松比与脆性呈负相关的基本规律。开展了AVO属性反演、井约束叠前反演，提出了角道集弹性参数变化率直接反演方法，其中YPD方法密度变化率反演储层识别效果好、分辨率高，值得在类似勘探区块推广使用。分析比较了4种脆性表征方法的物理含义，其中$ \rho E/\sigma $表征脆性具有“甜点”属性放大作用，实际应用效果最好。