裂缝通常会引起地震反射异常[1],增加岩石有效孔隙度,提高渗透率[2-3]。裂缝密度是表征储层裂缝的关键参数之一[4]。为准确获取裂缝密度参数,学者们利用方位各向异性地震资料开展了大量研究[5-9]。Bakulin等[10]认为当裂缝分别充填油、水、气三种不同类型的流体时,Schoenberg线性滑动模型参数和Thomsen各向异性参数均与裂缝密度存在定量关系。随后,Zhang等[11]、Downton等[12]实现了裂缝岩石物理参数与地震反射系数之间的相互转换,为裂缝密度定量预测奠定了基础。Isabel[13]首次在横向各向同性(Horizontally Transverse Isotropic,HTI)介质的裂缝密度反演过程中添加了奇异值分解(Singular Value Decomposition,SVD)方法,但该方法中各向异性对反射系数的贡献度并不高。于是,刘财等[14]运用不同方位相交测线反射系数取差的办法改善了这一缺点。Li等[4]提出了一种基于SVD的受光滑先验弹性参数约束的裂缝密度和裂缝方位反演方法。由于各向异性梯度可作为裂缝密度的指示因子[15],Al-marzoug等[16]将多方位振幅随炮检距(Amplitude Versus Offset,AVO)的梯度拟合成椭圆,并使用拟合椭圆的主轴方向和椭圆率分别表征裂缝方位和裂缝密度的分布特征。秦海旭等[17]推导了各向异性梯度与裂缝密度之间的关系,通过各向异性梯度间接反演获得裂缝密度。为充分利用炮检距向量片(Offset Vector Tile,OVT)域地震数据包含的叠前各向异性信息,魏欣伟等[18]提出了一种叠前AVAZ(振幅随炮检距和方位角变化)的裂缝密度预测方法。针对弹性波阻抗[19],Martin等[20]指出弱各向异性介质中的弹性阻抗为各向同性弹性阻抗背景部分与各向异性弹性阻抗扰动部分的乘积。陈超等[21]将组稀疏引入到方位弹性阻抗反演目标函数中,利用反演获得的裂缝弱度参数计算裂缝密度。
直接反演裂缝密度的方法比间接换算更具优势,可以有效地避免累积误差,提高反演结果的精度。根据这一思想,本文基于具有水平对称轴的HTI介质推导出具有裂缝密度表示的反射系数公式,并开展了裂缝密度参数的直接反演。同时,为了进一步提高反演结果的横向分辨率和稳定性,在ADMM(Alternate Direction Multiplier Method,交替方向乘子法)[22]中引入了反距离加权插值算法[23]的思想,对横向差分算子进行修改以增强反演方法的空间约束能力,进而提高反演目标的横向连续性。最后,通过理论数据测试和实际资料应用验证了本文提出的裂缝密度预测方法(简称“本文方法”)的有效性。
1 基本原理 1.1 含裂缝密度的反射系数近似方程在长波长假设条件下,线性滑动模型与Hudson薄硬币状裂隙模型具有相同的一阶表示形式,因此根据Hudson模型一阶等效弹性刚度矩阵可建立线性滑动模型参数与裂缝岩石相关参数之间的关系[24-25]
| $ {\delta }_{\mathrm{N}}=\frac{4e}{3g\left(1-g\right)\left[1+\frac{1}{\mathrm{\pi }\left(1-g\right)}\left(\frac{k\mathrm{\text{'}}+\frac{4}{3}\mu \mathrm{\text{'}}}{\mu \chi }\right)\right]} $ | (1) |
| $ {\delta }_{\mathrm{T}}=\frac{16e}{3\left(3-2g\right)\left[1+\frac{4}{\mathrm{\pi }\left(3-2g\right)}\left(\frac{\mu \mathrm{\text{'}}}{\mu \chi }\right)\right]} $ | (2) |
式中:
从式(2)可以看出,裂缝弱度与横纵波速度比、裂缝密度、裂缝填充物有关。当裂缝为干裂缝或充填气体时,可以将裂缝充填物的剪切模量和体积模量均设置为0(即
| $ \left\{\begin{array}{c}{\delta }_{\mathrm{N}}=\frac{4e}{3g\left(1-g\right)}\\ {\delta }_{\mathrm{T}}=\frac{16e}{3\left(3-2g\right)}\end{array}\right. $ | (3) |
由于流体剪切模量为0并且体积模量较小,因此当裂缝中饱含流体时,对于纵横比小的裂缝
| $ \left\{\begin{array}{l}{\delta }_{\mathrm{N}}=0\\ {\delta }_{\mathrm{T}}=\frac{16e}{3\left(3-2g\right)}\end{array}\right. $ | (4) |
可见法向裂缝弱度受到裂缝中流体的影响,而切向裂缝弱度不论裂缝充填流体与否,都保持不变。定义裂缝流体因子为
| $ f=\frac{1}{\left[1-g+\left(\frac{k\mathrm{\text{'}}+\frac{4}{3}\mu \mathrm{\text{'}}}{\mu \chi \mathrm{\pi }}\right)\right]} $ | (5) |
由于水的体积模量比油气大,因此当裂缝中含油气量增加时,裂缝流体因子增大。此时,法向裂缝弱度可表示为裂缝密度与裂缝流体因子的乘积,即
| $ \begin{array}{l}{\delta }_{\mathrm{N}}=\frac{4}{3g}\frac{e}{1-g+\frac{k\mathrm{\text{'}}+\frac{4}{3}\mu \mathrm{\text{'}}}{\mu \chi \mathrm{\pi }}}\\ \;\;\;\;=\frac{4}{3g}ef=\frac{4}{3g}F\end{array} $ | (6) |
式中
| $ {R}_{\mathrm{P}\mathrm{P}}\left(\theta ;\varphi \right)={R}_{\mathrm{P}\mathrm{P}}^{\mathrm{i}\mathrm{s}\mathrm{o}}\left(\theta \right)+{R}_{\mathrm{P}\mathrm{P}}^{\mathrm{a}\mathrm{n}\mathrm{i}}\left(\theta ;\varphi \right) $ | (7) |
| $ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}^{\mathrm{i}\mathrm{s}\mathrm{o}}\left(\theta \right)=\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\stackrel{-}{\theta }\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}-4g\mathrm{s}\mathrm{i}\mathrm{n}\theta \frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\left(1-4g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right)\frac{\mathrm{\Delta }\rho }{\stackrel{-}{\rho }}\end{array} $ | (8) |
| $ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}^{\mathrm{a}\mathrm{n}\mathrm{i}}\left(\theta ;\varphi \right)=-\left[g\left(1-2g\right)\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right.\left(1+\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left.{g}^{2}\mathrm{c}\mathrm{o}{\mathrm{s}}^{4}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right]\mathrm{\Delta }{\delta }_{\mathrm{N}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \left(1-\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\varphi \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right)\mathrm{\Delta }{\delta }_{\mathrm{T}}\left(9\right)\end{array} $ |
式中:
当
| $ {R}_{\mathrm{P}\mathrm{P}}^{\mathrm{a}\mathrm{n}\mathrm{i}}\left(\theta ;\varphi \right)=-g\left(1-2g\right)\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{\Delta }{\delta }_{\mathrm{N}}+\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;g\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{\Delta }{\delta }_{\mathrm{T}} $ | (10) |
将式(3)、式(4)代入到式(10),可得
| $ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}^{\mathrm{a}\mathrm{n}\mathrm{i}}\left(\theta ;\varphi \right)=-\frac{4}{3}\left(1-2g\right)\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{\Delta }F+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{16g}{3\left(3-2g\right)}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{\Delta }e\end{array} $ | (11) |
利用两个方位(
| $ \mathrm{\Delta }{R}_{\mathrm{P}\mathrm{P}}(\theta ;{\varphi }_{1},{\varphi }_{2})={A}_{1}(\theta ;{\varphi }_{1},{\varphi }_{2})\mathrm{\Delta }F+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{A}_{2}(\theta ;{\varphi }_{1},{\varphi }_{2})\mathrm{\Delta }e $ | (12) |
其中
| $ \left\{\begin{array}{l}{A}_{1}(\theta ;{\varphi }_{1},{\varphi }_{2})=-\frac{4}{3}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta (1-2g)(\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}-\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{1})\\ {A}_{2}(\theta ;{\varphi }_{1},{\varphi }_{2})=\frac{16g}{3\left(3-2g\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta (\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}-\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{1})\end{array}\right. $ | (13) |
式中
方位差数据可以表示为
| $ \mathrm{\Delta }\boldsymbol{S}=\boldsymbol{G}\boldsymbol{L} $ | (14) |
其中
| $ \left\{\begin{array}{l}\mathrm{\Delta }\boldsymbol{S}={\left[\begin{array}{c}\begin{array}{c}{\boldsymbol{S}}_{\mathrm{P}\mathrm{P}}^{}({\theta }_{1};{\varphi }_{2})-{\boldsymbol{S}}_{\mathrm{P}\mathrm{P}}^{}({\theta }_{1};{\varphi }_{1})\\ {\boldsymbol{S}}_{\mathrm{P}\mathrm{P}}^{}({\theta }_{2};{\varphi }_{2})-{\boldsymbol{S}}_{\mathrm{P}\mathrm{P}}^{}({\theta }_{2};{\varphi }_{1})\end{array}\\ \begin{array}{c}⋮\\ {\boldsymbol{S}}_{\mathrm{P}\mathrm{P}}^{}({\theta }_{m};{\varphi }_{2})-{\boldsymbol{S}}_{\mathrm{P}\mathrm{P}}^{}({\theta }_{m};{\varphi }_{1})\end{array}\end{array}\right]}_{mn\times t}\\ \boldsymbol{L}={\left[\begin{array}{c}\mathrm{\Delta }F\\ \mathrm{\Delta }e\end{array}\right]}_{2n\times t}\\ {\boldsymbol{S}}_{\mathrm{P}\mathrm{P}}^{}={\left[\begin{array}{c}{S}_{{}_{\mathrm{P}\mathrm{P}}}^{1}\\ ⋮\\ {S}_{{}_{\mathrm{P}\mathrm{P}}}^{n}\end{array}\right]}_{n\times t}\end{array}\right. $ | (15) |
式中:
| $ \boldsymbol{G}={\left[\begin{array}{cc}{\boldsymbol{W}}_{0}{\boldsymbol{B}}_{1}\left({\theta }_{1}\right)& {\boldsymbol{W}}_{0}{\boldsymbol{B}}_{2}\left({\theta }_{1}\right)\\ {\boldsymbol{W}}_{0}{\boldsymbol{B}}_{1}\left({\theta }_{2}\right)& {\boldsymbol{W}}_{0}{\boldsymbol{B}}_{2}\left({\theta }_{2}\right)\\ ⋮& ⋮\\ {\boldsymbol{W}}_{0}{\boldsymbol{B}}_{1}\left({\theta }_{m}\right)& {\boldsymbol{W}}_{0}{\boldsymbol{B}}_{2}\left({\theta }_{m}\right)\end{array}\right]}_{mn\times 2n} $ | (16) |
其中
| $ \left\{\begin{array}{l}{\boldsymbol{W}}_{0}^{}={\left[\begin{array}{cccc}{w}_{1}& & & \\ ⋮& {w}_{1}& & \\ {w}_{k}& ⋮& \ddots & \\ & {w}_{k}& \ddots & {w}_{1}\\ & & \ddots & ⋮\\ & & & {w}_{k}\end{array}\right]}_{(n+k-1)\times n}\\ {\boldsymbol{B}}_{1}\left({\theta }_{i}\right)={\left[\begin{array}{ccc}{A}_{1}({\theta }_{i};{\varphi }_{1},{\varphi }_{2})& & \\ & \ddots & \\ & & {A}_{1}({\theta }_{i};{\varphi }_{1},{\varphi }_{2})\end{array}\right]}_{n\times n}\\ {\boldsymbol{B}}_{2}\left({\theta }_{i}\right)={\left[\begin{array}{ccc}{A}_{2}({\theta }_{i};{\varphi }_{1},{\varphi }_{2})& & \\ & \ddots & \\ & & {A}_{2}({\theta }_{i};{\varphi }_{1},{\varphi }_{2})\end{array}\right]}_{n\times n}\\ i=\mathrm{1,2},\cdots ,m\end{array}\right. $ | (17) |
式中
| $ \boldsymbol{B}={\left[\begin{array}{cc}{\boldsymbol{B}}_{1}\left({\theta }_{1}\right)& {\boldsymbol{B}}_{2}\left({\theta }_{1}\right)\\ {\boldsymbol{B}}_{1}\left({\theta }_{2}\right)& {\boldsymbol{B}}_{2}\left({\theta }_{2}\right)\\ ⋮& ⋮\\ {\boldsymbol{B}}_{1}\left({\theta }_{m}\right)& {\boldsymbol{B}}_{2}\left({\theta }_{m}\right)\end{array}\right]}_{mn\times 2n} $ | (18) |
并引入纵向差分矩阵
| $ \boldsymbol{L}={\boldsymbol{D}}_{y}\boldsymbol{M} $ | (19) |
其中
| $ \left\{\begin{array}{l}{\boldsymbol{D}}_{y}={\left[\begin{array}{ccc}{\boldsymbol{D}}_{1}& & \\ & \ddots & \\ & & {\boldsymbol{D}}_{1}\end{array}\right]}_{mn\times 2n}\\ {\boldsymbol{D}}_{1}={\left[\begin{array}{ccccc}-1& 1& & & \\ & -1& 1& & \\ & & \ddots & \ddots & \\ & & & -1& 1\end{array}\right]}_{n\times n}\\ \boldsymbol{M}={\left[\begin{array}{cccc}{F}_{11}& {F}_{21}& \cdots & {F}_{t1}\\ & & ⋮& \\ {F}_{1n}& {F}_{1n}& \cdots & {F}_{tn}\\ {e}_{11}& {e}_{21}& \cdots & {e}_{t1}\\ & & ⋮& \\ {e}_{1n}& {e}_{2n}& \cdots & {e}_{tn}\end{array}\right]}_{2n\times t}\end{array}\right. $ | (20) |
式中:D为差分矩阵;M为待反演参数构成的矩阵。
为了提高多个参数反演的横向稳定性,ATV(Anisotropic Total Variation)算法引入横向差分
| $ \mathrm{A}\mathrm{T}\mathrm{V}\left(\boldsymbol{M}\right)={‖\boldsymbol{M}{\boldsymbol{D}}_{x}‖}_{1}+{‖{\boldsymbol{D}}_{y}\boldsymbol{M}‖}_{1} $ | (21) |
式中
反距离加权插值法基于相近、相似原理,认为两个物体距离越近,性质就越相似,因而以插值点与样本点间的距离为权重进行加权平均,离插值点越近的样本点赋予的权重越大。反距离加权插值为
| $ \widehat{Z}\left({h}_{0}\right)=\sum\limits _{j=1}^{N}{\vartheta }_{j}Z\left({h}_{j}\right) $ | (22) |
式中:
| $ {\vartheta }_{j}=\frac{{d}_{j,0}^{-p}}{\sum\limits _{j=1}^{N}{d}_{j,0}^{-p}} $ | (23) |
式中:p为指数值,一般取2;
根据式(22),利用邻近两道地震数据和初始模型进行约束,可以得到反演目标函数为
| $ \begin{array}{l}J\left(\boldsymbol{M}\right)=\underset{\boldsymbol{M}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left[\right||\boldsymbol{W}\boldsymbol{B}{\boldsymbol{D}}_{y}\boldsymbol{M}-\mathrm{\Delta }\boldsymbol{S}|{|}_{2}^{2}+\kappa \left|\right|\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \alpha \left(\left|\right|\boldsymbol{M}{\boldsymbol{D}}_{x}|{|}_{1}+|\left|{\boldsymbol{D}}_{y}\boldsymbol{M}\right|{|}_{1}\right)]\end{array} $ | (24) |
其中
| $ {\boldsymbol{D}}_{x}={{\left[\begin{array}{cccc}-1& & & \\ {\vartheta }_{12}& -1& & \\ {\vartheta }_{13}& \lambda {\vartheta }_{23}& \ddots & \\ & {\vartheta }_{24}& \ddots & -1\\ & & \ddots & {\vartheta }_{\left(n-2\right)\left(n-1\right)}\\ & & & {\vartheta }_{\left(n-2\right)n}\end{array}\right]}_{t\times }}_{t} $ | (25) |
式中:
本文采用ADMM[30]对含多个未知参数的待解目标函数(式(24))求解,将目标函数分解成多个单一参数的子问题。首先引入矩阵
| $ \begin{array}{l}J\left(\boldsymbol{M}\right)=\underset{\boldsymbol{M}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left[\right||\boldsymbol{W}\boldsymbol{B}{\boldsymbol{D}}_{y}\boldsymbol{M}-\mathrm{\Delta }\boldsymbol{S}|{|}_{2}^{2}+\kappa \left|\right|\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\\ \;\;\;\;\;\;\;\;\;\;\;\alpha \left(\left|\right|{\boldsymbol{M}}_{x}|{|}_{1}+|\left|{\boldsymbol{M}}_{y}\right|{|}_{1}\right)]\mathrm{s}.\mathrm{t}.{\boldsymbol{M}}_{x}=\boldsymbol{M}{\boldsymbol{D}}_{\mathrm{x}}{\boldsymbol{M}}_{y}={\boldsymbol{D}}_{y}\boldsymbol{M}\end{array} $ | (26) |
再引入对偶项
| $ \begin{array}{l}J\left(\boldsymbol{M}\right)=\underset{\boldsymbol{M}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left[\right||\boldsymbol{W}\boldsymbol{B}{\boldsymbol{D}}_{y}\boldsymbol{M}-\mathrm{\Delta }\boldsymbol{S}|{|}_{2}^{2}+\kappa \left|\right|\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\\\;\;\;\;\;\;\;\;\;\;\; \alpha \left(\left|\right|{\boldsymbol{M}}_{x}|{|}_{1}+|\left|{\boldsymbol{M}}_{y}\right|{|}_{1}\right)+\eta {‖{\boldsymbol{M}}_{x}-\boldsymbol{M}{\boldsymbol{D}}_{x}-{\boldsymbol{C}}_{x}‖}_{2}^{2}+\\ \;\;\;\;\;\;\;\;\;\;\;\eta {‖{\boldsymbol{M}}_{y}-{\boldsymbol{D}}_{y}\boldsymbol{M}-{\boldsymbol{C}}_{y}‖}_{2}^{2}\left]\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\right(27)\end{array} $ |
式中
于是,将式(27)拆解成分别关于
| $ \begin{array}{l}{K}_{1}\left(\boldsymbol{M}\right)=\underset{\boldsymbol{M}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\right||\boldsymbol{W}\boldsymbol{B}{\boldsymbol{D}}_{y}\boldsymbol{M}-\mathrm{\Delta }\boldsymbol{S}|{|}_{2}^{2}+\kappa \left|\right|\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\\\;\;\;\;\;\;\;\;\;\;\;\;\; \eta {‖{\boldsymbol{M}}_{x}-\boldsymbol{M}{\boldsymbol{D}}_{x}-{\boldsymbol{C}}_{x}‖}_{2}^{2}+\eta {‖{\boldsymbol{M}}_{y}-{\boldsymbol{D}}_{y}\boldsymbol{M}-{\boldsymbol{C}}_{y}‖}_{2}^{2})\end{array} $ | (28) |
| $ {K}_{2}\left({\boldsymbol{M}}_{x}\right)=\underset{{\boldsymbol{M}}_{x}}{\mathrm{m}\mathrm{i}\mathrm{n}}(\alpha {‖{\boldsymbol{M}}_{x}‖}_{1}+\eta {‖{\boldsymbol{M}}_{x}-\boldsymbol{M}{\boldsymbol{D}}_{x}-{\boldsymbol{C}}_{x}‖}_{2}^{2}) $ | (29) |
| $ {K}_{3}\left({\boldsymbol{M}}_{y}\right)=\underset{{\boldsymbol{M}}_{y}}{\mathrm{m}\mathrm{i}\mathrm{n}}(\alpha {‖{\boldsymbol{M}}_{y}‖}_{1}+\eta {‖{\boldsymbol{M}}_{y}-{\boldsymbol{D}}_{y}\boldsymbol{M}-{\boldsymbol{C}}_{y}‖}_{2}^{2}) $ | (30) |
| $ {K}_{4}\left({\boldsymbol{C}}_{x}\right)=\underset{{\boldsymbol{C}}_{x}}{\mathrm{m}\mathrm{i}\mathrm{n}}\eta {‖{\boldsymbol{M}}_{x}-\boldsymbol{M}{\boldsymbol{D}}_{x}-{\boldsymbol{C}}_{x}‖}_{2}^{2} $ | (31) |
| $ {K}_{5}\left({\boldsymbol{C}}_{y}\right)=\underset{{\boldsymbol{C}}_{y}}{\mathrm{m}\mathrm{i}\mathrm{n}}\eta {‖{\boldsymbol{M}}_{y}-{\boldsymbol{D}}_{y}\boldsymbol{M}-{\boldsymbol{C}}_{y}‖}_{2}^{2} $ | (32) |
针对式(28)关于
| $ \begin{array}{l}\left[\right(\boldsymbol{W}\boldsymbol{B}{\boldsymbol{D}}_{y}{)}^{\mathrm{T}}\left(\boldsymbol{W}\boldsymbol{B}{\boldsymbol{D}}_{y}\right)+\kappa \boldsymbol{E}+\eta {\boldsymbol{D}}_{y}^{\mathrm{T}}{\boldsymbol{D}}_{y}]\boldsymbol{M}+\boldsymbol{M}·\eta {\boldsymbol{D}}_{x}^{\mathrm{T}}{\boldsymbol{D}}_{x}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; =(\boldsymbol{W}\boldsymbol{B}{\boldsymbol{D}}_{y}{)}^{\mathrm{T}}\mathrm{\Delta }\boldsymbol{S}+\kappa {\boldsymbol{M}}_{0}+\eta {\boldsymbol{D}}_{y}^{\mathrm{T}}{\boldsymbol{M}}_{y}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \eta {\boldsymbol{M}}_{x}{\boldsymbol{D}}_{x}^{\mathrm{T}}-\eta {\boldsymbol{D}}_{y}^{\mathrm{T}}{\boldsymbol{C}}_{y}-\eta {\boldsymbol{C}}_{x}{\boldsymbol{D}}_{x}^{\mathrm{T}}\left(33\right)\end{array} $ |
式中“·”表示标量乘法运算。
由于式(33)符合二维西尔维特方程的基本形式,因此可通过特征值分解技术显式求解。
针对式(29)和式(30)同时含有L1范数和L2范数的子目标函数,引入软阈值收缩算法[23]求解,可依次求解得
| $ {\boldsymbol{M}}_{x}^{(r+1)}=\mathrm{m}\mathrm{a}\mathrm{x}(\left|{\boldsymbol{M}}^{(r+1)}{\boldsymbol{D}}_{x}+{\boldsymbol{C}}_{x}^{\left(r\right)}\right|-\frac{\alpha }{\eta },0)\mathrm{ }·\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left[{\boldsymbol{M}}^{(r+1)}{\boldsymbol{D}}_{x}+{\boldsymbol{C}}_{x}^{\left(r\right)}\right] $ | (34) |
| $ {\boldsymbol{M}}_{y}^{(r+1)}=\mathrm{m}\mathrm{a}\mathrm{x}\left[\left|{\boldsymbol{D}}_{y}{\boldsymbol{M}}^{(r+1)}+{\boldsymbol{C}}_{y}^{\left(r\right)}\right|-\frac{\alpha }{\eta },0\right]·\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left[{\boldsymbol{D}}_{y}{\boldsymbol{M}}^{(r+1)}+{\boldsymbol{C}}_{y}^{\left(r\right)}\right] $ | (35) |
式中:
| $ \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(Z\right)=\left\{\begin{array}{cc}1& Z > 0\\ 0& Z=0\\ -1& Z < 0\end{array}\right. $ | (36) |
针对式(31)和式(32)为仅含有2范数的凸优化问题,采用凸优化算法进行求解,得
| $ {\boldsymbol{C}}_{x}^{(r+1)}={\boldsymbol{C}}_{x}^{\left(r\right)}+\left[{\boldsymbol{M}}^{(r+1)}{\boldsymbol{D}}_{x}-{\boldsymbol{M}}_{x}^{(r+1)}\right] $ | (37) |
| $ {\boldsymbol{C}}_{y}^{(r+1)}={\boldsymbol{C}}_{y}^{\left(r\right)}+\left[{\boldsymbol{D}}_{y}{\boldsymbol{M}}^{(r+1)}-{\boldsymbol{M}}_{y}^{(r+1)}\right] $ | (38) |
本文反演方法流程及框架如表 1所示。
|
|
表 1 本文方法框架 |
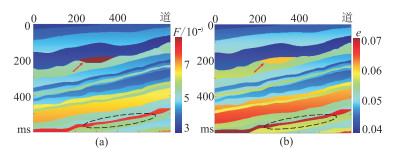
测试模型为Marmousi Ⅱ,选取其中纵向300个采样点、横向650道的数据用于建立可采性因子F和裂缝密度e的理论模型(图 1),采样时间间隔为2ms。该模型地层产状相对平缓,在剖面中部、底部位置分别发育透镜体状(图 1中红色箭头)和薄层状油气储层(图 1中黑色虚线圈)。油气储层均表现出F和e高值异常,表明该理论模型建立的合理性,同时存在的高值突变异常有利于验证本文方法具有能够改善地层横向连续性、提高横向分辨率的优点。
|
图 1 可采因子(a)和裂缝密度(b)理论模型 |
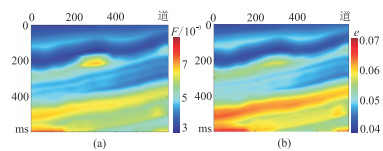
首先,将理论模型进行高斯低通滤波处理,构建用于补充背景信息待反演参数F和e的低频模型(图 2)。其次,基于式(8)、式(11)计算出四组包含各向异性扰动部分的纵波反射系数(
|
图 2 可采因子(a)和裂缝密度(b)低频模型 |
|
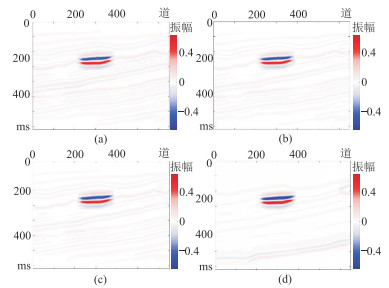
图 3 无噪情况下不同入射角、不同方位的合成地震记录 (a) |
|
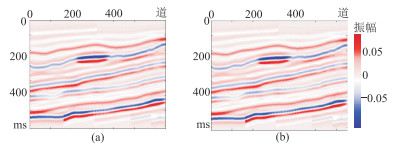
图 4 无噪情况下的不同方位差地震记录 (a) |
|
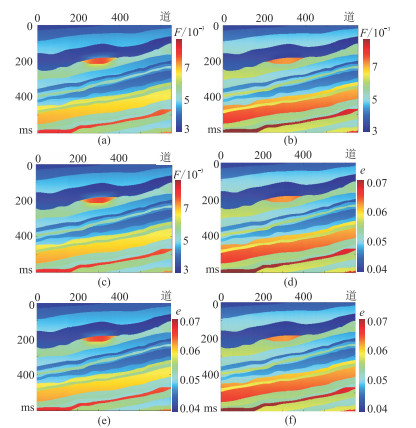
图 5 无噪情况下的不同方法的反演结果 (a)、(b)、(c)依次为单道、传统多道、本文方法的F;(d)、(e)、(f)依次为单道、传统多道、本文方法的e。 |
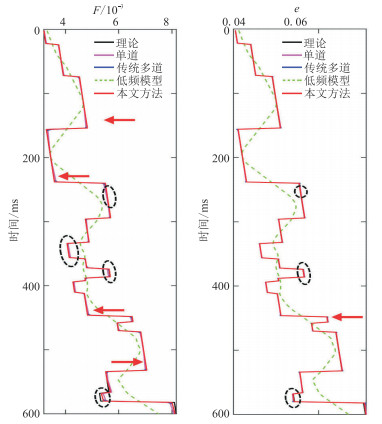
由图 5可知,在无噪情况下分别采用三种方法(单道、传统多道、本文方法)反演获得的F和e无明显差异,无法直观评价反演效果。为了更加准确地反映三种方法之间的差异,体现本文方法的优势,选取剖面的第100道数据,对比三种方法获得的无噪情况下F和e单道反演结果(图 6)。由图可见,在同一地层中(图 6中黑色虚线圈),传统多道的反演精度比单道更高,但本文方法的反演结果比传统多道更加准确。同时,在地层边界处(图 6中红色箭头处)存在F和e的突变,本文方法能更准确刻画地层边界,表明本文方法针对参数突变(异常)具有更高的稳定性。
|
图 6 无噪情况下不同方法的单道(第100道) F(左)、e(右)反演结果对比 |
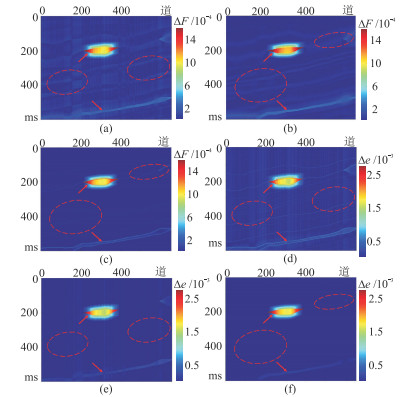
为了更好地体现这种差异,分别利用三种方法反演获得的F和e与对应的理论模型做差,得到残差剖面(图 7)。由图可见,单道(图 7a)、传统多道(图 7b)和本文方法(图 7c)得到的F残差剖面整体上逐渐“干净”,即残差值依次减小,且位于透镜体状和薄层状的油气储层(红色箭头处)的F残差也依次减小,这说明本文方法的反演结果最准确,传统多道方法次之,单道方法效果最差。同时,“竖条状”[31]反射也依次减少,说明相对于单道和传统多道,本文方法反演的F结果(图 5c)地层的横向连续性最好,传统多道方法(图 5b)次之,单道方法(图 5a)最差。同理,三种方法反演e结果的残差剖面(图 7d、7e、7f)也表明了采用本文方法结果更准确,地层横向连续性更好。
|
图 7 无噪情况下不同方法反演结果的残差剖面 (a)、(b)、(c)依次为单道、传统多道、本文方法的F;(d)、(e)、(f)依次为单道、传统多道、本文方法的e。 |
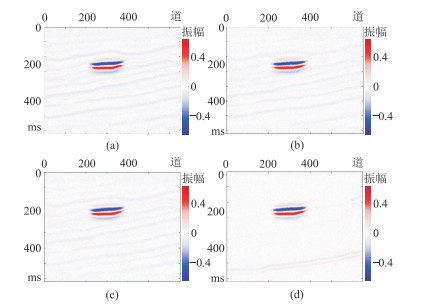
为测试本文方法的抗噪性,对图 3中的合成地震记录添加随机高斯白噪,分别得到四组信噪比(SNR)为5的不同入射角、不同方位的地震记录(图 8),并获得两组相应的方位差地震记录(图 9);再分别采用单道、传统多道和本文方法反演,最后得到SNR=5地震资料的F和e反演结果(图 10)。
|
图 8 SNR=5的不同入射角、不同方位的合成地震记录 (a) |
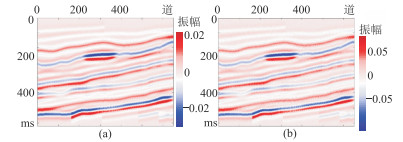
|
图 9 SNR=5的方位差地震记录 (a) |
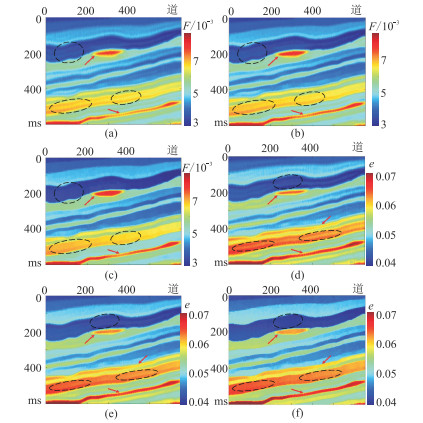
|
图 10 SNR=5的反演结果剖面 (a)(b)(c)依次为单道、传统多道、本文方法的F;(d)(e)(f)依次为单道、传统多道、本文方法的e。 |
由图 10可见,三种方法对透镜体状和薄层状的油气储层(红色箭头处)形态逐渐刻画得更好,且储层四周的伪层厚度逐渐变薄,说明本文方法受到油气储层F高值异常影响最小,反演效果最好,而传统多道方法次之,单道方法效果最差。同时,剖面的“竖条状”反射(黑色虚线圈内)得到削弱,表明横向连续性更好,由于本文方法通过反距离加权的原理对相邻道之间的关系考虑更充分,所以采用本文方法的反演获得的F剖面的“竖条状”反射明显减少,这表明进一步优化了地层横向连续性,提高了剖面的横向分辨率。
同理,三组SNR=5地震资料的e反演结果(图 10d~图 10f)也表现出和F相同的效果。因此,加噪测试结果表明:本文方法能表现出最好的准确性和横向连续性,对裂缝密度的预测更加准确、可靠。
同样,SNR=5地震资料的三种方法F和e的第100道单道反演结果如图 11所示。由图可见,采用本文方法反演获得的F和e更准确(黑色虚线圈),传统多道方法次之,单道方法最差,这反映了传统多道方法的抗噪性比单道更好,而本文方法在传统多道方法的基础上又更准确,证明了本文方法可有效提高了F和e反演结果的准确性,同时表现出更强的抗噪性。
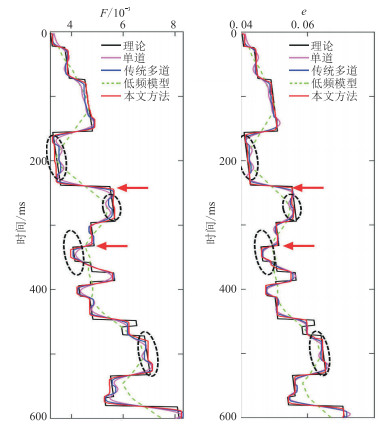
|
图 11 SNR=5时不同方法的单道(第100道) F(左)、e(右)反演结果对比 |
另外,从图 12可见,三种方法均受到噪声不同程度的影响,但本文方法获得的F残差剖面中的“竖条状”反射得到明显削弱,说明了本文方法获得的剖面横向连续性最好(红色虚线内)。尤其是在透镜体状和薄层状储层的边界及内部(红色箭头处),残差均明显得到削弱,进一步说明了本文方法预测的F和e结果最准确。因此,通过加噪测试,相比于单道和传统多道方法,本文方法表现出更高的准确性和抗噪性,地层横向连续性更好,对裂缝密度的预测更加准确、可靠,有利于油气储层的有效预测。
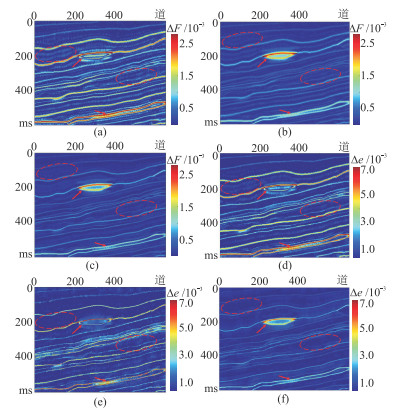
|
图 12 SNR=5反演结果的残差剖面 (a)、(b)、(c)依次为单道、传统多道、本文方法的F;(d)、(e)、(f)依次为单道、传统多道、本文方法的e。 |
引入信噪比和均方根误差(RMSE)[32]对三种方法的反演结果进行定量评价。信噪比和均方根误差表达式分别为
| $ \mathrm{S}\mathrm{N}\mathrm{R}=10\times \mathrm{l}\mathrm{g}\frac{\sum\limits_{i=1}^{{N}_{\mathrm{t}\mathrm{r}}}\sum\limits_{j=1}^{{N}_{\mathrm{s}}}({H}_{i,j}{-\overline{H})}^{2}}{\sum\limits_{i=1}^{{N}_{\mathrm{t}\mathrm{r}}}\sum\limits_{j=1}^{{N}_{\mathrm{s}}}({H}_{i,j}-{X}_{i,j}{)}^{2}} $ | (39) |
| $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{\sum\limits_{i=1}^{{t}_{}}\sum\limits_{j=1}^{{n}_{}}({H}_{i,j}-{X}_{i,j}{)}^{2}}{tn}} $ | (40) |
式中:
表 2为无噪情况下三种方法F和e反演结果的定量评价结果,表 3为SNR=5的地震资料三种方法F和e反演结果的定量评价结果。由表 2、表 3可知,本文方法反演获得的剖面信噪比均比单道和传统多道方法更高,且均方根误差最小。
|
|
表 2 无噪地震资料不同方法定量评价结果 |
|
|
表 3 SNR=5地震资料不同方法定量评价结果 |
为了更直观评价以上三种方法的反演精度,对不同方法的残差进行统计,获得不加噪和SNR=5时的残差统计直方图,分别如图 13和图 14所示。由图 13、图 14可见,在相同信噪比条件下,三种反演方法的反演精度由高到低依次为本文方法、传统多道、单道的反演方法;随着信噪比降低,三种方法的残差总量均增加,反演精度相比下降。
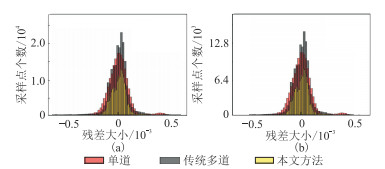
|
图 13 无噪情况下不同方法反演结果的残差统计直方图 (a)F;(b)e |
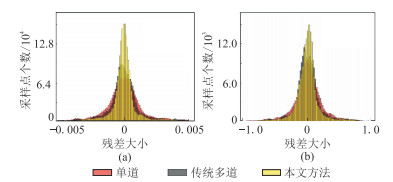
|
图 14 SNR=5时不同方法反演结果的残差统计直方图 (a)F;(b)e |
因此,从定量角度看,本文方法比单道和传统多道方法的反演精度更高,抗噪性更好。
3 实际资料应用选取塔里木盆地YM区块实际资料(图 15)测试本文方法的应用效果。该区块碳酸盐岩埋藏深,非均质性强,裂缝较为发育。储层段发育大量高角度裂缝,具有明显的HTI介质特征。研究区OVT道集炮检距范围为565~8456 m,主要分布在3000~8000 m,方位角分布均匀,非常有利于本文方法进行各向异性反演。
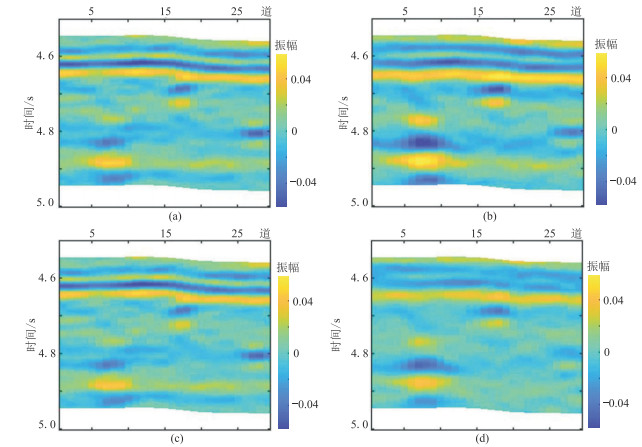
|
图 15 不同方位、不同角度叠加剖面 (a) |
采用方位差数据反演e和F仅需两个方位即可。综合各方位覆盖次数、最大炮检距以及各角度资料质量,将OVT叠前道集等分为2个方位,并在这2个方位下进行了入射角部分叠加,共得到不同方位、不同入射角的4个地震数据。数据的中心方位角分别为90°(75°~105°)、135°(120°~150°),中心入射角分别为10°(6°~14°)、19°(15°~23°),叠加数据如图 15所示。由图可见,振幅在不同方位和不同入射角下均存在较大的差异,适合用于各向异性反演。
分别采用本文方法与常规单道反演方法预测裂缝密度,结果如图 16所示。由图可见,两种反演方法均表明在过水平井轨迹的位置裂缝密度较大;本文方法与常规单道反演方法相比,剖面在横向上存在的“竖条状”反射(红色箭头所指)明显削弱,同时本文方法反演结果中横向上地层具有更好的连续性(图 16中红色圆圈内),反演结果的信噪比相对有所提升。
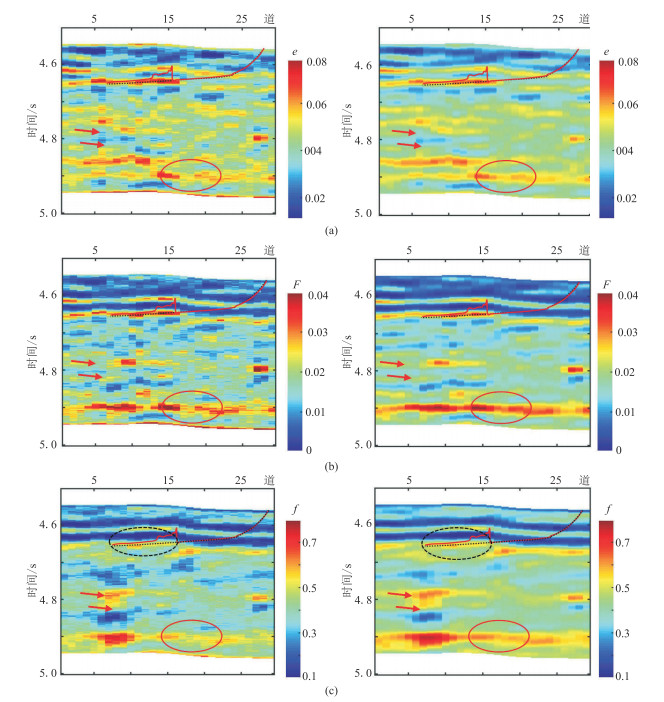
|
图 16 常规单道方法(左)与本文方法(右)不同参数的反演结果 (a)e;(b)F;(c)f。图中黑色虚线为井轨迹,红色曲线为气测曲线。 |
为了进一步验证反演结果的准确性,将反演结果进一步换算成裂缝流体因子f(图 16c)。由图可见,水平井段f为高值,表明整体含气;大值与气测曲线大值(黑色虚线圆圈)吻合较好,但水平井段气测具有差异,后段含气测显示更高,与裂缝发育密度相关;水平井段后段裂缝发育密度更高,与气测全烃结果对应较好。因此,可采性因子的预测结果与水平井段气测全烃显示具有很好的一致性。这证实了本文方法具有较高的精度,通过直接反演获得的裂缝密度更加准确。
4 结论本文提出的基于空间约束的碳酸盐岩裂缝密度直接反演的方法实现了裂缝密度的直接反演与反演算法的优化,通过模型测试和实际资料应用,得出如下结论:
(1) 引入反距离加权插值优化的横向差分算子充分利用了相邻多个地震道之间的相关性,提高了反演结果中地层的横向连续性和稳定性;
(2) 通过推导裂缝密度与包含各向异性纵波反射系数之间的关系实现了裂缝密度的直接反演,提高了裂缝预测的准确性和可靠性;
(3) 本文方法可以间接求取裂缝流体因子,能为油气开采提供指导。
| [1] |
GOODWAY B, VARSEK J, ABACO C. Anisotropic 3D amplitude variation with azimuth (AVAZ) methods to detect fracture prone zones in tight gas resource plays[C]. 2007 CSPG CSEG Convention, 2007, 590-596.
|
| [2] |
LIU E, MARTINEZ A. Seismic Fracture Characterization: Concepts and Practical Applications[M]. EAGE Publications, Houten, Netherlands, 2012.
|
| [3] |
陈怀震, 印兴耀, 高建虎, 等. 基于等效各向异性和流体替换的地下裂缝地震预测方法[J]. 中国科学(地球科学), 2015, 45(5): 589-600. CHEN Huaizhen, YIN Xingyao, GAO Jianhu, et al. Seismic inversion for underground fractures detection based on effective anisotropy and fluid substitution[J]. Scientia Sinica(Terrae), 2015, 45(5): 589-600. |
| [4] |
LI L, ZHANG G, LIU J, et al. Estimation of fracture density and orientation from azimuthal elastic impedance difference through singular value decomposition[J]. Petroleum Science, 2021, 18(6): 1675-1688. DOI:10.1016/j.petsci.2021.09.037 |
| [5] |
XUE J, GU H, CAI C. Model-based amplitude versus offset and azimuth inversion for estimating fracture parameters and fluid content[J]. Geophysics, 2017, 82(2): M1-M17. DOI:10.1190/geo2016-0196.1 |
| [6] |
PAN X P, LI L, ZHANG G Z. Multiscale frequency-domain seismic inversion for fracture weakness[J]. Journal of Petroleum Science and Engineering, 2020, 195(3): 107845. |
| [7] |
WANG Y, WANG C, LI J, et al. Frequency-dependent S-wave splitting parameters analysis: a case study from azimuthal PS data, Sanhu area of the Qaidam Basin, China[J]. Geophysics, 2019, 84(6): B375-B386. DOI:10.1190/geo2018-0627.1 |
| [8] |
刘开元. 三维方位各向异性分析及裂缝检测[D]. 四川成都: 成都理工大学, 2011. LIU Kaiyuan. Three-dimensional Research of Azimuthal Anisotropy and Fracture Detection Methods[D]. Chengdu University of Technology, Chengdu, Sichuan, 2011. |
| [9] |
陈怀震, 印兴耀, 高成国, 等. 基于各向异性岩石物理的缝隙流体因子AVAZ反演[J]. 地球物理学报, 2014, 57(3): 968-978. CHEN Huaizhen, YIN Xingyao, GAO Chengguo, et al. AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory[J]. Chinese Journal of Geophysics, 2014, 57(3): 968-978. |
| [10] |
BAKULIN A, GRECHKA V, TSVANKIN I. Estimation of fracture parameters from reflection seismic data- Part Ⅰ: HTI model due to a single fracture set[J]. Geophysics, 2000, 65(6): 1788-1802. DOI:10.1190/1.1444863 |
| [11] |
ZHANG F, LI X. Generalized approximations of reflection coefficients in orthorhombic media[J]. Journal of Geophysics and Engineering, 2013, 10(5): 054004. DOI:10.1088/1742-2132/10/5/054004 |
| [12] |
DOWNTON J E, ROURE B. Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters[J]. Interpretation, 2015, 3(3): ST9-ST27. DOI:10.1190/INT-2014-0235.1 |
| [13] |
ISABEL V G. Fracture Studies from Amplitude Versus Offset and Azimuth and Vertical Seismic Profile Data[D]. The University of Edinburgh, Edinburgh, Britain, 2009.
|
| [14] |
刘财, 刘宇巍, 冯晅, 等. 基于方位相交的纵波AVA数据运用SVD反演HTI介质裂缝密度[J]. 吉林大学学报(地球科学版), 2013, 43(5): 1655-1662. LIU Cai, LIU Yuwei, FENG Xuan, et al. Invert crack density of HTI media by using SVD based on PP-wave AVA data from crossing seismic survey lines[J]. Journal of Jilin University(Earth Science Edition), 2013, 43(5): 1655-1662. |
| [15] |
BAKULIN A, GRECHKA V, TSVANKIN I. Estimation of fracture parameters from reflection seismic data-Part Ⅱ: fractured models with orthorhombic symmetry[J]. Geophysics, 2000, 65(6): 1803-1817. DOI:10.1190/1.1444864 |
| [16] |
AL-MARZOUG A M, NEVES F A, KIM J J, et al. P-wave anisotropy from azimuthal AVO and velocity estimates using 3D seismic data from Saudi Arabia[J]. Geophysics, 2006, 71(2): E7-E11. DOI:10.1190/1.2187724 |
| [17] |
秦海旭, 吴国忱. 基于各向异性梯度的裂缝密度反演[J]. 地震学报, 2014, 36(6): 1062-1074, 1155. QIN Haixu, WU Guochen. Fracture density inversion based on the anisotropic gradient[J]. Acta Seismologica Sinica, 2014, 36(6): 1062-1074, 1155. |
| [18] |
魏欣伟, 薛姣, 罗霞. 基于OVT域地震数据的叠前AVOA裂缝密度反演[J]. 石油物探, 2021, 60(5): 816-825. WEI Xinwei, XUE Jiao, LUO Xia. Fracture density estimation using an amplitude-versus-offset-and-azimuth inversion based on prestack seismic data in the offset vector tile domain[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 816-825. DOI:10.3969/j.issn.1000-1441.2021.05.012 |
| [19] |
CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [20] |
MARTIN S, JORGE L. Elastic impedance in weakly anisotropic media[J]. Geophysics, 2006, 71(3): D73-D83. DOI:10.1190/1.2195448 |
| [21] |
陈超, 印兴耀, 刘晓晶, 等. 基于方位各向异性的裂缝密度反演方法及应用[J]. 地球物理学报, 2022, 65(1): 371-383. CHEN Chao, YIN Xingyao, LIU Xiaojing, et al. Fracture density inversion based on azimuthal aniso- tropy and its application[J]. Chinese Journal of Geophysics, 2022, 65(1): 371-383. |
| [22] |
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1): 1-122. |
| [23] |
LIU Z Q, XU B, CHENG B, et al. Interpolation parameters in inverse distance-weighted interpolation algorithm on DEM interpolation error[J]. Journal of Sensors, 2021, 2021: 3535195. |
| [24] |
SCHOENBERG M, DOUMA J. Elastic wave propagation in media with parallel fractures and aligned cracks[J]. Geophysical Prospecting, 1988, 36(6): 571-590. DOI:10.1111/j.1365-2478.1988.tb02181.x |
| [25] |
TENG L. Seismic and Rock-Physics Characterization of Fractured Reservoirs[D]. Stanford University, Palo Alto, USA, 1998.
|
| [26] |
周城, 杨宇勇, 周怀来, 等. 基于HTI介质走时反演的各向异性参数建模与AVAZ反演[J]. 石油地球物理勘探, 2023, 58(4): 949-960, 969. ZHOU Cheng, YANG Yuyong, ZHOU Huailai, et al. Modeling of anisotropic parameters based on HTI medium travel-time inversion and AVAZ inversion[J]. Oil Geophysical Prospecting, 2023, 58(4): 949-960, 969. |
| [27] |
周晓越, 甘利灯, 杨昊, 等. 利用叠前振幅和速度各向异性的联合反演方法[J]. 石油地球物理勘探, 2020, 55(5): 1084-1091. ZHOU Xiaoyue, GAN Lideng, YANG Hao, et al. A joint inversion method using amplitude and velocity anisotropy[J]. Oil Geophysical Prospecting, 2020, 55(5): 1084-1091. |
| [28] |
刘晓晶, 陈祖庆, 陈超, 等. 方位弹性阻抗傅里叶级数裂缝预测方法[J]. 石油地球物理勘探, 2022, 57(2): 423-433. LIU Xiaojing, CHEN Zuqing, CHEN Chao, et al. Fracture prediction method based on Fourier series of azimuthal elastic impedance[J]. Oil Geophysical Prospecting, 2022, 57(2): 423-433. |
| [29] |
于晓东, 桂志先, 汪勇, 等. 叠前AVAZ裂缝预测技术在车排子凸起的应用[J]. 石油地球物理勘探, 2019, 54(3): 624-633. YU Xiaodong, GUI Zhixian, WANG Yong, et al. Prestack AVAZ fracture prediction applied in Che-paizi Uplift[J]. Oil Geophysical Prospecting, 2019, 54(3): 624-633. |
| [30] |
EUHANNA G, ANDRE T, IMAN S, et al. Optimal parameter selection for the alternating direction method of multipliers (ADMM): Quadratic problems[J]. IEEE Transactions on Automatic Control, 2015, 60(3): 644-658. DOI:10.1109/TAC.2014.2354892 |
| [31] |
ZHAO L, LIN K, WEN X T, et al. Anisotropic total variation pre-stack multitrace inversion based on Lp norm constraint[J]. Journal of Petroleum Science and Engineering, 2023, 220: 111212. DOI:10.1016/j.petrol.2022.111212 |
| [32] |
张雨强, 文晓涛, 吴昊, 等. 基于Lp拟范数稀疏约束和交替方向乘子算法的波阻抗反演[J]. 石油物探, 2022, 61(5): 856-864. ZHANG Yuqiang, WEN Xiaotao, WU Hao, et al. Seismic acoustic impedance inversion using Lp quasi-norm sparse constraint and alternating direction multiplier algorithm[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 856-864. |



 袁敬一, 新疆库尔勒市塔指东路中国石油塔里木油田公司,841000。Email:
袁敬一, 新疆库尔勒市塔指东路中国石油塔里木油田公司,841000。Email: