2. 中国石油大学(华东), 山东青岛 266580;
3. 中国石油勘探开发研究院, 北京 100083
2. School of Geoscience, China University of Petroleum (East China), Qingdao, Shandong 266580, China;
3. Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China
页岩气是以吸附或游离状态赋存于富有机质页岩孔隙和裂缝等储集空间中的非常规天然气,页岩储层具有沉积环境复杂、优质储层薄、致密且压裂难度大等特点,是全球重要的油气资源[1-3]。利用地震资料预测“甜点”是描述页岩气储层的重要内容,地应力作为“甜点”预测的主要内容,对页岩气储层的压裂方案设计、水平井井位部署等具有重要的指导意义。
地应力计算方法分为直接测量法和间接计算法。直接测量法包括水力压裂、声发射测量等;间接计算法包括测井计算、有限元模拟及地震预测等[4-7]。测井计算法有声波测井、成像测井、声波速度各向异性等方法,同时,地应力是电成像测井曲线计算的重要影响因素[8-11]。地震预测法可有效地评价地应力横向展布特征,而地应力与水力压裂裂缝形态、储层裂缝参数密切相关[12-14]。近年来基于各向异性介质理论的裂缝预测方法发展迅速,从螺旋道集出发,综合岩石物理、测井等先验信息利用叠前AVAZ(Amplitude Versus Azimuth)反演裂缝参数[15-17]。Pan等[18-19]将裂缝型储层等效为HTI(Horizontal Transverse Isotropy)介质及正交各向异性介质,直接利用宽方位地震资料反演裂缝与流体参数。基于裂缝预测的地应力预测技术取得了显著进步,如:Gray等[20]运用基于宽方位角、大入射角的叠前道集资料估测与岩石力学相关的主应力,利用水平应力差与最大水平主应力的比值——水平应力差异比(Differential Horizontal Stress Ratio, DHSR)定量判断储层的地应力特征;马妮等[21-22]考虑了正交各向异性特征,利用弹性阻抗反演方法预测非常规储层的地应力特征;Dubinya等[14]研发了裂缝网络模型区分烃类液压导电和非液压导电裂缝,利用这两种裂缝的差异可以动态地描述储层的地质力学特征,其中通过叠前反演λ、μ、ρ(λ、μ为拉梅系数,ρ为密度)、垂向和横向泊松比等参数预测最大水平主应力、闭合应力梯度等[23-24]。目前,地震预测法通常运用弹性参数计算DHSR,但是存在不足:一是预测方程中含有各向异性参数(裂缝柔度),不容易求取,造成地应力预测难度较大;二是预测方程中的杨氏模量、泊松比等参数是由间接反演求取的,精度较低,难以满足页岩气地质工程一体化的要求。
为克服上述不足,本文提出基于裂缝密度反演的页岩储层地应力地震预测方法。为了有效提高预测精度,建立了基于杨氏模量、泊松比和裂缝密度的纵波方位各向异性AVO方程直接反演弹性参数[25],推导了由泊松比和裂缝密度表示的DHSR公式。最后,利用所提方法预测川南试验区龙马溪组页岩气储层的地应力。
1 页岩气储层地应力地震预测方法从页岩气储层特征(基质特征、矿物组分、孔隙类型和流体特征)出发,基于井数据建立各向异性岩石物理模型,利用基于贝叶斯理论的叠前各向异性直接反演估算储层的DHSR,以评价页岩气储层地应力。页岩气储层地应力地震预测法包括叠前方位各向异性AVO直接反演及DHSR定量估算。
1.1 叠前方位各向异性AVO直接反演基于页岩储层各向异性岩石物理模型[26]开展叠前方位各向异性反演。叠前方位各向异性AVO直接反演充分利用螺旋道集的方位角和入射角信息预测储层的非均质性和流体特征[27-29],裂缝作为页岩储层的有效储集空间,明显影响地震波传播,通常将含有裂缝的页岩等效为HTI介质。Rüger[30]研究了地震波在各向同性介质和HTI介质界面的反射特征,推导了纵波方位AVO近似方程,分析了振幅随方位角和入射角的变化特征。杜炳毅等[15]基于Rüger近似推导了由杨氏模量E、泊松比ν和各向异性梯度Γ表示的纵波方位各向异性AVO方程
| $ {R}_{\mathrm{P}\mathrm{P}}^{}\left(\theta ,\phi \right)=\left[\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{2\left(a+2\right)}+\frac{a}{2\left(a+2\right)}-2g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right]\frac{\mathrm{\Delta }E}{\stackrel{-}{E}}+\left\{2g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{1-2g}{3-4g}+\left[\frac{1}{2\left(a+2\right)}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta +\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{a}{2\left(a+2\right)}\right]\frac{\left(2g-3\right){\left(2g-1\right)}^{2}}{g\left(4g-3\right)}\right\}\frac{\mathrm{\Delta }\nu }{\stackrel{-}{\nu }}+\mathrm{\Delta }\mathit{\Gamma} \mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\phi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (1) |
式中:θ为入射角;
Bakulin等[31]在干岩石或流体充填裂缝的介质中利用Hudson模型建立了硬币状模型的各向异性参数与裂缝密度e之间的线性关系,结合Γ与Thomsen参数关系得到e与Γ之间的关系
| $ \mathit{\Gamma} =\frac{4}{3}e\left(\frac{8{g}^{2}-4g-3}{3-5g+2{g}^{2}}\right) $ | (2) |
为了直接反演e,需要建立新反演方程。将式(2)代入式(1),得到基于E、ν和e的纵波方位各向异性AVO方程
| $ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}^{}\left(\theta ,\phi \right)=\left\{2g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{1-2g}{3-4g}+\left[\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{2\left(a+2\right)}+\frac{a}{2\left(a+2\right)}\right]\frac{\left(2g-3\right){\left(2g-1\right)}^{2}}{g\left(4g-3\right)}\right\}\frac{\mathrm{\Delta }\nu }{\stackrel{-}{\nu }}+\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left.\left[\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{2\left(a+2\right)}\right.+\frac{a}{2\left(a+2\right)}-2g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right]\frac{\mathrm{\Delta }E}{\stackrel{-}{E}}+\frac{4\mathrm{\Delta }e}{3}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\phi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{8{g}^{2}-4g-3}{2{g}^{2}-5g+3}\end{array} $ | (3) |
在不同θ和
| $ \left(\begin{array}{c}{\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}\left({\theta }_{1},{\phi }_{1}\right)\\ {\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}^{}\left({\theta }_{2},{\phi }_{1}\right)\\ \vdots \\ {\boldsymbol{R}}_{\mathrm{P}\mathrm{P}}^{}\left({\theta }_{N},{\phi }_{M}\right)\end{array}\right)=\left(\begin{array}{ccc}{\boldsymbol{C}}_{1}\left({\theta }_{1}\right)& {\boldsymbol{C}}_{2}\left({\theta }_{1}\right)& {\boldsymbol{C}}_{3}\left({\theta }_{1},{\phi }_{1}\right)\\ {\boldsymbol{C}}_{1}\left({\theta }_{2}\right)& {\boldsymbol{C}}_{2}\left({\theta }_{2}\right)& {\boldsymbol{C}}_{3}\left({\theta }_{2},{\phi }_{1}\right)\\ \vdots & \vdots & \vdots \\ {\boldsymbol{C}}_{1}\left({\theta }_{N}\right)& {\boldsymbol{C}}_{2}\left({\theta }_{N}\right)& {\boldsymbol{C}}_{3}\left({\theta }_{N},{\phi }_{M}\right)\end{array}\right)\left(\begin{array}{c}{\boldsymbol{R}}_{E}\\ {\boldsymbol{R}}_{\nu }\\ {\boldsymbol{R}}_{e}\end{array}\right) $ | (4) |
其中
| $\boldsymbol {C}_{1}\left({\theta }_{i}\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({C}_{1}{\left({\theta }_{i}\right)}_{1}\cdots {C}_{1}{\left({\theta }_{i}\right)}_{K}\right) $ |
| $ \boldsymbol{C}_{2}\left({\theta }_{i}\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({C}_{2}{\left({\theta }_{i}\right)}_{1}\cdots {C}_{2}{\left({\theta }_{i}\right)}_{K}\right) $ |
| $ \boldsymbol{C}_{3}\left({\theta }_{i},{\phi }_{j}\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({C}_{3}{\left({\theta }_{i},{\phi }_{j}\right)}_{1}\cdots {C}_{3}{\left({\theta }_{i},{\phi }_{j}\right)}_{K}\right) $ |
| $ {\boldsymbol{R}}_{E}={\left(\begin{array}{ccc}{R}_{E1}& \cdots & {R}_{EK}\end{array}\right)}^{\mathrm{T}} $ |
| $ {\boldsymbol{R}}_{\nu }={\left(\begin{array}{ccc}{R}_{\nu 1}& \cdots & {R}_{\nu K}\end{array}\right)}^{\mathrm{T}} $ |
| $ {\boldsymbol{R}}_{e}={\left(\begin{array}{ccc}{R}_{e1}& \cdots & {R}_{eK}\end{array}\right)}^{\mathrm{T}} $ |
式中:i=1, 2, …, N为入射角序号,N为入射角个数;j=1, 2, …, M为方位角序号,M为方位角个数;k=1, 2, …, K为采样点序号,K为采样点个数;
不同θ和
| $ {\boldsymbol{d}}_{(N\times M\times K)\times 1}={\boldsymbol{G}}_{(N\times M\times K)\times 3K}{\boldsymbol{m}}_{3K\times 1} $ | (5) |
其中
| $ {\boldsymbol{m}}_{3K\times 1}=\left(\begin{array}{c}{\boldsymbol{R}}_{E}\\ {\boldsymbol{R}}_{\nu }\\ {\boldsymbol{R}}_{e}\end{array}\right) $ |
| $ {\boldsymbol{G}}_{(N\times M\times K)\times 3K}=\boldsymbol{W}\left(\begin{array}{ccc}\boldsymbol{C}_{1}\left({\theta }_{1}\right)& \boldsymbol{C}_{2}\left({\theta }_{1}\right)& \boldsymbol{C}_{3}\left({\theta }_{1},{\phi }_{1}\right)\\ \boldsymbol{C}_{1}\left({\theta }_{2}\right)& \boldsymbol{C}_{2}\left({\theta }_{2}\right)& \boldsymbol{C}_{3}\left({\theta }_{2},{\phi }_{1}\right)\\ \vdots & \vdots & \vdots \\ \boldsymbol{C}_{1}\left({\theta }_{N}\right)& \boldsymbol{C}_{2}\left({\theta }_{N}\right)& \boldsymbol{C}_{3}\left({\theta }_{N},{\phi }_{M}\right)\end{array}\right) $ |
式中W为子波矩阵。
在贝叶斯理论框架下,给定观测数据d(包含不同θ和ϕ的叠前道集)和先验地质信息I,并假定噪声和参数向量m均服从高斯分布,得到m的估计值,使合成角度道集和叠前角道集误差最小
| $ \boldsymbol{m}={\left[{{\boldsymbol{G}}_{(\boldsymbol{N}}^{\boldsymbol{T}}}_{\times M\times K)\times 3K}{\boldsymbol{G}}_{(N\times M\times K)\times 3K}+{\sigma }_{n}^{2}\boldsymbol{Q}/\boldsymbol{I}\right]}^{-1}{{\boldsymbol{G}}_{(\boldsymbol{N}}^{\mathbf{T}}}_{\times M\times K)\times 3K}\boldsymbol{d} $ | (6) |
式中:
为了有效地预测DHSR,利用裂缝柔度和e间的关系建立计算DHSR的新方程。Gray等[20]利用宽方位、大角度地震数据AVAZ反演E、ν有效评价地应力特征,包括最大水平主应力σH、最小水平主应力σh 和垂直主应力σv。Schoenberg等[32]基于线性滑动理论根据胡克定律构建应变—应力关系
| $ \begin{array}{l}\left(\begin{array}{c}{\varepsilon }_{1}\\ {\varepsilon }_{2}\\ {\varepsilon }_{3}\\ {\varepsilon }_{4}\\ {\varepsilon }_{5}\\ {\varepsilon }_{6}\end{array}\right)=\left(\begin{array}{cccccc}\frac{1}{E}+{Z}_{\mathrm{N}}& -\frac{\nu }{E}& -\frac{\nu }{E}& 0& 0& 0\\ -\frac{\nu }{E}& \frac{1}{E}& -\frac{\nu }{E}& 0& 0& 0\\ -\frac{\nu }{E}& -\frac{\nu }{E}& \frac{1}{E}& 0& 0& 0\\ 0& 0& 0& \frac{1}{\mu }& 0& 0\\ 0& 0& 0& 0& \frac{1}{\mu }+{Z}_{\mathrm{T}}& 0\\ 0& 0& 0& 0& 0& \frac{1}{\mu }+{Z}_{\mathrm{T}}\end{array}\right)\left(\begin{array}{c}{\sigma }_{1}\\ {\sigma }_{2}\\ {\sigma }_{3}\\ {\sigma }_{4}\\ {\sigma }_{5}\\ {\sigma }_{6}\end{array}\right)\\ \end{array} $ | (7) |
式中:εl(l=1, 2, …, 6)为应变张量;σl为应力张量;ZN和ZT分别为法向和切向裂缝柔度。
假设最大水平应变和最小水平应变等于零,得到
| $ {\sigma }_{\mathrm{h}}={\sigma }_{\mathrm{v}}\frac{\nu \left(1+\nu \right)}{1+E{Z}_{\mathrm{N}}-{\nu }^{2}} $ | (8) |
| $ {\sigma }_{\mathrm{H}}={\sigma }_{\mathrm{v}}\frac{\nu \left(1+E{Z}_{\mathrm{N}}+\nu \right)}{1+E{Z}_{\mathrm{N}}-{\nu }^{2}} $ | (9) |
利用DHSR定量描述页岩气储层地应力特征[20]
| $ \mathrm{D}\mathrm{H}\mathrm{S}\mathrm{R}=\frac{{\sigma }_{\mathrm{H}}-{\sigma }_{\mathrm{h}}}{{\sigma }_{\mathrm{H}}}=\frac{E{Z}_{\mathrm{N}}}{1+E{Z}_{\mathrm{N}}-{\nu }^{2}} $ | (10) |
裂缝弱度
| $ {\Delta }_{\mathrm{N}}=\frac{\lambda +2\mu }{1+\left(\lambda +2\mu \right){Z}_{\mathrm{N}}} $ | (11) |
将式(11)代入式(10),得到
| $ \mathrm{D}\mathrm{H}\mathrm{S}\mathrm{R}=\frac{{\Delta }_{\mathrm{N}}\left(1-2\nu \right)}{\left(1-{\Delta }_{\mathrm{N}}\right)\left(1-\nu \right)+{\Delta }_{\mathrm{N}}\left(1-2\nu \right)} $ | (12) |
Bakulin等[31]建立了干岩石或流体充填裂缝介质的
| $ {\Delta }_{\mathrm{N}}=\frac{4e}{3g\left(1-g\right)} $ | (13) |
将式(13)代入式(12),得到
| $ \mathrm{D}\mathrm{H}\mathrm{S}\mathrm{R}=\frac{4e\left(1-2\nu \right)}{\left[3g\left(1-g\right)-4e\right]\left(1-\nu \right)+4e\left(1-2\nu \right)} $ | (14) |
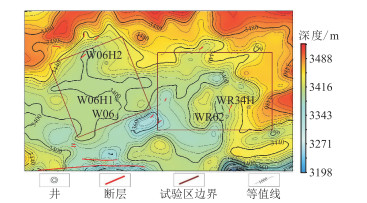
选取W06井区和WR02井区作为地应力预测试验区(图 1)。北东向的宽缓箱式向斜与隔档式褶皱带为该区基本构造格局:宽缓箱式向斜北西翼以北东向单斜为主,局部发育鼻状构造;中部向斜主体区岩层起伏相对平缓,局部存在构造高点和鼻状构造;宽缓箱式向斜东南翼呈北东向隔档式褶皱带。
|
图 1 试验区及周边五峰组底界构造图 |
室内地应力实验结果表明,σv>σH>σh,测井解释的五峰组—龙一1的σH平均值为101.8 MPa,σh平均值为89.4 MPa,水平压力差平均值为12.4 MPa,σH呈近东西向(100°~120°)。
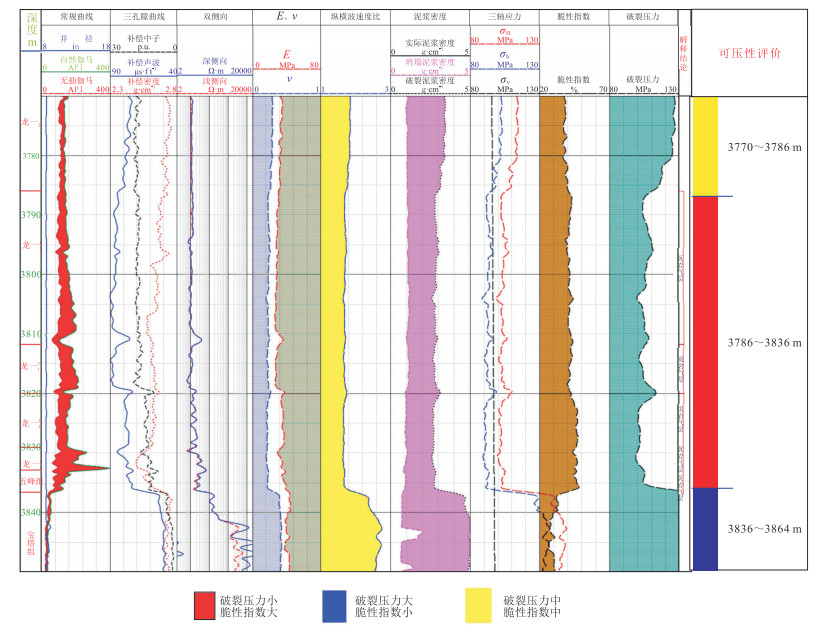
图 2为WR34H导眼井测井解释结果。岩石力学分析认为,纵向上破裂压力较小、脆性指数较大的层段为有利压裂段,在3786~3836 m深度段储层的压裂效果较好,可验证地应力预测结果。
|
图 2 WR34H导眼井测井解释结果 |
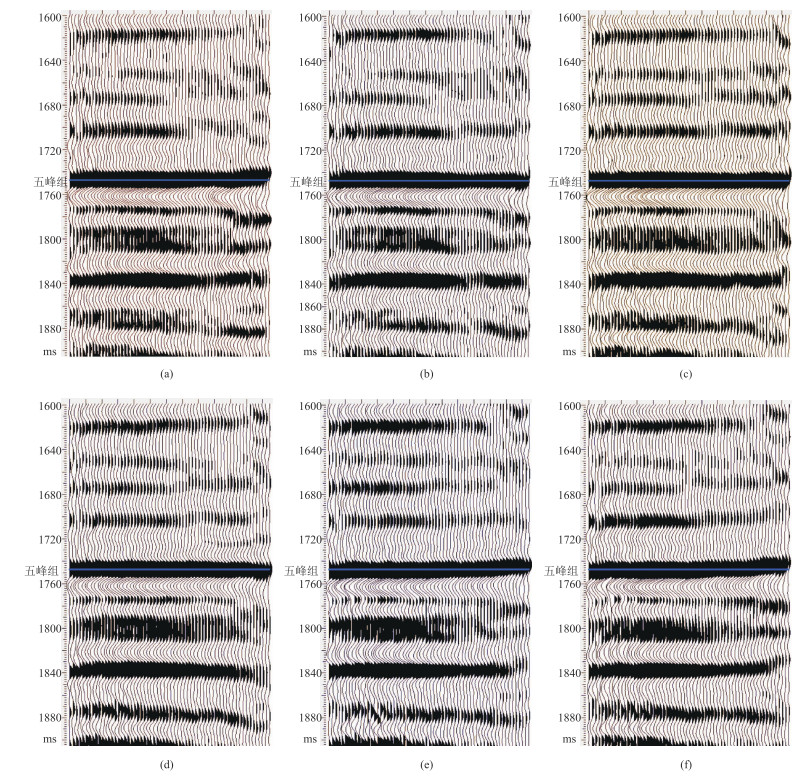
根据井数据对W06井区和WR02井区进行页岩储层各向异性岩石物理建模,并开展叠前方位各向异性反演,利用反演的泊松比和裂缝密度估算DHSR。由式(4)可见,为了更好地反演裂缝信息,需要不同方位角的叠前角道集。图 3为不同方位的CRP道集。由图可见,方位角道集整体信噪比较高、纵向分辨率较高,且不同方位角的叠前道集特征存在一定差异,为叠前方位各向异性反演提供了较好的资料基础。
|
图 3 不同方位的CRP(Inline515、Crossline497)道集 (a)30°;(b)60°;(c)90°;(d)120°;(e)150°;(f)180° |
试验区的优质页岩气储层的TOC、孔隙度、含气饱和度、脆性矿物含量等均较高,因此产能较大,矿物组分中的有机质以硅质页岩和混合硅质页岩为主。通过V-R-H模型计算碳酸盐岩、石英及有机质等组分的基质弹性模量,再利用Backus平均模型将泥质加入基质计算岩石基质的模量;孔隙主要为有机质孔隙和无机质孔隙,因此通过微分等效介质(DEM)模型添加粒间无机质孔隙,利用Kuster-Toksöz模型添加有机质孔隙,得到干岩石模量;裂缝主要是层间页理缝(近似水平)和构造缝(近似垂直),因此使用Hudson模型添加近垂直裂缝,利用Pade近似添加近水平裂缝,得到含裂缝的干岩石模量;孔隙流体主要由气和水组成,因此选取Brown-Korringa各向异性岩石流体替换添加气和水,得到饱和岩石模量;利用弱各向异性理论计算井点弹性参数及Thomesen各向异性参数,并进一步计算泊松比和裂缝密度曲线。
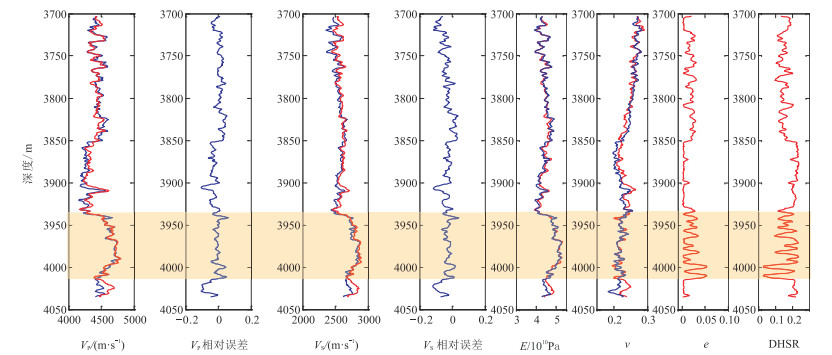
图 4为WR34H井岩石物理建模预测的弹性参数和各向异性参数。由图可见,由各向异性岩石物理模型获得的纵、横波速度较准确,预测相对误差均小于10%,裂缝密度和DHSR曲线均呈异常特征,表明各向异性岩石物理模型较合理,具有一定的可靠性和实用性。
|
图 4 WR34H井岩石物理建模预测的弹性参数和各向异性参数 红色为预测值,蓝色为实测值或计算值,阴影部分为裂缝较发育层段。 |
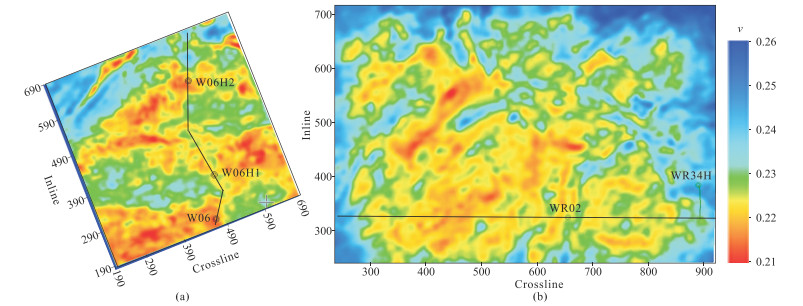
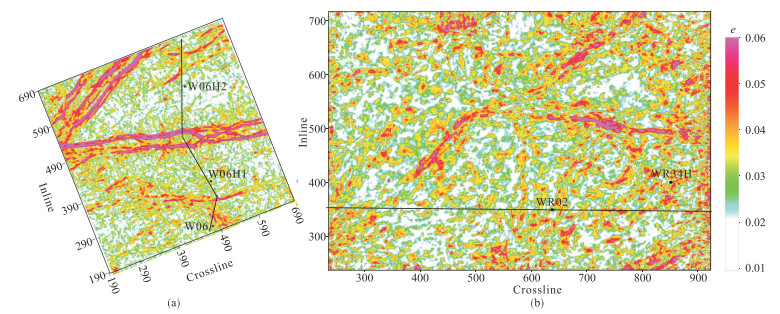
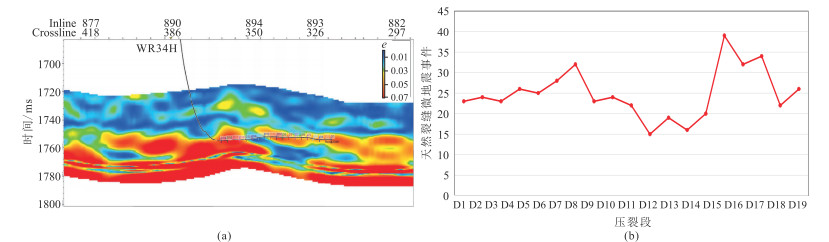
图 5、图 6分别为W06井区和WR02井区五峰组—龙一1泊松比、裂缝密度反演平面图。反演结果表明:W06H2井处泊松比呈低值(图 5a),WR34H井处泊松比呈高值(图 5b);W06H2井附近裂缝相对欠发育,裂缝密度较低(图 6a),WR34H井附近裂缝密度较大,裂缝较发育(图 6b)。上述特征与图 2、图 4的储层特征较吻合。岩心照片和成像测井资料揭示,五峰组、龙一段和龙二段的纵向裂缝密度较大,包括层间页理缝和构造缝,地质分析认为裂缝类型分为高阻充填缝、张开缝和应力释放缝等,裂缝预测结果与现有的地质和测井信息吻合度较高。图 7分析了裂缝密度与微地震事件位置关系。由图可见,WR34H井共有19个压裂段(图 7a),压裂段D11~D14的天然裂缝微地震事件较少(图 7b),说明D11~D14裂缝欠发育,与图 7a较吻合。
|
图 5 W06井区(a)和WR02井区(b)五峰组—龙一1泊松比反演平面图 |
|
图 6 W06井区(a)和WR02井区(b)五峰组—龙一1裂缝密度反演平面图 |
|
图 7 裂缝密度与微地震事件位置关系 (a)过WR34H井裂缝密度反演剖面与压裂段的关系;(b)不同压裂段的天然裂缝微地震事件 |
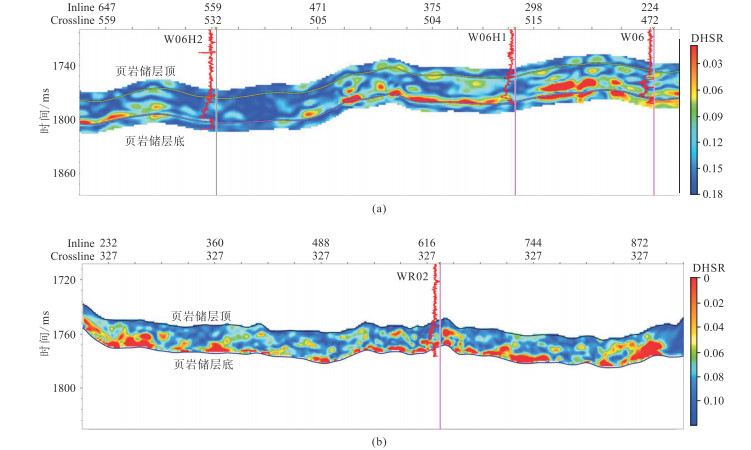
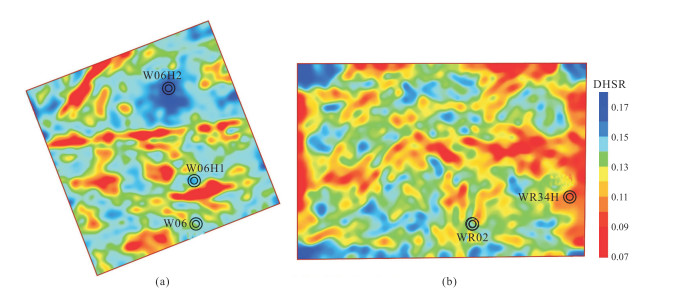
图 8为DHSR预测剖面。由图可见,DHSR剖面低值对应DHSR曲线低值,说明反演精度较高。图 9为试验区五峰组—龙一1 DHSR预测平面图。由图可见:①W06H2附近(工区北部)DHSR较大,与图 8a一致(图 9a);W06H1和W06附近(工区南部)DHSR相对较小,DHSR低值区域以条带状分布,可能为有利压裂区域(图 9a),与图 8a较吻合。②WR02附近(工区南部)DHSR较大,WR34H附近(工区中部和东部)DHSR较小,WR34H北部DHSR低值区域呈片状分布,因此可以判定WR34H附近为有利压裂区域——页岩气高产富集区(图 9b),与图 8b吻合。
|
图 9 W06井区(a)和WR02井区(b)五峰组—龙一1DHSR预测平面图 |
表 1为试验区五峰组—龙一1测井地应力算数平均值统计表。可见,WR34H和WR02井的水平应力差较小,W06H1和W06H2井水平应力差较大,相对误差小于9%,表明地应力预测结果与测井地应力解释结果的吻合度很高。
|
|
表 1 试验区五峰组—龙一1测井地应力算数平均值统计表 |
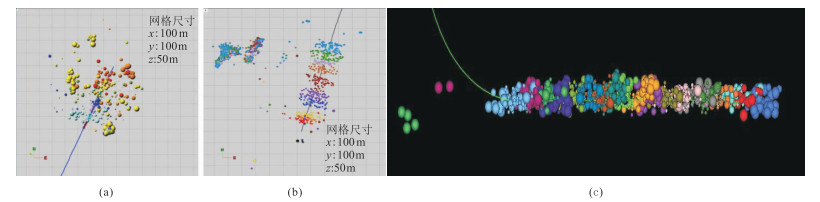
图 10为W06H1井、W06H2井、WR34H井微地震事件监测结果。由图可见,W06H1井、W06H2井、WR34H井压裂后获得的改造体积分别为2244×104(图 10a)、2066×104(图 10b)、5526×104 m3(图 10c)。因此,W06H1井和W06H2井储层改造体积较小、裂缝复杂程度较低,限制了储层改造效果,WR34H井储层改造体积较大,形成了复杂的裂缝缝网,提高了储层疏通能力。结合图 8a、图 9和图 10a可知,W06H1井的微地震事件更分散,说明可能存在与天然裂缝有关的相对孤立的裂缝系统,且各向异性特征较强,即DHSR值较高、储层改造程度较低、压裂效果较差。
|
图 10 W06H1井(a)、W06H2井(b)、WR34H井(c)微地震事件监测结果 不同的颜色代表不同的压裂段。 |
产量测试表明,W06H1井、W06H2井和WR34H井的测试产量分别为5.3×104、6.2×104和16.77×104 m3。压裂效果及试油、试气结果均表明WR34H井附近为有利压裂区和高产富集区——有利“甜点”区域。
3 结束语地应力评价对页岩储层“地质工程一体化”尤为重要,基于叠前方位各向异性直接反演的地应力预测方法有效提高了地应力预测精度。该方法避免了间接反演的误差,同时解决了裂缝柔度不易求取的难题,为地应力的高精度预测提供了可行方案。
应用实例表明:DHSR越小,水力压裂会产生不同方向的正交复杂裂缝网,可以更好地改造储层的物性和渗流通道,储层改造体积越大,越利于储层压裂;DHSR越大,水力压裂会产生平行于水平最大主应力的非正交平面裂缝,形成孤立裂缝,不利于体积改造。同时,DHSR预测结果与现有的测井地应力计算、压裂监测及产量测试等结果的一致性很高,并且符合地质认识,说明了所提方法的有效性和可靠性。
| [1] |
邹才能, 董大忠, 王玉满, 等. 中国页岩气特征、挑战及前景(一)[J]. 石油勘探与开发, 2015, 42(6): 689-701. ZOU Caineng, DONG Dazhong, WANG Yuman, et al. Shale gas in China: Characteristics, challenges and prospects(Ⅰ)[J]. Petroleum Exploration and Development, 2015, 42(6): 689-701. |
| [2] |
邹才能, 董大忠, 王玉满, 等. 中国页岩气特征、挑战及前景(二)[J]. 石油勘探与开发, 2016, 43(2): 166-178. ZOU Caineng, DONG Dazhong, WANG Yuman, et al. Shale gas in China: Characteristics, challenges and prospects(Ⅱ)[J]. Petroleum Exploration and Development, 2016, 43(2): 166-178. |
| [3] |
董大忠, 邹才能, 戴金星, 等. 中国页岩气发展战略对策建议[J]. 天然气地球科学, 2016, 57(3): 397-406. DONG Dazhong, ZOU Caineng, DAI Jinxing, et al. Suggestion on the development strategy of shale gas in China[J]. Natural Gas Geoscience, 2016, 57(3): 397-406. |
| [4] |
印兴耀, 马妮, 马正乾, 等. 地应力预测技术的研究现状与进展[J]. 石油物探, 2018, 57(4): 488-504. YIN Xingyao, MA Ni, MA Zhengqian, et al. Review of in-situ stress prediction technology[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 488-504. |
| [5] |
张少华, 邓小江, 冯许魁, 等. 川南地区深层页岩气地球物理勘探技术新进展与攻关方向[J]. 石油地球物理勘探, 2023, 58(1): 238-248. ZHANG Shaohua, DENG Xiaojiang, FENG Xukui, et al. New progress and research direction of geophysical prospecting techniques for deep shale gas in southern Sichuan Basin[J]. Oil Geophysical Prospecting, 2023, 58(1): 238-248. |
| [6] |
刘建伟, 张云银, 曾联波, 等. 非常规油藏地应力和应力甜点地球物理预测——渤南地区沙三下亚段页岩油藏勘探实例[J]. 石油地球物理勘探, 2016, 51(4): 792-800. LIU Jianwei, ZHANG Yunyin, ZENG Lianbo, et al. Geophysical prediction of stress and stress desserts in unconventional reservoirs: an example in Bonan area[J]. Oil Geophysical Prospecting, 2016, 51(4): 792-800. |
| [7] |
张帆, 何振华, 黄德济, 等. 预测裂隙发育带的构造应力场数值模拟技术[J]. 石油地球物理勘探, 2000, 35(2): 154-163. ZHANG Fan, HE Zhenhua, HUANG Deji, et al. Structural stress field numerical simulation technique for fracture zone prediction[J]. Oil Geophysical Prospecting, 2000, 35(2): 154-163. |
| [8] |
胡耀方. 页岩储层地应力场数值模拟方法[D]. 北京: 中国石油大学(北京), 2018.
|
| [9] |
张恒荣, 肖立志, 曾少军, 等. 基于裂缝柔度和地应力模型的声电测井正、反演方法及应用[J]. 石油地球物理勘探, 2023, 58(2): 431-442. ZHANG Hengrong, XIAO Lizhi, ZENG Shaojun, et al. Forward and inversion methods and application of acoustoelectric logging based on fracture compliance and crustal stress model[J]. Oil Geophysical Prospecting, 2023, 58(2): 431-442. |
| [10] |
袁龙, 章海宁, 李国利, 等. 库车前陆盆地强挤压应力条件下的测井电阻率校正方法[J]. 石油地球物理勘探, 2018, 53(5): 1085-1094. YUAN Long, ZHANG Haining, LI Guoli, et al. Logging resistivity correction under the strong extrusion stress condition in the Kuqa foreland basin[J]. Oil Geophysical Prospecting, 2018, 53(5): 1085-1094. |
| [11] |
刘忠华, 宋连腾, 王长胜, 等. 各向异性快地层最小水平主应力测井计算方法[J]. 石油勘探与开发, 2017, 44(5): 745-752. LIU Zhonghua, SONG Lianteng, WANG Changsheng, et al. Evaluation method of the least horizontal principal stress by logging data in anisotropic fast formations[J]. Petroleum Exploration and Development, 2017, 44(5): 745-752. |
| [12] |
WARPINSKI N R. Rock mechanics and fracture geometry∥Hydraulic Fracturing: Fundamentals and Advancements[M]. Society of Petroleum Engineers, 2019, 47-73.
|
| [13] |
LIU H, LING Y, GUO X, et al. Fracture prediction based on stress analysis and seismic information: a case study[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 1118-1123.
|
| [14] |
DUBINYA N, BAYUK I O, TIKHOTSKIY S, et al. Localization and characterization of hydraulically conductive fractured zones at seismic scale with the help of geomecha[C]. Extended Abstracts of 80th EAGE Conference and Exhibition, 2018, DOI: 10.3997/2214-4609.201800722.
|
| [15] |
杜炳毅, 杨午阳, 王恩利, 等. 基于杨氏模量、泊松比和各向异性梯度的裂缝介质AVAZ反演方法[J]. 石油物探, 2015, 54(2): 218-225. DU Bingyi, YANG Wuyang, WANG Enli, et al. AVAZ inversion based on Young's modulus, Poisson's ratio and anisotropy gradient in fracture media[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 218-225. |
| [16] |
CHEN H, JI Y, INNANEN K A. Estimation of modified fluid factor and dry fracture weaknesses using azimuthal elastic impedance[J]. Geophysics, 2018, 83(1): WA73-WA88. DOI:10.1190/geo2017-0075.1 |
| [17] |
PAN X, ZHANG G. Fracture detection and fluid identification based on anisotropic Gassmann equation and linear-slip model[J]. Geophysics, 2019, 84(1): R99-R112. DOI:10.1190/geo2017-0727.1 |
| [18] |
PAN X, ZHANG G. Bayesian seismic inversion for estimating fluid content and fracture parameters in a gas-saturated fractured porous reservoir[J]. Science China Earth Sciences, 2019, 62(5): 798-811. DOI:10.1007/s11430-018-9284-2 |
| [19] |
PAN X, ZHANG G, YIN X. Azimuthally pre-stack seismic inversion for orthorhombic anisotropy driven by rock physics[J]. Science China Earth Sciences, 2018, 61(4): 425-440. DOI:10.1007/s11430-017-9124-6 |
| [20] |
GRAY D, ANDERSON P, LOGEL J, et al. Estimation of stress and geomechanical properties using 3D seismic data[J]. First Break, 2012. DOI:10.3997/1365-2397.2011042 |
| [21] |
马妮, 印兴耀, 孙成禹, 等. 基于方位地震数据的地应力反演方法[J]. 地球物理学报, 2018, 61(2): 697-706. MA Ni, YIN Xingyao, SUN Chengyu, et al. Inversion for crustal stress based on azimuthal seismic data[J]. Chinese Journal of Geophysics, 2018, 61(2): 697-706. |
| [22] |
马妮, 印兴耀, 孙成禹, 等. 基于正交各向异性介质理论的地应力地震预测方法[J]. 地球物理学报, 2017, 60(12): 4766-4775. MA Ni, YIN Xingyao, SUN Chengyu, et al. The in-situ stress seismic prediction method based on the theory of orthorhombic anisotropic media[J]. Chinese Journal of Geophysics, 2017, 60(12): 4766-4775. |
| [23] |
PEREZ M, GOODWAY B, PURDUE G. Stress estimation through seismic analysis[C]. SEG Technical Program Expanded Abstracts, 2012, 31, SEG-2012-1480.
|
| [24] |
STARR J. Closure stress gradient estimation of the Marcellus shale from seismic data[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 1789-1793.
|
| [25] |
宗兆云, 印兴耀, 吴国忱. 基于叠前地震纵横波模量直接反演的流体检测方法[J]. 地球物理学报, 2012, 55(1): 284-292. ZONG Zhaoyun, YIN Xingyao, WU Guochen. Fluid identification method based on compressional and shear modulus direct inversion[J]. Chinese Journal of Geophysics, 2012, 55(1): 284-292. |
| [26] |
张广智, 陈娇娇, 陈怀震, 等. 基于页岩岩石物理等效模型的地应力预测方法研究[J]. 地球物理学报, 2015, 58(6): 2112-2122. ZHANG Guangzhi, CHEN Jiaojiao, CHEN Huaizhen, et al. Prediction for in-situ formation stress of shale based on rock physics equivalent model[J]. Chinese Journal of Geophysics, 2015, 58(6): 2112-2122. |
| [27] |
DU B, YANG W, ZHANG J, et al. Stress prediction and evaluation of heterogeneous reservoir[C]. Extended Abstracts of 80th EAGE Conference and Exhibition, 2018, DOI: https:∥DOI.org/10.3997/2214-4609.201800717.
|
| [28] |
DOWNTON J, GRAY D. AVAZ parameter uncertainty estimation[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 234-238.
|
| [29] |
陈怀震, 印兴耀, 高成国, 等. 基于各向异性岩石物理的缝隙流体因子AVAZ反演[J]. 地球物理学报, 2014, 57(3): 968-978. CHEN Huaizhen, YIN Xingyao, GAO Chengguo, et al. AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory[J]. Chinese Journal of Geophysics, 2014, 57(3): 968-978. |
| [30] |
RÜGER A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[D]. Colorado School of Mines, 1996.
|
| [31] |
BAKULIN A, GRECHKA V, TSVANKIN I. Estimation of fracture parameters from reflection seismic data-Part I: HTI model due to a single fracture set[J]. Geophysics, 2000, 65(6): 1788-1802. DOI:10.1190/1.1444863 |
| [32] |
SCHOENBERG M, SAYERS C. Seismic anisotropy of fractured rock[J]. Geophysics, 1995, 60(1): 204-211. DOI:10.1190/1.1443748 |



 杜炳毅, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院地球物理研究所,730020。Email:
杜炳毅, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院地球物理研究所,730020。Email: