2. 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
3. 东北石油大学地球科学学院, 黑龙江大庆 163318;
4. 大庆油田勘探事业部, 黑龙江大庆 163453
2. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum (Beijing), Beijing 102249, China;
3. School of Earth Sciences, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
4. Exploration Department of Daqing Oilfield Company Ltd, Daqing, Heilongjiang 163453, China
陆相碎屑岩储层作为中国油气资源的主要载体,具有砂体薄、纵横向非均质性强的特征。现今多数主力油田已进入开发中后期,有利储层的勘探、开发难度不断增大,传统储层剩余油开采、精细刻画储层内部细节的关键是发展高精度、高分辨率的储层预测理论与方法。
通过叠前地震反演获得储层弹性参数是定量预测及评价储层的核心方法,可表达为基于贝叶斯框架的概率推断问题[1]。在获得模型参数的后验概率分布后,以最优化理论获得最大后验概率解的方法称为确定性反演,而以随机采样方法探索后验分布解空间获得多个可能解的方法称为随机反演[2]。在通常情况下,受地震资料的带限性以及测井、地震数据信噪比影响,确定性反演获得的储层弹性参数缺少小尺度的非均质信息,影响储层参数评价,难以满足高精度预测有利储层的要求,并且无法评价反演结果的不确定性[3-4]。相比确定性反演,随机反演可以输出一组满足特定约束条件的解,便于评价不确定性。此外,随机反演可以有效耦合测井数据的高频信息,突破了确定性反演受地震频带限制的不足,从而获得高分辨率的随机结果,预测薄砂体的效果较好[5-7]。
当前,随机反演方法主要分为迭代类随机反演和线性贝叶斯随机反演[8]。迭代类随机反演框架最初由Haas等[9]提出,通过地质统计学随机模拟表征先验信息,利用蒙特卡洛迭代更新模型参数,从而获得多个等概率的反演解。随着迭代类随机反演的发展,一些全局优化策略被引入反演框架,避免迭代过程陷入局部最优,从而提高了算法的稳定性[10]。然而,迭代类随机反演的模型更新效率低,计算耗时长,降低了该方法的实用性[11]。线性贝叶斯随机反演基于线性贝叶斯理论,在井震数据约束下直接获取目标参数的后验概率分布,计算模型参数的效率远高于迭代类随机反演[12-13]。Hansen等[14]首先将由地质统计学表征的先验信息引入线性贝叶斯框架,有效避免了蒙特卡洛运算,实现了非迭代地质统计学随机反演。近年来,线性贝叶斯随机反演发展迅速。Yu等[15]用去相关方法改进地质统计学先验表征,以提高线性随机反演的精度;de Figueiredo等[16]结合线性贝叶斯框架与马尔可夫—蒙特卡洛抽样,提高了模型参数后验估计的精度;李祺鑫等[17]借鉴序贯高斯模拟的思想,将测井数据巧妙地融入线性贝叶斯框架,实现井震数据联合约束的高分辨率线性随机反演。可以看出,目前主流随机反演是将地质统计学模拟纳入贝叶斯反演框架,获得井震数据约束的反演结果。然而,井震数据约束随机反演大多利用测井低频信息以及地震中、低频信息,极少利用丰富的测井高频信息。因此,利用测井高频信息约束随机反演降低反演结果的不确定性对于储层精细刻画具有重要意义。
无论是迭代类随机反演还是线性贝叶斯随机反演,一般采用序贯类随机模拟表征油藏的非均质性。序贯类方法大多依赖变差函数[18]或训练图像[19]描述模型参数的空间相关性,需要逐点计算模拟结果,因此并行实现困难、计算效率低。相比序贯模拟,快速傅里叶变换滑动平均(FFT-MA)[20]是一种高效、快速的非条件谱模拟方法,广泛用于地震反演[21]、随机建模[22-23]等领域。FFT-MA可在频率域融合随机项与空间相关项,在空间域产生一系列具有空间相关的随机数用于后续模拟。目前利用FFT-MA进行随机反演获得空间解时多采用迭代更新的方式[21-24],计算效率虽较序贯类方法略有提升,但是迭代运算成本仍昂贵。因此,在高分辨率储层预测的基础上减少计算耗时,是提高随机反演实用性的迫切需要。
为高效地预测薄储层,本文将基于FFT-MA的空间相关协模拟引入线性反演框架,提出基于空间协模拟的叠前地震随机反演方法。首先,在贝叶斯框架下整合地震数据和测井数据的低频信息,获得弹性参数的后验概率分布。然后,根据FFT-MA算法生成概率场,以测井数据为条件数据实现概率场协同采样,从而获得井震数据约束的叠前三参数高分辨率随机反演结果。该方法无需迭代更新模型参数,能极大地提高随机反演的计算效率。最后,由理论模型试算和实际资料应用测试方法的效果。
1 方法原理 1.1 地震约束贝叶斯后验推断AVO正演中,观测地震数据d可以表示为地震子波W与反射系数rPP的褶积
| $ \boldsymbol{d}=\boldsymbol{W}{\boldsymbol{r}}_{\mathrm{P}\mathrm{P}}+\boldsymbol{e} $ | (1) |
式中e为观测误差。本文选择Aki-Richards近似公式[25]计算反射系数
| $ \begin{array}{l} {r}_{\mathrm{P}\mathrm{P}}\left(t,\theta \right)=\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{2}\frac{\partial \mathrm{l}\mathrm{n}\;{v}_{\mathrm{P}}\left(t\right)}{\partial t}-\frac{4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{{\gamma }^{2}}\frac{\partial \mathrm{l}\mathrm{n}\;{v}_{\mathrm{S}}\left(t\right)}{\partial t}+\\ \;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\; \;\;\frac{1}{2}\left(1-\frac{4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{{\gamma }^{2}}\right)\frac{\partial \mathrm{l}\mathrm{n}\;\rho \left(t\right)}{\partial t}\end{array} $ | (2) |
式中:t为时间;θ为入射角;vP、vS和ρ分别为岩石的纵波速度、横波速度和密度;γ为纵横波速度比。结合式(1)和式(2),获得地震AVO正演表达式
| $ \boldsymbol{d}=\boldsymbol{Gm}+\boldsymbol{e}=\boldsymbol{W}\boldsymbol{ADm}+\boldsymbol{e} $ | (3) |
式中:G为正演算子;A为与θ相关的系数矩阵;
假设e为高斯白噪,m和d分别服从以下分布
| $ p\left(\boldsymbol{m}\right)=N\left({\boldsymbol{\mu }}_{\boldsymbol{m}},{\boldsymbol{\Sigma }}_{\boldsymbol{m}}\right) $ | (4) |
| $ p\left(\boldsymbol{d}\left|\boldsymbol{m}\right.\right)=N\left({\boldsymbol{G\mu }}_{\boldsymbol{m}},{\boldsymbol{G\Sigma }}_{\boldsymbol{m}}\boldsymbol{G}+{\boldsymbol{\Sigma }}_{\boldsymbol{e}}\right) $ | (5) |
式中:
在贝叶斯线性框架下,m的后验概率分布为
| $ p\left(\boldsymbol{m}\left|\boldsymbol{d}\right.\right)\propto p\left(\boldsymbol{d}\left|\boldsymbol{m}\right.\right)p\left(\boldsymbol{m}\right) $ | (6) |
对应的后验均值
| $ {\boldsymbol{\mu }}_{\boldsymbol{m}|\boldsymbol{d}}={\boldsymbol{\mu }}_{\boldsymbol{m}}+{\boldsymbol{\Sigma }}_{\boldsymbol{m}}{\boldsymbol{G}}^{\mathrm{T}}(\boldsymbol{G}{\boldsymbol{\Sigma }}_{\boldsymbol{m}}{\boldsymbol{G}}^{\mathrm{T}}+{\boldsymbol{\Sigma }}_{\boldsymbol{e}}{)}^{-1}\left(\boldsymbol{d}-\boldsymbol{G}{\boldsymbol{\mu }}_{\boldsymbol{m}}\right) $ | (7) |
| $ {\boldsymbol{\Sigma }}_{\boldsymbol{m}|\boldsymbol{d}}={\boldsymbol{\Sigma }}_{\boldsymbol{m}}-{\boldsymbol{\Sigma }}_{\boldsymbol{m}}{\boldsymbol{G}}^{\mathrm{T}}(\boldsymbol{G}{\boldsymbol{\Sigma }}_{\boldsymbol{m}}{\boldsymbol{G}}^{\mathrm{T}}+{\boldsymbol{\Sigma }}_{\boldsymbol{e}}{)}^{-1}\boldsymbol{G}{\boldsymbol{\Sigma }}_{\boldsymbol{m}} $ | (8) |
根据地质统计学理论,
相比随机反演,确定性反演结果往往在小尺度上缺乏对储层的细节刻画。然而大部分的随机反演方法在更新多元模型参数时,往往忽略参数的空间相关性和参数之间的统计相关性,会导致两个问题:一是反演结果的随机性过强,导致地下参数的空间展布估计错误;二是破坏参数间的统计相关关系,使反演结果的联合分布偏离原始测井数据。为此,本文提出一种考虑空间相关性的井约束多参数协模拟方法,通过FFT-MA模拟表征空间相关性,可以构建一组具有空间相关特征的随机扰动项,从而降低模拟过程的随机性。通常情况下,FFT-MA模拟是非条件模拟,模拟结果无法满足测井数据。因此,本文通过协同条件变换对FFT-MA模拟进行条件化处理。
1.2.1 FFT-MA空间相关模拟FFT-MA模拟是在频率域实现的[25]。MA将n维高斯随机噪声
| $\boldsymbol{y}=\boldsymbol{g\varepsilon} $ | (9) |
通过协方差函数
| $\boldsymbol {C}=\boldsymbol{g{g}}^{\mathrm{T}} $ | (10) |
通过变差函数求取
| $ \boldsymbol{\varPhi }={\mathrm{F}}^{-1}\left[\mathrm{F}\left(\boldsymbol{g}\right)\mathrm{F}\left(\boldsymbol{\varepsilon }\right)\right] $ | (11) |
式中:F[•]和F-1[•]分别为傅里叶变换和反傅里叶变换;
根据FFT-MA构建空间相关随机噪声的流程如下:①生成一组高斯随机噪声
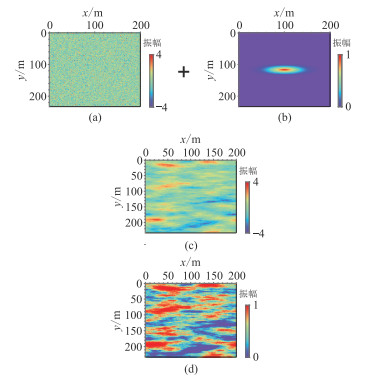
|
图 1 FFT-MA方法构建均匀扰动概率场 (a)高斯白噪;(b)空间结构模型;(c)构建的高斯扰动概率场;(d)均匀扰动概率场 |
FFT-MA条件模拟是在条件数据(测井数据)约束下进行协同条件变换实现的。对于一组随机变量
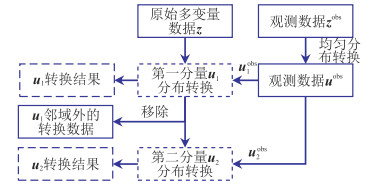
|
图 2 利用条件数据进行协同条件变换示意图 |
(1)对观测数据
(2)选择待模拟分量
(3)从
(4)定义邻域值
(5)选取下一模拟分量
(6)从
(7)重复步骤(5)、步骤(6),直到n个变量的第j个节点均完成分布转换;
(8)重复步骤(2)~步骤(7),直到n个变量的所有节点均完成分布转换,转换后的背景值为
(9)利用
| $ {\boldsymbol{u}}^{\text{'}}={\boldsymbol{\varPhi }}_{\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}\boldsymbol{u}+{\boldsymbol{\sigma }}_{\boldsymbol{u}} $ | (12) |
式中:
(10)对
综上所述,测井数据约束的多变量FFT-MA条件模拟流程(图 3)为:首先,以测井数据为条件数据,获得弹性参数的条件累计概率分布;其次,根据条件累计概率分布,将高斯概率场的贝叶斯后验均值转化到均匀概率场;再次,应用FFT-MA模拟计算服从均匀分布且具有空间相关性的随机噪声,以此对均匀概率场的贝叶斯后验概率进行随机扰动,获得模拟实现;最后,通过测井累计概率分布将模拟结果转换到高斯概率场实现条件化协同模拟,获得高分辨率弹性参数表征结果。
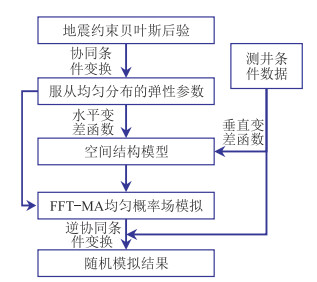
|
图 3 测井数据约束的多变量FFT-MA条件模拟流程 |
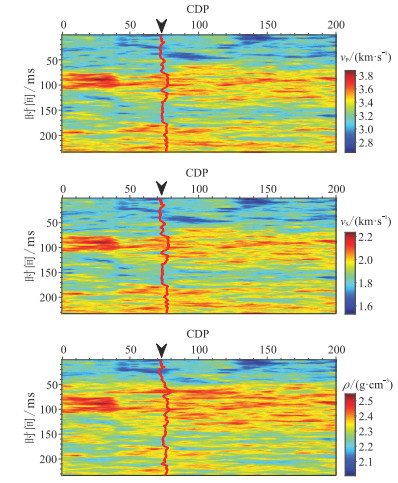
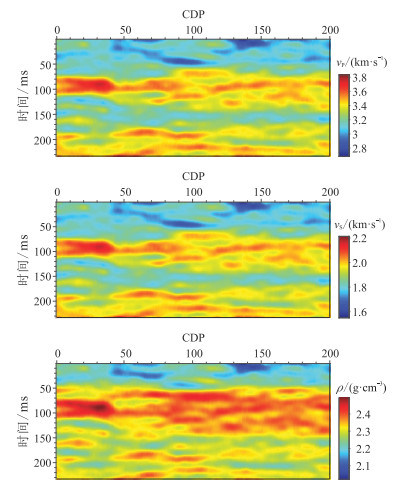
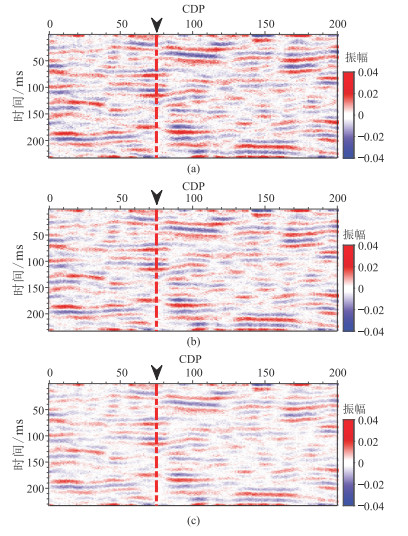
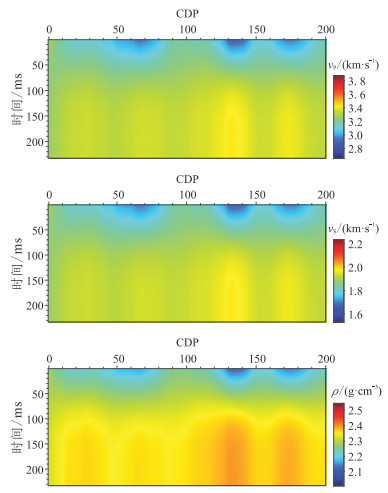
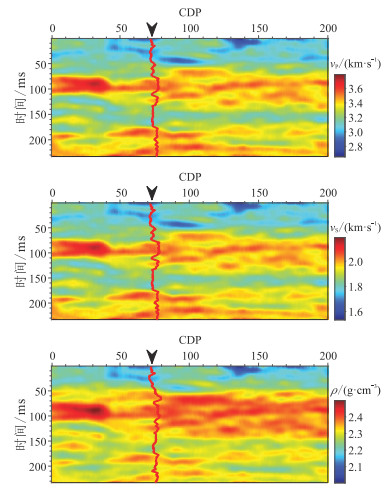
为验证本文所提方法的效果,选取中国M区的一道测井数据作为条件数据,利用条件模拟构造二维薄互层模型(图 4)作为实际地层的真实参考模型。对图 4滤波保留90 Hz的有效信号,获得平滑参考模型(图 5),利用图 5与主频为30Hz的雷克子波褶积,并添加随机噪声,得到不同入射角的含噪合成地震记录(图 6)。对图 5进一步滤波,仅保留10~15 Hz的有效信号,获得初始背景模型(图 7)。以图 6为观测数据,基于图 7逐道进行叠前地震反演,获得地震数据约束的模型参数的贝叶斯后验均值(图 8)——确定性反演结果。可以看出,图 8的分辨率与图 5相当,仅大致反映了图 5的参数变化趋势,无法进一步刻画测井数据的细节变化。
|
图 4 二维薄互层模型 横向共200道,测井数据位于第75道,纵向采样点数为233,时间采样间隔为1 ms。 |
|
图 5 二维薄互层平滑模型 |
|
图 6 不同入射角的含噪合成地震记录(信噪比为6 dB) (a)5°;(b)15°;(c)25° |
|
图 7 初始背景模型 |
|
图 8 确定性反演结果 |
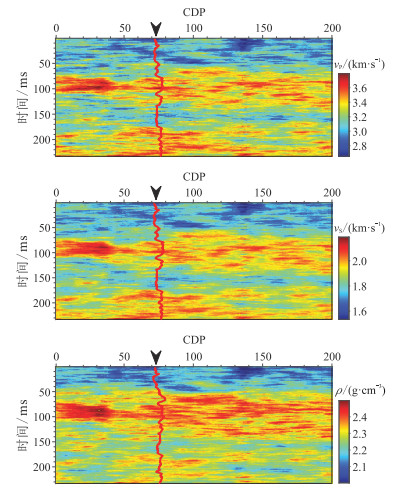
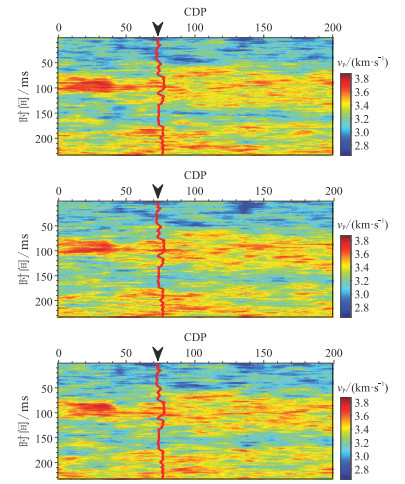
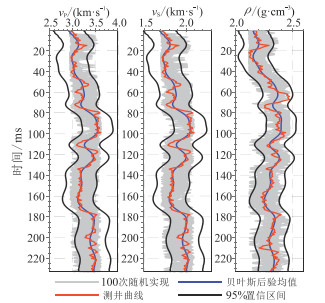
以图 8作为克里金均值,后验方差作为克里金方差,在测井数据约束下实现一次协同模拟,获得测井数据约束的一次随机反演结果(图 9)。可见,图 9的分辨率与图 4相当,且井位处的反演结果与测井数据完全吻合。图 10为纵波速度的三次随机反演结果。由图可见:①井位处的三次随机反演结果均与测井数据高度吻合,且分辨率与图 4相当,说明随机反演结果的不确定性较低;②三次随机反演结果整体特征相似,进一步证明了所提方法的稳定性,而三次随机反演结果在小尺度的差异性反映了地下介质的非均质性。图 11为井位处100次随机反演结果。由图可见,100次随机反演结果与95%的置信区间几乎重合,说明地震数据与低频测井数据的整合反演结果等价于真实解的后验分布。
|
图 9 测井数据约束的一次随机反演结果 |
|
图 10 纵波速度的三次随机反演结果 |
|
图 11 井位处100次随机反演结果 |
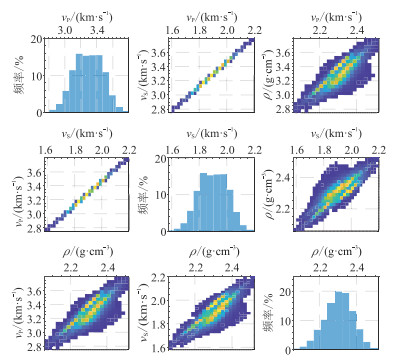
统计图 8、图 9和图 4的垂直变差函数(图 12)及水平变差函数(图 13)可知,图 9与图 4的水平变差函数及垂直变差函数的匹配程度均好于图 8。图 14、图 15分别为图 4、图 9的非参数概率密度函数。由图可见,图 15与图 14接近,说明所提方法的反演结果的非参数概率密度函数逼近真实参考模型。
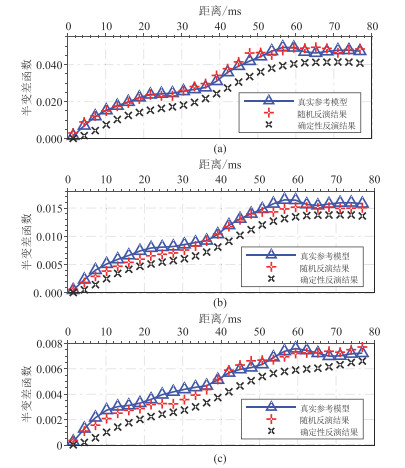
|
图 12 不同反演结果与图 4的垂直变差函数对比 (a)vP;(b)vS;(c)ρ |
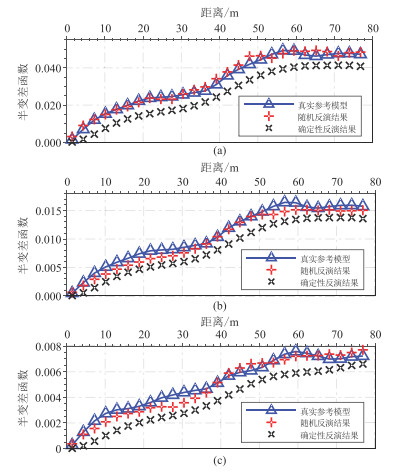
|
图 13 不同反演结果与图 4的水平变差函数对比 (a)vP;(b)vS;(c)ρ |
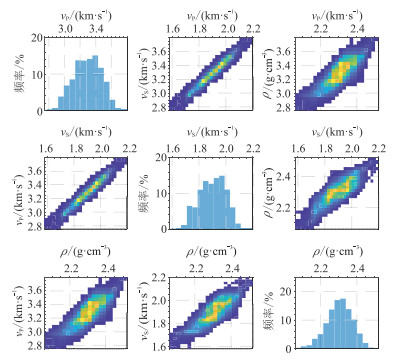
|
图 15 图 9的非参数概率密度函数 |
图 16为vP一次随机反演结果。由图可见,本文方法反演结果(图 16a)的分辨率与基于条件化FFT-MA的迭代随机反演结果(图 16b)相近。分析二者的计算效率可知,图 16a、图 16b的计算时间分别为52.78、675.86 s。可见,本文方法在保证高分辨率随机反演的情况下大幅提高了计算效率。
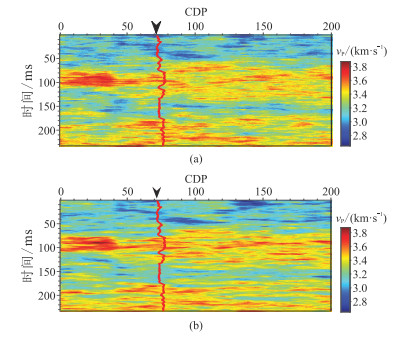
|
图 16 vP一次随机反演结果 (a)本文方法;(b)基于条件化FFT-MA的迭代随机反演 |
由A区过井二维地震角道集(图 17)提取反演地震子波(图 18),由测井数据获得低频初始背景模型(图 19)。
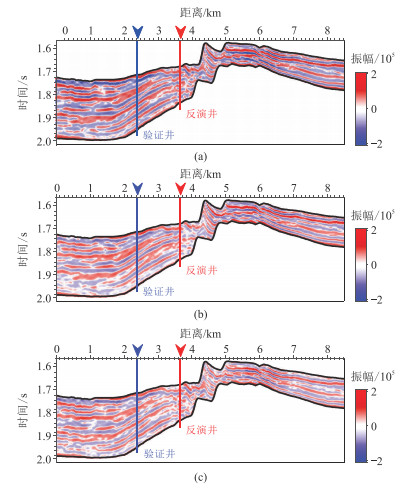
|
图 17 A区过井二维地震角道集 (a)7.5°;(b)17.5°;(c)27.5° 共341道,道间距为25 m,横向跨度为8.5 km。目的层以砂泥薄互层为主,反演井(红色竖线)位于3.7 km(第148道)处,验证井(蓝色竖线)位于2.4 km(第96道)处。目的层大致位于1700~2000 ms,时间采样间隔为2 ms。 |

|
图 18 由图 17提取的地震子波 |
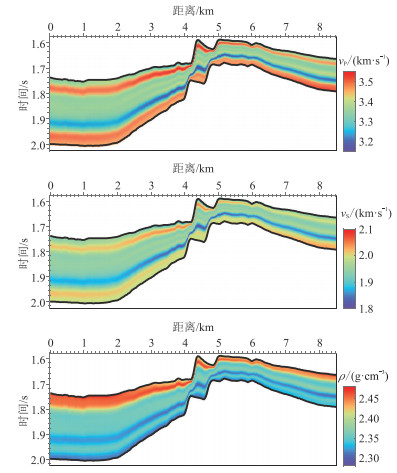
|
图 19 低频初始背景模型 |
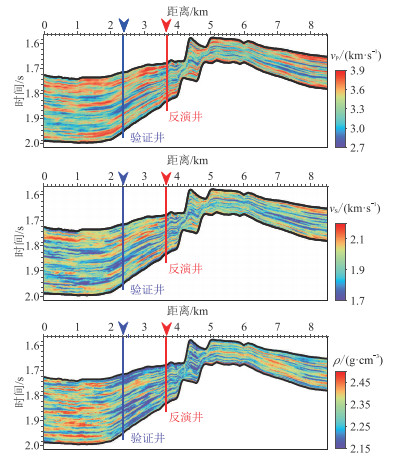
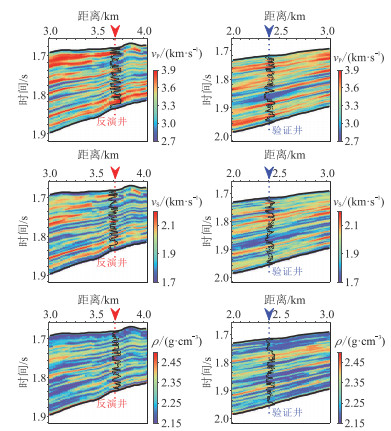
图 20为地震数据约束的确定性反演结果。可见,仅依赖地震数据的反演结果较平滑,横向连续性较好,但纵向分辨率与图 17一致。图 21为图 20的局部放大。由图可见,确定性反演结果与测井数据的趋势相当,但是分辨率远低于测井数据。统计图 20获得水平变差函数、统计测井数据得到纵向变差函数,从而构建空间结构模型。为了反映测井数据的高频结构信息,以测井数据为条件数据,将空间相关协模拟方法用于贝叶斯后验均值和方差。图 22为井约束一次随机反演结果,图 23为图 22的局部放大。可见,随机反演结果的分辨率与测井数据相当,且随机反演结果与反演井数据、验证井数据吻合度良好,说明反演结果可靠。
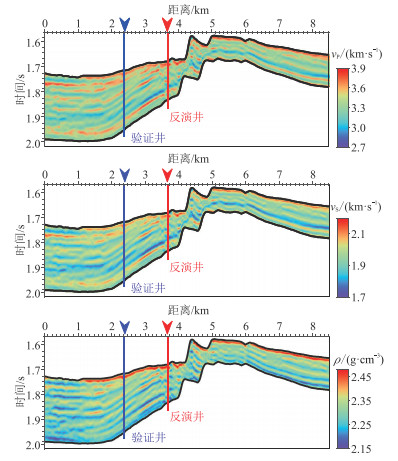
|
图 20 地震数据约束的确定性反演结果 |
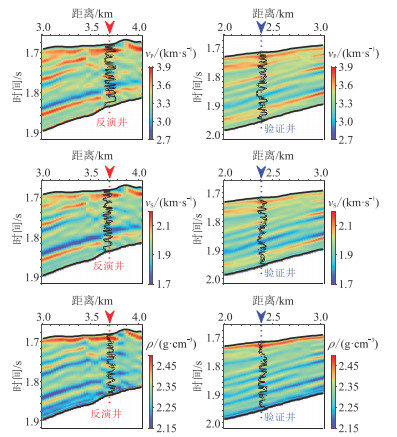
|
图 21 图 20的局部放大 |
|
图 22 井约束一次随机反演结果 |
|
图 23 图 22的局部放大 |
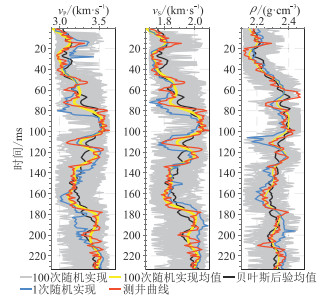
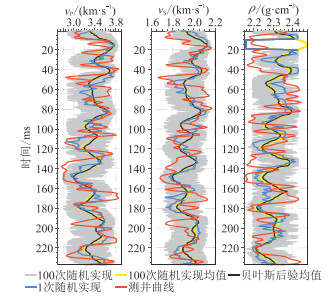
图 24和图 25分别为反演井、验证井的井旁道随机反演结果。可见:井约束随机反演结果的中、低频趋势的分辨率与测井数据基本一致,且显示了小尺度参数变化(图 24);在验证井处,100次随机结果几乎涵盖原始测井数据,即反演结果的不确定性较小,很好地反映了测井数据的高频信息(图 25)。
|
图 24 反演井的井旁道随机反演结果 |
|
图 25 验证井的井旁道随机反演结果 |
本文从高效、实用的高分辨率储层表征角度出发,耦合线性贝叶斯反演理论与条件化FFT-MA模拟,发展了一种井震数据联合的叠前地震随机反演方法。该方法在地震数据约束下获得贝叶斯后验推断,为反演结果提供准确的储层横向展布及地震频带信息,以测井数据为条件数据进行随机模拟,将测井高频有效信息引入反演结果,实现储层的精细刻画。模型试算和实际资料应用表明,本文方法可以有效地获得高分辨率储层表征结果,即中低频趋势服从地震数据、高频趋势遵循测井数据的特征。相较传统的随机反演方法,本文方法考虑了空间相关性的约束,无需通过迭代更新模型参数,缩短了运算时间,具有良好的应用前景。
| [1] |
撒利明, 杨午阳, 姚逢昌, 等. 地震反演技术回顾与展望[J]. 石油地球物理勘探, 2015, 50(1): 184-202. SA Liming, YANG Wuyang, YAO Fengchang, et al. Past, present, and future of geophysical inversion[J]. Oil Geophysical Prospecting, 2015, 50(1): 184-202. |
| [2] |
DOWNTON J E. Seismic Parameter Estimation from AVO Inversion[D]. Department of Geology and Geophysics, University of Calgary, 2005.
|
| [3] |
TIHONOV A N. Solution of incorrectly formulated problems and the regularization method[J]. Soviet Math Dokl, 1963, DOI. DOI:10.11499/sicejl1962.36.468 |
| [4] |
裴松, 印兴耀, 李坤. 全域正则化快速匹配追踪稀疏地震反演方法[J]. 石油地球物理勘探, 2022, 57(6): 1400-1408, 1426. PEI Song, YIN Xingyao, LI Kun. Sparse seismic inversion method based on full-domain regularized fast matching pursuit[J]. Oil Geophysical Prospecting, 2022, 57(6): 1400-1408, 1426. |
| [5] |
ZHANG R, SEN M K, PHAN S, et al. Stochastic and deterministic seismic inversion methods for thin-bed resolution[J]. Journal of Geophysics and Engineering, 2012, 9(5): 611-618. DOI:10.1088/1742-2132/9/5/611 |
| [6] |
张枫, 贾学成, 张晓敏, 等. 相控反演薄储层预测技术在鄂尔多斯盆地东缘的应用[J]. 石油地球物理勘探, 2022, 57(增刊1): 215-222. ZHANG Feng, JIA Xuecheng, ZHANG Xiaomin, et al. Application of thin reservoir prediction technology based on facies-controlled inversion at eastern margin of Ordos Basin[J]. Oil Geophysical Prospecting, 2022, 57(S1): 215-222. |
| [7] |
郭同翠, 姜明军, 纪迎章, 等. 叠前地质统计学反演在页岩甜点和薄夹层预测中的应用——以西加拿大盆地W区块为例[J]. 石油地球物理勘探, 2020, 55(1): 167-175. GUO Tongcui, JIANG Mingjun, JI Yingzhang, et al. The application of prestack geostatistical inversion in the prediction of shale sweet spots and thin interbeds: a case study of Block W in Western Canada Basin[J]. Oil Geophysical Prospecting, 2020, 55(1): 167-175. |
| [8] |
PEREIRA P, BORDIGNON F, AZEVEDO L, et al. Strategies for integrating uncertainty in iterative geostatistical seismic inversion[J]. Geophysics, 2019, 84(2): R207-R219. DOI:10.1190/geo2017-0758.1 |
| [9] |
HAAS A, DUBRULE O. Geostatistical inversion: a sequential method of stochastic reservoir modeling constrained by seismic data[J]. First Break, 1994, 12(11): 561-569. |
| [10] |
郭强, 雒聪, 刘红达, 等. 自适应优化参数模拟退火的叠前地震联合反演方法[J]. 石油地球物理勘探, 2023, 58(3): 670-679. GUO Qiang, LUO Cong, LIU Hongda, et al. Prestack seismic hybrid inversion based on simulated annealing algorithm with adaptive optimization parameters[J]. Oil Geophysical Prospecting, 2023, 58(3): 670-679. |
| [11] |
PEREIRA Â, NUNES R, AZEVEDO L, et al. Geostatistical seismic inversion for frontier exploration[J]. Interpretation, 2017, 5(4): T477-T485. DOI:10.1190/INT-2016-0171.1 |
| [12] |
LIU M, GRANA D. Stochastic nonlinear inversion of seismic data for the estimation of petroelastic properties using the ensemble smoother and data reparamete- rization[J]. Geophysics, 2018, 83(3): M25-M39. DOI:10.1190/geo2017-0713.1 |
| [13] |
YU B, ZHOU H, WANG L, et al. Prestack Bayesian statistical inversion constrained by reflection features[J]. Geophysics, 2020, 85(4): R349-R363. |
| [14] |
HANSEN T M, JOURNEL A G, TARANTOLA A, et al. Linear inverse Gaussian theory and geostatistics[J]. Geophysics, 2006, 71(6): R101-R111. DOI:10.1190/1.2345195 |
| [15] |
YU B, ZHOU H, WANG L, et al. Prestack Bayesian linearized inversion with decorrelated prior information[J]. Mathematical Geosciences, 2021, 53(3): 437-464. DOI:10.1007/s11004-020-09899-6 |
| [16] |
DE FIGUEIREDO L P, GRANA D, ROISENBERG M, et al. Gaussian mixture Markov chain Monte Carlo method for linear seismic inversion[J]. Geophysics, 2019, 84(3): R463-R476. DOI:10.1190/geo2018-0529.1 |
| [17] |
李祺鑫, 罗亚能, 张生, 等. 高分辨率波阻抗贝叶斯序贯随机反演[J]. 石油地球物理勘探, 2020, 55(2): 389-397. LI Qixin, LUO Yaneng, ZHANG Sheng, et al. High-resolution Bayesian sequential stochastic inversion[J]. Oil Geophysical Prospecting, 2020, 55(2): 389-397. |
| [18] |
樊鹏军, 马良涛, 王宗俊, 等. 地质统计学反演中变差函数地质含义及求取方法探讨[J]. 地球物理学进展, 2017, 32(6): 2444-2450. FAN Pengjun, MA Liangtao, WANG Zongjun, et al. Variogram geological implication and its calculating method discussing for geostatistical inversion[J]. Progress in Geophysics, 2017, 32(6): 2444-2450. |
| [19] |
LIU X, LI J, CHEN X, et al. Stochastic inversion of facies and reservoir properties based on multi-point geostatistics[J]. Journal of Geophysics and Engineering, 2018, 15(6): 2455-2468. DOI:10.1088/1742-2140/aac694 |
| [20] |
LE RAVALEC M, NOETINGER B, HU L Y. The FFT moving average (FFT-MA) generator: an efficient numerical method for generating and conditioning Gaussian simulations[J]. Mathematical Geology, 2000, 32(6): 701-723. DOI:10.1023/A:1007542406333 |
| [21] |
印兴耀, 刘婵娟, 王保丽. 基于混合遗传算法的叠前随机反演方法[J]. 中国石油大学学报(自然科学版), 2017, 41(4): 65-70. YIN Xingyao, LIU Chanjuan, WANG Baoli. Pre-stack stochastic inversion based on hybrid genetic algorithm[J]. Journal of China University of Petroleum (Edition of Natural Science), 2017, 41(4): 65-70. |
| [22] |
杨修伟, 朱培民, 毛宁波, 等. 基于FFT-MA的随机介质建模方法[J]. 地球物理学报, 2018, 61(12): 5007-5018. YANG Xiuwei, ZHU Peimin, MAO Ningbo, et al. Random medium modeling based on FFT-MA[J]. Chinese Journal of Geophysics, 2018, 61(12): 5007-5018. |
| [23] |
DE FIGUEIREDO L P, SCHMITZ T, LUNELLI R, et al. Direct multivariate simulation-a stepwise conditional transformation for multivariate geostatistical simulation[J]. Computers & Geosciences, 2021. DOI:10.1016/j.cageo.2020.104659 |
| [24] |
王保丽, 印兴耀, 丁龙翔, 等. 基于FFT-MA谱模拟的快速随机反演方法研究[J]. 地球物理学报, 2015, 58(2): 664-673. WANG Baoli, YIN Xingyao, DING Longxiang, et al. Study of fast stochastic inversion based on FFT-MA spectrum simulation[J]. Chinese Journal of Geophy-sics, 2015, 58(2): 664-673. |
| [25] |
AKI K, RICHARDS P G. Quantitative Seismology(2nd Edition)[M]. University Science Books, 2002.
|
| [26] |
BORDIGNON F L, DE FIGUEIREDO L P, AZEVEDO L, et al. Hybrid global stochastic and Bayesian linearized acoustic seismic inversion methodo- logy[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8): 4457-4464. DOI:10.1109/TGRS.2017.2692388 |
| [27] |
OLIVER D S. Moving averages for Gaussian simulation in two and three dimensions[J]. Mathematical Geology, 1995, 27(8): 939-960. DOI:10.1007/BF02091660 |



 周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: