叠前反演可揭示地下储层空间展布与含油气性等特征,在油气勘探、开发中具有重要作用[1-3]。根据正演问题所用解析表达式的不同,叠前反演分为基于波动方程的反演和基于各种反射系数公式的反演[4]。对于叠前三参数反演来说,受限于各种假设和条件[5],导致物理先验认识(AVA理论公式,如Aki公式[6]、Gray公式[7]、Fatti公式[8]等)中的角度不易准确给定,加之大型稀疏矩阵的病态性,导致反演过程不稳定。为此,本文提出物理、数据先验认识融合(Harmonicon of Physical and Data Prior Knowledge, HPDPK)的叠前解耦分步反演方法。首先,对基于物理先验认识构建的正演框架进行非稀疏化,以保持反演的稳定性,同时也为后续解耦分步反演奠定基础;然后,以井资料作为数据先验认识,对正演框架进行修正,并利用修正后的正演框架对地震数据进行解耦,以获得稳定且准确的叠前地震属性数据;最后,利用井数据的低频信息作为先验约束,对叠前地震属性数据进行反演,获得地层弹性参数。
本文的反演方法如何获取高质量的叠前地震属性数据是关键。因常规方法利用物理先验认识直接提取的叠前地震属性数据不准确,不能与井合成记录匹配。作为改进,Levenberg-Marguarot方法在矩阵对角线引入单位矩阵和拉格朗日系数[9-10]。后来,有人在贝叶斯概率化反演理论框架[11]下,引入协方差[12]以提高解耦精度。但在实际应用中,此方法对解耦性能的改善有限,根本原因在于无法获得符合工区实际情况的角度系数项,导致物理先验认识不适用。
为获取准确的角度项,本文将井控思想[13-15]引入叠前三参数反演过程,提出物理、数据先验认识融合的地震数据解耦方法。通过地震数据与井数据的匹配,求取物理先验认识中的角度项,解决仅利用物理先验认识带来的解耦精度不足的问题。
1 方法原理 1.1 基于物理先验认识的非稀疏正演框架以物理先验认识中的Gray公式为例介绍方法原理
| $ R\left(\theta \right)={R}_{\lambda }\left(\frac{1}{2}-\frac{{\beta }^{2}}{{\alpha }^{2}}\right)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta +\frac{{\beta }^{2}}{{\alpha }^{2}}\left(\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -\\ \;\;\;\;\;\;\;\;4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right){R}_{\mu }+\frac{1}{2}\left(1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right){R}_{\rho } $ | (1) |
式中:
| $ d({\theta }_{i},t)=\left(\frac{1}{2}-\frac{{\beta }^{2}}{{\alpha }^{2}}\right)\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{\mathrm{i}}w\left(t\right){R}_{\mathrm{\lambda }}\left(t\right)+\frac{{\beta }^{2}}{{\alpha }^{2}}\left(\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{\mathrm{i}}-4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{\mathrm{i}}\right)w\left(t\right){R}_{\mathrm{\mu }}\left(t\right)+\frac{1}{2}\left(1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right)w\left(t\right){R}_{\mathrm{\rho }}\left(t\right) $ | (2) |
式中
| $\underbrace{\left[\begin{array}{c} d\left(\theta_1, t_1\right) \\ \vdots \\ d\left(\theta_1, t_n\right) \\ d\left(\theta_2, t_1\right) \\ \vdots \\ d\left(\theta_2, t_n\right) \\ \vdots \\ d\left(\theta_m, t_1\right) \\ \vdots \\ d\left(\theta_m, t_n\right) \end{array}\right]}_ \boldsymbol{d}= \underbrace{\left[ {\begin{array}{*{20}{l}} {{w_1}a\left( {{\theta _1}} \right)\;\;\;\;{w_1}b\left( {{\theta _1}} \right)\;\;\;\;{w_1}c\left( {{\theta _1}} \right)}\\ {\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots }\\ {\;\;\;\;\;\;\;\;\;\;\;{w_n}a\left( {{\theta _1}} \right)\;\;\;\;{w_n}b\left( {{\theta _1}} \right)\;\;\;\;{w_n}c\left( {{\theta _1}} \right)}\\ {{w_1}a\left( {{\theta _2}} \right)\;\;\;\;{w_1}b\left( {{\theta _2}} \right)\;\;\;\;{w_1}c\left( {{\theta _2}} \right)}\\ {\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots }\\ {\;\;\;\;\;\;\;\;\;\;\;{w_n}a\left( {{\theta _2}} \right)\;\;\;\;{w_n}b\left( {{\theta _2}} \right)\;\;\;\;{w_n}c\left( {{\theta _2}} \right)}\\ \ldots \\ {{w_1}a\left( {{\theta _m}} \right)\;\;\;\;{w_1}b\left( {{\theta _m}} \right)\;\;\;\;{w_1}c\left( {{\theta _m}} \right)}\\ {\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots }\\ {\;\;\;\;\;\;\;\;\;\;\;{w_n}a\left( {{\theta _m}} \right)\;\;\;\;{w_n}b\left( {{\theta _m}} \right)\;\;\;\;{w_n}c\left( {{\theta _m}} \right)} \end{array}} \right]}_\boldsymbol{G} \underbrace{\left[\begin{array}{c}R_\lambda\left(t_1\right) \\ \vdots \\ R_\lambda\left(t_n\right) \\ R_\mu\left(t_1\right) \\ \vdots \\ R_\mu\left(t_n\right) \\ R_\rho\left(t_1\right) \\ \vdots \\ R_\rho\left(t_n\right)\end{array}\right]}_\boldsymbol{R}$ | (3) |
式中:
| $ {\boldsymbol{d}}_{mn\times 1}={\boldsymbol{G}}_{mn\times 3n}{\boldsymbol{R}}_{3n\times 1} $ | (4) |
从式(3)、式(4)不难看出,常规叠前反演希望从地震道集直接反演地层弹性参数。因不同参数相互耦合,且需求解大型稀疏矩阵
在大数据领域,数据解耦是指将含有多个变量的数学方程变成用单个变量表示的方程组,从而简化计算。将此思路用于叠前三参数反演问题,如果消除参数之间的耦合作用,实现各个参数的独立存在,就可实现各弹性参数的稳定反演。对此,提出物理、数据先验认识融合的叠前解耦分步反演方法。首先根据褶积运算的交换律,将式(3)进行非稀疏化分解,得到如下正演框架
| $ \underbrace{\left[\begin{array}{ccc} d\left(\theta_1, t_1\right) & \cdots & d\left(\theta_1, t_n\right) \\ d\left(\theta_2, t_1\right) & \cdots & d\left(\theta_2, t_n\right) \\ & \vdots & \\ d\left(\theta_m, t_1\right) & \cdots & d\left(\theta_m, t_n\right) \end{array}\right]}_\boldsymbol{d}=\underbrace{\left[\begin{array}{ccc} a\left(\theta_1\right) & b\left(\theta_1\right) & c\left(\theta_1\right) \\ a\left(\theta_2\right) & b\left(\theta_2\right) & c\left(\theta_2\right) \\ &\vdots & \\ a\left(\theta_m\right) & b\left(\theta_m\right) & c\left(\theta_m\right) \end{array}\right]}_\boldsymbol{A} \underbrace{\left[\begin{array}{ccc} R_\lambda\left(t_1\right) & \cdots & R_\lambda\left(t_n\right) \\ R_\mu\left(t_1\right) & \cdots & R_\mu\left(t_n\right) \\ R_\rho\left(t_1\right) & \cdots & R_\rho\left(t_n\right) \end{array}\right] \boldsymbol{w}}_{\boldsymbol{m} = \boldsymbol{R} \times \boldsymbol{w}} $ | (5) |
式(5)的矩阵形式如下
| $ {\boldsymbol{d}}_{m\times n}={\boldsymbol{A}}_{m\times 3}{\boldsymbol{R}}_{3\times n}{\boldsymbol{w}}_{n\times n}={\boldsymbol{A}}_{m\times 3}{\boldsymbol{m}}_{3\times n} $ | (6) |
式中:A为与角度有关的系数矩阵,称为叠前角度项;
对比式(3)和式(5)、式(4)和式(6)中的G和A可知,因G为稀疏矩阵,且矩阵维数较大,这给矩阵求逆带来了挑战。非稀疏化后,矩阵A的维数及病态性大大降低,为解耦分步反演奠定了基础。如何准确获取叠前地震属性数据是解耦分步反演的关键,具体解耦过程如下。
1.1.1 常规叠前数据解耦对于式(6),期望得到一组与叠前地震数据之间误差
| $ E={\boldsymbol{e}}^{\mathrm{T}}\boldsymbol{e}={(\boldsymbol{d}-\boldsymbol{A}\boldsymbol{m})}^{\mathrm{T}}(\boldsymbol{d}-\boldsymbol{A}\boldsymbol{m})\to \mathrm{m}\mathrm{i}\mathrm{n} $ | (7) |
对上式求导,可得
| $ \boldsymbol{m}={\left({\boldsymbol{A}}^{T}\boldsymbol{A}\right)}^{-1}{\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{d} $ | (8) |
从式(8)看出,利用叠前角度项
作为改进,引入协方差提高解耦精度[16]。由贝叶斯理论[17-18],当
| $ P\left(\boldsymbol{d}\left|\boldsymbol{m}\right.\right)=\frac{1}{\sigma \sqrt{2\mathrm{\pi }}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}\frac{{(\boldsymbol{A}\boldsymbol{m}-\boldsymbol{d})}^{\mathbf{T}}(\boldsymbol{A}\boldsymbol{m}-\boldsymbol{d})}{{\sigma }^{2}}\right] $ | (9) |
| $ P\left(\boldsymbol{m}\right)=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}{(\boldsymbol{m}-\overline{\boldsymbol{m}})}^{\mathrm{T}}{\boldsymbol{C}}_{\boldsymbol{m}}^{-1}(\boldsymbol{m}-\overline{\boldsymbol{m}})\right]}{{\left(2\mathrm{\pi }\right)}^{\frac{3}{2}}\sqrt{|\mathrm{d}\mathrm{e}\mathrm{t}{\boldsymbol{C}}_{\boldsymbol{m}}{|}^{3}}} $ | (10) |
式中:“det”表示行列式;
| $ \begin{array}{l}P\left(\boldsymbol{m}\right|\boldsymbol{d})\propto \mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}\frac{{(\boldsymbol{A}\boldsymbol{m}-\boldsymbol{d})}^{\mathbf{T}}(\boldsymbol{A}\boldsymbol{m}-\boldsymbol{d})}{{\sigma }^{2}}\right]\times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{1}{2}{\boldsymbol{m}}^{\mathrm{T}}{\boldsymbol{C}}_{\boldsymbol{m}}^{-1}\boldsymbol{m}\right)\end{array} $ | (11) |
取式(11)的对数,可得解耦目标函数
| $ J\left(\boldsymbol{m}\right|\boldsymbol{d})=\frac{1}{2}{\boldsymbol{m}}^{\mathrm{T}}{\boldsymbol{C}}_{m}^{-1}\boldsymbol{m}+\frac{{(\boldsymbol{A}\boldsymbol{m}-\boldsymbol{d})}^{\mathbf{T}}(\boldsymbol{A}\boldsymbol{m}-\boldsymbol{d})}{2{\sigma }^{2}} $ | (12) |
令其梯度为零可得
| $ \boldsymbol{m}={\left[{\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{A}+{\sigma }^{2}{\boldsymbol{C}}_{m}^{-1}\right]}^{-1}{\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{d} $ | (13) |
对比式(8)与式(13),虽然协方差约束方法引入
为获得精确的解耦结果,以测井数据为先验认识,利用HPDPK方法对叠前数据进行解耦。即利用井控计算的叠前角度项
| $ \boldsymbol{d}=\boldsymbol{A}\boldsymbol{R}\boldsymbol{w}=\boldsymbol{A}\boldsymbol{m}\to \boldsymbol{d}={\boldsymbol{A}}_{wc}\boldsymbol{R}\boldsymbol{w}={\boldsymbol{A}}_{wc}\boldsymbol{m} $ | (14) |
具体步骤如下:
(1) 通过井震标定,将地震数据与井数据进行匹配。
(2) 利用井数据计算
(3) 利用d与
| $ \boldsymbol{e}=\boldsymbol{d}-\boldsymbol{A}{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}=0 $ | (15) |
| $ \boldsymbol{L}={\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{A}=\sum {\boldsymbol{A}}_{kl}^{2} $ | (16) |
即在
不失一般性,设地震数据
| $ \varphi \left(\boldsymbol{A}\right)=\boldsymbol{L}+\sum\limits_{k=1}^{M}{\beta }_{k}{e}_{l}=\\\;\;\;\;\;\;\sum\limits_{k=1}^{M}\sum\limits_{l=1}^{N}{\boldsymbol{A}}_{kl}^{2}+\sum\limits_{k=1}^{M}{\beta }_{k}\left({\boldsymbol{d}}_{k}-\sum\limits_{l=1}^{N}{\boldsymbol{A}}_{kl}{{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}}_{l}\right) $ | (17) |
求式(17)的梯度并令其为
| $ \begin{array}{l}\frac{\partial \varphi \left(\boldsymbol{A}\right)}{\partial \boldsymbol{A}}=\sum\limits_{k=1}^{M}\sum\limits_{l=1}^{N}2\frac{\partial {\boldsymbol{A}}_{kl}^{}}{\partial \boldsymbol{A}}{\boldsymbol{A}}_{kl}^{}-\sum\limits_{k=1}^{M}{\beta }_{k}\sum\limits_{l=1}^{N}\frac{\partial {\boldsymbol{A}}_{kl}^{}}{\partial \boldsymbol{A}}{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}l}\\ \;\;\;\;\;\;\;\;\;\; =2\sum\limits_{k=1}^{M}\sum\limits_{l=1}^{N}{\boldsymbol{A}}_{kl}^{}-\sum\limits_{k=1}^{M}{\beta }_{k}\sum\limits_{l=1}^{N}{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}l}=0\end{array} $ | (18) |
由式(18)可得
| $ 2\boldsymbol{A}=\boldsymbol{\beta }{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}^{\mathrm{T}} $ | (19) |
式中
| $ \boldsymbol{\beta }=2\boldsymbol{d}({\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}^{\mathrm{T}}{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}{)}^{-1} $ | (20) |
将式(20)代入式(19),消元后得到
| $ {\boldsymbol{A}}_{wc}=\boldsymbol{d}({\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}^{\mathrm{T}}{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}{)}^{-1}{\boldsymbol{m}}_{\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}}^{\mathrm{T}} $ | (21) |
根据式(21)可以得到符合实际工区的叠前角度项
(4) 将
| $ \boldsymbol{m}={\left[{\boldsymbol{A}}_{wc}^{\mathrm{T}}{\boldsymbol{A}}_{wc}\right]}^{-1}{\boldsymbol{A}}_{wc}^{\mathrm{T}}\boldsymbol{d} $ | (22) |
通过式(22)可得到精确的叠前地震属性数据。
1.2 叠前地震属性的井约束反演鉴于地震反演的多解性,引入测井低频信息约束和稀疏约束[21-22],可得反演目标函数
| $ F\left(\boldsymbol{r}\right)={‖\boldsymbol{m}-\boldsymbol{w}\boldsymbol{r}‖}_{2}^{2}+\gamma {‖\boldsymbol{r}-{\boldsymbol{r}}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}‖}_{2}^{2}+\eta {‖\boldsymbol{r}‖}_{1} $ | (23) |
式中:r为
输入不同的叠前地震属性数据,利用梯度投影稀疏重构法[23]对式(23)求解,得到
利用某工区W48井的测井曲线,根据Zoeppritz方程得到不同角度的纵波反射系数,与主频30 Hz的Ricker子波褶积得到1°~30°的叠前地震数据(图 1)。分别将1°~10°、11°~20°、21°~30°的数据部分叠加,得到小角度、中角度、大角度地震数据。
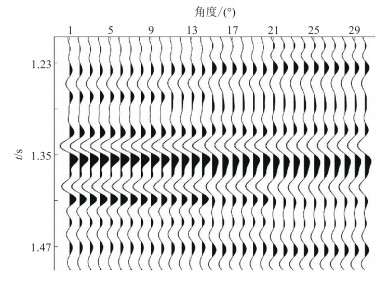
|
图 1 叠前地震记录 |
利用角度部分叠加数据作为d与W48井中
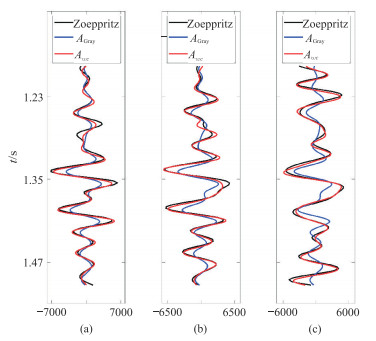
|
图 2 正演结果对比 (a)小角度地震数据;(b)中角度叠前数据;(c)大角度叠前数据 |
根据式(21)和式(22),将HPDPK方法应用于某工区实际地震资料1°~10°、11°~20°、21°~30°三个部分角度叠加数据和W48井数据,解耦获得
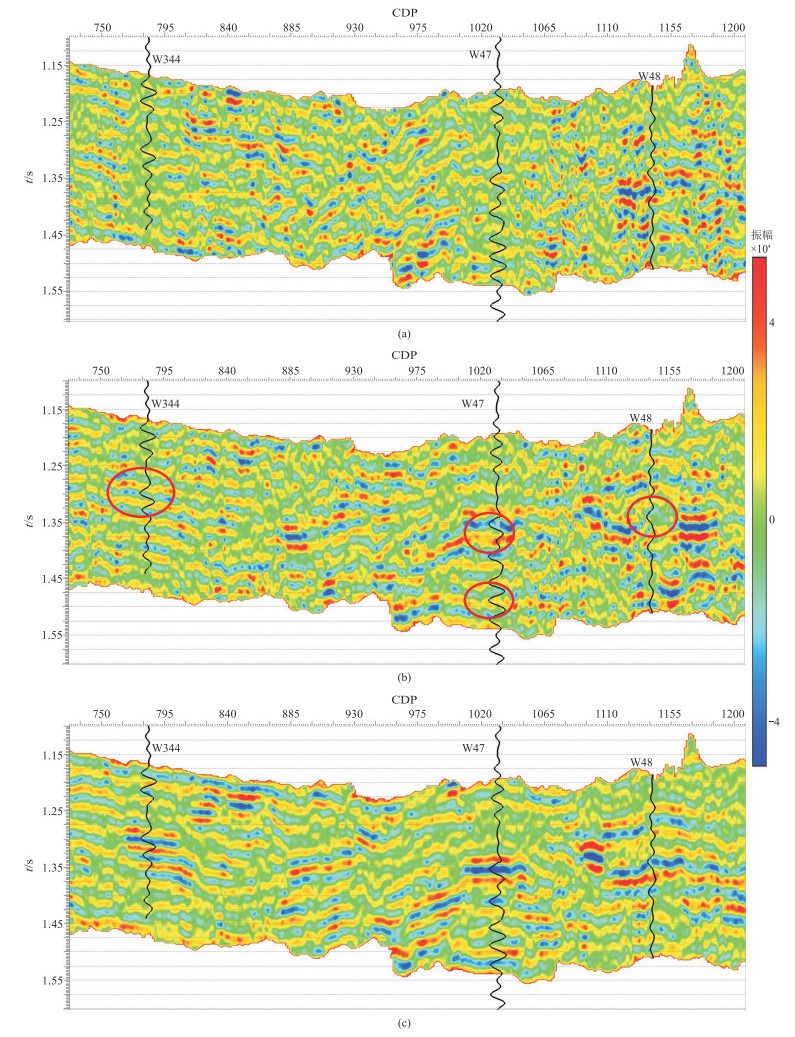
|
图 3 λ叠前地震属性剖面 (a)直接解耦;(b)协方差约束方法解耦;(c)HPDPK方法解耦 |
为更细致地观察各方法解耦结果与
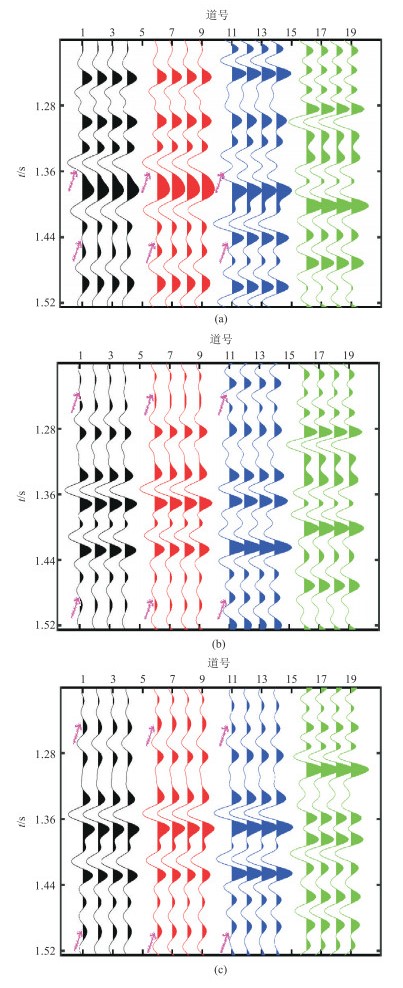
|
图 4 W48井叠前地震属性对比 (a)λ叠前地震属性;(b)μ叠前地震属性;(c)ρ叠前地震属性 黑色为测井合成属性数据,红、蓝、绿分别为HPDPK方法、协方差约束方法和直接解耦的解耦结果。 |
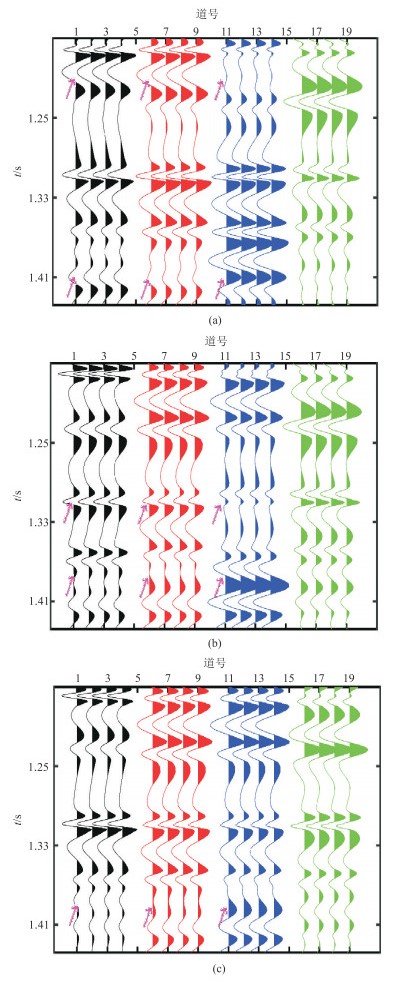
为进一步验证HPDPK方法的稳定性,图 5给出了W344盲井的验证结果。由图可见,直接解耦的结果、协方差约束的解耦结果与W344盲井的
|
图 5 W344盲井叠前地震属性对比验证 (a)λ叠前地震属性;(b)μ叠前地震属性;(c)ρ叠前地震属性 黑色为测井合成属性数据,红、蓝、绿分别为HPDPK方法、协方差约束方法和直接解耦的解耦结果。 |
根据式(23),利用HPDPK解耦的叠前地震属性数据进行反演,得到相应的地层弹性参数,如图 6~图 8所示。图 6是剪切模量的反演结果,可见反演结果的低值区(蓝色区域)对应测井曲线低值,高值区(红色区域)对应测井曲线高值,反演结果与井曲线吻合度较高。图 7、图 8分别是拉梅参数和密度反演结果。与图 6类似,反演结果均与井曲线吻合。

|
图 6 HPDPK方法反演的剪切模量剖面 |
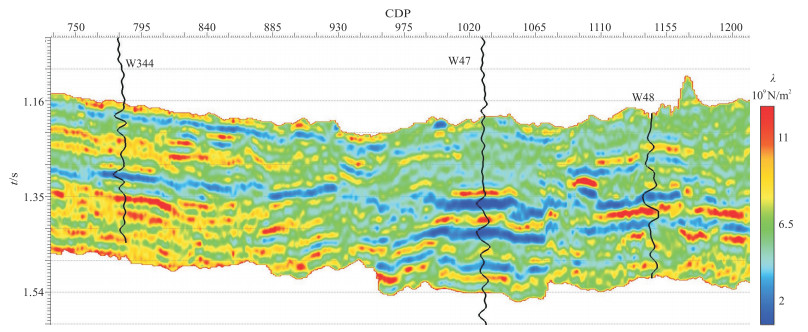
|
图 7 HPDPK方法反演的拉梅参数剖面 |
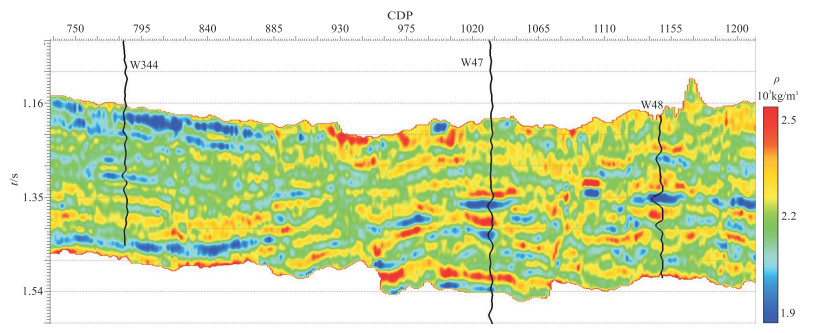
|
图 8 HPDPK方法反演的密度剖面 |
为更直观地观察HPDPK方法的反演精度,提取协方差约束方法和HPDPK方法在W48井处的反演曲线,并与原始井曲线对比,如图 9所示。由图可见,HPDPK方法的反演结果与测井曲线最相似,其中
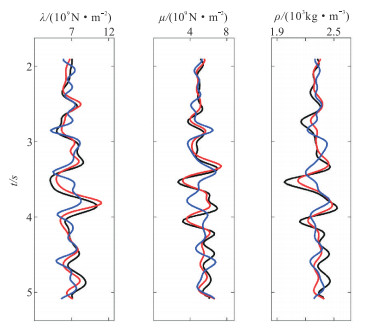
|
图 9 不同方法反演结果对比 黑色曲线为原始井数据;蓝色曲线为协方差约束方法的反演结果;红色曲线为HPDPK方法的反演结果。 |
|
|
表 1 反演结果与井数据的相似系数 |
针对叠前三参数反演存在的不稳定和精度不高问题,提出了物理、数据先验认识融合(HPDPK)的叠前解耦分步反演方法。先对AVA正演框架进行非稀疏化分解,增加了参数反演的稳定性;然后利用HPDPK方法从叠前部分叠加数据中解耦获得叠前地震属性数据,避免了角度不准而带来的巨大偏差,有利于提高地层弹性参数的反演精度;最后通过叠前地震属性数据反演得到对应的地层弹性参数。模型和实际数据试验结果表明,相比于业界常用的叠前反演方法,本文方法获得的叠前地震属性及反演结果更稳定,而且具有更高的精度。
本文方法将物理、数据先验认识融合,可以利用叠前数据进行任意敏感参数的反演,不限于模量、纵横波速度、泊松比等弹性参数,也可以自然扩展到AVAZ五维地震数据反演。
| [1] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing Russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. |
| [2] |
罗辑, 吴国忱, 宗兆云, 等. 基于方位弹性阻抗反演的裂缝型储层流体检测方法[J]. 石油地球物理勘探, 2015, 50(6): 1154-1165. LUO Ji, WU Guochen, ZONG Zhaoyun, et al. Fluid detection method for fractured reservoirs based on azimuthal elastic impedance inversion[J]. Oil Geophysical Prospecting, 2015, 50(6): 1154-1165. |
| [3] |
周路, 周江辉, 代瑞雪, 等. OVT域五维地震属性在双鱼石地区栖霞组裂缝预测中的应用[J]. 地学前缘, 2023, 30(1): 213-228. ZHOU Lu, ZHOU Jianghui, DAI Ruixue, et al. Application of OVT-domain 5-dimensional seismic attributes in fracture prediction in the Qixia formation of the Shuangyushi area[J]. Earth Science Frontiers, 2023, 30(1): 213-228. |
| [4] |
撒利明, 杨午阳, 姚逢昌, 等. 地震反演技术回顾与展望[J]. 石油地球物理勘探, 2015, 50(1): 184-202. SA Liming, YANG Wuyang, YAO Fengchang, et al. Review and exhibition of seismic inversion technology[J]. Oil Geophysical Prospecting, 2015, 50(1): 184-202. |
| [5] |
RABBEN T E, TJELMELAND H, URSIN B. Non-linear Bayesian joint inversion of seismic reflection coefficients[J]. Geophysical Journal International, 2008, 173(1): 265-280. DOI:10.1111/j.1365-246X.2007.03710.x |
| [6] |
AKI K, RICHARDS P G. Quantitative Seismology: Theory and Methods[M]. Freeman and Co, San Francisco, 1980.
|
| [7] |
GRAY D, GOODWAY B, CHEN T W. Bridging the gap: using AVO to detect changes in fundamental elastic constants[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 2061.
|
| [8] |
FATTI J L, SMITH G C, VAIL P J, et al. Detection of gas in sandstone reservoirs using AVO analysis: a 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [9] |
MARQUARDT D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441. DOI:10.1137/0111030 |
| [10] |
LEVENBERG K. A method for the solution of certain non-linear problems in least squares[J]. Quarterly of Applied Mathematics, 1944, 2(2): 164-168. DOI:10.1090/qam/10666 |
| [11] |
BULAND A, OMRE H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |
| [12] |
DOWNTON J E. Seismic Parameter Estimation from AVO Inversion[D]. University of Calgary, Calgary, 2005.
|
| [13] |
印兴耀, 崔维, 宗兆云, 等. 基于弹性阻抗的储层物性参数预测方法[J]. 地球物理学报, 2014, 57(12): 4132-4140. YIN Xingyao, CUI Wei, ZONG Zhaoyun, et al. Prediction method of reservoir physical parameters based on elastic impedance[J]. Chinese Journal of Geophysics, 2014, 57(12): 4132-4140. DOI:10.6038/cjg20141224 |
| [14] |
MACKAY S, JIMÉNEZ H R, SAN MARTÍN ROMERO J, et al. Calibrating prestack depth migration volumes with well control[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 3541.
|
| [15] |
王迪, 张益明, 张繁昌, 等. 利用先验信息约束的深度学习方法定量预测致密砂岩"甜点"[J]. 石油地球物理勘探, 2023, 58(1): 65-74. WANG Di, ZHANG Yiming, ZHANG Fanchang, et al. Quantitative prediction of tight sandstone sweet spots based on deep learning method with prior information constraints[J]. Oil Geophysical Prospecting, 2023, 58(1): 65-74. |
| [16] |
曲志鹏, 温瑨, 韩宏伟, 等. 基于BISQ模型的储层物性参数贝叶斯反演方法[J]. 石油地球物理勘探, 2023, 58(4): 942-948. QU Zhipeng, WEN Jin, HAN Hongwei, et al. Baye-sian inversion based on BISQ model for reservoir physical properties[J]. Oil Geophysical Prospecting, 2023, 58(4): 942-948. |
| [17] |
张猛. 基于自注意力机制的卷积自编码器多次波压制方法[J]. 石油物探, 2022, 61(3): 454-462. ZHANG Meng. A multiple suppression method based on self-attention convolutional auto-encoder[J]. Geophysical Prospecting for Petroleum, 2022, 61(3): 454-462. |
| [18] |
GARDNER G H F, GARDNER L W, GREGORY A R. Formation velocity and density: the diagnostic basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780. DOI:10.1190/1.1440465 |
| [19] |
陈建江, 印兴耀, 张广智. 基于贝叶斯理论的振幅随偏移距变化三参数同步反演[J]. 中国石油大学学报(自然科学版), 2007, 31(3): 33-38. CHEN Jianjiang, YIN Xingyao, ZHANG Guangzhi. Simultaneous three-term AVO inversion based on Bayesian theorem[J]. Journal of China University of Petroleum (Edition of Natural Science), 2007, 31(3): 33-38. |
| [20] |
姚姚. 地球物理反演基本理论与应用方法[M]. 湖北武汉: 中国地质大学出版社, 2002. YAO Yao. Basic Theory and Application Methods of Geophysical Inversion[M]. Wuhan, Hubei: China University of Geosciences Press, 2002. |
| [21] |
印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34, 46. YIN Xingyao, CAO Danping, WANG Baoli, et al. Research progress of fluid discrimination with pre-stack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34, 46. |
| [22] |
张丰麒, 金之钧, 盛秀杰, 等. 基于低频软约束的叠前AVA稀疏层反演[J]. 石油地球物理勘探, 2017, 52(4): 770-782. ZHANG Fengqi, JIN Zhijun, SHENG Xiujie, et al. AVA sparse layer inversion with the soft-low frequency constraint[J]. Oil Geophysical Prospecting, 2017, 52(4): 770-782. |
| [23] |
杨震, 刘俊州, 时磊, 等. 基于快速反射率法的AVA反演技术在致密砂岩薄储层勘探中的应用[J]. 石油物探, 2023, 62(1): 130-141. YANG Zhen, LIU Junzhou, SHI Lei, et al. Application of AVA inversion technique based on rapid reflectivity method in thin tight gas reservoir exploration[J]. Geophysical Prospecting for Petroleum, 2023, 62(1): 130-141. |



 张繁昌, 山东省青岛市经济技术开发区长江西路中国石油大学(华东)地球科学与技术学院,266580。Email:
张繁昌, 山东省青岛市经济技术开发区长江西路中国石油大学(华东)地球科学与技术学院,266580。Email: