裂缝既可以作为流体的主要渗流通道控制油气的运移,也可以作为油气的储集空间控制油气藏的分布。因此,随着油气勘探和开发的不断深入,裂缝型油气藏已成为当今油气勘探的重要领域,是中国含油气盆地中的一种重要油气藏类型。
常用的裂缝介质岩石物理等效模型有Hudson模型[1]、Thomsen模型[2]和Schoenberg线性滑动模型[3],其中Hudson模型和Thomsen模型假设裂缝密度较小,裂缝呈硬币状;Schoenberg线性滑动模型将裂缝假设为无限薄的柔软平面,忽略裂缝的结构和形状,裂缝面为位移间断面,两侧保持应力连续,位移间断与连续应力呈线性关系。Bakulin等[4-5]提出了币状裂缝假设,用岩石骨架参数、裂缝密度和充填流体参数表征裂缝弱度。Mallick等[6]发现垂直定向排列裂缝的各向异性介质中纵波反射振幅响应是炮检方向的周期函数,对不同方位的纵波反射振幅进行椭圆拟合,椭圆长轴和短轴可以指示裂缝走向,而椭圆扁率与裂缝密度有关。薛姣等[7]提出用广义裂隙弱度表征Gurevich准静态等效介质中的含流体裂缝,可用于实现准静态孔缝模型地震数据的定量解释。
随着宽方位地震数据采集和处理技术的发展,叠前AVOA(Amplitude Variation with Offset and Azimuth)数据反演应用于裂缝参数预测。Shaw等[8]推导了线性滑动模型纵波反射系数与裂缝弱度的关系,并利用AVOA数据反演裂缝弱度。Ruger[9]推导的近似方程对地震振幅方位各向异性反演做出了极大贡献,在裂缝和储层预测方面应用广泛。刘洋等[10]根据各向异性介质弹性波波动方程推导出TI介质分界面上36个反射和透射系数的计算公式,指出P波方位AVO特征与裂缝的方位、倾角和密度密切相关。朱培民等[11]提出了分布削减参数反演方法,利用两条相互垂直测线的纵波AVO数据反演裂缝介质各向异性参数,并进行了数值试验。张世俊等[12]在对裂缝介质的研究中通过遗传算法反演HTI介质中的各向异性参数。姚姚等[13]对深层碳酸盐岩的裂缝及储层预测进行了数值模拟、波场分析,推进了深层裂缝预测的研究。朱兆林等[14]利用HTI模型比较了反射系数Vavrycuk近似、Ruger的近似与真实反射系数曲线,认为在大入射角情况下Vavrycuk近似比Ruger近似精度更高。李录明等[15]利用了多分量地震资料通过纵、横波联合反演求解裂缝储层的各向异性参数。张广智等[16]、陈怀震等[17]针对HTI介质中的各向异性AVO特征,利用叠前反演求解弹性参数。Xue等[18]提出了新的流体因子表达式,给出了纵波方位反射振幅与裂缝弱度的矩阵表达式,并基于AVOA数据反演了裂缝弱度和新的流体因子。
Downton等[19]利用傅里叶系数重写方位纵波反射系数并实现了各向异性梯度估算。Pan等[20]基于纵波反射系数方位差异利用非线性马尔可夫链—蒙特卡罗算法反演了裂缝弱度。李林等[21]分析了傅里叶系数对裂缝弱度反射系数的敏感性,认为二阶傅里叶系数对裂缝弱度反射系数的变化最敏感。宋维琪等[22]基于傅里叶级数进行各向异性参数估计,利用二倍角公式将纵波反射系数傅里叶级数进一步展开,提高了各向异性参数估计和裂缝预测精度。Li等[23]基于弹性波阻抗傅里叶系数反演裂缝弱度,给出了由二阶方位傅里叶系数求取裂缝对称轴方位角存在90°不确定性问题的解决方法,指出裂缝对称轴方位角估测值偏差在30°以内反演结果较为可靠。魏欣伟等[24]基于等效裂缝介质理论推导了不同方位地震道集差异与裂缝密度之间的矩阵关系,利用OVT(炮检距向量片)域地震数据反演裂缝密度。陈超等[25]提出了先基于方位弹性波阻抗反演裂缝弱度,再结合裂缝密度与裂缝弱度关系间接定量预测裂缝密度的方法。李林等[26]将扩展弹性阻抗推广到水平横向各向同性介质,提出了一种基于扩展方位弹性阻抗预测裂缝参数及水平应力差异比的方法。汤伟等[27]提出一种基于非下采样剪切波变换(NSST)—参数自适应脉冲耦合神经网络(PA-PCNN)的属性融合裂缝预测方法。范廷恩等[28]基于M气田宽方位地震资料,提出基于高角度断裂约束的方位傅里叶系数叠前裂缝参数反演方法。
本文基于HTI模型,推导了不同流体充填条件下纵波反射振幅方位傅里叶系数与裂缝密度的关系式,利用二阶傅里叶系数预测裂缝对称轴方位角。研究了在地震数据含有噪声时二阶傅里叶系数正、余弦分量信噪比的比值随裂缝对称轴方位角的变化规律,提出了应用二阶傅里叶系数正、余弦分量加权的裂缝密度反演方法。
1 方法原理 1.1 裂缝等效介质模型裂缝等效介质理论基于特定假设条件将岩石理想化,建立裂缝介质中裂缝密度、裂缝尺寸以及裂缝高宽比与弹性参数的关系。裂缝密度不仅反映了裂缝的发育程度,也是影响裂缝孔隙度和渗透率的重要参数。在上覆地层压实作用下,储层中广泛发育定向分布的高角度裂缝,可以将裂缝储层等效为HTI介质。Schoenberg等[3]提出用分别代表纵波和横波各向异性的法向裂隙弱度ΔN和切向裂隙弱度ΔT表征裂缝。
对于流体充填裂缝介质,根据线性滑动模型与Hudson模型刚度矩阵的等价性,
| $ {\varDelta }_{\mathrm{T}}=\frac{16e}{3(3-2g)} $ | (1) |
式中:
当裂缝饱含气时,
| $ {\varDelta }_{\mathrm{N}}=\frac{4e}{3g(1-g)} $ | (2) |
当裂缝中充填油、水时,
| $ {\varDelta }_{\mathrm{N}}\approx 0 $ | (3) |
饱和气裂缝介质模型可以看成是HTI介质,其纵波反射系数近似公式[20]为
| $ \begin{array}{l}R(\theta , \phi )=\frac{1}{2}A\left(\theta \right)\frac{\mathtt{δ}\alpha }{\overline{\alpha }}+\frac{1}{2}B\left(\theta \right)\frac{\mathtt{δ}\beta }{\overline{\beta }}+\\ \frac{1}{2}C\left(\theta \right)\frac{\mathtt{δ}\rho }{\overline{\rho }}+\frac{1}{2}D(\theta , \phi )\mathtt{δ}{\varDelta }_{\mathrm{N}}+\frac{1}{2}E(\theta , \phi )\mathtt{δ}{\varDelta }_{\mathrm{T}}\end{array} $ | (4) |
式中:θ为入射角;
| $ A\left(\theta \right)=\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta $ | (5) |
| $ B\left(\theta \right)=-8g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (6) |
| $ C\left(\theta \right)=1-4g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (7) |
| $ \begin{array}{l}D(\theta , \phi )=-2g\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \times \\ \begin{array}{cc}& \left[(1-2g)(1+\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\varphi \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta )+\right.\end{array}\\ \begin{array}{cc}& \left.(1-g)\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right]\end{array}\end{array} $ | (8) |
| $ E(\theta , \phi )=2g\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\varphi \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta (1-\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\varphi \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta ) $ | (9) |
其中:
根据式(1)、式(2)和式(4)可得由各向同性背景参数和裂缝密度表示的纵波反射系数
| $ \begin{array}{l}R(\theta , \phi )=\frac{1}{2}\left[A\left(\theta \right)\frac{\mathtt{δ}\alpha }{\overline{\alpha }}+B\left(\theta \right)\frac{\mathtt{δ}\beta }{\overline{\beta }}+C\left(\theta \right)\frac{\mathtt{δ}\rho }{\overline{\rho }}\right]+\\ \begin{array}{cc}& \left[\frac{2}{3g(1-g)}D(\theta , \phi )+\frac{8}{3(3-2g)}E(\theta , \phi )\right]\end{array}\mathtt{δ}e\end{array} $ | (10) |
将式(10)展开成傅里叶级数形式
| $ \begin{array}{l}R(\theta , \phi )={a}_{0}\left(\theta \right)+{a}_{2}\left(\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(2\phi \right)+{b}_{2}\left(\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(2\phi \right)+\\ \begin{array}{cc}& {a}_{4}\left(\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(4\phi \right)+{b}_{4}\left(\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(4\phi \right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left(11\right)\end{array}\end{array} $ |
式中系数为
| $ \begin{array}{l}{a}_{0}\left(\theta \right)=\frac{1}{2}\left[A\left(\theta \right)\frac{\mathtt{δ}\alpha }{\overline{\alpha }}+B\left(\theta \right)\frac{\mathtt{δ}\beta }{\overline{\beta }}+C\left(\theta \right)\frac{\mathtt{δ}\rho }{\overline{\rho }}\right]+\\ \begin{array}{cc}& \left[\frac{2}{3g(1-g)}F\left(\theta \right)+\frac{8}{3(3-2g)}G\left(\theta \right)\right]\end{array}\mathtt{δ}e\end{array} $ | (12) |
| $ {a}_{2}\left(\theta \right)=\frac{1}{2}H\left(\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (13) |
| $ {b}_{2}\left(\theta \right)=\frac{1}{2}H\left(\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (14) |
| $ {a}_{4}\left(\theta \right)=\frac{1}{2}I\left(\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(4{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (15) |
| $ {b}_{4}\left(\theta \right)=\frac{1}{2}I\left(\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(4{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (16) |
其中F、G、H、I分别为
| $ F\left(\theta \right)=\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \left[g(2g-1)+g\left(\frac{5}{4}g-1\right)\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right] $ | (17) |
| $ G\left(\theta \right)=g\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \left(1-\frac{1}{4}\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right) $ | (18) |
| $ H\left(\theta \right)=\frac{4}{3}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \left(\frac{12g-8{g}^{2}-3}{2{g}^{2}-5g+3}-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right) $ | (19) |
| $ I\left(\theta \right)=\frac{g(3g-4)}{2{g}^{2}-5g+3}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta $ | (20) |
傅里叶余弦系数an(θ)(n=0、2、4)和正弦系数bn(θ)可由纵波反射系数计算
| $ {a}_{n}\left(\theta \right)=\frac{1}{\mathrm{\pi }}\sum\limits_{k=1}^{K}R(\theta , {\phi }_{k})\mathrm{c}\mathrm{o}\mathrm{s}\left(n{\phi }_{k}\right)\mathtt{δ}\phi $ | (21) |
| $ {b}_{n}\left(\theta \right)=\frac{1}{\mathrm{\pi }}\sum\limits_{k=1}^{K}R(\theta , {\phi }_{k})\mathrm{s}\mathrm{i}\mathrm{n}\left(n{\phi }_{k}\right)\mathtt{δ}\phi $ | (22) |
式中:K为观测方位个数;
二阶傅里叶系数余弦分量a2(θ)和正弦分量b2(θ)为裂缝对称轴方位角
| $ {\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}=\frac{1}{2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{{b}_{2}\left(\theta \right)}{{a}_{2}\left(\theta \right)} $ | (23) |
当裂缝中饱含油或水时,其法向弱度近似为零,则式(10)可简化为
| $ \begin{array}{l}R(\theta , \phi )=\frac{1}{2}\left[A\left(\theta \right)\frac{\mathtt{δ}\alpha }{\overline{\alpha }}+B\left(\theta \right)\frac{\mathtt{δ}\beta }{\overline{\beta }}+C\left(\theta \right)\frac{\mathtt{δ}\rho }{\overline{\rho }}\right]+\\ \begin{array}{cc}& \end{array}\frac{8}{3(3-2g)}E(\theta , \phi )\mathtt{δ}e\end{array} $ | (24) |
则纵波反射系数傅里叶级数的系数可简化为
| $ \begin{array}{l}{a}_{0}\left(\theta \right)=\frac{1}{2}\left[A\left(\theta \right)\frac{\mathtt{δ}\alpha }{\overline{\alpha }}+B\left(\theta \right)\frac{\mathtt{δ}\beta }{\overline{\beta }}+C\left(\theta \right)\frac{\mathtt{δ}\rho }{\overline{\rho }}\right]+\\ \begin{array}{cc}& \end{array}\frac{8}{3(3-2g)}G\left(\theta \right)\mathtt{δ}e\end{array} $ | (25) |
| $ {a}_{2}\left(\theta \right)=\frac{1}{2}J\left(\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (26) |
| $ {b}_{2}\left(\theta \right)=\frac{1}{2}J\left(\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (27) |
| $ {a}_{4}\left(\theta \right)=\frac{1}{2}T\left(\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(4{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (28) |
| $ {b}_{4}\left(\theta \right)=\frac{1}{2}T\left(\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(4{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\mathtt{δ}e $ | (29) |
式中J、
| $ J\left(\theta \right)=\frac{16g}{3(3-2g)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $ | (30) |
| $ T\left(\theta \right)=-\frac{4g}{3(3-2g)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta $ | (31) |
由于正切函数周期性,通过式(23)计算得到的裂缝对称轴方位角可能存在90°的不确定性,利用二阶方位傅里叶系数及其正、余弦分量正负性可判别计算结果是否存在90°偏差[23]。但大多情况下二阶傅里叶系数的符号难以确定,需结合地质信息判断是否旋转90°,即根据已知地质信息选择一个参考裂缝对称轴方位角,如果计算的方位角与参考值偏差超出45°,则旋转90°。地层裂缝发育方向具有一定的连续性,在没有先验地质信息时,可将目的层段内二阶傅里叶系数计算的裂缝对称轴方位角的均值作为参考。
1.4 裂缝密度反演方法地震记录可表示为地震子波与地层反射系数的褶积
| $ S(\theta , \phi )=w(\theta , \phi )\mathrm{*}R(\theta , \phi ) $ | (32) |
式中:
由于二阶方位傅里叶系数对裂缝参数变化最敏感[23],本文利用二阶傅里叶系数预测裂缝对称轴方位角和裂缝密度。地震记录二阶傅里叶系数余弦分量
| $ {X}_{2}\left(\theta \right)=\frac{1}{\mathrm{\pi }}\sum\limits_{k=1}^{K}S(\theta , {\phi }_{k})\mathrm{c}\mathrm{o}\mathrm{s}\left(2{\phi }_{k}\right)\mathtt{δ}\phi $ | (33) |
| $ {Y}_{2}\left(\theta \right)=\frac{1}{\mathrm{\pi }}\sum\limits_{k=1}^{K}S(\theta , {\phi }_{k})\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\phi }_{k}\right)\mathtt{δ}\phi $ | (34) |
假设入射角为M个,地震记录时间采样点为
| $ \boldsymbol{d}=\boldsymbol{Q}\boldsymbol{m} $ | (35) |
式中: m=e; 而
| $ \begin{array}{l} \boldsymbol{d}={\left[{\boldsymbol{X}}_{2}\left({\theta }_{1}\right), {\boldsymbol{Y}}_{2}\left({\theta }_{1}\right), \cdots , {\boldsymbol{X}}_{2}\left({\theta }_{M}\right), {\boldsymbol{Y}}_{2}\left({\theta }_{M}\right)\right]}^{\mathrm{T}}\end{array} $ | (36) |
| $ \boldsymbol{Q}=\frac{1}{2}\left[\begin{array}{c}\boldsymbol{W}\left({\theta }_{1}\right)\boldsymbol{L}\left({\theta }_{1}\right)\boldsymbol{P}\mathrm{c}\mathrm{o}\mathrm{s}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\\ \boldsymbol{W}\left({\theta }_{1}\right)\boldsymbol{L}\left({\theta }_{1}\right)\boldsymbol{P}\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\\ ⋮\\ \boldsymbol{W}\left({\theta }_{M}\right)\boldsymbol{L}\left({\theta }_{M}\right)\boldsymbol{P}\mathrm{c}\mathrm{o}\mathrm{s}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\\ \boldsymbol{W}\left({\theta }_{M}\right)\boldsymbol{L}\left({\theta }_{M}\right)\boldsymbol{P}\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\phi }_{\mathrm{s}\mathrm{y}\mathrm{m}}\right)\end{array}\right] $ | (37) |
其中:P为一阶差分矩阵;
| $ {\boldsymbol{X}}_{2}\left({\theta }_{i}\right)=\left[{X}_{2}^{1}\right({\theta }_{i}), {X}_{2}^{2}({\theta }_{i}), \cdots , {X}_{2}^{N}({\theta }_{i}{\left)\right]}^{\mathrm{T}} $ | (38) |
| $ {\boldsymbol{Y}}_{2}\left({\theta }_{i}\right)=\left[{Y}_{2}^{1}\right({\theta }_{i}), {Y}_{2}^{2}({\theta }_{i}), \cdots , {Y}_{2}^{N}({\theta }_{i}{\left)\right]}^{\mathrm{T}} $ | (39) |
| $ \boldsymbol{L}\left({\theta }_{i}\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[{L}^{1}\right({\theta }_{i}), {L}^{2}({\theta }_{i}), \cdots , {L}^{N}({\theta }_{i}\left)\right] $ | (40) |
式中i=1,2,…,M。由于含有子波影响的傅里叶系数与方位无关,因而采用的子波仅为入射角的函数。特别地,对于饱含油或水裂缝介质,有
| $ L\left(\theta \right)=\frac{16g}{3(3-2g)}\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta $ | (41) |
对于饱含气裂缝介质,有
| $ L\left(\theta \right)=\frac{4}{3}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \left(\frac{12g-8{g}^{2}-3}{2{g}^{2}-5g+3}-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right) $ | (42) |
由式(13)和式(14)及式(26)和式(27)可知,二阶傅里叶系数正弦分量与余弦分量比值为
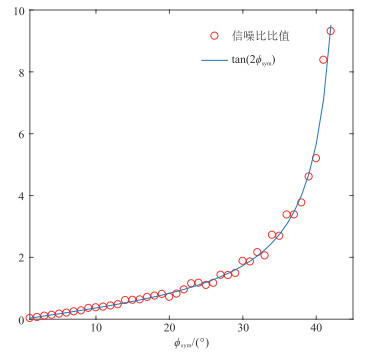
|
图 1 振幅二阶傅里叶系数信噪比比值随裂缝对称轴方位角的变化 |
假设地震数据似然函数及其噪声满足高斯分布,噪声相互独立,将模型先验分布和观测数据似然函数结合得到后验概率分布,再将后验概率最大化,得到目标函数
| $ \begin{array}{l}\varPhi \left(\boldsymbol{m}\right)={\left[\boldsymbol{U}(\boldsymbol{d}-\boldsymbol{Q}\boldsymbol{m})\right]}^{\mathrm{T}}\left[\boldsymbol{U}(\boldsymbol{d}-\boldsymbol{Q}\boldsymbol{m})\right]+\\ \lambda {\boldsymbol{m}}^{\mathrm{T}}{\boldsymbol{P}}^{\mathrm{T}}\boldsymbol{P}\boldsymbol{m}+\mu {\boldsymbol{m}}^{\mathrm{T}}\boldsymbol{m}\end{array} $ | (43) |
式中:
| $ \left\{\begin{array}{l}\boldsymbol{U}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[{\boldsymbol{u}}_{1}^{1}, {\boldsymbol{u}}_{2}^{1}, {\boldsymbol{u}}_{1}^{2}, {\boldsymbol{u}}_{2}^{2}, \cdots , {\boldsymbol{u}}_{1}^{M}, {\boldsymbol{u}}_{2}^{M}]\\ {\boldsymbol{u}}_{1}={[\mathrm{1, 1}, \cdots , 1]}_{1\times N}\\ {\boldsymbol{u}}_{2}=\left[\mathrm{t}\mathrm{a}\mathrm{n}\right(2{\overline{\phi }}_{\mathrm{s}\mathrm{y}\mathrm{m}}), \mathrm{t}\mathrm{a}\mathrm{n}(2{\overline{\phi }}_{\mathrm{s}\mathrm{y}\mathrm{m}}), \cdots , \mathrm{t}\mathrm{a}\mathrm{n}(2{\overline{\phi }}_{\mathrm{s}\mathrm{y}\mathrm{m}}{\left)\right]}_{1\times N}\end{array}\right. $ | (44) |
通过调节系数
本文提出的裂缝密度反演方法基于宽方位叠前地震数据,需将地震数据按方位和入射角抽取道集。为提高信噪比将地震数据进行部分角度叠加再计算二阶傅里叶系数,利用二阶傅里叶系数预测裂缝对称轴方位角,继而反演裂缝密度。
2 模型试算建立裂缝等效介质模型,参数如图 2所示。选取峰值频率为25 Hz的Ricker子波,设定裂缝对称轴方位角为35°,利用模型参数分别正演饱和气裂缝储层模型叠前地震道集和饱和油裂缝储层模型叠前地震道集,入射角为1°~40°,间隔为1°;每个入射角包含四个观测方位(30°、75°、120°和165°),然后分别添加信噪比(SNR,信号平均功率与噪声平均功率比值)分别为5、2和1的随机噪声。大角度入射时地震记录各向异性更明显,因而选择大入射角地震数据预测裂缝更为可靠。首先利用合成地震记录进行部分角度叠加,将入射角为21°~29°地震记录叠加作为入射角为25°的地震记录,入射角为31°~39°地震记录叠加作为入射角为35°的地震记录;以部分角度叠加地震记录计算二阶傅里叶系数正弦分量和余弦分量,通过式(23)初步计算裂缝对称轴方位角,将目的层段内裂缝对称轴方位角的均值作为裂缝对称轴方位角预测参考值,然后将初步估算的裂缝对称轴方位角与参考值偏差超出45°的部分旋转90°,最后应用本文提出的对二阶傅里叶系数加权反演方法预测裂缝密度。
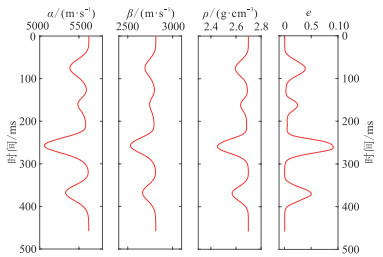
|
图 2 裂缝储层模型参数 |
图 3为饱和气裂缝储层模型不同噪声水平叠前地震道集。由图可知。大入射角条件下地震记录各向异性特征更为明显。图 4为饱和气储层模型不同信噪比条件下裂缝对称轴方位角估算结果,当地震数据SNR=1时,裂缝对称轴方位预测结果仍与模型符合较好;图 5为饱和气储层模型裂缝密度反演结果,反演结果与模型相符,地震数据含噪声较大时裂缝密度预测结果稳定且误差较小。
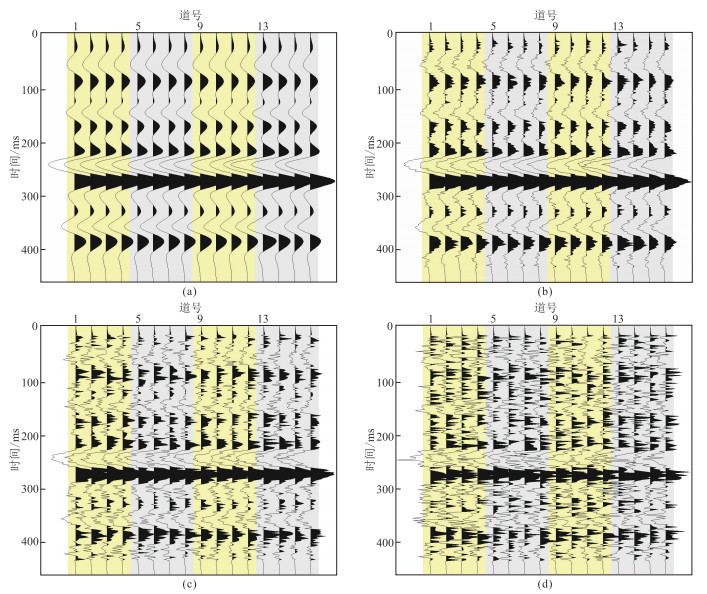
|
图 3 饱含气裂缝储层模型的不同信噪比正演叠前道集 (a)不含噪声;(b)SNR=5;(c)SNR=2;(d)SNR=1 每4道入射角相同,分别为5°、15°、25°和35°;4道的方位角依次为30°、75°、120°和165°。 |

|
图 4 饱含气模型不同信噪比数据的裂缝对称轴方位角估算结果(红线)与理论值(蓝线)对比 (a)不含噪声;(b)SNR=5;(c)SNR=2;(d)SNR=1 |
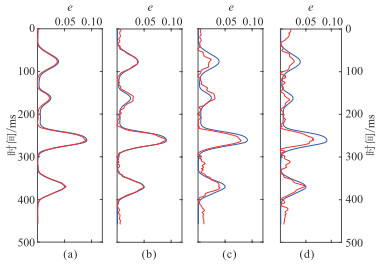
|
图 5 饱含气模型不同信噪比数据的裂缝密度反演结果(红线)与理论值(蓝线)对比 (a)不含噪声;(b)SNR=5;(c)SNR=2;(d)SNR=1 |
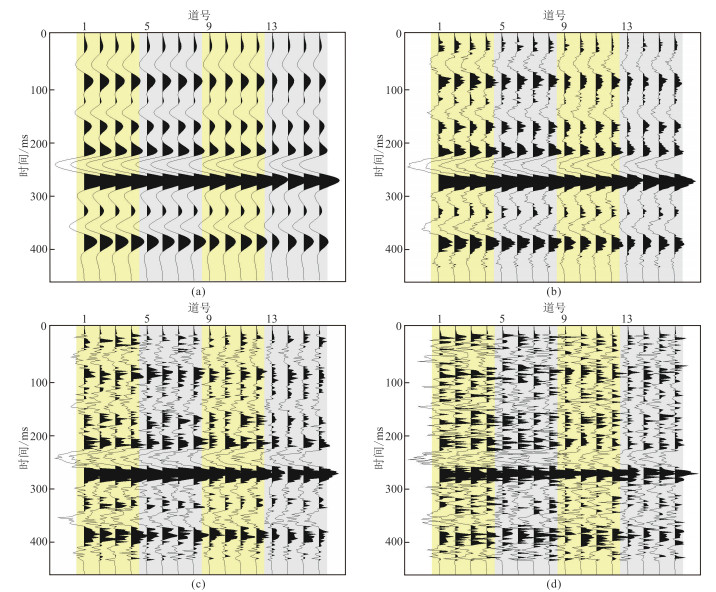
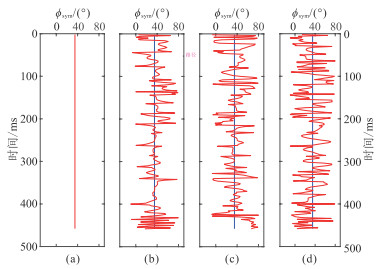
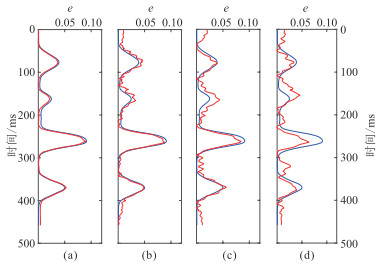
图 6为饱和油裂缝储层模型不同噪声水平叠前正演道集,图 7为饱和油模型不同噪声水平条件下裂缝对称轴方位角预测结果,图 8为饱和油模型裂缝密度反演结果。随着地震数据噪声水平增加,饱和油裂缝储层模型裂缝对称轴方位及裂缝密度预测准确度虽有所降低,但预测结果均与真值吻合。表 1为裂缝对称轴方位角估算值的统计结果。由表可见,地震数据SNR大于1时,目的层段内预测的裂缝对称轴方位角均值与模型参数吻合,裂缝对称轴方位角预测值偏差在30°以内的占比可达70%以上,裂缝对称轴方位角预测准确度随地震数据噪声减弱而不断提升,尤其在裂缝发育层段裂缝对称轴方位角估计较为准确。由饱含气和饱含油储层模型裂缝密度反演结果可知,在地震记录SNR=1时,裂缝密度预测结果仍与模型参数符合较好,而只在非裂缝层段裂缝密度反演结果受噪声影响较大,模型试算结果表明本文提出的裂缝密度反演方法具有较强的抗噪性和稳定性。
|
图 6 饱含油裂缝储层模型的不同信噪比正演叠前道集 (a)不含噪声;(b)SNR=5;(c)SNR=2;(d)SNR=1 每4道入射角相同,分别为5°、15°、25°和35°;4道的方位角依次为30°、75°、120°和165°。 |
|
图 7 饱含油模型不同信噪比数据的裂缝对称轴方位角估算结果(红线)与理论值(蓝线)对比 (a)不含噪声;(b)SNR=5;(c)SNR=2;(d)SNR=1 |
|
图 8 饱含油模型不同信噪比数据的裂缝密度反演结果(红线)与理论值(蓝线)对比 (a)不含噪声;(b)SNR=5;(c)SNR=2;(d)SNR=1 |
|
|
表 1 裂缝对称轴方位角估算结果统计 |
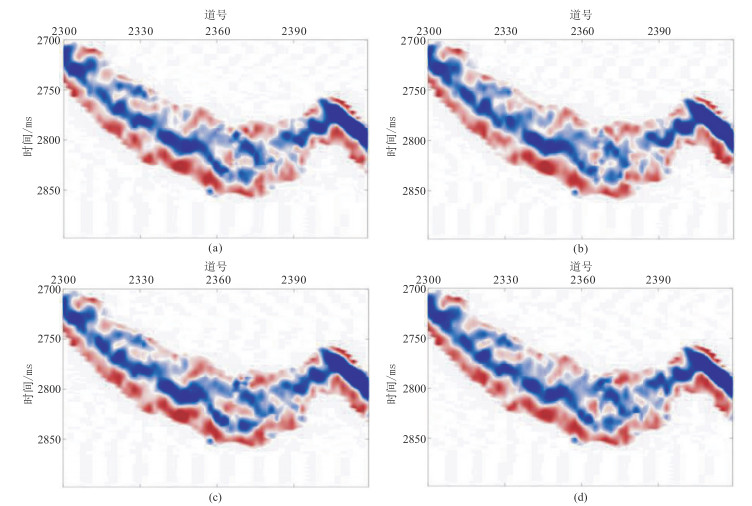
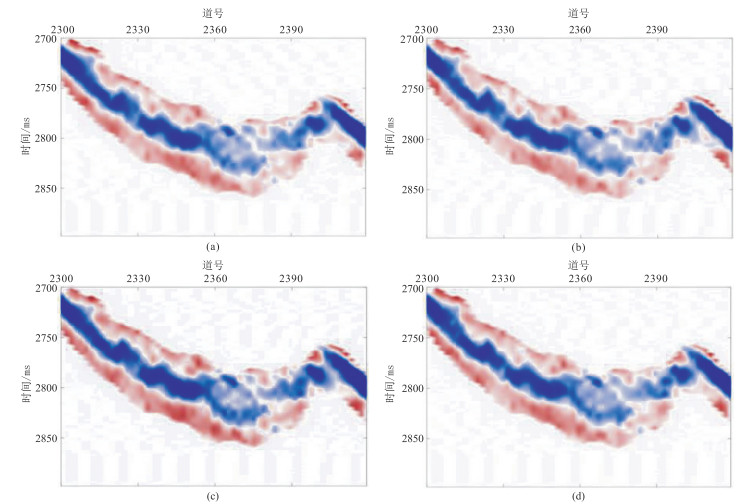
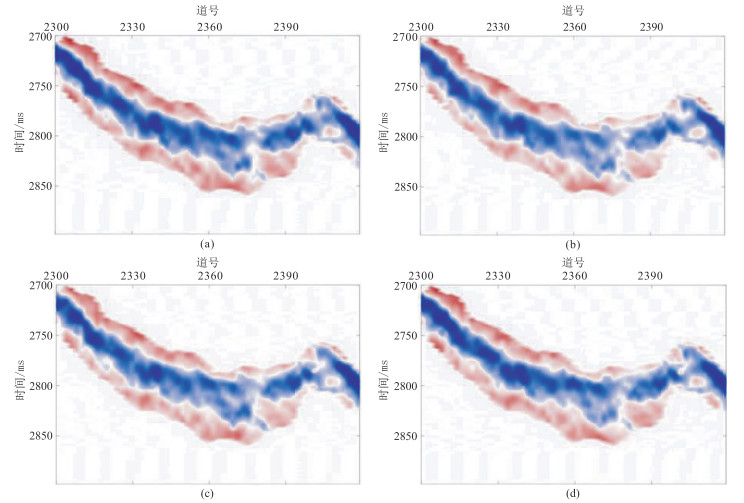
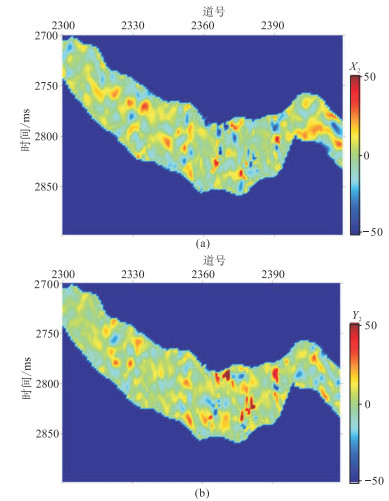
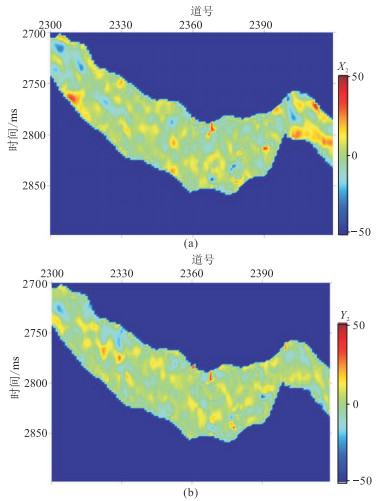
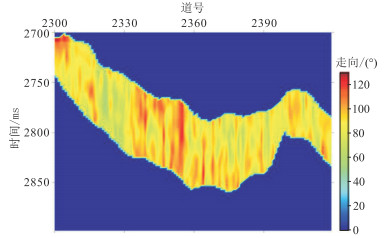
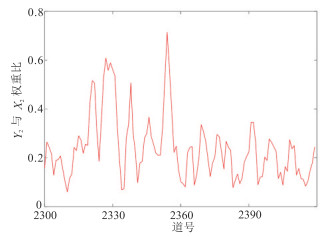
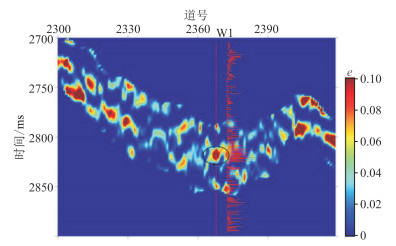
将本文储层裂缝密度反演方法应用于中国C油田致密砂岩工区。实际地震数据为OVT域地震道集,为了提高地震数据信噪比,依据该工区OVT地震道集展布,将地震道按方位角均匀划分为0°~45°,45°~90°,90°~135°和135°~180°,得到方位角分别为22.5°、67.5°、112.5°和157.5°的叠加数据。再抽取入射角为6°~13°、13°~20°、20°~27°地震数据体,进行部分角度叠加后得到入射角分别为10°、17°和24°的分方位、分入射角叠加剖面(图 9 ~图 11)。由图 9~图 11可知,随着入射角增大,目的层段地震记录能量逐渐降低,各向异性信息也相对减弱。首先应用统计方法对实际地震数据提取角度子波,再利用傅里叶级数分析方法计算二阶傅里叶系数(图 12~图 14),随着入射角增大,二阶傅里叶系数能量依次减弱。二阶傅里叶系数的能量大小反映了地震记录各向异性强度,间接指示了地层裂缝发育程度。然后预测目的层段裂缝对称轴方位角,旋转90°后得到裂缝走向,大部分集中在100°附近(图 15),与工区断裂带延展方向一致(由知地质信息可知该工区断裂带主要呈近东西向走向)。图 16为根据裂缝目的层对称轴方位预测均值计算的二阶傅里叶系数正、余弦分量反演权重比曲线。最后应用含气条件下二阶傅里叶系数正、余弦分量加权反演裂缝密度(图 17)。由图 17可知,目的层发育的裂缝呈条带状和块状分布,图中红色曲线为W1井的正交多极子声波阵列各向异性强度测井曲线,在井位处目的层段裂缝密度反演结果与测井信息吻合,验证了本文裂缝密度预测方法的实用性。
|
图 9 入射角为10°的不同方位角叠加剖面 (a)22.5°;(b)67.5°;(c)112.5°;(d)157.5° |
|
图 10 入射角为17°的不同方位角叠加剖面 (a)22.5°;(b)67.5°;(c)112.5°;(d)157.5° |
|
图 11 入射角为24°的不同方位角叠加剖面 (a)22.5°;(b)67.5°;(c)112.5°;(d)157.5° |
|
图 12 入射角为10°的二阶傅里叶系数剖面 (a)余弦分量;(b)正弦分量 |
|
图 13 入射角为17°的二阶傅里叶系数剖面 (a)余弦分量;(b)正弦分量 |
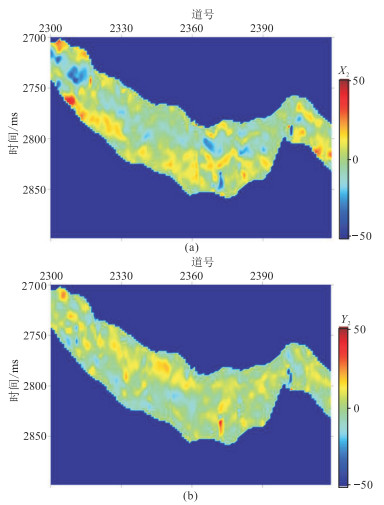
|
图 14 入射角为24°的二阶傅里叶系数剖面 (a)余弦分量;(b)正弦分量 |
|
图 15 过W1井的裂缝走向估算剖面 |
|
图 16 过W1井剖面二阶傅里叶系数正、余弦分量反演权重比 |
|
图 17 过W1井裂缝密度反演剖面 |
本文利用二阶分方位傅里叶系数估计裂缝对称轴方位角,分析了二阶傅里叶系数正、余弦分量信噪比的比值随裂缝对称轴变化规律,提出了利用二阶傅里叶系数正、余弦分量加权并运用非负约束迭代反演裂缝密度方法。建立HTI模型并分别正演了含油和含气条件下的分方位、分入射角地震记录,添加不同噪声后,运用本文方法估计裂缝对称轴方位和反演裂缝密度,结果证明了本文裂缝密度反演方法的准确性和稳定性。实际数据裂缝密度反演结果与测井信息吻合,验证了本文方法的有效性。
| [1] |
HUDSON J A. Overall properties of a cracked solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1980, 88(2): 371-384. DOI:10.1017/S0305004100057674 |
| [2] |
THOMSEN L. Elastic anisotropy due to aligned cracks in porous rock[J]. Geophysical Prospecting, 1995, 43(6): 805-829. DOI:10.1111/j.1365-2478.1995.tb00282.x |
| [3] |
SCHOENBERG M, SAYERS C M. Seismic anisotropy of fractured rock[J]. Geophysics, 1995, 60(1): 204-211. DOI:10.1190/1.1443748 |
| [4] |
BAKULIN A, GRECHKA V, TSVANKIN I. Estimation of fracture parameters from reflection seismic data, part Ⅰ: HTI model due to a single fracture set[J]. Geophysics, 2000, 65(6): 1788-1802. DOI:10.1190/1.1444863 |
| [5] |
BAKULIN A, GRECHKA V, TSVANKIN I. Estimation of fracture parameters from reflection seismic data, part Ⅱ: Fractured models with orthorhombic symmetry[J]. Geophysics, 2000, 65(6): 1803-1817. DOI:10.1190/1.1444864 |
| [6] |
MALLICK S, CRAFT K L, MEISTER L J, et al. Determination of the principal directions of azimuthal anisotropy from P-wave seismic data[J]. Geophysics, 1998, 63(2): 697-706. |
| [7] |
薛姣, 顾汉明, 蔡成国. 准静态孔缝介质广义裂隙弱度研究[J]. 石油地球物理勘探, 2015, 50(6): 1146-1153. XUE Jiao, GU Hanming, CAI Chengguo. General fracture weaknesses for quasi-static porous fractured media[J]. Oil Geophysical Prospecting, 2015, 50(6): 1146-1153. |
| [8] |
SHAW R K, SEN M K. Use of AVOA data to estimate fluid indicator in a vertically fractured medium[J]. Geophysics, 2006, 71(3): C15-C21. DOI:10.1190/1.2194896 |
| [9] |
RUGER A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J]. Geophysics, 1998, 63(3): 935-947. DOI:10.1190/1.1444405 |
| [10] |
刘洋, 董敏煜. 各向异性介质中的方位AVO[J]. 石油地球物理勘探, 1999, 34(3): 260-268. LIU Yang, DONG Minyu. Azimuthal AVO in anisotropic medium[J]. Oil Geophysical Prospecting, 1999, 34(3): 260-268. |
| [11] |
朱培民, 王家映, 於文辉, 等. 用纵波AVO数据反演储层裂隙密度参数[J]. 石油物探, 2001, 40(2): 1-12. ZHU Peimin, WANG Jiaying, YU Wenhui, et al. Inverting reservoir fracture density using P-wave AVO data[J]. Geophysical Prospecting for Petroleum, 2001, 40(2): 1-12. |
| [12] |
张世俊, 杨慧珠, 董渊, 等. 遗传算法反演HTI介质各向异性参数[J]. 石油地球物理勘探, 2002, 37(1): 24-28. ZHANG Shijun, YANG Huizhu, DONG Yuan, et al. Inversion of anisotropic parameters in HTI medium by genetic algorithm[J]. Oil Geophysical Prospecting, 2002, 37(1): 24-28. |
| [13] |
姚姚, 唐文榜. 深层碳酸盐岩岩溶风化壳洞缝型油气藏可检测性的理论研究[J]. 石油地球物理勘探, 2003, 38(6): 623-629. YAO Yao, TANG Wenbang. Theoretical study of detectable cavern-fractured reservoir in weathered Karst of deep carbonatite[J]. Oil Geophysical Prospecting, 2003, 38(6): 623-629. |
| [14] |
朱兆林, 赵爱国. 裂缝介质的纵波方位AVO反演研究[J]. 石油物探, 2005, 44(5): 499-503. ZHU Zhaolin, ZHAO Aiguo. Azimuthal AVO inversion of P-wave in fractured medium[J]. Geophysical Prospecting for Petroleum, 2005, 44(5): 499-503. |
| [15] |
李录明, 罗省贤, 王明春, 等. 各向异性介质三维纵横波联合叠前反演方法及应用[J]. 石油地球物理勘探, 2010, 45(1): 60-65. LI Luming, LUO Shengxian, WANG Mingchun, et al. 3D PP-PS joint inversion method and application in anisotropic medium[J]. Oil Geophysical Prospecting, 2010, 45(1): 60-65. |
| [16] |
张广智, 陈怀震, 王琪, 等. 基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测[J]. 地球物理学报, 2013, 56(5): 1707-1715. ZHANG Guangzhi, CHEN Huaizhen, WANG Qi, et al. Estimation of S-wave velocity and anisotropic parameters using fractured carbonate rock physics model[J]. Chinese Journal of Geophysics, 2013, 56(5): 1707-1715. |
| [17] |
陈怀震, 印兴耀, 高成国, 等. 基于各向异性岩石物理的缝隙流体因子AVAZ反演[J]. 地球物理学报, 2014, 57(3): 968-978. CHEN Huaizhen, YIN Xingyao, GAO Chengguo, et al. AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory[J]. Chinese Journal of Geophysics, 2014, 57(3): 968-978. |
| [18] |
XUE J, GU H M, CAI C G. Model-based amplitude versus offset and azimuth inversion for estimating fracture parameters and fluid content[J]. Geophysics, 2017, 82(2): M1-M17. DOI:10.1190/geo2016-0196.1 |
| [19] |
DOWNTON J E, ROURE B. Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters[J]. Interpretation, 2015, 3(3): T9-T27. |
| [20] |
PAN X P, ZHANG G Z, CHEN H Z, et al. McMC-based AVAZ direct inversion for fracture weaknesses[J]. Journal of Applied Geophysics, 2017, 138(1): 50-61. |
| [21] |
李林, 张广智, 张佳佳, 等. 基于反射振幅傅里叶系数的裂缝弱度反演方法[J]. 中国石油大学学报(自然科学版), 2020, 44(6): 36-45. LI Lin, ZHANG Guangzhi, ZHANG Jiajia, et al. Fracture weakness inversion based on reflection amplitude Fourier coefficient[J]. Journal of China University of Petroleum(Edition of Natural Science), 2020, 44(6): 36-45. |
| [22] |
宋维琪, 徐月森, 张云银, 等. 基于傅里叶级数分析的各向异性参数估计及裂缝预测[J]. 石油物探, 2020, 59(1): 108-113. SONG Weiqi, XU Yuesen, ZHANG Yunyin, et al. Anisotropy parameter estimation and fracture prediction based on Fourier series analysis[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 108-113. |
| [23] |
LI L, ZHANG J J, PAN X P, et al. Azimuthal elastic impedance-based Fourier coefficient variation with angle inversion for fracture weakness[J]. Petroleum Science, 2020, 17(1): 86-104. DOI:10.1007/s12182-019-00405-0 |
| [24] |
魏欣伟, 薛姣, 罗霞. 基于OVT域地震数据的叠前AVOA裂缝密度反演[J]. 石油物探, 2021, 60(5): 816-825. WEI Xinwei, XUE Jiao, LUO Xia. Fracture density estimation using an amplitude-versus-offset-and-azimuth inversion based on prestack seismic data in the offset vector tile domain[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 816-825. |
| [25] |
陈超, 印兴耀, 刘晓晶, 等. 基于方位各向异性的裂缝密度反演方法及应用[J]. 地球物理学报, 2022, 65(1): 371-383. CHEN Chao, YIN Xingyao, LIU Xiaojing, et al. Fracture density inversion based on azimuthal anisotropy and its application[J]. Chinese Journal of Geophysics, 2022, 65(1): 371-383. |
| [26] |
李林, 张广智. 基于扩展方位弹性阻抗的裂缝参数及地应力参数预测方法[J]. 地球物理学报, 2022, 65(8): 3172-3185. LI Lin, ZHANG Guangzhi. Estimation of fracture parameters and in-situ stress parameters based on extended azimuthal elastic impedance[J]. Chinese Journal of Geophysics, 2022, 65(8): 3172-3185. |
| [27] |
汤韦, 李景叶, 王建花, 等. 基于非下采样剪切波变换—参数自适应脉冲耦合神经网络的属性融合裂缝预测方法[J]. 石油地球物理勘探, 2022, 57(1): 52-61. TANG Wei, LI Jingye, WANG Jianhua, et al. Attribute fusion method based on NSST-PAPCNN for fracture prediction.[J]. Oil Geophysical Prospecting, 2022, 57(1): 52-61. |
| [28] |
范廷恩, 杜昕, 马淑芳, 等. 高角度断裂约束的方位傅里叶系数裂缝预测方法及在M气田的应用[J]. 石油地球物理勘探, 2022, 57(6): 1436-1444. FAN Tingen, DU Xin, MA Shufang, et al. Application of high-angle-fault constrained azimuthal Fourier coefficient fracture prediction in M gas field.[J]. Oil Geophysical Prospecting, 2022, 57(6): 1436-1444. |



 薛姣, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院,430070。Email:
薛姣, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院,430070。Email: