0 引言

地震反演是地震勘探中重要的解释方法，它可以利用地震资料解释地下弹性参数，进一步进行储层预测，其中弹性参数包括纵波速度、横波速度和密度等。地震反演可以分为叠后反演和叠前反演，叠后反演具有简便、高效的特点，在储层预测中得到了广泛的应用，但是只能得到少数类型的参数，不能得到反映物理性质和流体特性的参数。与叠后反演相比，叠前地震反演利用地震振幅和炮检距的信息，为研究岩性和储层变化提供了充足有效的数据量^[1-2]，因此叠前地震反演是油气储层定量解释的一种重要手段^[3-5]。

纵横波速度比(v_P/v_S)是表征储层和区分岩性的重要参数。各种实验测量表明，v_P/v_S在岩性识别和异常孔隙压力预测方面具有广泛的应用^[6]。特别是，由于该比值与泊松比直接相关^[7-8]，对流体性质高度敏感^[9-10]，已广泛用为有效油气鉴别器。

鉴于v_P/v_S的重要性，已开发了多种估计方法。较常用的是基于振幅随炮检距的变化(AVO)理论，使用AVO近似式从地震数据中反演纵、横波速度或模量或阻抗，以间接方式计算v_P/v_S^[11]。这种间接的弹性参数转换会引起累积误差。因此，本文在前人研究的基础上提出一种从地震数据中直接获得v_P/v_S的反演方法，避免了间接方法的不稳定性。

Connolly^[12]首次提出了弹性阻抗(EI)的概念。EI是在改进的Zoeppritz方程基础上推导而来，包含了纵波速度、横波速度和密度等信息，较常规波阻抗能反映更多的信息。然而，常规的EI方程存在一个不良特征，数值随入射角有较大尺度的变化。Whitcombe^[13]对EI方程进行了标准化，使EI在一定角度范围内可以直观对比。Whitcombe等^[14]对常规的EI定义进行了扩展，使其能够满足对流体和岩性的预测。为了平衡反演精度和稳定性，EI反演中嵌入的v_P/v_S通常是一个恒定值。马劲风^[15]考虑了v_P/v_S随深度的变化，导出了递推形式的广义弹性阻抗(GEI)表达式。根据马劲风的研究，GEI的精度高于EI，但是GEI表达式较复杂，限制了反演的适用性。本文对GEI方程进行了改进，导出了关于v_P/v_S的反射系数近似方程，将v_P/v_S作为一个模型参数，可直接由叠前地震数据反演。

由于地球物理反演问题的多解性，导致反演结果精度较低。较常用的方法是通过正则化方法对反演问题添加先验信息。印兴耀等^[16]在基于L₁范数约束的基追踪反演算法基础上，加入低频模型约束，对波阻抗进行反演，发现该方法能够消除子波旁瓣对反演结果的影响。刘晓晶等^[17]基于反射系数奇偶分解实现了关于流体因子在深部储层的基追踪EI反演方法。She等^[18]在一阶纵向差分的基础上，提出了基于L₁范数约束的高阶差分叠前地震反演方法，可以有效应对地质结构更复杂的情况。文晓涛等^[19]在L₁范数稀疏约束的基础上，加入低频模型残差约束项，提出一种低频稀疏双约束的波阻抗反演方法，有效提高反演结果的分辨率。虽然L₁范数正则化方法提高了反演的稀疏性，但是对稀疏先验信息挖掘程度不够。Woodworth等^[20]指出L_p拟范数比L₁范数更接近L₀范数。Chen等^[21]基于L_p拟范数的稀疏性约束，提出了一种新的时频分析方法。张雨强等^[22]将L_p拟范数稀疏约束项引入叠后反演，得到了精度更高的反演结果。综合来看，与L₁范数相比，L_p拟范数是一种更为稀疏的L₀范数近似。

基于以上分析，本文提出了一种基于L_p拟范数稀疏约束的叠前v_P/v_S直接反演方法。

1 基本原理 1.1 改进的GEI公式

EI由于含有地震AVO信息，在地震解释和流体识别中得到广泛的应用。但常规弹性阻抗中的v_P/v_S通常设为常数，未考虑到随深度的变化。马劲风^[15]将GEI表示为

$ \mathrm{G}\mathrm{E}{\mathrm{I}}_{i}=\frac{{\rho }_{i}{{v}_{\mathrm{P}}}_{i}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{i}}{\left(1-\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i}}{{r}_{i}^{2}}\right)}^{4} $

(1)

式中：r_i=v_Pi/v_Si，为第i层纵横波速比；ρ为岩石密度；θ为P波入射角。式(1)是关于v_P/v_S、纵波速度和密度的表达式。P波反射系数可以表示为

$ R\left(\theta \right)=\frac{1}{2}\frac{\mathrm{\Delta }\mathrm{G}\mathrm{E}\mathrm{I}}{\mathrm{G}\mathrm{E}\mathrm{I}}\approx \frac{1}{2}\mathrm{l}\mathrm{n}\frac{\mathrm{G}\mathrm{E}{\mathrm{I}}_{i+1}}{\mathrm{G}\mathrm{E}{\mathrm{I}}_{i}} $

(2)

对式(1)进行对数运算，简化为

$ \mathrm{l}\mathrm{n}\left(\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{i}\mathrm{G}\mathrm{E}{\mathrm{I}}_{i}\right)=\mathrm{l}\mathrm{n}{\rho }_{i}+\mathrm{l}\mathrm{n}{{v}_{\mathrm{P}}}_{i}+4\mathrm{l}\mathrm{n}\left(1-\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i}}{{r}_{i}^{2}}\right) $

(3)

当$ \theta $小于30°时，$ 1/{r}_{i}^{2} $最大值为0.5，$ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i} $最大值为0.25，所以$ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i}/{r}_{i}^{2} $的最大值为0.125，是一个较小的值，将$ \mathrm{l}\mathrm{n}(1-\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i}/{r}_{i}^{2}) $用泰勒公式展开，有

$ \mathrm{l}\mathrm{n}\left(1-\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i}}{{r}_{i}^{2}}\right)\approx -\frac{\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i}}{{r}_{i}^{2}} $

(4)

将式(4)代入式(3)，可得到新的GEI表达式

$ \mathrm{G}\mathrm{E}{\mathrm{I}}_{i}=\frac{{\rho }_{i}{{v}_{\mathrm{P}}}_{i}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{i}}{\mathrm{e}}^{\left(-\frac{4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{i}}{{r}_{i}^{2}}\right)} $

(5)

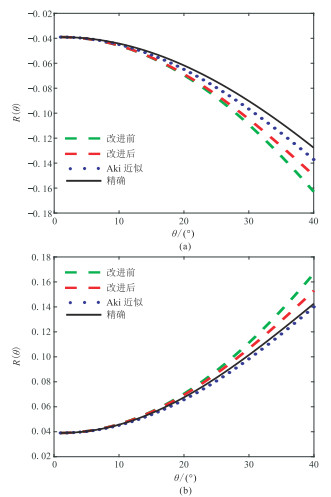
应用Goodway等^[23]根据实际资料给出的含气砂岩模型(表 1)进一步说明改进的GEI公式准确性。改进前、后计算的反射系数与精确Zoeppritz方程及Aki-Richards近似方程^[24]计算的反射系数对比如图 1所示。该模型包含两个反射系数：上两层之间的负反射系数和下两层之间的正反射系数。由图 1可以看出，改进后计算的反射系数比改进前更接近Zoeppritz方程，因为改进前忽略密度反射率而产生了较大的误差；在入射角小于25°时，改进后的反射系数计算结果与Zoeppritz方程及Aki-Richards方程基本一致。

1.2 反射系数公式

在上、下介质弹性参数差异小的情况下，使用改进的GEI建立线性化的纵波反射系数方程。对式(5)进行微分，可得

$ \begin{array}{l}\mathrm{\Delta }\mathrm{G}\mathrm{E}\mathrm{I}=\left[\frac{{v}_{\mathrm{P}}\mathrm{\Delta }\rho +\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \rho \mathrm{\Delta }{v}_{\mathrm{P}}}{\mathrm{c}\mathrm{o}\mathrm{s}\theta }-8\mathrm{s}\mathrm{i}\mathrm{n}\theta \times \right.\\ \begin{array}{cc}& \left.\mathrm{t}\mathrm{a}\mathrm{n}\theta {\left(\frac{1}{r}\right)}^{2}\rho \mathrm{\Delta }{v}_{\mathrm{P}}-\frac{8\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\mathrm{c}\mathrm{o}\mathrm{s}\theta }\rho {v}_{\mathrm{S}}\mathrm{\Delta }\left(\frac{1}{r}\right)\right]{\mathrm{e}}^{\left(\frac{-4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{{r}^{2}}\right)}\end{array}\end{array} $

(6)

式中$ \mathrm{\Delta }\left(1/r\right)=-\mathrm{\Delta }r/{r}^{2} $。结合式(2)、式(6)可得纵波反射系数的线性公式

$ \begin{array}{l}R\left(\theta \right)=4{\left(\frac{{v}_{\mathrm{S}}}{{v}_{\mathrm{P}}}\right)}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }r}{r}+\\ \begin{array}{cc}& \left[\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -4{\left(\frac{{v}_{\mathrm{S}}}{{v}_{\mathrm{P}}}\right)}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right]\frac{\mathrm{\Delta }{v}_{\mathrm{P}}}{{v}_{\mathrm{P}}}+\frac{1}{2}\frac{\mathrm{\Delta }\rho }{\rho }\end{array}\end{array} $

(7)

式中$ \mathrm{\Delta }r/r $、$ \mathrm{\Delta }{v}_{\mathrm{P}}/{v}_{\mathrm{P}} $、$ \mathrm{\Delta }\rho /\rho $分别为纵横波速比、纵波速度和密度的反射系数，具体分别为

$ \frac{\mathrm{\Delta }r}{r}=\frac{2\left({r}_{i+1}-{r}_{i}\right)}{{r}_{i+1}+{r}_{i}} $

(8)

$ \frac{\mathrm{\Delta }{v}_{\mathrm{P}}}{{v}_{\mathrm{P}}}=\frac{2\left({{v}_{\mathrm{P}}}_{i+1}-{{v}_{\mathrm{P}}}_{i}\right)}{{{v}_{\mathrm{P}}}_{i+1}+{{v}_{\mathrm{P}}}_{i}} $

(9)

$ \frac{\mathrm{\Delta }\rho }{\rho }=\frac{2\left({\rho }_{i+1}-{\rho }_{i}\right)}{{\rho }_{i+1}+{\rho }_{i}} $

(10)

1.3 反演算法

式(7)可以写为矩阵形式

$ \boldsymbol{R}\left(\theta \right)=a\left(\theta \right)\frac{\mathrm{\Delta }\boldsymbol{r}}{\boldsymbol{r}}+b\left(\theta \right)\frac{\mathrm{\Delta }{\boldsymbol{v}}_{\mathrm{P}}}{{\boldsymbol{v}}_{\mathrm{P}}}+c\left(\theta \right)\frac{\mathrm{\Delta }\boldsymbol{\rho }}{\boldsymbol{\rho }} $

(11)

式中$ a\left(\theta \right) $、$ b\left(\theta \right) $、$ c\left(\theta \right) $为纵横波速比、纵波速度和密度反射系数的参数项，表示为

$ \left\{\begin{array}{l}a\left(\theta \right)=4{\left(\frac{{v}_{\mathrm{S}}}{{v}_{\mathrm{P}}}\right)}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \\ b\left(\theta \right)=\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -4{\left(\frac{{v}_{\mathrm{S}}}{{v}_{\mathrm{P}}}\right)}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \\ c\left(\theta \right)=\frac{1}{2}\end{array}\right. $

(12)

$ \mathrm{\Delta }\boldsymbol{r}/\boldsymbol{r} $的元素$ \mathrm{\Delta }{r}_{i, j}/{r}_{i, j} $表示为

$ \frac{\mathrm{\Delta }{r}_{i, j}}{{r}_{i, j}}=\mathrm{\Delta }\mathrm{l}\mathrm{n}{r}_{i, j}=\mathrm{l}\mathrm{n}{r}_{i+1, j}-\mathrm{l}\mathrm{n}{r}_{i, j} $

(13)

式中j为道号。于是

$ \frac{\mathrm{\Delta }\boldsymbol{r}}{\boldsymbol{r}}=\boldsymbol{D}{\boldsymbol{L}}_{r} $

(14)

式中：$ {\boldsymbol{L}}_{r}=\mathrm{l}\mathrm{n}\boldsymbol{r} $，表示对矩阵r中每一个元素都取对数；D为差分矩阵，即

$ \boldsymbol{D}=\left(\begin{array}{ccccc}-1& 1& & & \\ & -1& 1& & \\ & & \ddots & \ddots & \\ & & & -1& 1\end{array}\right) $

(15)

类似地，有

$ \frac{\mathrm{\Delta }{\boldsymbol{v}}_{\mathrm{P}}}{{\boldsymbol{v}}_{\mathrm{P}}}=\boldsymbol{D}{\boldsymbol{L}}_{{v}_{\mathrm{P}}} $

(16)

$ \frac{\mathrm{\Delta }\boldsymbol{\rho }}{\boldsymbol{\rho }}=\boldsymbol{D}{\boldsymbol{L}}_{\rho } $

(17)

则式(11)可以表示为

$ \boldsymbol{R}\left(\theta \right)=a\left(\theta \right)\boldsymbol{D}{\boldsymbol{L}}_{r}+b\left(\theta \right)\boldsymbol{D}{\boldsymbol{L}}_{{v}_{\mathrm{P}}}+c\left(\theta \right)\boldsymbol{D}{\boldsymbol{L}}_{\rho } $

(18)

式中：$ {\boldsymbol{L}}_{{v}_{\mathrm{P}}}=\mathrm{l}\mathrm{n}{\boldsymbol{v}}_{\mathrm{P}} $；$ {\boldsymbol{L}}_{\rho }=\mathrm{l}\mathrm{n}\boldsymbol{\rho } $。根据褶积模型可以得到地震记录和反射系数的关系表达式

$ \boldsymbol{S}\left(\theta \right)=\boldsymbol{W}\boldsymbol{R}\left(\theta \right) $

(19)

式中$ \boldsymbol{W} $表示子波矩阵。如果有N个入射角，S可写为

$ \boldsymbol{S}={\left[\begin{array}{cccc}\boldsymbol{S}\left({\theta }_{1}\right)& \boldsymbol{S}\left({\theta }_{2}\right)& \cdots & \boldsymbol{S}\left({\theta }_{N}\right)\end{array}\right]}^{\mathrm{T}} $

(20)

式(19)可进一步表示为

$ \boldsymbol{S}=\boldsymbol{A}\boldsymbol{L} $

(21)

式中：$ \boldsymbol{L}={\left[\begin{array}{ccc}{{\boldsymbol{L}}_{r}}^{\mathrm{T}}& {{\boldsymbol{L}}_{{v}_{\mathrm{P}}}}^{\mathrm{T}}& {{\boldsymbol{L}}_{\rho }}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}} $；$ \boldsymbol{A} $可以表示为

$ \boldsymbol{A}=\left[\begin{array}{ccc}a\left({\theta }_{1}\right)\boldsymbol{W}\boldsymbol{D}& b\left({\theta }_{1}\right)\boldsymbol{W}\boldsymbol{D}& c\left({\theta }_{1}\right)\boldsymbol{W}\boldsymbol{D}\\ a\left({\theta }_{2}\right)\boldsymbol{W}\boldsymbol{D}& b\left({\theta }_{2}\right)\boldsymbol{W}\boldsymbol{D}& c\left({\theta }_{2}\right)\boldsymbol{W}\boldsymbol{D}\\ & ⋮& \\ a\left({\theta }_{N}\right)\boldsymbol{W}\boldsymbol{D}& b\left({\theta }_{N}\right)\boldsymbol{W}\boldsymbol{D}& c\left({\theta }_{N}\right)\boldsymbol{W}\boldsymbol{D}\end{array}\right] $

(22)

反演的目标函数可表示为

$ J\left(\boldsymbol{L}\right)=\underset{\boldsymbol{L}}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖\boldsymbol{S}-\boldsymbol{A}\boldsymbol{L}‖}_{2}^{2} $

(23)

为了提高反演的稳定性，加入了纵横波速比、纵波速度、密度的初始模型约束项，同时采用L_p拟范数构造反射稀疏约束项

$ \begin{array}{l}J\left(\boldsymbol{L}\right)\mathrm{ }=\underset{\boldsymbol{L}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left({‖\boldsymbol{S}-\boldsymbol{A}\boldsymbol{L}‖}_{2}^{2}+\alpha {‖{\boldsymbol{L}}_{r}-\mathrm{l}\mathrm{n}{\boldsymbol{r}}_{0}‖}_{2}^{2}+\right.\\ \left.\mu {‖{\boldsymbol{A}}_{1}\boldsymbol{L}‖}_{p}^{p}+\beta {‖{\boldsymbol{L}}_{{v}_{\mathrm{P}}}-\mathrm{l}\mathrm{n}{\boldsymbol{v}}_{\mathrm{P}0}‖}_{2}^{2}+\gamma {‖{\boldsymbol{L}}_{\rho }-\mathrm{l}\mathrm{n}{\boldsymbol{\rho }}_{0}‖}_{2}^{2}\right)\end{array} $

(24)

式中：α、β、γ分别为纵横波速比、纵波速度和密度的初始模型约束项参数；μ为稀疏约束项参数；r₀、v_P0、ρ₀分别为纵横波速比、纵波速度和密度的初始模型；$ {‖·‖}_{p}^{p} $表示L_p拟范数，其中p的取值范围为0~1，p值越小，反演结果会越稀疏，可根据实际情况取最优值；矩阵$ {\boldsymbol{A}}_{1} $满足反射系数$ \boldsymbol{R}={\boldsymbol{A}}_{1}\boldsymbol{L} $，可表示为

$ {\boldsymbol{A}}_{1}=\left[\begin{array}{ccc}a\left({\theta }_{1}\right)\boldsymbol{D}& b\left({\theta }_{1}\right)\boldsymbol{D}& c\left({\theta }_{1}\right)\boldsymbol{D}\\ a\left({\theta }_{2}\right)\boldsymbol{D}& b\left({\theta }_{2}\right)\boldsymbol{D}& c\left({\theta }_{2}\right)\boldsymbol{D}\\ & ⋮& \\ a\left({\theta }_{N}\right)\boldsymbol{D}& b\left({\theta }_{N}\right)\mathbf{W}\mathbf{D}& c\left({\theta }_{N}\right)\boldsymbol{D}\end{array}\right] $

(25)

因为目标函数包括了L_p和$ {\mathrm{L}}_{2} $范数，因此采用交替方向乘子法求解^[25]。引入拉格朗日项$ {\boldsymbol{L}}_{\mathrm{y}} $代替L_p拟范数的运算，将式(24)转换为可以直接求解的优化问题

$ \begin{array}{l}J\left(\boldsymbol{L}\right)=\underset{\boldsymbol{L}, {\boldsymbol{L}}_{y}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left({‖\boldsymbol{S}-\boldsymbol{A}\boldsymbol{L}‖}_{2}^{2}+\alpha {‖{\boldsymbol{L}}_{r}-\mathrm{l}\mathrm{n}{\boldsymbol{r}}_{0}‖}_{2}^{2}+\right.\\ \mu {‖{\boldsymbol{L}}_{\mathrm{y}}‖}_{p}^{p}+\left.\beta {‖{\boldsymbol{L}}_{{v}_{\mathrm{P}}}-\mathrm{l}\mathrm{n}{\boldsymbol{v}}_{\mathrm{P}0}‖}_{2}^{2}+\gamma {‖{\boldsymbol{L}}_{\rho }-\mathrm{l}\mathrm{n}{\boldsymbol{\rho }}_{0}‖}_{2}^{2}\right)\\ \mathrm{s}\mathrm{t}{\boldsymbol{L}}_{\mathrm{y}}={\boldsymbol{A}}_{1}\boldsymbol{L}\end{array} $

(26)

再引入对偶项$ \boldsymbol{C} $，将式(26)转换成无约束的最优化问题

$ \begin{array}{l}J\left(\boldsymbol{L}\right)=\underset{\boldsymbol{L}, {\boldsymbol{L}}_{y}, \boldsymbol{C}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left({‖\boldsymbol{S}-\boldsymbol{A}\boldsymbol{L}‖}_{2}^{2}+\mu {‖{\boldsymbol{L}}_{\mathrm{y}}‖}_{p}^{p}+\right.\\ \alpha {‖{\boldsymbol{L}}_{r}-\mathrm{l}\mathrm{n}{\boldsymbol{r}}_{0}‖}_{2}^{2}+\beta {‖{\boldsymbol{L}}_{{v}_{\mathrm{P}}}-\mathrm{l}\mathrm{n}{\boldsymbol{v}}_{\mathrm{P}0}‖}_{2}^{2}+\\ \left.\gamma {‖{\boldsymbol{L}}_{\rho }-\mathrm{l}\mathrm{n}{\boldsymbol{\rho }}_{0}‖}_{2}^{2}+\lambda {‖{\boldsymbol{L}}_{\mathrm{y}}-{\boldsymbol{A}}_{1}\boldsymbol{L}-\boldsymbol{C}‖}_{2}^{2}\right)\end{array} $

(27)

式中λ为对偶项的约束参数。将含有多参数的目标函数分解为多个单参数问题，其中关于$ \boldsymbol{L} $的子目标函数为

$ \begin{array}{l}{J}_{1}\left(\boldsymbol{L}\right)=\underset{\boldsymbol{L}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left({‖\boldsymbol{S}-\boldsymbol{A}\boldsymbol{L}‖}_{2}^{2}+\alpha {‖{\boldsymbol{L}}_{r}-\mathrm{l}\mathrm{n}{\boldsymbol{r}}_{0}‖}_{2}^{2}+\right.\\ \beta {‖{\boldsymbol{L}}_{{v}_{\mathrm{P}}}-\mathrm{l}\mathrm{n}{\boldsymbol{v}}_{\mathrm{P}0}‖}_{2}^{2}+\gamma {‖{\boldsymbol{L}}_{\rho }-\mathrm{l}\mathrm{n}{\boldsymbol{\rho }}_{0}‖}_{2}^{2}+\\ \left.\lambda {‖{\boldsymbol{L}}_{\mathrm{y}}-{\boldsymbol{A}}_{1}\boldsymbol{L}-\boldsymbol{C}‖}_{2}^{2}\right)\end{array} $

(28)

拉格朗日项$ {\boldsymbol{L}}_{\mathrm{y}} $的子目标函数为

$ {J}_{2}\left({\boldsymbol{L}}_{\mathrm{y}}\right)=\underset{{\boldsymbol{L}}_{\mathrm{y}}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\mu {‖{\boldsymbol{L}}_{\mathrm{y}}‖}_{p}^{p}+\lambda {‖{\boldsymbol{L}}_{\mathrm{y}}-{\boldsymbol{A}}_{1}\boldsymbol{L}-\boldsymbol{C}‖}_{2}^{2}\right) $

(29)

关于对偶项$ \boldsymbol{C} $的子目标函数为

$ {J}_{3}\left(\boldsymbol{C}\right)=\underset{\boldsymbol{C}}{\mathrm{m}\mathrm{i}\mathrm{n}}\lambda {‖{\boldsymbol{L}}_{\mathrm{y}}-{\boldsymbol{A}}_{1}\boldsymbol{L}-\boldsymbol{C}‖}_{2}^{2} $

(30)

引入交替方向乘子算法及软阈值收缩算法对上述不同目标函数交替求解

$ \begin{array}{l}{\boldsymbol{L}}^{(k+1)}={\left({\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{A}+\boldsymbol{\eta }\boldsymbol{E}+\lambda {\boldsymbol{A}}_{1}^{\mathbf{T}}{\boldsymbol{A}}_{1}\right)}^{-1}\left[{\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{S}+\right.\\ \begin{array}{cc}& \left.\boldsymbol{\eta }{\boldsymbol{L}}_{0}+\lambda {\boldsymbol{A}}_{1}^{\mathbf{T}}{\boldsymbol{L}}_{\mathrm{y}}^{\left(k\right)}-\lambda {\boldsymbol{A}}_{1}^{\mathbf{T}}{\boldsymbol{C}}^{\left(k\right)}\right]\end{array}\end{array} $

(31)

$ \begin{array}{l}{{\boldsymbol{L}}_{\mathrm{y}}}^{(k+1)}=\mathrm{m}\mathrm{a}\mathrm{x}\left[\left|{\boldsymbol{A}}_{1}{\boldsymbol{L}}^{(k+1)}+{\boldsymbol{C}}^{\left(k\right)}\right|-{(\lambda /\mu )}^{p-2}\times \right.\\ \left.{\left|{\boldsymbol{A}}_{1}{\boldsymbol{L}}^{(k+1)}+{\boldsymbol{C}}^{\left(k\right)}\right|}^{p-1}, 0\right]\times \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left[{\boldsymbol{A}}_{1}{\boldsymbol{L}}^{(k+1)}+{\boldsymbol{C}}^{\left(k\right)}\right]\end{array} $

(32)

$ {\boldsymbol{C}}^{(k+1)}={\boldsymbol{C}}^{\left(k\right)}+{\boldsymbol{A}}_{1}{\boldsymbol{L}}^{(k+1)}-{{\boldsymbol{L}}_{\mathrm{y}}}^{(k+1)} $

(33)

式中：$ {\boldsymbol{L}}_{0}={\left[\begin{array}{ccc}\mathrm{l}\mathrm{n}{\boldsymbol{r}}_{0}^{\mathrm{T}}& \mathrm{l}\mathrm{n}{\boldsymbol{v}}_{\mathrm{P}0}^{\mathrm{T}}& \mathrm{l}\mathrm{n}{\boldsymbol{\rho }}_{0}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}} $；k为迭代次数；E为单位矩阵；$ \left|•\right| $表示对矩阵每个元素取绝对值；max(·，0)表示比较矩阵各个元素与0，取最大值，即对矩阵中值为负的元素置零；$ {\left|•\right|}^{p-1} $表示对矩阵每个元素取绝对值后计算p$ - $1次方；sign(·)表示对矩阵每个元素取正、负号；而

$ \boldsymbol{\eta }=\left(\begin{array}{ccc}\alpha & 0& 0\\ 0& \beta & 0\\ 0& 0& \gamma \end{array}\right) $

(34)

2 模型测试与实际应用 2.1 模型测试

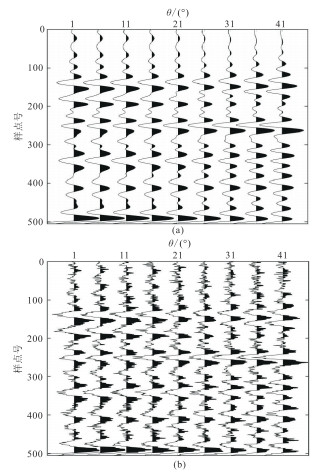
为验证本文提出反演方法的效果，根据A井测井数据设计了一维地震模型。该模型是利用A井纵波速度、横波速度和密度测井数据通过Zoeppritz方程计算得到纵波反射系数，并与主频为30 Hz的Ricker子波褶积得到不同角度的合成地震道集(图 2a)。为了验证本文方法的抗噪性，对合成地震数据加上其最大振幅30%的高斯噪声(图 2b)。

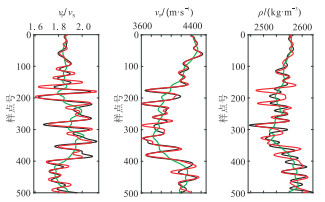
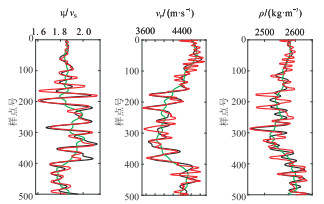
将L_p拟范数稀疏约束的纵横波速比直接反演方法应用于该模型。图 3为无噪条件下的反演结果，与理论模型很接近，验证了本文方法的可行性。图 4为含噪条件下的反演结果，可以发现：纵波速度和密度由于噪声的影响，反演精度降低，但仍能反映基本趋势；纵横波速比反演结果受噪声干扰较小，仍具有较高的精度，说明本文方法具有较强的抗噪性。

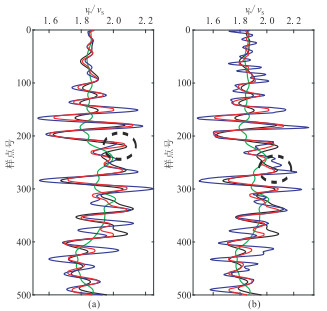
为了进一步验证直接反演方法的优势，将利用Aki-Richards近似方程间接得到的纵横波速比与直接得到的反演结果进行对比(图 5)。由图 5可见，无论是无噪条件下还是含噪条件下，直接反演结果均更接近理论模型，尤其是黑色虚线圈处更加明显。

为了定量分析提出方法与间接反演方法的反演效果，使用信噪比(Signal-to-noise Ratio，SNR)定量评估不同反演方法的反演效果。具体定义为

$ \mathrm{S}\mathrm{N}\mathrm{R}=10\times \mathrm{l}\mathrm{g}\frac{{‖\boldsymbol{r}-\stackrel{-}{\boldsymbol{r}}‖}_{2}^{2}}{{‖{\boldsymbol{r}}^{\mathrm{i}\mathrm{n}\mathrm{v}}-\stackrel{-}{\boldsymbol{r}}‖}_{2}^{2}} $

(35)

式中：r为理论纵横波速度比模型；$ \stackrel{-}{\boldsymbol{r}} $表示理论模型的平均值；$ {\boldsymbol{r}}^{\mathrm{i}\mathrm{n}\mathrm{v}} $表示反演结果。

表 2为两种方法反演结果的SNR，可见，无论在无噪或含噪的条件下，本文方法都具有更高的信噪比，从而验证了方法的有效性。

2.2 实际数据应用

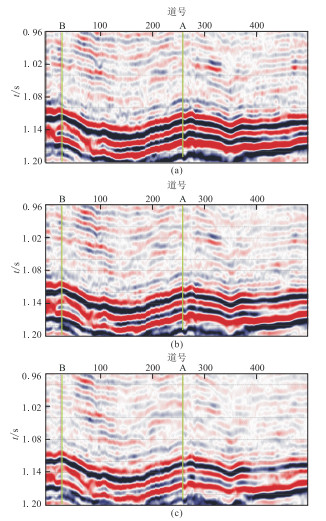
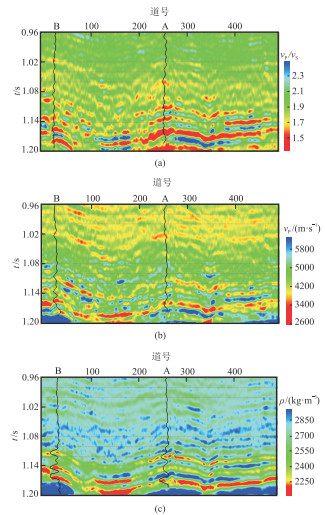
将本文的直接反演方法应用于M工区实际地震数据。该区目的层主要为砂岩含气储层。图 6是入射角为10°、17°和24°的部分角度叠加剖面，共500道，每道含有241个采样点，采样间隔为1 ms。该地震剖面过A、B两口井，均钻遇含气储层，因此具有较高的研究价值。图 7为本文方法反演的纵横波速比、纵波速度和密度剖面，从图中可以看出，反演剖面与A、B两井测井曲线趋势吻合较好，验证了本文方法实用性。

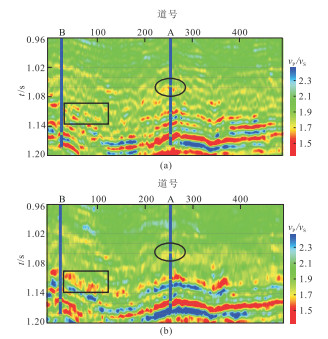
对比本文方法得到的v_P/v_S反演结果与基于Aki-Richards近似方程得到的间接反演结果(图 8)可进一步说明本文方法的优越性。气层的纵横波速比反映为异常低值，与测井解释结论对比可知，两种方法得到的反演剖面与测井解释结论基本吻合，但是由于间接反演方法存在累积误差，对部分含气储层不能有效识别(黑色椭圆处)。并且由于直接反演方法得到的反演结果不存在累积误差，其对储层边界刻画更为清晰(黑色矩形框处)。

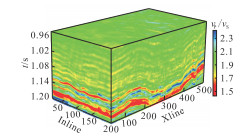
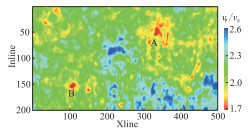
为了进一步验证本文方法应用于实际数据的可行性，对该工区进行三维反演。数据由500条Xline和200条Inline组成。图 9为本文方法的三维直接反演结果，可见，横向连续性较高、气藏分布较清晰。图 10是提取三维反演结果的沿层切片，可以看出，低值区(红色)显示为气藏异常，与A井和B井吻合较好，验证了本文方法的有效性。

3 结论

(1) 本文在广义弹性阻抗基础上提出了新的广义弹性阻抗方程，该方程与纵横波速比、纵波速度和密度有关，计算的纵波反射系数更接近Zoeppritz方程。为了直接反演纵横波速比，由新的广义弹性阻抗方程导出了一个与纵横波速比、纵波速度、密度相关的纵波反射系数近似方程。

(2) 为了提高反演精度，在稀疏反演理论的基础上引入L_p拟范数对反演参数进行稀疏约束，应用交替方向乘子算法求解。模型数据测试及实际数据应用结果表明本文方法反演精度较高。

(3) 本文的直接反演方法避免了间接反演方法产生的累积误差，具有一定的抗噪能力，提高了反演的稳定性，同时提高了对含气储层的识别能力。